Výpis souhrnů
Geometrie
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
- Geometrie
- Prostorová představivost
- Prostorová představivost v rovině
- Prostorová představivost: 3D objekty
- Nárys, půdorys, bokorys
- Počty vrcholů, stěn, hran
- Síť krychle
- Sítě těles
- Řezy krychle
- Řezy těles
- Geometrické pojmy
- Názvy geometrických útvarů a těles
- Pojmy související s úhly
- Pojmy související s trojúhelníkem
- Pojmy související s kružnicí
- Rovinné útvary
- Trojúhelník
- Obsah trojúhelníku
- Obvod trojúhelníku
- Pythagorova věta
- Pythagorova věta: základní použití
- Pythagorova věta: aplikace
- Euklidovy věty
- Úhly v trojúhelníku
- Konstrukční úlohy: trojúhelníky
- Konstrukce trojúhelníků: známé délky stran
- Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
- Konstrukce trojúhelníků: věty sss, sus, usu, Ssu
- Konstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
- Čtverec a obdélník
- Obvod čtverce a obdélníku
- Obsah čtverce a obdélníku
- Rovnoběžník
- Obvod rovnoběžníku
- Obsah rovnoběžníku
- Lichoběžník
- Obvod lichoběžníku
- Obsah lichoběžníku
- Kruh a kružnice
- Obvod kruhu, délka kružnice
- Obsah kruhu
- Úhly a kružnice
- Obsah kruhové výseče
- Délka oblouku
- Prostorové útvary
- Krychle a kvádr
- Objem krychle a kvádru
- Povrch krychle a kvádru
- Hranol
- Objem hranolu
- Povrch hranolu
- Jehlan
- Objem jehlanu
- Povrch jehlanu
- Válec
- Objem válce
- Povrch válce
- Koule
- Objem koule
- Povrch koule
- Kužel
- Objem kužele
- Povrch kužele
- Obsah a obvod
- Obvod: mix
- Obsah: mix
- Objem a povrch
- Objem hranatých těles
- Objem kulatých těles
- Povrch hranatých těles
- Povrch kulatých těles
- Úhly
- Poznávání úhlů
- Úhly ve čtyřúhelníku
- Úhly a mnohoúhelníky
- Geometrické konstrukce
- Geometrické konstrukce: značení
- Polopřímky a poloroviny
- Rovnoběžky a kolmice
- Konstrukční úlohy: čtyřúhelníky
- Konstrukční úlohy průřezově
- Operace a vlastnosti v rovině
- Osová souměrnost
- Středová souměrnost
- Shodnost
- Podobnost
- Posunutí
- Otočení
- Stejnolehlost
- Analytická geometrie
- Body
- Souřadnice bodů v rovině
- Souřadnice bodů v prostoru
- Vzdálenost bodů v rovině
- Vzdálenost bodů v prostoru
- Úsečky
- Délka úsečky v rovině
- Střed úsečky v rovině
- Vzájemná poloha úseček v rovině
- Délka úsečky v prostoru
- Střed úsečky v prostoru
- Vzájemná poloha úseček v prostoru
- Vektory
- Vektory: pojmy
- Souřadnice vektoru
- Velikost vektoru
- Vzájemná poloha vektorů
- Operace s vektory
- Vektory: násobení konstantou, součet, rozdíl
- Vektory: skalární součin
- Přímky
- Přímky: pojmy
- Určení přímky
- Parametrické rovnice přímky v rovině
- Obecná rovnice přímky v rovině
- Směrnicový tvar rovnice přímky
- Vzájemná poloha přímek v rovině
- Vzájemná poloha přímky a bodu v rovině
- Polohové úlohy
- Metrické úlohy
- Vzdálenost bodu od přímky
- Odchylka dvou přímek
- Roviny
- Roviny: pojmy
- Parametrické rovnice roviny
- Obecná rovnice roviny
- Vzájemná poloha bodu a roviny
- Kuželosečky
- Kružnice (kuželosečka)
- Elipsa
- Parabola
- Hyperbola
Geometrie
Geometrie je oblast matematiky, která se zabývá studiem tvarů, velikostí a prostorových vztahů mezi objekty. Geometrie rozvíjí naši prostorovou představivost a hraje důležitou roli v každodenním životě – pomáhá nám chápat a popisovat svět kolem nás, od měření vzdáleností až po architektonické návrhy budov. Na její bohaté využití narazí nejen inženýři a architekti, ale třeba i grafičtí návrháři při tvorbě plakátu či vývojáři počítačových her při vykreslování pohybu postavičky.
Geometrie je široké téma, které má řadu podtémat:
- Prostorová představivost – rozvíjení schopnosti vnímat a představit si tvary v rovině i v prostoru
- Geometrické pojmy – základní pojmy jako jsou body, přímky, roviny, úhly
- Rovinné útvary – seznámení s různými tvary v rovině, například s trojúhelníky, čtverci a kruhy
- Prostorové útvary – studium trojrozměrných objektů jako jsou krychle, koule nebo válce
- Obsah a obvod – výpočet obsahu a obvodu různých rovinných útvarů
- Objem a povrch – výpočet objemu a povrchu prostorových útvarů
- Úhly – práce s úhly, jejich měření a vztahy mezi nimi
- Geometrické konstrukce – postupy a nástroje potřebné pro konstrukci geometrických objektů
- Operace a vlastnosti v rovině – souměrnosti, posunutí, otáčení a další operace s rovinnými tvary
- Analytická geometrie – využití souřadnicového systému k popisu geometrických útvarů a jejich vlastností
Prostorová představivost
Prostorová představivost nám pomáhá vnímat a rozumět tvarům kolem nás, ať už na papíře nebo ve skutečném světě. Procvičování je děleno do více podtémat rozličné obtížnosti:
- Prostorová představivost v rovině – práce s tvary na ploché rovině
- Prostorová představivost: 3D objekty – schopnost představit si, jak vypadá trojrozměrné těleso z jiného úhlu pohledu
- Nárys, půdorys, bokorys – různé způsoby zobrazení objektů
- Počty vrcholů, stěn, hran – počítání základních prvků prostorových těles
- Síť krychle – skládání krychle z plochých částí
- Sítě těles – navazuje na předchozí téma a zabývá se i složitějšími 3D tělesy
- Řezy krychle – řezání krychle rovinou
- Řezy těles – řezání dalších prostorových těles
Prostorová představivost v rovině
Představivost v rovině využíváme, aniž bychom si to uvědomili, v každodenním životě - při orientaci ve městě, v přírodě, při práci s mapu i při pohledu do zrcadla. Měli bychom být schopni rozeznat vzájemnou polohu dvou objektů, určit jejich sjednocení, průnik nebo změnu polohy.
Doplňování v rovině
Při doplňování v rovině budeme pracovat nejen se základními rovinnými útvary, ale i s jejich kombinacemi - hvězdy, domečky, sítě. Při řešení úloh je vhodné si, v duchu či na papíře, představit, jak má výsledný tvar vypadat. Pozor, chybějící dílek může být otočený či překlopený.
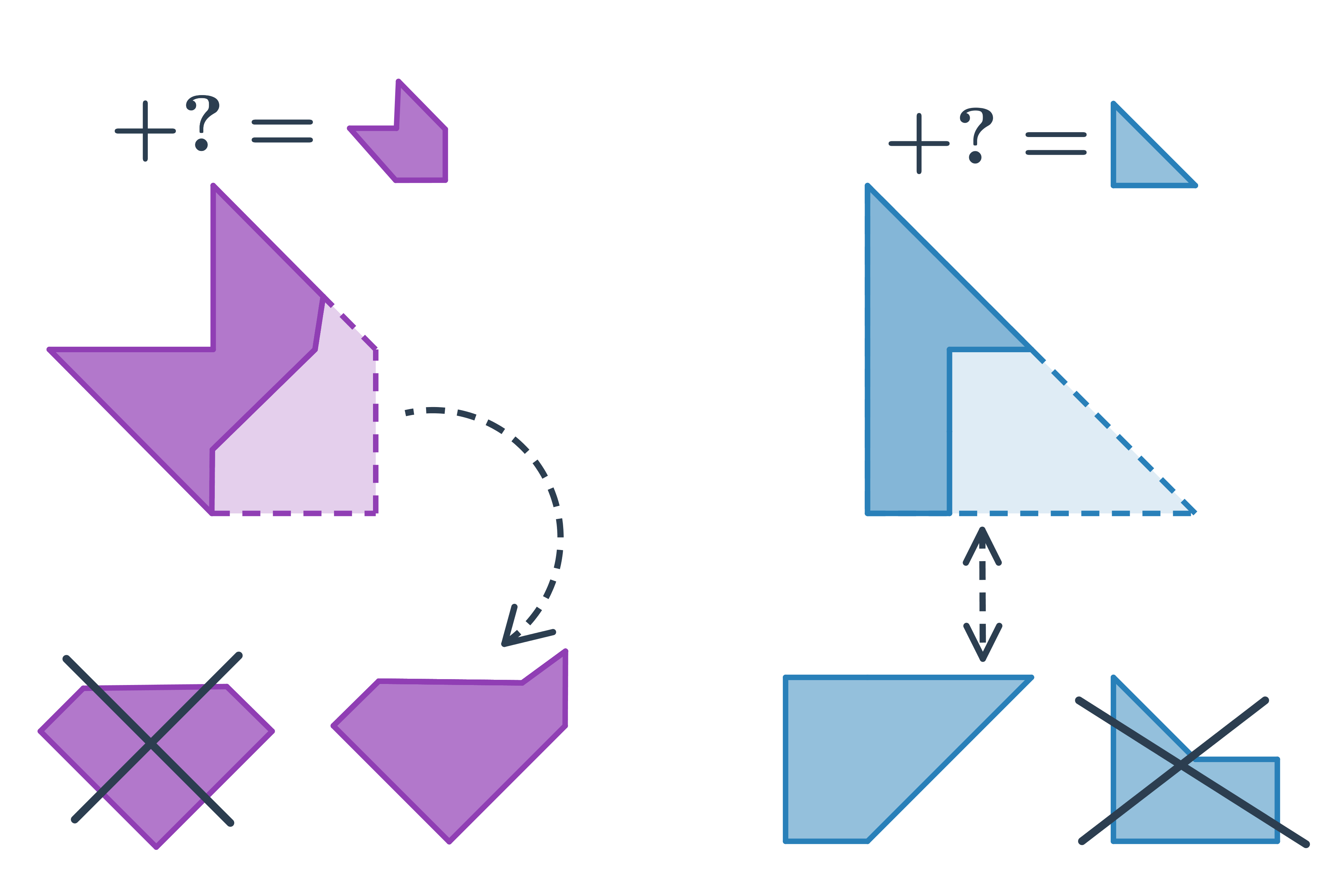
Otočení a překlopení v rovině
Při hledání správného dílku, který vznikne otočením nebo překlopením daného útvaru využíváme základních vlastností otáčení, osové a středové souměrnosti.
Stačí si pamatovat pár jednoduchých pravidel:
- Při otočení ani překlopení nemění jednotlivé části objektů své vzájemné polohy. Například, pokud je kruh na straně trojúhelníku, nemůže se „přestěhovat“ na vrchol.
- Překlopení je osová souměrnost. To mimo jiné znamená, že bod, který je nejdál od osy překlopení, bude i v překlopení nejdál od osy.
- Otočení o 180° je středová souměrnost.
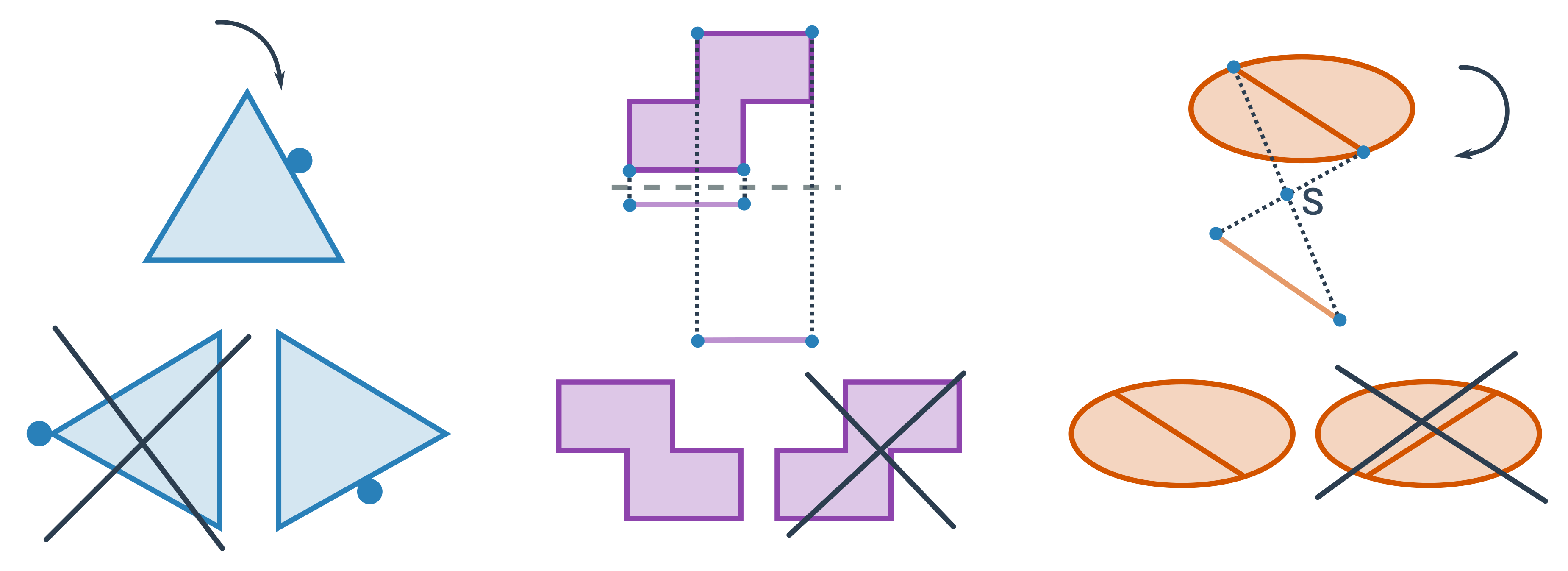
Prostorová představivost: 3D objekty
Při zobrazení prostorových objektů (těles, staveb z kostek a jiných) narážíme na základní problém: papír či obrazovka má pouze dva rozměry a neumíme tedy reálně modelovat prostorové situace.
Při zobrazení 3D objektů často využíváme pravoúhlého promítání z přední, boční a horní strany, tzv. nárys, bokorys a půdorys.
Při řešení úloh s prostorovou tematikou můžeme například postupovat takto:
- Začneme u jednodušších pohledů.
- Zaměříme se na odlišnosti, tedy zkusíme najít, v čem se dané útvary liší.
Příklad: Výběr správného pohledu na těleso

- Úkol: Vyberte, který ze tří dolních obrázků je jiným pohledem na těleso nad nimi.
- Pozorování: Těleso se skládá ze dvou delších ramen a jednoho kratšího ramene.
- Můžeme tedy škrtnout první obrázek. Na něm má těleso jedno dlouhé a dvě kratší ramena.
- Stejně tak můžeme škrtnout i třetí obrázek, na kterém má těleso tři stejně dlouhá ramena.
- Řešením je prostřední obrázek.
Nárys, půdorys, bokorys
Nárys, bokorys a půdorys slouží k dvojrozměrnému zakreslení trojrozměrného objektu pomocí pravoúhlého promítání. Každý z nich zachycuje pohled na objekt z jiného směru.
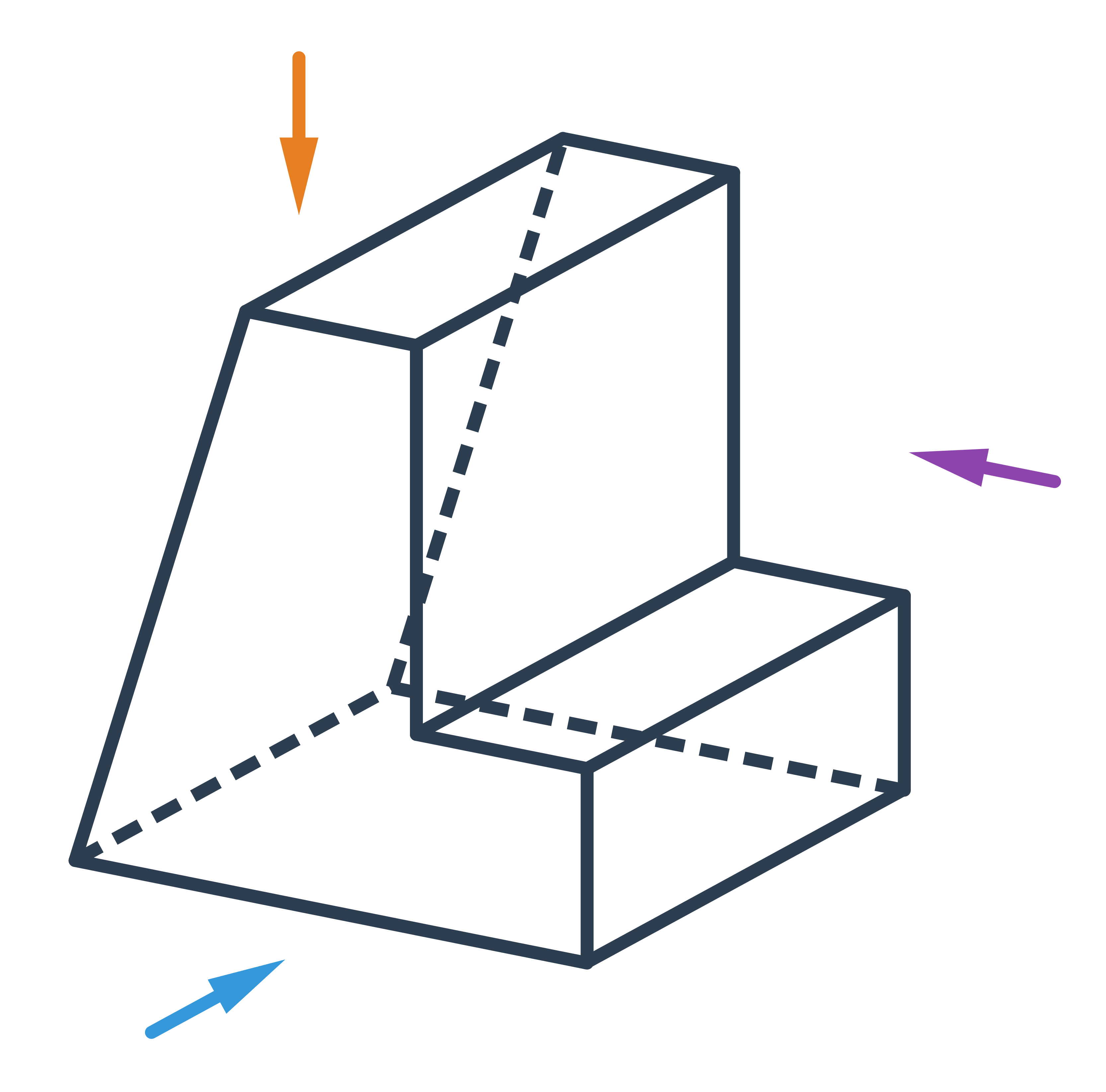
Nárys je pohled na těleso zepředu: 
Bokorys je pohled z boční strany: 
Půdorys je pohled shora: 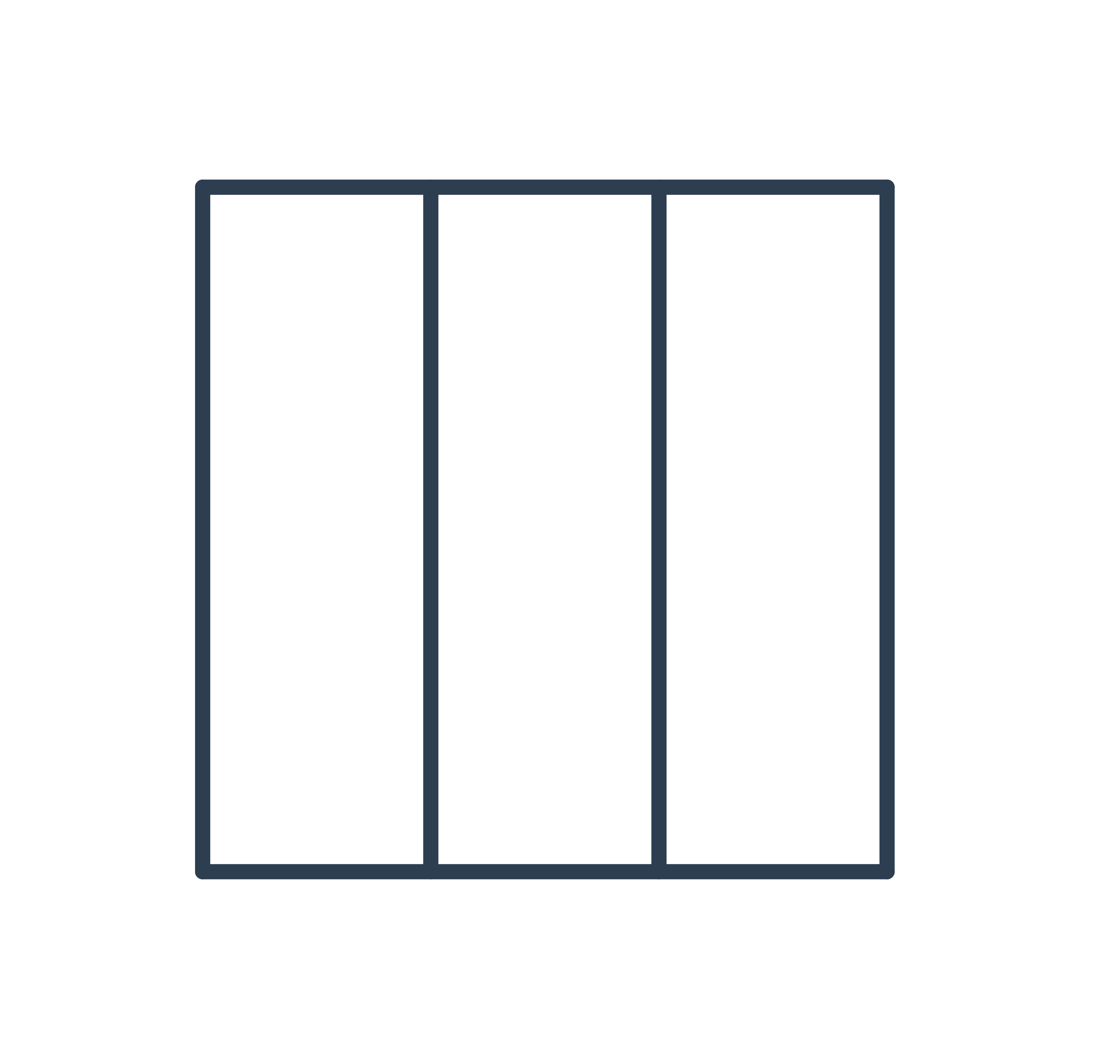
Příklad: 3 pohledy na těleso
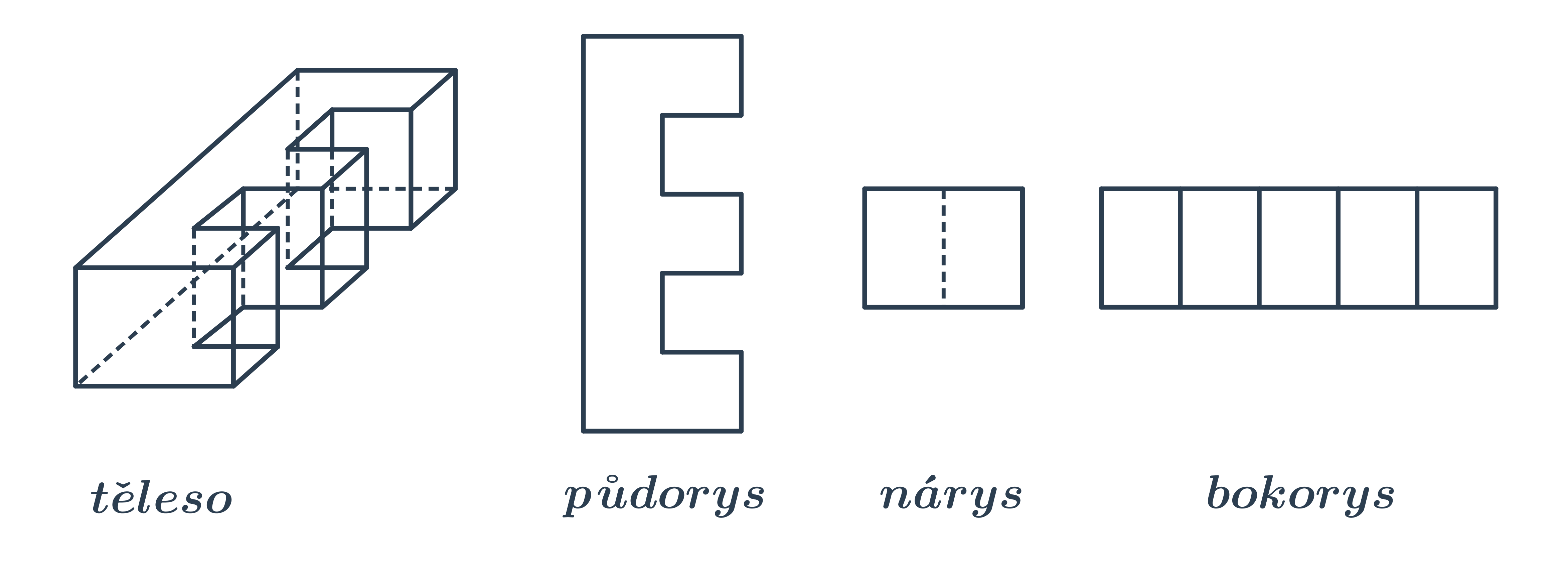
Nejčastěji se v technických aplikacích používá jen půdorys a nárys. Někdy však tyto dva pohledy nestačí.
Příklad: Je to hranol nebo není?
Jaké těleso vidíme na obrázku?
V tuto chvíli řešení není zcela jednoznačné. Těleso může být hranol (což nás asi napadne nejdřív), ale i válec. Aby bylo řešení jednoznačné, museli bychom přidat i bokorys.
Počty vrcholů, stěn, hran
Pro počet vrcholů v, hran h a stěn s konvexního mnohostěnu platí Eulerova věta: v - h + s = 2.
Počty vrcholů, stěn a hran pro pravidelné mnohostěny:
| mnohostěn | počet stěn | počet vrcholů | počet hran |
|---|---|---|---|
| čtyřstěn | 4 | 4 | 6 |
| krychle | 6 | 8 | 12 |
| osmistěn | 8 | 6 | 12 |
| dvanáctistěn | 12 | 20 | 30 |
| dvacetistěn | 20 | 12 | 30 |
Sítě těles
Síť tělesa je rovinné zakreslení, ze kterého jde poskládat plášť tělesa. Příklady sítí:
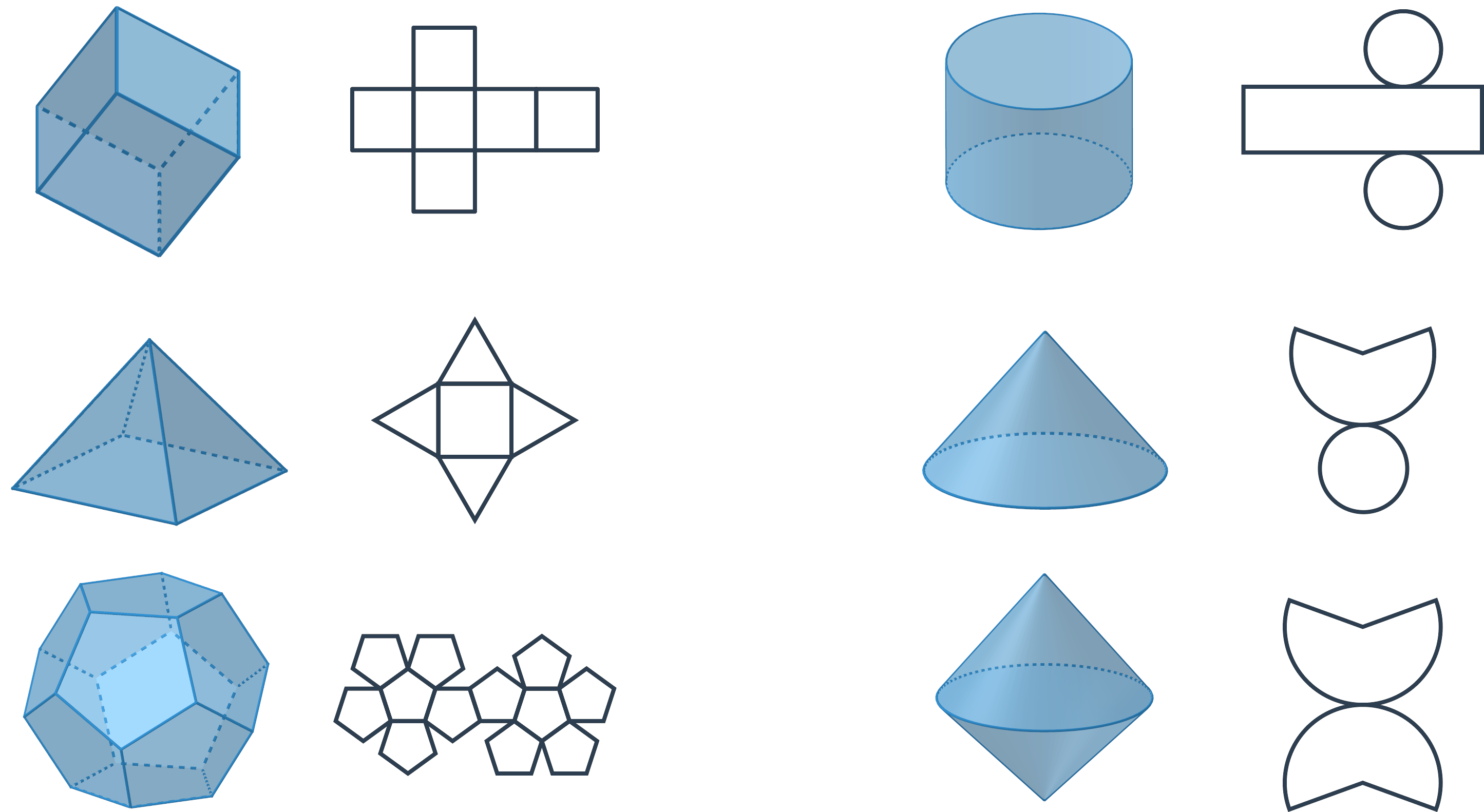
Síť tělesa jde většinou zakreslit mnoha různými způsoby. Síť krychle můžeme zakreslit takto:
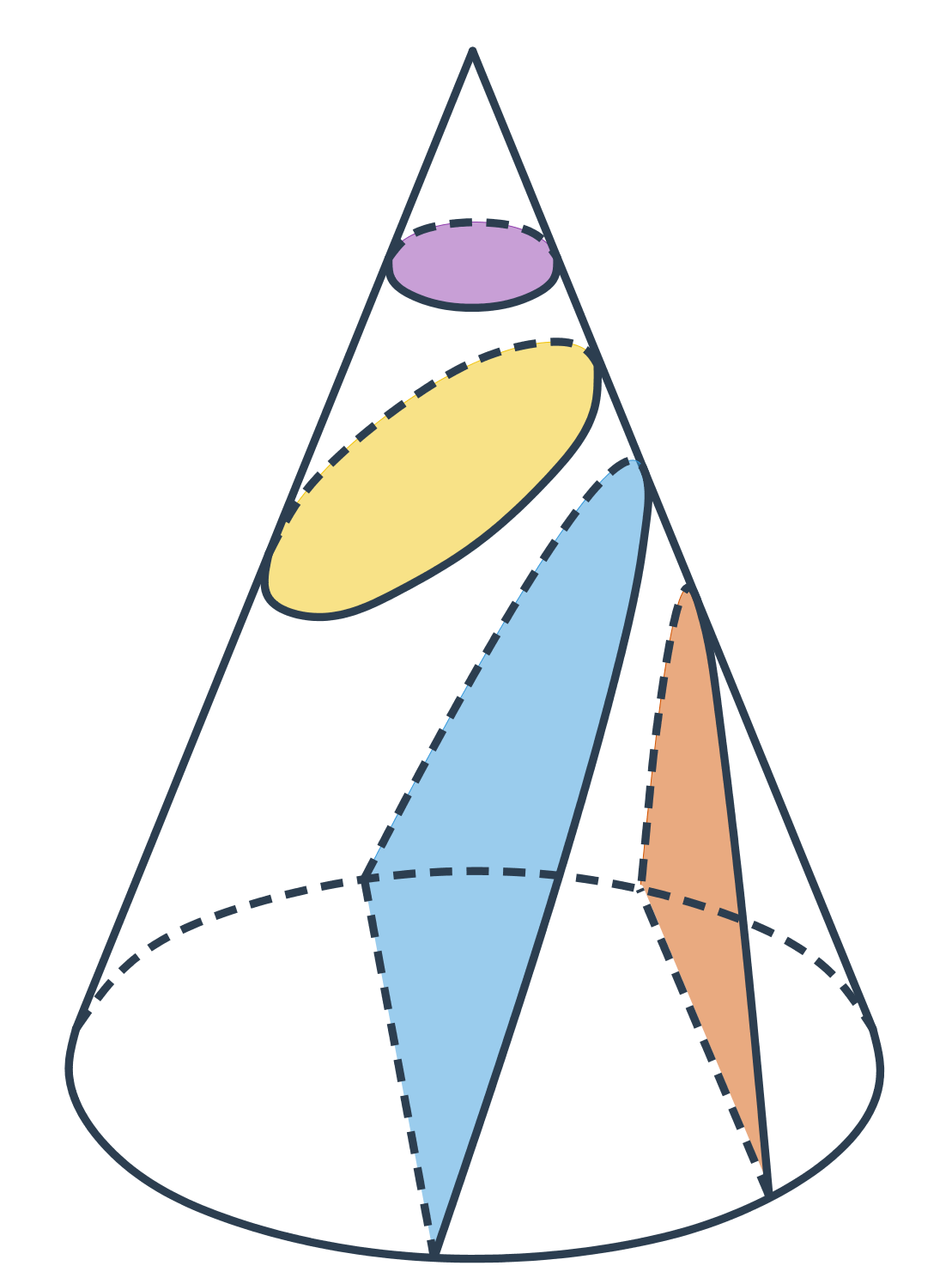
Řezy krychle
Sestrojit řez krychle znamená sestrojit průnik roviny a krychle. Půjde o mnohoúhelník, který leží v rovině řezu a jeho strany jsou okraje řezu, tedy čáry, kudy rovina řízne stěny krychle. Tyto průsečnice řezné roviny se stěnami tělesa chceme sestrojit. Při konstrukci řezů (nejen krychle) můžeme použít tři základní pravidla:
- Pokud leží dva různé body v rovině, pak přímka, která jimi prochází, leží také v této rovině. Když známe ve stěně tělesa dva různé body, které oba leží v rovině řezu, nakreslíme jejich spojnici. Průnik stěny a této spojnice je jednou stranou řezu.
- Dvě rovnoběžné roviny protíná každá další k nim různoběžná rovina ve dvou rovnoběžných přímkách. To znamená, že strany řezu v rovnoběžných stěnách jsou navzájem rovnoběžné.
- Tři navzájem různoběžné roviny se vždy protínají v jednom bodě. Tímto bodem prochází všechny tři průsečnice jednotlivých dvojic rovin. Tedy dvě průsečnice rovin dvou sousedních stěn s rovinou řezu a přímka, na které leží společná hrana stěn, se protínají v jednom bodě.
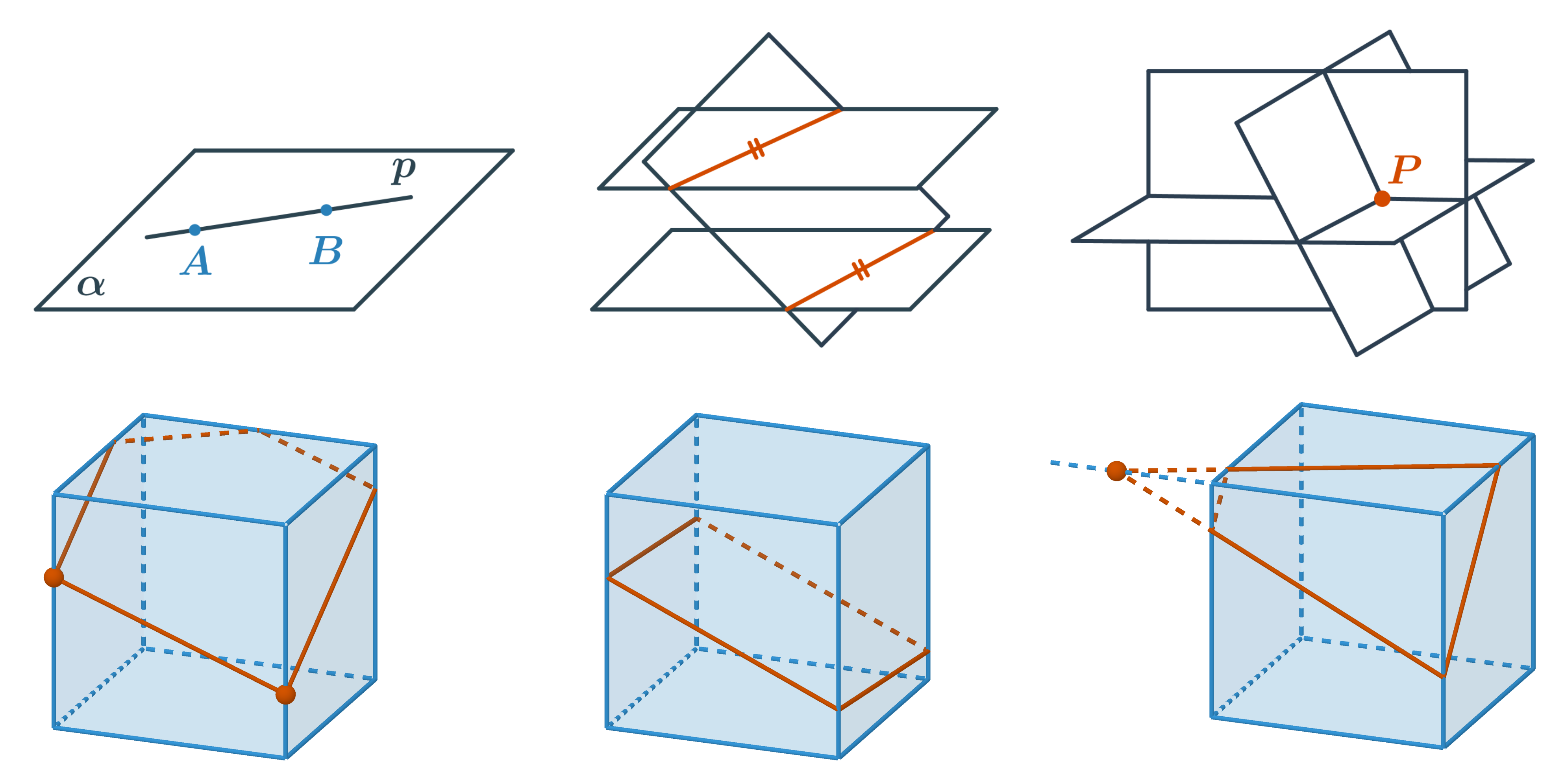
Pozor si dáváme na nejčastější chyby:
- zalomení řezu v jedné stěně (část řezu v jedné stěně musí vždy tvořit jedna úsečka)
- čára řezu jde vnitřkem nebo vnějškem tělesa (okraj řezu musí být celý ve stěnách tělesa)
- čára řezu nekončí na hraně (těleso na hraně končí, řez tělesa také)
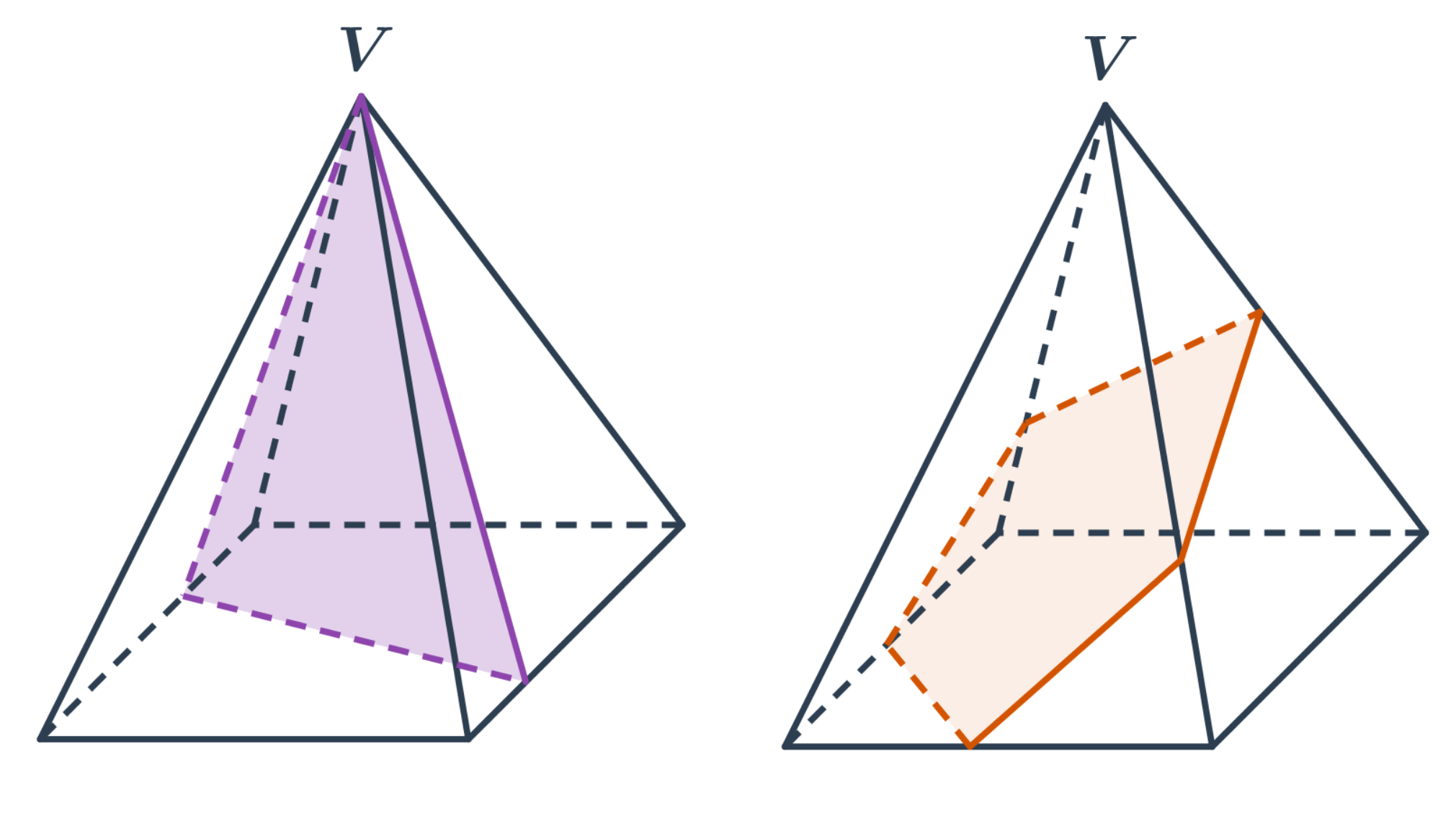
Řez krychle rovinou procházející body K, L, M.
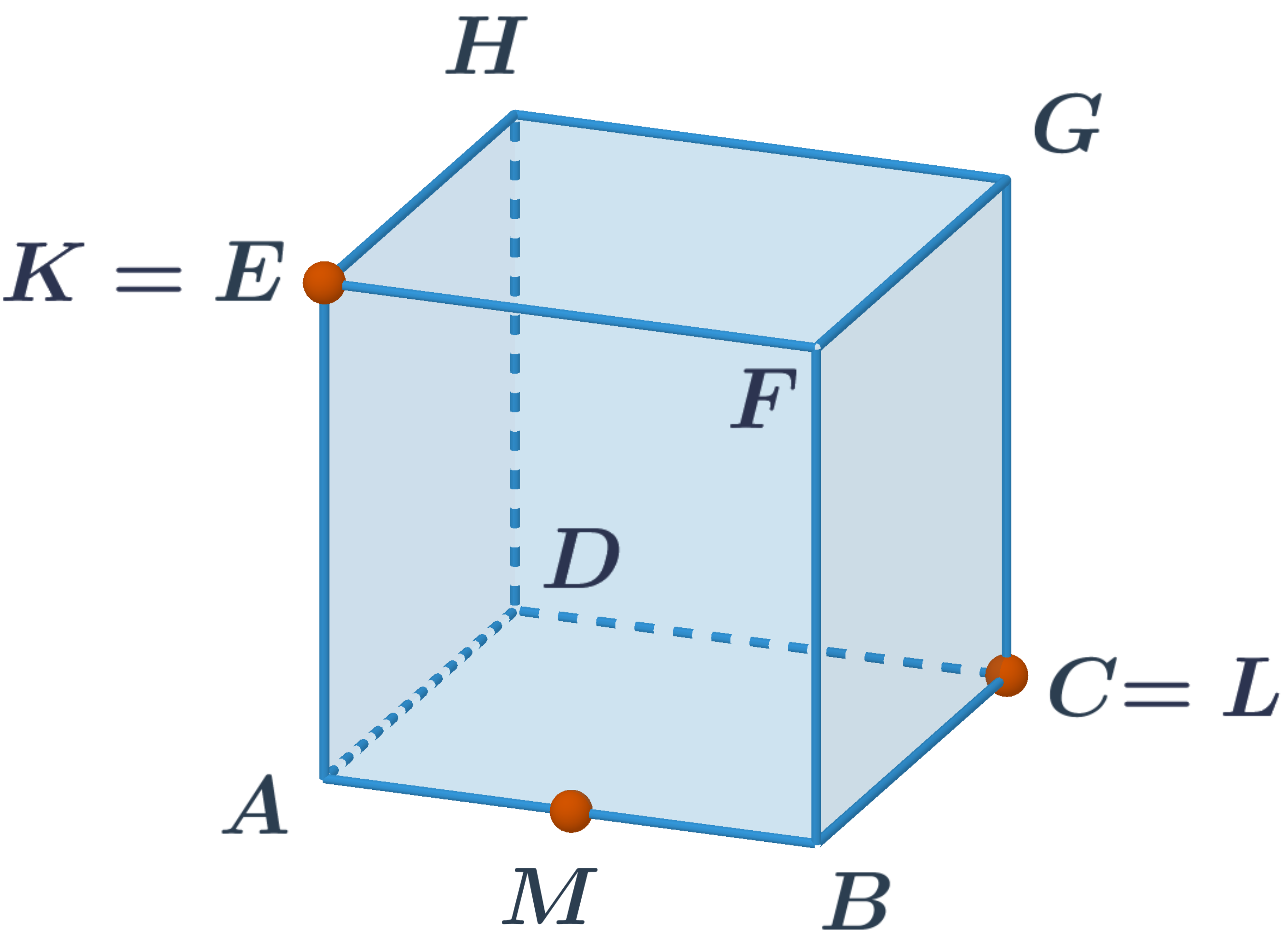
- Body K, M leží v jedné rovině – v přední stěně ABFE. Úsečka KM je tedy první část řezu.
- Stejně tak body L, M leží v jedné rovině – v dolní stěně ABCD. Úsečka LM je tedy druhá část řezu.
- Bod K leží v horní stěně EFGH. Ta je rovnoběžná se stěnou ABCD. Další část řezu KN je tedy rovnoběžná s úsečkou LM.
- Podobně je i poslední část řezu NL v zadní stěně CDHG rovnoběžná s úsečkou KM ve stěně ABFE.
- Řezem je v tomto případě rovnoběžník.
Řezy těles
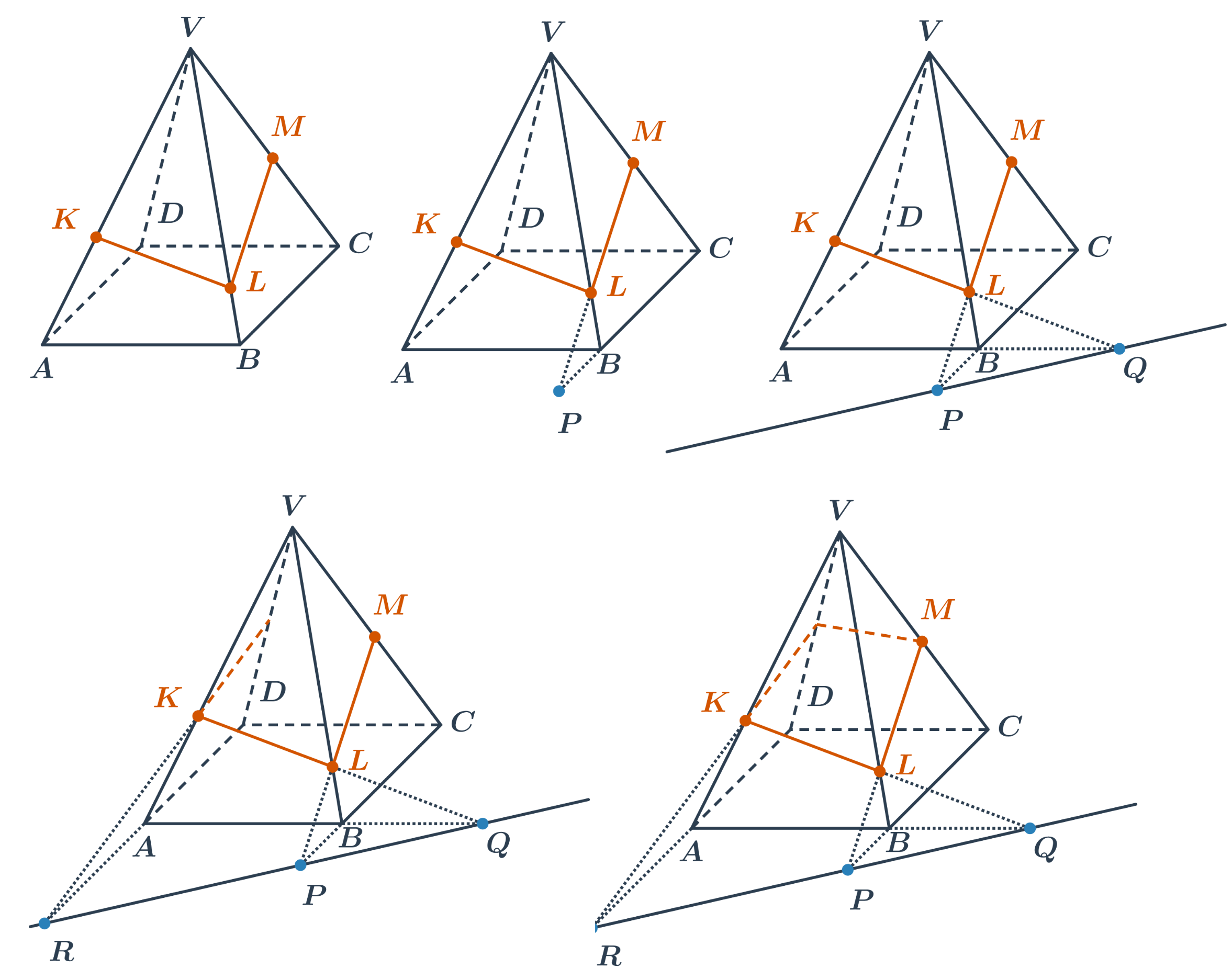
Sestrojit řez tělesa znamená sestrojit průnik roviny a tělesa. K základní principům konstrukce řezů, které známe z řezů krychle si u složitějších případů přidáme ještě jedno pravidlo:
- Když známe jednu stranu řezu, můžeme ji protáhnout do ostatních stěn. Průsečíky s ostatními stěnami určíme tak, že protáhneme společnou hranu hranu stěny, kde leží známá úsečka řezu a stěny, ve které chceme řez najít. Výhodné je najít průsečnici roviny podstavy a roviny řezu.
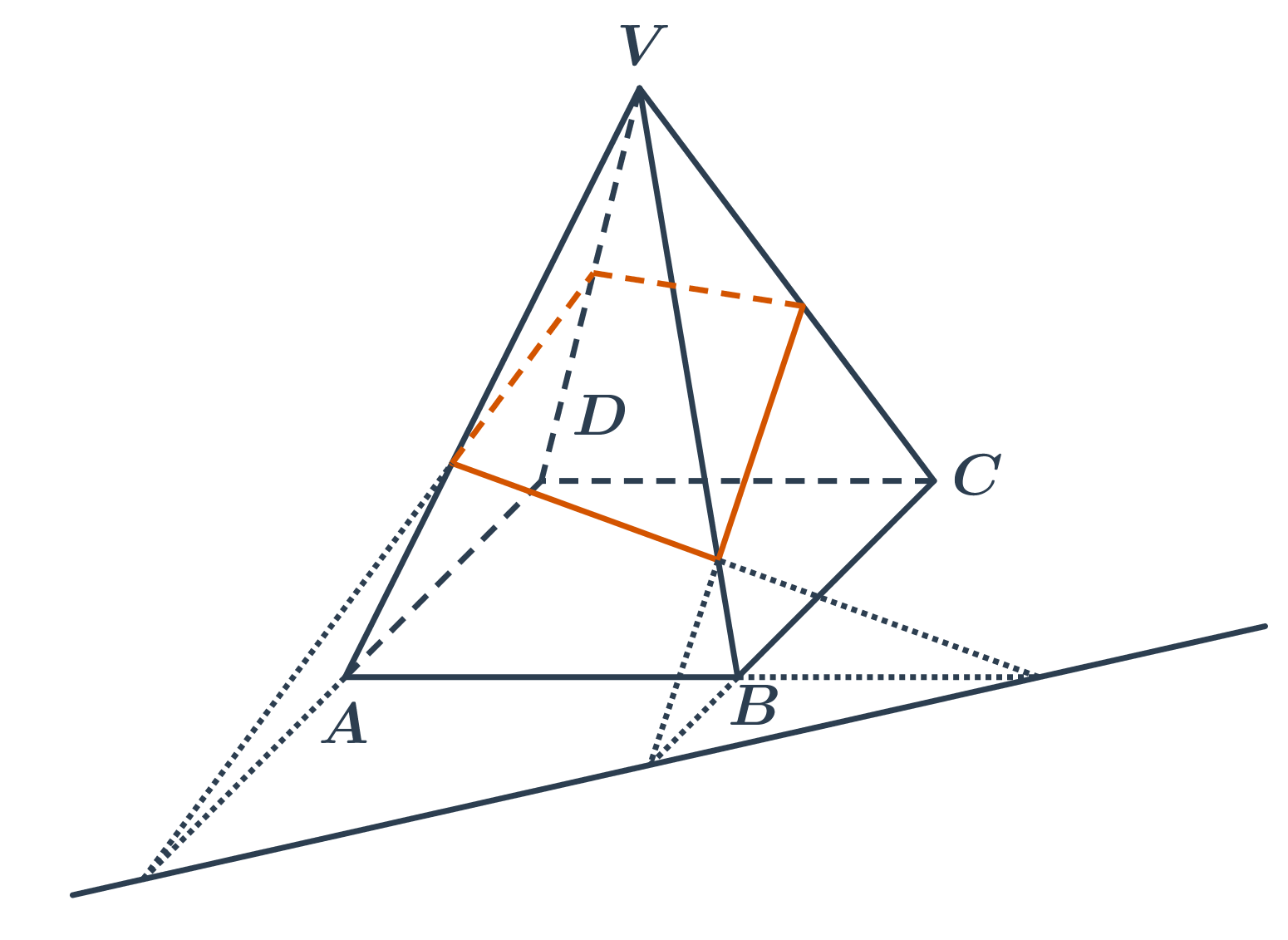
Zobecněním tohoto principu je tzv. středová kolineace, která se využívá pro přesné sestrojení řezu jehlanu a kužele.
Řez jehlanu rovinou procházející body K, L, M.
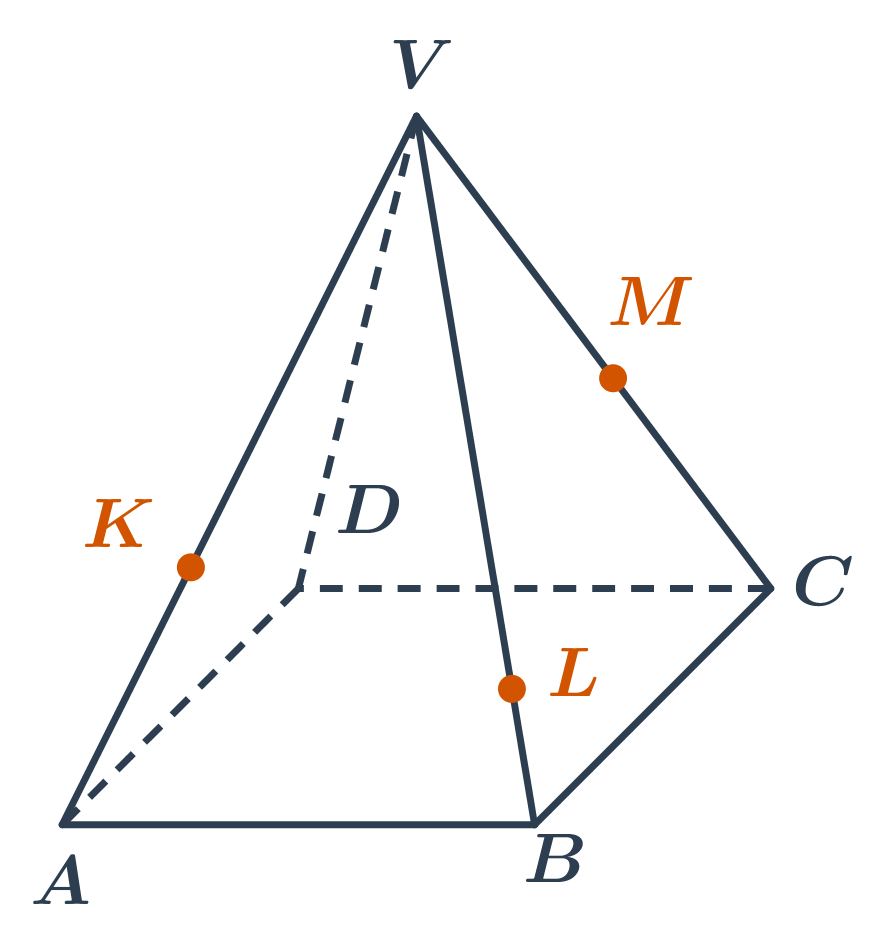
- Známe body na hranách, můžeme rovnou sestrojit dvě části řezu - úsečky KL a LM.
- Najdeme průsečnici roviny podstavy a roviny řezu. Ve stěne BCV leží hrana podstavy BC a úsečka LM. Jejich protažením získáme společný bod P tří rovin: roviny stěny BCV, roviny podstavy a roviny řezu.
- Stejným způsobem získáme společný bod Q tří rovin: roviny stěny ABV, roviny podstavy a roviny řezu. Přímka PQ je pak průsečnice roviny podstavy a roviny řezu.
- Protažením hrany AD získáme na průsečnici bod R. Na přímce RK pak leží další část řezu ve stěně ADV.
- V zadní stěne CDV nyní máne na hranách dva body řezu a můžeme doplnit poslední stranu řezného čtyřúhelníku.
Stejně jako u řezu krychle záleží na poloze roviny a tělesa:
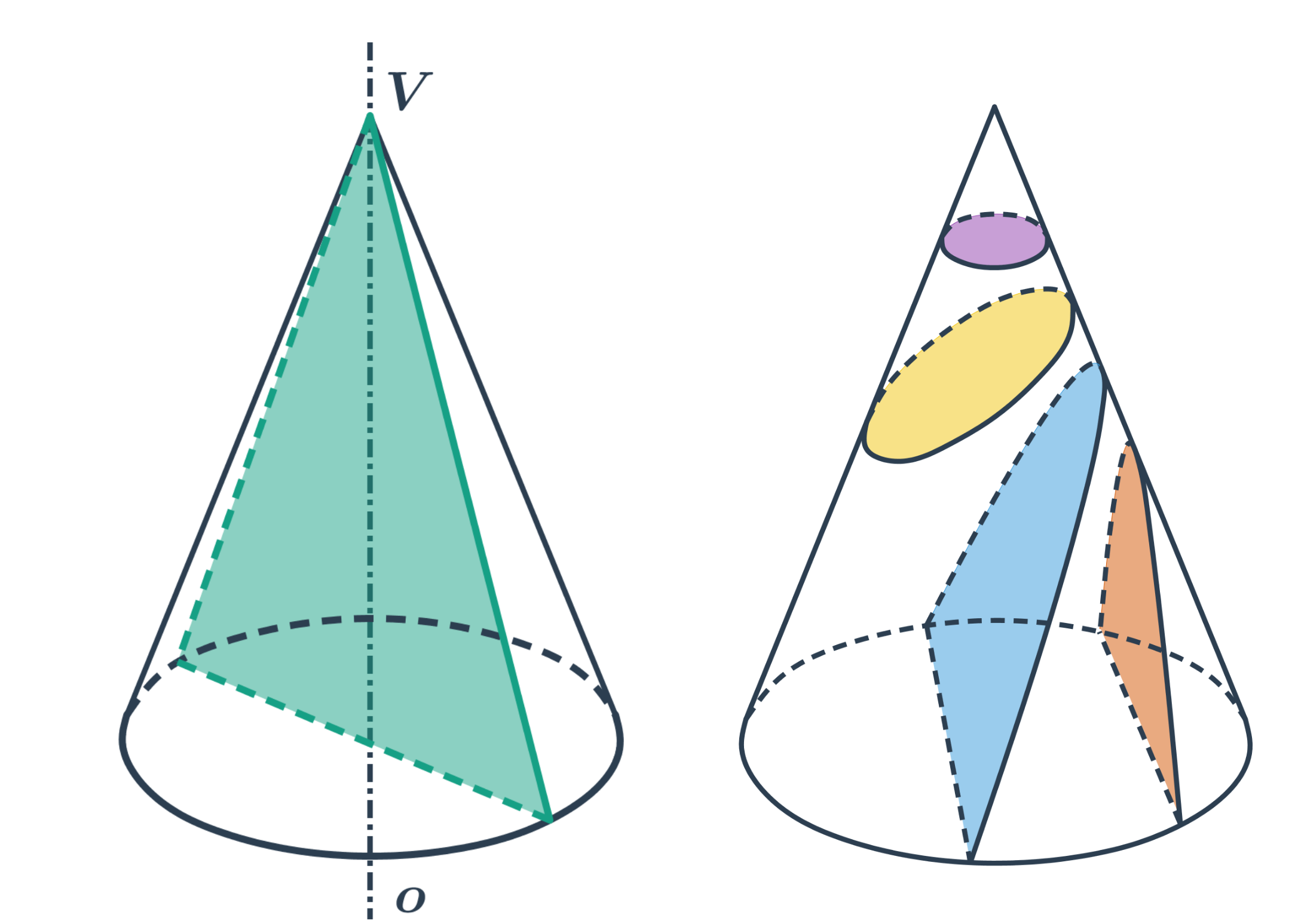
Jehlan
- Rovina prochází vrcholem jehlanu - řezem je trojúhelník.
- Rovina neprochází vrcholem - řezem je obecný n-úhelník.
Kužel
- Rovina prochází vrcholem kužele - řezem je trojúhelník.
- Rovina neprochází vrcholem - řezem je kuželosečka.
Válec
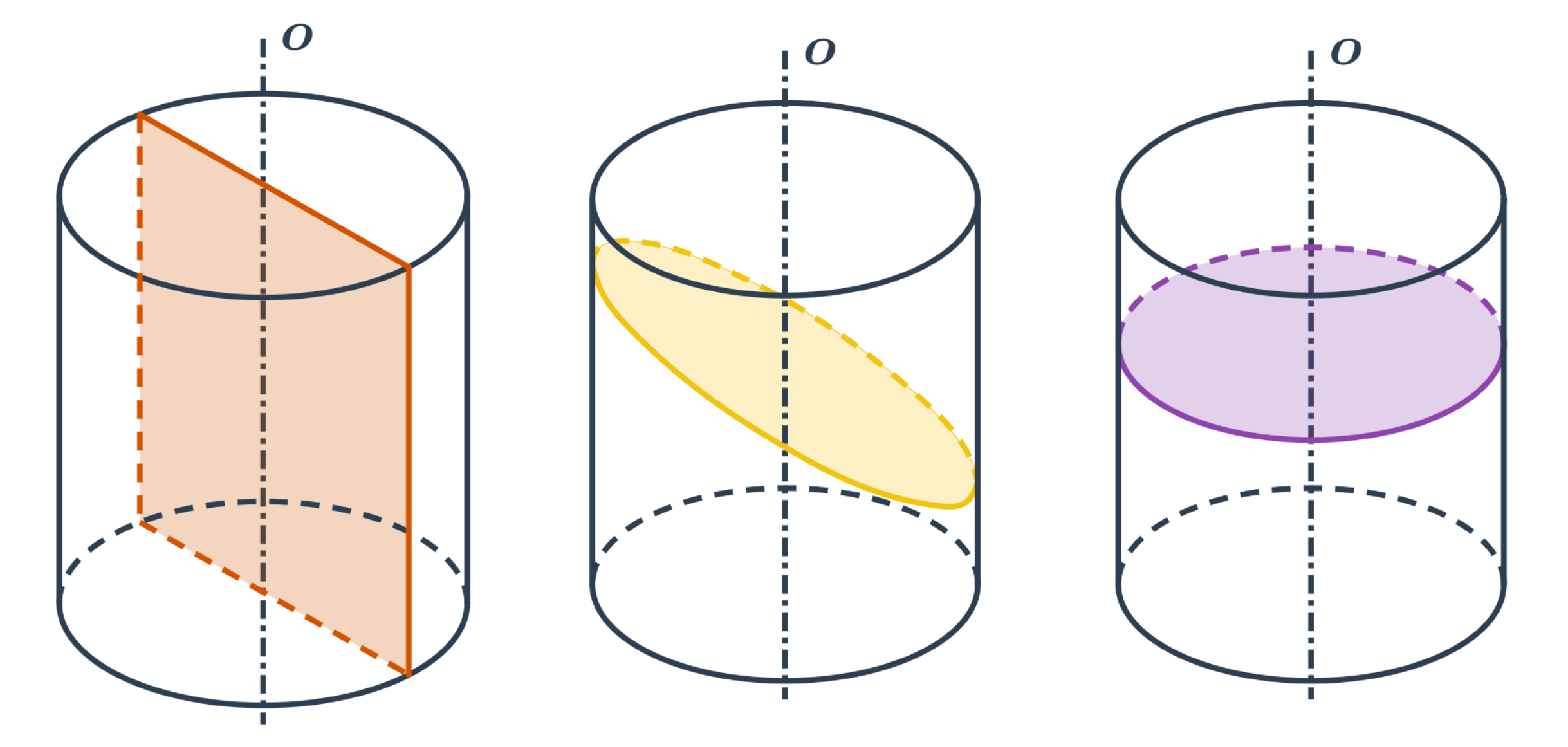
- Rovina je rovnoběžná s osou válce - řezem je obdélník.
- Rovina není rovnoběžná s osou válce - řezem je kružnice nebo elipsa.
Koule
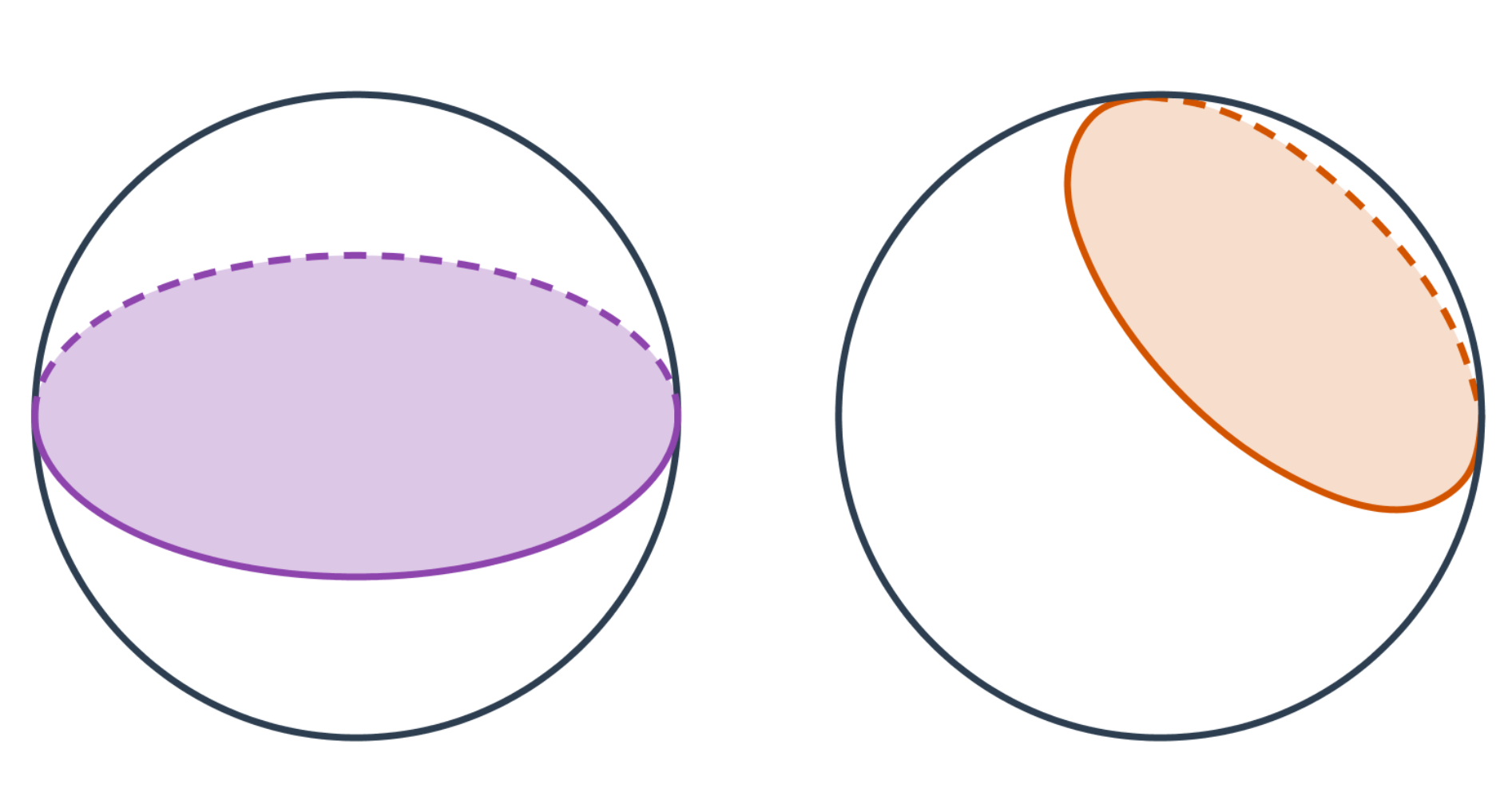
Řezem koule je vždy kružnice. Na papíře či obrazovce ji ale můžeme vidět i jako elipsu.
Geometrické pojmy
Na rozdíl od běžného jazyka, kde mají slova většinou několik významů, v matematice používáme pojmy s přesně definovaným významem. To je velmi užitečné, protože se díky tomu můžeme vyjadřovat stručně a přitom jednoznačně. V geometrii se využívá řada pojmů.
| téma | příklady pojmů |
|---|---|
| Názvy geometrických útvarů a těles | obdélník, kosodélník, trojúhelník, kružnice, krychle, kvádr, jehlan, koule |
| Pojmy související s úhly | úhel tupý, ostrý, pravý, plný, střídavý, vrcholový |
| Pojmy související s trojúhelníkem | těžiště, výška, přepona, odvěsna, kružnice vepsaná, rovnoramenný trojúhelník |
| Pojmy související s kružnicí | průměr, poloměr, tětiva, tečna, sečna, výseč, úseč, středový úhel |
| Kuželosečky: pojmy | elipsa, hyperbola, parabola, osa, vrchol, střed, asymptota |
Pojmy související s úhly
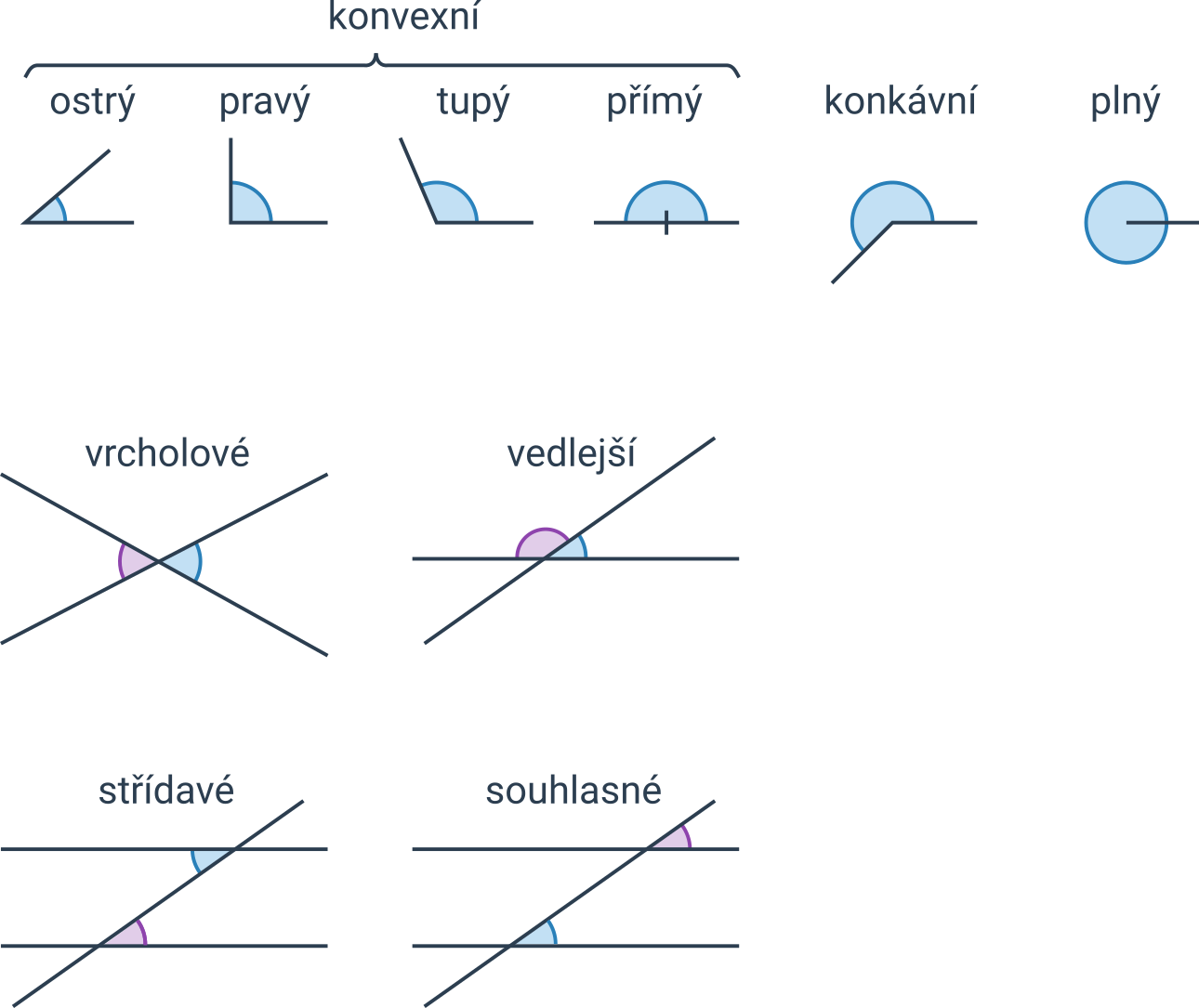
Úhly podle velikosti
| plný úhel | úhel o velikosti 360° |
| přímý úhel | úhel o velikosti 180° |
| pravý úhel | úhel o velikosti 90° |
| ostrý úhel | úhel menší než 90° |
| tupý úhel | úhel větší než 90° a menší než 180° |
| konvexní úhel | úhel menší nebo roven 180° |
| nekonvexní, konkávní úhel | úhel větší než 180° |
Pojmy související s dvojicemi úhlů
| vrcholové úhly | dvojice úhlů, jejichž ramena jsou opačné polopřímky | mají stejnou velikost |
| vedlejší úhly | dvojice úhlů, jejichž jedno rameno je společné a druhá ramena jsou opačné polopřímky | součet jejich velikostí je 180° |
| souhlasné úhly | dvojice úhlů, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je stejný | mají stejnou velikost |
| střídavé úhly | dvojice úhlů, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je opačný | mají stejnou velikost |
Pojmy související s trojúhelníkem
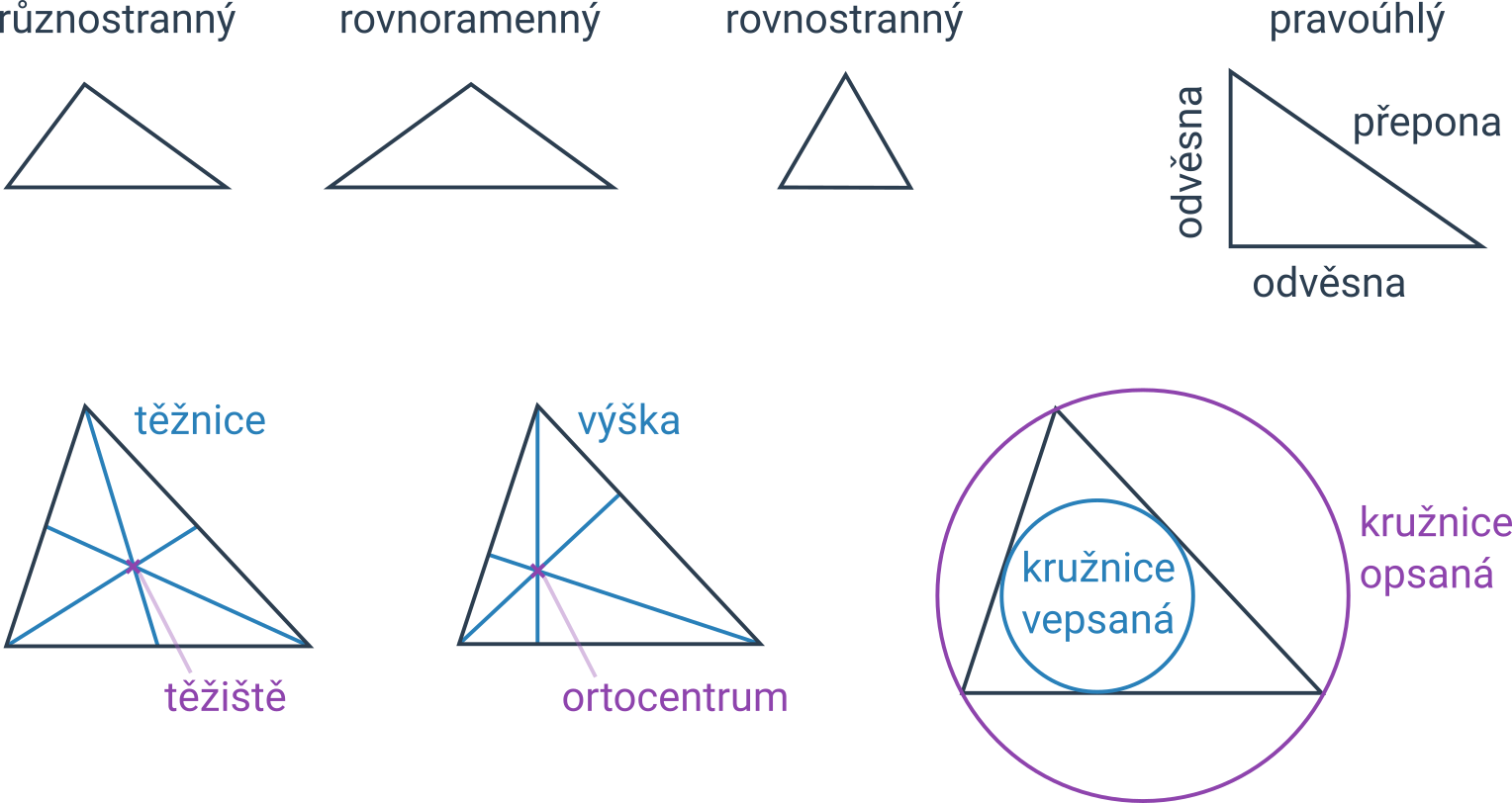
| obecný (různostranný) trojúhelník | trojúhelník, ve kterém žádné dvě strany nejsou shodné |
| rovnoramenný trojúhelník | trojúhelník, který má dvě strany shodné |
| rovnostranný trojúhelník | trojúhelník, který má všechny tři strany shodné |
| pravoúhlý trojúhelník | trojúhelník, který má jeden úhel pravý |
| odvěsna | strana sousedící s pravým úhlem v pravoúhlém trojúhelníku |
| přepona | strana protilehlá k pravému úhlu v pravoúhlém trojúhelníku |
| těžnice | úsečka spojující střed strany a protilehlý vrchol trojúhelníku |
| těžiště | průsečík těžnic |
| výška | úsečka spojující vrchol trojúhelníku a patu kolmice vedené tímto vrcholem na protější stranu |
| ortocentrum | průsečík výšek |
| kružnice opsaná | kružnice, která prochází všemi vrcholy trojúhelníku |
| kružnice vepsaná | kružnice, která se dotýká všech stran trojúhelníku |
| střed kružnice opsané | průsečík os stran |
| střed kružnice vepsané | průsečík os úhlů |
Pozn. Přesné definice rovnoramenného trojúhelníku se liší: někteří autoři vyžadují „alespoň“ dvě strany shodné, jiní „právě“ dvě strany shodné. Rozdíl je v tom, zda rovnostranné trojúhelníky považujeme za rovnoramenné.
NahoruPojmy související s kružnicí
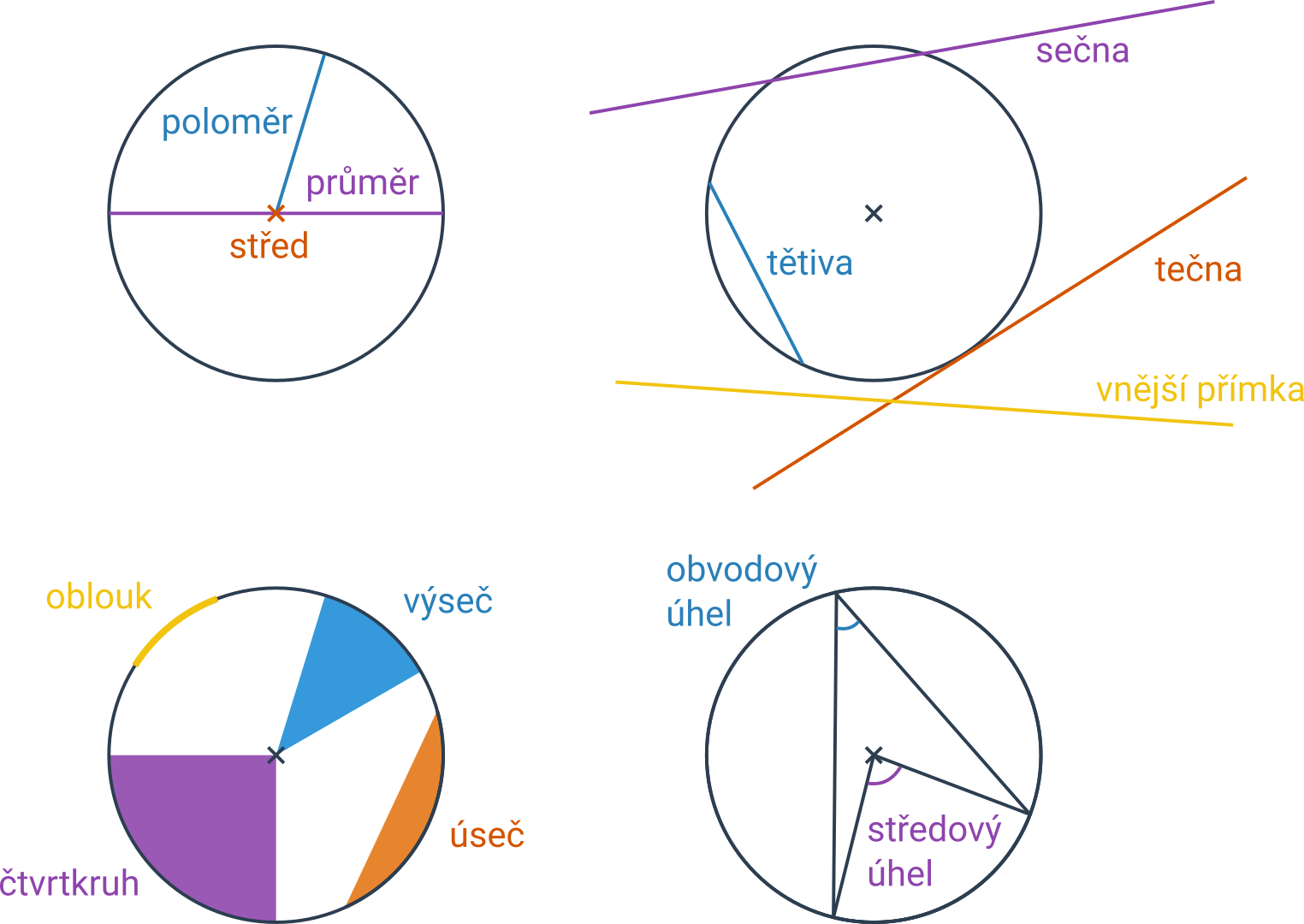
| poloměr | jejíž jeden koncový bod leží na kružnici a druhý koncový bod ve středu kružnice |
| průměr | úsečka, která prochází středem kružnice a jejíž oba krajní body leží na této kružnici |
| tečna | přímka, která se kružnice dotýká právě v jednom bodě |
| sečna | přímka, která kružnici protíná ve dvou bodech |
| vnější přímka | přímka, která kružnici neprotíná |
| tětiva | úsečka spojující dva body na kružnici |
| kruhová výseč | část kruhu příslušná středovému úhlu |
| mezikruží | plocha mezi dvěma soustřednými kružnicemi |
| půlkruh | výseč příslušná přímému úhlu (180°) |
| čtvrtkruh | výseč příslušná pravému úhlu (90°) |
| úseč | část kruhu vymezená tětivou a kruhovým obloukem vzniklá rozdělením kruhu sečnou |
| středový úhel | úhel, jehož vrcholem je střed kružnice a jehož ramena procházejí krajními body oblouku |
| obvodový úhel | úhel, jehož vrchol leží na kružnici a ramena procházejí krajními body oblouku |
Komiks pro zpestření

Rovinné útvary
Rovinné útvary jsou množiny bodů v rovině, tedy jde o dvourozměrné útvary. Nejznámější rovinné útvary jsou například čtverec, obdélník, trojúhelník, kružnice, kruh, rovnoběžník, lichoběžník, pravidelný nebo nepravidelný mnohoúhelník.
U některých rovinných útvarů umíme jednoduše spočítat jejich obvod a obsah.
NahoruTrojúhelník
Trojúhelník je základní geometrický útvar, který má tři vrcholy a tři strany. Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi.
Značení stran a úhlů v trojúhelníku:
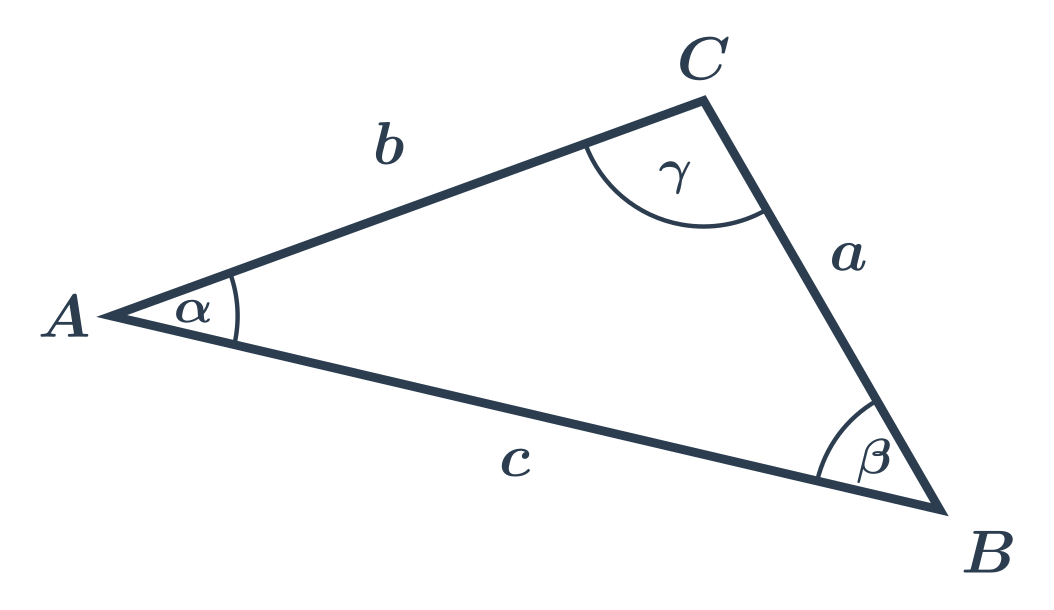
Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
Výšky příslušné stranám v trojúhelníku:
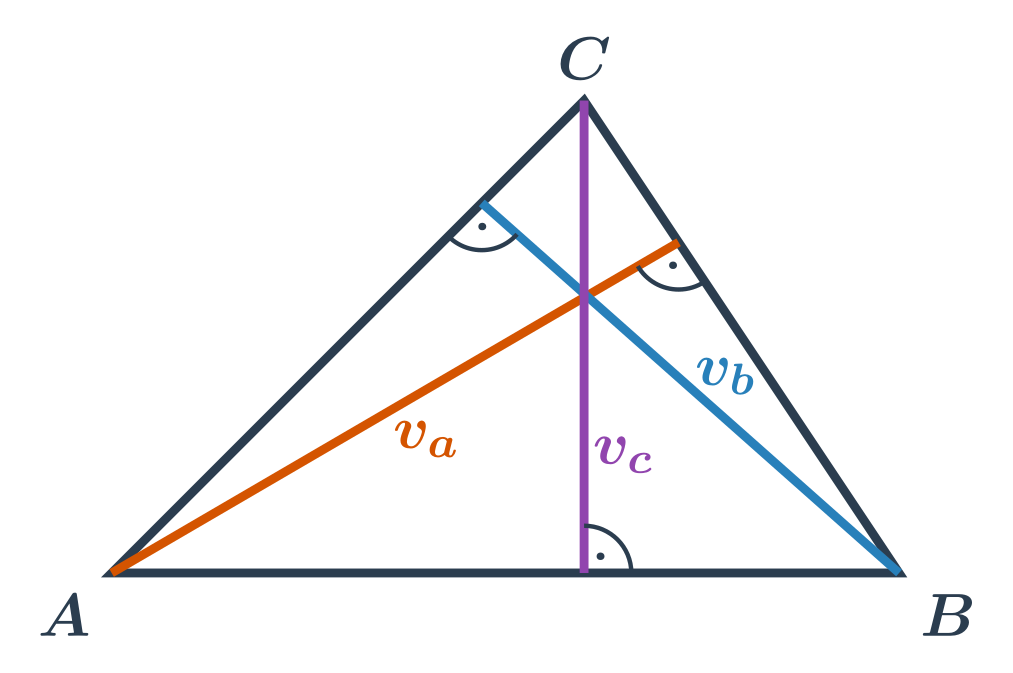 Výška v_a je vzdálenost bodu A od přímky, na které leží strana a. Tedy je to vzdálenost bodu A od paty kolmice na přímku BC vedené bodem A. Tato pata kolmice může a nemusí ležet přímo na straně a.
Výška v_a je vzdálenost bodu A od přímky, na které leží strana a. Tedy je to vzdálenost bodu A od paty kolmice na přímku BC vedené bodem A. Tato pata kolmice může a nemusí ležet přímo na straně a.
Témata související s trojúhelníkem:
- Pojmy související s trojúhelníkem – rovnoramenný, rovnostranný, výška, tečna, kružnice opsaná
- Obvod trojúhelníku, Obsah trojúhelníku – výpočty na základě zadaných údajů o trojúhelníku
- Úhly v trojúhelníku – součet úhlů, výpočty úhlů
- Konstrukční úlohy s trojúhelníky – narýsování trojúhelníku na základě zadaných údajů, např. za využití vět sss, sus, usu
- Pythagorova věta, Euklidovy věty, Goniometrické funkce – témata související s pravoúhlými trojúhelníky
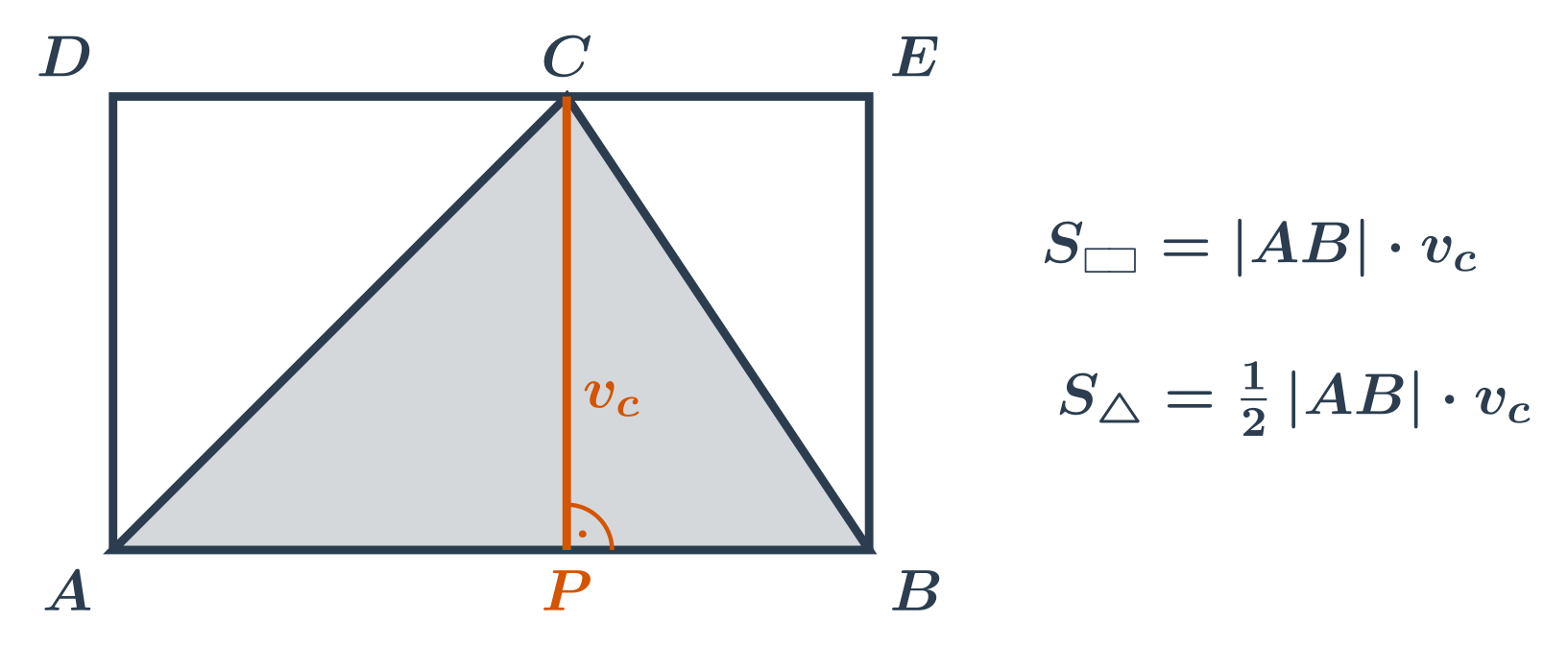
Obsah trojúhelníku
Obsah trojúhelníku spočítáme jako součin délky libovolné strany trojúhelníka a výšky příslušné k této straně, takže: S_{\triangle} = \frac12 \cdot a \cdot v_a = \frac12 \cdot b \cdot v_b = \frac12 \cdot c \cdot v_c
Což si můžeme představit jako polovinu obsahu obdélníku, ve kterém je náš trojúhelník takto vepsán:
Příklady: obsah ostroúhlých trojúhelníků
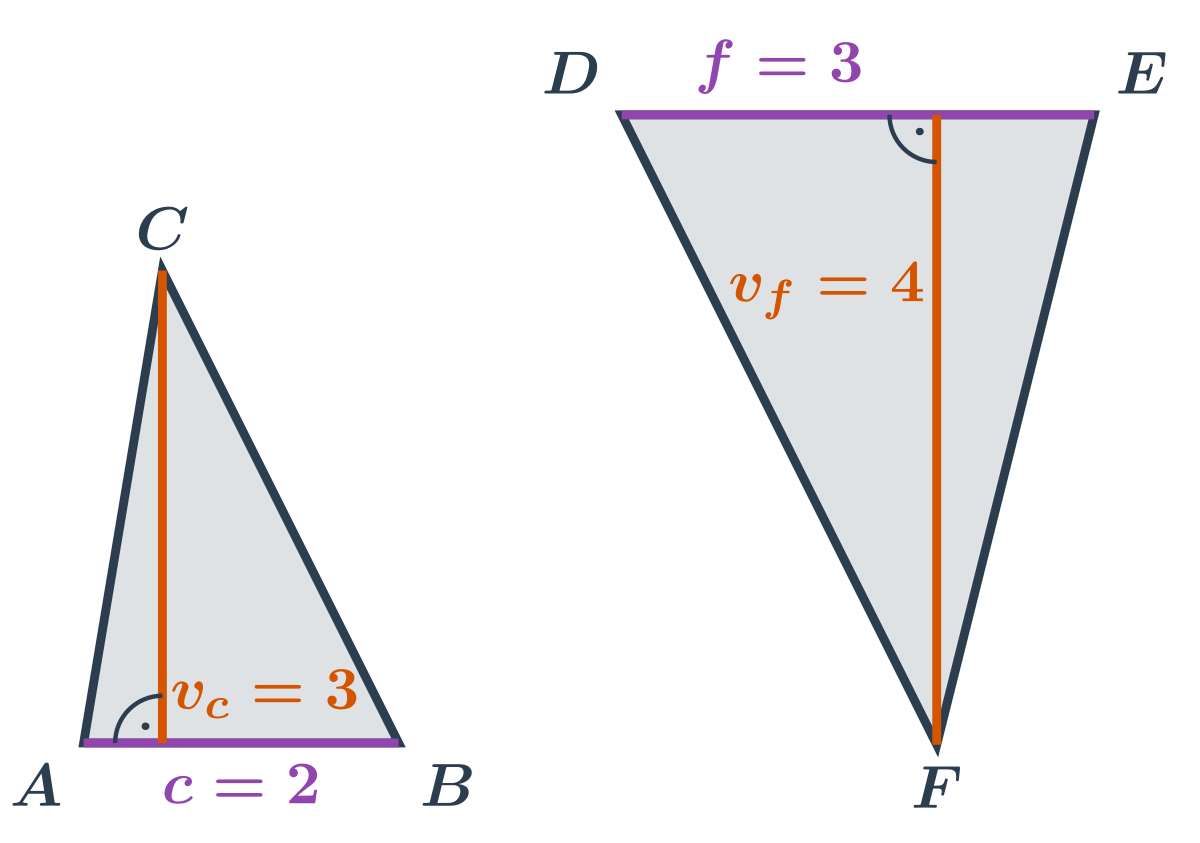
- Trojúhelník ABC: Délka strany \left| AB \right| je 2. Velikost k ní příslušné výšky v_c je 3. Obsah trojúhelníku ABC je roven \frac12 \cdot 2 \cdot 3 = 3.
- Trojúhelník DEF: Nevadí nám, že trojúhelník na náčrtku vypadá zvláštně natočený. Známe délku strany \left| DE \right|, což je 3. Velikost k ní příslušné výšky v_f je 4. Obsah trojúhelníku DEF je roven \frac12 \cdot 3 \cdot 4 = 6.
Příklady: obsah tupoúhlého a pravoúhlého trojúhelníku
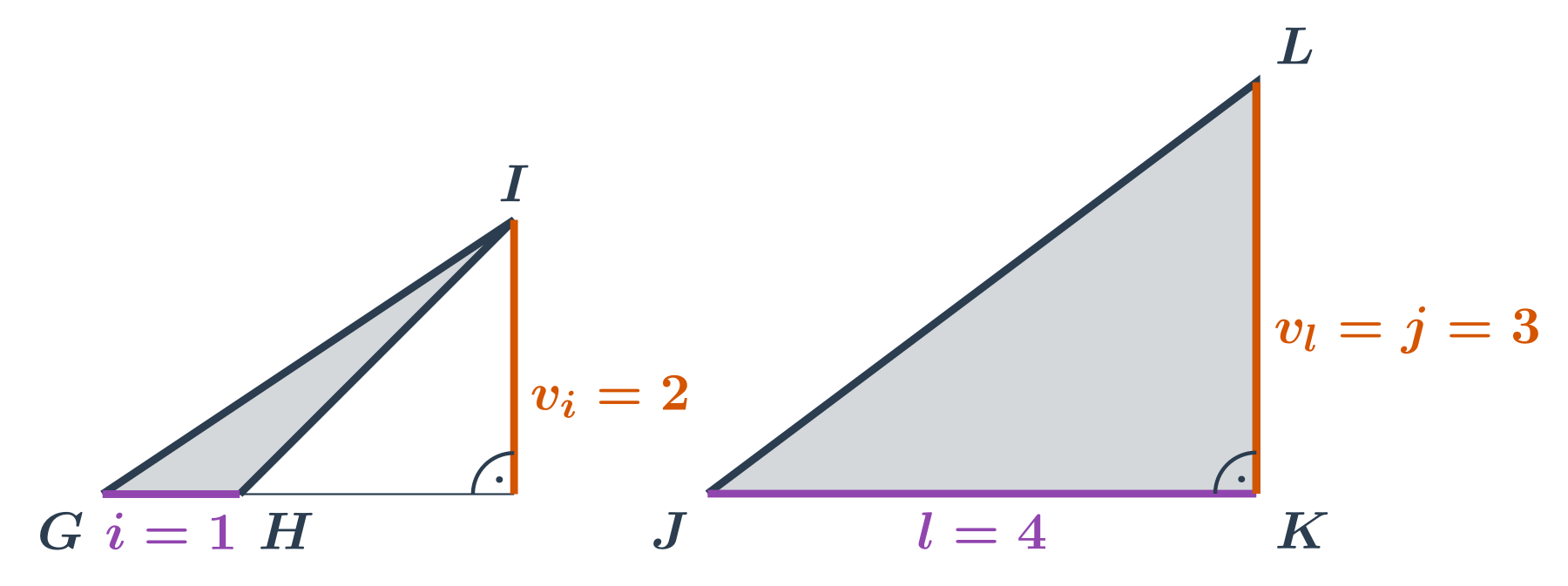
- Trojúhelník GHI: Nevadí nám ani když je pata kolmice, na které leží výška, mimo stranu trojúhelníka. Délka strany \left| GH \right| je 1. Velikost k ní příslušné výšky v_i je 2. Obsah trojúhelníku GHI je \frac12 \cdot 2 \cdot 1 = 1.
- Trojúhelník JKL: S pravoúhlým trojúhelníkem si také poradíme. Délka strany \left| JK \right| je 4. Velikost k ní příslušné výšky v_l je 3 (a je to zároveň i délka strany KL našeho trojúhelníku). Obsah trojúhelníku JKL je \frac12 \cdot 4 \cdot 3 = 6.
Obvod trojúhelníku
Obvod trojúhelníku spočítáme jako součet délek jeho stran: o=a+b+c
Příklad: obvod trojúhelníku
Trojúhelník na obrázku má délky stran a=10, b=8, c=14, takže jeho obvod je o=a+b+c=10+8+14=32.
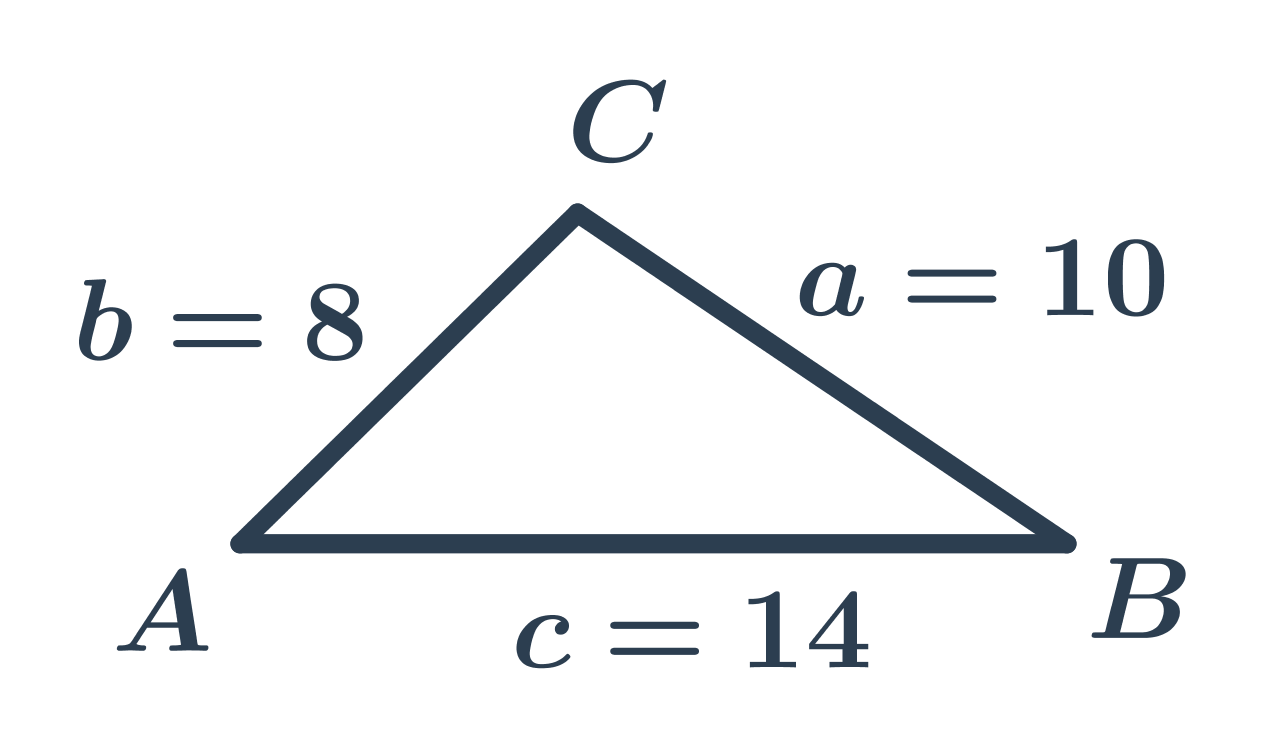
Pythagorova věta
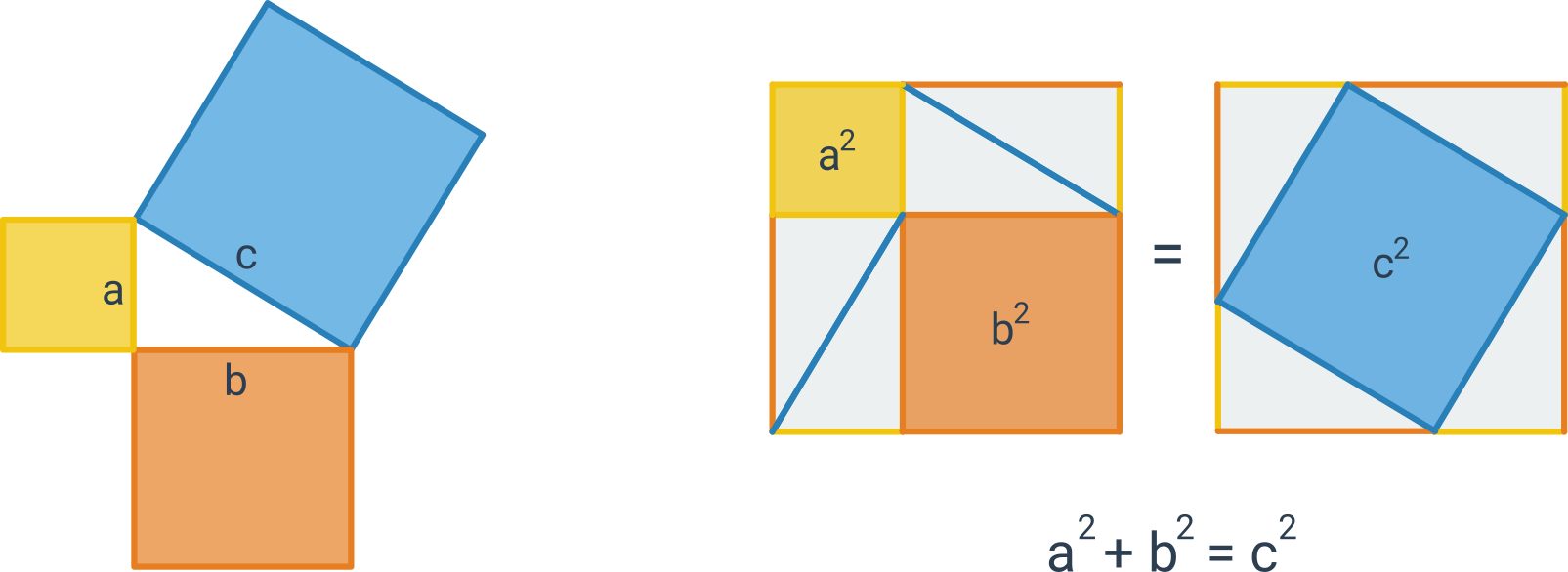
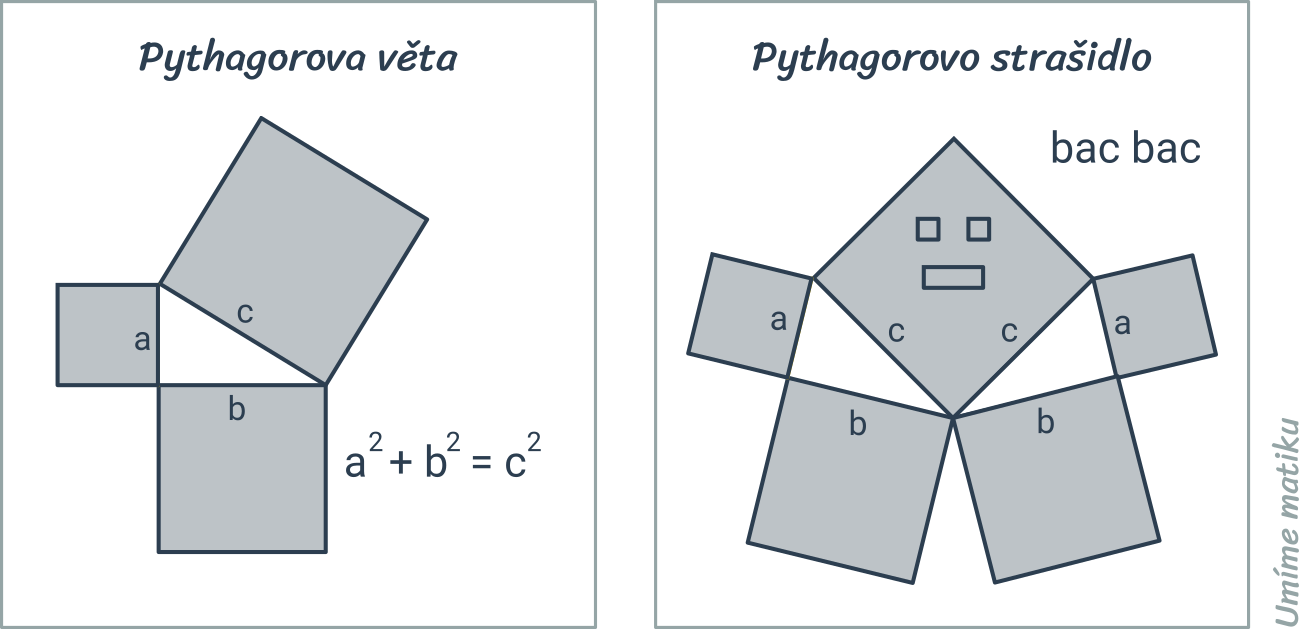
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Pythagorovu větu můžeme zapsat vztahem c^2 = a^2 + b^2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b. Platí i opačný směr: Pokud má trojúhelník strany délek a, b, c, které splňují rovnost c^2 = a^2 + b^2, pak musí jít o pravoúhlý trojúhelník s přeponou c.
Následující obrázek znázorňuje graficky znění věty a také „obrázkový důkaz“ této věty:
Procvičování Pythagorovy věty máme rozdělené do dvou podtémat:
- Základní použití – základní aplikace vzorce a^2+b^2=c^2, výpočty délky strany pravoúhlého trojúhelníku při znalosti zbylých dvou stran
- Aplikace – využití Pythagorovy věty v různých geometrických případech (např. výška trojúhelníku, uhlopříčka kvádru) a slovních úlohách
Komiks pro zpestření
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
Délka přepony c = \sqrt{a^2 + b^2}. Pokud má pravoúhlý trojúhelník odvěsny délky 3 metry a 6 metrů, přepona má délku \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6{,}41 metrů.
Délka odvěsny a = \sqrt{c^2-b^2}. Pokud má trojúhelník přeponu délky 8 metrů a jedna z odvěsen má délku 4 metry, druhá odvěsna má délku \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6{,}93 metrů.
Pythagorejské trojice jsou trojice celých čísel, které splňují a^2+b^2=c^2, tj. trojúhelník s příslušnými délkami stran je pravoúhlý. Typickým příkladem Pythagorejské trojice je (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.
Další příklady Pythagorejských trojic: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). Mezi Pythagorejské trojice patří také všechny násobky těchto trojic, např. (6, 8, 10); (9, 12, 15); (10, 24, 26). Pokud si zapamatujeme některé základní Pythagorejské trojice, především nejjednodušší trojici (3, 4, 5), tak nám to může usnadnit výpočty.
NahoruPythagorova věta: aplikace
Pythagorova věta má v geometrii velice široké využití, protože mnoho složitějších útvarů můžeme rozložit na pravoúhlé trojúhelníky.
Typickým příkladem aplikace Pythagorovy věty je výpočet délky uhlopříčky čtverce nebo výšky rovnostranného trojúhelníku:
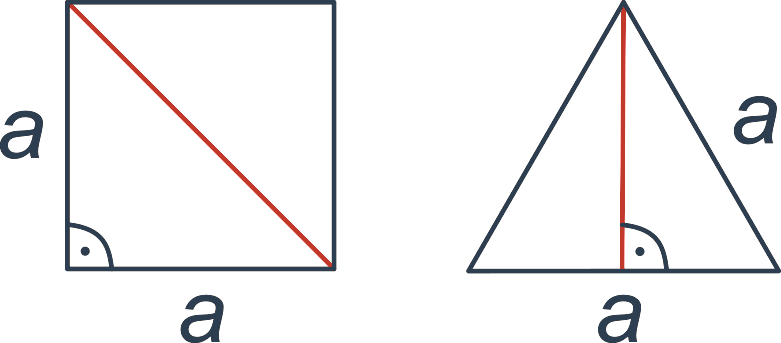
Ve čtverci o straně a tvoří uhlopříčka přeponu pravoúhlého trojúhelníku s odvěsnami délky a. Pro délku uhlopříčky u tedy platí u^2 = a^2 + a^2. Po úpravách: u = \sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}. Například čtverec o straně 10 cm tedy má uhlopříčku délky 10\cdot \sqrt{2} \doteq 14,1 cm.
V rovnostranném trojúhelníku o straně a tvoří výška odvěsnu pravoúhlého trojúhelníku s přeponou délky a a odvěsnou délky \frac{a}{2}. Pro délku výšky v tedy platí v^2 + \large(\frac{a}{2}\large)^2 = a^2. Po úpravách dostáváme v^2 = a^2 - \frac{a^2}{2^2} = \frac{3}{4}a^2, v = a\frac{\sqrt{3}}{2}. Například v rovnostranném trojúhelníku o straně 5 metrů má tedy výška délku \frac{\sqrt{3}}{2}\cdot 5 \doteq 4,33 metru.
NahoruEuklidovy věty
Euklidovy věty jsou dvě tvrzení o vlastnostech pravoúhlého trojúhelníku.
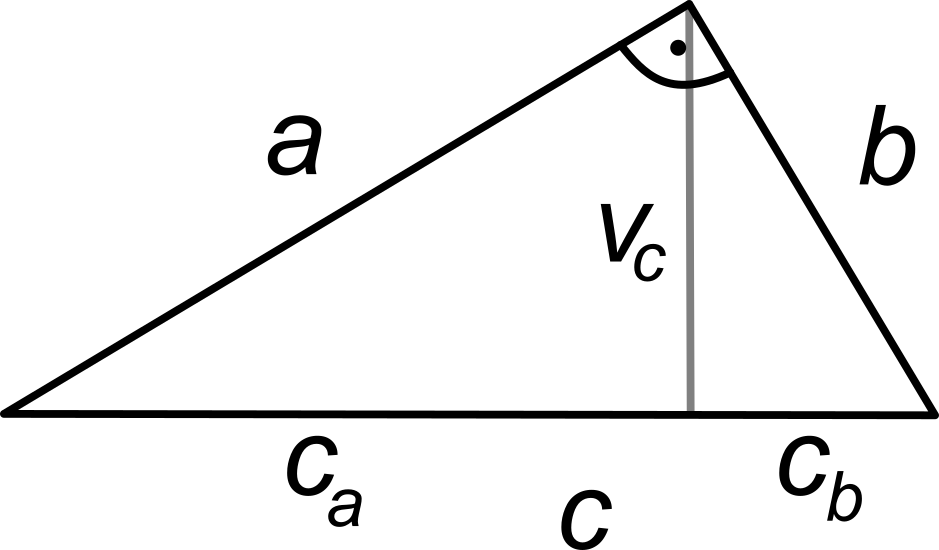
Euklidova věta o výšce
Obsah čtverce sestrojeného nad výškou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z obou úseků přepony:
v_c^2 = c_a\cdot c_b
Euklidova věta o odvěsně
Obsah čtverce sestrojeného nad odvěsnou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z přepony a úseku přepony k této odvěsně přilehlého.
- a^2 = c\cdot c_a
- b^2 = c\cdot c_b
Úhly v trojúhelníku
Při výpočtu velikosti neznámého úhlu v trojúhelníku využíváme základní vlastnosti, že součet vnitřních úhlů v trojúhelníku je 180°.
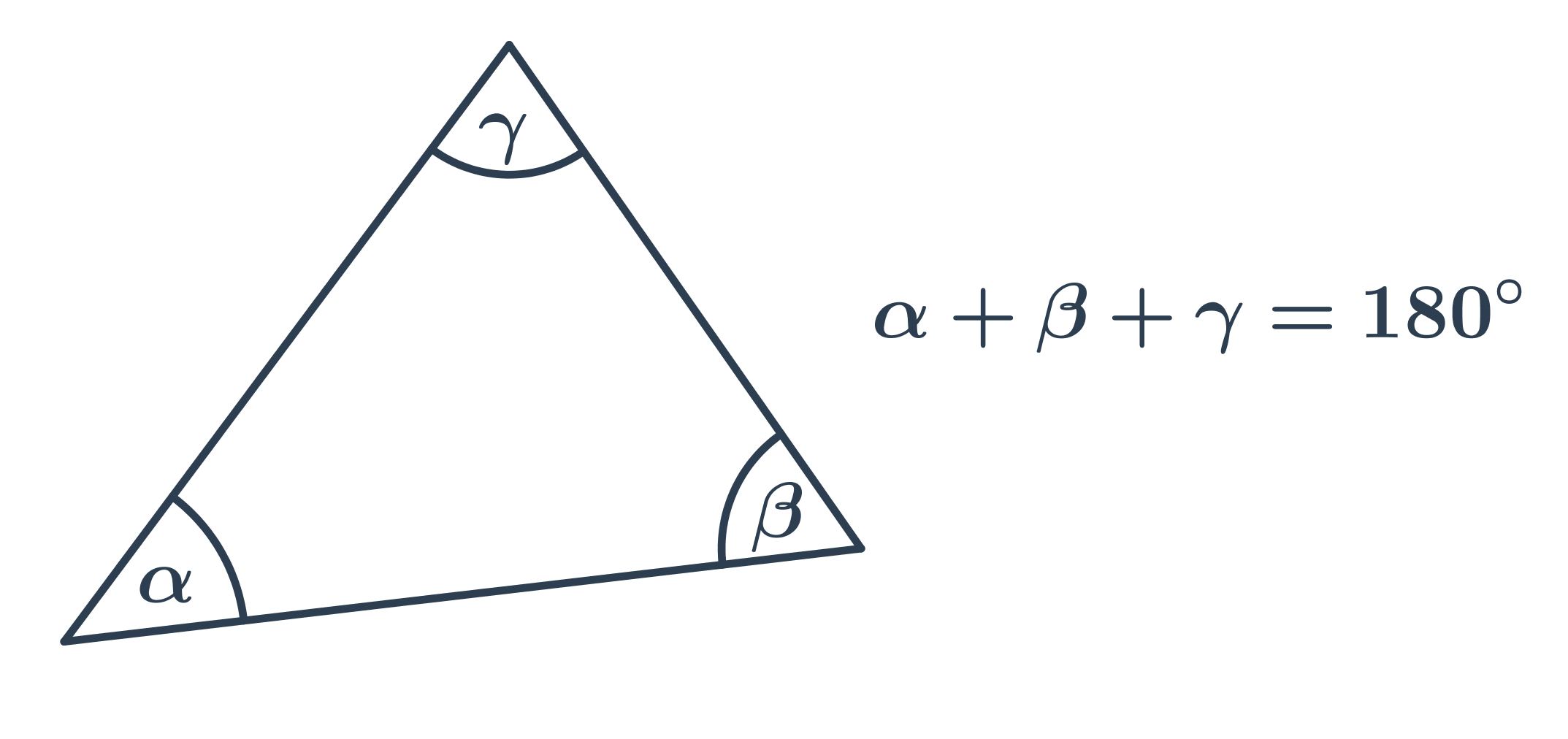
Speciální případy:
- V rovnostranném trojúhelníku mají všechny vnitřní úhly velikost 60°.
- V rovnoramenném trojúhelníku jsou oba úhly u základny stejné.
- V pravoúhlém trojúhelníku je velikost jednoho úhlu 90°, součet velikostí zbývajících dvou úhlů je také 90°.
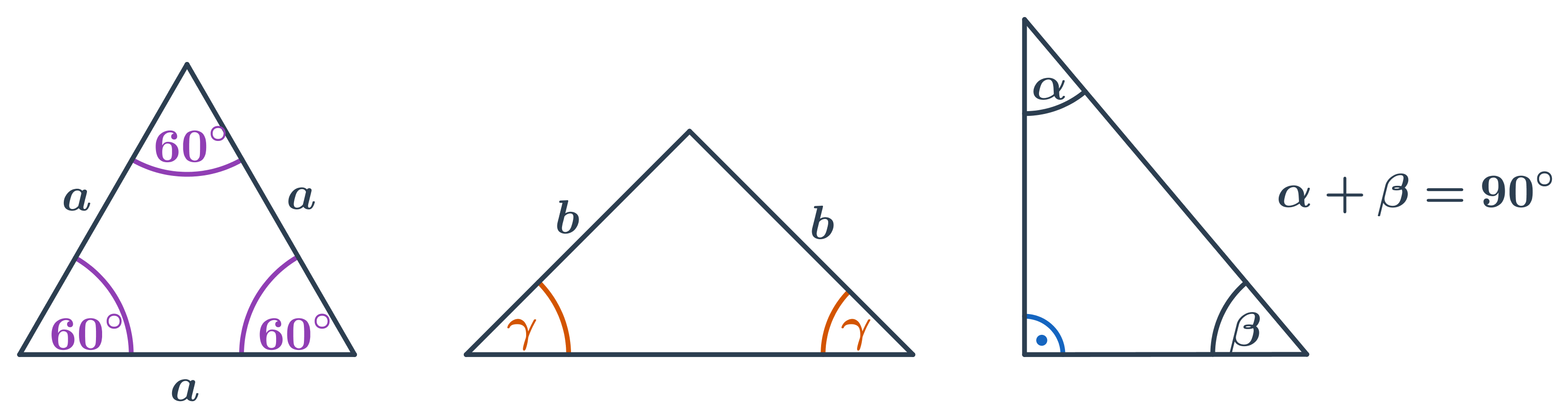
Při výpočtu lze využít i vrcholových a vedlejších úhlů.
Příklad: výpočet velikosti úhlu
Určete velikost oranžového úhlu:
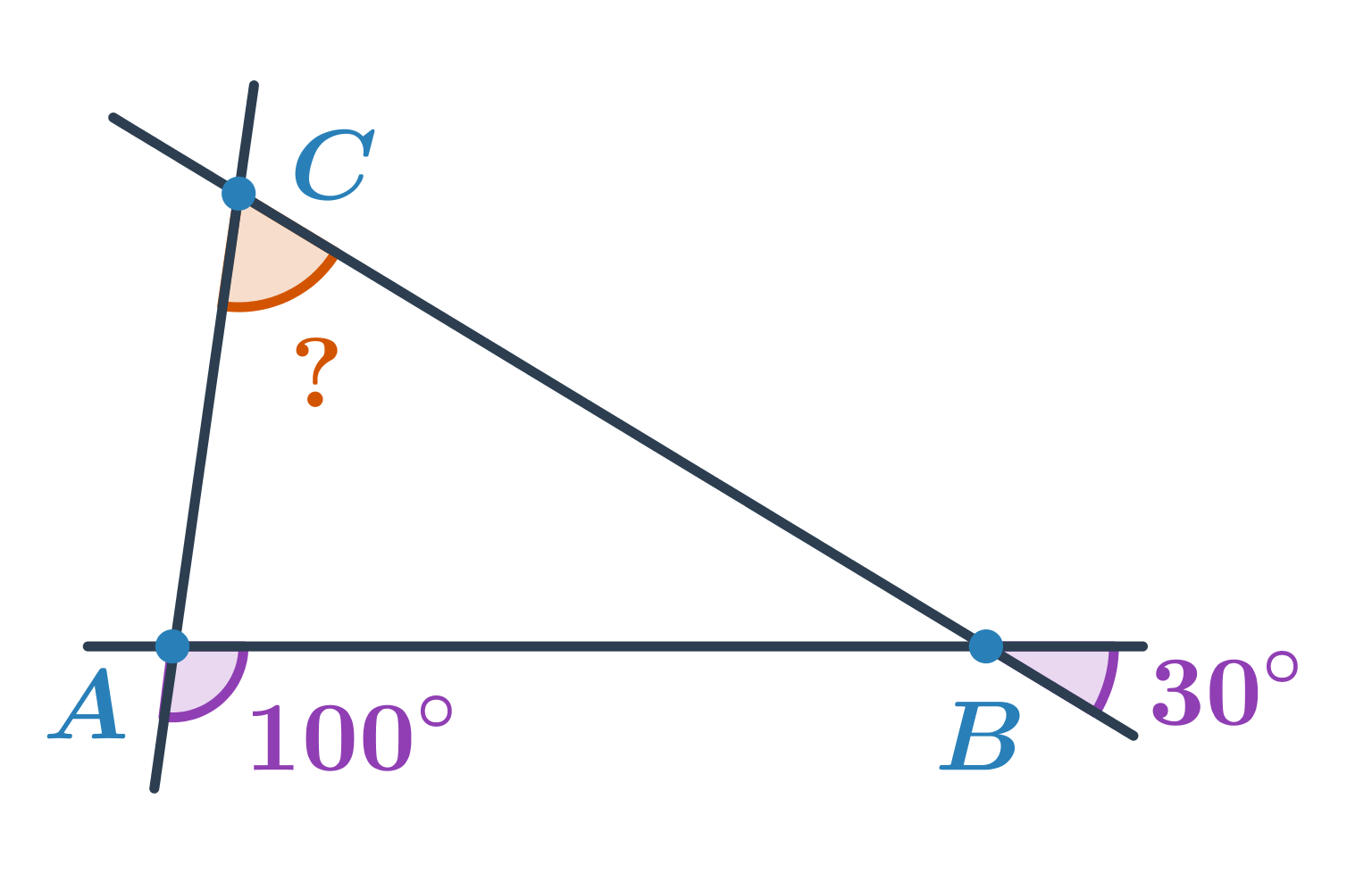
- Úhel u vrcholu B tvoří s úhlem o velikosti 30° dvojici vrcholových úhlů. Jeho velikost je tedy 30°.
- Úhel u vrcholu A tvoří s úhlem o velikosti 100° dvojici vedlejších úhlů. Jeho velikost je tedy 180°-100°=80°.
- Pro velikost neznámého úhlu u vrcholu C pak platí: 180°-80°-30°=70°
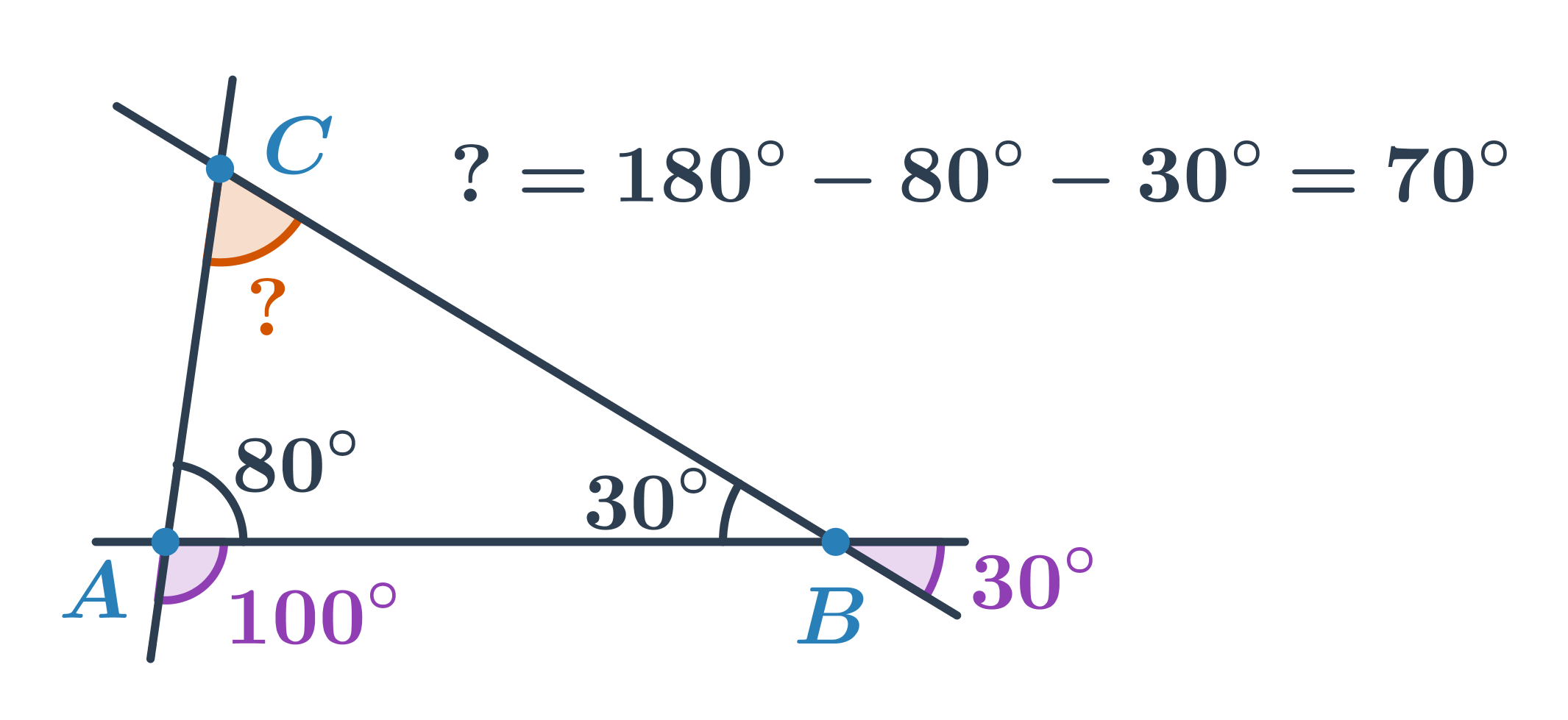
Konstrukční úlohy: trojúhelníky
Při řešení jednodušších úloh provádíme konstrukce trojúhelníků se známými délkami stran. Nesmíme přitom zapomínat, že platí tzv. trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, jedině pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
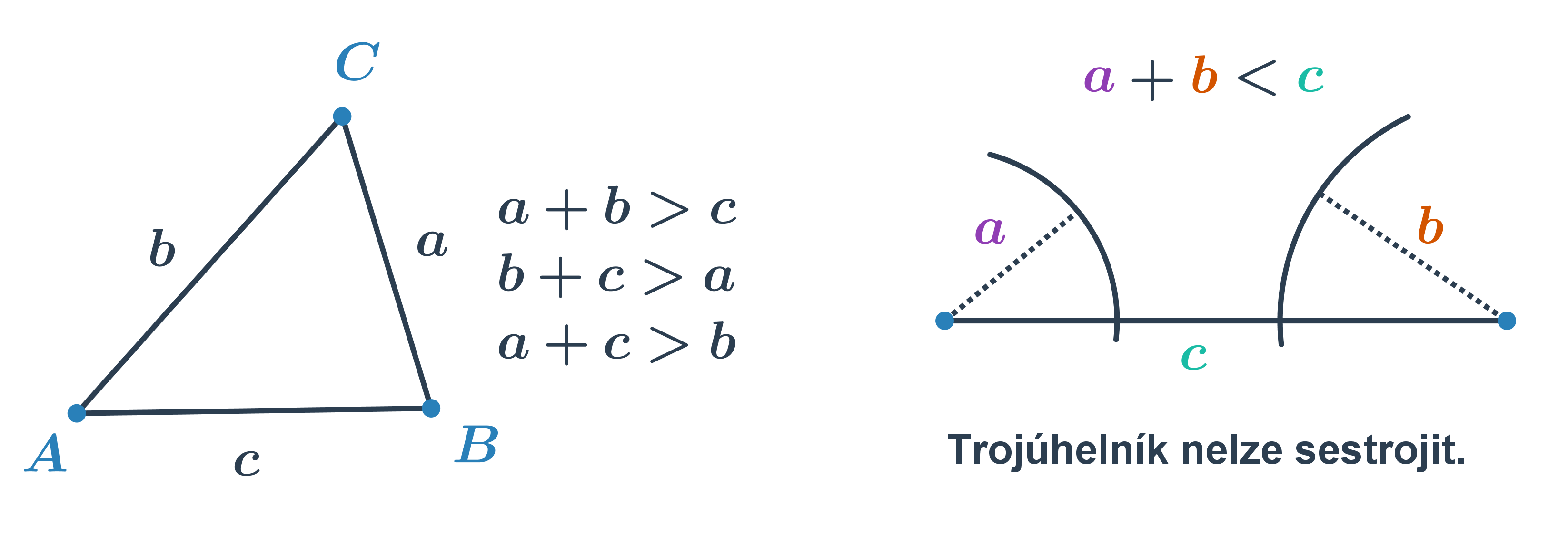
Občas má některý trojúhelník zajímavou vlastnost, která nám pomůže odvodit si potřebné informace k jeho sestrojení — může jít např. o konstrukci rovnoramenného nebo rovnostranného trojúhelníku.
Při řešení složitějších příkladů provádíme konstrukci trojúhelníků podle vět sss, sus, usu, Ssu, využíváme přitom známé věty o sestrojitelnosti trojúhelníků.
U nejtěžších příkladů, jako je konstrukce trojúhelníků, kdy známé údaje zahrnují těžnice, výšky, opsanou nebo vepsanou kružnici trojúhelníka využíváme při konstrukci další pojmy související s trojúhelníkem, či množiny bodů daných vlastností.
NahoruKonstrukce trojúhelníků: známé délky stran
Při konstrukci trojúhelníků můžeme každou stranu označit dvěma způsoby:
- přímo – strana a
- pomocí vrcholů – strana BC
Při konstrukcích také můžeme zaměňovat označení strany a její délky. Můžeme psát a=|BC|. Je třeba myslet i na pravidlo, že strana je pojmenovaná podle protějšího vrcholu.
Příklad: Je v trojúhelníku na obrázku délka strany a=8 cm?
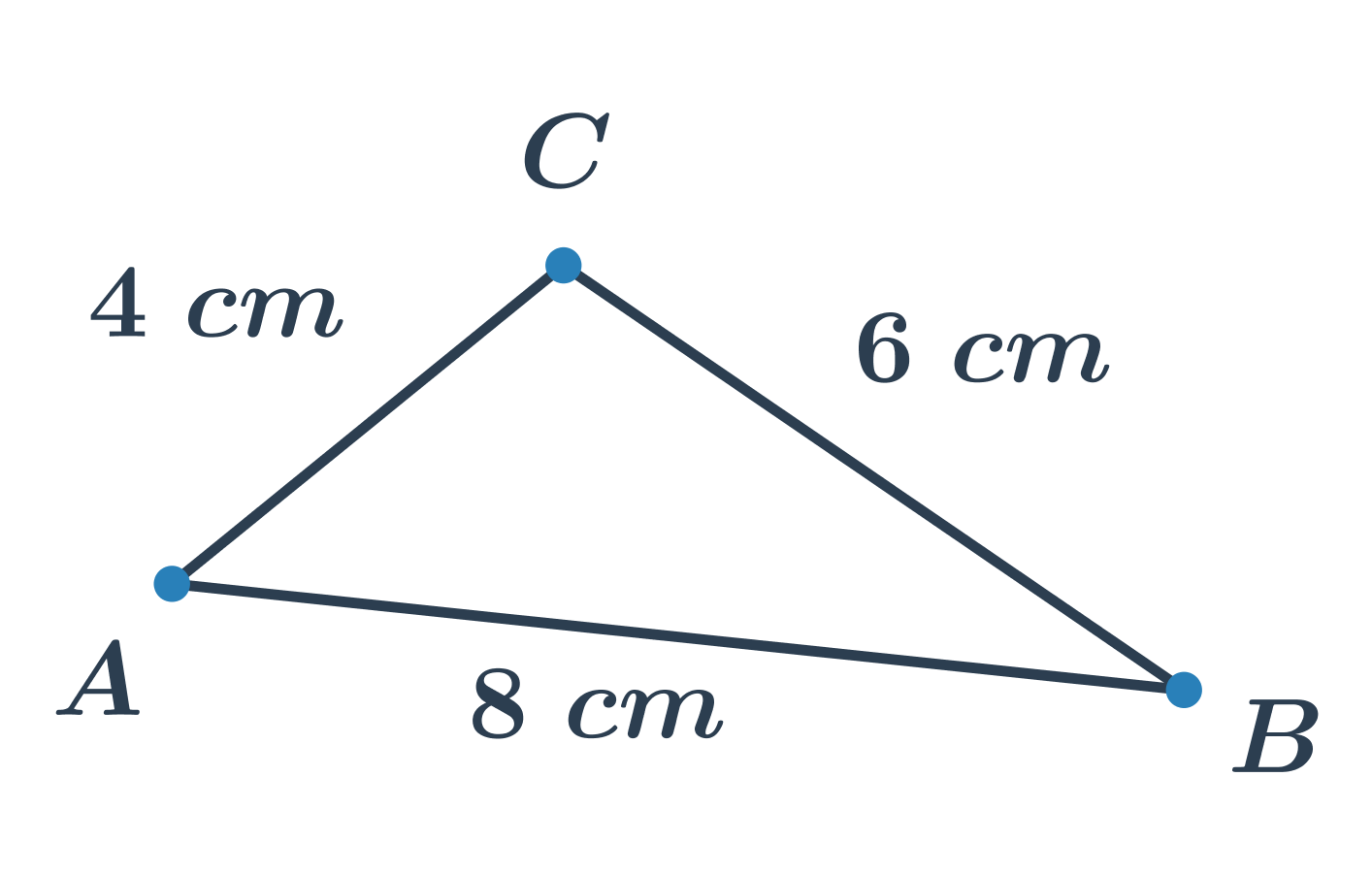
- Strana a leží proti vrcholu A. Je to tedy strana BC.
- Z obrázku vidíme, že |BC|=6 cm.
- Strana a tedy nemá délku 8 cm.
- Délku 8 cm má v tomto trojúhelníku strana AB, tedy strana c.
Lze sestrojit trojúhelník se stranami zadané délky?
- 6\ \text{cm}, 5\ \text{cm}, 4\ \text{cm} - součet dvou nejkratších stran je 4 + 5= 9 \ \text{cm}, to je více než 6\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.
- 6\ \text{cm}, 5\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 5 = 6\ \text{cm}, to je rovno délce třetí strany, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
- 5\ \text{cm}, 2\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 2 = 3\ \text{cm}, to je menší než délka třetí strany 5\ \text{cm}, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
- 7\ \text{cm}, 7\ \text{cm}, 7\ \text{cm} - součet dvou nejkratších stran je 7 + 7= 14\ \text{cm}, to je více než 7\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.
Při konstrukcích trojúhelníků, u kterých známe tři strany, postupujeme tak, že sestrojíme jako první libovolnou stranu, na obrázku například AB. K nalezení posledního vrcholu C použijeme dvě kružnice nebo jejich části. Výsledkem konstrukce jsou dva shodné (stejné) trojúhelníky, proto stačí sestrojit jen jeden.
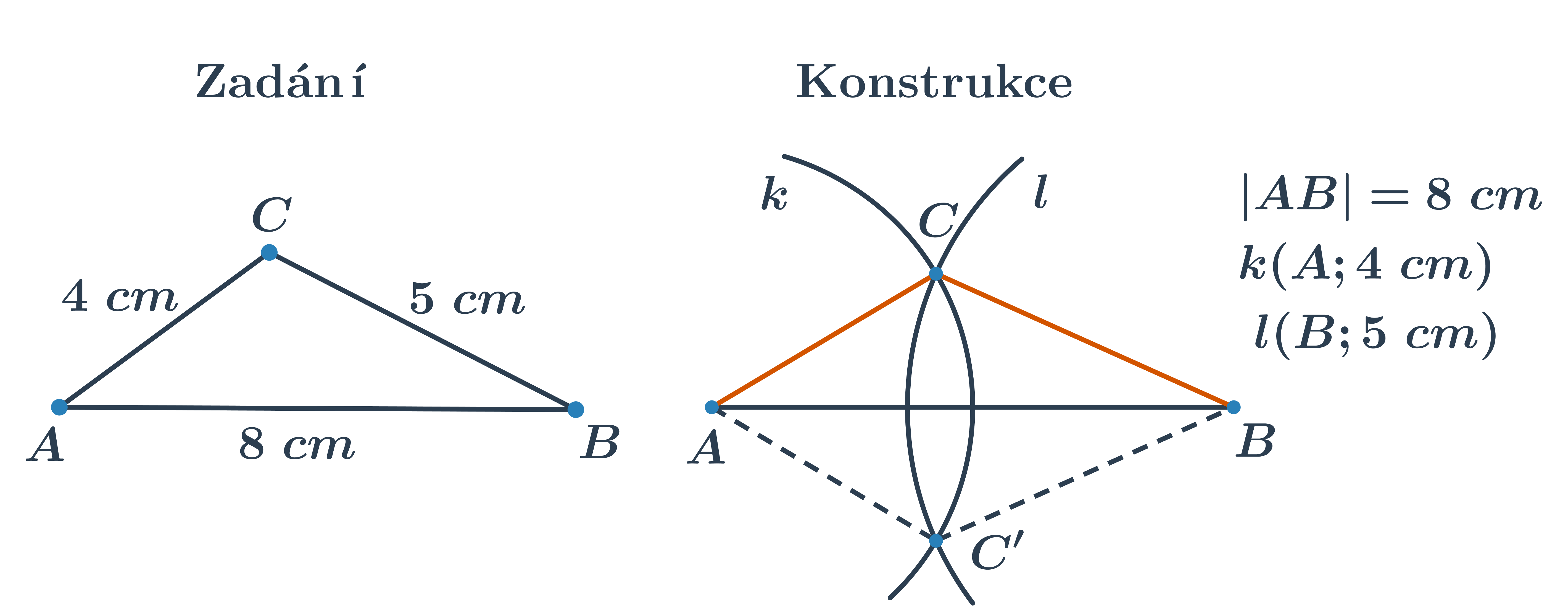
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
Při konstrukci rovnoramenného trojúhelníku využíváme jeho základní vlastnosti:
- Má dvě strany (ramena) shodné. Vrchol proti základně tedy leží na ose základny.
- Shodné (stejně velké) jsou i vnitřní úhly při základně.
- Výška kolmá na základnu leží na ose základny a dělí rovnoramenný trojúhelník na dva shodné trojúhelníky.
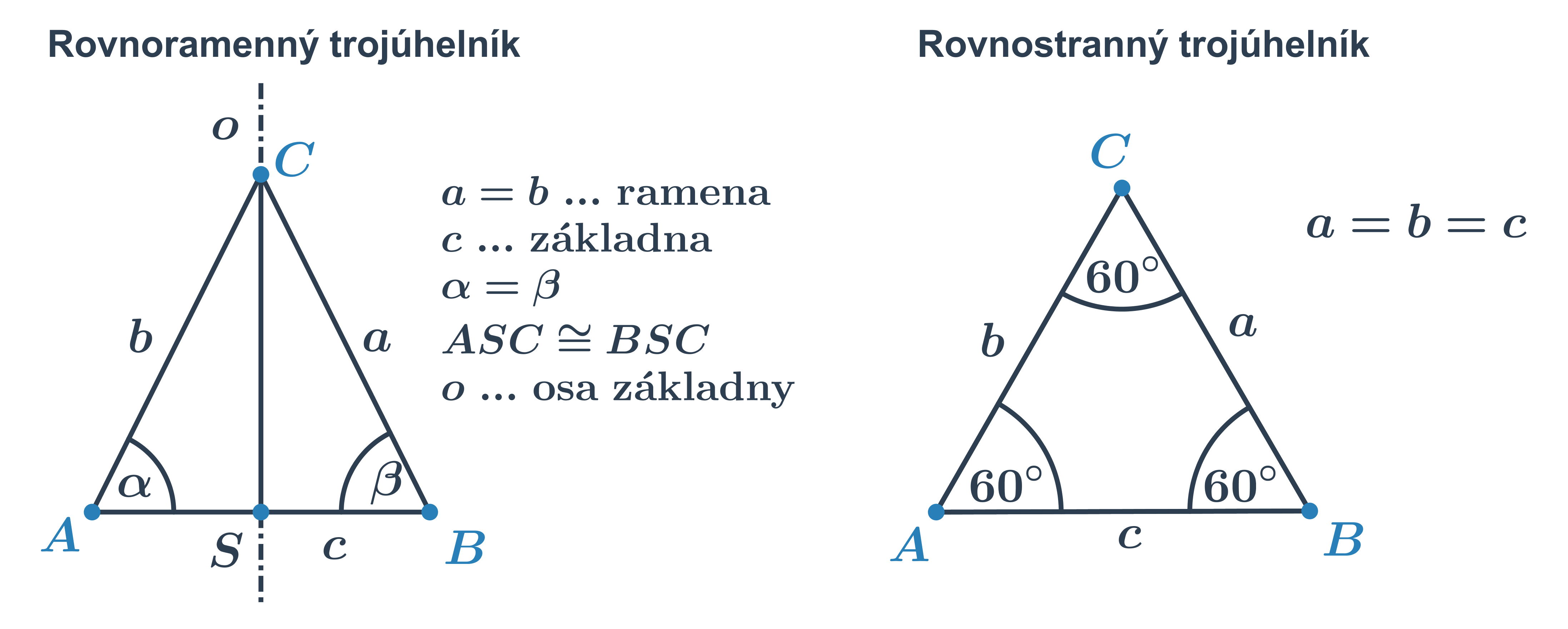
Rovnostranný trojúhelník můžeme chápat jako speciální případ rovnoramenného trojúhelníka. Má všechny strany stejně dlouhé a velikost všech jeho vnitřních úhlů je 60°.
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: věty sss, sus, usu, Ssu
Při složitějších příkladech využíváme věty o sestrojitelnosti trojúhelníků (kde s značí stranu a u úhel):
- Věta sss — v trojúhelníku jsou dány délky všech stran, pro které platí trojúhelníková nerovnost.
- Věta sus— v trojúhelníku jsou dány délky dvou stran a velikost úhlu, který svírají (menší než 180°).
- Věta usu — v trojúhelníku je dána délka jedné strany a velikosti 2 úhly k ní přiléhající (součet velikostí daných úhlů je menší než 180°).
- Věta Ssu — známe velikosti dvou stran trojúhelníka a velikost úhlu proti větší z těchto stran (velikost zadaného úhlu je menší než 180°).

Tyto věty také používáme při určení shodnosti trojúhelníků.
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
Při řešení složitějších příkladů použijeme další pojmy související s trojúhelníkem, například výška, těžnice, střední příčka, kružnice opsaná či vepsaná.
Těžnice je úsečka, která spojuje vrchol trojúhelníku se středem protější strany. Každý trojúhelník má tři těžnice a jejich průsečík tvoří těžiště trojúhelníku. Těžiště rozděluje každou těžnici v poměru 2 : 1. Delší část těžnice je úsečka mezi vrcholem a těžištěm.
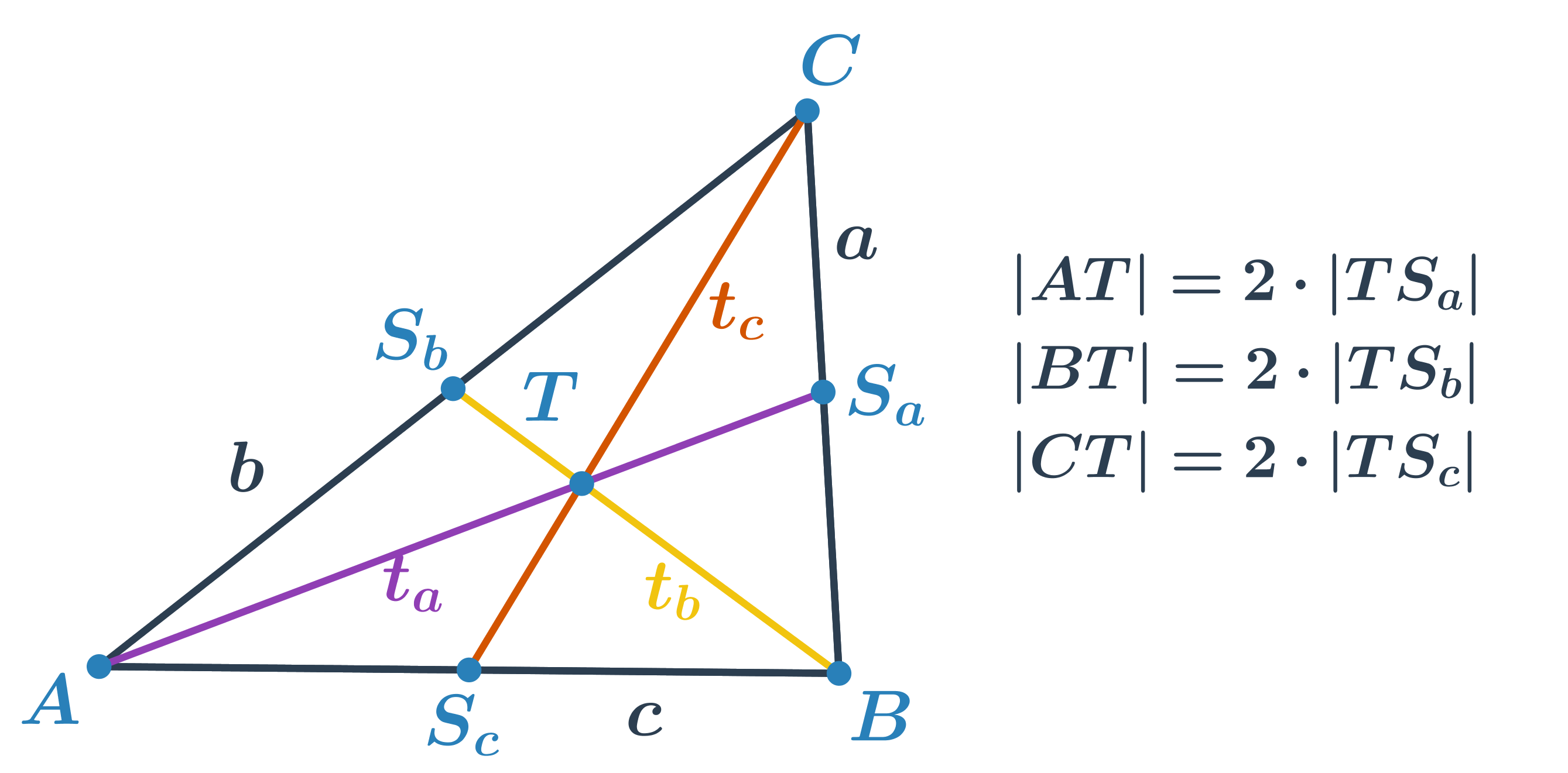
Střední příčka trojúhelníku je úsečka, která spojuje středy dvou stran v trojúhelníku. Je rovnoběžná se stranou, jejíž střed nespojuje a její délka je rovna polovině délky této strany.
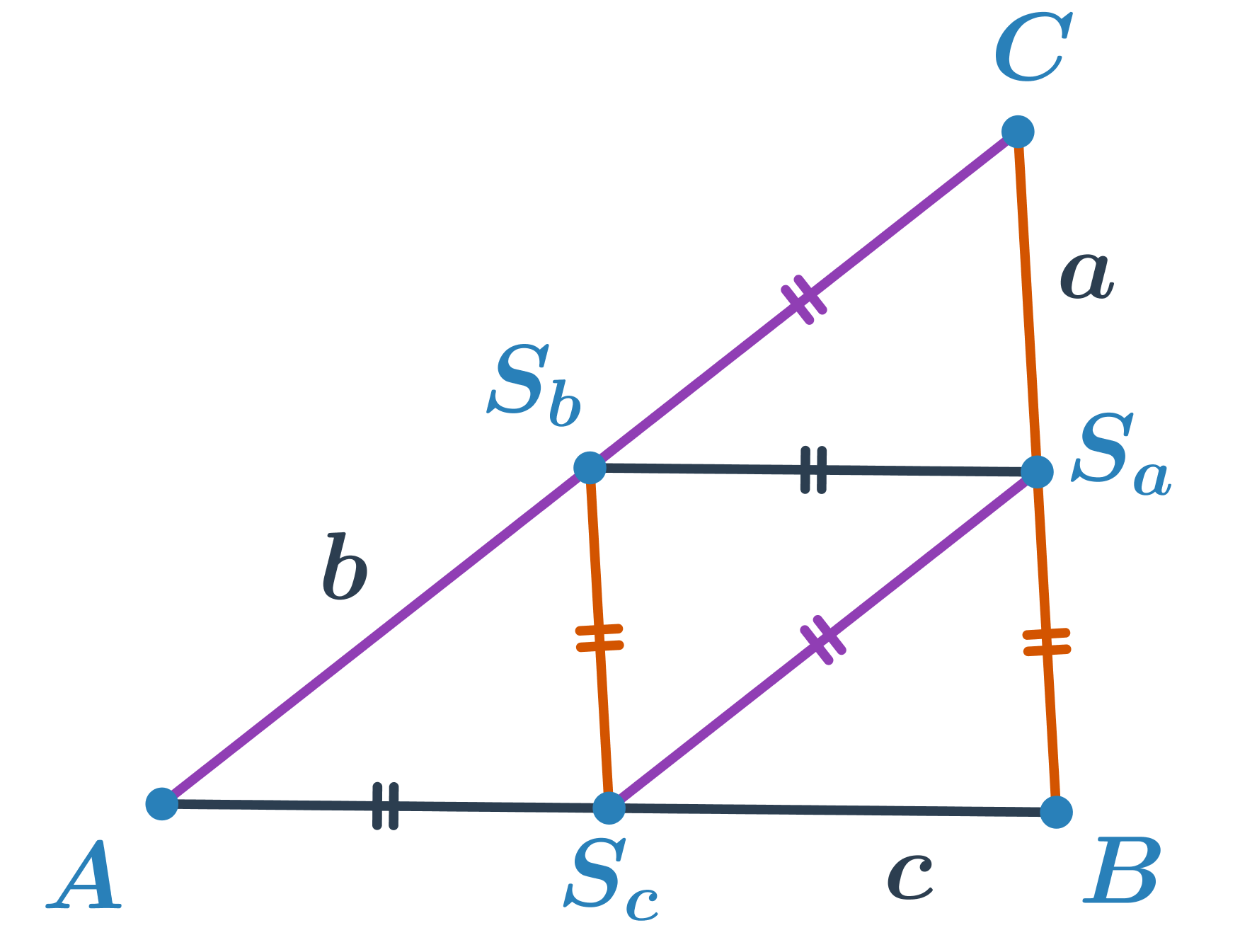
Kružnice opsaná je kružnice, která prochází všemi vrcholy trojúhelníka. Její střed leží v průsečíku os stran. To znamená, že střed kružnice opsané je stejně vzdálen od všech vrcholů trojúhelníku.
Kružnice vepsaná je kružnice, která se dotýká všech stran trojúhelníku. Její střed leží v průsečíku os vnitřních úhlů trojúhelníku. To znamená, že střed kružnice vepsané je stejně vzdálen od všech tří přímek, na kterých leží strany trojúhelníku.
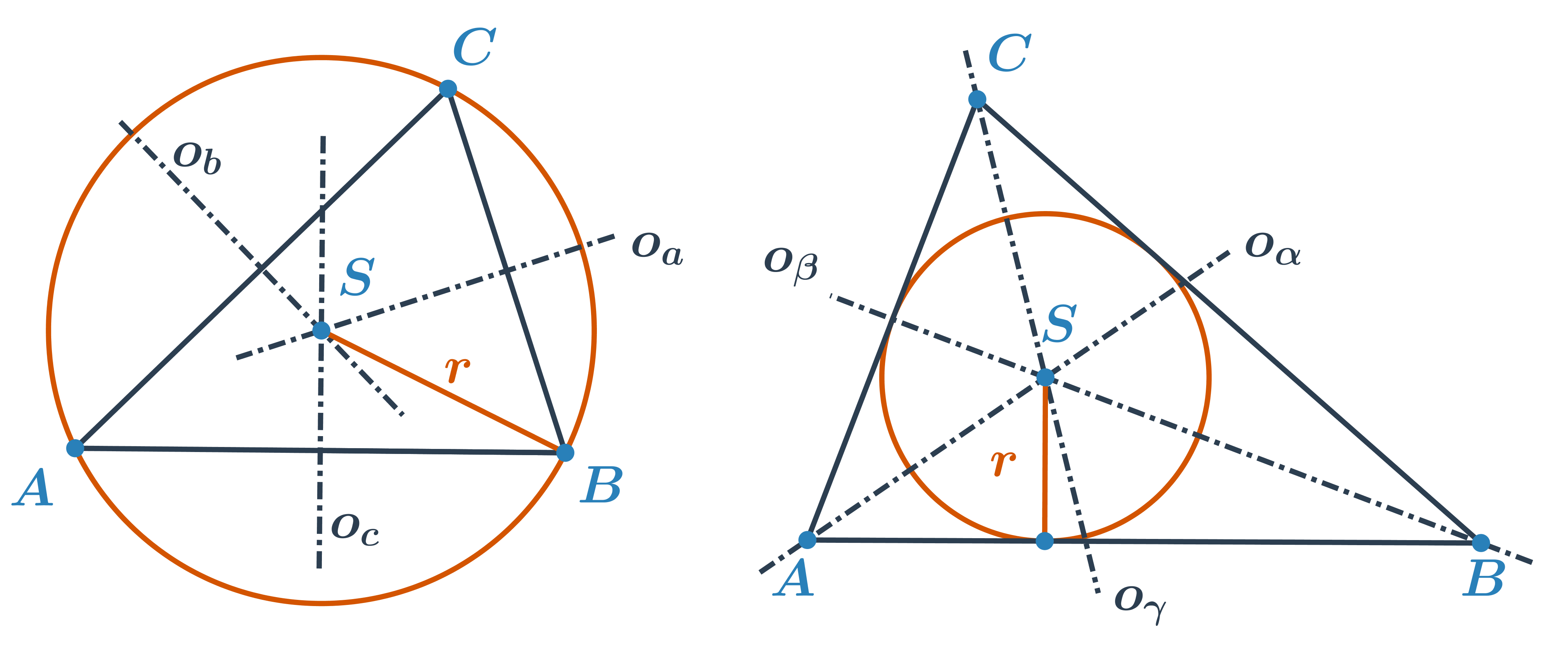
Kromě níže uvedených interaktivních cvičení jsou k dispozici také pracovní listy k vytištění a rýsování na papíře:
NahoruČtverec a obdélník
Obdélník patří mezi čtyřúhelníky. Je to rovnoběžník, který má všechny vnitřní úhly pravé.
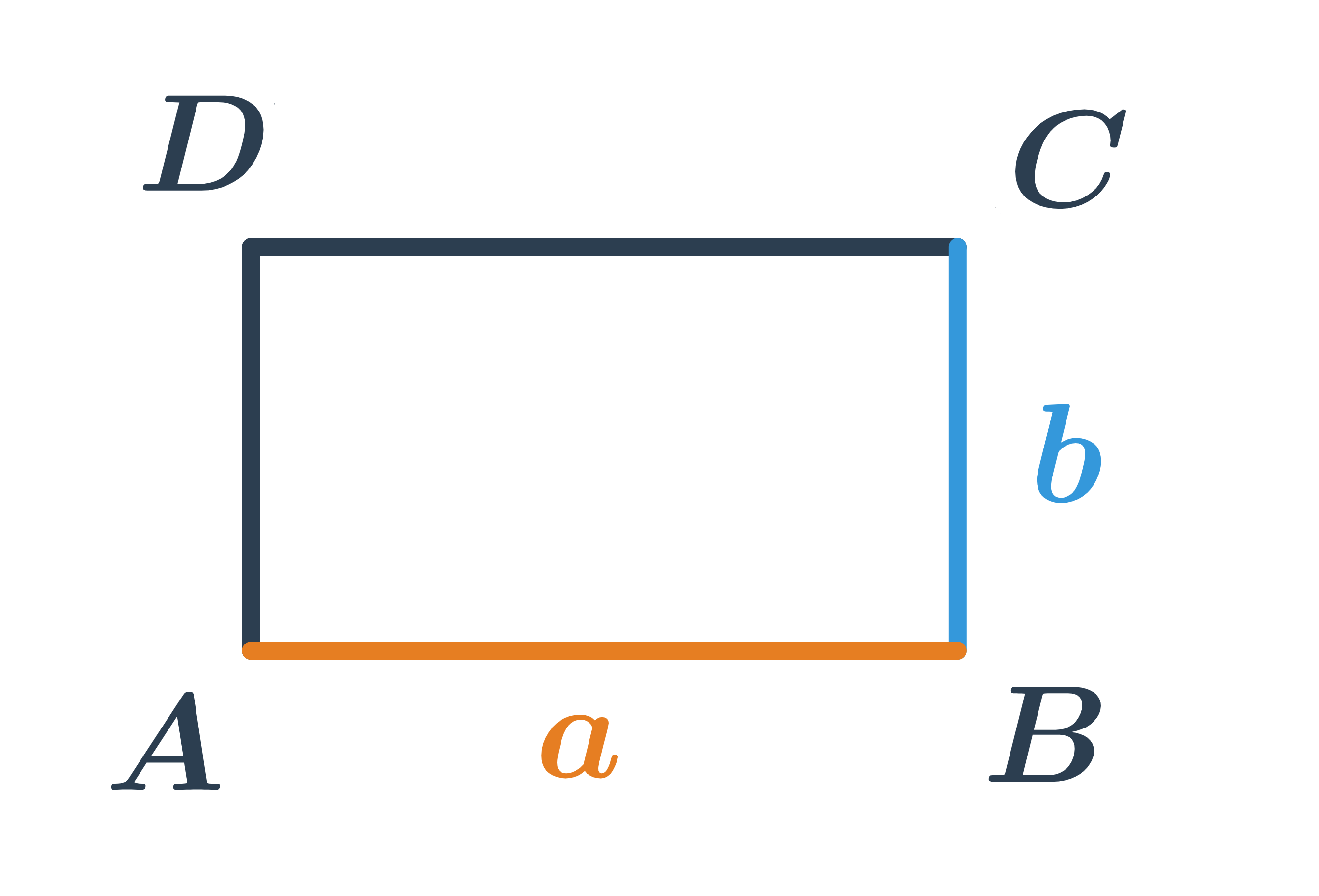
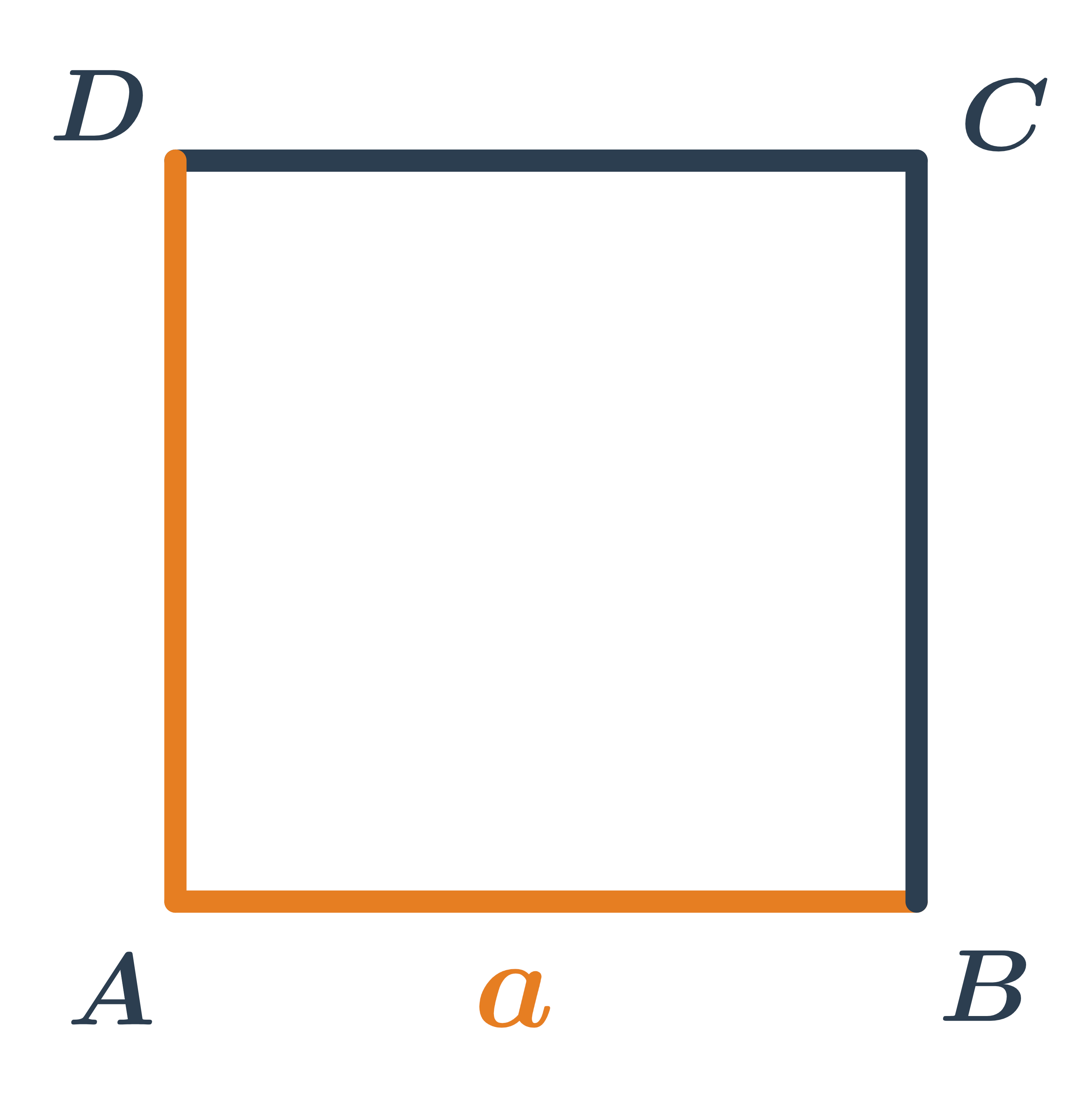
Čtverec je zvláštní případ obdélníku, který má všechny strany stejně dlouhé.
Obvod čtverce a obdélníku
Obvod čtverce o straně délky a je o=a+ a+a+a= 4a.
Obvod obdélníku se stranami o délkách a,b je roven o=a + b + a + b = 2\cdot (a+b).
NahoruObsah čtverce a obdélníku
Obsah čtverce o straně délky a je S=a\cdot a=a^2.
Obsah obdélníku se stranami o délkách a,b je roven S=a\cdot b.
NahoruRovnoběžník
Rovnoběžník je čtyřúhelník, jehož protilehlé strany jsou rovnoběžné. Dříve se označoval také jako kosodélník.
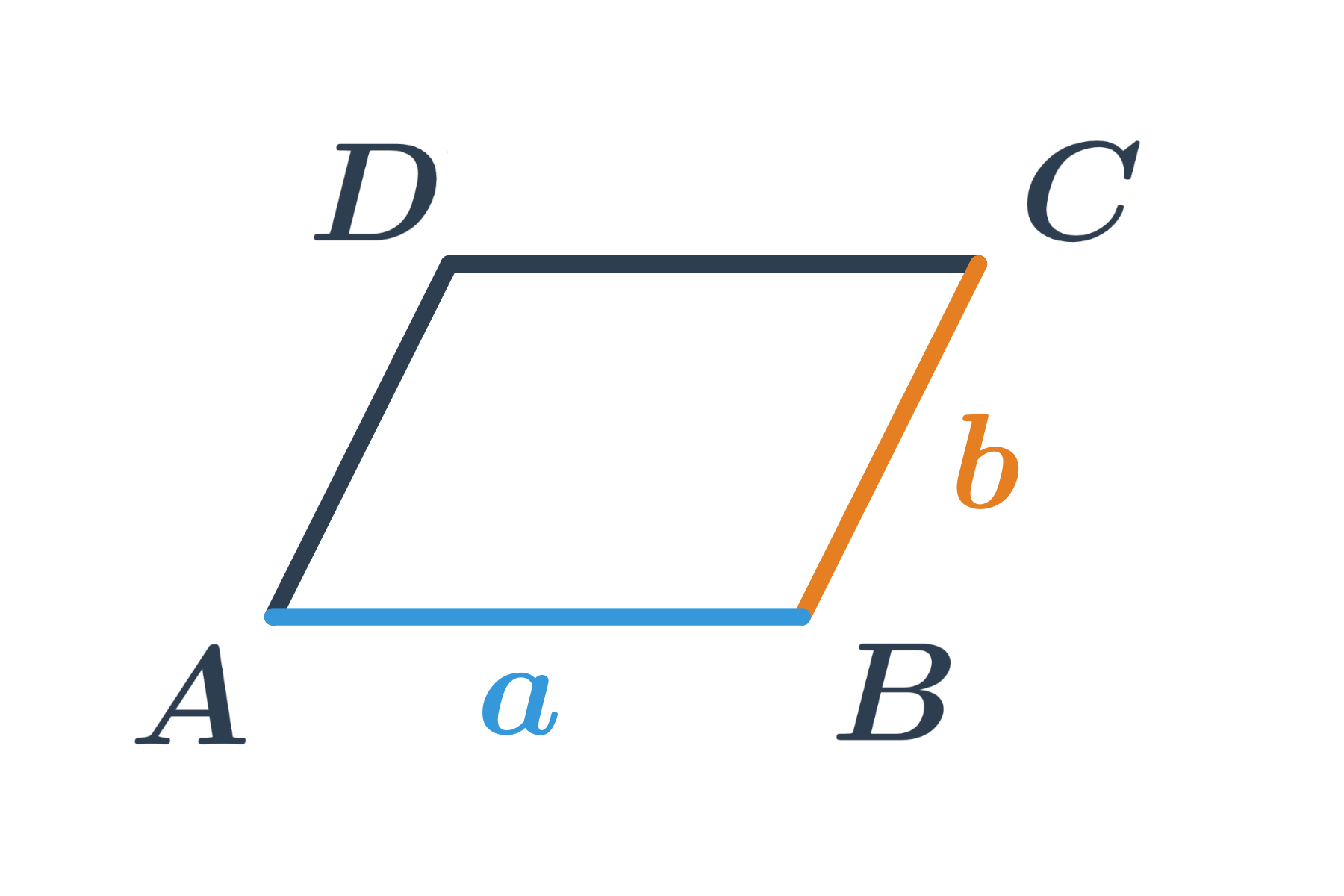
Speciální případy rovnoběžníku:
- Kosočtverec má všechny strany stejně dlouhé.
- Obdélník má vnitřní úhly pravé.
- Čtverec má vnitřní úhly pravé a všechny strany stejně dlouhé.
Obvod rovnoběžníku
Obvod rovnoběžníku se stranami o délkách a,b je roven S=a + b + a + b = 2\cdot (a+b).
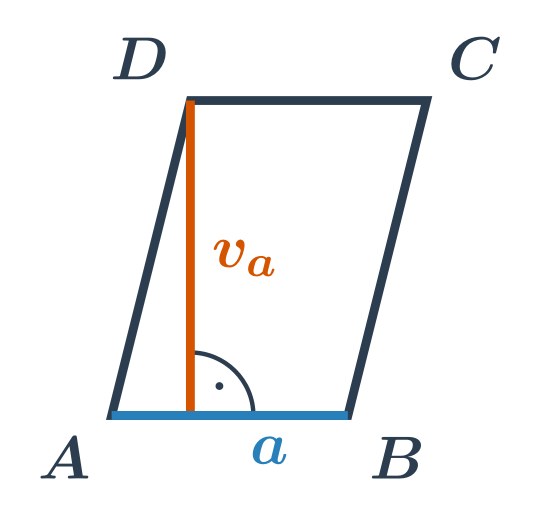
NahoruObsah rovnoběžníku
Obsah rovnoběžníku je roven součinu délky strany a k ní příslušné výšky. Tedy obsah rovnoběžníku ABCD, ve kterém ke straně o délce a přísluší výška v_a spočítáme jako S= a\cdot v_a.
Lichoběžník
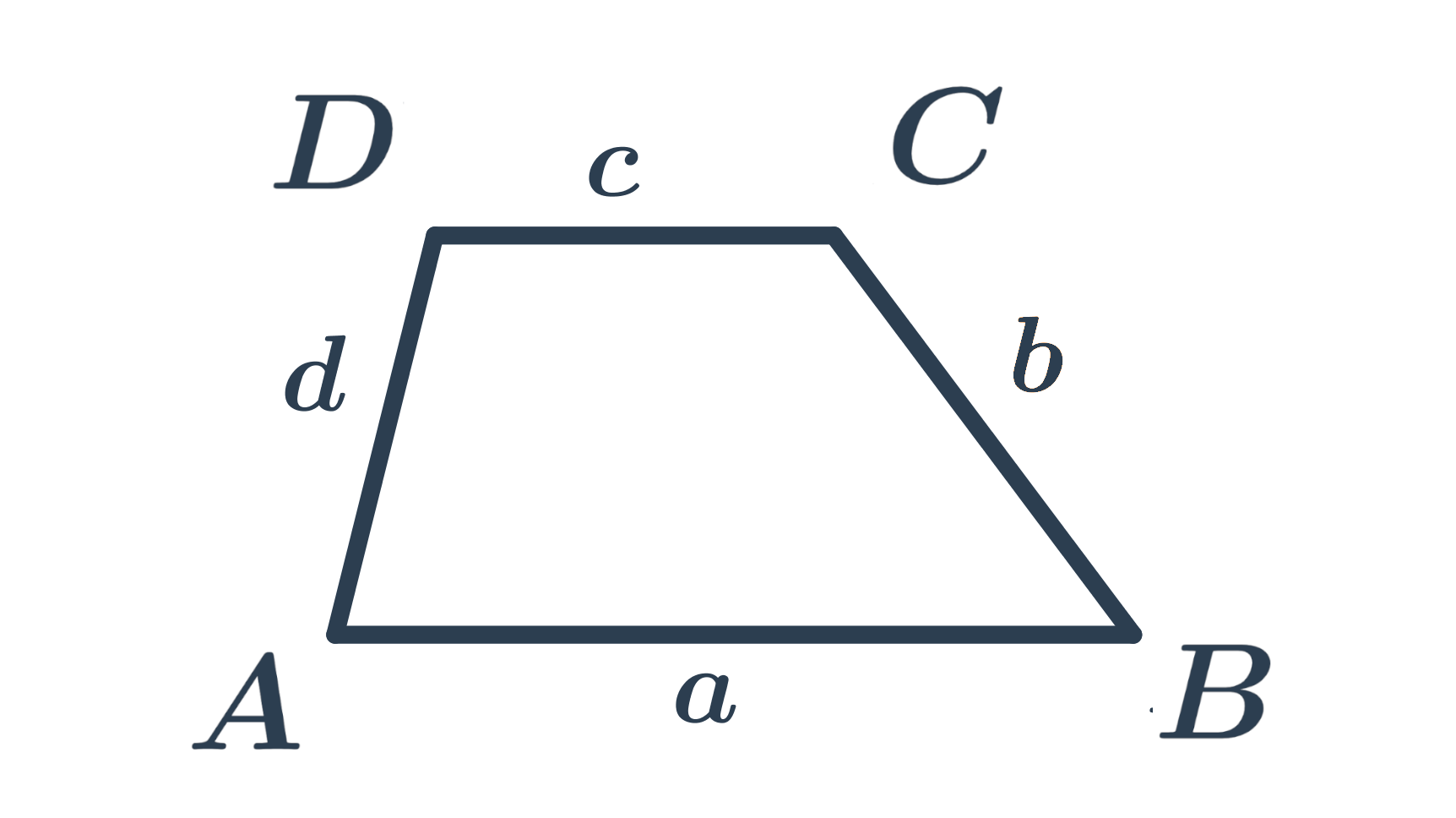
Lichoběžník je čtyřúhelník, jehož dvě protější strany jsou rovnoběžné (říkáme jim základny) a zbývající dvě protější strany jsou různoběžné.
Pravoúhlý lichoběžník má dva z vnitřních úhlů pravé (základny lichoběžníku jsou rovnoběžné, je‑li jeden vnitřní úhel pravý, musí být jeho doplněk do 180° u druhé základny také pravý).
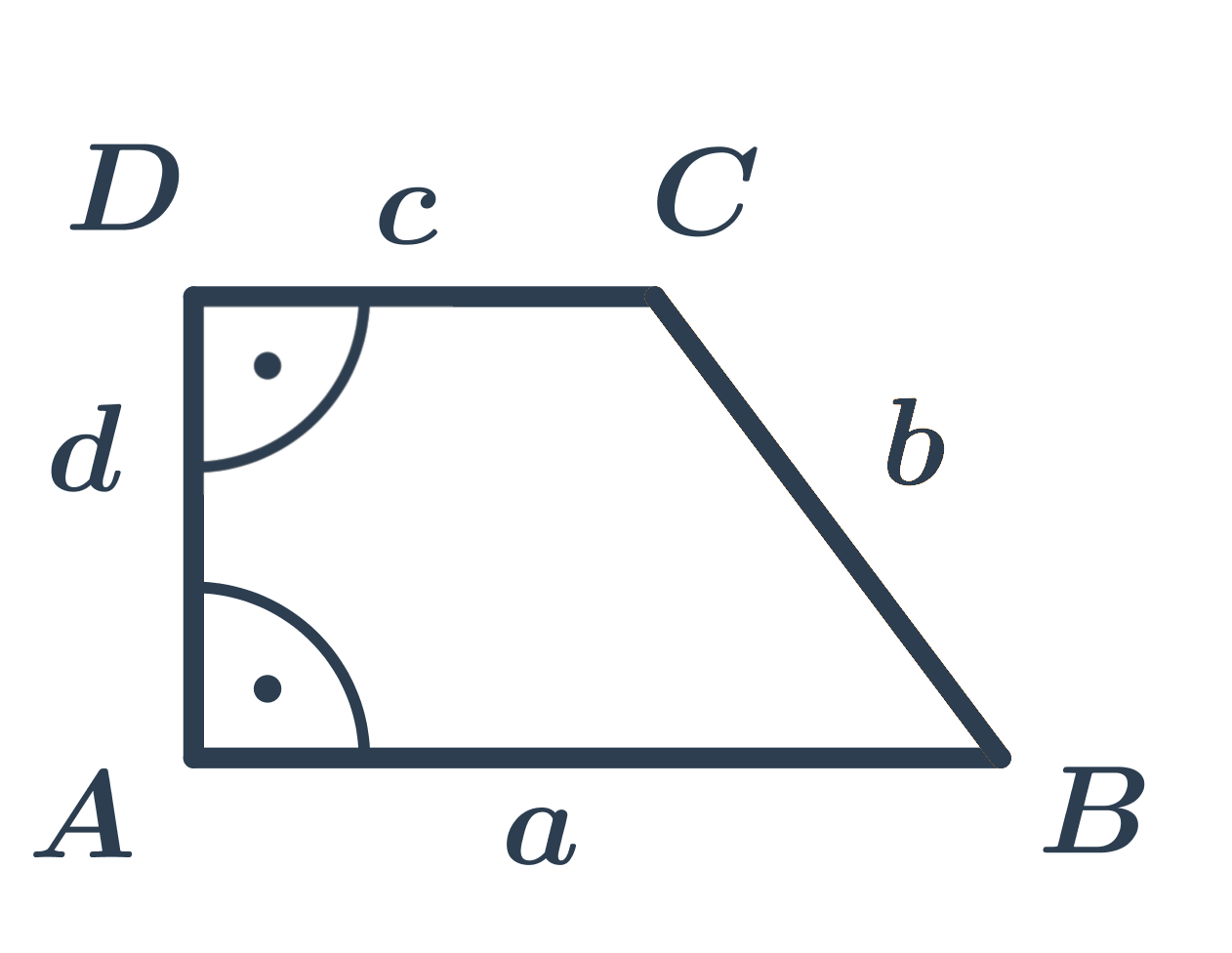
Rovnoramenný lichoběžník má ramena stejné délky.
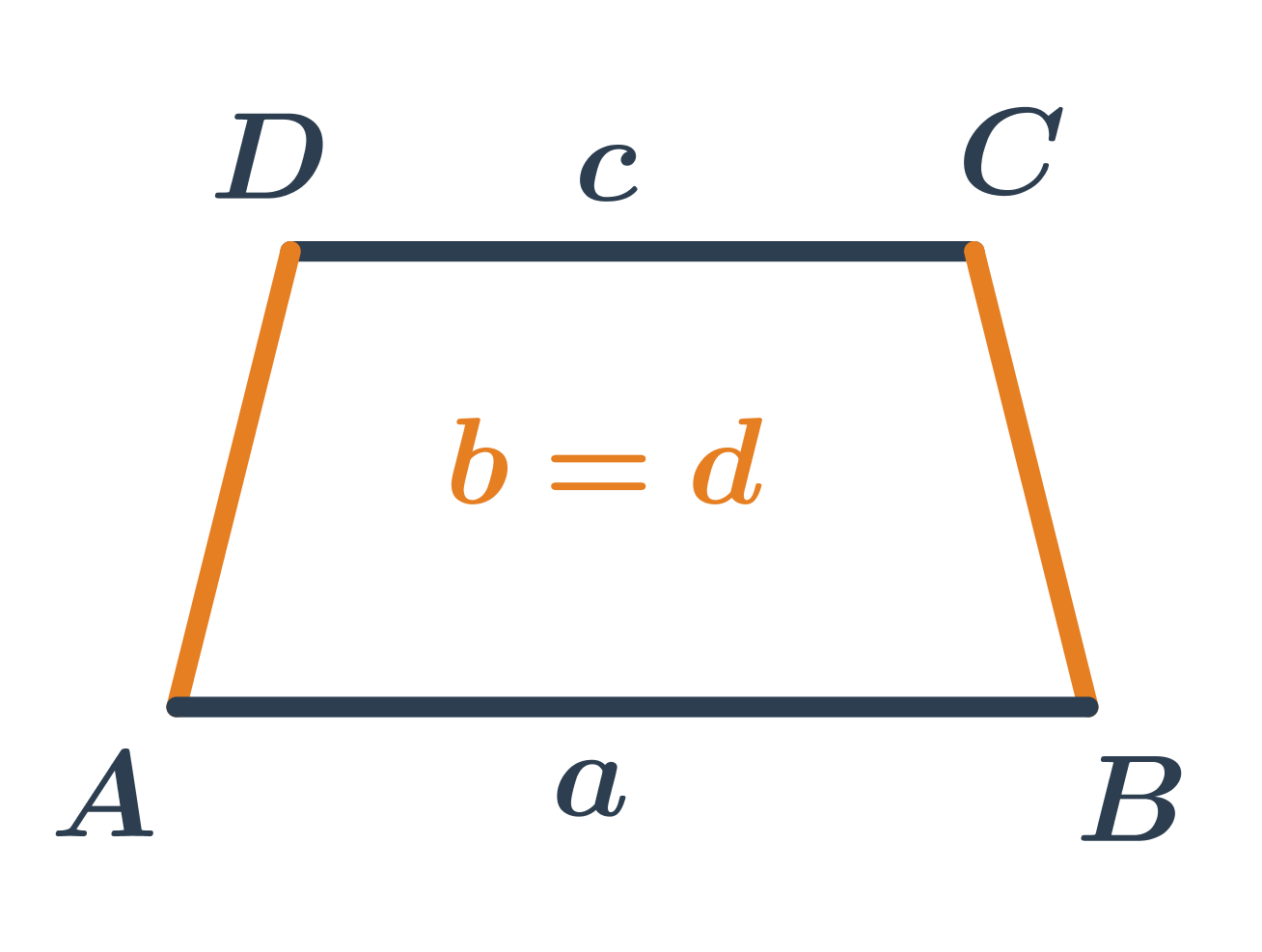
Obvod lichoběžníku
Obvod lichoběžníku je součet délek jeho stran. Tedy obvod lichoběžníku ABCD se stranami o délkách a,b,c,d vypočítáme podle vzorečku o=a+b+c+d.

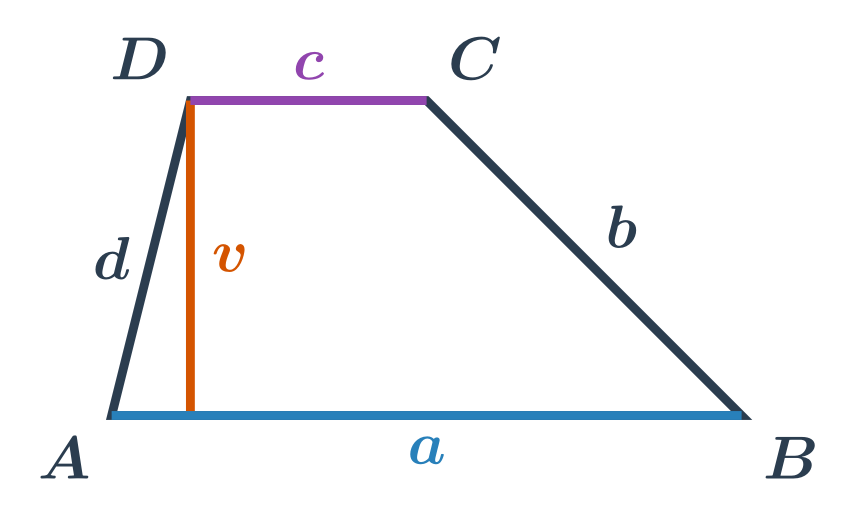
Obsah lichoběžníku
Obsah lichoběžníku se základnami o délkách a,c a výškou v spočítáme podle vzorečku S=\frac{1}{2} \cdot (a+c) \cdot v.
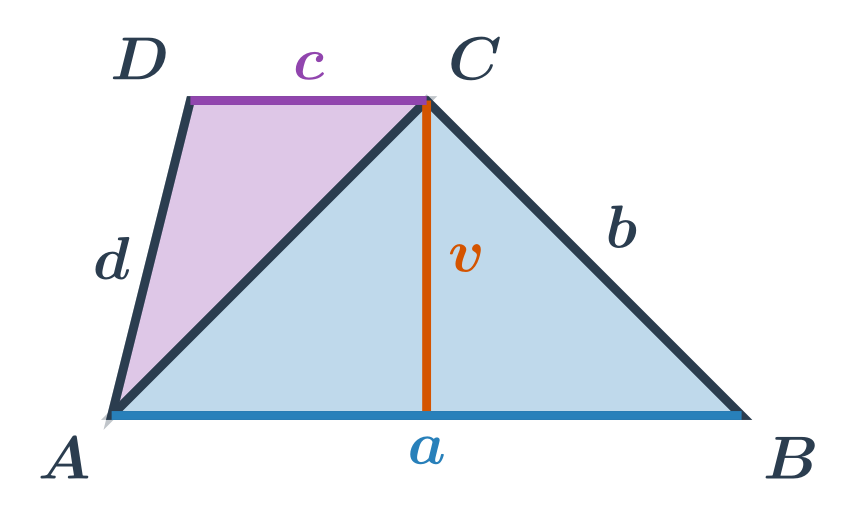
Intuice za tímto vzorečkem je vidět na následujícím obrázku. Obsah lichoběžníku je roven součtu obsahů dvou trojúhelníků.
- První trojúhelník má výšku v příslušnou ke straně délky a. Jeho obsah je S_{ABC}=\frac{1}{2} \cdot a \cdot v.
- Druhý trojúhelník má výšku v příslušnou ke straně délky c. Jeho obsah je S_{ACD}=\frac{1}{2} \cdot c \cdot v.
Součet obsahů těchto dvou trojúhelníků je S = S_{ABC} + S_{ACD} = \frac{1}{2} \cdot a \cdot v + \frac{1}{2} \cdot c \cdot v = \frac{1}{2} \cdot (a+c) \cdot v
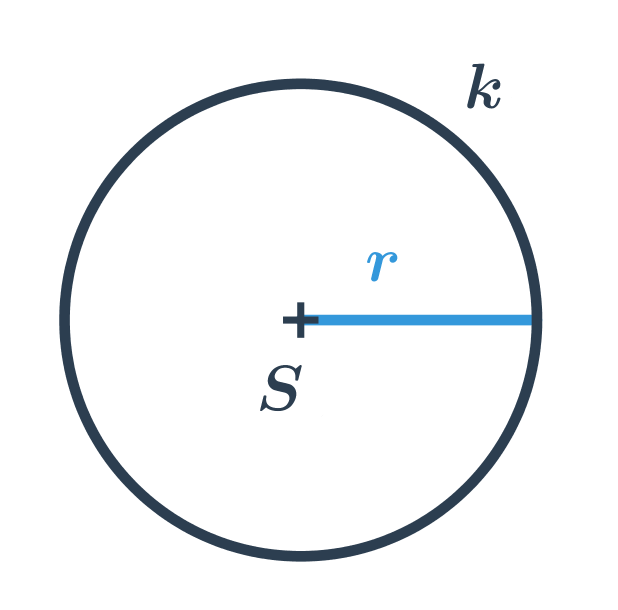
Kruh a kružnice
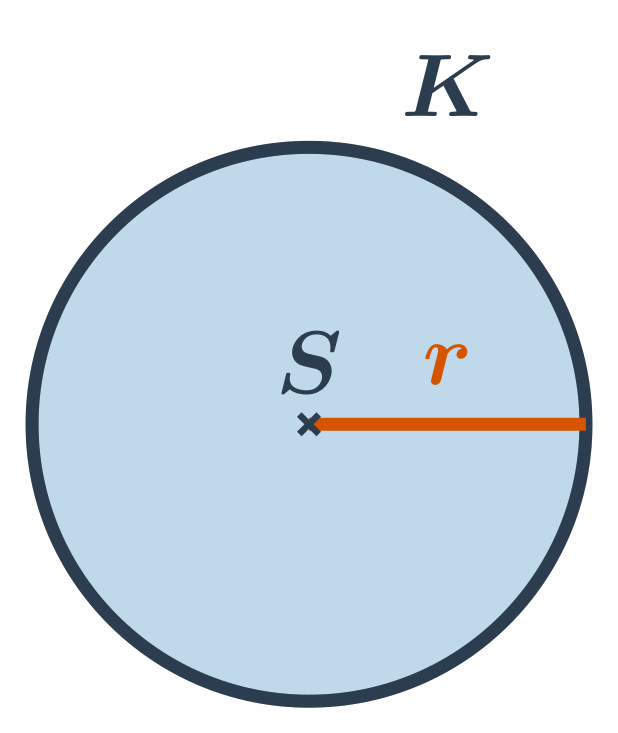
Kružnice s daným středem S a poloměrem r je tvořena všemi body v rovině, které jsou od středu vzdáleny přesně o r. U každého bodu v rovině pak můžeme určit, kde leží:
- na kružnici (jejich vzdálenost od S je rovna r)
- ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici)
- ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)
Kruh s daným středem S a poloměrem r je tvořen všemi body v rovině, které jsou od středu vzdáleny nejvýše o r. Kruh s daným středem a poloměrem je tedy sjednocení kružnice se stejným středem a poloměrem a její vnitřní oblasti. Střed S kruhu je bod, který patří do kruhu. (Zatímco střed kružnice neleží na kružnici, ale v její vnitřní oblasti.)
Obvod kruhu, délka kružnice
Vzorec pro obvod kruhu
Obvod kruhu (i kružnice) o poloměru r je o=2\pi r. Pro průměr d platí o = \pi d.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obvodu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru r nebo průměru d = 2r. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obvodu kruhu přibližuje níže uvedený obrázek. Obvod oranžového čtverce je 8\cdot r. Obvod kruhu je „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Příklady: obvod kruhu
- Mějme kruh o poloměru 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Kružnice o průměru 2 cm má délku \pi \cdot 2 \approx 6,3 cm.
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud jej chceme obejít po jeho okrajové čáře, ujdeme 2 \pi \cdot 9{,}1 \approx 57 metrů.
Obsah kruhu
Vzorec pro obsah kruhu
Obsah kruhu o poloměru r je S=\pi r^2. Pro průměr d platí S = \frac{1}{4} \pi d^2.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obsahu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru nebo průměru. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obsahu kruhu přibližuje níže uvedený obrázek. Žluté čtverce mají obsah r^2. Oranžový čtverec se skládá ze čtyř žlutých čtverců, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový čtverec, což odpovídá tomu, že obsah kruhu je přibližně 3{,}14 \cdot r^2.

Příklady
- Mějme kruh o poloměru 3 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Uvažujme kružnici o průměru 2 cm. Její vnitřní oblast má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud bychom chtěli veškerou trávu v kruhu nabarvit na růžovo, museli bychom nabarvit \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Komiks pro zpestření
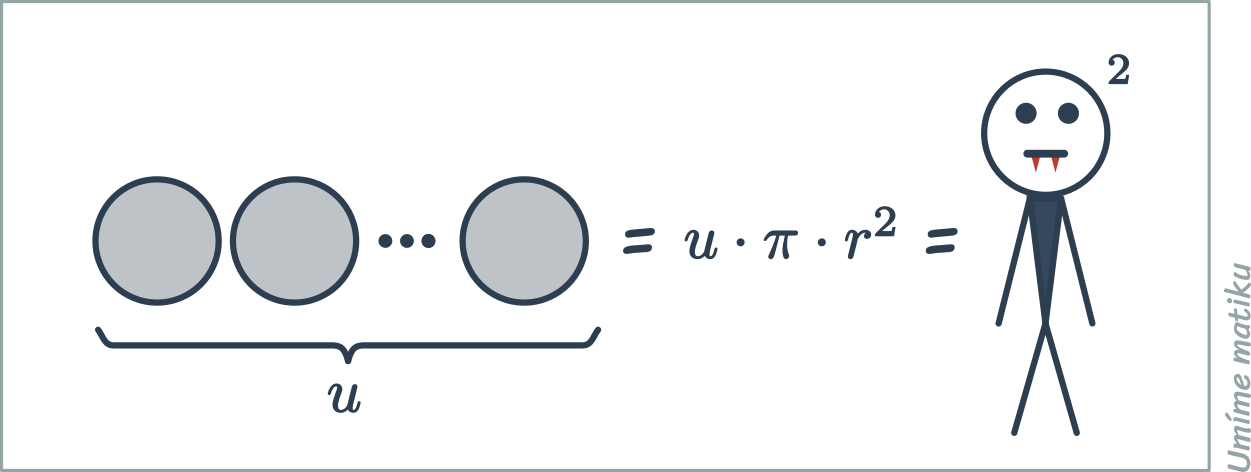
Úhly a kružnice
Středový úhel
- Úhel s vrcholem ve středu S kružnice k, jehož ramena procházejí krajními body A, B oblouku kružnice k.
- Pro každé dva body na kružnici lze určit dva středové úhly. Každý přísluší tomu oblouku, který v daném úhlu leží.
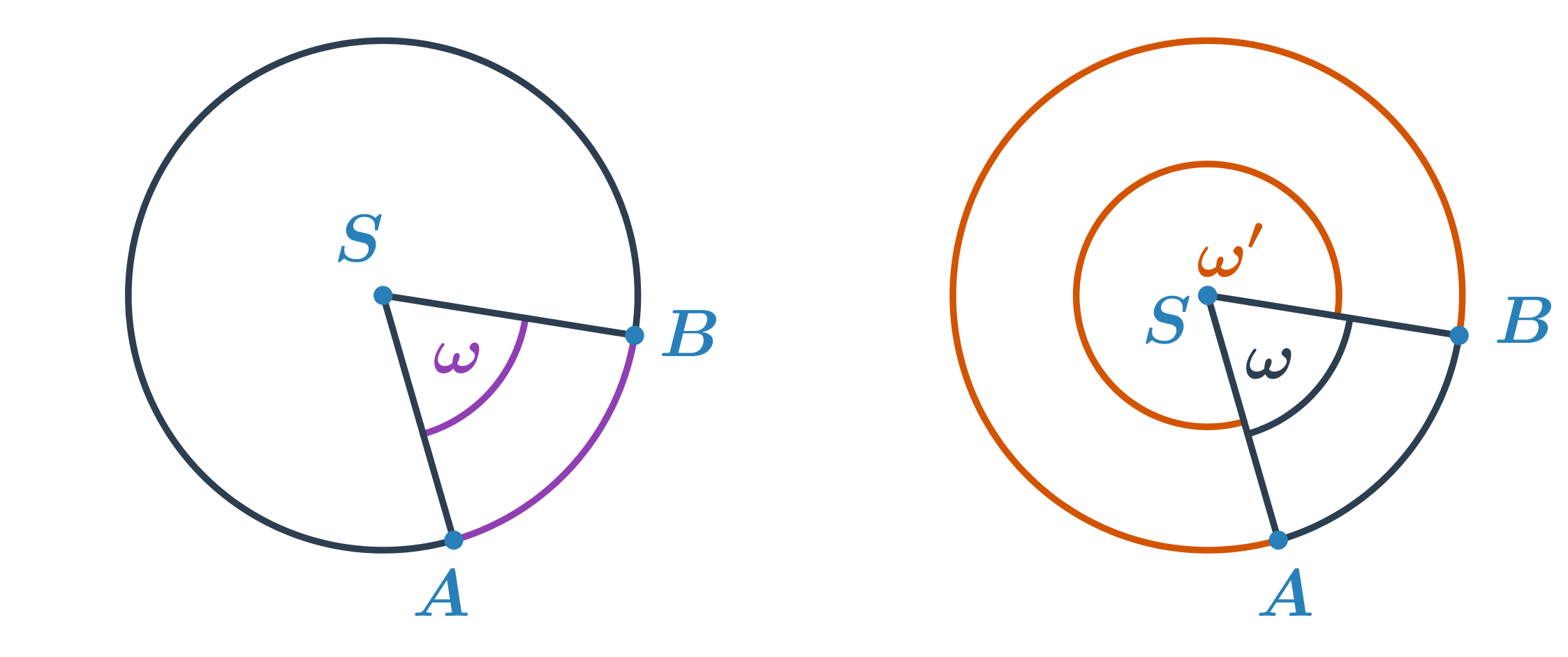
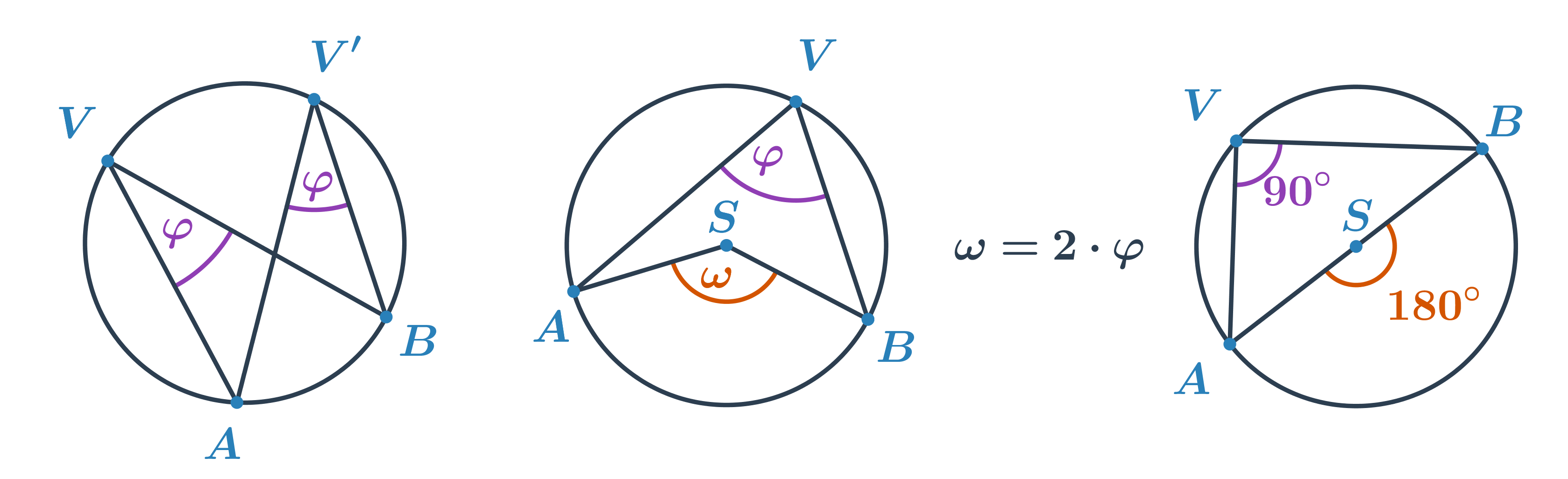
Obvodový úhel
- Úhel, jehož vrchol V leží na kružnici k a jeho ramena procházejí body A, B oblouku kružnice k (A \neq V \neq B)
- Všechny obvodové úhly příslušné oblouku AB s vrcholem V, který na oblouku neleží, mají stejnou velikost.
- Velikost středového úhlu \omega se rovná dvojnásobku velikosti obvodového úhlu \varphi příslušného ke stejnému oblouku, \omega = 2\cdot\varphi.
- Thaletova věta: Obvodový úhel nad průměrem kružnice je pravý.
Úsekový úhel
- Úhel, jenž svírá tětiva AB kružnice k s tečnou t kružnice v bodě A nebo B.
- Velikost úsekového úhlu je stejná jako velikost obvodového úhlu nad obloukem AB.
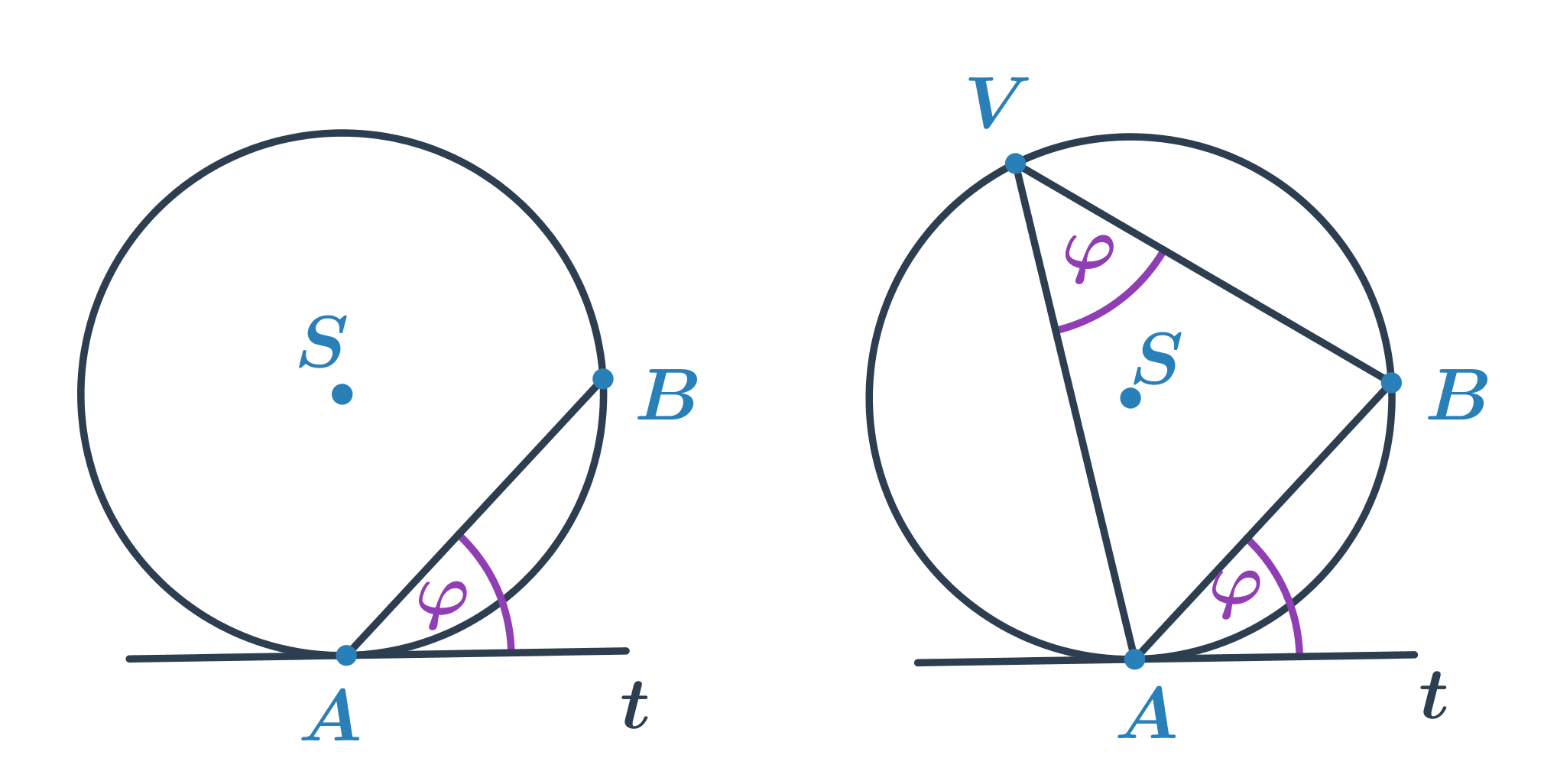
Příklad 1: Určete velikost úhlu
Určete velikost oranžového úhlu.
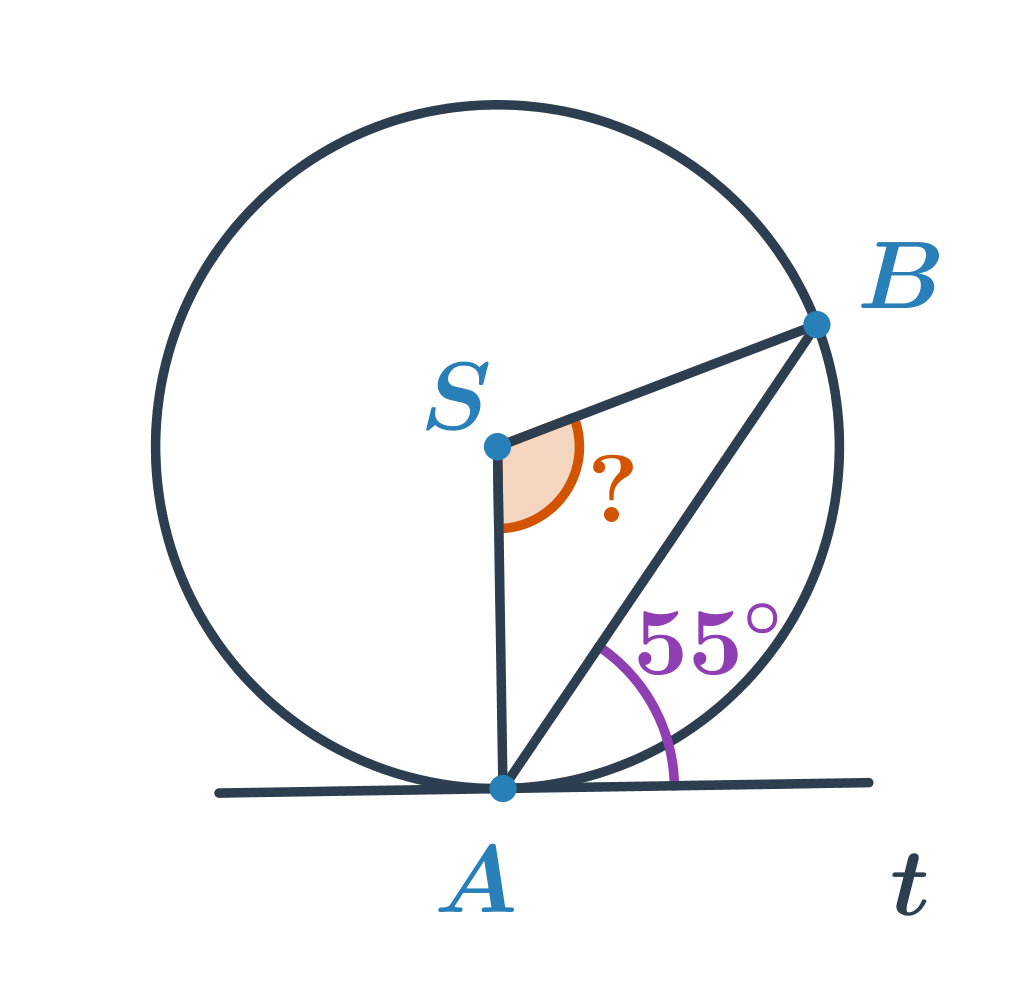
Úhel o velikosti 55^\circ je úsekový úhel příslušný tětivě AB. Víme, že velikosti úsekového a příslušného obvodového úhlu jsou stejné, tedy 55^\circ. Neznámý úhel je středový úhel příslušný menšímu oblouku AB. Jeho velikost je dvojnásobkem velikosti obvodového úhlu, tedy 2\cdot55^\circ=110^\circ.
Příklad 2: Určete velikost úhlu
Určete velikost oranžového úhlu.
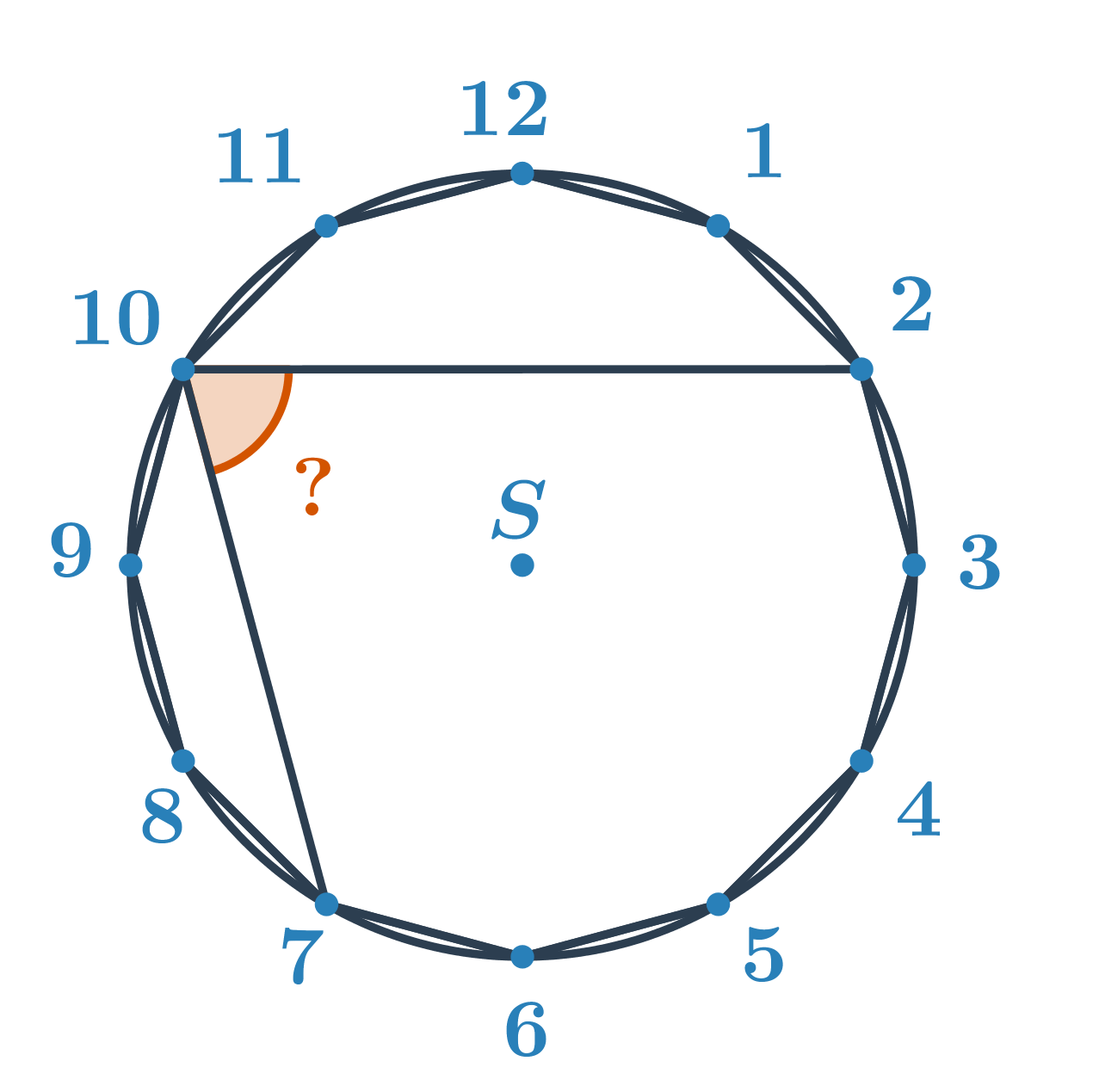
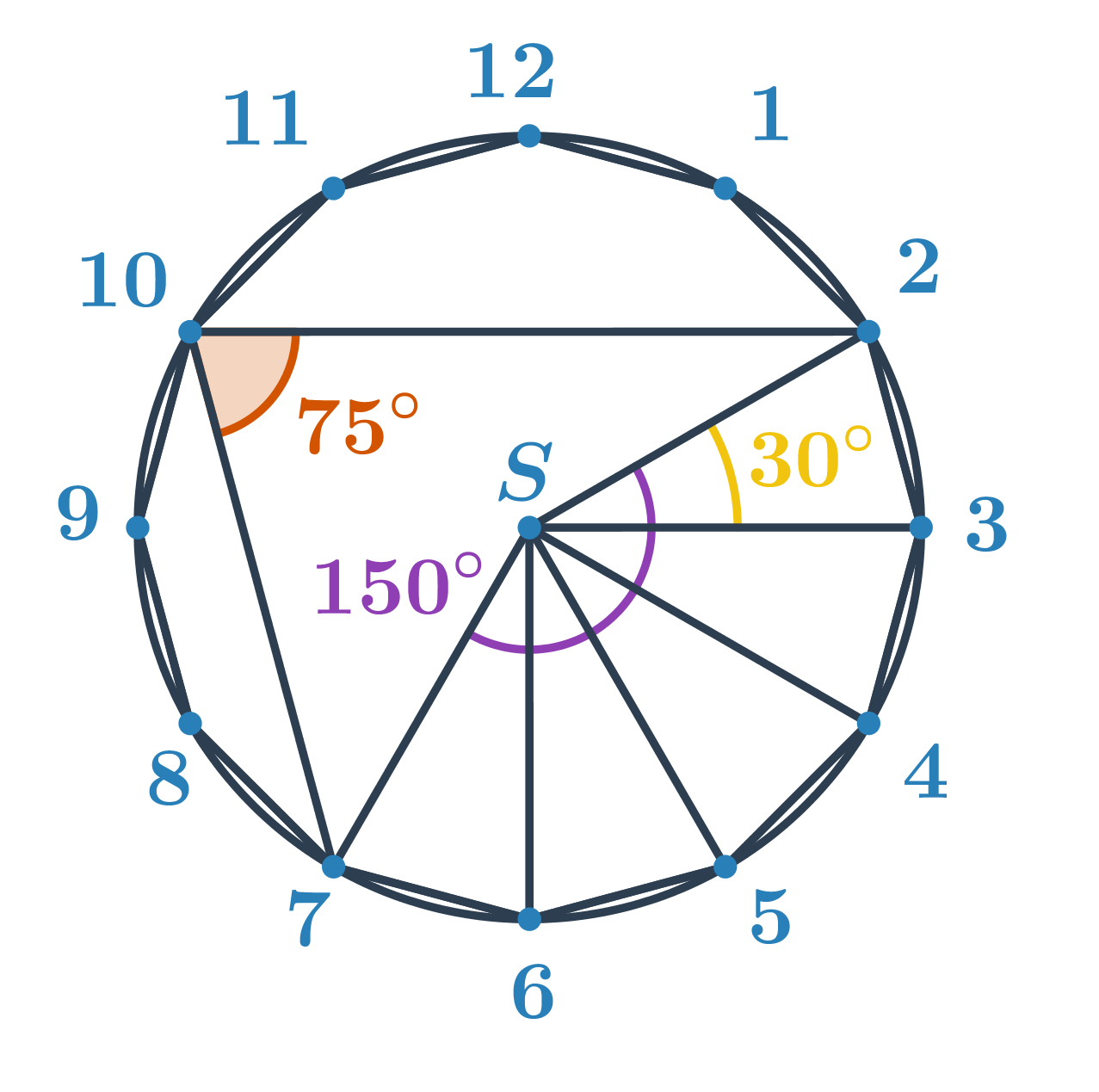
Neznámý úhel je obvodovým úhlem nad menším obloukem s koncovými body 2 a 7. Určíme velikost příslušného středového úhlu. Z kapitoly úhly a mnohoúhelníky víme, že velikost středového úhlu pravidelného n-úhelníku je \frac{360^\circ}{n}. Pro pravidelný dvanáctiúhelník je tedy úhel mezi spojnicemi dvou vedlejších vrcholů a středu \frac{360^\circ}{12}=30^\circ. Středový úhel příslušný oblouku 2 a 7 je pak 5\cdot30^\circ=150^\circ. Hledaný obvodový úhel má poloviční velikost, tedy 150^\circ:2=75^\circ.
Obsah kruhové výseče
Obsah kruhové výseče
Obsah kruhové výseče se středovým úhlem \alpha a poloměrem r spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Příklady
- Kruhová výseč na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
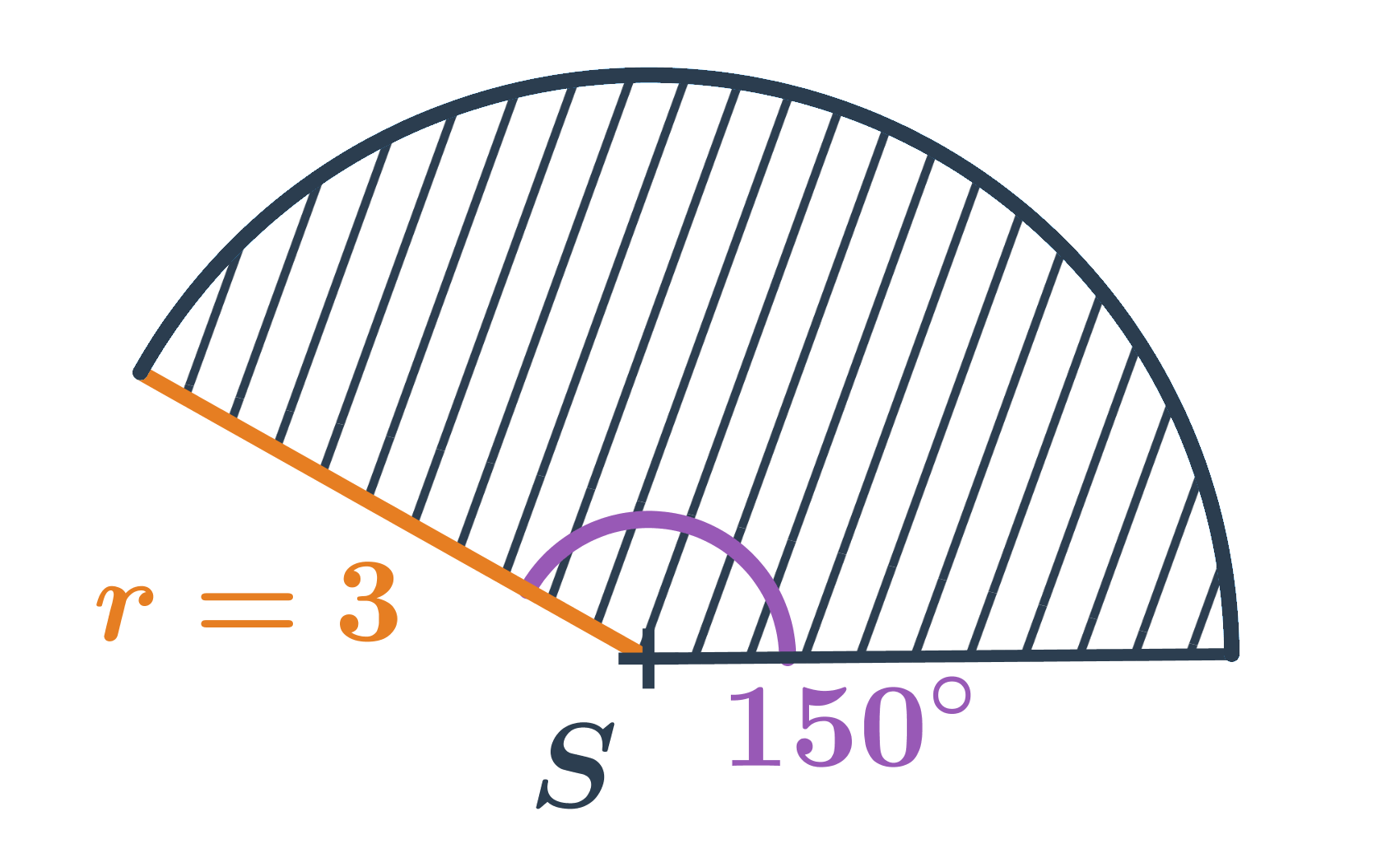
- Obsah celého kruhu (výseče se středovým úhlem 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2
Délka oblouku
Délku oblouku, který na kružnici o poloměru r odpovídá středovému úhlu \alpha spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Příklad – délka oblouku odpovídajícího 90^{\circ}
Délka oblouku na obrázku je:
\frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
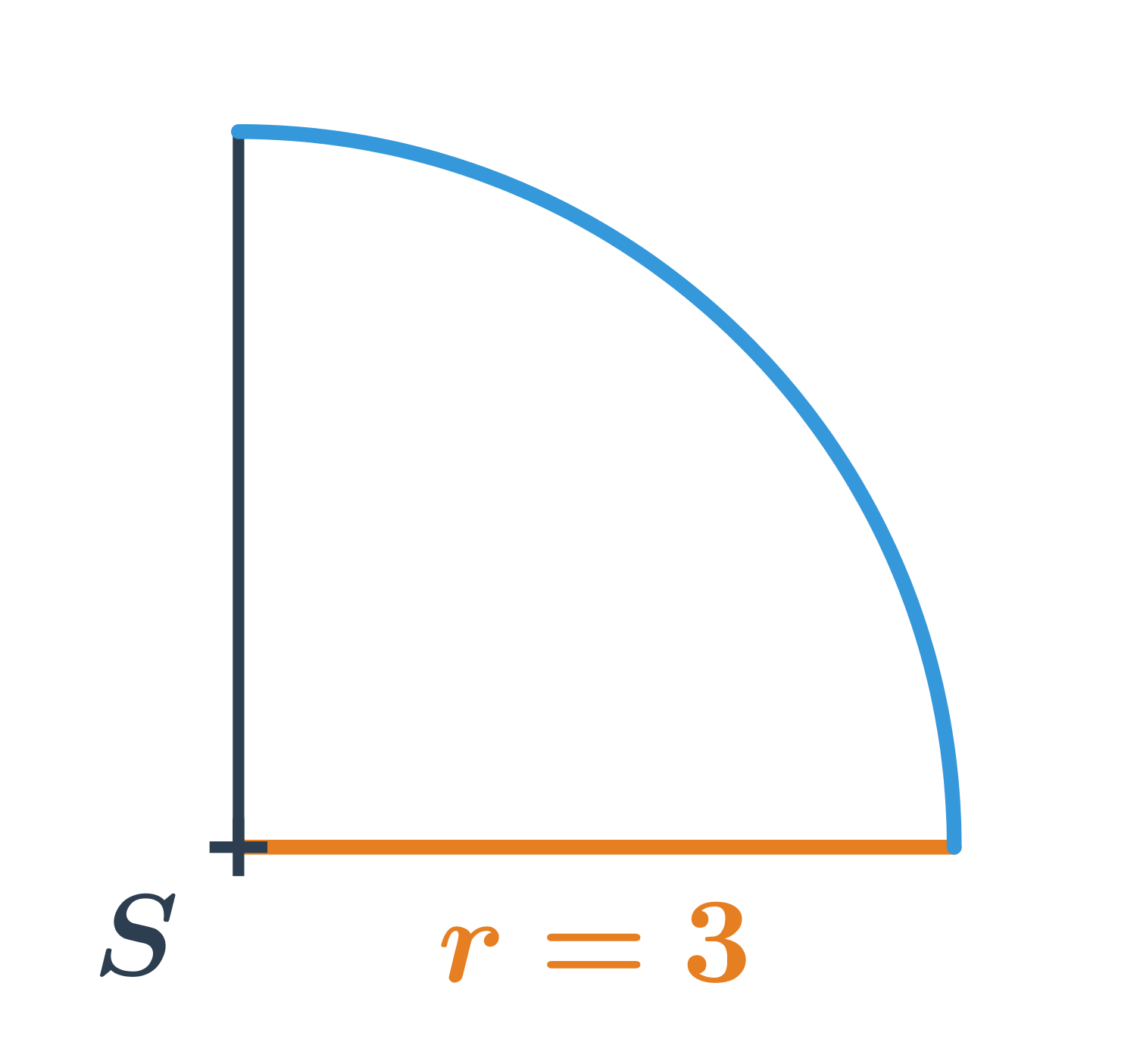 Jedná se o čtvrtinu délky kružnice.
Jedná se o čtvrtinu délky kružnice.
Příklad – délka oblouku odpovídajícího 360^{\circ}
Délka celé kružnice (tedy pro celých 360^{\circ}) je:
\frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Prostorové útvary
Prostorové útvary jsou množiny bodů v prostoru, tedy jde o třírozměrné útvary. Nejznámější prostorové útvary jsou krychle, kvádr, jehlan, koule, hranol, válec a kužel.
U některých prostorových útvarů umíme jednoduše spočítat jejich objem a povrch.
NahoruKrychle a kvádr
Krychle a kvádr jsou oba prostorové geometrické útvary, které patří mezi mnohostěny, speciálněji jde o zvláštní případy hranolů.
Krychle je prostorový útvar, který má šest stěn, tvar každé stěny je čtverec. Všechny hrany krychle mají stejnou délku a všechny vnitřní úhly jsou pravé, tedy jejich velikost je 90°. Příklady krychlí v běžném životě zahrnují kostky cukru nebo Rubikovu kostku.
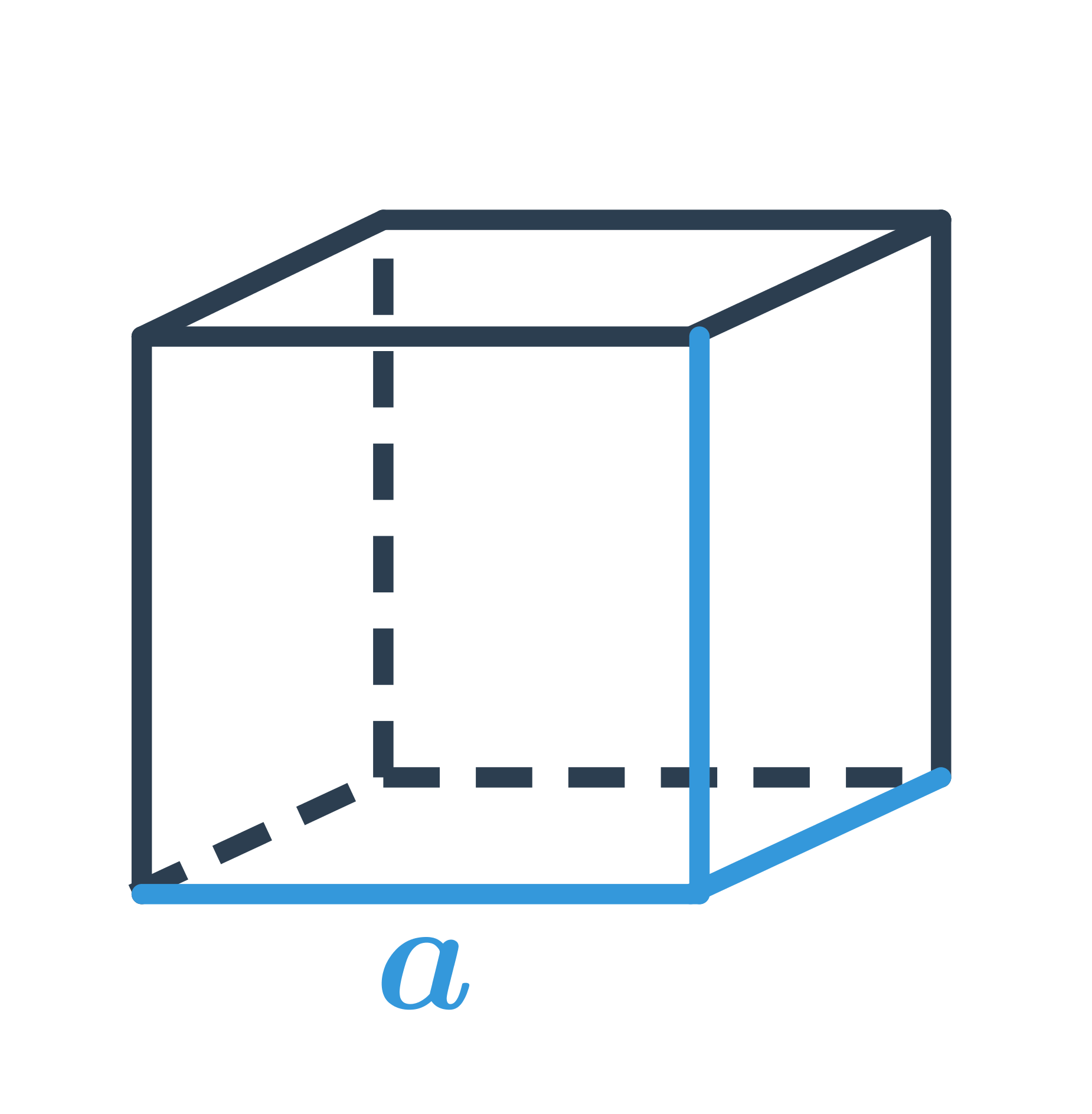
Pro výpočet objemu krychle použijeme vzorec V = a^3, kde a je délka hrany krychle.
Povrch krychle s délkou hrany a se vypočítá pomocí vzorce S = 6a^2.
Kvádr je také hranol, ale na rozdíl od krychle mají jeho stěny tvar obdélníků. Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle. Kvádr má šest stěn, tvar každé stěny je obdélník nebo čtverec, pokud jsou všechny stěny tvaru čtverce, jde o krychli.
Příklady kvádrů v běžném životě zahrnují krabice, knihy nebo cihly.
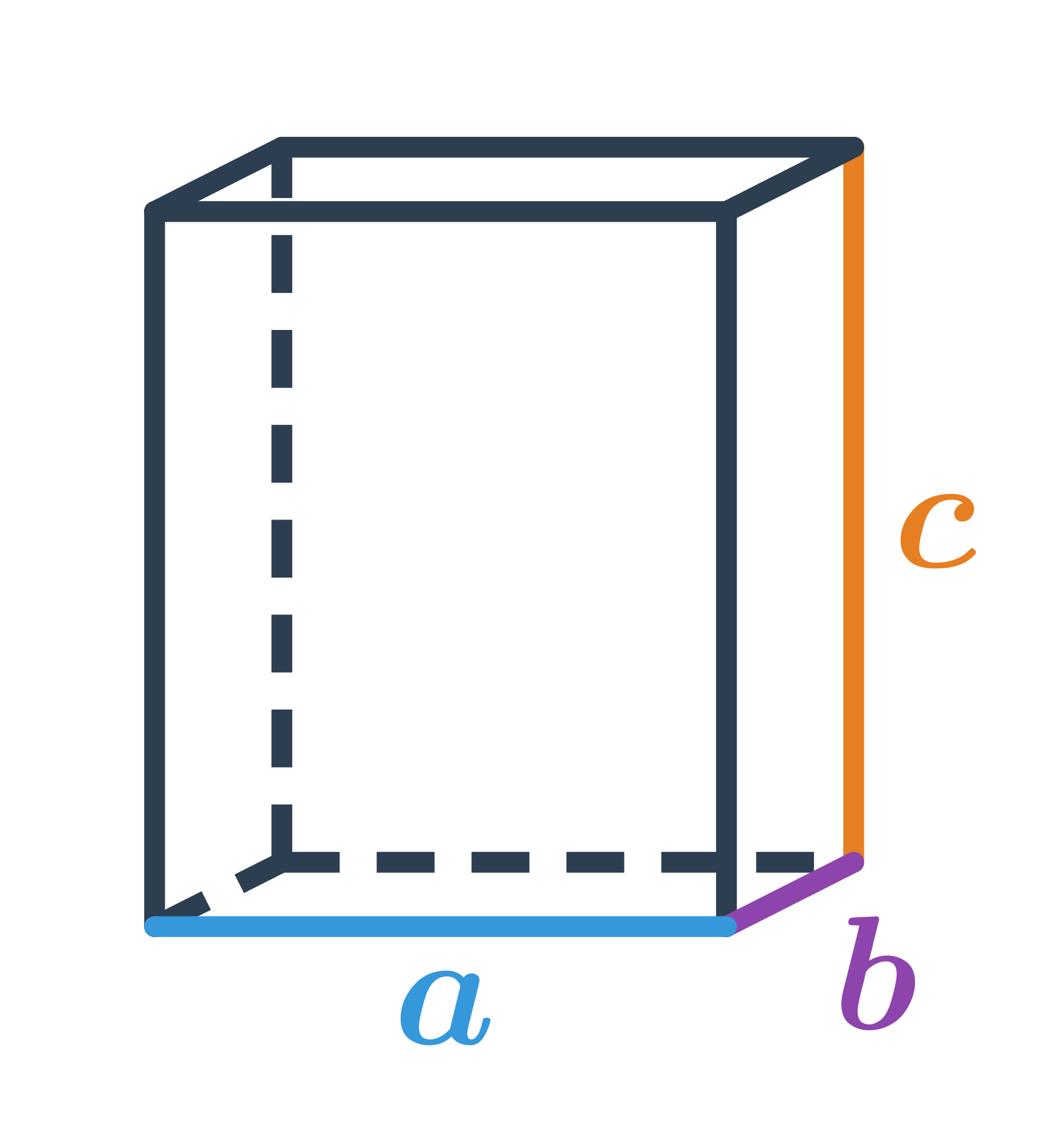
Objem kvádru získáme vzorcem V = a \cdot b \cdot c, kde a,b,c jsou rozměry kvádru.
Povrch kvádru vypočítáme jako součet obsahů všech jeho šesti obdélníkových stěn S = 2(ab + bc + ac). Všechny dvojice protějších stěn jsou dvojice shodných obdélníků, které mají stejné obsahy.
NahoruObjem krychle a kvádru
Objem kvádru s délkami hran a,b,c je: V=a\cdot b\cdot c
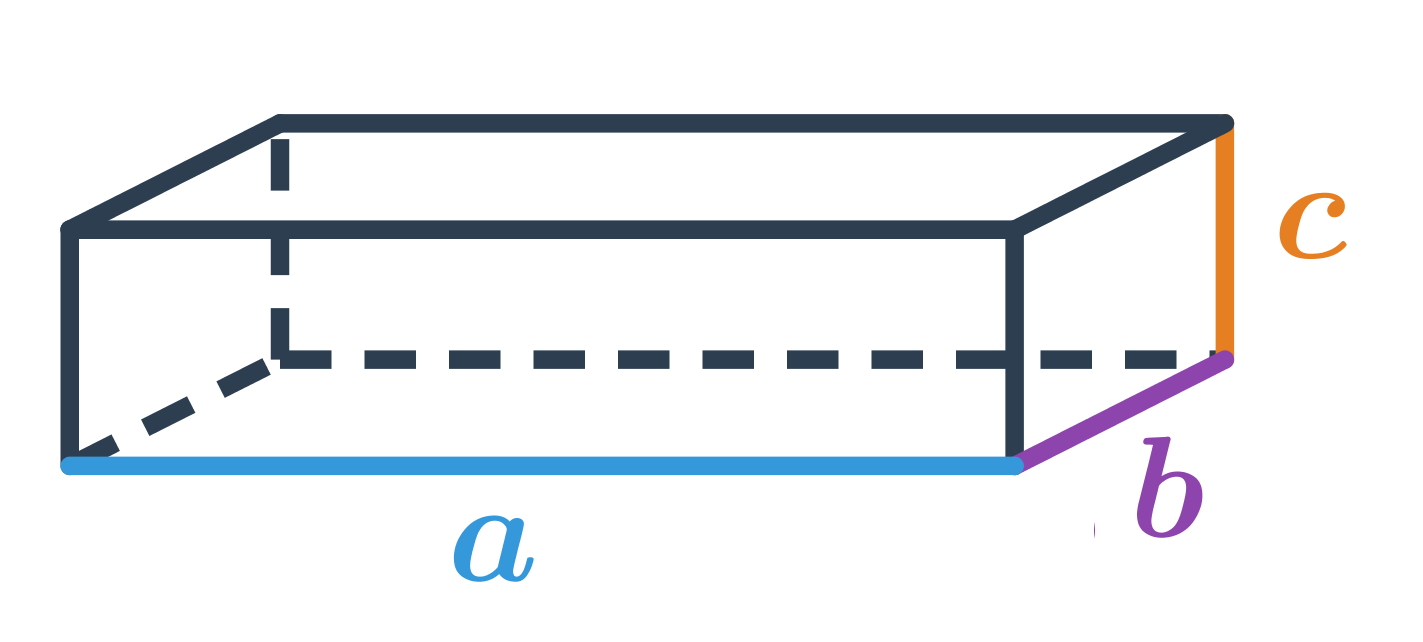
Objem krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako objem kvádru s a=b=c, tedy: V=a\cdot a\cdot a=a^3
NahoruPovrch krychle a kvádru
Povrch kvádru s délkami hran a,b,c spočítáme jako součet obsahů všech jeho stěn. Tedy: S=2 (a\cdot b + a\cdot c + b \cdot c)
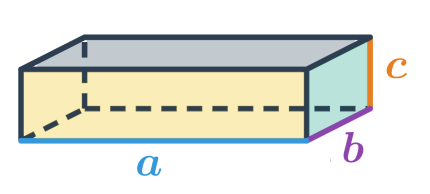
Povrch krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako povrch kvádru s a=b=c, tedy šestkrát obsah jedné čtvercové stěny krychle: S = 6\cdot a\cdot a = 6a^2
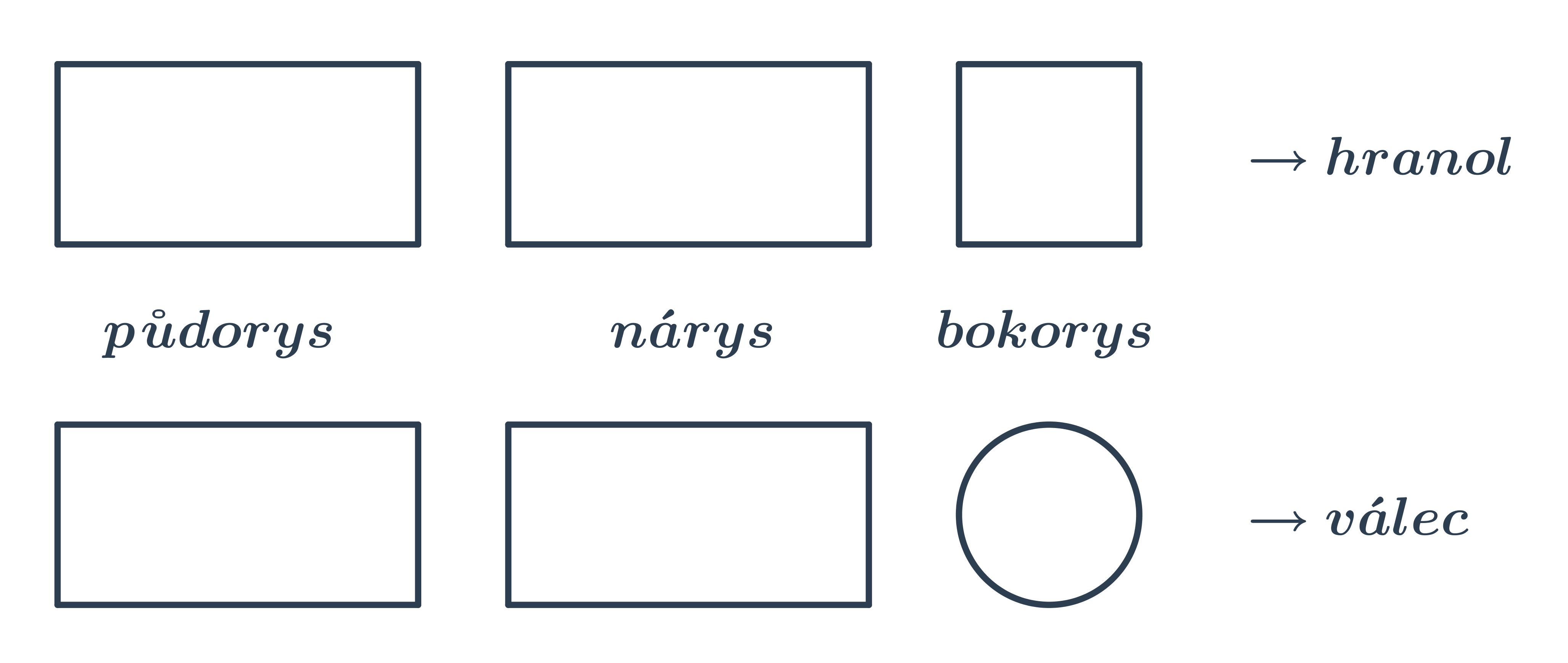
NahoruHranol je prostorový geometrický útvar, který má dvě shodné podstavy umístěné v různých rovinách. Budeme se zabývat kolmými hranoly, ve kterých odpovídající strany podstavy jsou vždy spojené boční stěnou tvaru obdélníka nebo čtverce. (Pro kosé hranoly jsou boční stěny rovnoběžníky.) Podstavy hranolu mohou mít rozličné tvary, například mohou být trojúhelníkové, čtvercové, obdélníkové nebo i mnohoúhelníkové.
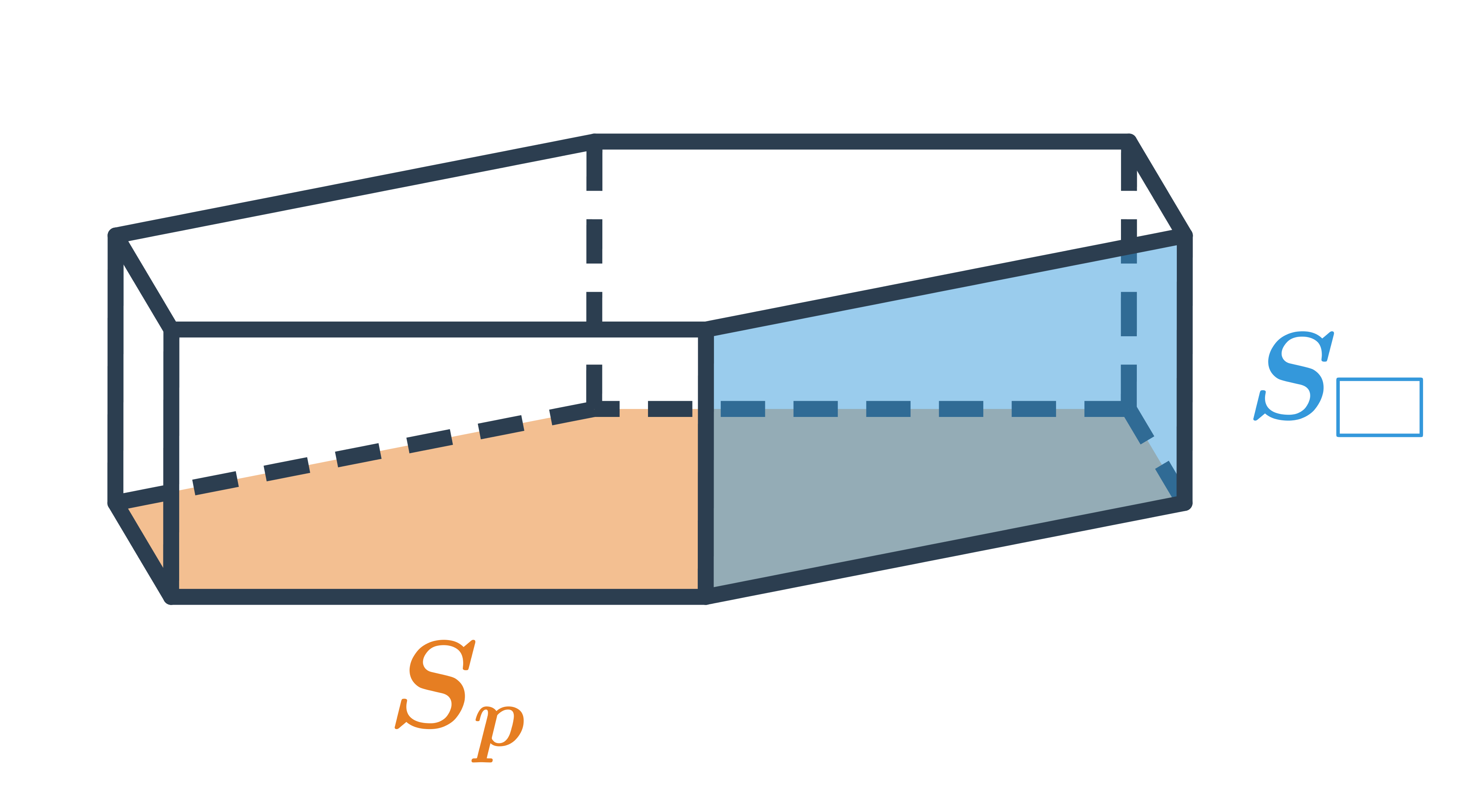
Vzorečky pro objem a povrch hranolu
Pro výpočet objemu hranolu používáme vzorec V = S_p \cdot v, kde S_p je obsah jedné podstavy a v je výška hranolu.
Síť hranolu se skládá ze dvou podstav a pláště, proto jeho povrch vypočítáme jako součet obsahů podstav a obsahu pláště: S = 2S_p + S_{pl}, kde S_{pl} je obsah pláště, což je součet obsahů všech obdélníkových nebo čtvercových stěn tvořících plášť.
Příklady hranolů
Pravidelný n-boký hranol má jako podstavy dva pravidelné n-úhelníky.
Speciální případy čtyřbokých hranolů jsou kvádr a krychle. Kvádr může a nemusí být pravidelný čtyřboký hranol. Krychle je pravidelný čtyřboký hranol, který navíc splňuje a=v.
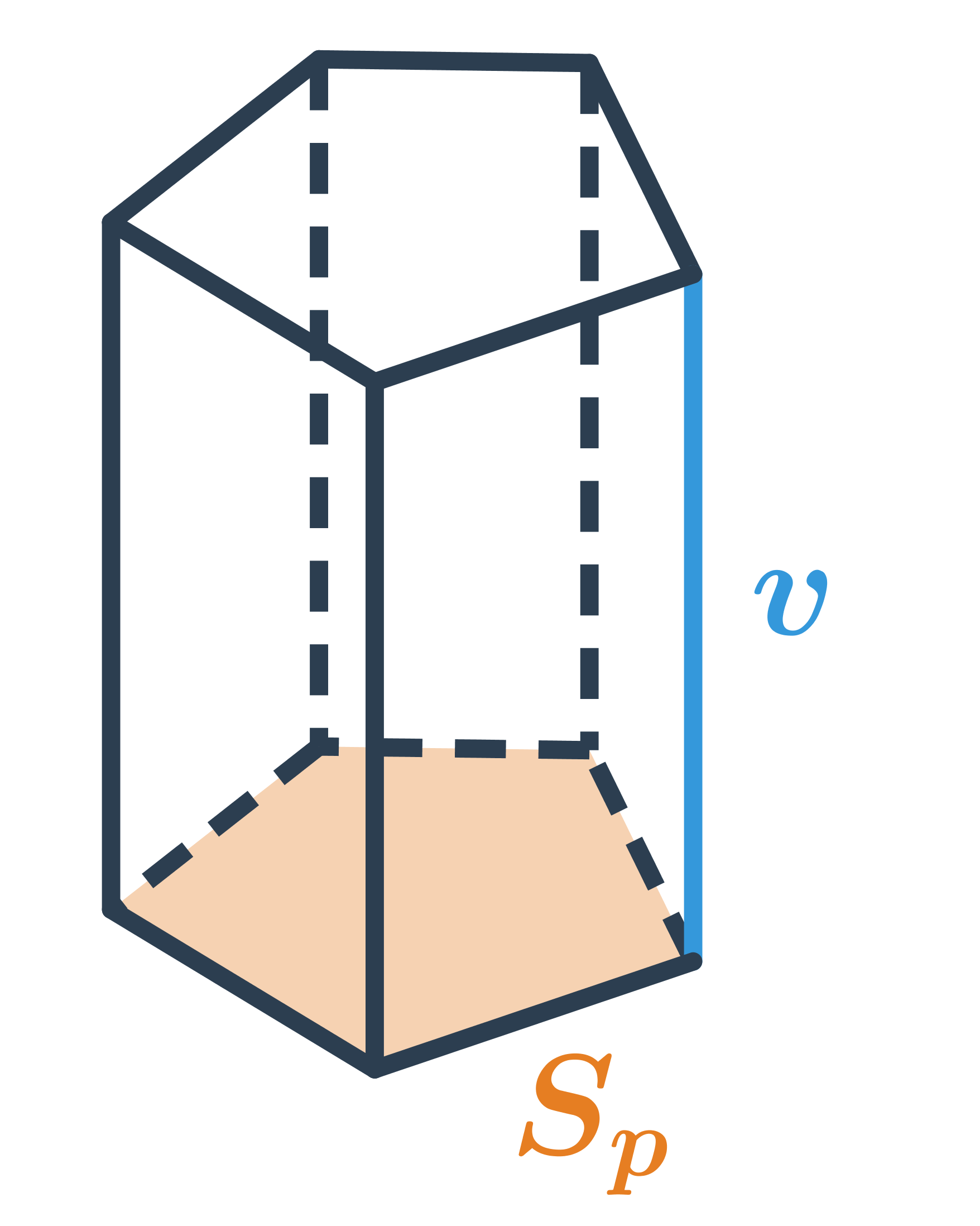
Objem hranolu
Objem hranolu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=S_p \cdot v.
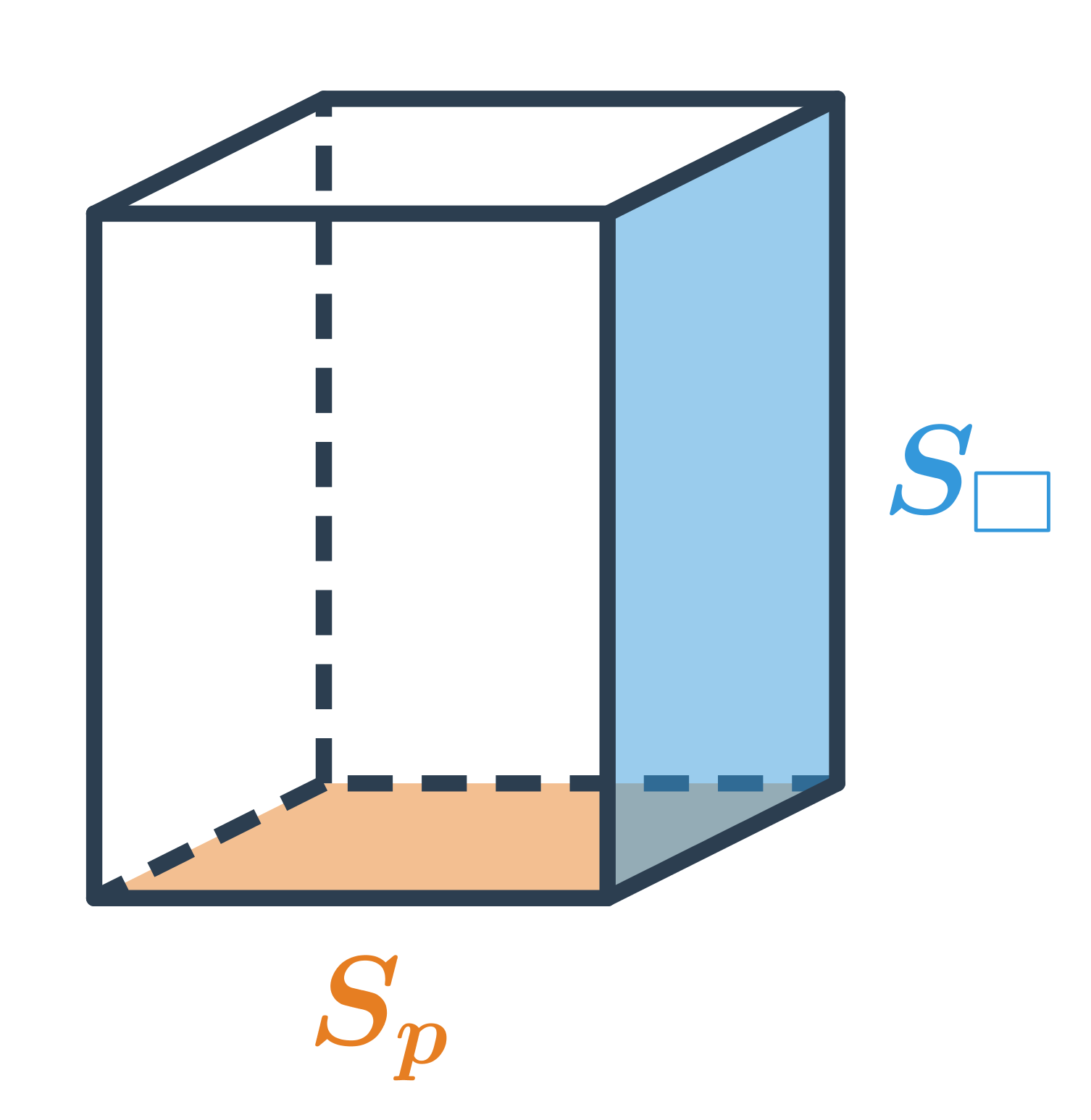
Povrch hranolu
Povrch hranolu, který má podstavu o obsahu S_p plášť o obsahu S_{pl}, spočítáme jako S=2S_p + S_{pl}. Plášť hranolu je tvořen všemi jeho stěnami kromě dvou podstav.
Povrch pravidelného n‑bokého hranolu, který má dvě podstavy ve tvaru pravidelných n‑úhelníků a potom n stejných obdélníkových stěn (obsah jedné označme S_1), spočítáme takto: S=2S_p + n\cdot S_1
NahoruJehlan je prostorový geometrický útvar, který má jednu podstavu a plášť tvořený trojúhelníky. Podstava jehlanu může být libovolný mnohoúhelník (například čtverec, obdélník nebo trojúhelník) a všechny boční stěny (plášť) se setkávají v jednom společném bodě nazývaném vrchol jehlanu. Příkladem jehlanů jsou pyramidy ze starověkého Egypta, vypadají zhruba jako jehlany se čtvercovou podstavou a čtyřmi trojúhelníkovými bočními stěnami.
Vzorce pro objem a povrch
Objem jehlanu V = \frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy a v je výška jehlanu, což je vzdálenost vrcholu od roviny podstavy. (Velikost výšky jehlanu získáme jako délku úsečky, která vede od vrcholu k rovině podstavy a je kolmá na tuto rovinu.)
Povrch jehlanu získáme jako součet obsahu podstavy S_p a obsahu pláště S_{pl} (obsah pláště je roven součtu obsahů všech bočních trojúhelníkových stěn jehlanu). Celkově je povrch jehlanu S = S_p + S_{pl}, v případě pravidelného šestibokého jehlanu na obrázku je: S=Sp + 6 \cdot S_{\Delta}
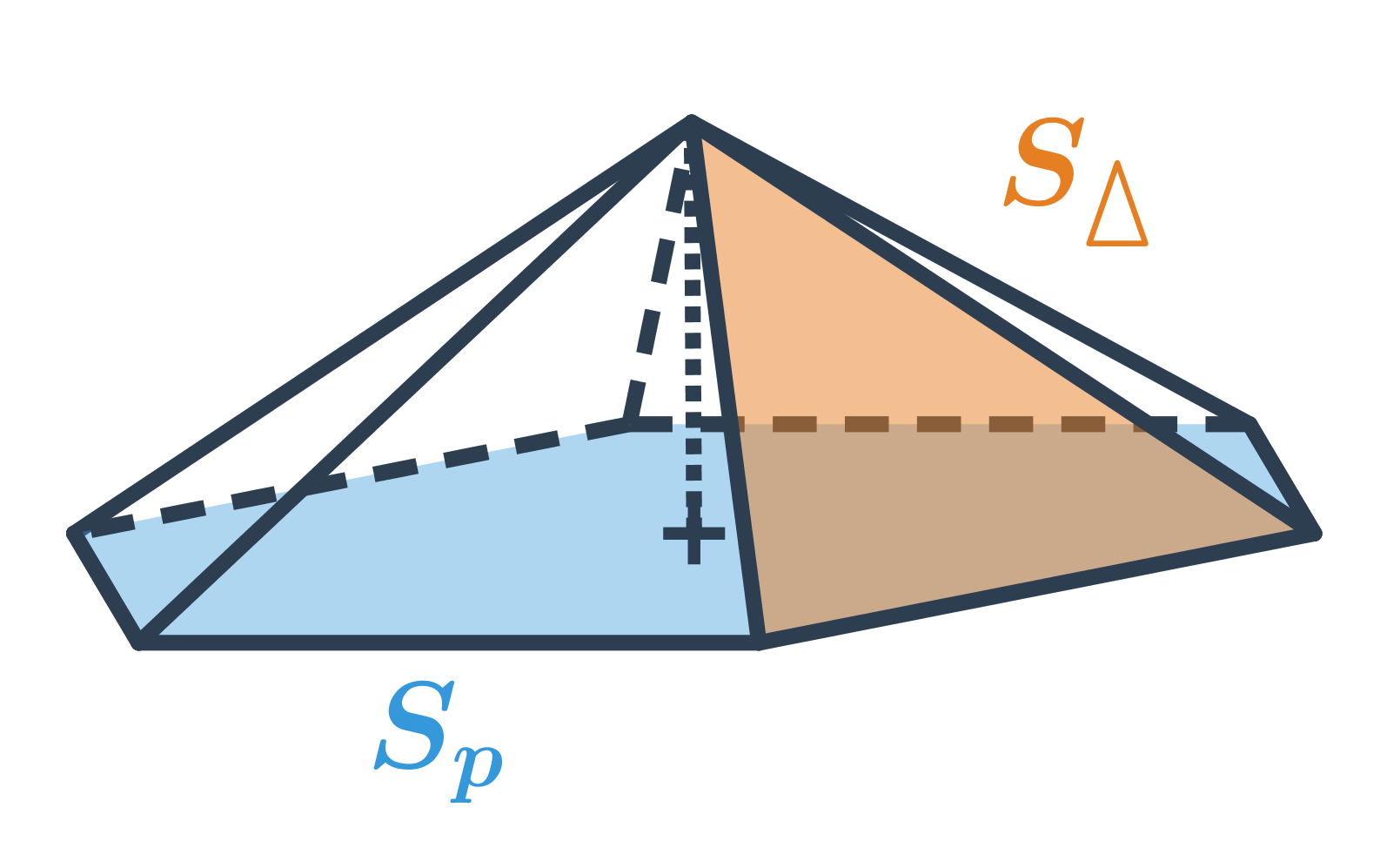
Některé jehlany mají pravidelnou podstavu, vrchol umístěný přímo nad středem podstavy a všechny trojúhelníkové stěny z pláště stejné, ale obecně se může výpočet obsahu každé z těchto trojúhelníkových stěn lišit v závislosti na tvaru podstavy jehlanu.
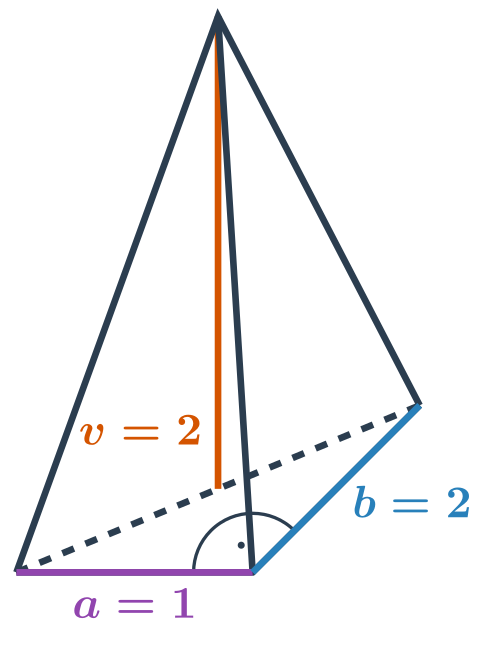
Speciální případy
Pravidelný čtyřstěn je jehlan, jehož základna i všechny tři boční stěny jsou rovnostranné trojúhelníky. Je jedním z Platónských těles.
Pokud máme pravidelný čtyřstěn, jehož stěny jsou rovnostranné trojúhelníky s délkou každé strany a, umíme si pomocí Pythagorovy věty spočítat výšku každého z těchto rovnostranných trojúhelníků \frac{\sqrt{3}}{2} a.
Povrch pravidelného čtyřstěnu
- Obsah podstavy pravidelného čtyřstěnu se stranou délky a je obsah jednoho ze čtyř stejných rovnostranných trojúhelníků: S_p = \frac{1}{2} \cdot a \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} a^2.
- Povrch pravidelného čtyřstěnu se stranou délky a je: 4 \cdot S_p = \sqrt{3} \cdot a^2
Objem pravidelného čtyřstěnu
- V rovnostranném trojúhelníku leží těžnice na výškách a zároveň na osách vnitřních úhlů. Vrchol pravidelného čtyřstěnu leží na přímce, která je kolmá k jeho podstavě a protíná ji v ortocentru (což je zároveň také těžiště rovnostranného trojúhelníka).
- Můžeme tedy spočítat pomocí Pythagorovy věty nejen výšku trojúhelníků, které tvoří stěny pravidelného čtyřstěnu, ale také výšku celého tělesa:
- v^2 = a^2 - (\frac{2}{3} \cdot \frac{\sqrt{3}}{2} a )^2 = (1-\frac{1}{\sqrt{3}})\cdot a^2
- v = \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a
- Objem pravidelného čtyřstěnu se stranou délky a je:
- \frac{1}{3} S_p \cdot v = \frac{1}{3}\cdot \frac{\sqrt{3}}{4} a^2 \cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a = \frac{1}{4\cdot \sqrt{3}}\cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a^3
Pravidelný n-boký jehlan má jako podstavu pravidelný n-úhelník, jeho plášť tvoří n rovnoramenných trojúhelníků. Například podstava pravidelného čtyřbokého jehlanu je čtverec, jeho plášť tvoří čtyři rovnoramenné trojúhelníky.
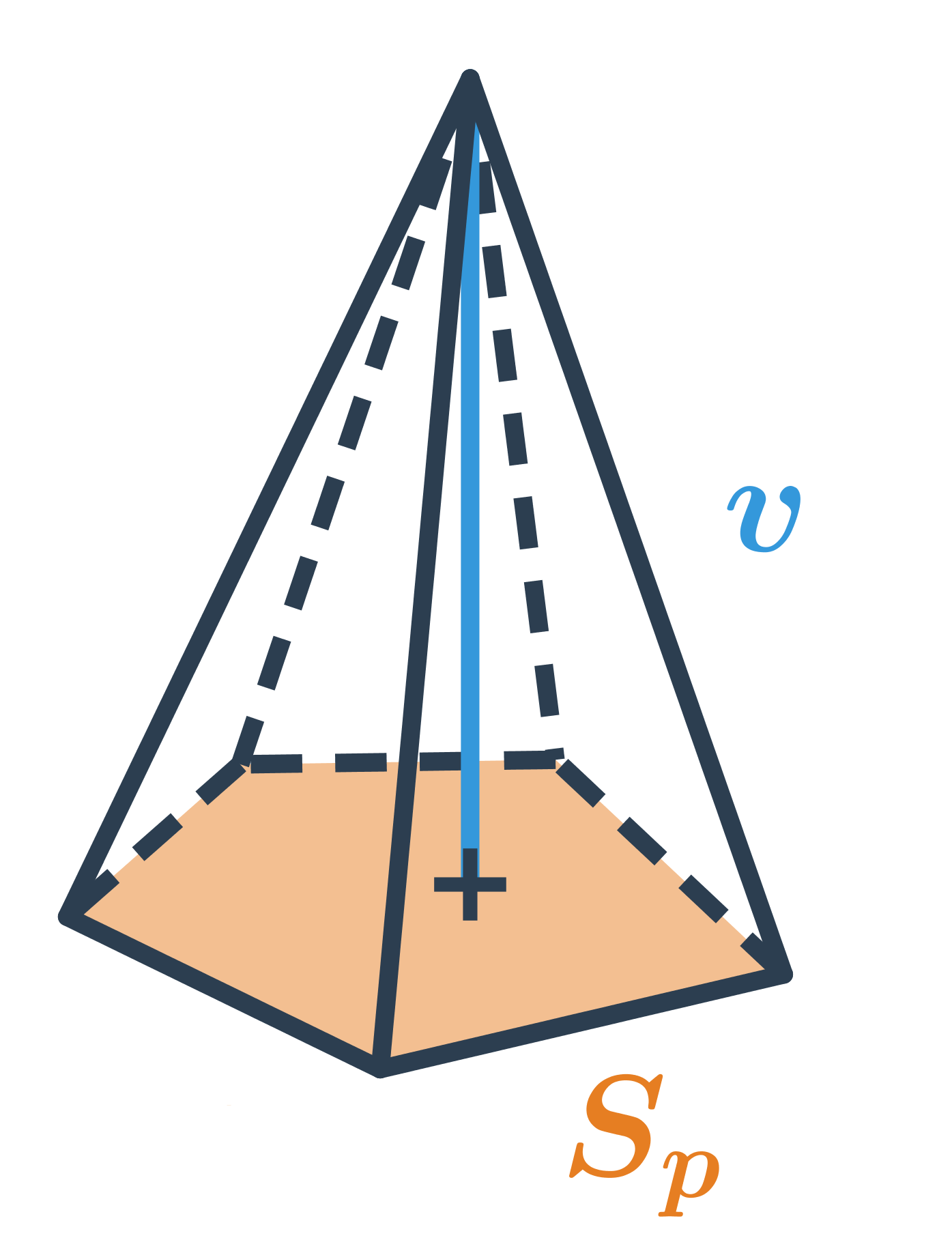
Objem jehlanu
Objem jehlanu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=\frac{1}{3} S_p \cdot v.
Oproti hranolu se stejnou výškou a tvarem podstavy má jehlan třikrát menší objem.
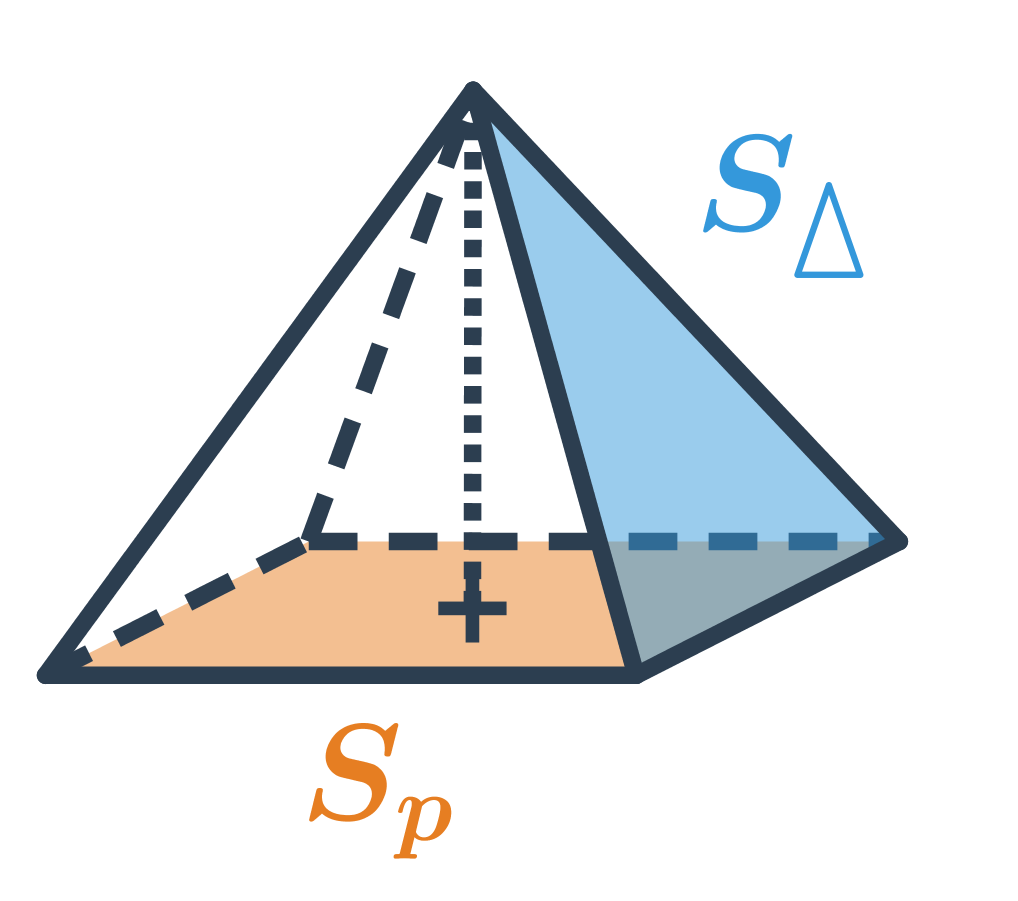
Povrch jehlanu
Povrch jehlanu spočítáme jako součet obsahu jeho podstavy S_p a obsahu jeho pláště S_{pl}. Obsah pláště spočítáme jako součet obsahů stěn jehlanu, které tvoří plášť (tj. všechny stěny jehlanu kromě jeho podstavy).
Povrch pravidelného n‑bokého jehlanu, který má podstavu ve tvaru pravidelného n‑úhelníka a potom n stejných trojúhelníkových stěn (obsah jedné označme S_1), spočítáme takto: S= S_p + n\cdot S_1
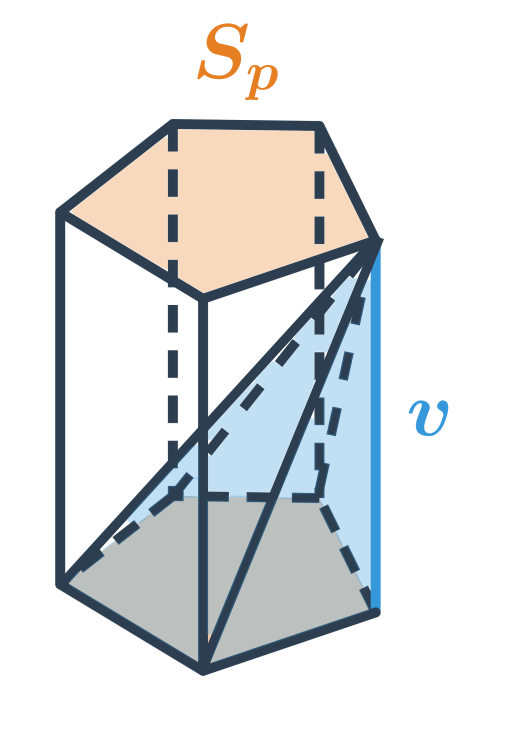
NahoruVálec je těleso, které vznikne rotací obdélníku v prostoru okolo jedné strany.
Válec má dvě podstavy tvaru kruhu, je jednoznačně určen poloměrem (nebo průměrem) podstavy a výškou.
Vzorečky pro objem a povrch válce
Objem válce spočítáme podobně jako u hranolu V=S_p \cdot v, kde S_p je obsah kruhové podstavy. Celkově je tedy objem válce: V=\pi \cdot r^2 \cdot v
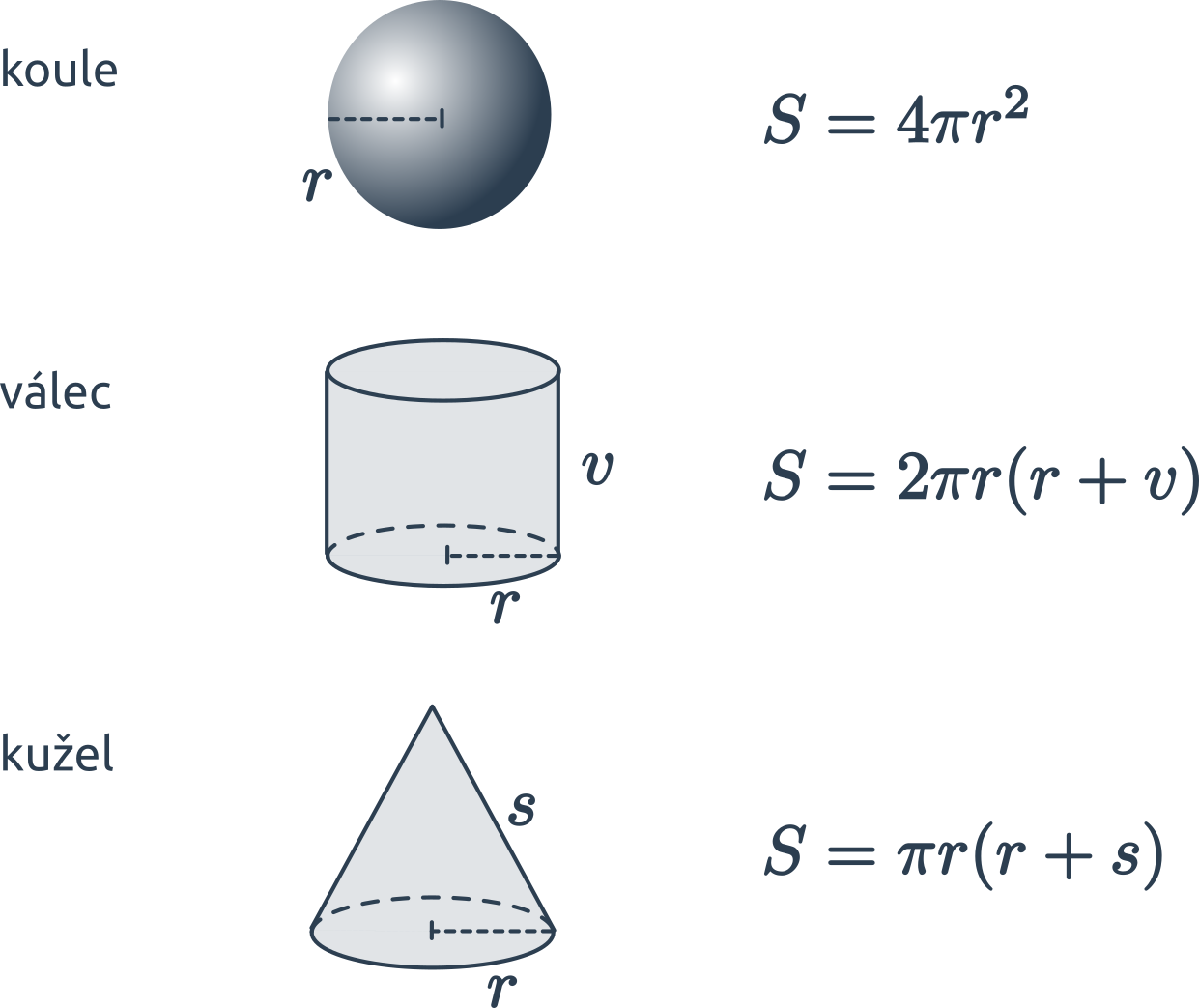
Povrch válce je součet obsahů jeho dvou podstav a obsahu pláště S = 2\cdot S_p + S_{pl}. Podstavy jsou ve tvaru kruhu a plášť můžeme rozvinout do roviny jako obdélník o rozměrech v a 2\pi \cdot r (výška válce a obvod jeho podstavy). Povrch válce je roven: V = 2\pi \cdot r^2 + 2\pi \cdot r \cdot v = 2\pi r (r+v)
NahoruObjem válce
Objem válce s poloměrem podstavy r a výškou v spočítáme jako: V=\pi \cdot r^2 \cdot v
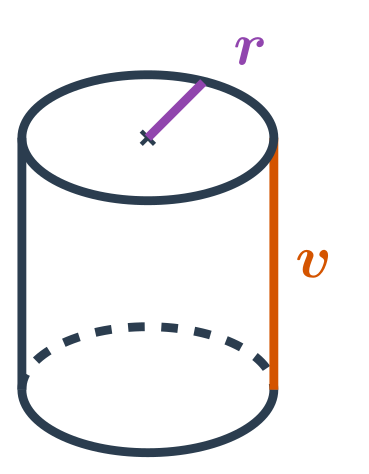
Platí V=S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
NahoruPovrch válce
Povrch válce s poloměrem podstavy r a výškou v spočítáme jako: S = 2\pi r \cdot(r + v)
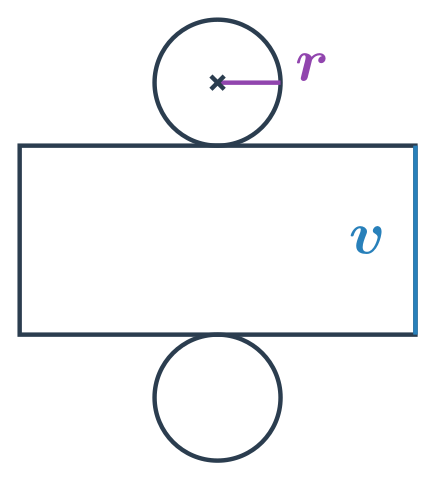
Platí S=2S_p + S_{pl}, kde S_p je obsah podstavy válce a S_{pl} obsah pláště válce. Podstava válce má tvar kruhu s poloměrem r a plášť válce je obdélník o stranách v a 2\pi r. Celkem máme:
- Obsah podstavy: S_p = \pi \cdot r^2
- Obsah pláště: S_{pl}=2\pi r \cdot v
- Povrch válce: S=2\pi r \cdot (r + v)
Koule je prostorový geometrický útvar, který má tvar dokonale kulatého tělesa. Všechny body na povrchu koule jsou stejně daleko od středu, tato vzdálenost se nazývá poloměr koule. Koule je symetrická ve všech směrech, což znamená, že nezáleží na tom, jak ji otočíme, její tvar zůstane stejný.
Příklady koule v běžném životě zahrnují basketbalový míč, zeměkouli nebo kuličku z ložiska.
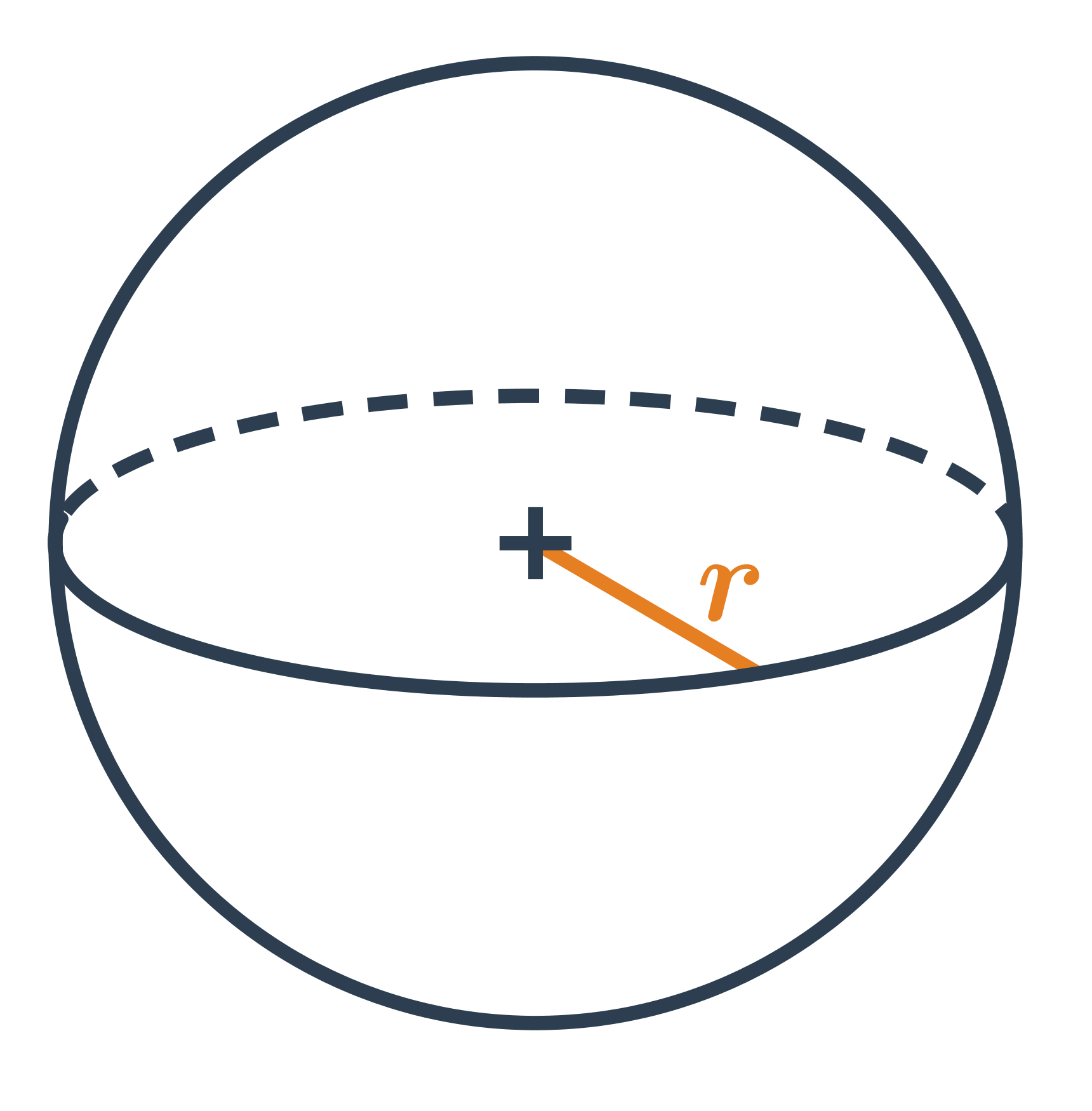
Pro výpočet objemu koule používáme vzorec V = \frac{4}{3} \pi r^3, kde r je poloměr koule.
Povrch koule se vypočítá pomocí vzorce S = 4 \pi r^2, kde opět r značí poloměr koule.
Koule nemá rohy ani hrany, což ji odlišuje od mnoha jiných geometrických útvarů. Tato jedinečná vlastnost dává kouli významnou roli v různých oblastech, včetně fyziky, kde se používá například pro modelování ideálních těles v teorii gravitace. Předmětem studia v neeuklidovské geometrii mohou zase být útvary, které nejsou částí roviny, ale kulové plochy (pak jde o sférickou geometrii, neboli geometrii na sféře).
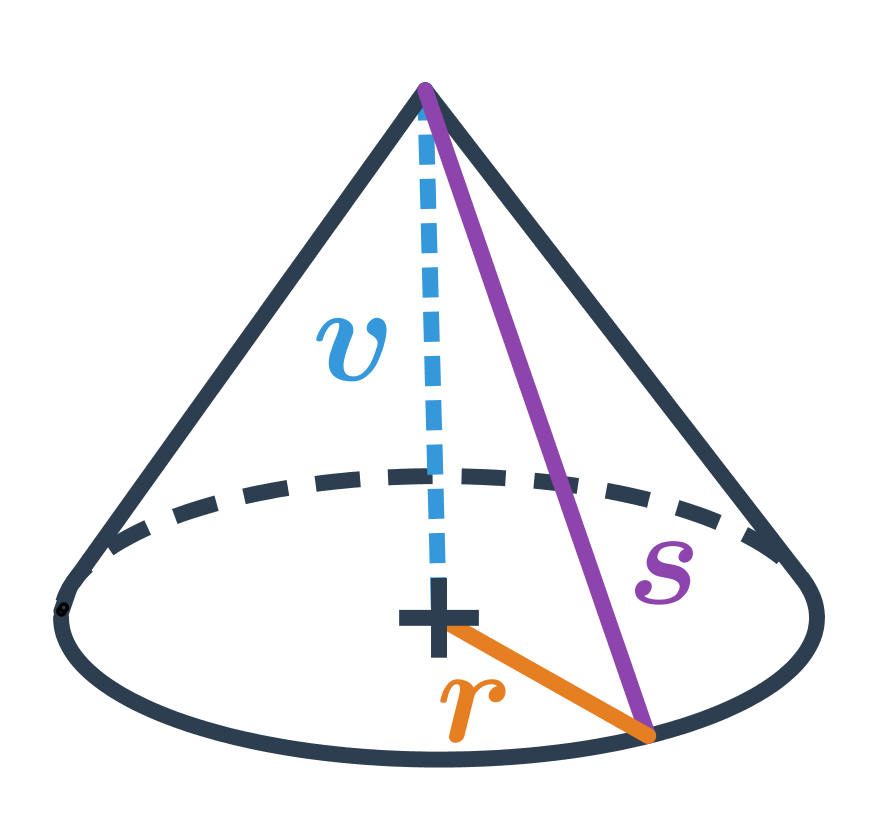
NahoruKužel je prostorový geometrický útvar s kruhovou podstavou. Zužuje se směrem k jednomu bodu zvanému vrchol. Jde o útvar, který vznikne, když se kolem své osy otáčí rovnoramenný trojúhelník. Příkladem kuželu v běžném životě je kornout zmrzliny nebo dopravní kužel.
Vzorce pro objem a povrch
Objem kuželu lze vypočítat pomocí vzorce: V = \frac{1}{3} \pi \cdot r^2 \cdot v, kde r je poloměr podstavy a v je výška kuželu, což je vzdálenost vrcholu od roviny, ve které leží podstava kuželu.
Povrch kuželu získáme sečtením obsahu základny a obsahu pláště S = \pi \cdot r^2 + \pi \cdot r s, kde s je tzv. strana kuželu, což je délka úsečky spojující vrchol kuželu s okrajem jeho základny.
Kuželosečky
Křivky, které vznikají průnikem kuželového povrchu s rovinou, se nazývají kuželosečky. Patří mezi ně například kružnice, elipsa, parabola a hyperbola.
Objem kužele
Objem kužele s poloměrem podstavy r a výškou v spočítáme jako: V=\frac{1}{3} \pi \cdot r^2 \cdot v
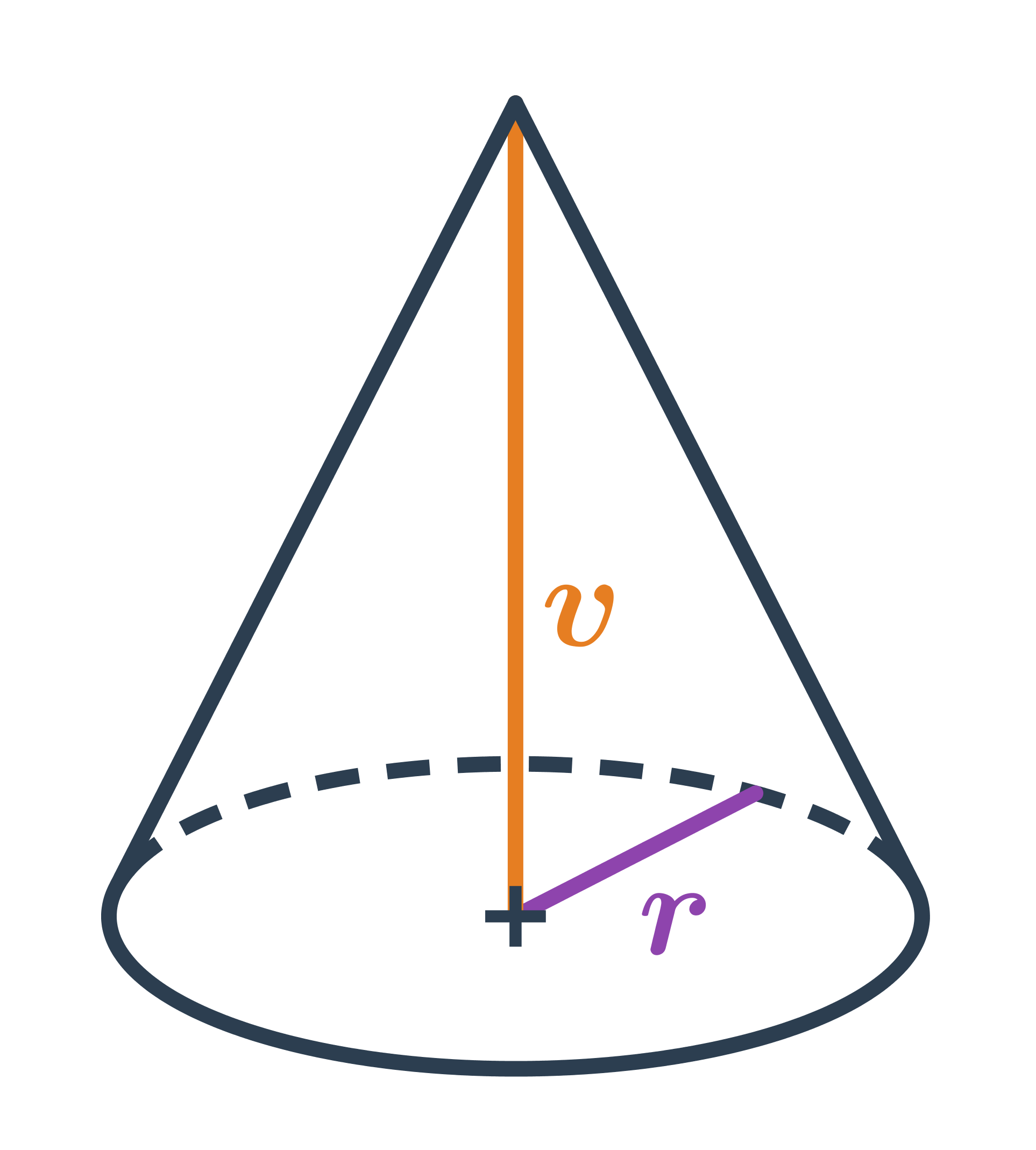
Pro kužel platí V=\frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
Oproti válci se stejnou výškou a poloměrem podstavy má kužel třikrát menší objem.
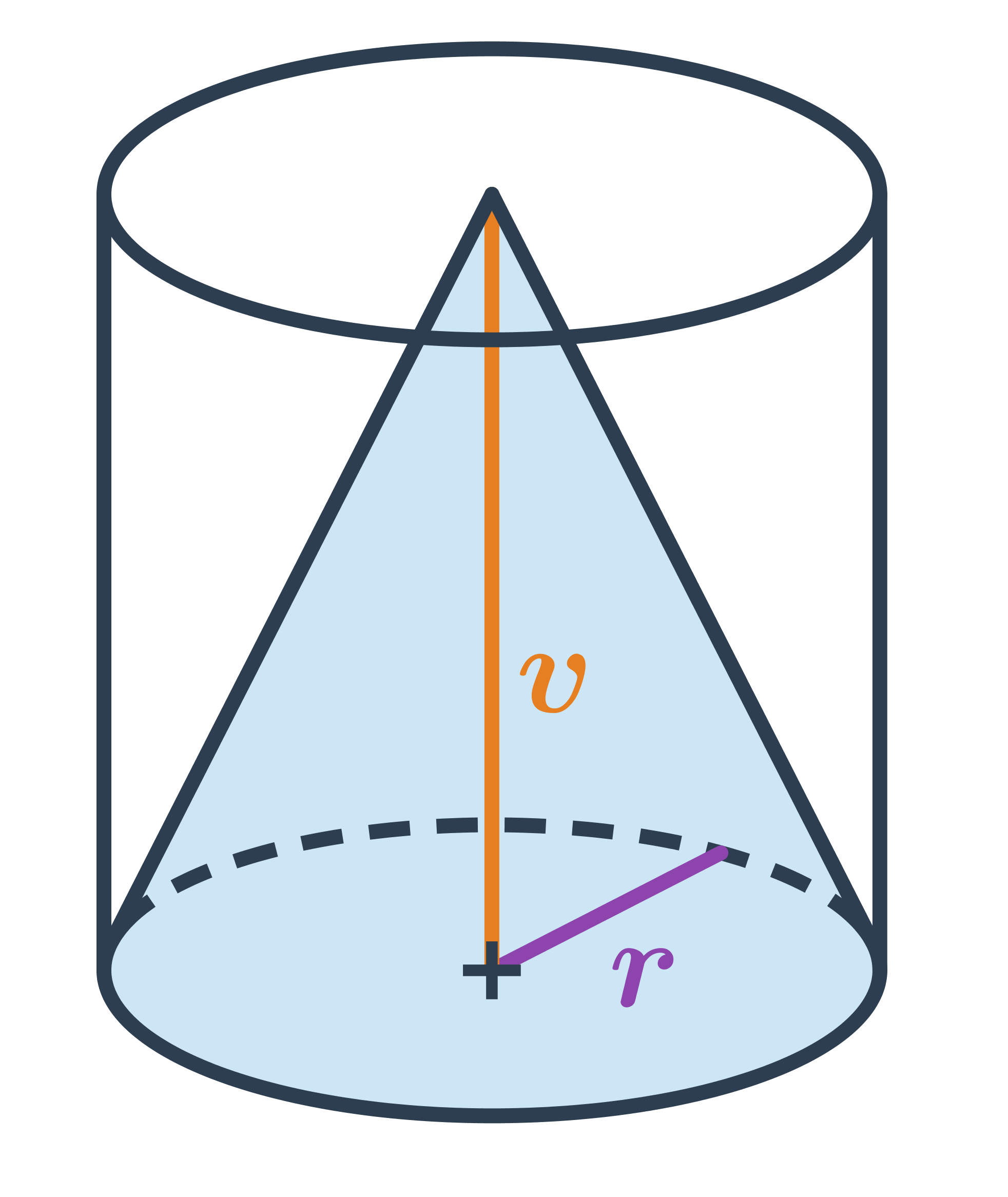
Povrch kužele
Povrch kužele s poloměrem podstavy r a délkou strany s spočítáme takto: V=\pi r^2 + \pi r s = \pi r \cdot (r+s)

Může se stát, že známe poloměr r podstavy kužele a jeho výšku v, ale nemáme zadanou jeho stranu s. Potom si stranu můžeme dopočítat jako přeponu pravoúhlého trojúhelníka s odvěsnami o délkách v a r. Platí: s=\sqrt{v^2+r^2}
- Obsah podstavy kužele: \pi r^2
- Obsah pláště kužele: \frac{1}{2} \cdot 2 \pi r \cdot s = \pi r s
Obsah a obvod
Obvod značíme o. Obvod je součet délek čar, které útvar vymezují. Se základním porozuměním tomu, co obvod vyjadřuje, pomůže téma délka a obvod na mřížce. Obvod se měří v jednotkách délky (např. centimetr, metr).
Obsah značíme S. Obsah vyjadřuje, kolik „místa v rovině“ útvar zaujímá. Se základním porozuměním tomu, co obsah vyjadřuje, pomůže téma obsah na mřížce. Obsah se měří v jednotkách obsahu (např. metr čtvereční, hektar).
Přehled vzorců pro obsah a obvod základních geometrických útvarů:
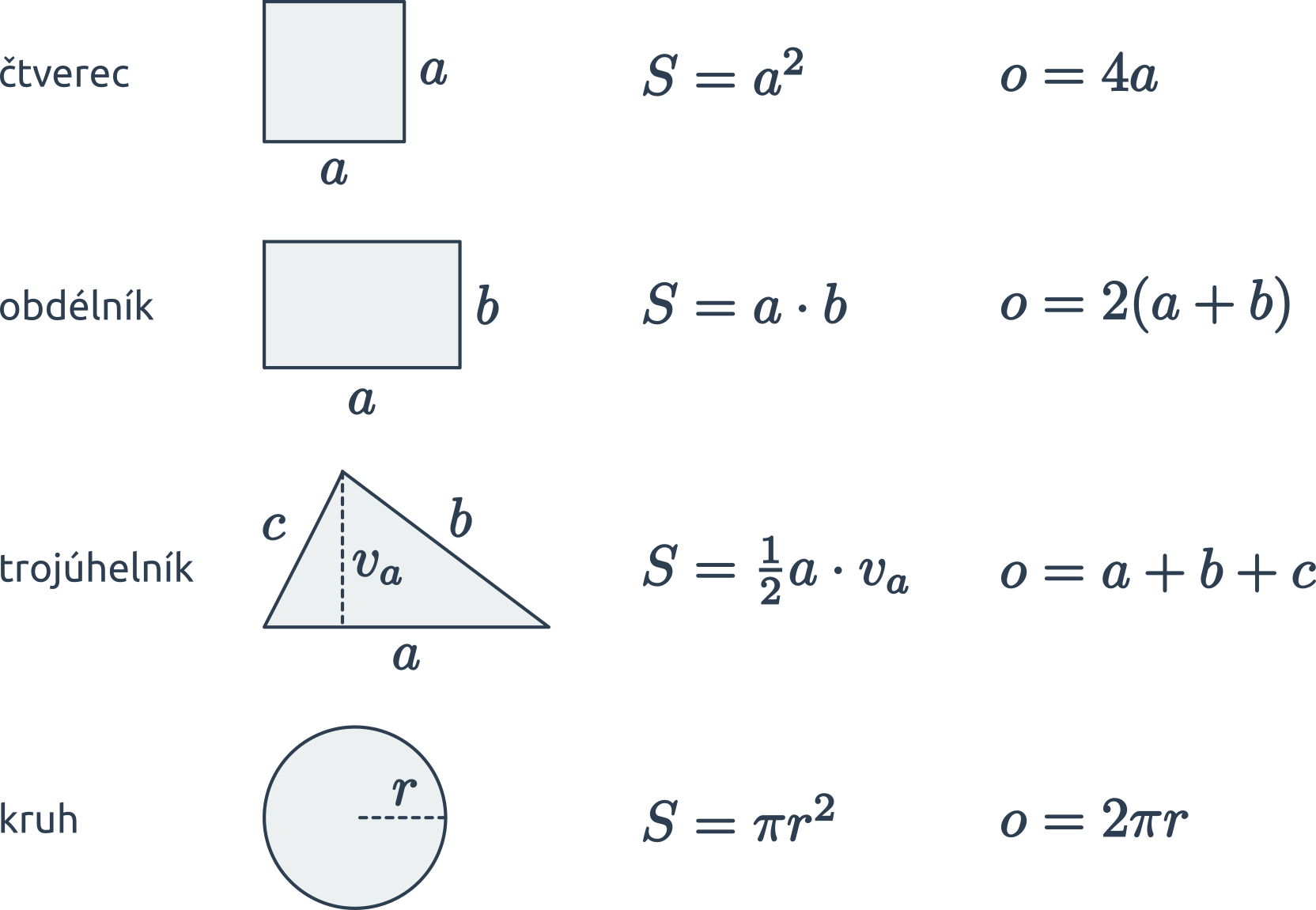
Přehled vzorců je dispozici také jako Obsah a obvod: pomůcka k vytištění.
NahoruObvod: mix
Obvod u trojúhelníků a čtyřúhelníků je prostě součet délek jejich stran.
| Útvar | Vlastnosti | Obvod |
|---|---|---|
| trojúhelník | strany a, b, c | o = a + b + c |
| čtverec | strana a | o = 4a |
| obdélník | strany a, b | o = 2(a+b) |
| rovnoběžník | strany a, b | o = 2(a+b) |
| obecný čtyřúhelník | strany a, b, c, d | o = a+b+c+d |
Objem a povrch
Objem tělesa vyjadřuje kolik místa v prostoru těleso zaujímá. Můžeme si jej představit jako množství vody, které bychom potřebovali, kdybychom chtěli těleso „napustit“. Pro vyjádření objemu využíváme jednotky objemu.
Povrch tělesa je součet obsahů všech ploch, které těleso ohraničují. Můžeme si jej představit jako velikost barevného papíru, který potřebujeme na „polepení“ tělesa. Pro vyjádření povrchu využíváme jednotky obsahu.
Značení ve vzorcích
| V | objem |
| S | povrch |
| S_p | obsah podstavy |
| S_{pl} | obsah pláště |
| a, b, c | délky stran |
| r | poloměr |
| v | výška |
| s | strana kužele |
Vzorce
| Útvar | Objem | Povrch |
|---|---|---|
| krychle | V = a^3 | S=6a^2 |
| kvádr | V = abc | S = 2(ab+ac+bc) |
| koule | V=\frac43\pi r^3 | S=4\pi r^2 |
| válec | V=S_p\cdot v =\pi r^2 v | S=2S_p+S_{pl} =2\pi r(r+v) |
| kužel | V=\frac{1}{3}S_p\cdot v =\frac13 \pi r^2 v | S =S_p+S_{pl} =\pi r(r+\sqrt{r^2+v^2})=\pi r^2 +\pi rs |
| jehlan | V=\frac{1}{3}S_p\cdot v | S=S_p+S_{pl} |
| pravidelný čtyřboký jehlan | V=\frac{1}{3}S_p\cdot v=\frac{1}{3} a^2v | |
| hranol | V= S_p\cdot v | S=2\cdot S_p+S_{pl} |
Komiks pro zpestření
Objem hranatých těles
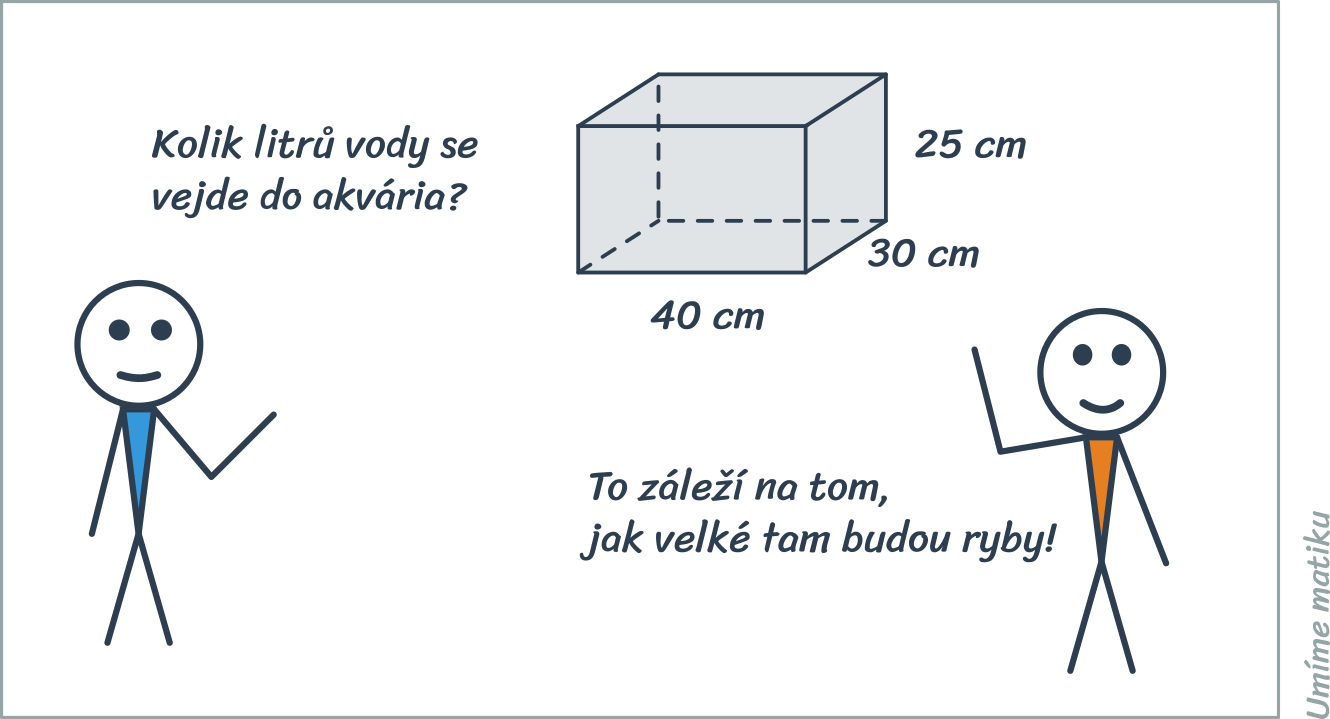
Vzorce pro objem „hranatých“ těles vychází z obsahu podstavy a výšky tělesa.
Objem libovolného hranolu je součin obsahu podstavy a výšky: V=S_p\cdot v.
Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = abc. Objem krychle vypočítáme stejným způsobem. Protože v krychli jsou všechny hrany stejně dlouhé, výraz se zjednoduší na V = a^3.
Příklad: objem krychle
Určete objem krychle o hraně délky 4 m.
- Objem krychle o hraně délky a spočítáme jako V=a^3.
- Dosadíme za a známou délku hrany.
- Takže daná krychle má objem V = 4^3 = 64 m³.
Délka hrany je zadaná v metrech, proto je výsledný objem krychle v metrech krychlových.
Příklad: objem kvádru
Určete objem kvádru s hranami 3, 6 a 10 cm.
- Objem kvádru s hranami a,b,c spočítáme jako V=a\cdot b\cdot c.
- Dosadíme za a,b,c známé délky hran.
- Takže daný kvádr má objem V = 3\cdot 6 \cdot 10 = 180 cm³.
Délky hran jsou zadány v centimetrech, proto je výsledný objem kvádru v centimetrech krychlových.
Objem jehlanu je jedna třetina součinu obsahu podstavy a výšky, tj. V=\frac{1}{3}S_p\cdot v. Pro pravidelný čtyřboký jehlan pak tedy V=\frac{1}{3} a^2v.
Příklad: objem pravidelného čtyřbokého jehlanu
Určete objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany 6 cm a výškou 4 cm.
- Objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany a a výškou v spočítáme jako V=\frac{1}{3} \cdot a^2 \cdot v.
- Dosadíme za a a v známé hodnoty.
- Takže daný jehlan má objem V=\frac{1}{3} 6^2 \cdot 4 = 48 cm³.
Délka hran podstavy a velikost výšky jsou zadány v centimetrech, proto je výsledný objem jehlanu v centimetrech krychlových.
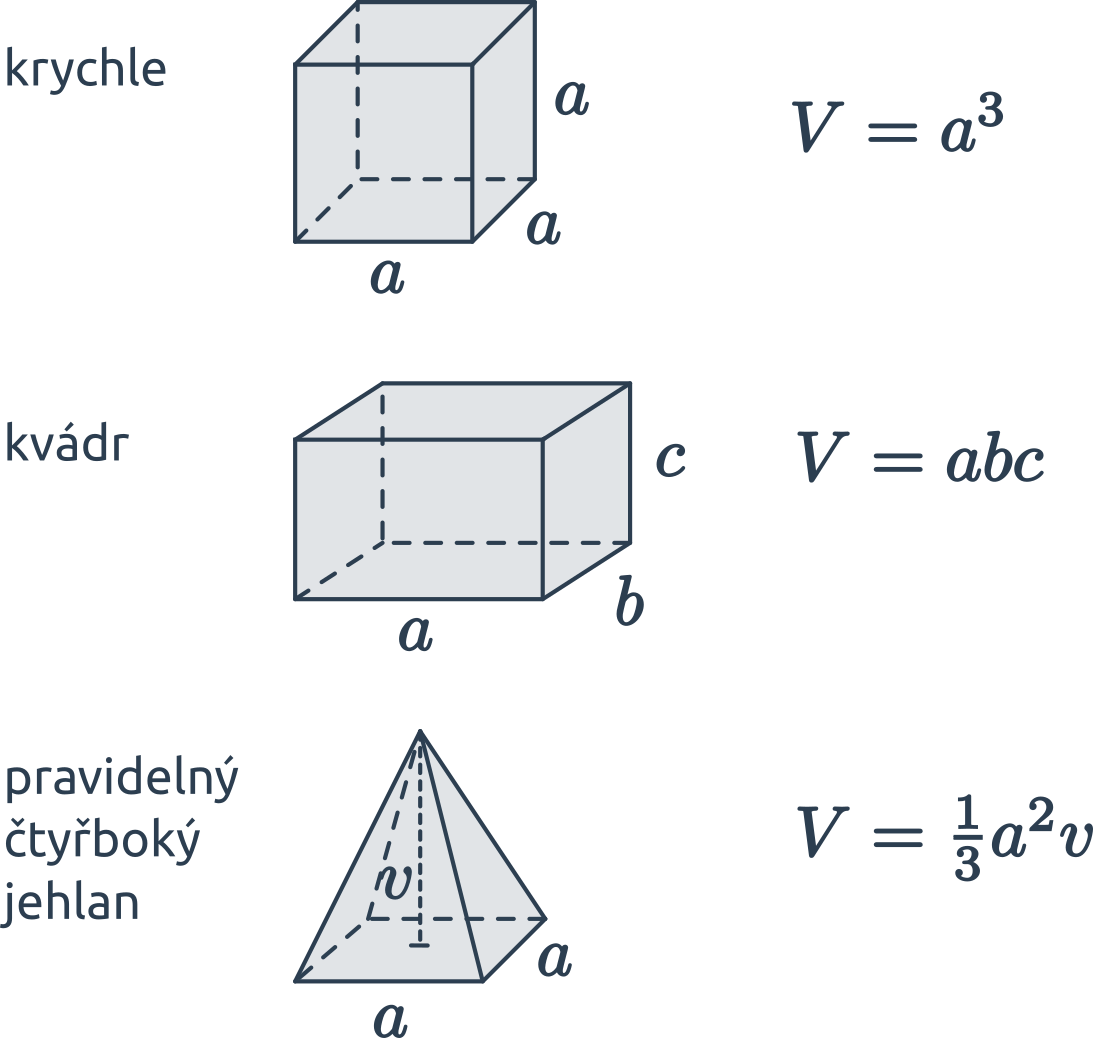
Objem kulatých těles
Objem „kulatých“ těles vypočítáme za využití konstanty \pi \approx 3{,}14 159 265. Ve vzorcích označuje r poloměr (koule či podstavy) a v výšku válce.
- Objem koule je V = \frac43 \pi r^3.
- Objem válce je obsah (kruhové) podstavy vynásobený výškou, tedy V = S_p \cdot v = \pi r^2 v.
- Objem kužele je jedna třetina obsahu podstavy vynásobeného výškou, tedy V = \frac13 S_p \cdot v = \frac13 \pi r^2 v.
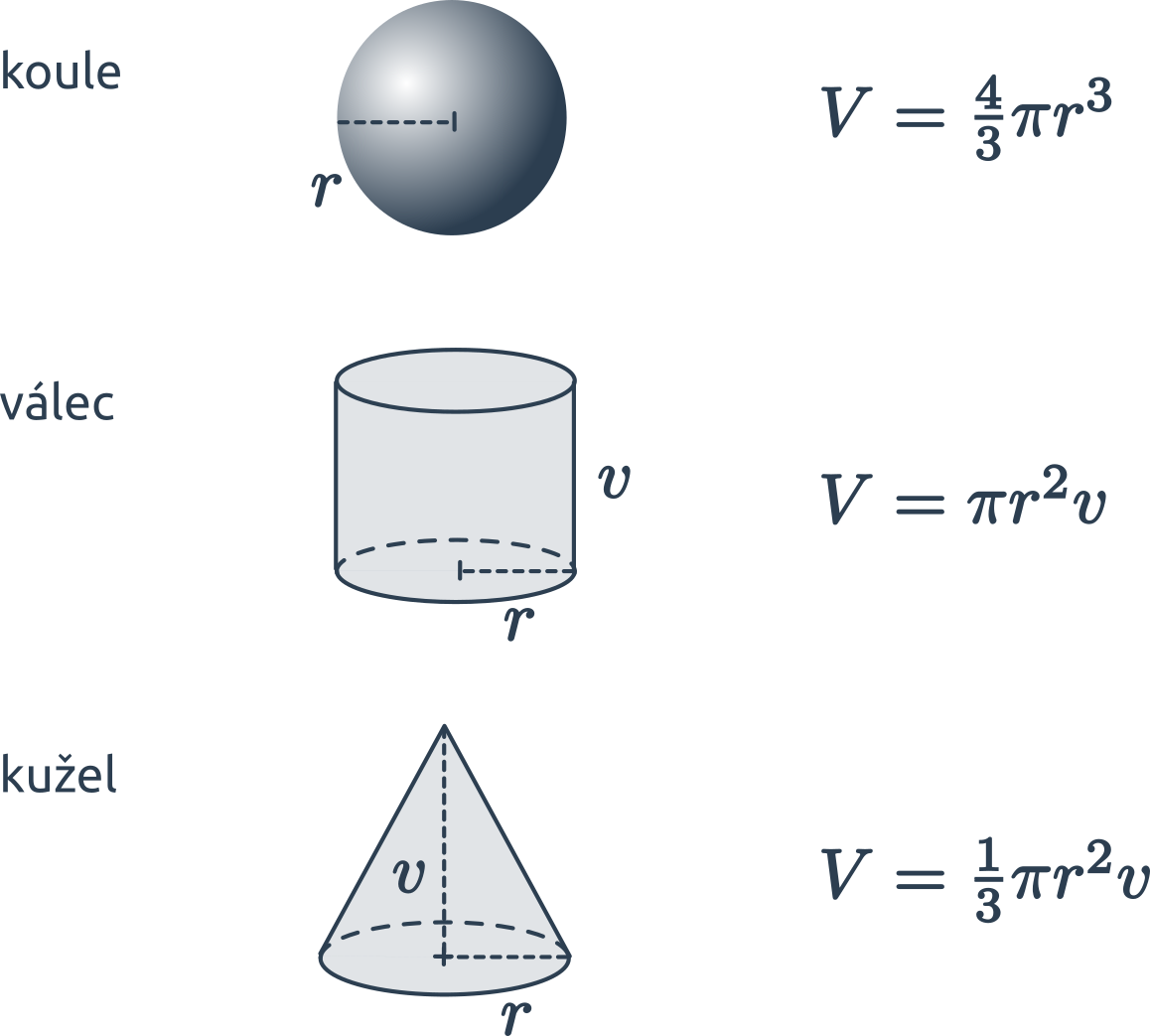
Příklad: objem koule s daným poloměrem
Určete objem koule o poloměru 3 m.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Dosadíme za r známou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 3^3 m³ = 36 \pi m³ \doteq 113 m³
Velikost poloměru je zadaná v metrech, proto je výsledný objem koule v metrech krychlových.
Příklad: objem koule s daným průměrem
Určete objem koule o průměru 4 dm.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Známe průměr, proto umíme určit poloměr koule jako polovinu průměru r=\frac42=2 dm
- Dosadíme za r spočítanou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 2^3 dm³ = \frac{32}{3} \pi dm³ \doteq 33{,}5 dm³
Velikost průměru je zadaná v decimetrech, proto je výsledný objem koule v decimetrech krychlových.
Příklad: objem válce
Určete objem válce o poloměru podstavy 5 mm a výšce 0{,}1 cm.
- Poloměr podstavy a výšku máme v různých jednotkách. Převedeme velikost výšky na milimetry, abychom měli všechny údaje v mm.
- r=5 mm, v=0{,}1 cm = 1 mm
- Objem válce se známým poloměrem podstavy r a výškou v spočítáme jako: V = \pi r^2 v
- Dosadíme za r a v známé hodnoty v mm.
- Daný válec má objem: V = \pi \cdot 5^2 \cdot 1 mm³ = 25 \pi mm³ \doteq 78{,}5 mm³
Výpočty provádíme s velikostí poloměru i výšky v milimetrech, proto je výsledný objem válce v milimetrech krychlových.
Povrch hranatých těles
Povrch „hranatých“ těles je prostě součet obsahů jednotlivých stran.
Hranol má dvě stejné podstavy a plášť, povrch je tedy S=2\cdot S_p+S_{pl}. Jehlan má jednu podstavu a plášť, povrch je tedy S=S_p+S_{pl}.
Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2(ab+ac+bc).
Krychle má šest stěn — jde o šest stejných čtverců. Povrch je S=6a^2.
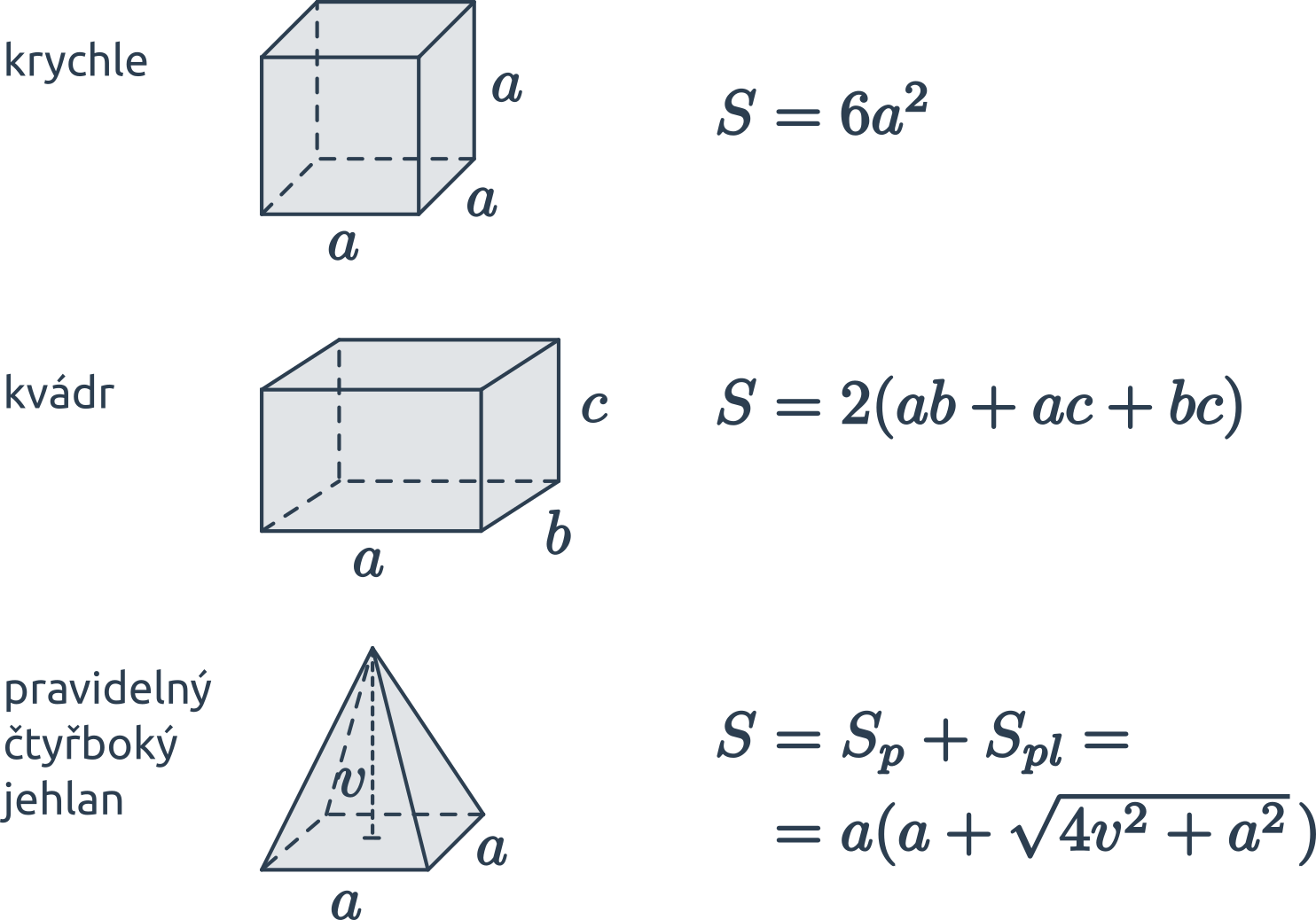
Povrch kulatých těles
Povrch „kulatých“ těles vypočítáme za využití konstanty \pi \approx 3{,}14 159 265. Ve vzorcích označuje r poloměr (koule či podstavy), v výšku válce, s stranu kužele.
- Povrch koule je S = 4\pi r^2.
- Povrch válce se skládá z podstavy (dvakrát) a pláště: S = 2\cdot \pi r^2 + 2\pi r v = 2\pi r (r+v).
- Povrch kužele se skládá z podstavy a pláště: S = \pi r^2 + \pi rs= \pi r(r+s).
Úhel je část roviny vymezená dvěma polopřímkami. Velikost úhlu měříme nejčastěji ve stupních, přičemž plný úhel má velikost 360°. Úhly využíváme v mnoha oblastech geometrie a mají bohaté praktické využití ve fyzice, navigaci (azimuty) a v podstatě kdekoliv, kde se něco staví.
Při práci s úhly je první krok základní poznávání úhlů – potřebujeme získat základní představu o úhlech a schopnost odhadnout velikost úhlu podle obrázku. Další krok je pak znalost pojmů souvisejících s úhly, mezi které patří třeba úhel ostrý, tupý, pravý, plný, vrcholový či střídavý.
Jakmile zvládneme základy práce s úhly, můžeme se pustit do práce s úhly v rovinných objektech:
Pokročilejší téma pak jsou radiány, což je alternativní vyjadřování velikosti úhlů, které se často používá ve spojitosti s goniometrickými funkcemi.
Úhly a želvy
Pro získání zběhlosti v práci s úhly může posloužit atraktivní cvičení Želví grafika zařazené v předmětu informatika.
Úhly ve čtyřúhelníku
Součet vnitřních úhlů ve čtyřúhelníku je 360°.
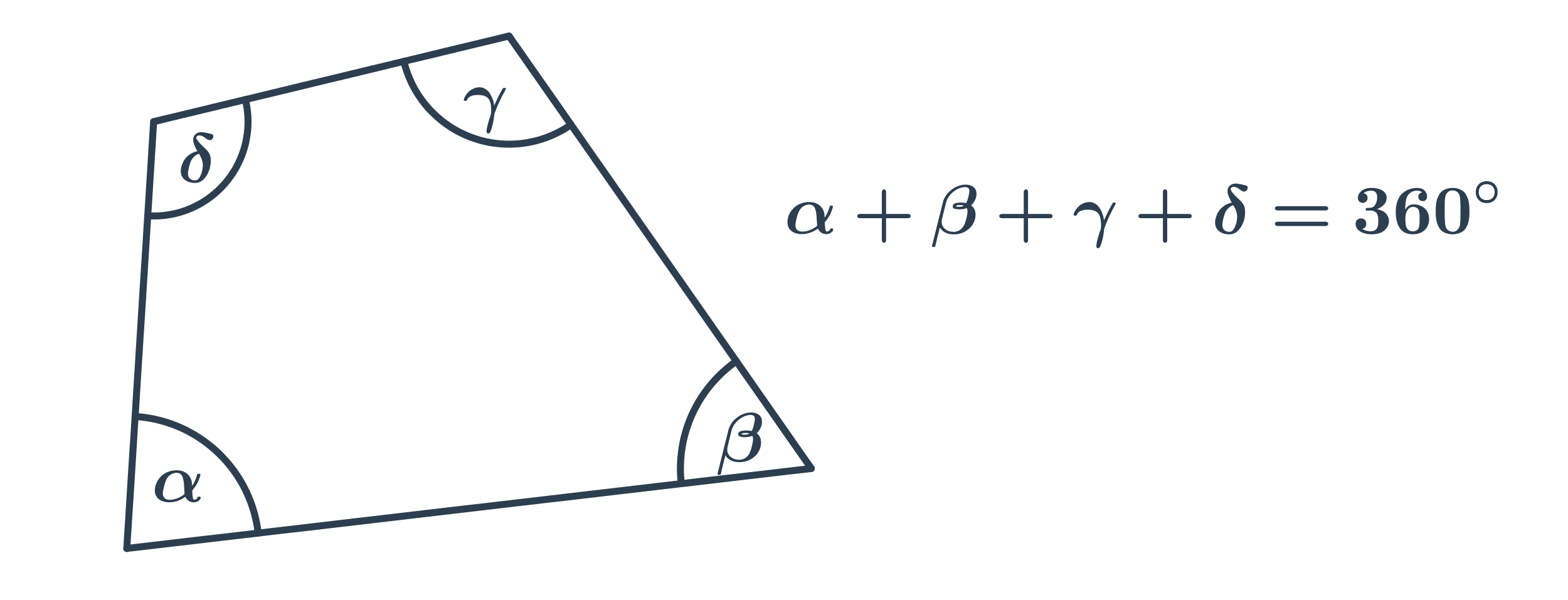
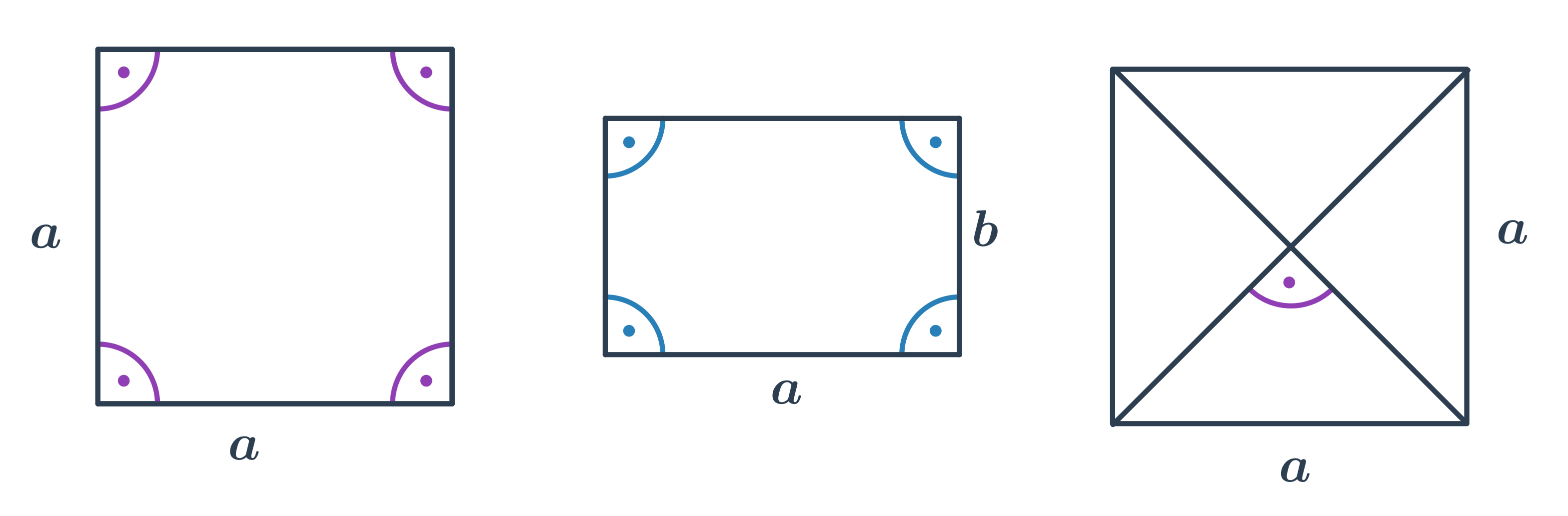
Čtverec, obdélník
- Ve čtverci i obdélníku je velikost všech vnitřních úhlů 90°.
- Ve čtverci svírají úhlopříčky úhel o velikosti 90°.
Rovnoběžník
- Protější úhly mají stejnou velikost.
- Součet velikostí sousedních úhlů je 180°.
- Speciálním případem rovnoběžníku je kosočtverec, jehož úhlopříčky svírají pravý úhel.
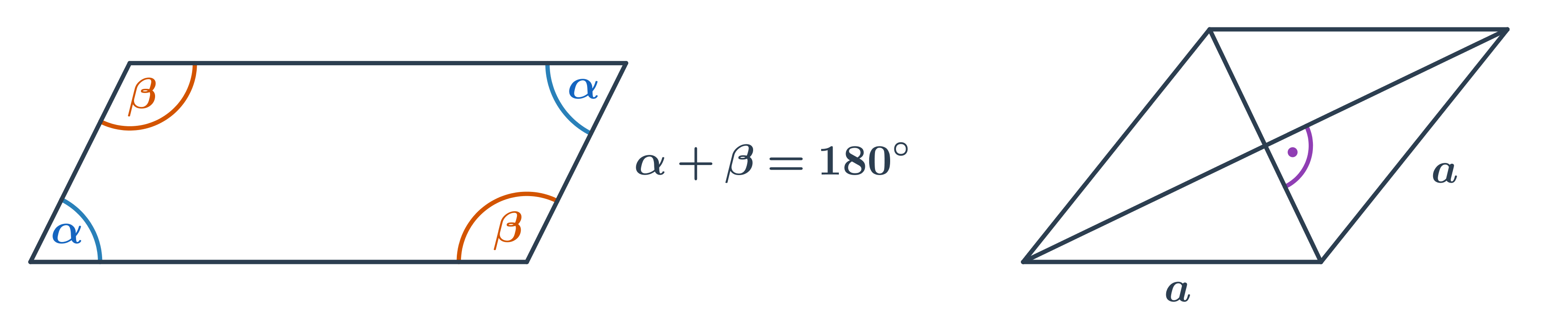
Lichoběžník
- Součet velikostí vnitřních úhlů u ramen je 180°.
- V rovnoramenném lichoběžníku jsou úhly u základen shodné.
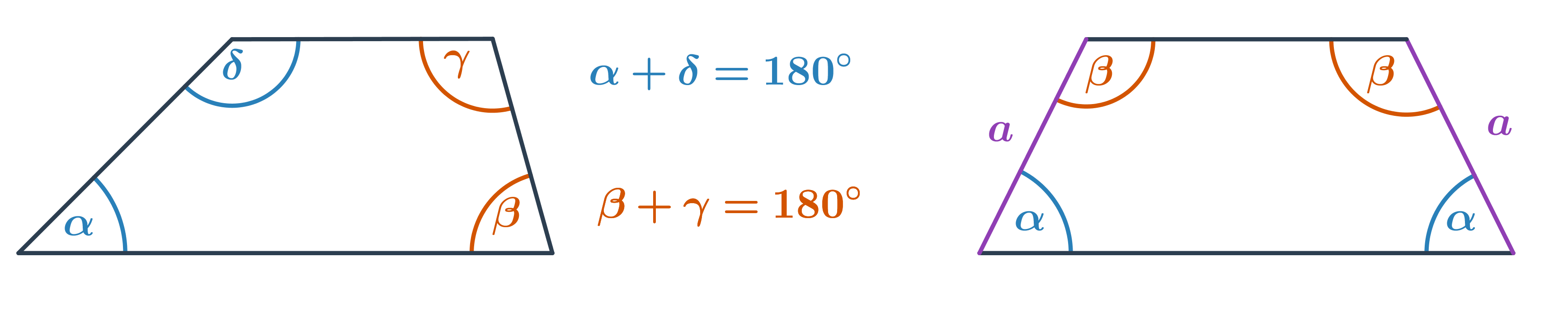
Při výpočtu neznámého úhlu můžeme také daný čtyřúhelník rozdělit na několik trojúhelníků a lze využít i vrcholových a vedlejších úhlů.
Příklad: určete velikost úhlu
Určete velikost oranžového úhlu v rovnoběžníku ABCD.
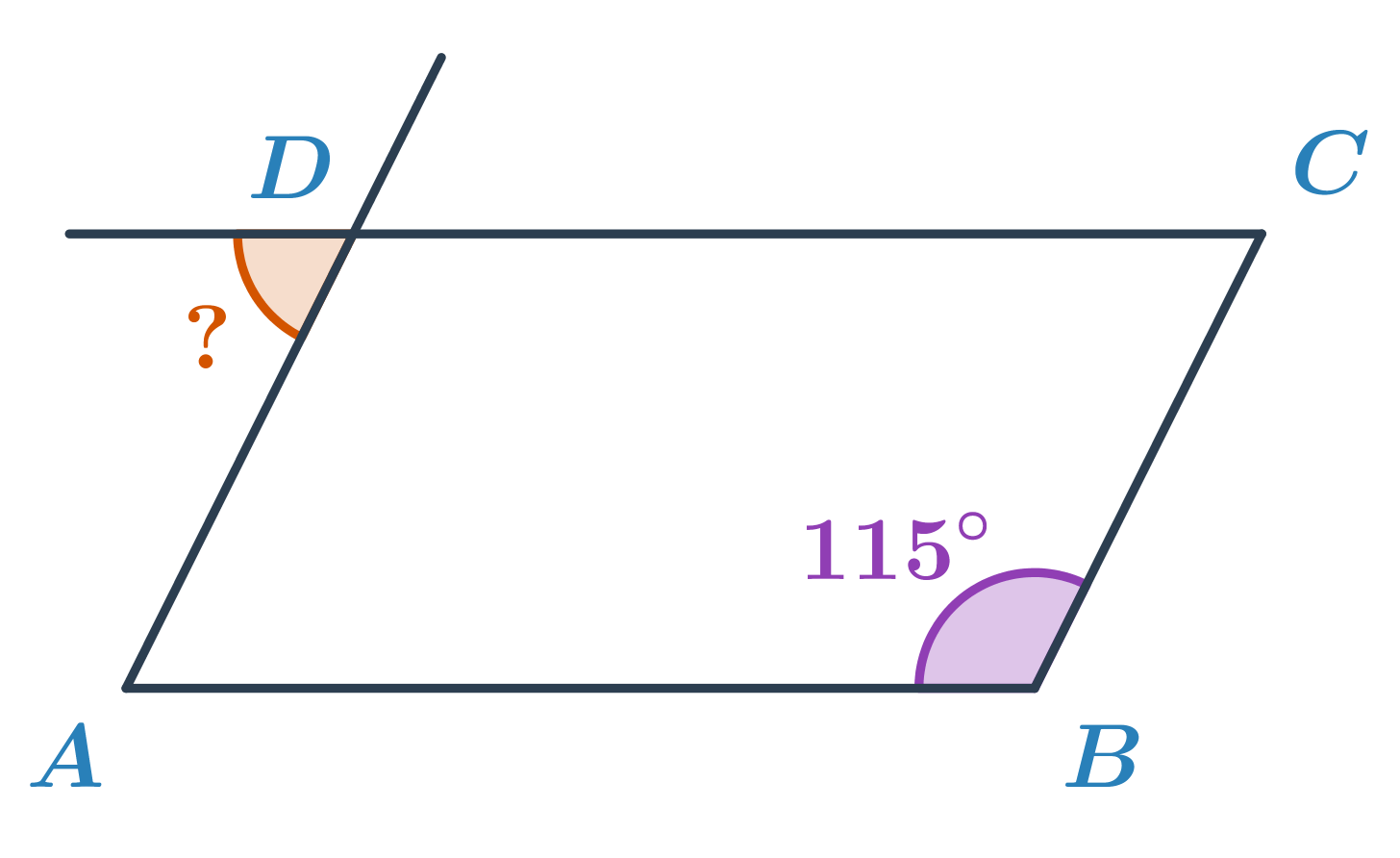
V rovnoběžníku mají protější úhly stejnou velikost, úhel ADC má tedy velikost 115°. Úhel ADC tvoří s neznámým úhlem dvojici vedlejších úhlů. Velikost neznámého úhlu je tedy 180°-115°=65°.
Úhly a mnohoúhelníky
Součet vnitřních úhlů v obecném mnohoúhelníku s n stranami (tedy n-úhelníku) je 180^\circ\cdot(n-2). Například v pětiúhelníku je součet vnitřních úhlů 180^\circ(5-2)=540^\circ. Každý vnitřní úhel pak může mít jinou velikost.
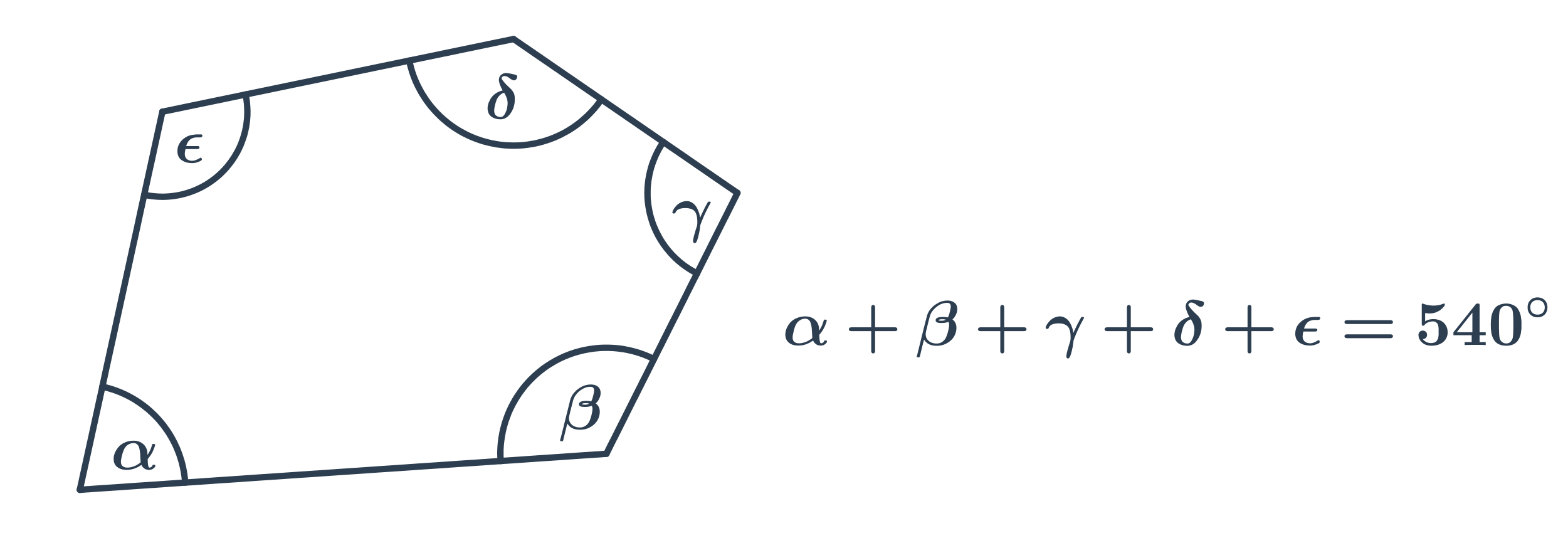
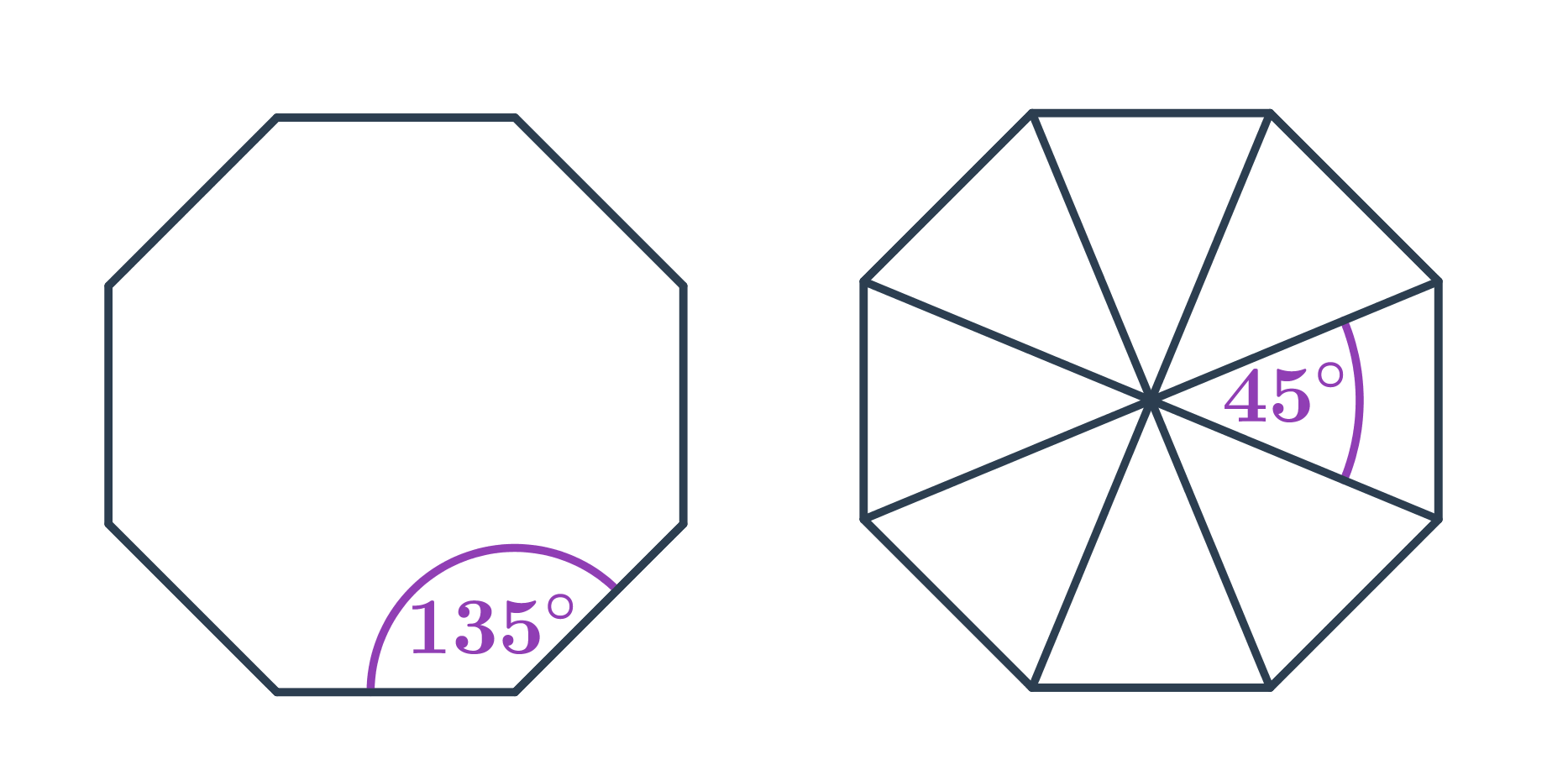
Pravidelné mnohoúhelníky
- Každý vnitřní úhel v pravidelném mnohoúhelníku s n vrcholy má velikost 180^\circ\cdot\frac{n-2}{n}. Například v pravidelném osmiúhelníku má každý vnitřní úhel velikost 180^\circ\cdot\frac{8-2}{6}=135^\circ.
- Velikost středového úhlu pravidelného n-úhelníku je \frac{360^\circ}{n}. Například v pravidelném osmiúhelníku má každý středový úhel velikost \frac{360^\circ}{8}=45^\circ.
Při výpočtu neznámého úhlu v mnohoúhelníku lze využít i vrcholových a vedlejších úhlů.
Příklad: Určete velikost úhlu
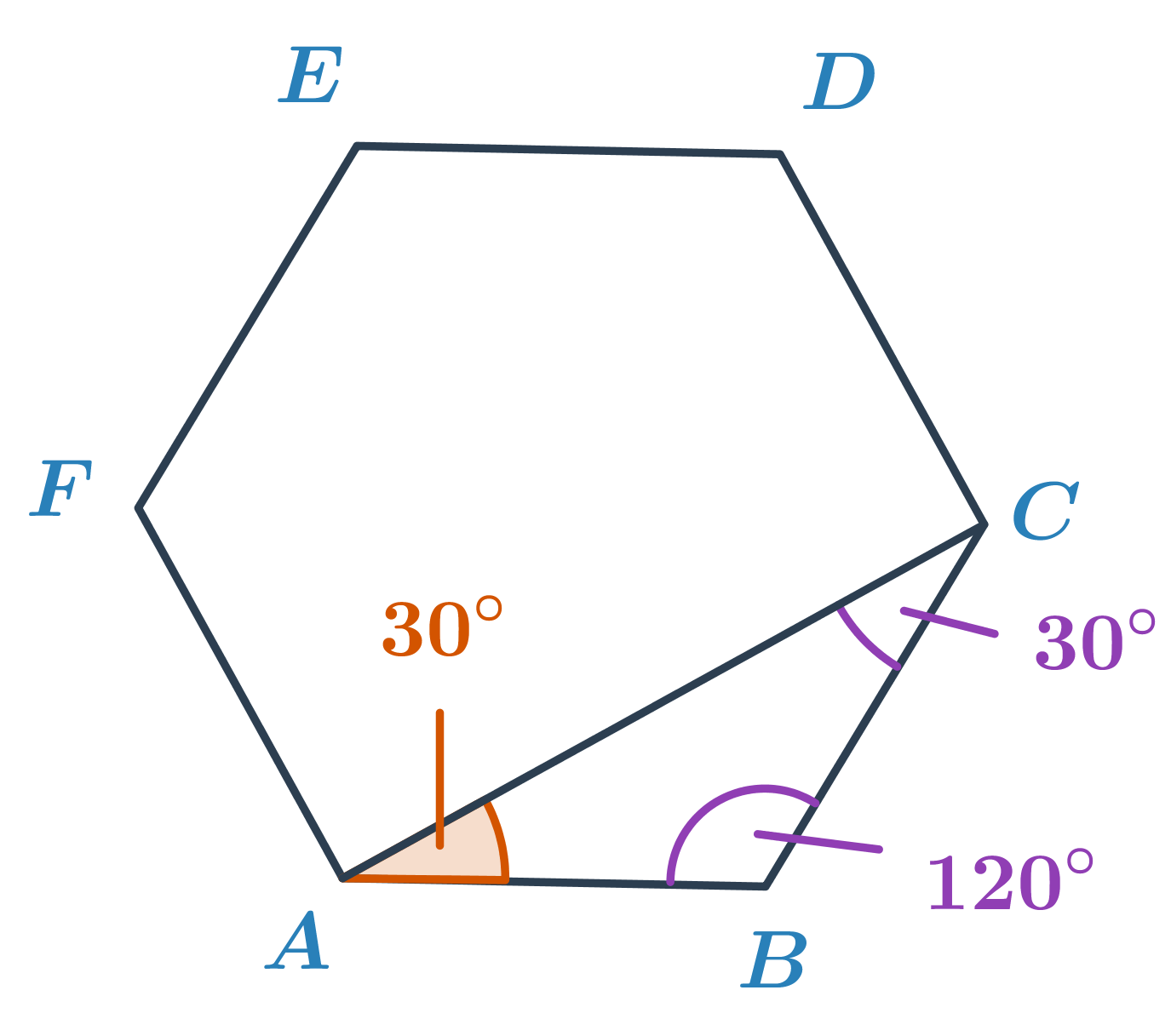
Určete velikost oranžového úhlu v pravidelném šestiúhelníku ABCDEF.
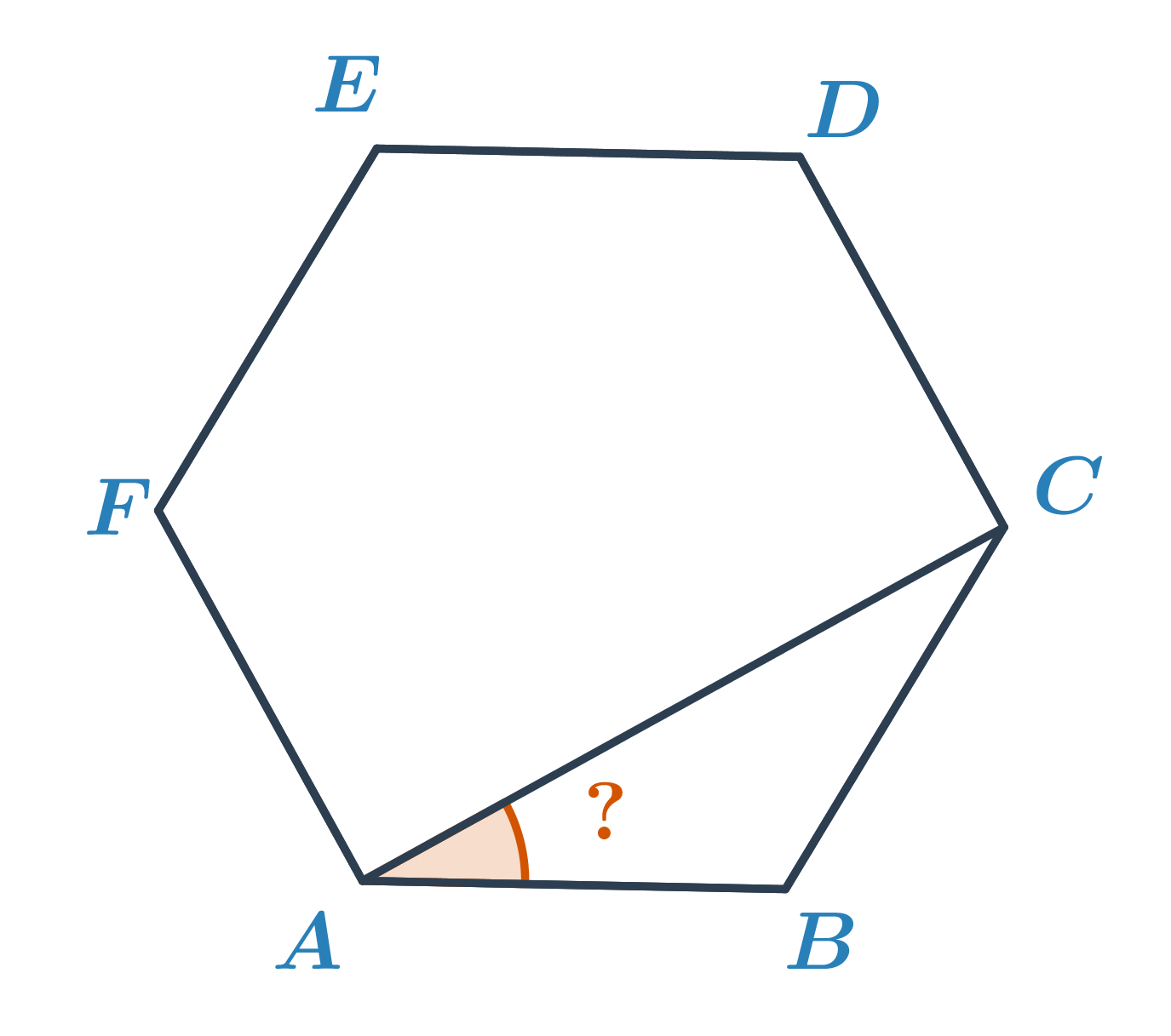
V pravidelném šestiúhelníku má každý úhel stejnou velikost, a to 180^\circ\cdot\frac{6-2}{6}=120^\circ. Úhel ABC má tedy velikost 120^\circ. Trojúhelník ABC je rovnoramenný, úhly u vrcholů A a C jsou pak shodné. Jejich velikost je (180^\circ-120^\circ):2=30^\circ.
Geometrické konstrukce
Konstrukční úlohou rozumíme úlohu, ve které chceme sestrojit určitý geometrický útvar (alespoň jeden, případně všechny) splňující dané podmínky. Jinými slovy, pomocí pravítka, kružítka a případně i úhloměru sestrojíme geometrický útvar (trojúhelník, obdélník atd.), pro který známe délky jeho stran, velikosti úhlů či jiné vlastnosti.
Před rýsováním je dobré si ujasnit:
- body značíme velkými písmeny, např bod A
- přímky značíme malými písmeny, např. přímka p
Obvyklé kroky řešení konstrukční úlohy
Náčrtek: Od ruky si nakreslíme obrázek hledaného útvaru se vším, co známe ze zadání. To nám pomůže představit si výsledek. Pro přehlednost můžeme jednotlivé prvky vyznačit barevně. Nezapomeňte, náčrtky děláme velké a přehledné. V obrázku velkém jako blecha nic neuvidíme.
Popis konstrukce: Popis jednotlivých kroků, které musíme udělat, abychom dospěli k výsledku. Popis píšeme proto, aby každý mohl náš postup zopakovat. Z výsledného obrázku to nejde vždy snadno udělat. Pro zápis konstrukce používáme geometrické značení. Popis konstrukce řešíme obvykle až ve vyšších ročnících.
Konstrukce: Jde o samotné rýsování příkladu.
Zkouška správnosti: Měli bychom ověřit, jestli obrázek opravdu splňuje všechny podmínky ze zadání.
Počet řešení (diskuse): Zjistíme počet výsledků, které vyhovují zadání úlohy. Ne vždy musíme všechny výsledky narýsovat. Například při konstrukci trojúhelníku se známými délkami stran nám typicky stačí narýsovat jeden trojúhelník „nad“ první narýsovanou stranou, i když oblouky mají dva průsečíky a mohly by nám vzniknout dva shodné trojúhelníky. U dalších jednodušších úloh většinou postupujeme podobně. Při řešení náročnějších konstrukčních úloh, kde je vyžadováno nalezení všech řešení, je dobré mít na paměti, v kolika bodech se útvary doopravdy protínají a zda uvažujeme skutečně celé množiny bodů daných vlastností.
Pracovní listy
Kromě níže uvedených interaktivních cvičení jsou k dispozici také následující pracovní listy k vytištění a rýsování na papíře:
- Konstrukce čtverce a obdélníku (pro 4. ročník) + řešení
- Konstrukce trojúhelníků: známé délky stran + řešení
- Konstrukce rovnostranných a rovnoramenných trojúhelníků + řešení
- Konstrukce trojúhelníků podle vět + řešení
- Konstrukce trojúhelníků: těžnice, výšky + řešení
- Konstrukce trojúhelníků: vepsaná a opsaná kružnice + řešení
- Konstrukce čtyřúhelníků: čtverce a obdélníky + řešení
- Konstrukce čtyřúhelníků: rovnoběžníky a lichoběžníky + řešení
- Konstrukce čtyřúhelníků: obecný čtyřúhelník + řešení
- Konstrukce s použitím osové souměrnosti + řešení
- Konstrukce s použitím středové souměrnosti + řešení
- Konstrukční úlohy: průřezově (pro 9. ročník) + řešení
Geometrické konstrukce: značení
| Značka | Význam |
|---|---|
| p \parallel q | rovnoběžné přímky |
| p \perp q | kolmé přímky |
| \sphericalangle BAC | úhel při vrcholu A |
| \triangle ABC | trojúhelník ABC |
| \vert AB\vert | délka úsečky AB |
| A \in p | A leží na přímce p |
| A \notin p | A neleží na přímce p |
| \leftrightarrow AB | přímka procházející body A, B |
| \mapsto AB | polopřímka začínající v bodě A, procházející bodem B |
| \mapsto ABC | polorovina s hraniční přímkou AB, obsahující bod C |
| \mapsto pK | polorovina s hraniční přímkou p, obsahující bod K |
| \leftrightarrow ABC | rovina určená body A, B, C |
| (p, q) | pás roviny, ohraničený rovnoběžkami p, q |
Dále využíváme pro zápis geometrických konstrukcí množinové operace, především průnik (\cap) a sjednocení (\cup).
NahoruPolopřímky a poloroviny
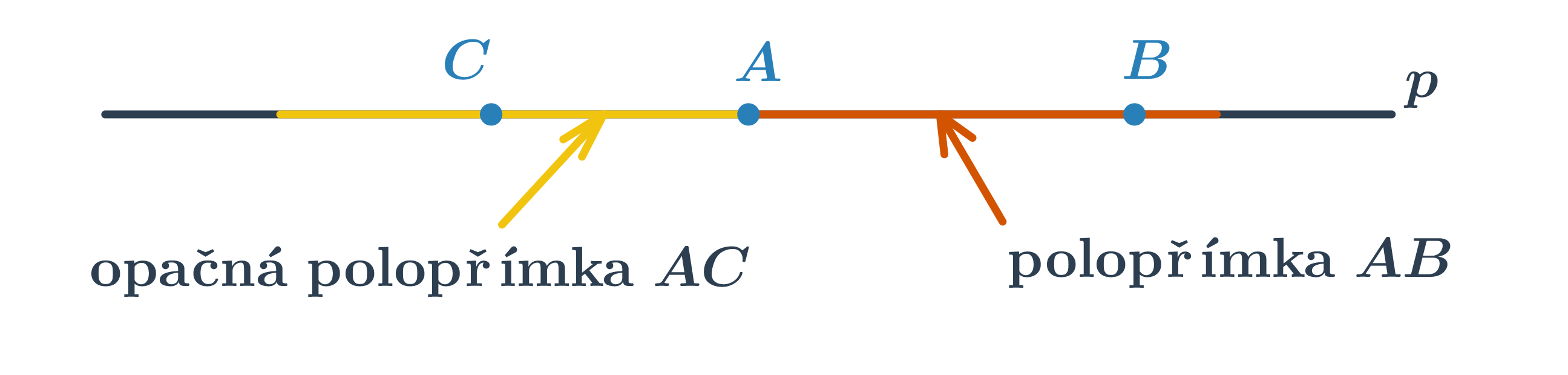
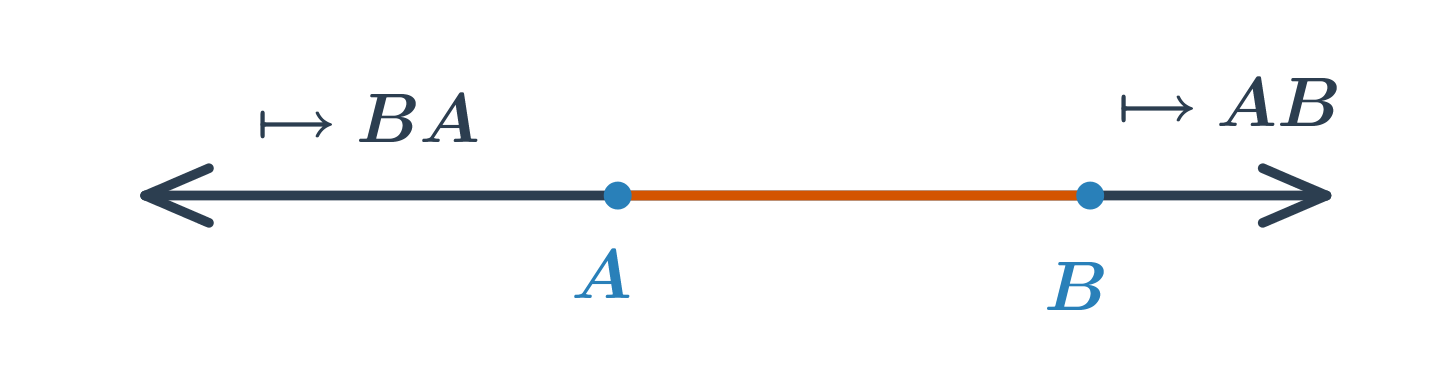
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem. Tento bod se nazývá počáteční. Polopřímku s počátečním bodem A procházející bodem B značíme \mapsto AB. Každý bod rozděluje přímku na dvě opačné polopřímky se společným počátečním bodem.
Základní vlastnosti polopřímek:
- Sjednocením dvou opačných polopřímek je přímka.
- Průnikem dvou opačných polopřímek je bod.
- Průnikem polopřímek \mapsto AB a \mapsto BA je úsečka AB.
Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme \mapsto pK. Je-li přímka p určena body A, B, můžeme také psát \mapsto ABK. Každá přímka rozděluje rovinu na dvě opačné poloroviny se společnou hraniční přímkou.
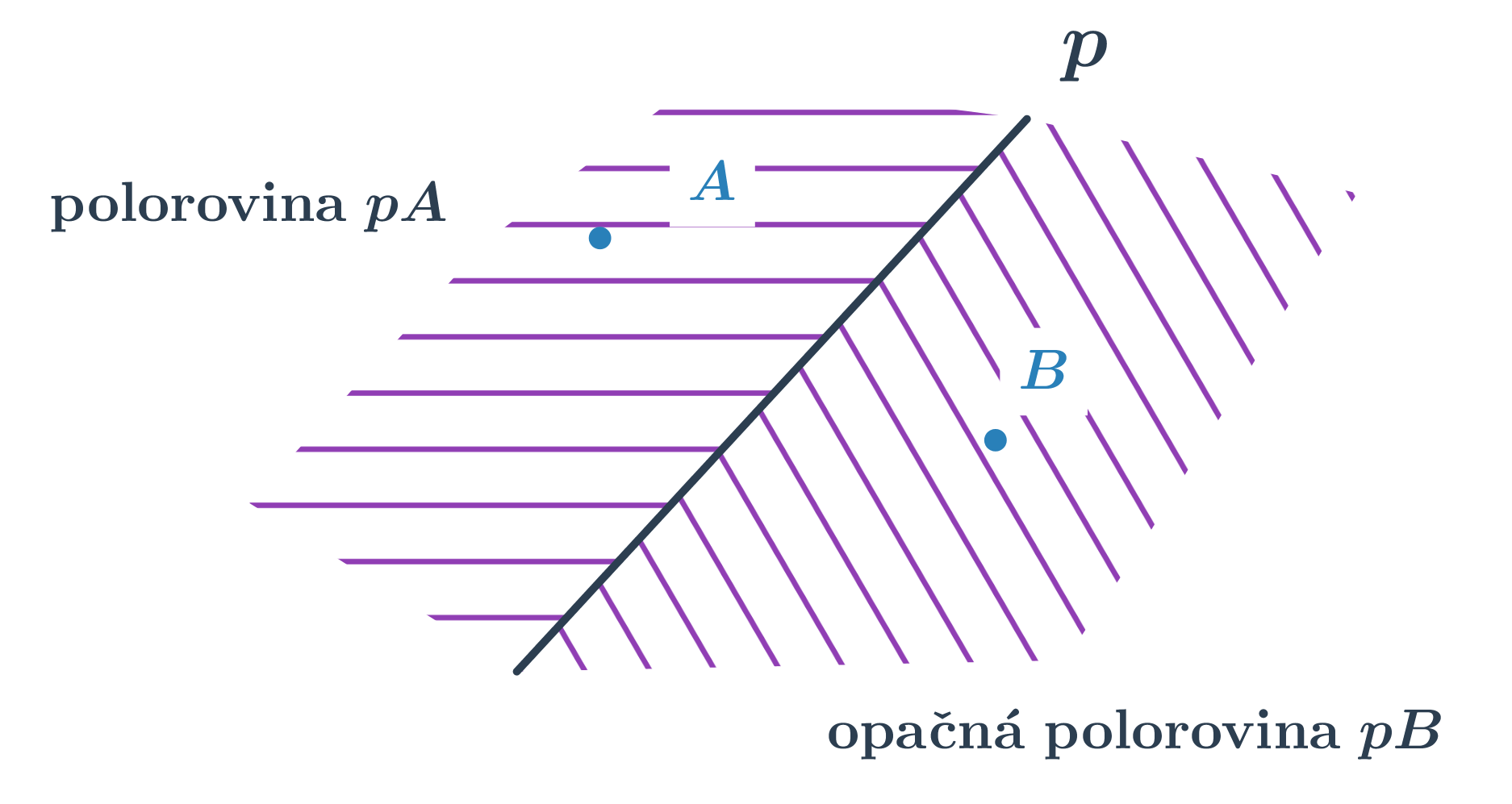
Základní vlastnosti polorovin:
- Sjednocením dvou opačných polorovin je rovina.
- Průnikem dvou opačných polorovin je hraniční přímka.
- Průnikem dvou polorovin s rovnoběžnými hraničními přímkami je pás rovnoběžek.
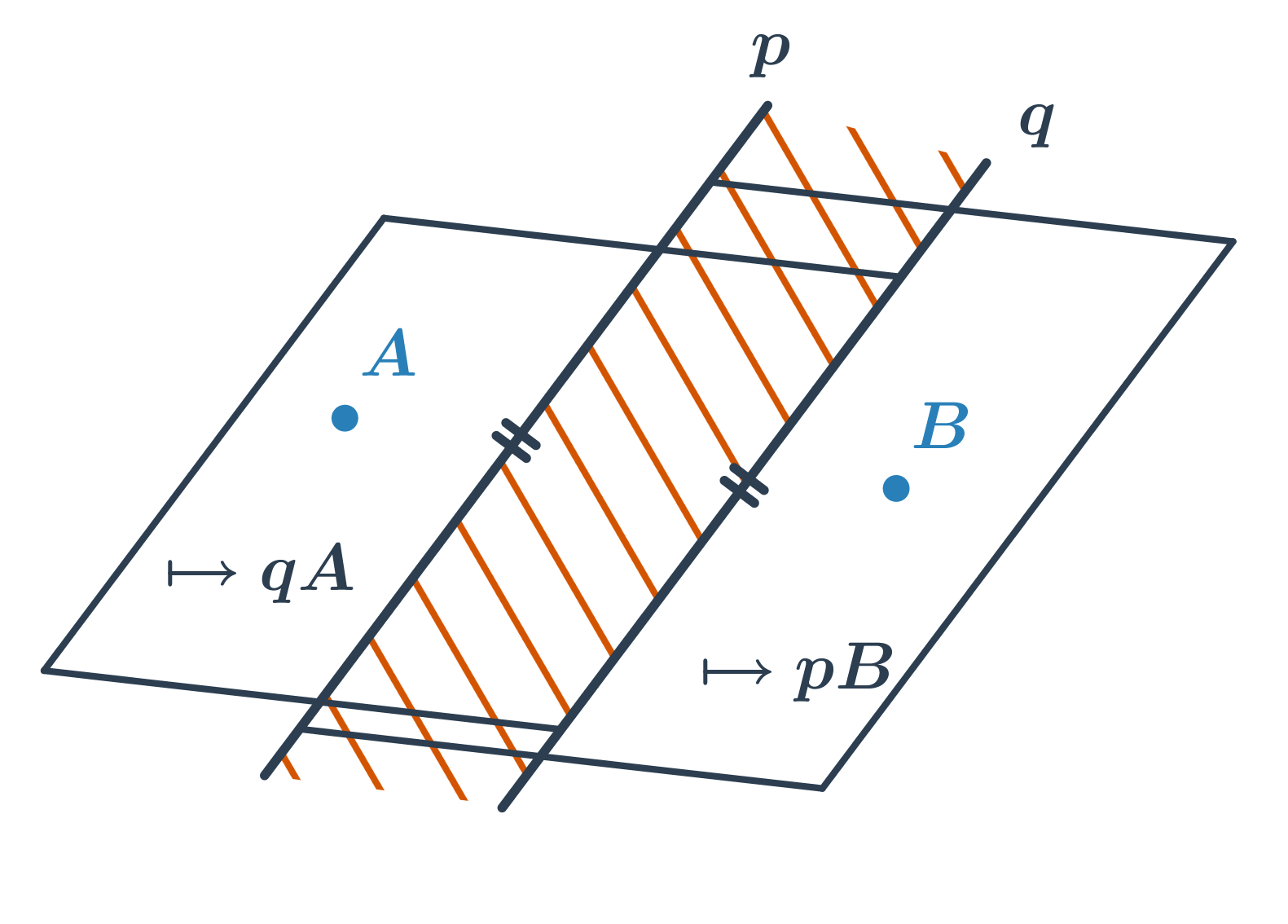
Pro zápis geometrických konstrukcí používáme množinové operace, především průnik \cap a sjednocení \cup.
Příklad: průnik přímky a poloroviny
Rozhodněte, co je průnikem polopřímky CA a poloroviny ABC.
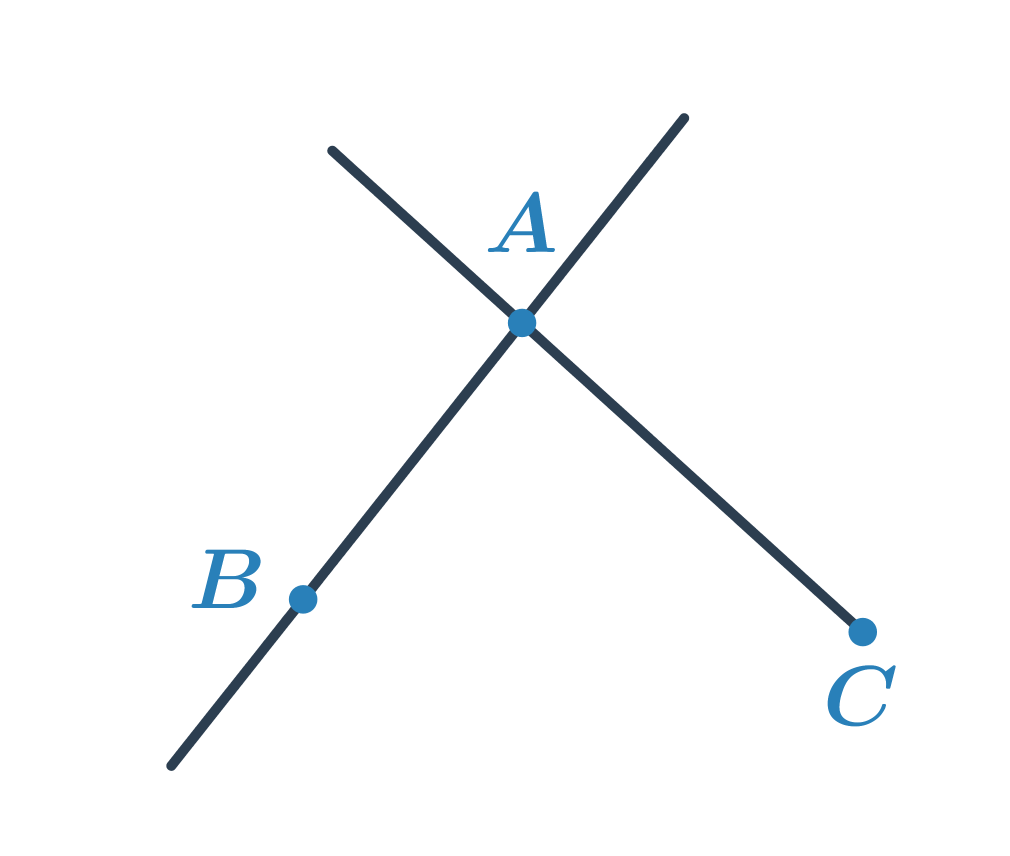
Polorovina ABC je určena hraniční přímkou AB a bodem C. Polopřímka CA má počáteční bod C a prochází bodem A. Průnikem je pak úsečka AC. Matematicky bychom úlohu zapsali: AC = \mapsto ABC \cap \mapsto CA.
Rovnoběžky a kolmice
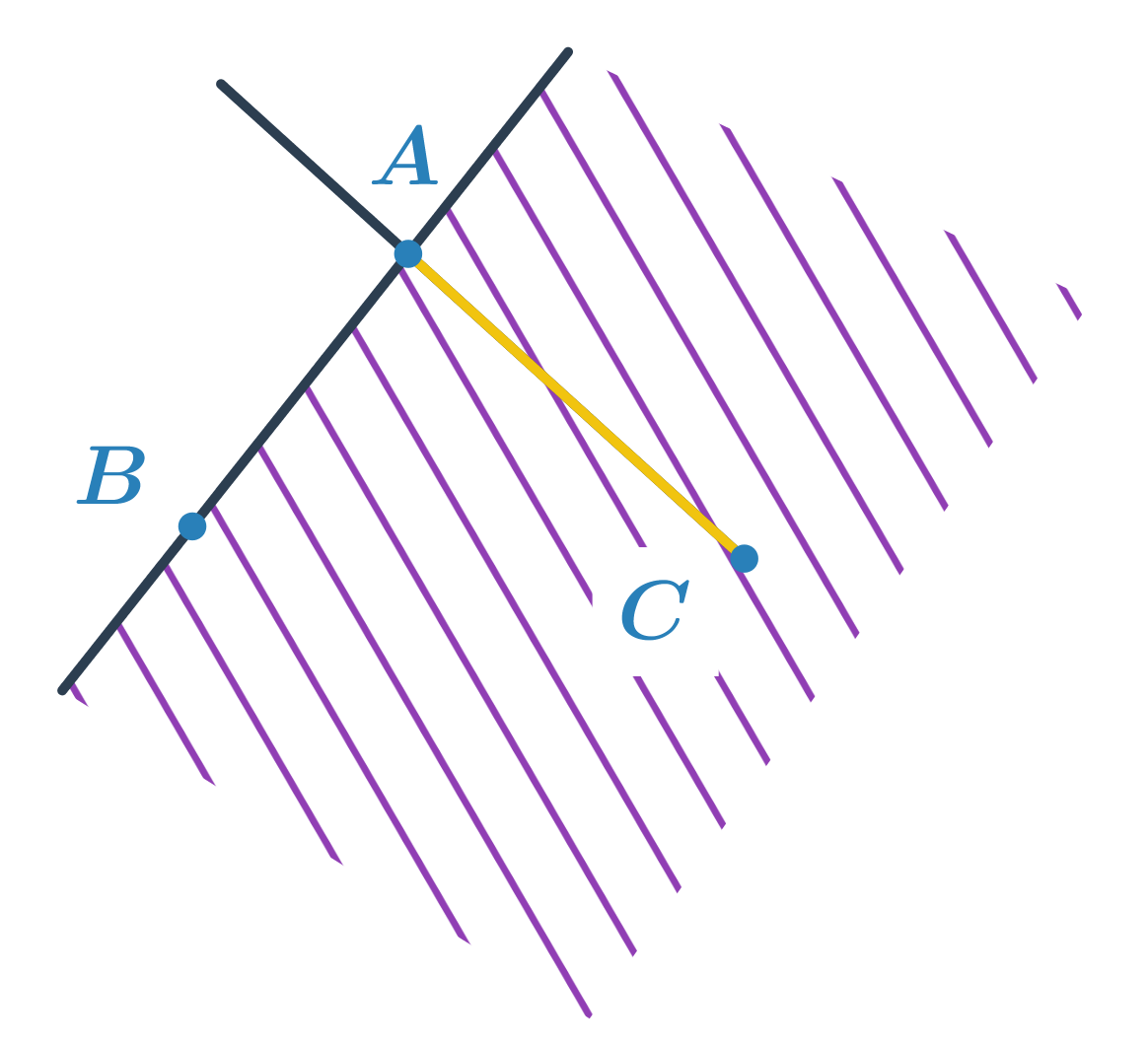
Rovnoběžky jsou dvě přímky ležící ve stejné rovině, které se nikde neprotínají. Rovnoběžnost přímek p a q zapisujeme p \parallel q.
Kolmice je přímka, která protíná jinou přímku a svírá s ní úhel 90°. Kolmost přímek p a q zapisujeme p \perp q.
Dvě přímky, které jsou kolmé na nějakou třetí přímku a současně obě leží v jedné rovině, jsou rovnoběžky.
Komiks pro zpestření
Konstrukční úlohy: čtyřúhelníky
Kromě níže uvedených interaktivních cvičení jsou k dispozici také následující pracovní listy k vytištění a rýsování na papíře:
NahoruKonstrukční úlohy průřezově
Při řešení složitějších konstrukčních úloh budeme využívat i množiny bodů daných vlastností. Připomeňme si ty nejdůležitější.
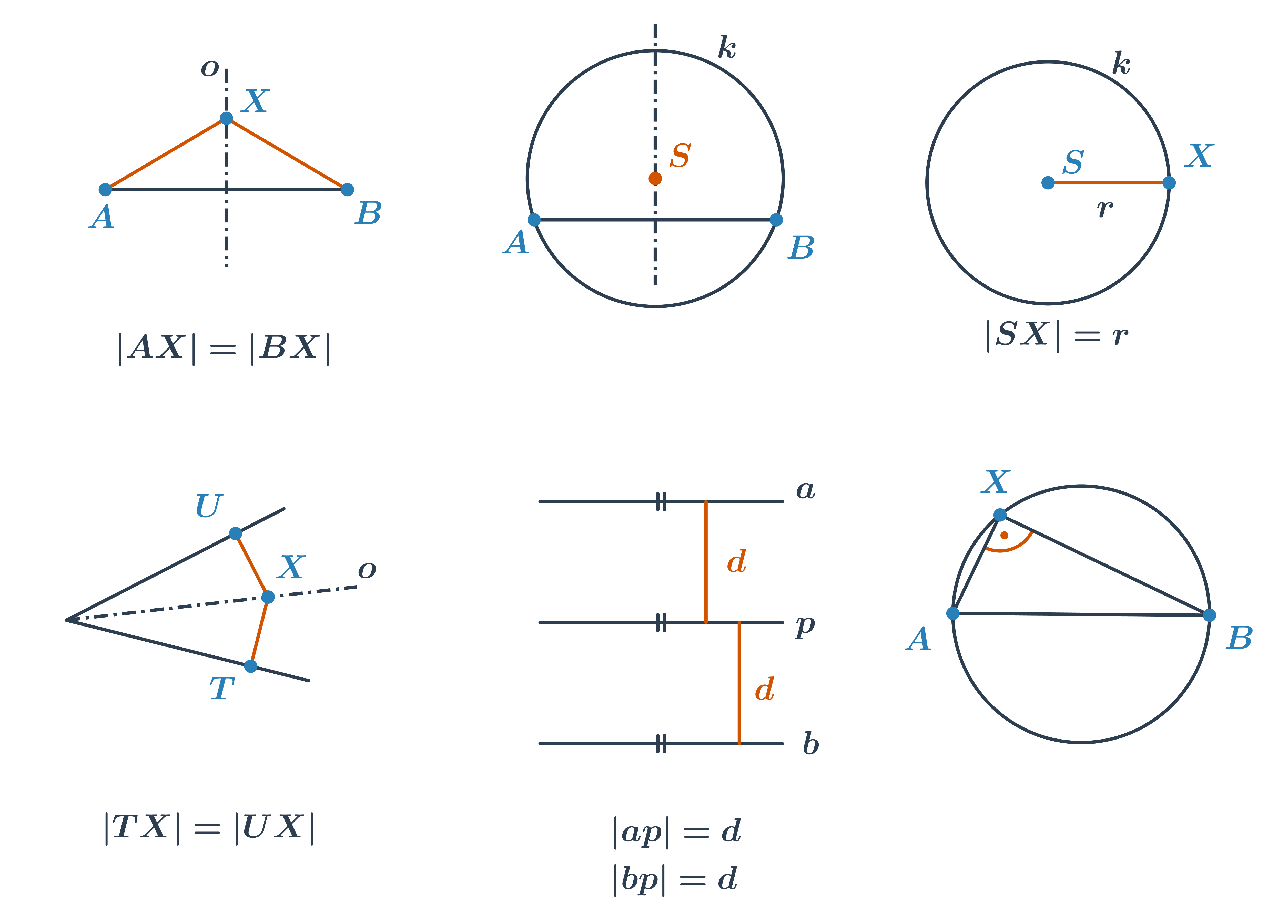
| osa úsečky AB | množina všech bodů, které mají od bodů A, B stejnou vzdálenost |
| osa úsečky AB | množina středů všech kružnic, které prochází body A, B |
| kružnice | množina všech bodů, které mají od bodu S stejnou vzdálenost (poloměr r) |
| osa úhlu | množina všech bodů, které mají od ramen úhlu stejnou vzdálenost |
| rovnoběžky | množiny všech bodů, které mají od přímky p stejnou vzdálenost |
| Thaletova kružnice nad úsečkou AB | množina všech vrcholů pravých úhlů, jejichž ramena procházejí body A, B |
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruOperace a vlastnosti v rovině
Základní intuitivní představa pro jednotlivé operace a vlastnosti:
- Osová souměrnost – děláme „zrcadlový“ obraz útvaru podle přímky
- Středová souměrnost – překlápíme útvar podle bodu
- Shodnost – dva útvary jsou shodné, pokud „mají stejný tvar a velikost“ (mohou se lišit natočením a umístěním)
- Otočení – otočíme útvar okolo určitého bodu o nějaký úhel po směru nebo proti směru hodinových ručiček
- Posunutí – posuneme útvar o určitou vzdálenost daným směrem
- Podobnost – dva útvary jsou podobné, pokud „mají stejný tvar“ (mohou se lišit velikostí, natočením a umístěním)
- Stejnolehlost – vzdálenost bodů útvaru vzhledem k danému bodu se mění v daném poměru
Podtéma určení zobrazení v rovině se pak zabývá rozlišováním mezi jednotlivými zobrazeními.
Podle velikosti a umístění útvarů v rovině lze rozhodnout, jestli je jeden útvar obrazem druhého v nějakém geometrickém zobrazení.
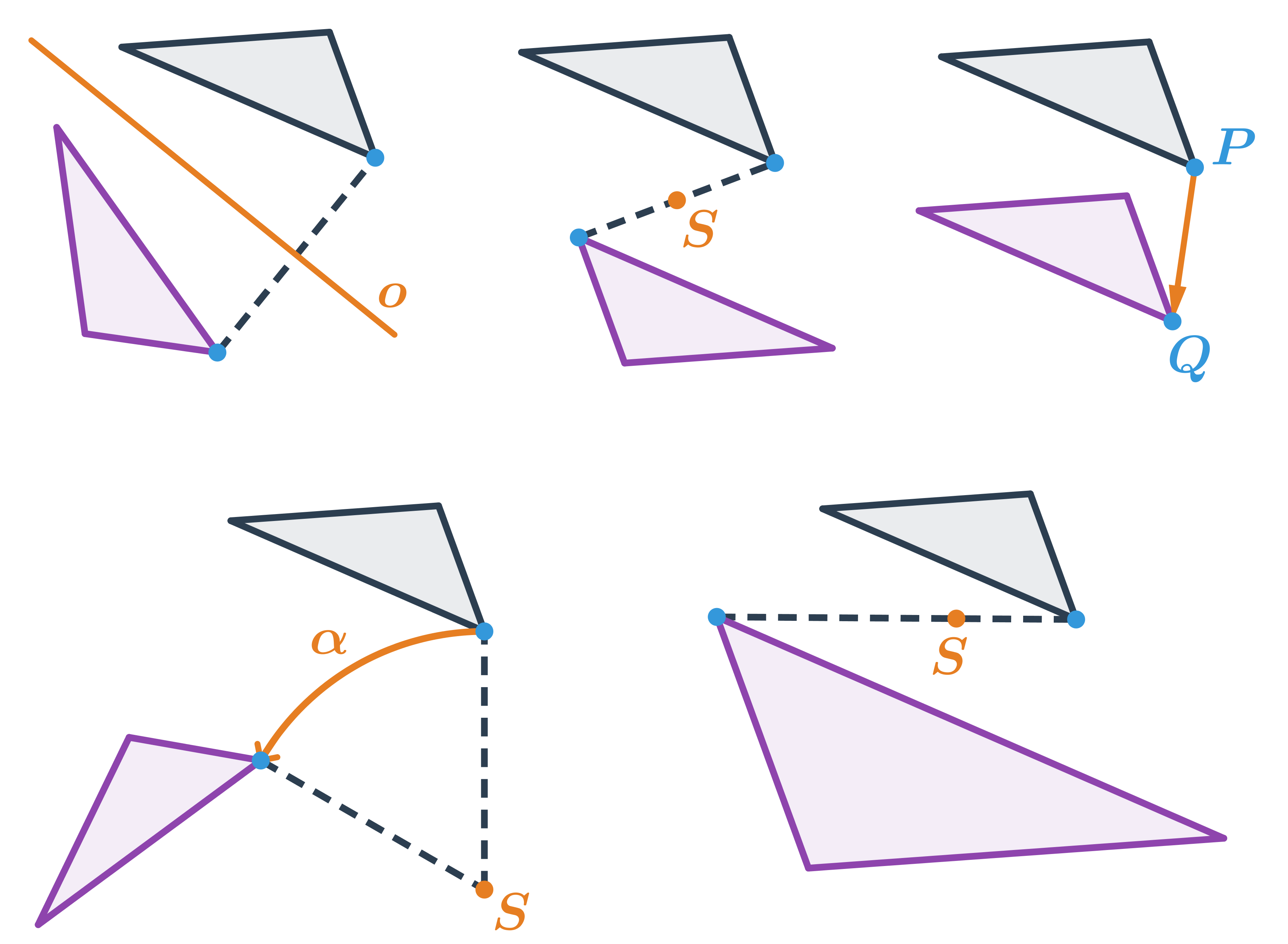
Na obrázku je obraz trojúhelníku v těchto zobrazeních:
- osová souměrnost s osou o
- středová souměrnost se středem S
- posunutí dané orientovanou úsečkou \overrightarrow{PQ}
- otočení dané středem S a orientovaným úhlem \alpha
- stejnolehlost daná středem S a koeficientem -2
Osová souměrnost
Osová souměrnost je dána přímkou o a přiřazuje každému bodu X mimo osu takový bod X', že přímka o je osou úsečky XX'. Jinými slovy: obraz má od osy stejnou vzdálenost jako původní bod a spojnice bodů je kolmá na osu. Osová souměrnost zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
Příklady
Modré a oranžové útvary jsou vzájemně osově souměrné podle osy o:
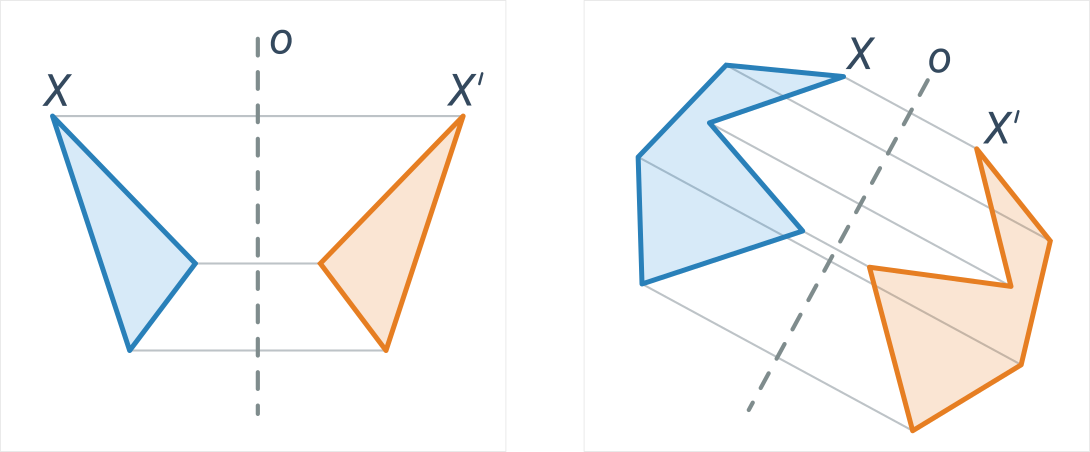
Pro lepší pochopení může být užitečné porovnat osovou a středovou souměrnost.
Osově souměrný útvar
Útvar označujeme za osově souměrný, pokud je v nějaké osové souměrnosti obrazem sebe sama. Osu této souměrnosti pak nazýváme osou útvaru. Obrázek uvádí příklady útvarů osově souměrných (zelené, s vyznačenými osami souměrnosti) i těch nesouměrných (červené):
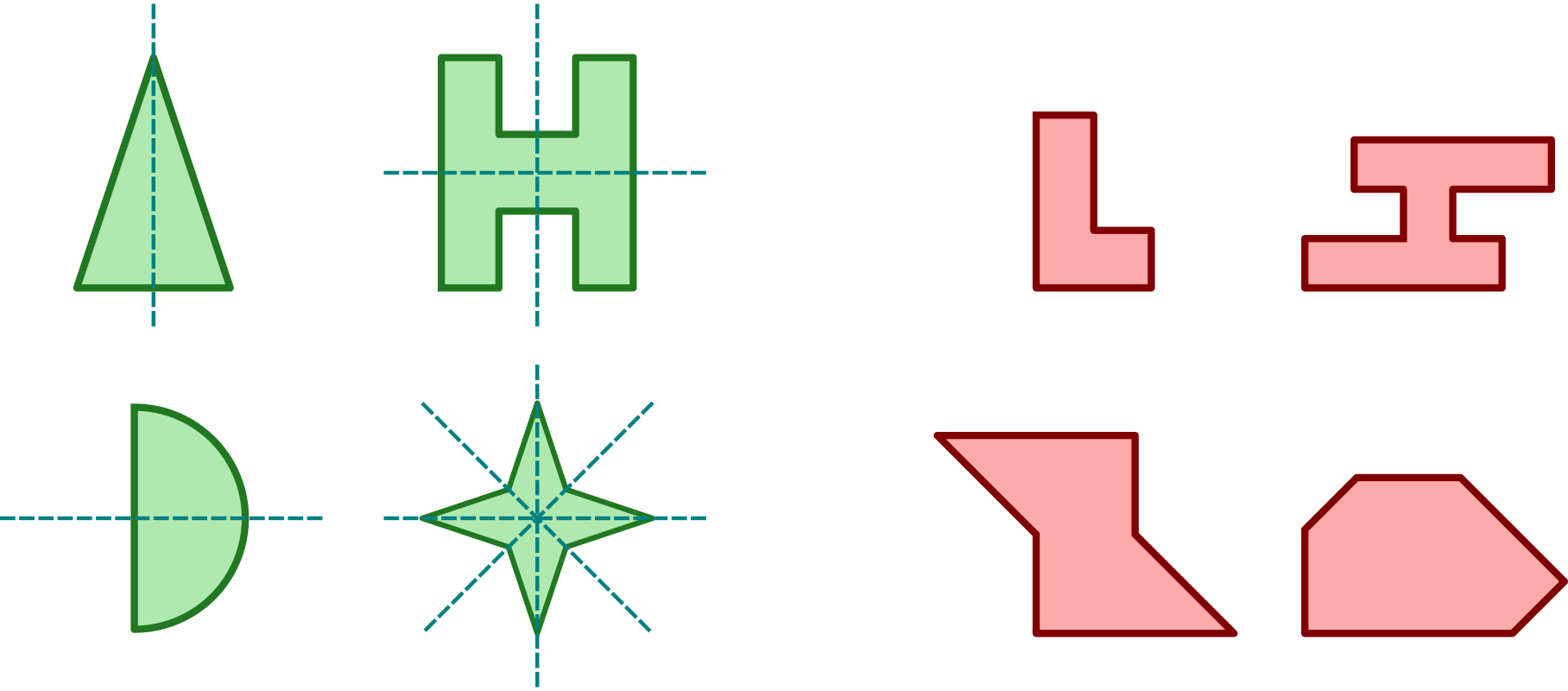
Další příklady:
- Úsečka je osově souměrná a má v rovině jedinou osu souměrnosti (kolmici v jejím středu).
- Rovnoramenný trojúhelník je osově souměrný.
- Trojúhelník, který není rovnoramenný, není osově souměrný.
- Všechny pravidelné mnohoúhelníky jsou osově souměrné. Počet os souměrnosti je roven počtu vrcholů mnohoúhelníku.
- Kruh je osově souměrný a má nekonečně mnoho os souměrnosti.
Komiks pro zpestření
Středová souměrnost
Středová souměrnost je dána bodem S a přiřazuje každému bodu X takový bod X', že bod S je středem úsečky XX'. Jinými slovy: obraz má od středu stejnou vzdálenost jako původní bod a leží na polopřímce opačné k SX.
Středová souměrnost zachovává vzdálenosti i úhly, jde tedy o druh shodnosti. Středová souměrnost se středem v bodě S je shodná s otočením o 180 stupňů podle středu S.
Příklady
Modré a oranžové útvary jsou vzájemně středově souměrné podle středu S:
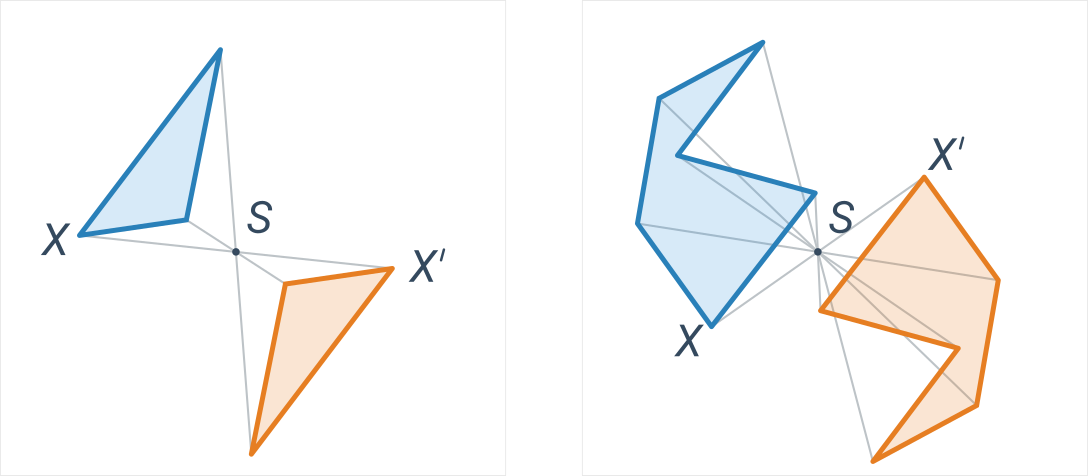
Pro lepší pochopení může být užitečné porovnat středovou a osovou souměrnost.
Středově souměrný útvar
Útvar označujeme za středově souměrný, pokud je v nějaké středové souměrnosti obrazem sebe sama. Střed této středové souměrnosti pak nazýváme středem souměrnosti objektu. Obrázek uvádí příklady útvarů středově souměrných (zelené, s vyznačeným středem souměrnosti) i těch nesouměrných (červené):
Další příklady:
Úsečka, obdélník, čtverec, kosočtverec, pravidelný šestiúhelník a kruh jsou středově souměrné.
Žádný trojúhelník není středově souměrný.
Dva geometrické útvary jsou shodné, pokud mají stejný tvar a velikost. Na následujícím obrázku mají shodné útvary stejnou barvu.

Značení
Mějme dva pojmenované útvary, např. dva trojúhelníky ABC a GEF.
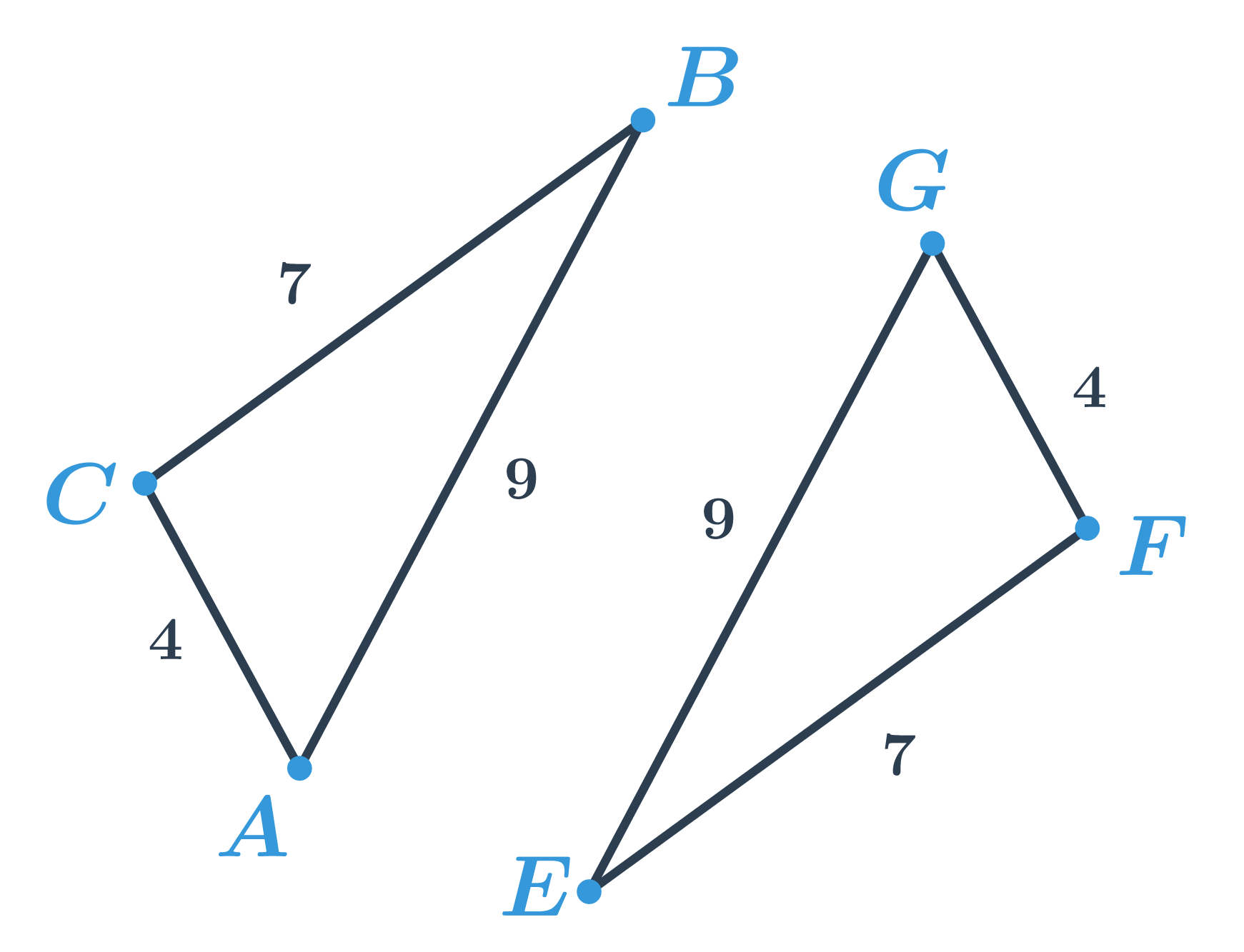
- \left|AB\right|=\left|GE\right|
- \left|BC\right|=\left|EF\right|
- \left|AC\right|=\left|GF\right|
Tyto dva trojúhelníky mají stejné délky stran, jsou tedy shodné. Zapíšeme jako ABC \cong GEF – pozor, na pořadí písmen záleží. Pořadí písmen v názvu trojúhelníku určuje, který vrchol ABC odpovídá kterému vrcholu trojúhelníku GEF. Máme \left|AB\right|=\left|GE\right|, ale \left|AB\right|\neq \left|EF\right|, takže ABC \ncong EFG.
NahoruPodobnost
Dva geometrické útvary jsou si podobné, pokud oba mají stejný tvar (bez ohledu na velikost). Na následujícím obrázku mají podobné útvary stejnou barvu:

Přesněji řečeno, útvary jsou podobné, pokud jeden můžeme získat z druhého kombinací rovnoměrného zmenšení či zvětšení a následným posunutím, otočením nebo překlopením.
Podobnost zachovává velikost úhlů a poměr délek.
Poměr délek odpovídajících úseček v obou útvarech se nazývá koeficient podobnosti.
Příklad 1
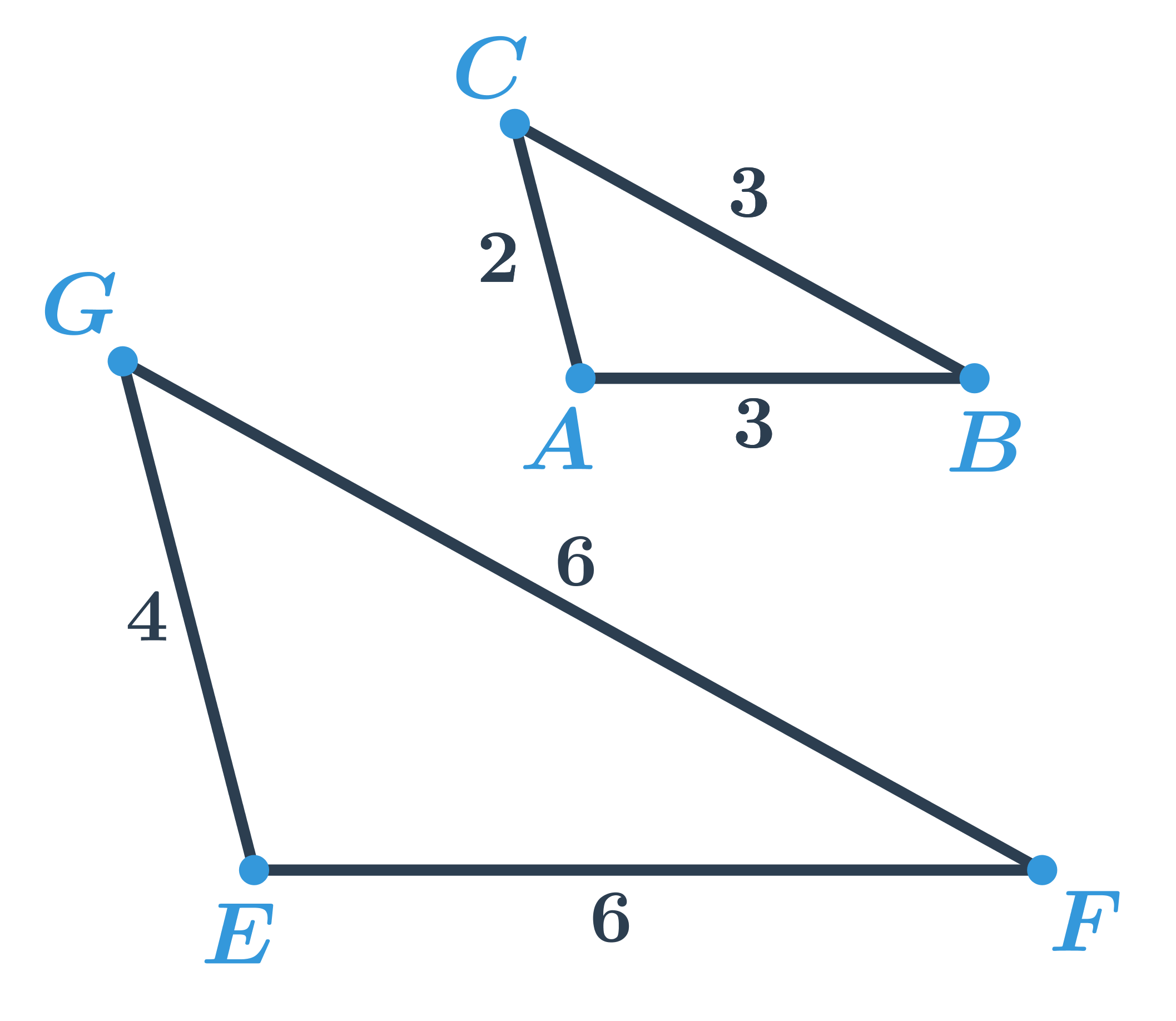
Trojúhelníky ABC a EFG jsou si podobné, protože poměr délek odpovídajících stran je stejný:
- \frac{EF}{AB}=\frac{6}{3}=2
- \frac{FG}{BC}=\frac{6}{3}=2
- \frac{GE}{CA}=\frac{4}{2}=2
Zapisujeme \bigtriangleup EFG\sim \bigtriangleup ABC, koeficient podobnosti je 2.
Příklad 2
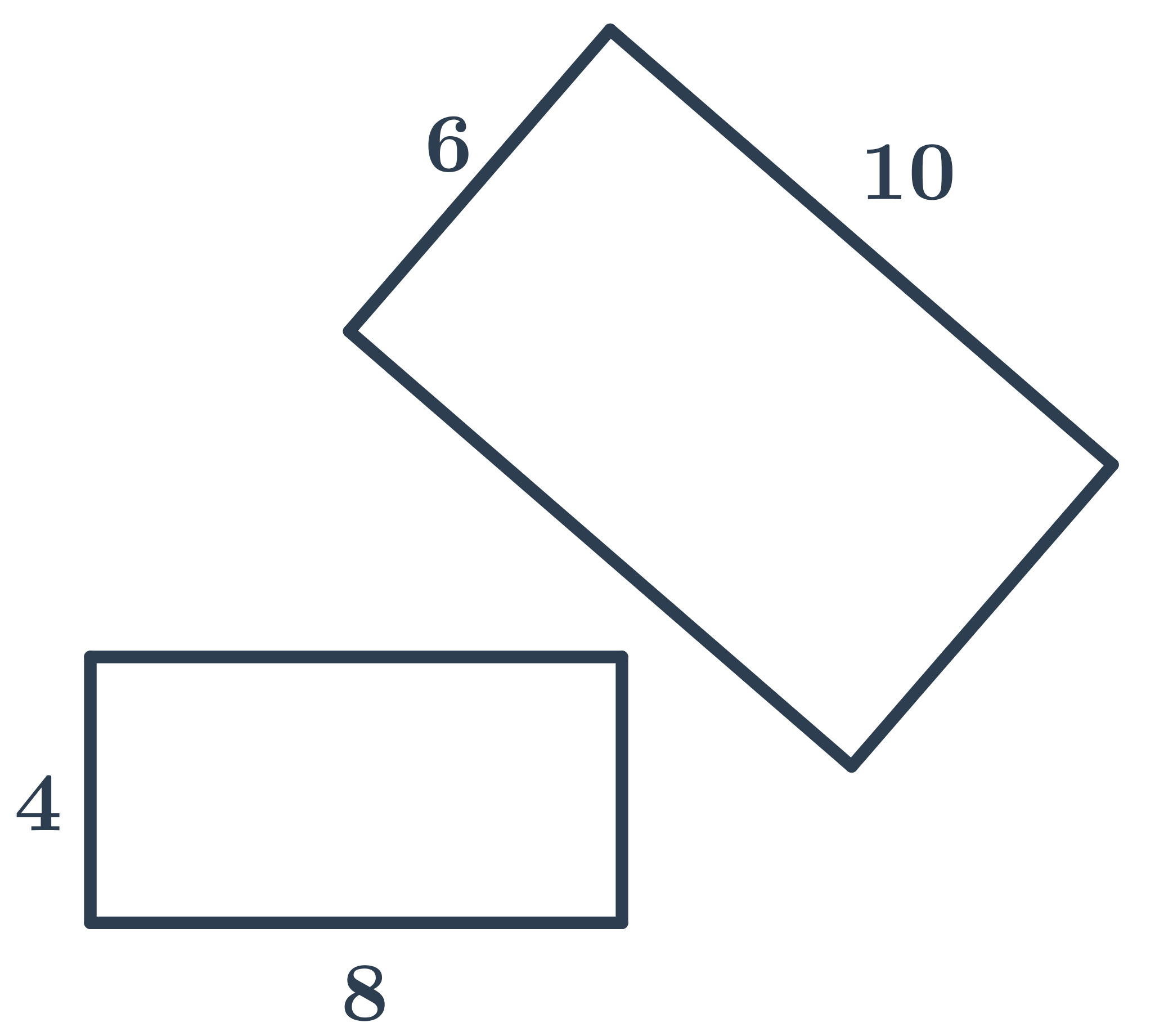
Obdélníky na obrázku nejsou podobné, protože poměr délek odpovídajících stran není stejný:
- poměr delších stran je \frac{10}{8}=\frac{5}{4}
- poměr kratších stran je \frac{6}{4}=\frac{3}{2}
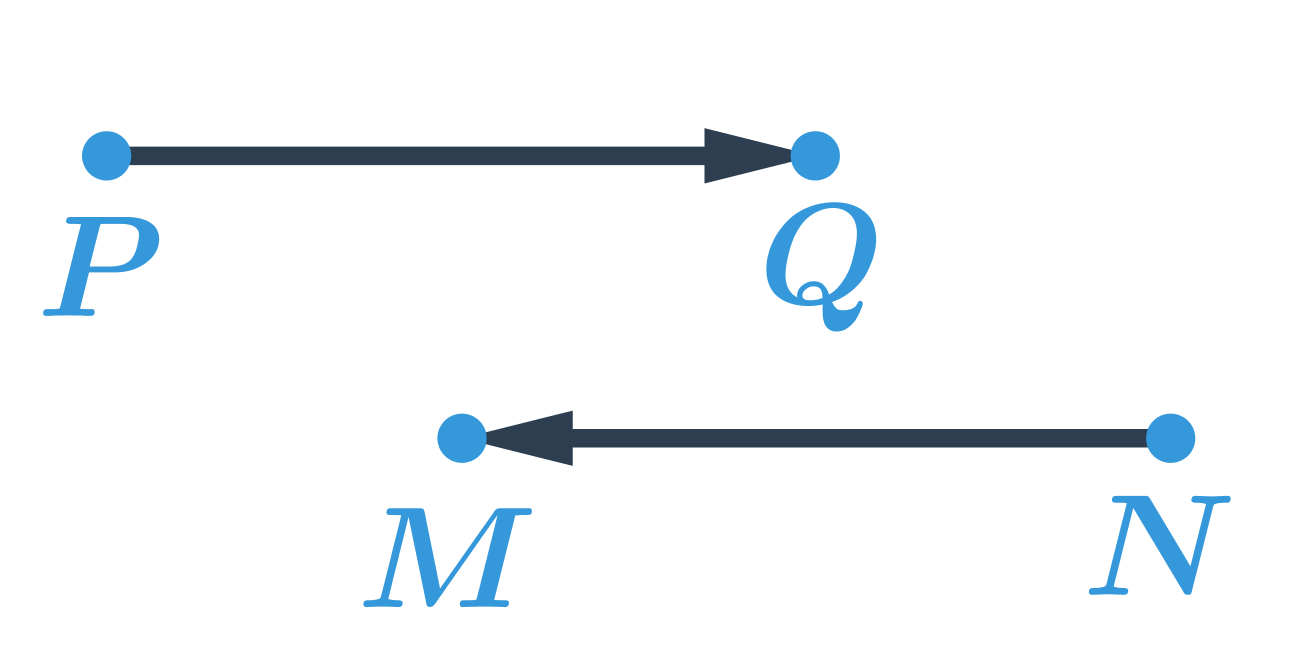
Posunutí je dané orientovanou úsečkou. Tato úsečka určuje směr a délku posunutí. Orientovaná úsečka je úsečka, u které rozlišujeme, který bod je počáteční a který koncový. Orientovanou úsečku označíme šipkou, která určí její směr. Zápis \overrightarrow{PQ} znamená, že počátečním bodem orientované úsečky je bod P a koncovým bodem bod Q. Na obrázku jsou orientované úsečky \overrightarrow{PQ} a \overrightarrow{NM}. Tyto úsečky mají stejnou délku, ale opačný směr.
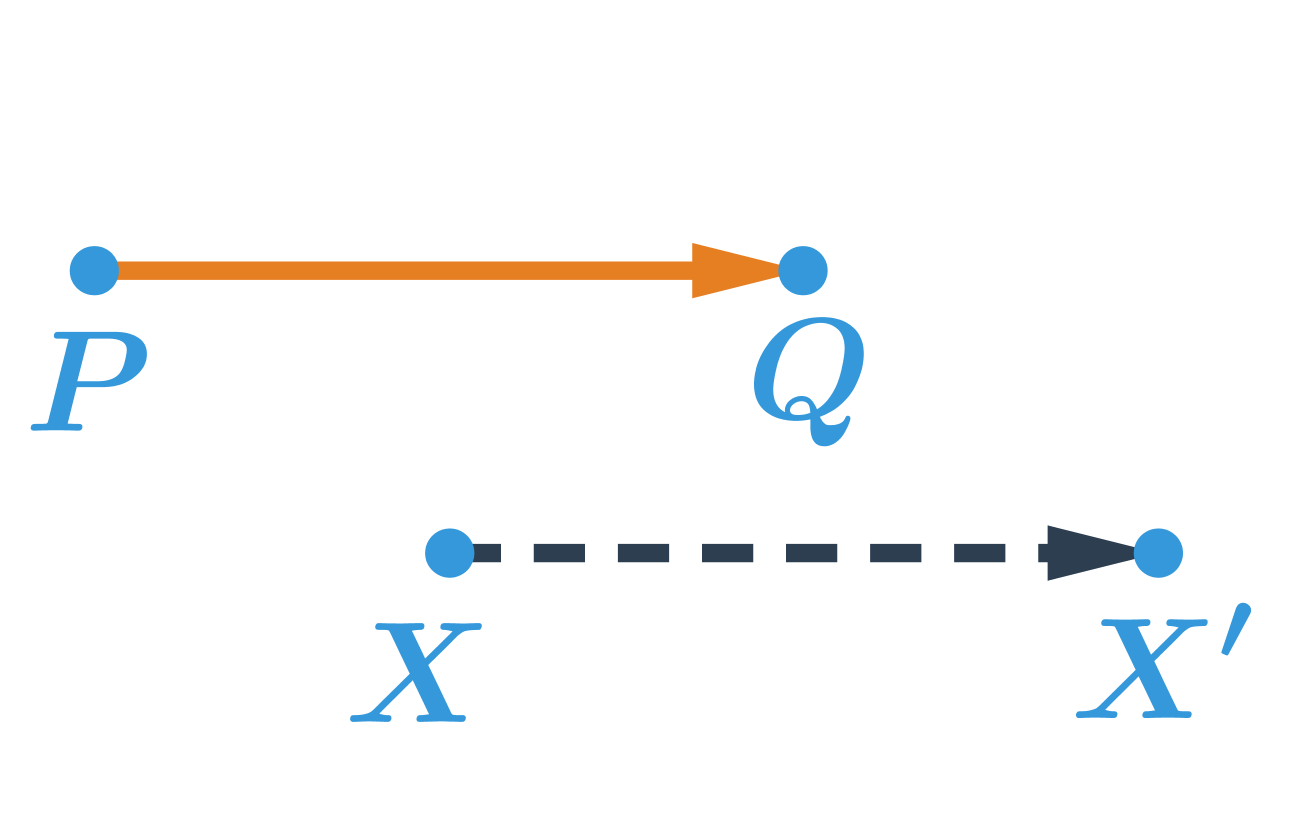
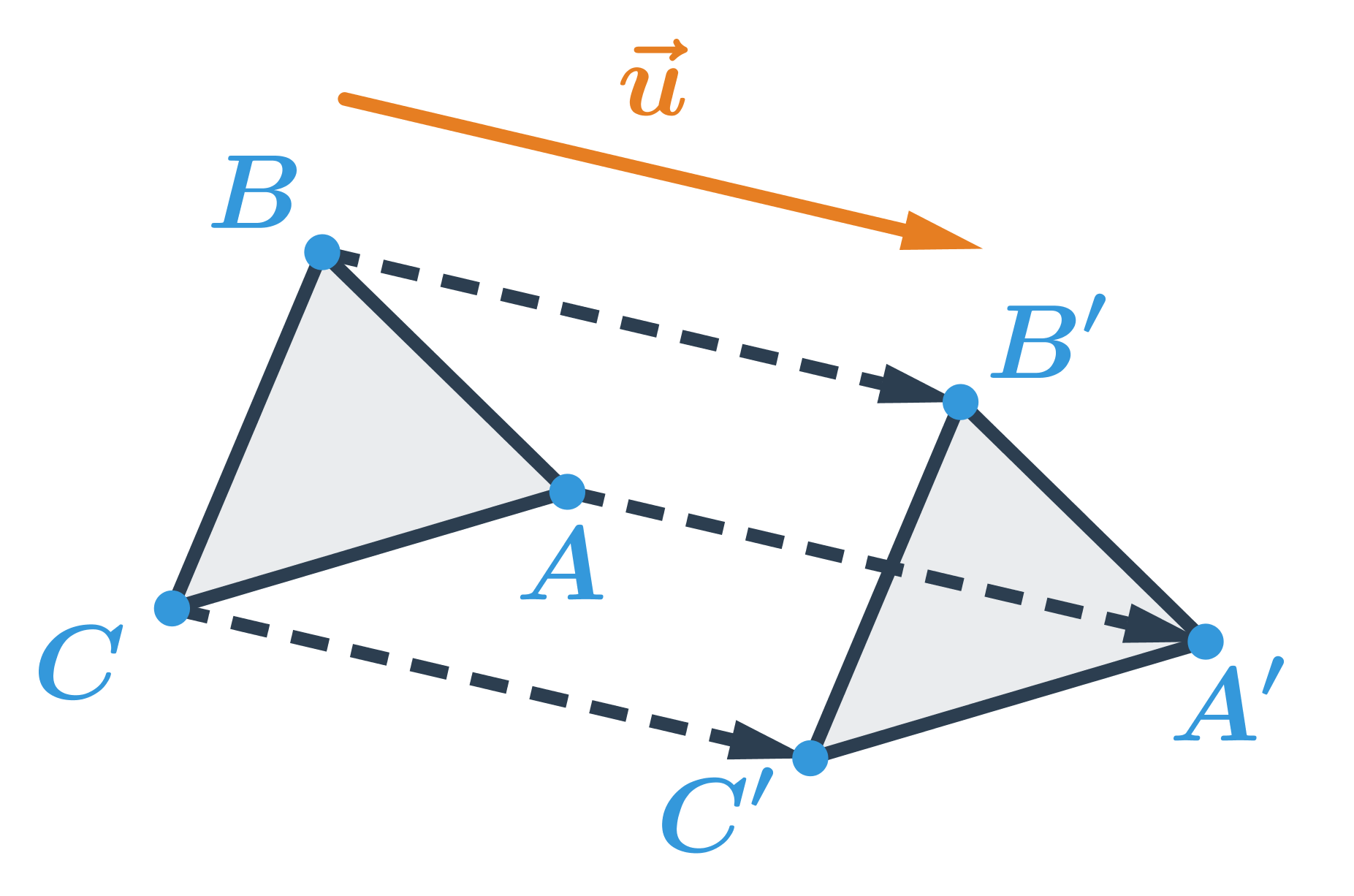
Obrazem bodu X v posunutí, které je určené orientovanou úsečkou \overrightarrow{PQ} je bod X', pro který platí, že orientovaná úsečka \overrightarrow{XX'} má stejnou velikost a stejný směr jako orientovaná úsečka \overrightarrow{PQ}.
Příklad: posunutí bodu
Obrazem bodu X v posunutí, které je určené orientovanou úsečkou \overrightarrow{PQ} je bod X':
Příklad: posunutí trojúhelníku
Obrazem trojúhelníku ABC v posunutí, které je určené orientovanou úsečkou \overrightarrow{PQ} je trojúhelník A'B'C': 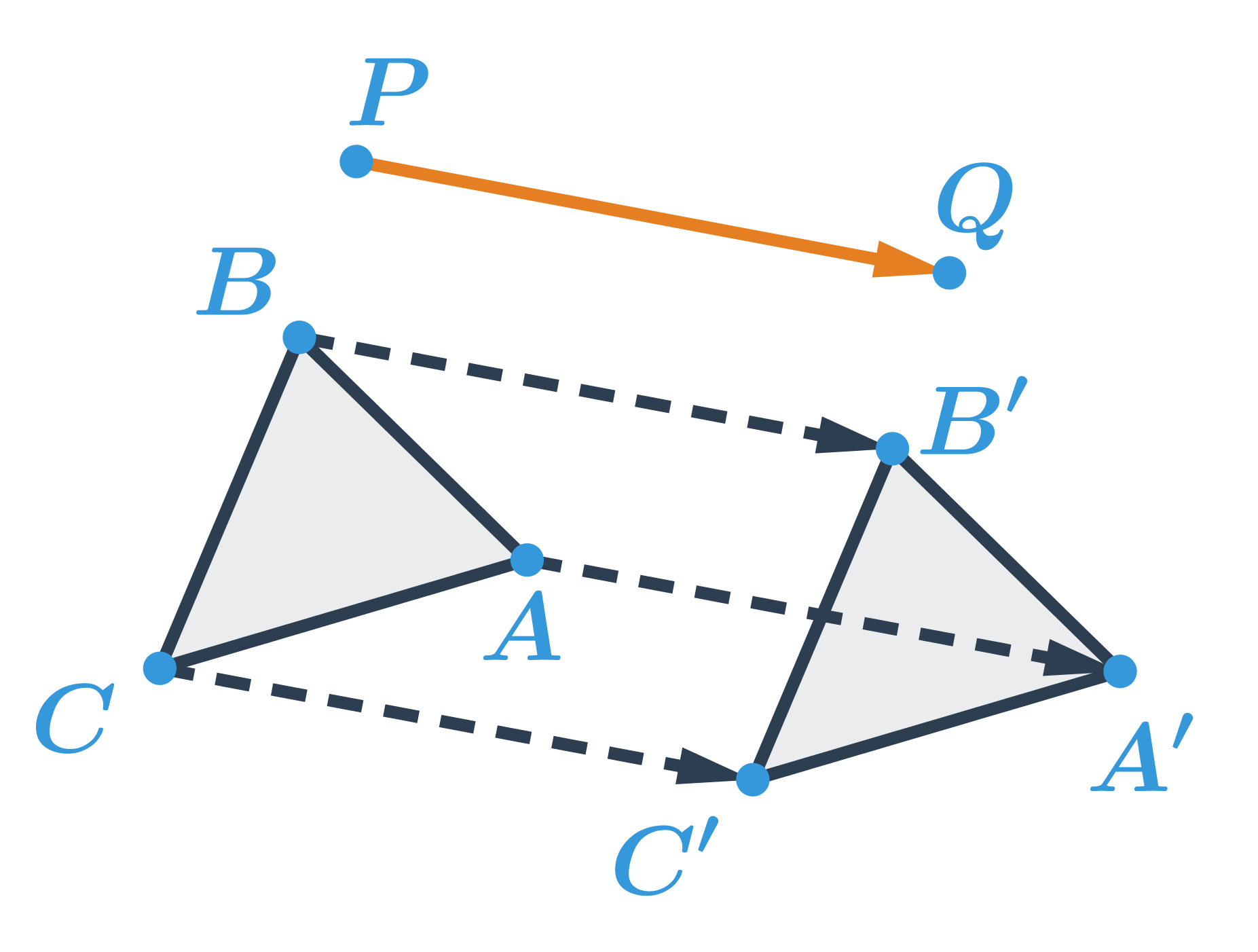
Posunutí zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
Posunutí s použitím vektorů
Posunutí můžeme definovat ještě druhým způsobem, známe‑li vektory. Posunutí je pak dané vektorem posunutí \vec{u}. Obrazem bodu X je bod X', pro který platí, že vektor \overrightarrow{XX'} má stejnou velikost a stejný směr jako vektor \vec{u}.
Příklad: posunutí bodu dané vektorem
Obrazem bodu X v posunutí, které je určené vektorem \vec{u} je bod X'
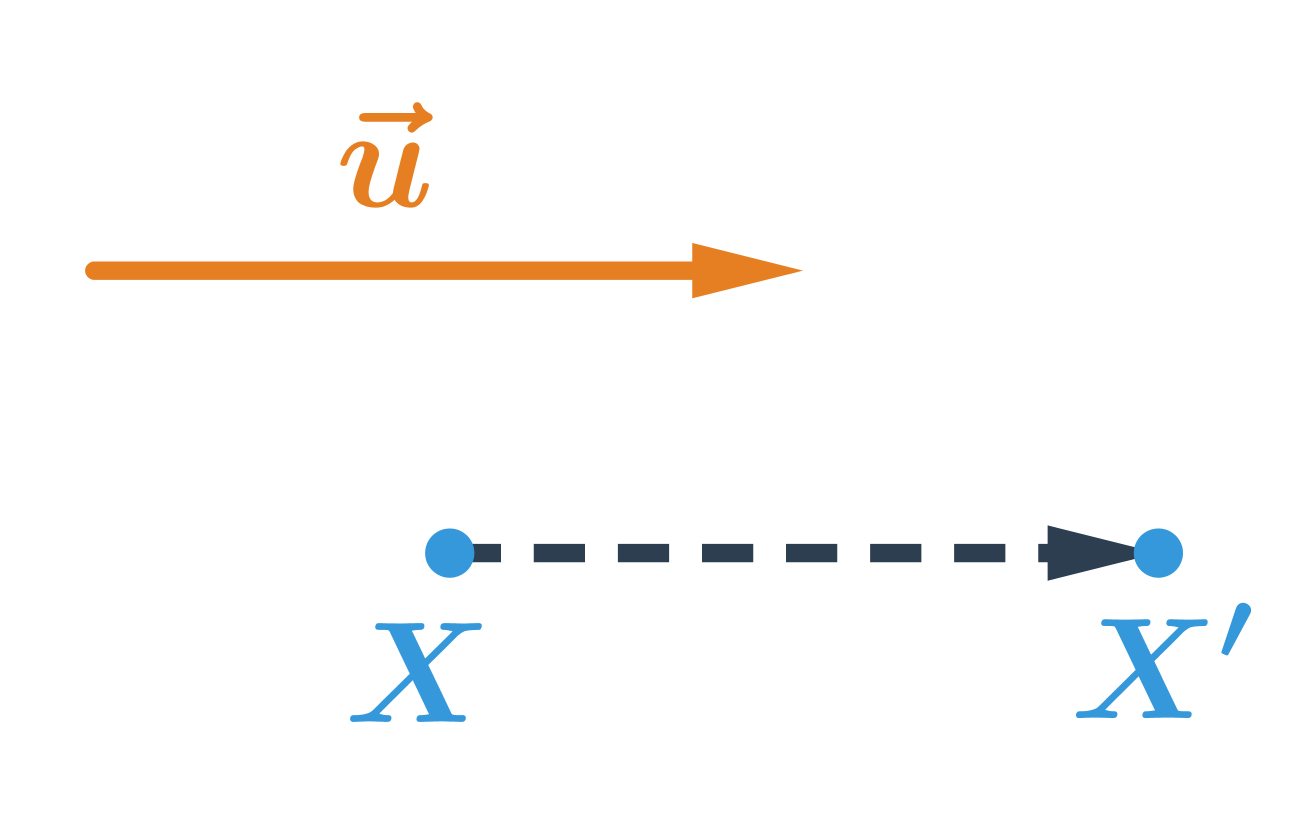
Příklad: posunutí trojúhelníku dané vektorem
Obrazem trojúhelníku ABC v posunutí, které je určené vektorem \vec{u} je trojúhelník A'B'C'
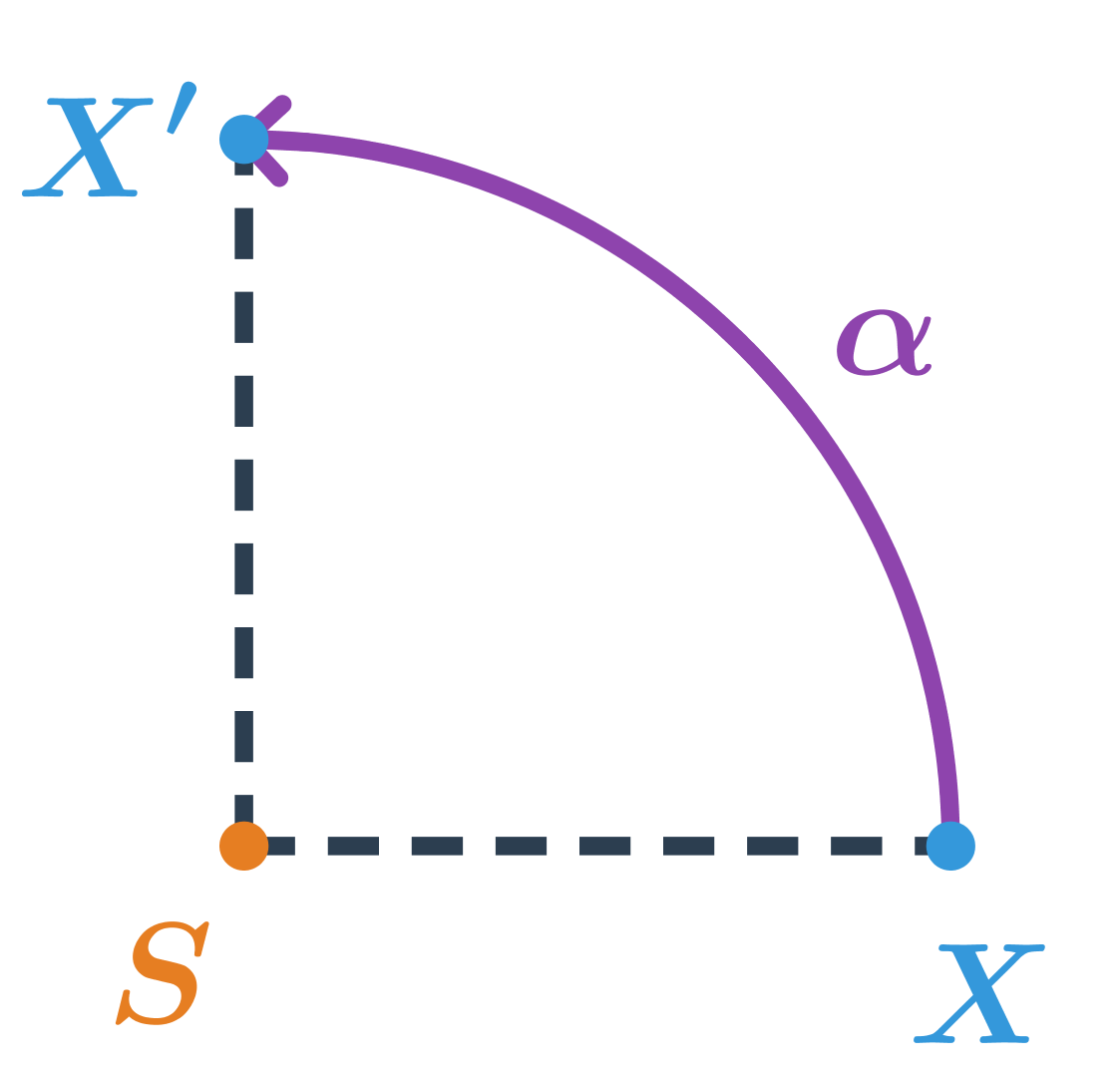
Otočení (rotace) je dané bodem S a orientovaným úhlem \alpha. Bod S se nazývá střed otočení. Pojem orientovaný úhel znamená, že rozlišujeme, zda otáčíme proti směru hodinových ručiček (kladný směr) nebo po směru hodinových ručiček (záporný směr). Obrazem bodu X je bod X', který má stejnou vzdálenost od středu S jako bod X a úhel XSX' má velikost \alpha.
Příklady
Bod X je otočený kolem středu S o 90^\circ proti směru hodinových ručiček.
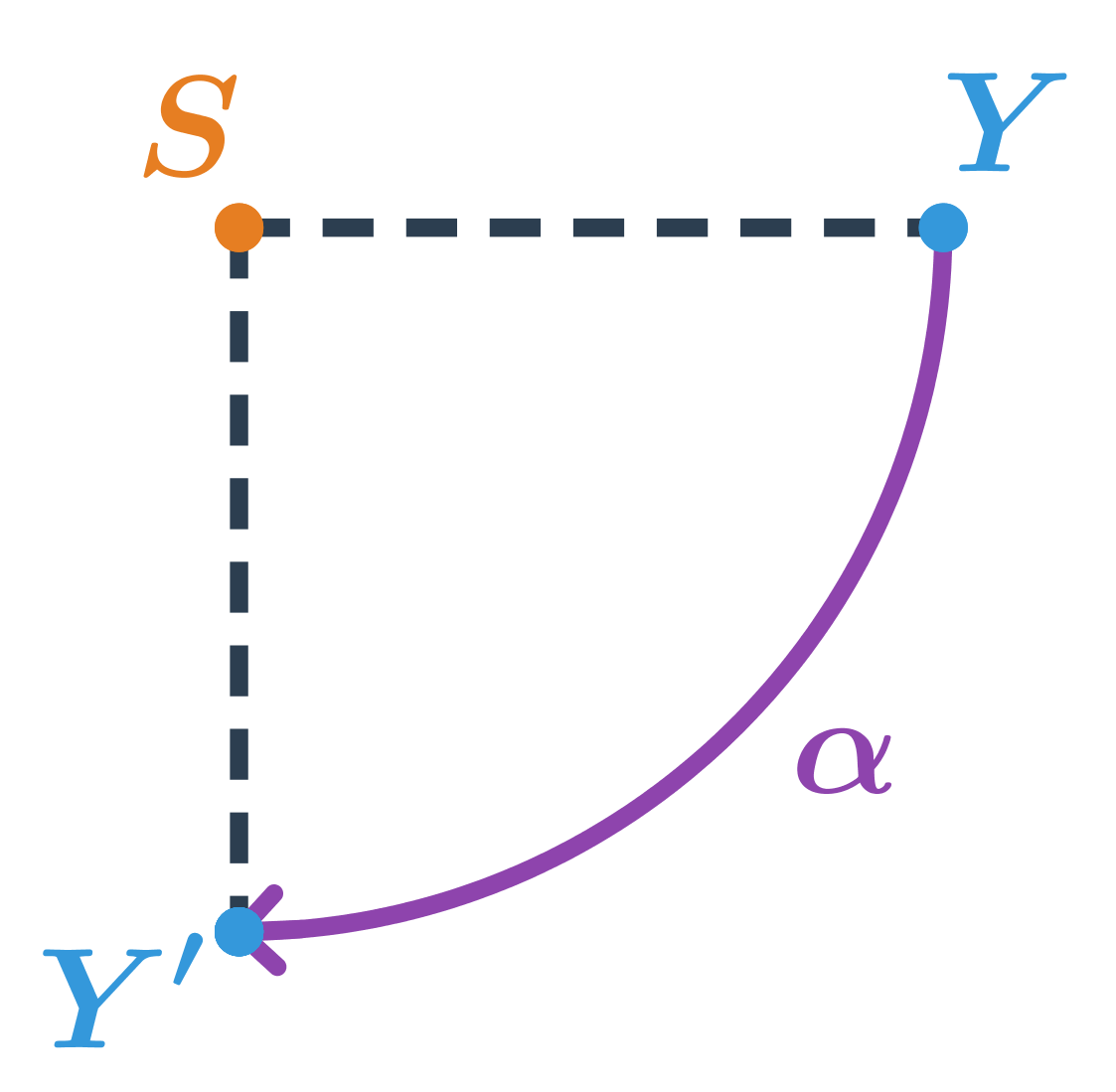
Bod Y je otočený kolem středu S o 90^\circ ve směru hodinových ručiček, tedy o úhel \alpha=-90^\circ.
Trojúhelník ABC je otočený kolem středu S o 60^\circ ve směru hodinových ručiček, tedy o úhel \alpha=-60^\circ.
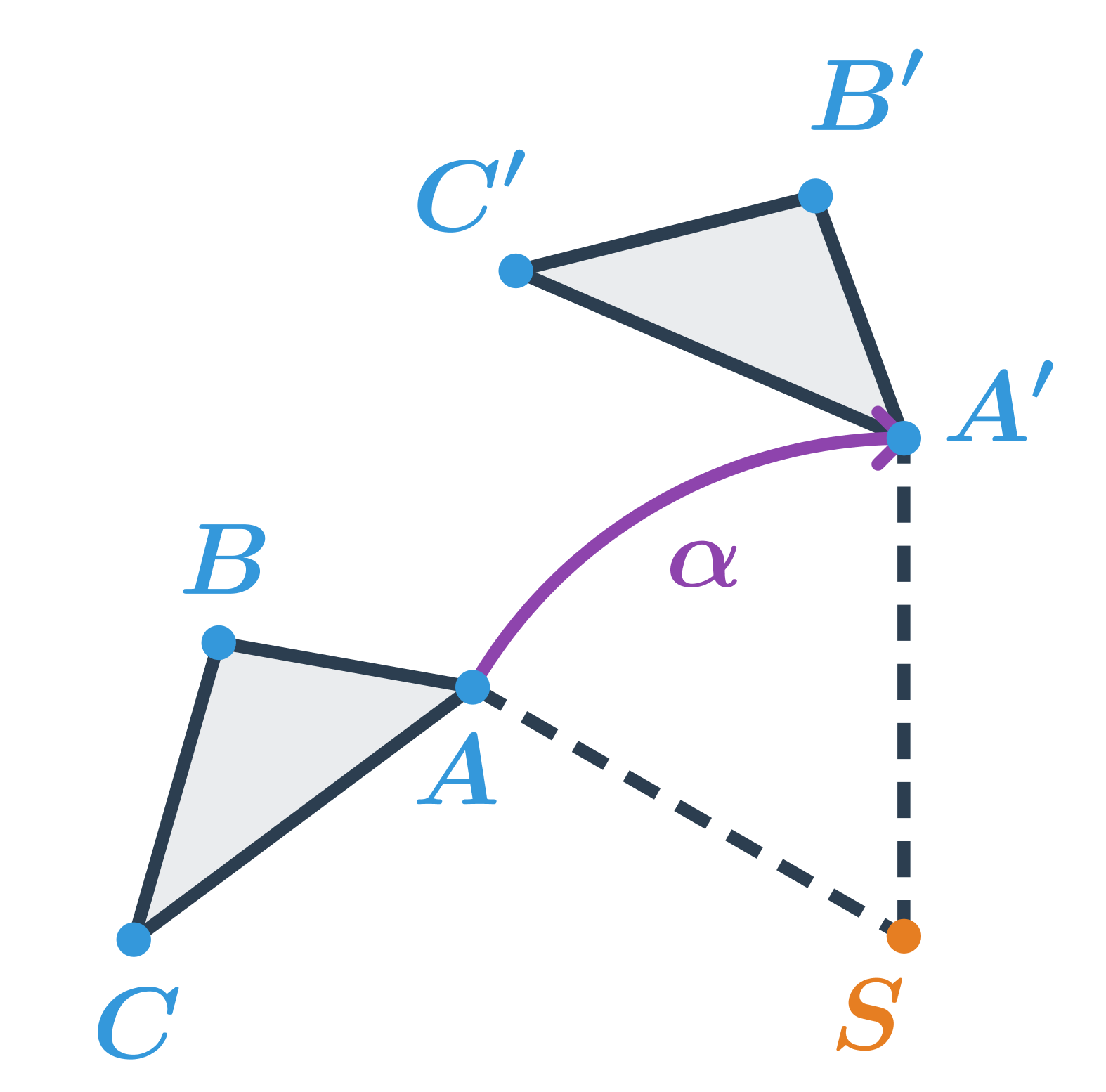
Otočení zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
NahoruStejnolehlost
Stejnolehlost je dána bodem S a nenulovým číslem \lambda. Bod S se nazývá střed stejnolehlosti, číslo \lambda je koeficient stejnolehlosti.
Obrazem bodu X je bod X', pro který platí:
- |SX'|=|\lambda| \cdot |SX|
- pro \lambda \gt 0 leží X, X' na stejné polopřímce s počátkem S
- pro \lambda \gt 0 leží X, X' na opačných polopřímkách s počátkem S
Na obrázku je vidět, kde leží obraz X' bodu X v závislosti na hodnotě koeficientu \lambda:
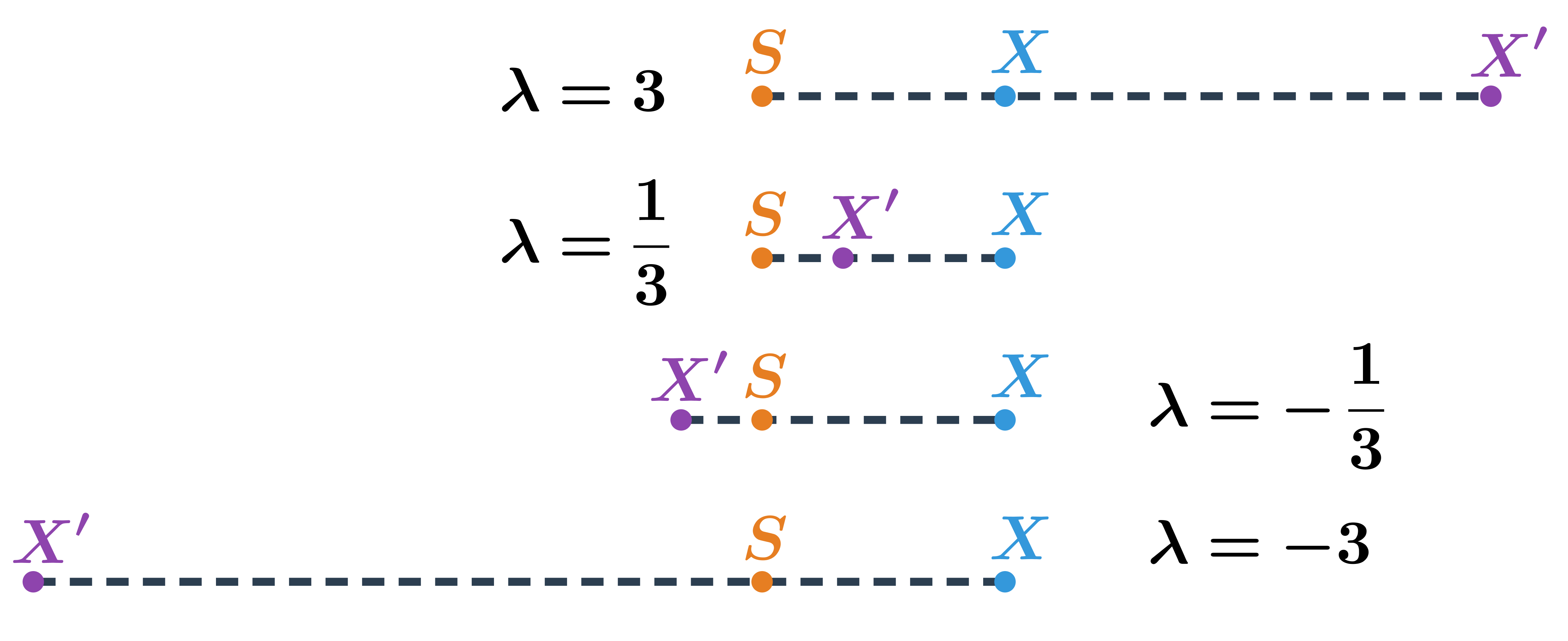
Přehled vlastností obrazu X' bodu X ve stejnolehlosti se středem S pro různé hodnoty koeficientu \lambda:
| \lambda \gt 0 | bod X' leží na polopřímce SX |
| \lambda \lt 0 | bod X' leží na polopřímce opačné k SX |
| |\lambda| \gt 1 | bod X' má od středu S větší vzdálenost než bod X |
| |\lambda| \lt 1 | bod X' má od středu S menší vzdálenost než bod X |
Příklad 1: obraz trojúhelníku ve stejnolehlosti
Obraz trojúhelníku ABC ve stejnolehlosti se středem S a koeficientem \lambda =\frac{1}{2}
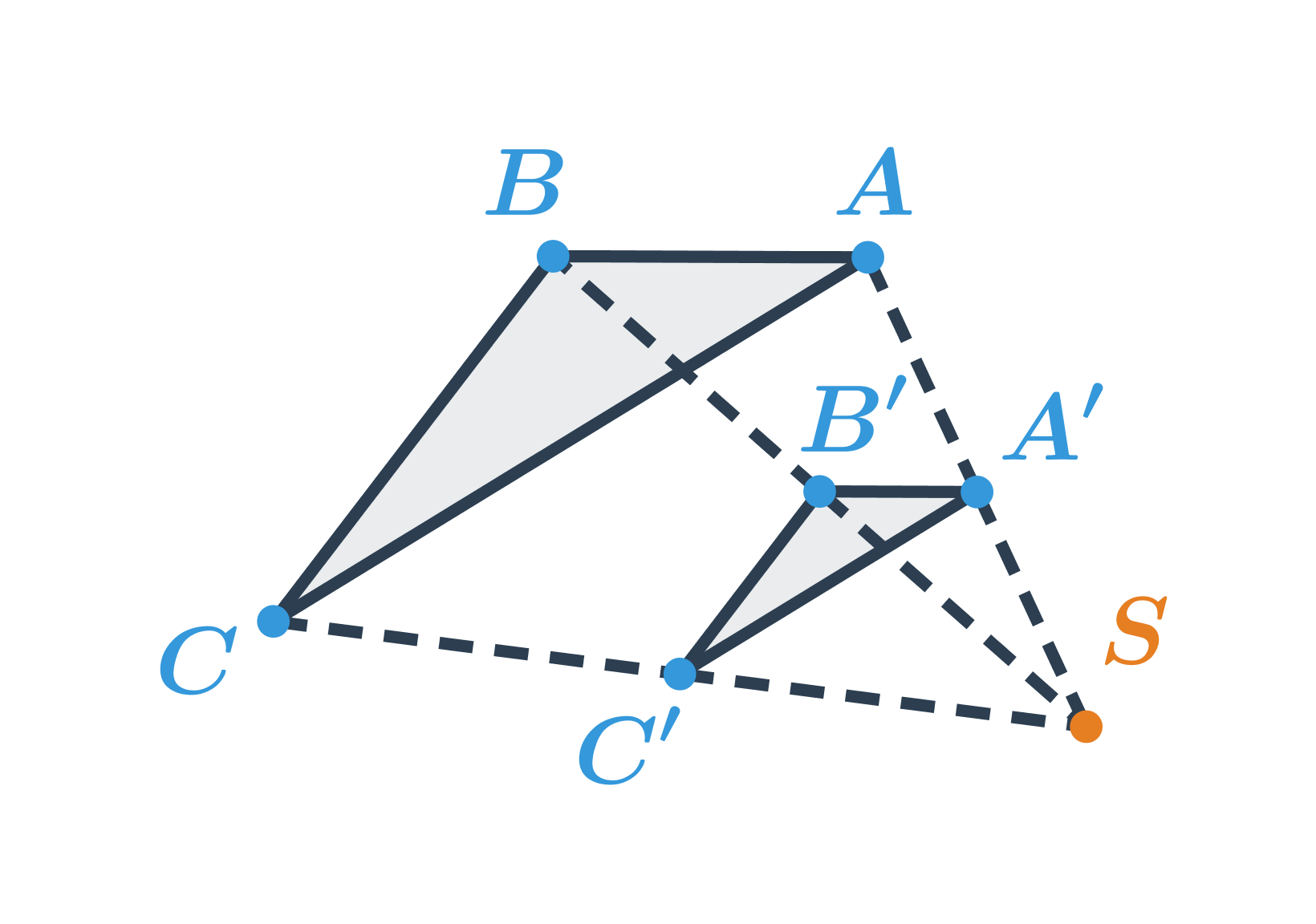
Pro délky odpovídajících si úseček platí: \frac{|SA'|} {|SA|}=\frac{|SB'|} {|SB|}=\frac{|SC'|} {|SC|}=\frac{1}{2}
Příklad 2: obraz kružnice ve stejnolehlosti
Obraz kružnice k ve stejnolehlosti se středem S a koeficientem \lambda =-3.
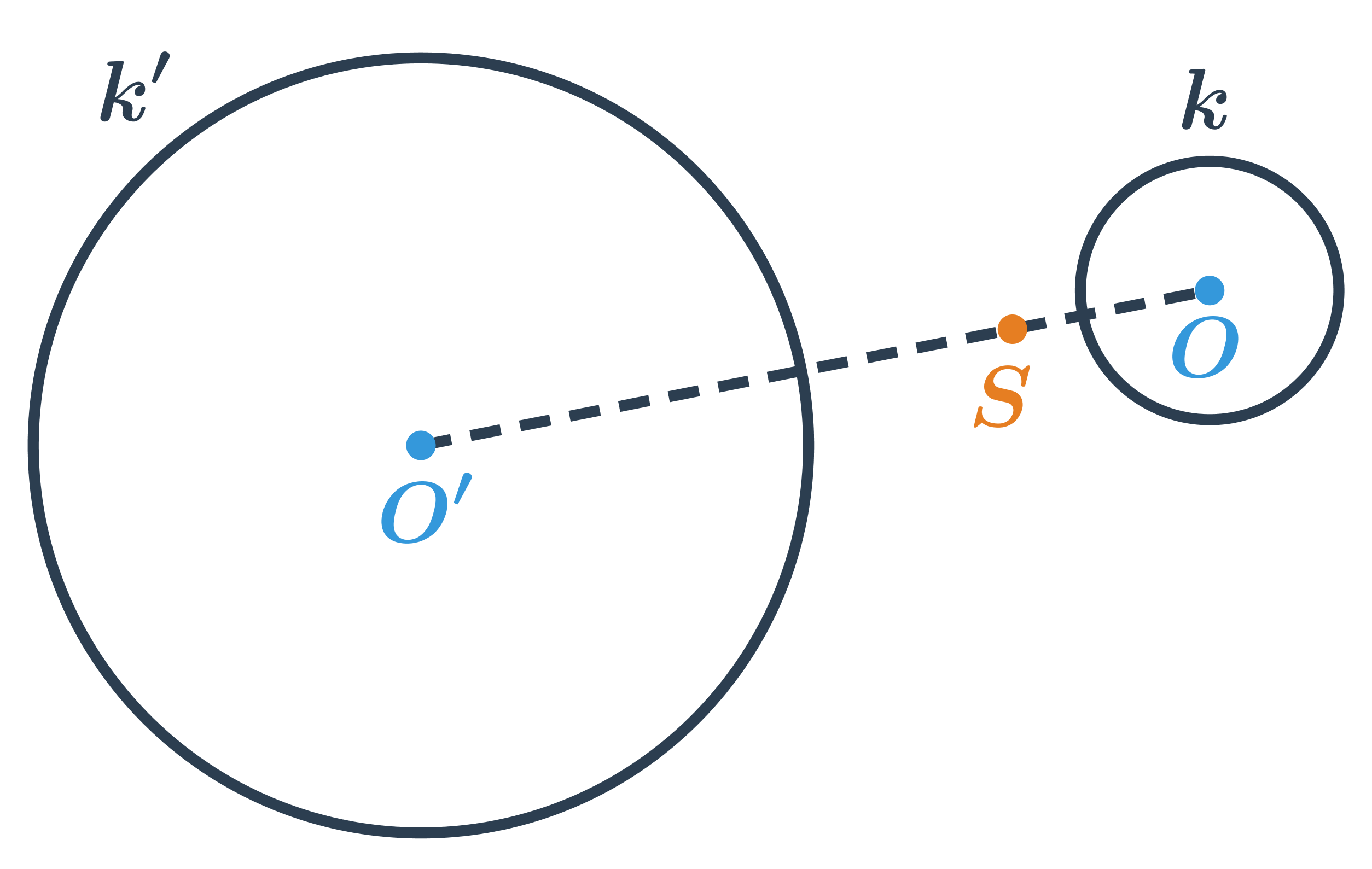
Stejnolehlost zachovává úhly a poměr délek, jde tedy o druh podobnosti.
NahoruAnalytická geometrie
Analytická geometrie nám dovoluje zapsat geometrické problémy algebraicky a vyřešit je pomocí rovnic.
Nejjednodušší objekty popsatelné analyticky jsou body, úsečky a vektory v rovině nebo v prostoru. Když už umíme manipulovat s vektory, můžeme je použít například k popisu přímky nebo roviny.
V případě přímek a rovin se pořád ještě jedná o objekty popsatelné lineárními rovnicemi nebo soustavami lineárních rovnic. Pokud se začneme zabývat i kvadratickými rovnicemi, dokážeme popsat i kuželosečky v rovině, například kružnici, elipsu, parabolu a hyperbolu.
Dva významné typy problémů, které řešíme v rámci analytické geometrie jsou polohové úlohy, ve kterých vyšetřujeme vzájemnou polohu geometrických objektů, a metrické úlohy, ve kterých počítáme konkrétní číselnou hodnotu výsledku, jako je např. vzdálenost dvou bodů nebo úhel svíraný dvěma protínajícími se přímkami.
NahoruUvažujeme‑li body v rovině nebo v prostoru, kde máme zavedenou kartézskou soustavu souřadnic (v rovině se dvěma osami x,y nebo v prostoru se třemi osami x,y,z), můžeme body popsat číselně souřadnicemi v rovině, případně souřadnicemi v prostoru.
Pomocí souřadnic pak umíme spočítat vzdálenost dvou bodů „vzdušnou čarou“ – délku úsečky v rovině, případně v prostoru.
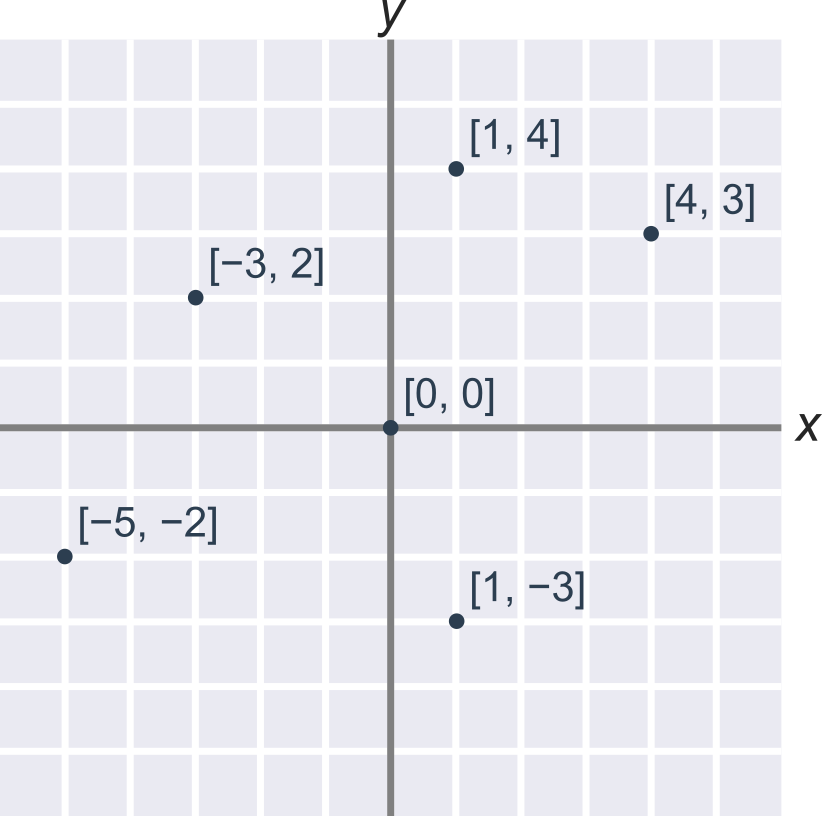
NahoruSouřadnice bodů v rovině
Souřadnice bodů většinou zapisujeme pomocí kartézské soustavy souřadnic v rovině, která má jako osy dvě kolmé přímky. Vodorovná přímka se tradičně označuje x a souřadnice podél této osy se zapisuje první. Svislá přímka se tradičně označuje y a souřadnice podle této osy se zapisuje druhá. Přímky x, y se protínají v bodě [0;0].
Přímky x a y jsou souřadné osy, bod [0;0] je počátek soustavy souřadnic.
Příklad: Souřadnice bodu A
Bod A na obrázku je v dané soustavě souřadnic určen jako x=1, y=2, což můžeme zapsat jako A[1;2].
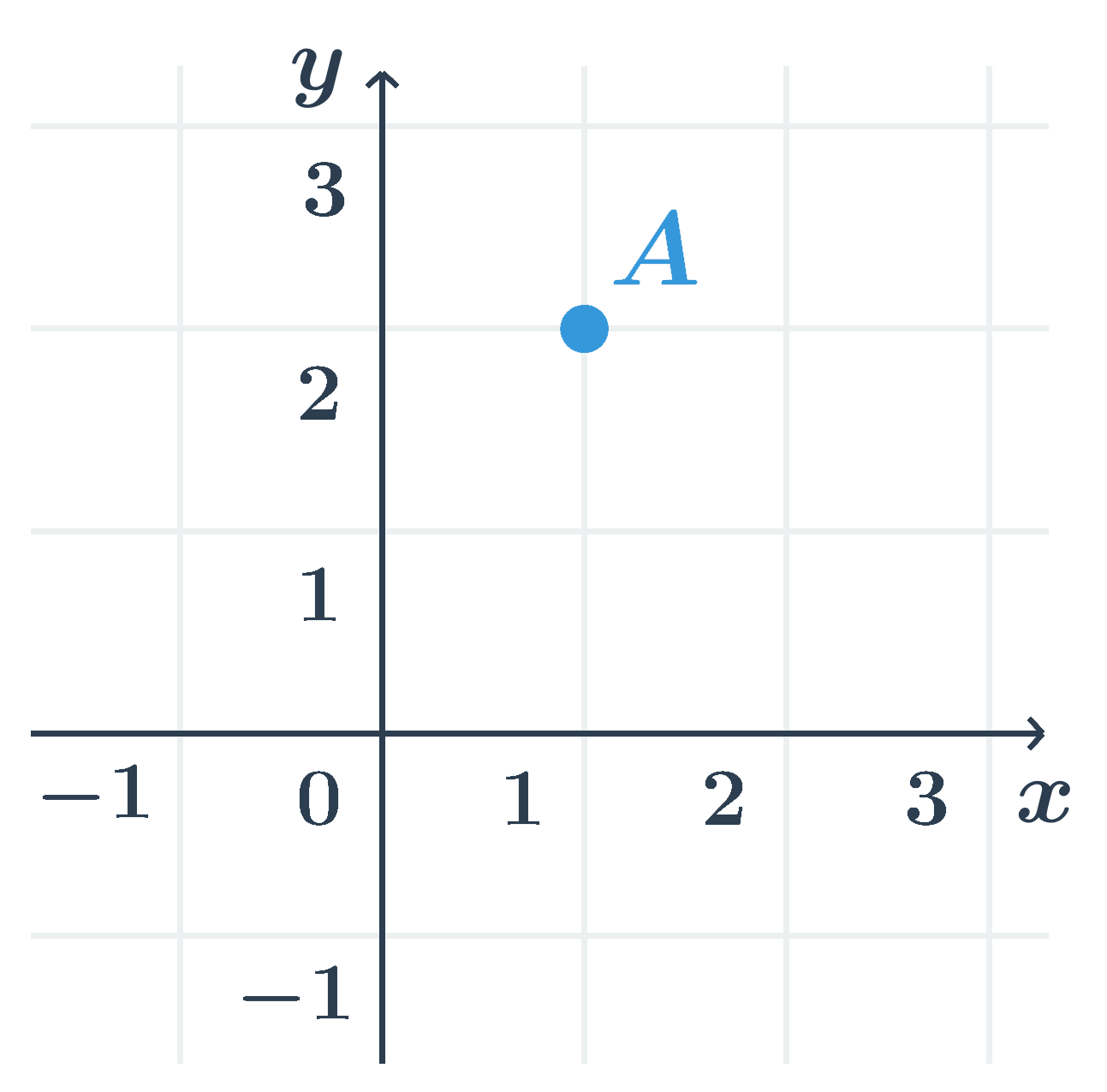
Další příklady souřadnic bodů
Souřadnice bodů v prostoru
Kartézská soustava souřadnic v rovině je daná trojicí navzájem kolmých číselných os x,y,z, které se protínají v bodě [0;0;0].
Přímky x,y,z jsou souřadné osy v prostoru, bod [0;0;0] je počátek soustavy souřadnic.
Příklad: Souřadnice bodu A
Bod A na obrázku je v dané soustavě souřadnic určen jako x=4, y=2, z=3, což můžeme zapsat jako A[4;2;3].
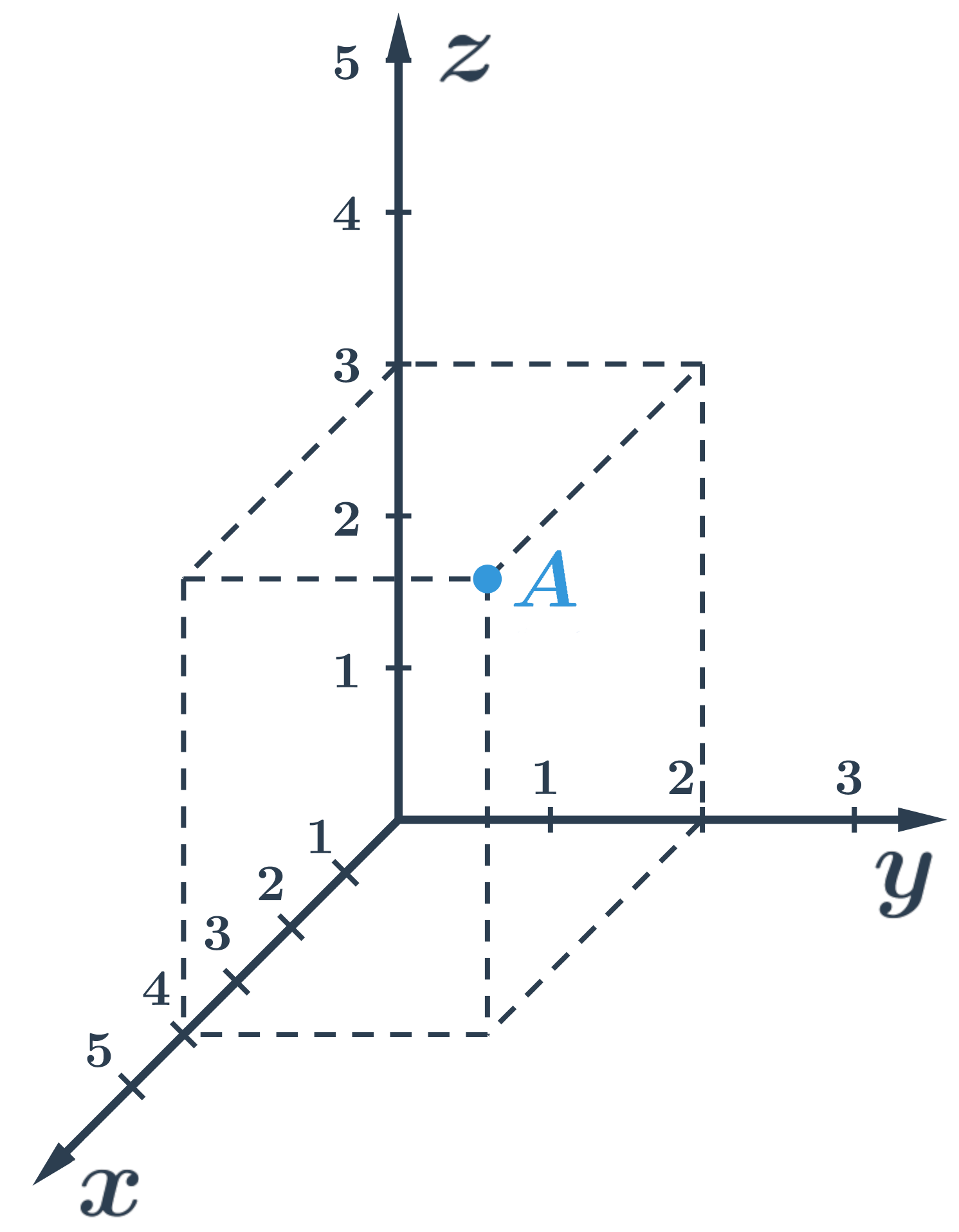
Vzdálenost bodů v rovině
Vzdálenost dvou bodů v rovině můžeme spočítat, když známe jejich souřadnice.
Jsou‑li dány souřadnice A=[a_x,a_y], B=[b_x,b_y], je vzdálenost bodu A od bodu B:
|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2}
Vzoreček vychází z Pythagorovy věty. Všimněme si pravoúhlého trojúhelníku s délkami odvěsen (b_x-a_x) a (b_y-a_y), jehož přepona má délku |AB|.
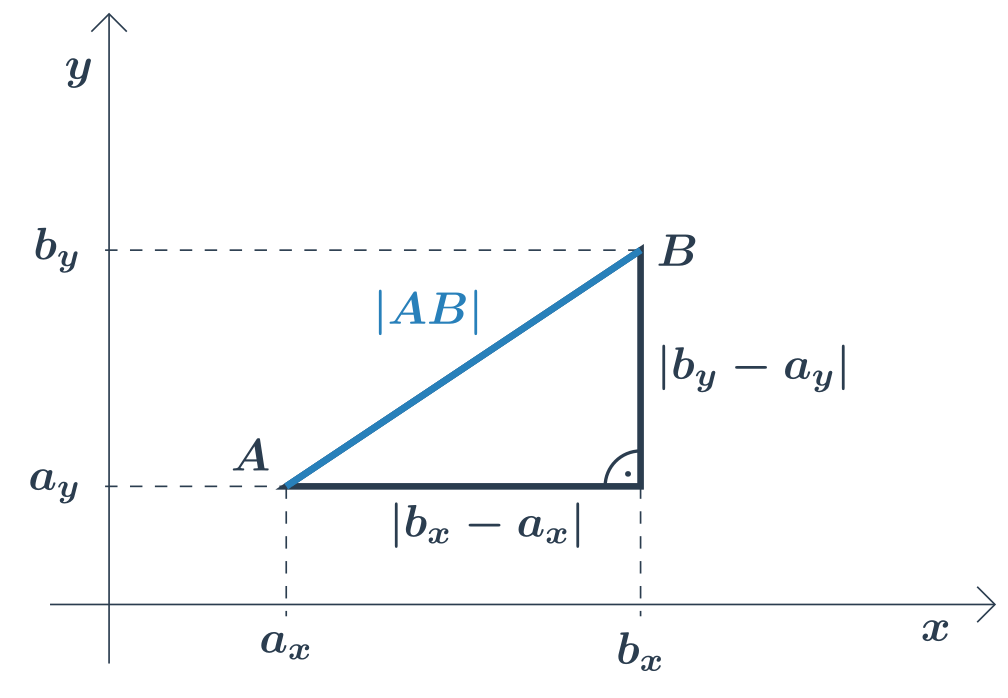
Příklad: vzdálenost C[0;1],D[4;4]
- |CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2}
- Dosadíme souřadnice bodů C[0;1] a D[4;4]:
\sqrt{(4-0)^2 + (4-1)^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5 - Vzdálenost je: |CD|=5
Příklad: vzdálenost M[2;-1], N[-1;-2]
- |MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2}
- Dosadíme souřadnice bodů M[2;-1] a N[-1;-2]:
\sqrt{(-1-2)^2 + (-2-(-1))^2}=\sqrt{(-3)^2 + (-1)^2}=\sqrt{10} - Vzdálenost je: |MN|=\sqrt{10}
Vzdálenost bodů v prostoru
Vzdálenost dvou bodů v prostoru spočítáme podobně jako v rovině pomocí jejich souřadnic. Máme‑li souřadnice bodů A=[a_x,a_y,a_z], B=[b_x,b_y,b_z], můžeme jejich vzdálenost určit takto:
|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2 + (b_z-a_z)^2}
Podobným způsobem (dvakrát po sobě použijeme Pythagorovu větu) počítáme délku tělesové úhlopříčky kvádru.
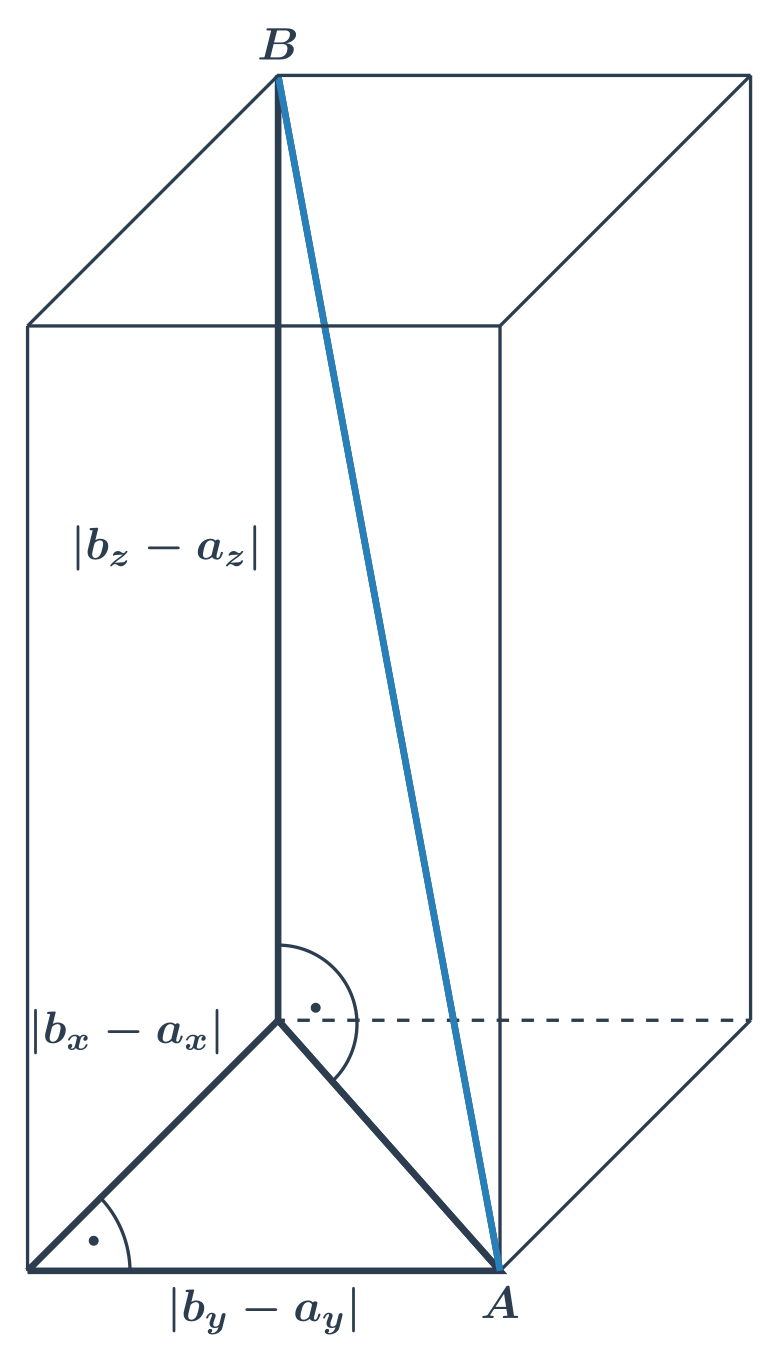
Příklad: vzdálenost C[1;2;0],D[4;5;1]
- |CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2 + (d_z-c_z)^2}
- Dosadíme souřadnice bodů C[1;2;0] a D[4;5;1]: \sqrt{(4-1)^2 + (5-2)^2 + (1-0)^2}=\sqrt{3^2 + 3^2 + 1^2}=\sqrt{19}
- Vzdálenost je: |CD|=\sqrt{19}
Příklad: vzdálenost M[0;-1;3], N[-4;1;-1]
- |MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2 + (n_y-m_y)^2}
- Dosadíme souřadnice bodů M[0;-1;3] a N[-4;1;-1]: \sqrt{(-4-0)^2 + (1-(-1))^2 + (-1-3)^2}=\sqrt{(-4)^2 + 2^2+(-4)^2}=\sqrt{36}=6
- Vzdálenost je: |MN|=6
Úsečka je část přímky mezi dvěma krajními body (včetně těchto bodů). Úsečka je v rovině i v prostoru jednoznačně zadaná svými krajními body.
NahoruDélka úsečky v rovině
Délku úsečky v rovině spočítáme stejně jako vzdálenost bodů v rovině.
Jsou‑li dány souřadnice A[x_A; y_A], B[x_B; y_B], je délka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}
Vzoreček vychází z Pythagorovy věty.
Je nutné počítat rozdíl souřadnic v pořadí „druhý bod mínus první“?
- Není. Výrazy x_B-x_A a x_A-x_B nejsou stejné. Ale jsou opačné a ve vzorci počítáme jejich druhé mocniny, které se rovnají.
- Navíc geometricky, délka úsečky AB je stejná jako délka úsečky BA.
- Důvodem zápisu právě v tomto tvaru je fakt, že délka úsečky je rovna velikosti vektoru \overrightarrow{AB} a u vektoru se jeho velikost vždy počítá „koncový bod mínus počáteční“.
Příklad: Délka úsečky EF: E[0;-1], F[-4;2]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
- Dosadíme souřadnice bodů E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
- Délka úsečky je: |EF|=5
Střed úsečky v rovině
Střed úsečky dělí úsečku na dvě stejné části. Pokud leží krajní body úsečky AB na číselné ose a jejich polohám odpovídají hodnoty a a b, potom jejímu středu S odpovídá číslo s=\frac{a+b}{2}. Střed úsečky je „průměrem“ jejích krajních bodů.
Pro úsečku v rovině bude situace následující. 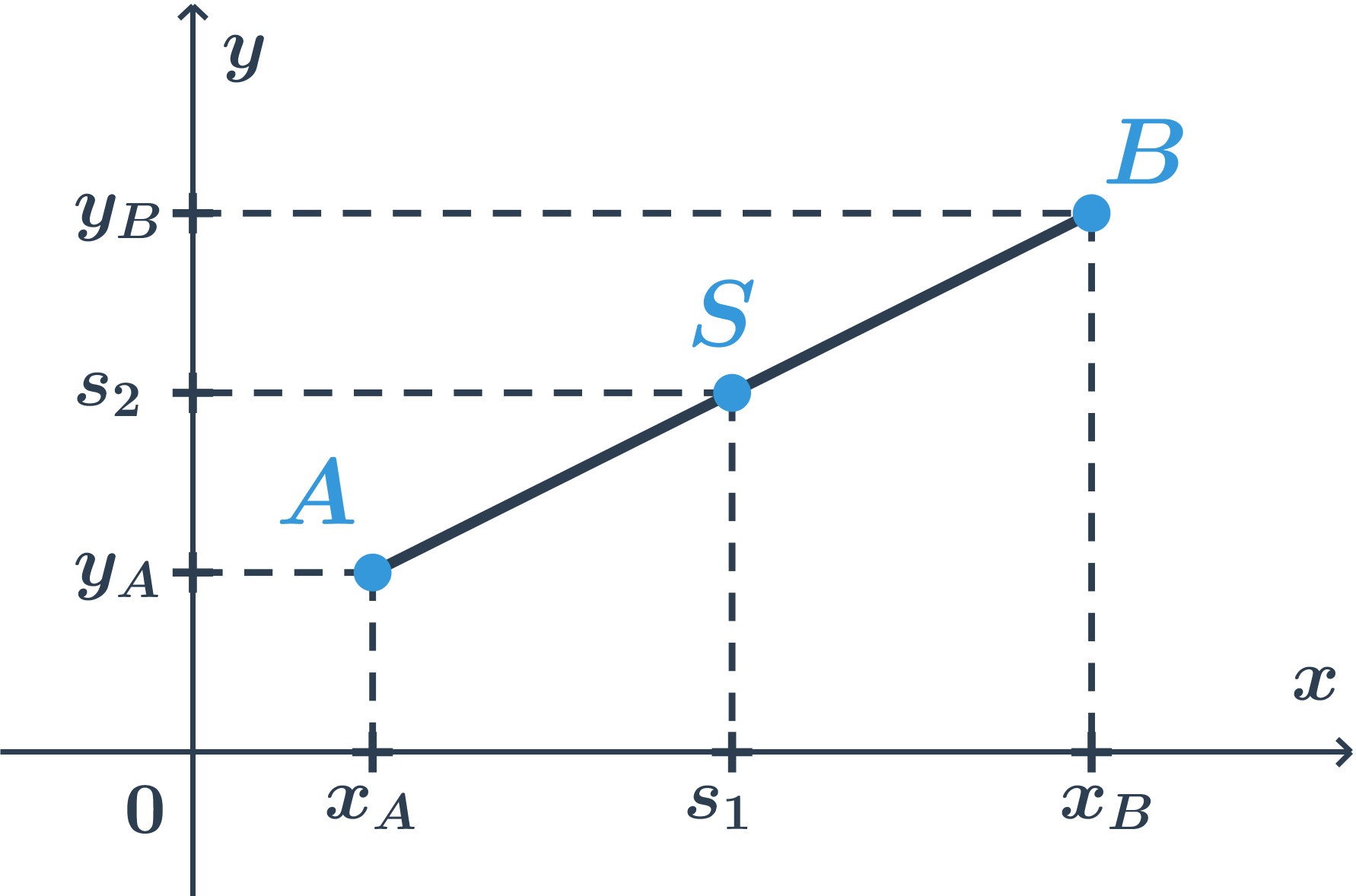 Situace na obou souřadných osách je stejná jako předtím. Spočítáme obě souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Situace na obou souřadných osách je stejná jako předtím. Spočítáme obě souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Pro střed S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Příklad: určení středu úsečky
Najděte střed úsečky AB: A[6;-1], B[2;3]
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Střed úsečky AB je bod S[4;1]
Příklad: určení druhého krajního bodu úsečky
Určete souřadnice druhého krajního bodu úsečky AB, je‑li dán bod A[-3;0] a její střed S[1;3].
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Dopočítáme neznámé x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Bod B má souřadnice [5;6].
Vzájemná poloha úseček v rovině
Dvě úsečky v rovině mohou mít společné krajní body, pak říkáme, že jsou totožné. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou různoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.
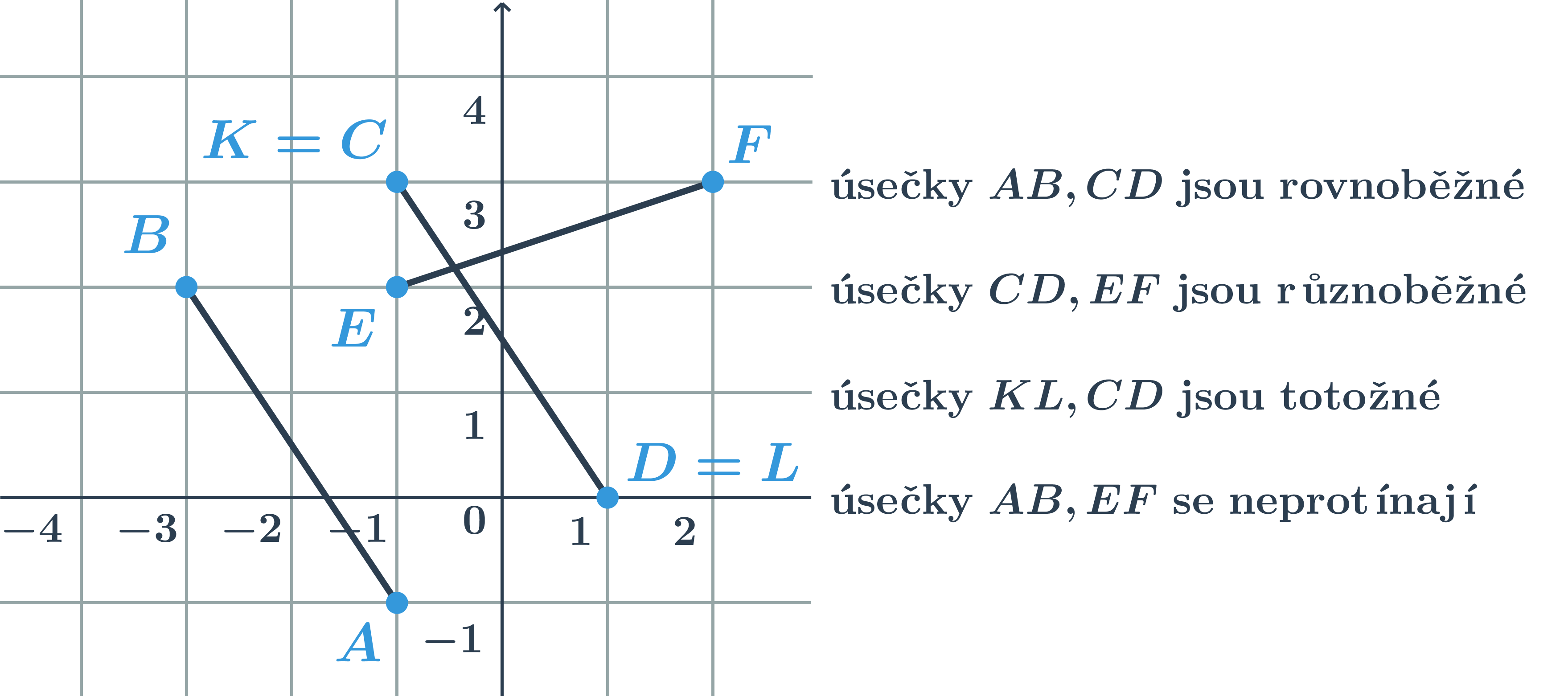
Délka úsečky v prostoru
Délku úsečky v prostoru spočítáme stejně jako vzdálenost bodů v prostoru.
Jsou‑li dány souřadnice A[x_A; y_A;z_A], B[x_B; y_B;z_B], je délka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2+(z_B-z_A)^2}
Příklad: Délka úsečky EF: E[-2;0;1], F[-4;2;0]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2+ (z_F-z_E)^2}
- Dosadíme souřadnice bodů EF; E[-2;0;1], F[-4;2;0]:
\sqrt{(-4-(-2))^2 + (2-0)^2+(0-1)^2}=\sqrt{(-2)^2 + 2^2+(-1)^2}=\sqrt{4+4+1}=\sqrt{9}=3 - Délka úsečky je: |EF|=3
Střed úsečky v prostoru
Střed úsečky v prostoru spočítáme podobně jako střed úsečky v rovině. Spočítáme všechny souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Pro střed S[s_1;s_2;s_3] úsečky AB, kde A[x_A; y_A;z_A], B[x_B; y_B;z_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2} , s_3 = \frac{z_A+z_B}{2}
Příklad: určení středu úsečky
Najděte střed úsečky AB: A[2;1;-3], B[2;-3;3]
Pro souřadnice středu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme souřadnice bodů A[2;1;-3], B[2;-3;3].
- s_1 = \frac{2+2}{2}=2, s_2 = \frac{1-3}{2}=-1, s_3 = \frac{-3+3}{2}=0
Střed úsečky AB je bod S[2;-1;0]
Příklad: určení druhého krajního bodu úsečky
Určete souřadnice druhého krajního bodu úsečky AB, je-li dán bod A[1;2;4] a její střed S[1;-3;0].
- Pro souřadnice středu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme souřadnice bodů A[1;2;4], S[1;-3;0].
- 1 = \frac{1+x_B}{2}, -3 = \frac{2+y_B}{2}, 0 = \frac{4+z_B}{2}
- Dopočítáme neznámé x_B, y_B, z_B:
\begin{array}{rclcrcr} 2&=&1+x_B &\Rightarrow& x_B&=&1\\ -6&=&2+y_B &\Rightarrow& y_B&=&-8\\ 0&=&4+z_B &\Rightarrow& z_B&=&-4 \end{array}
- Bod B má souřadnice [2;-8;-4].
Vzájemná poloha úseček v prostoru
Podobně jako v rovině mohou mít dvě úsečky společné krajní body, pak říkáme, že jsou totožné. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou různoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.
Tyto vzájemné polohy si dobře můžeme ilustrovat na krychli.
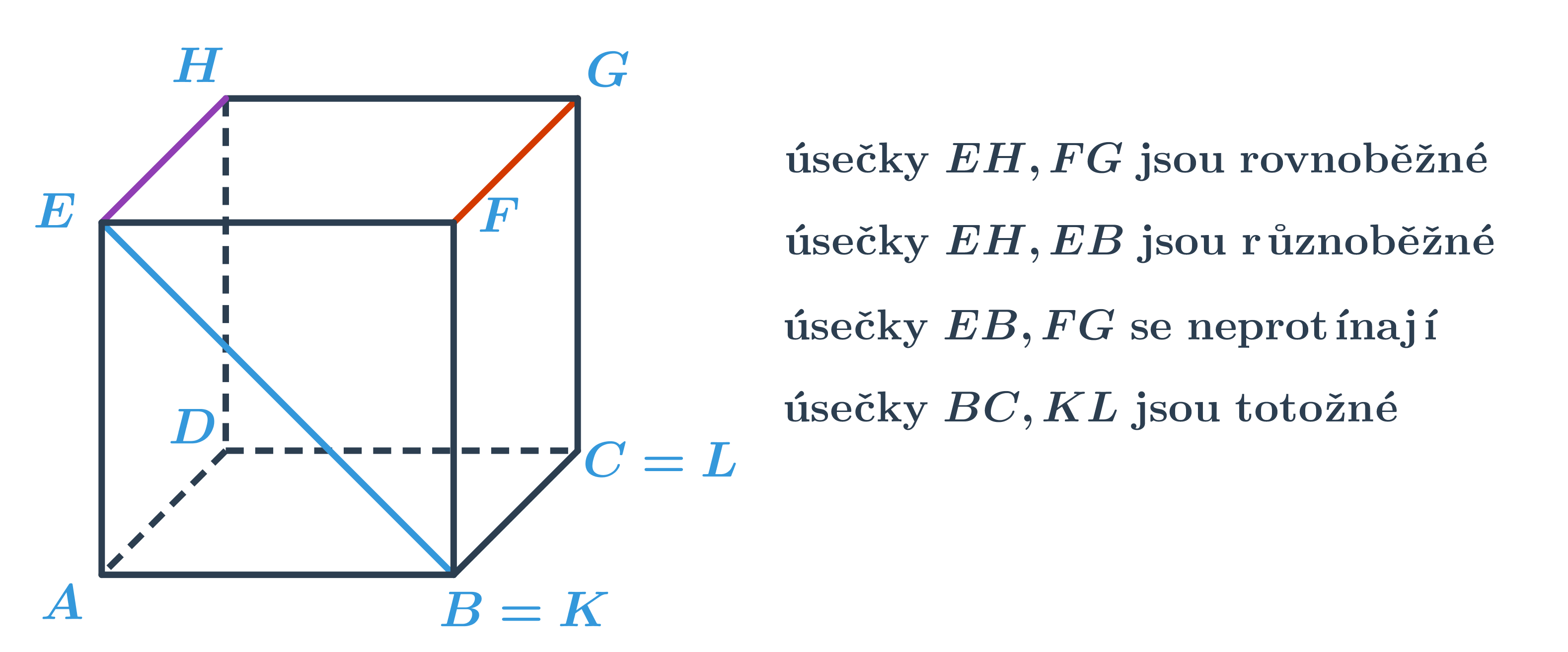
Vektory patří mezi základní objekty používané v analytické geometrii. Vektory mají hojné využití i ve fyzice. Intuitivně si je můžeme představit jako šipky, které udávají směr a současně mají určitou velikost.
Základní procvičování vektorů je rozdělené do několika témat:
- Vektory: pojmy – definice vektoru, vektory opačné, kolmé a kolineární, souřadnice vektoru, velikost vektoru
- Souřadnice vektoru – určování souřadnic vektorů, souvislost se souřadnicemi bodů
- Velikost vektoru – výpočet velikosti vektoru, aplikace Pythagorovy věty
- Vzájemná poloha vektorů – opačné, kolmé a kolineární vektory, určování vzájemné polohy na základě souřadnic
Vektory: pojmy
Vektor je množina všech shodně orientovaných úseček, které mají stejnou délku. Každou z těchto úseček nazýváme umístěním vektoru.
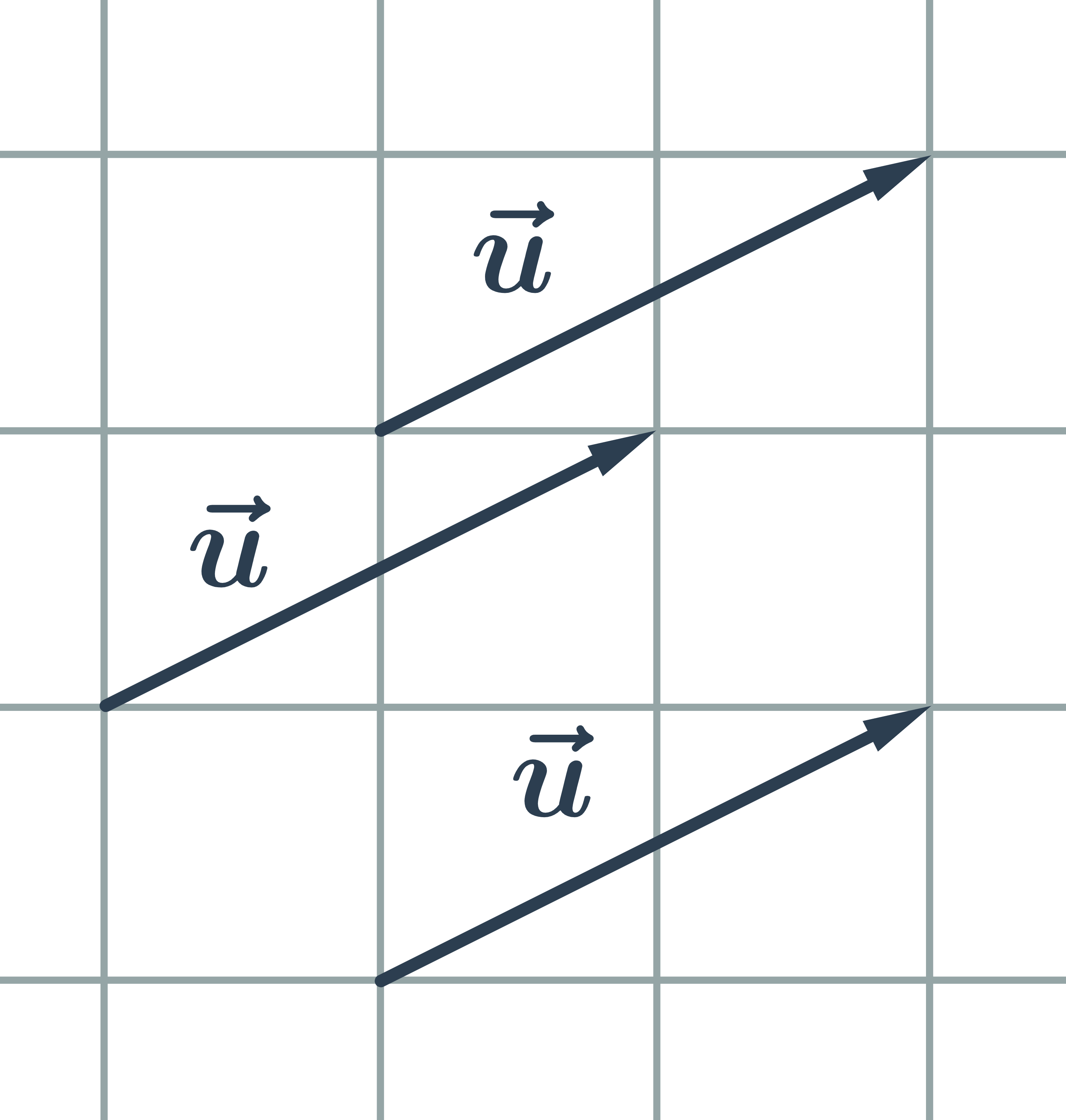
Vektor je určený počátečním a koncovým bodem, graficky znázorňujeme se šipkou u koncového bodu, zapisujeme: \vec{u}=\overrightarrow{AB}
Na obrázku je A počáteční bod vektoru \vec{u}, B je koncový bod vektoru \vec{u}.
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci:
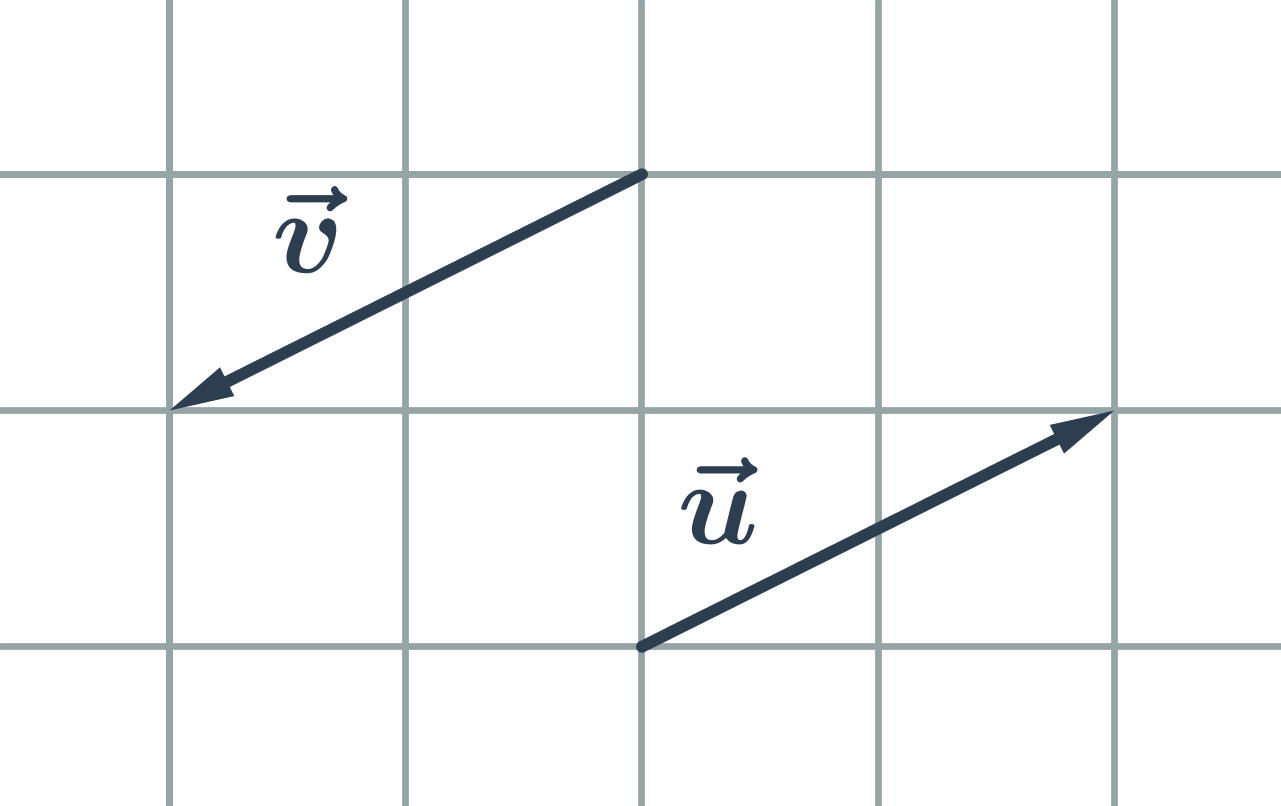
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. Tedy nemusí mít stejnou délku, mohou mít stejnou nebo opačnou orientaci:
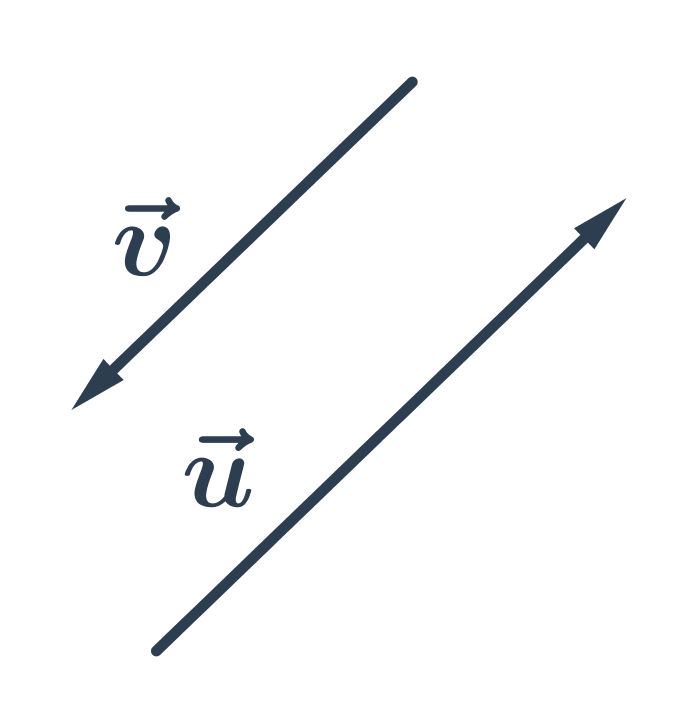
Kolmé vektory jsou vektory, které svírají pravý úhel:
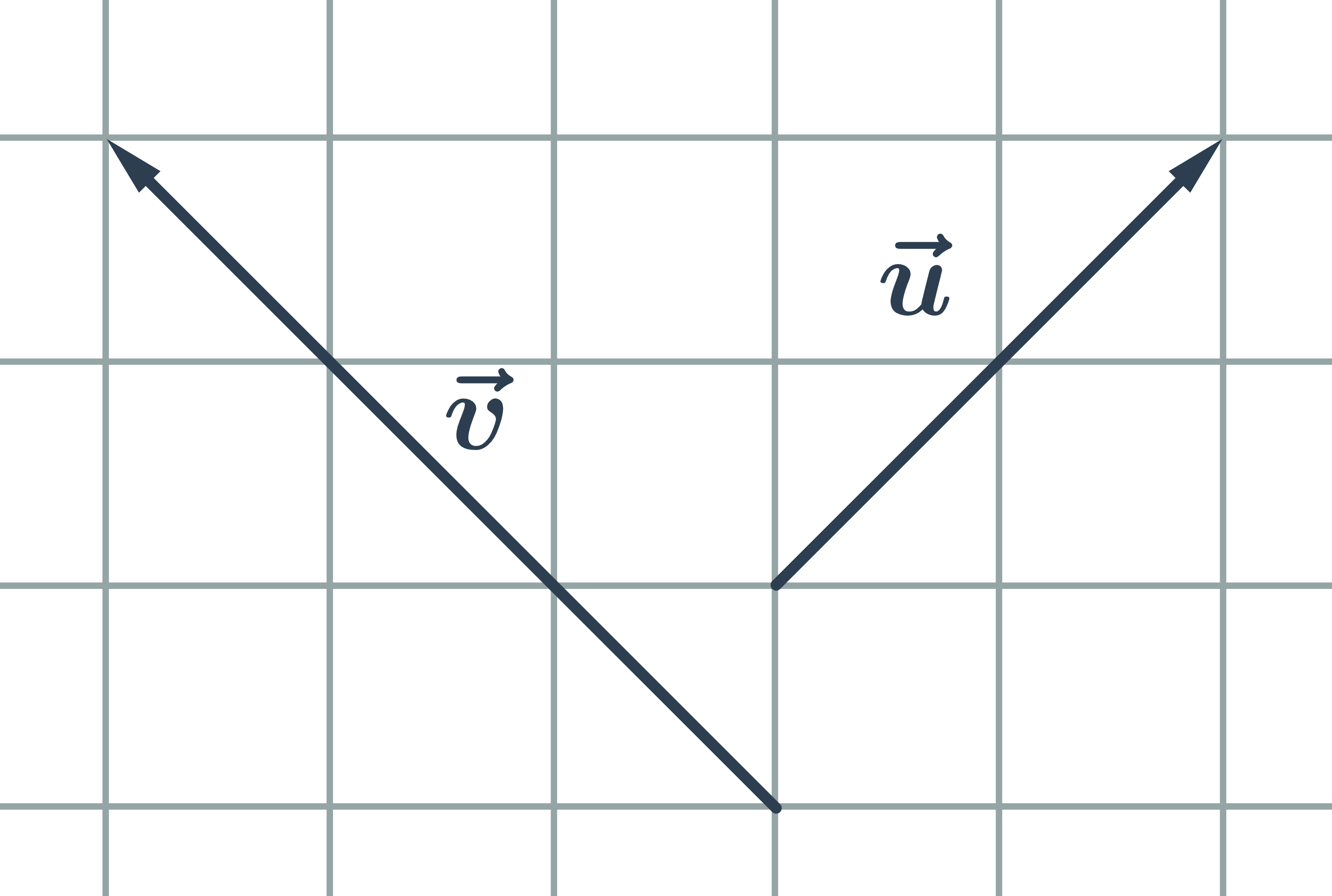
Souřadnice vektoru jsou pravoúhlé průměty vektoru do souřadných os, tedy vektor \vec{u}=\overrightarrow{AB} má souřadnice: \vec{u}=(u_1;u_2)=(b_1-a_1;b_2-a_2)
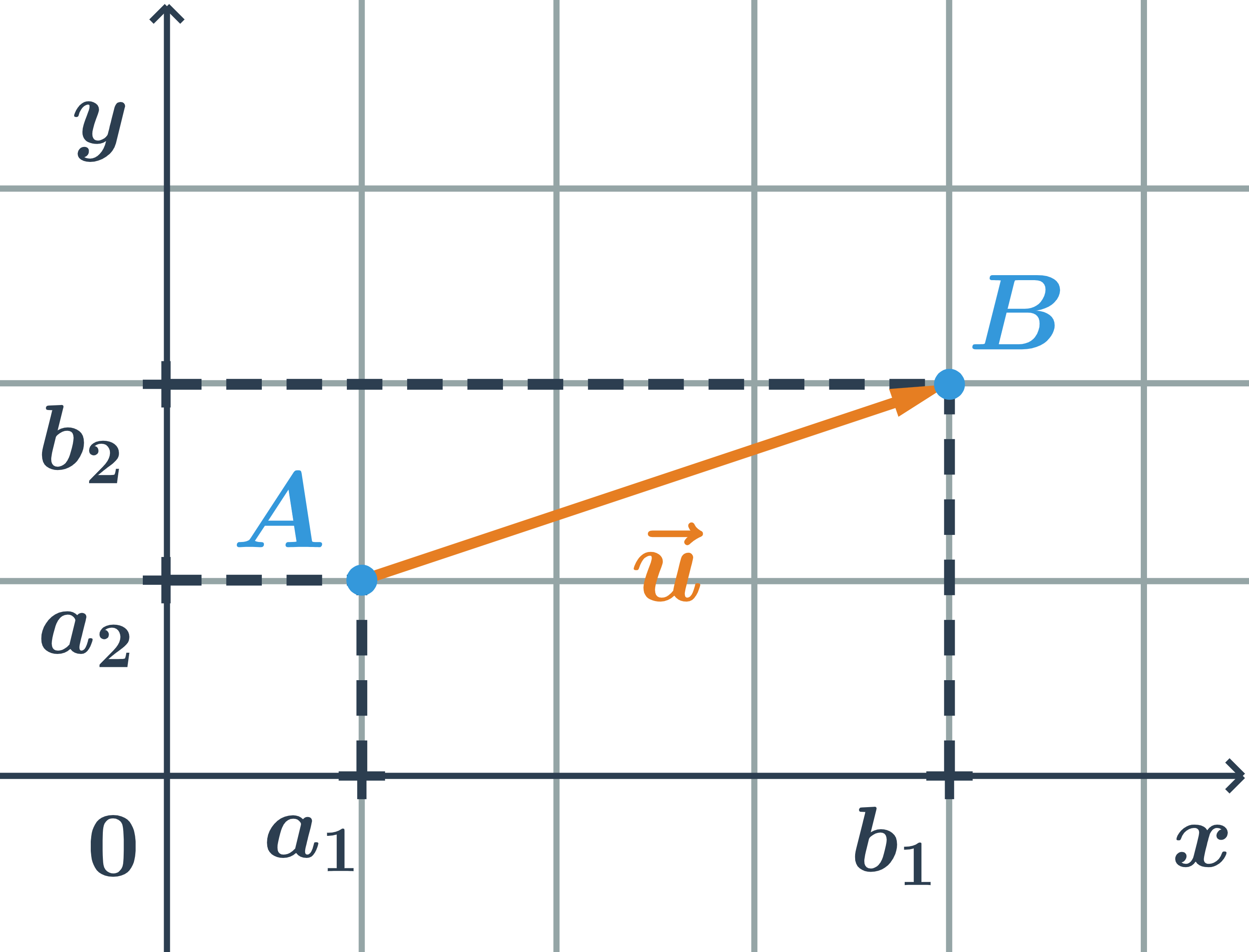
Velikost vektoru \vec {u}=\overrightarrow{AB} je délka úsečky AB, značíme \left| \vec{u} \right| a platí: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
Jednotkový vektor má délku 1.
Nulový vektor má nulovou délku, tedy splývá jeho počáteční a koncový bod.
NahoruSouřadnice vektoru
Již víme, že vektor je množina nekonečně mnoha orientovaných úseček, jedna z nich má počátek v počátku souřadného systému, v bodě O=[0;0]. Souřadnice koncového bodu jsou souřadnice daného vektoru.
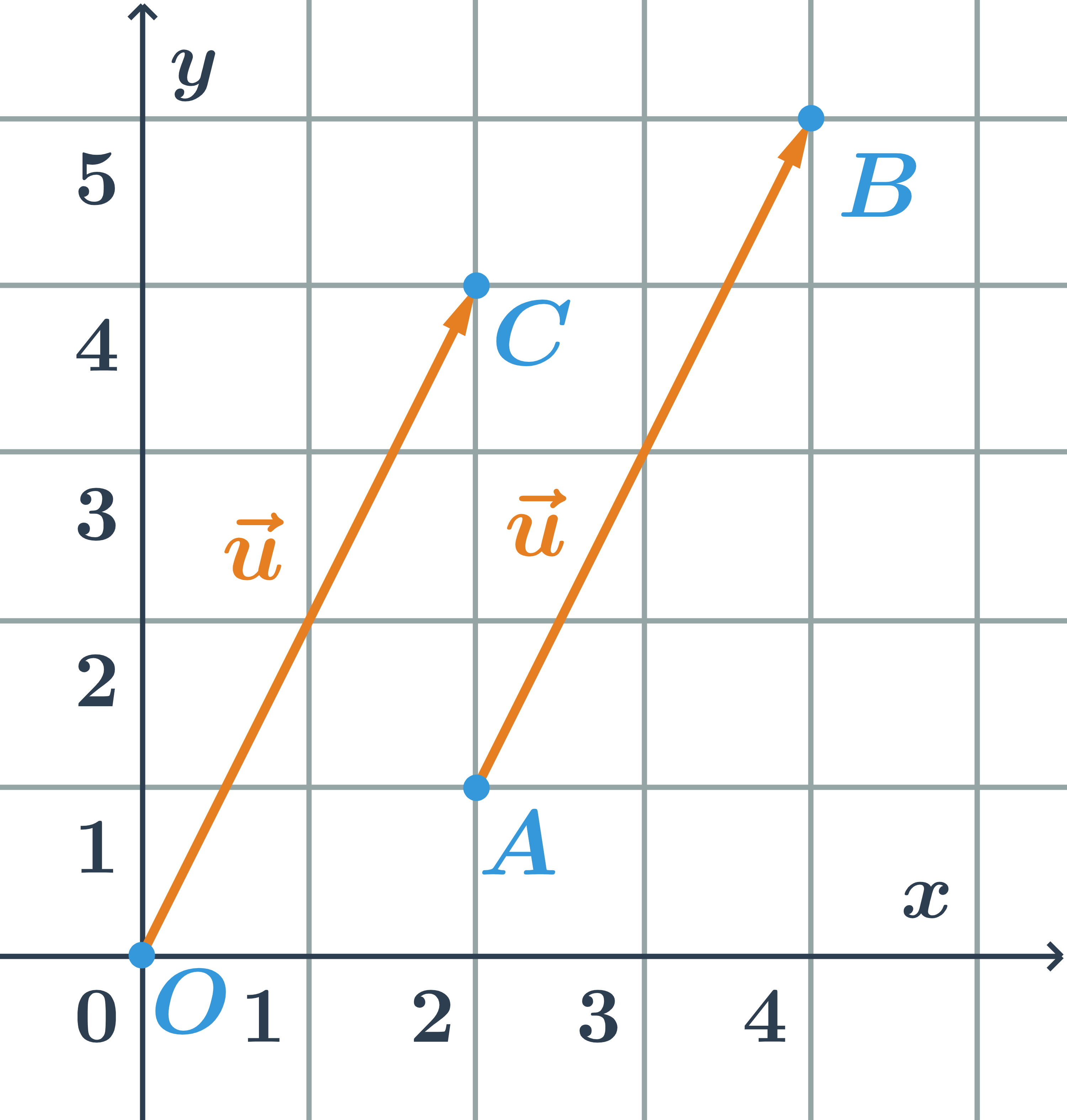
Souřadnice vektoru \overrightarrow{AB}
- Chceme-li vektor \overrightarrow{AB} posunout do počátku souřadného systému, posuneme ho o dva čtverečky vlevo a o jeden čtvereček dolů.
- Bod A se posune do bodu O, bod B se posune do bodu C. Tento posun můžeme vyjádřit takto:
- A se posune na [2-2;1-1]=[0;0]
- B se posune na [4-2;5-1]=[2;4]
- Souřadnice vektor na obrázku jsou: \vec{u}=\overrightarrow{AB}=\overrightarrow{OC}=(2;4)
Všimněte si, že souřadnice vektoru \overrightarrow{AB} jsme získali odečtením souřadnic bodu A od souřadnic bodu B
Pro souřadnice vektoru \overrightarrow{AB} určeného body A=[a_1;a_2], B=[b_1;b_2] platí: \overrightarrow{AB}=B-A=(b_1-a_1;b_2-a_2)
NahoruVelikost vektoru
Velikost vektoru \overrightarrow{AB} je délka úsečky AB. Vektor, který má délku 1, se nazývá jednotkový vektor:
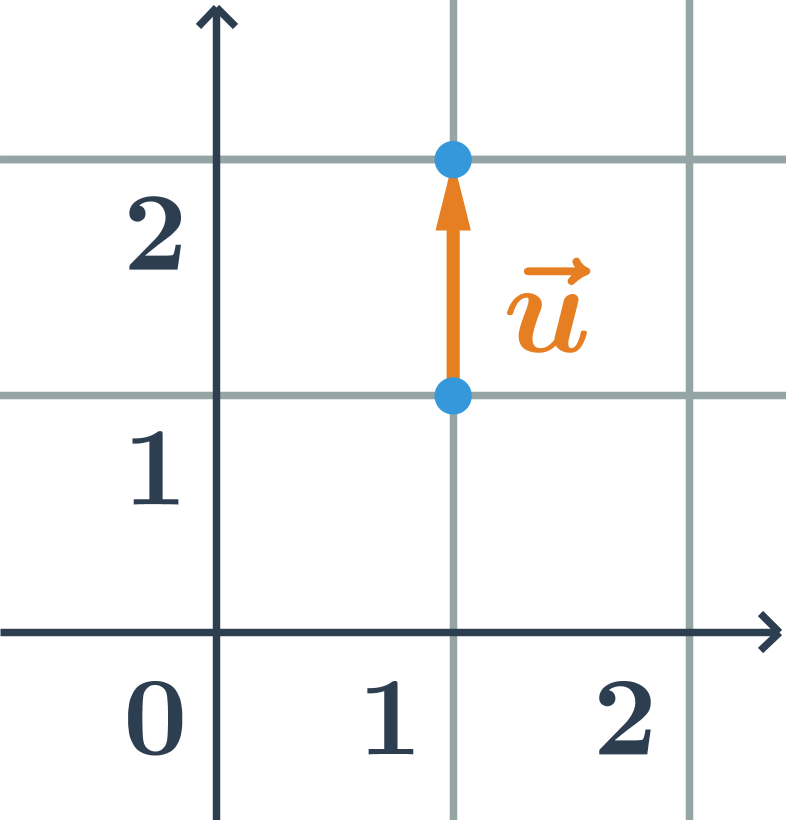
Vektor, který má nulovou délku (počáteční a koncový bod vektoru splývá) se nazývá nulový vektor:
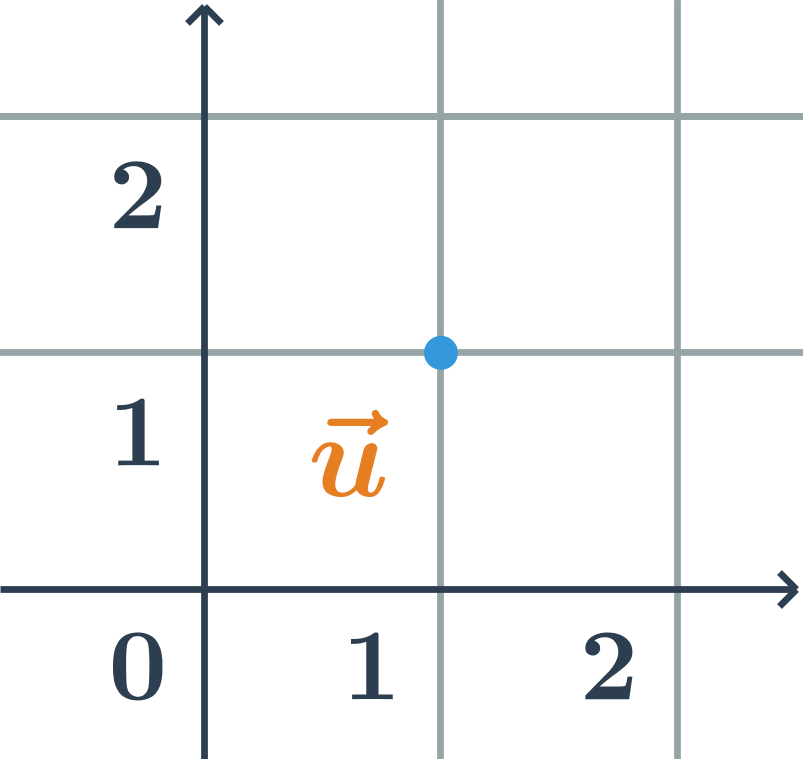
Velikost vektoru \vec{u}=(u_1;u_2) určíme s využitím Pythagorovy věty: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
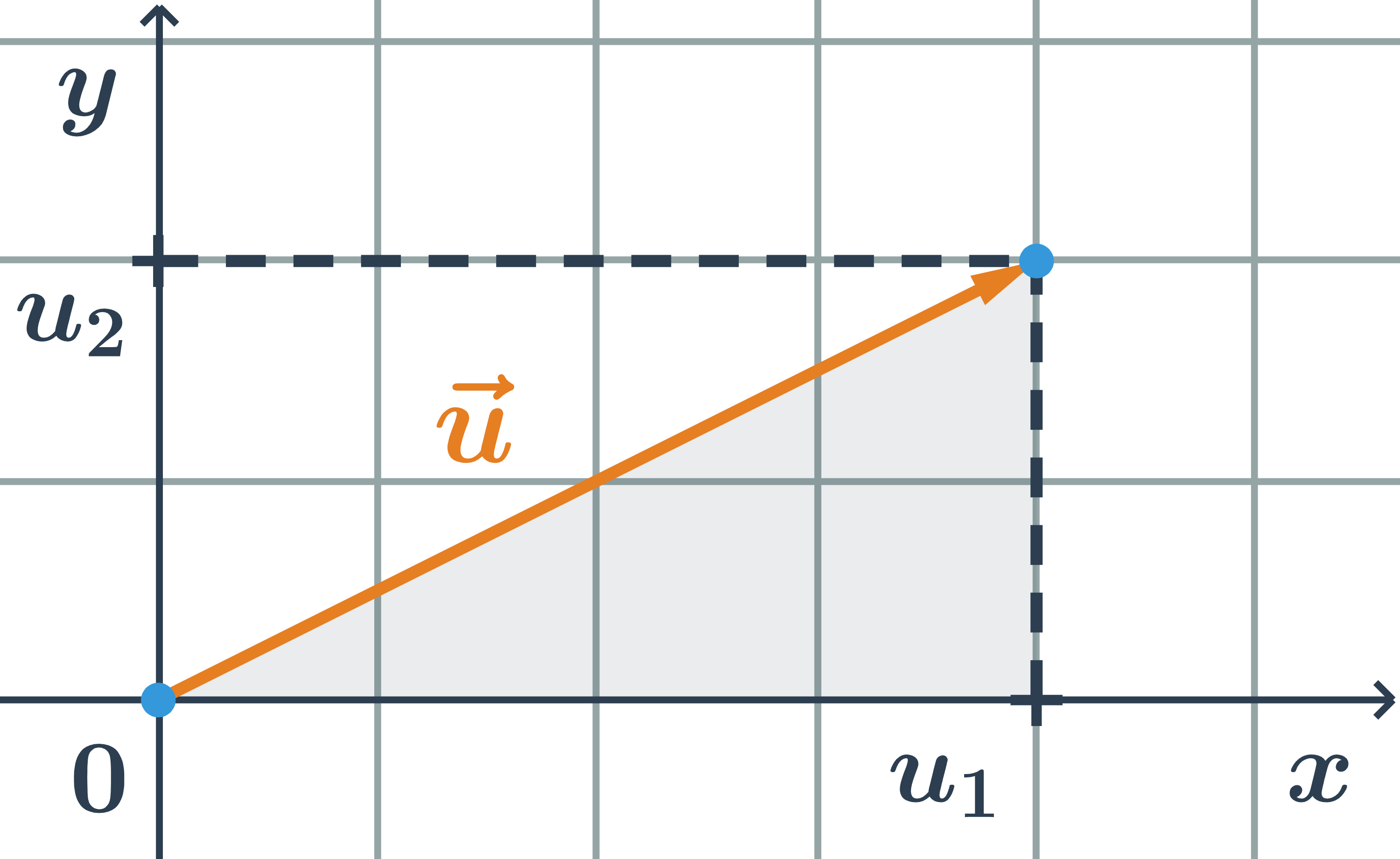
Ve vybarveném trojúhelníku je délka vektoru přepona, odvěsny mají délky u_1 a u_2.
Příklad: velikost vektoru
Určete velikost vektoru na obrázku:
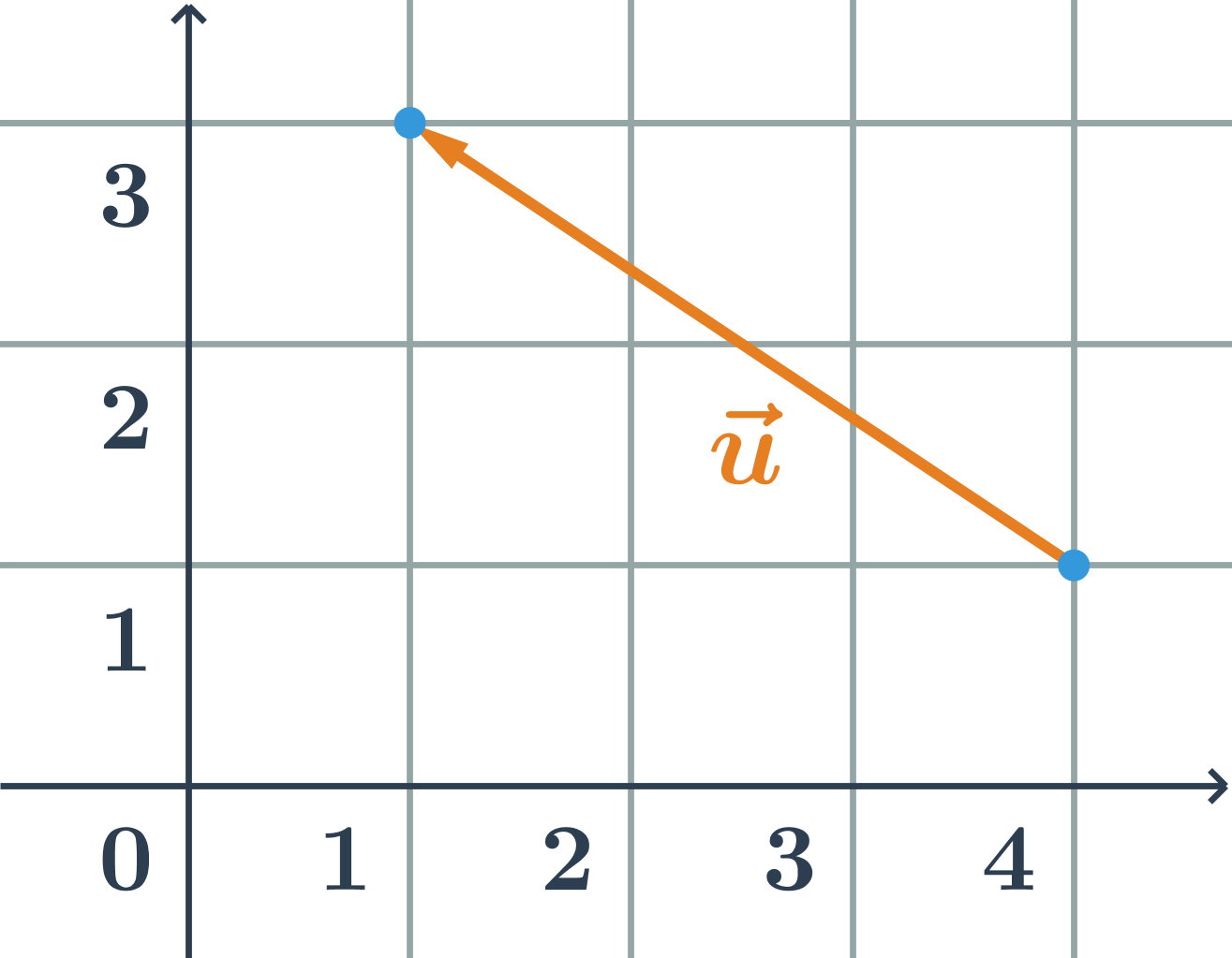
Vektor na obrázku má souřadnice \vec{u}=(-3;2), jeho velikost je \left| \vec{u} \right|=\sqrt{(-3)^2+2^2}=\sqrt{(-3)^2+2^2}=\sqrt{13}
Vzájemná poloha vektorů
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci. K vektoru \vec{u}=(u_1;u_2) je opačný vektor \vec{v}=(-u_1;-u_2)
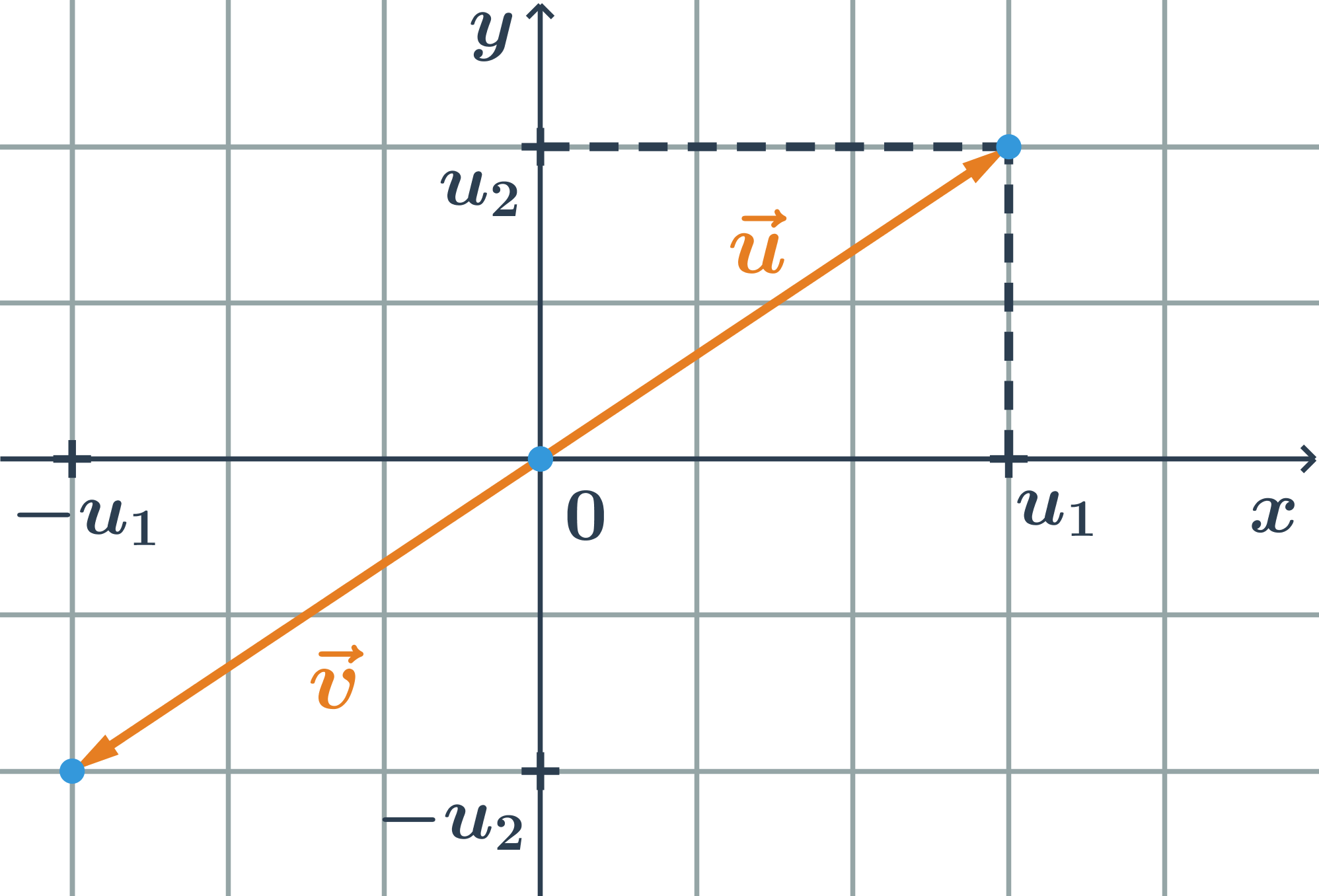
Příklad opačný vektor
- Určete opačný vektor k vektoru \vec{u}=(3;-1).
- Opačný vektor \vec{v} k vektoru \vec{u} má souřadnice: (-u_1;-u_2)=(-3;1)
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. S vektorem \vec{u}=(u_1;u_2) je kolineární každý vektor \vec{v}=(k\cdot u_1;k \cdot u_2), kde k je reálné nenulové číslo. Pro k \gt 0 vektory mají stejný směr, pro k \lt 0 mají vektory opačný směr.
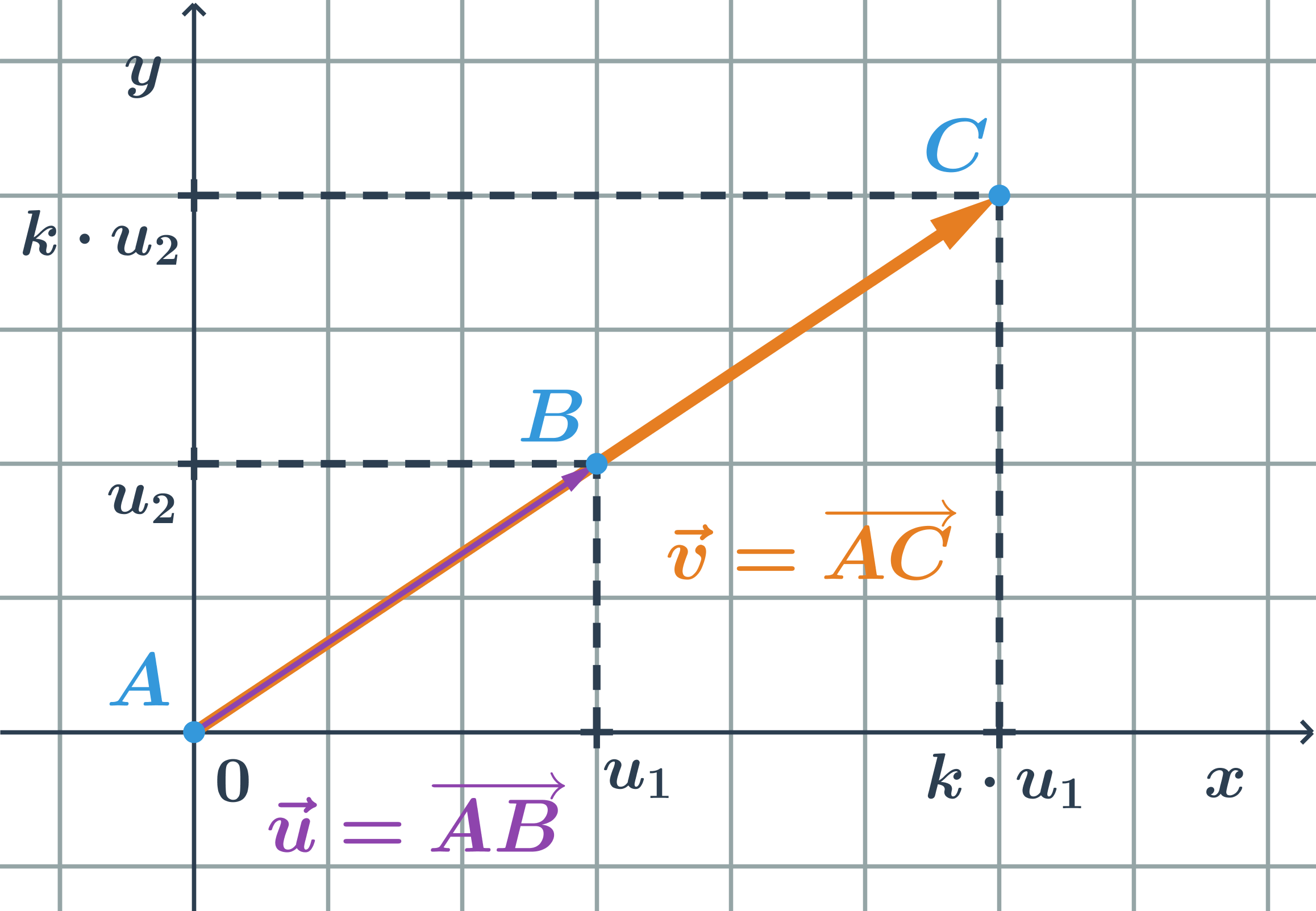
Příklad kolineární vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;3) tak, aby byl kolineární s vektorem \vec{u}=(2;-1).
- Pro druhou souřadnici platí: v_2=3, u_2=-1, tedy v_2= (-3) \cdot u_2
- Vidíme, že k=-3 je záporné, tj. \vec{u} a \vec{v} mají opačnou orientaci
- Pro první souřadnici musí platit: v_1= (-3) \cdot u_1= (-3)\cdot2=-6.
Kolmé vektory jsou vektory, které svírají pravý úhel K vektoru \vec{u}=(u_1;u_2) je kolmý každý vektor \vec{v}=(-k\cdot u_2;k \cdot u_1), kde k je reálné nenulové číslo.
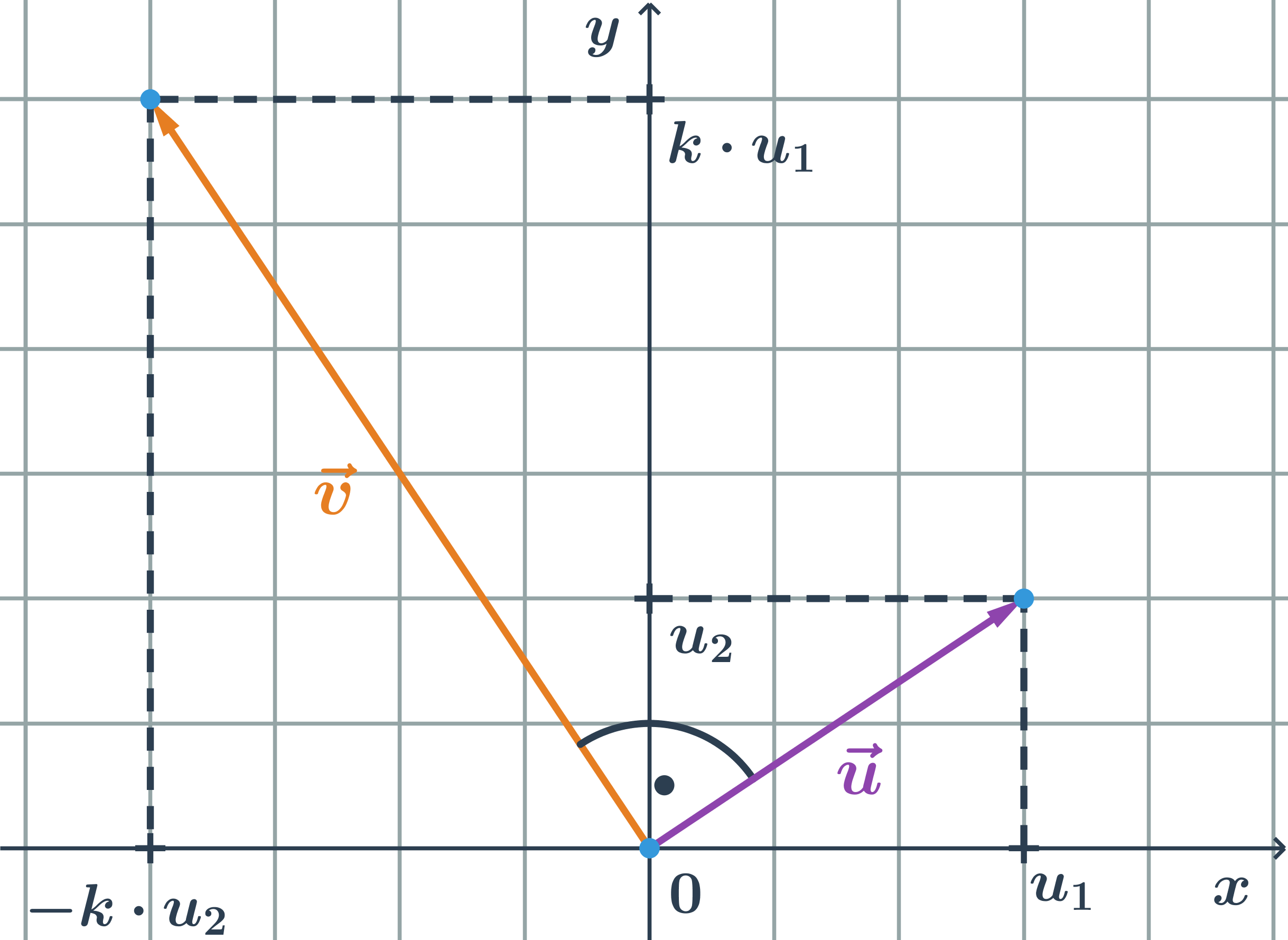
Příklad kolmý vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;4) tak, aby byl kolmý k vektoru \vec{u}=(2;-1).
- Platí: v_2=2 \cdot u_1, tedy musí platit: v_1 = - 2 \cdot u_2.
- Máme tedy v_1 = - 2 \cdot u_2 = -2 \cdot (-1) = 2.
Operace s vektory
Vektory v rovině mohou být zapsané jako dvojice čísel – souřadnic v rovině, podobně trojrozměrné vektory lze zapsat jako trojice čísel – souřadnic v prostoru.
Operace jako součet, rozdíl a vynásobení reálným číslem, které umíme jednoduše provádět s čísly, lze s vektory provádět po jednotlivých souřadnicích. Tím se zabývá kapitolka Vektory: násobení konstantou, součet, rozdíl. Příklady praktického použití těchto operací s vektory:
- vrabec letí stejným směrem jako moucha a dvakrát rychleji než moucha – vektor rychlosti vrabce získáme, když vektor rychlosti mouchy vynásobíme konstantou 2,
- satelitní snímky ukazují, že ráno ještě vozítko Marka Watneyho stálo na marsovské základně, za dnešek ujel 50 km na východ – jeho novou polohu získáme, když k souřadnicím základny přičteme vektor (50;0),
- šnek přelezl rovně po monitoru z levého horního rohu (souřadnice v pixelech [0;0]) do bodu [1007;555] – vektor, jehož souřadnice jsou počty pixelů, co šnek ulezl v horizontálním a vertikálním směru získáme jako rozdíl jeho umístění na konci pohybu a jeho umístění na začátku pohybu.
Speciální operace, kterou lze provést se dvěma vektory stejné dimenze (mají stejný počet souřadnic), je skalární součin. Vstup této operace jsou dva vektory, výstup je reálné číslo.
Díky skalárnímu součinu můžeme vypočítat kupříkladu jaký úhel vektory svírají, speciálně jestli jsou na sebe kolmé (v takovém případě jejich skalární součin vyjde nulový).
NahoruVektory: násobení konstantou, součet, rozdíl
Součet vektorů
Vektory \vec{u} a \vec{v} sečteme takto: počáteční bod vektoru \vec{v} posuneme do koncového bodu vektoru \vec{u}. Součet vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má počáteční bod stejný jako vektor \vec{u} a koncový bod stejný jako vektor \vec{v}. Píšeme: \vec{u}+\vec{v}=\vec{w}
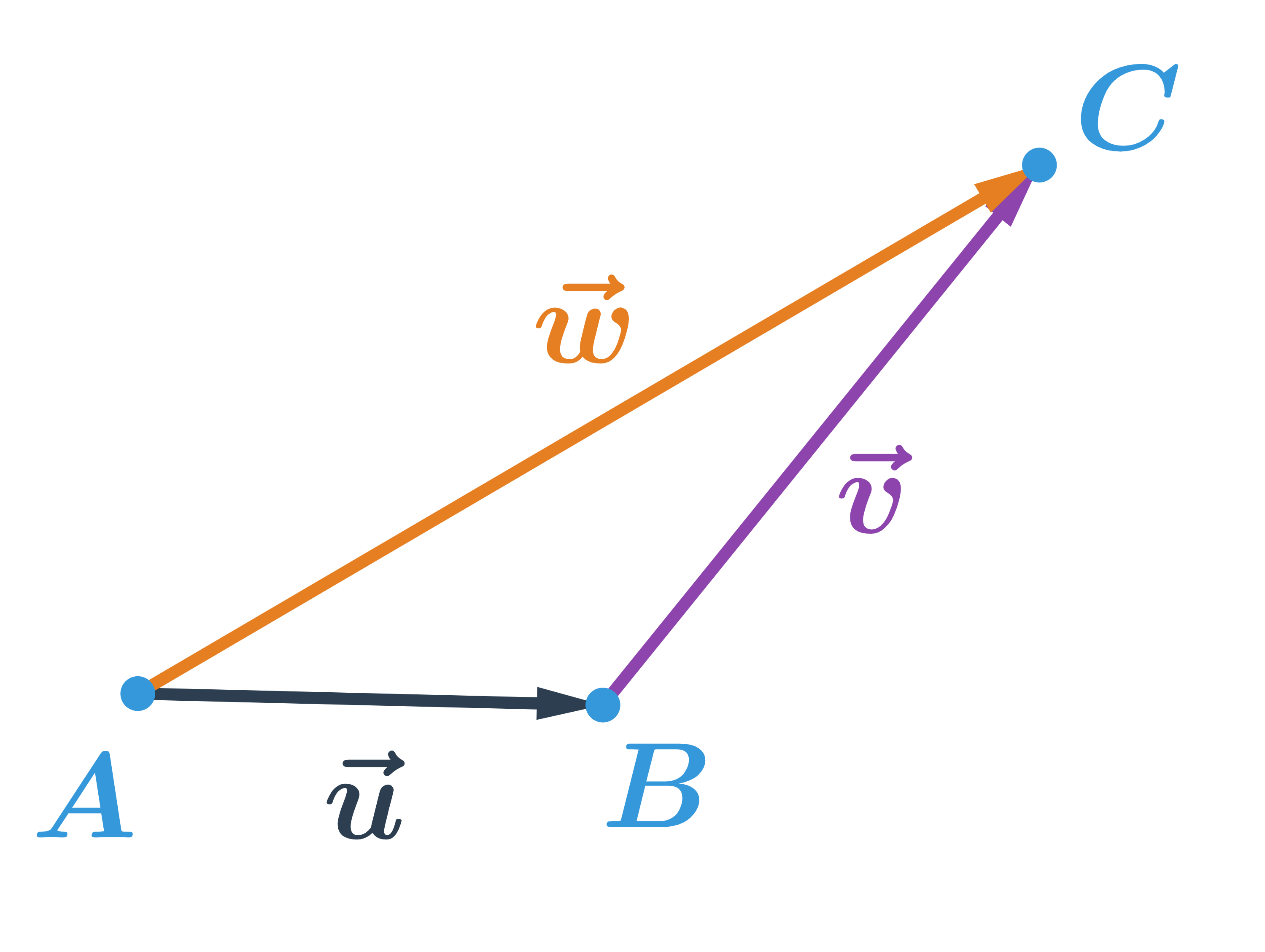
Vektory na obrázku jsou označené \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{BC}. Součet těchto vektorů: \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}
Mějme vektory se souřadnicemi \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2). Pak součet vektorů \vec{u} a \vec{v} je vektor \vec{w} se souřadnicemi \vec{w}=(u_1+v_1; u_2+v_2).
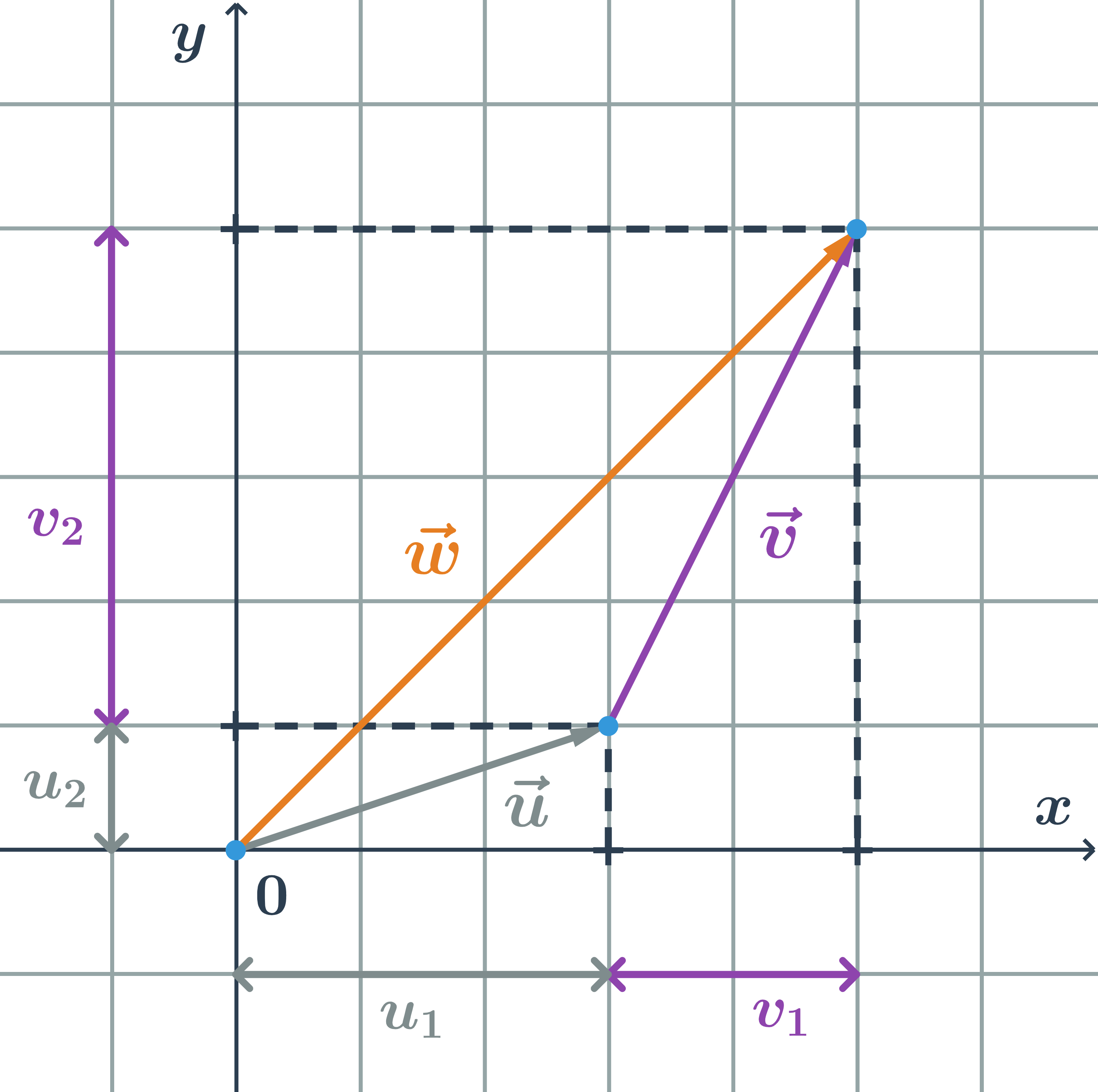
Rozdíl vektorů
Rozdíl vektorů \vec{u} a \vec{v} je součet vektoru \vec{u} s vektorem opačným k \vec{v}. Tedy:
\vec{u}-\vec{v}=\vec{u}+(-\vec{v})
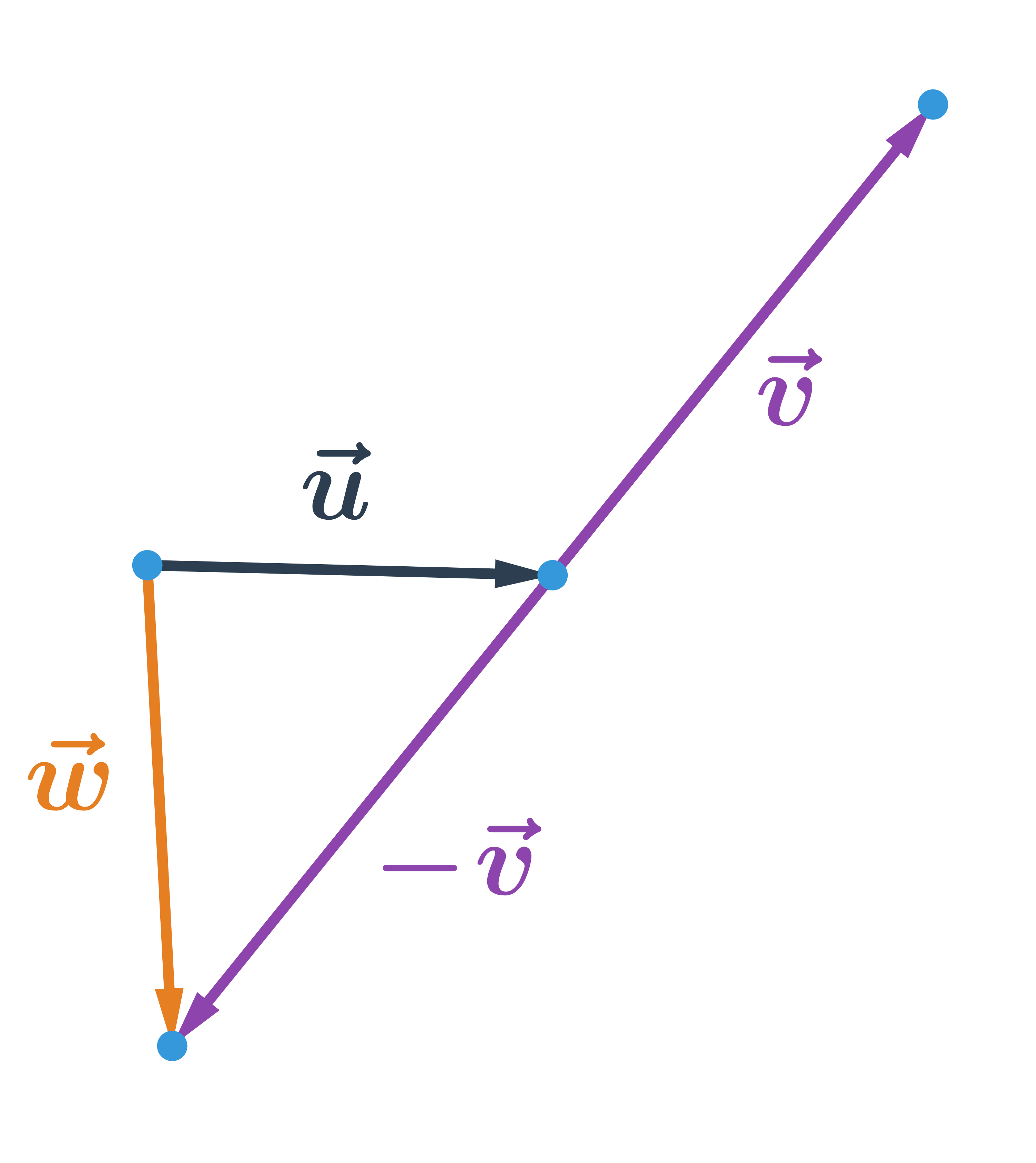
Máme-li souřadnice vektorů: \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), pak rozdíl vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má souřadnice: \vec{w}=(u_1-v_1; u_2-v_2).
Násobek vektoru
Vektor \vec{u} můžeme vynásobit libovolným reálným číslem k. Dostaneme vektor \vec{v}, kterému říkáme násobek vektoru. Píšeme \vec{v}=k \cdot \vec{u}
- Pokud k \gt 0, vektory \vec{u} a k \cdot \vec{u} mají stejný směr
- Pokud k \lt 0, vektory \vec{u} a k \cdot \vec{u} mají opačný směr
- Pokud k=0, vektor k \cdot \vec{u} je nulový vektor
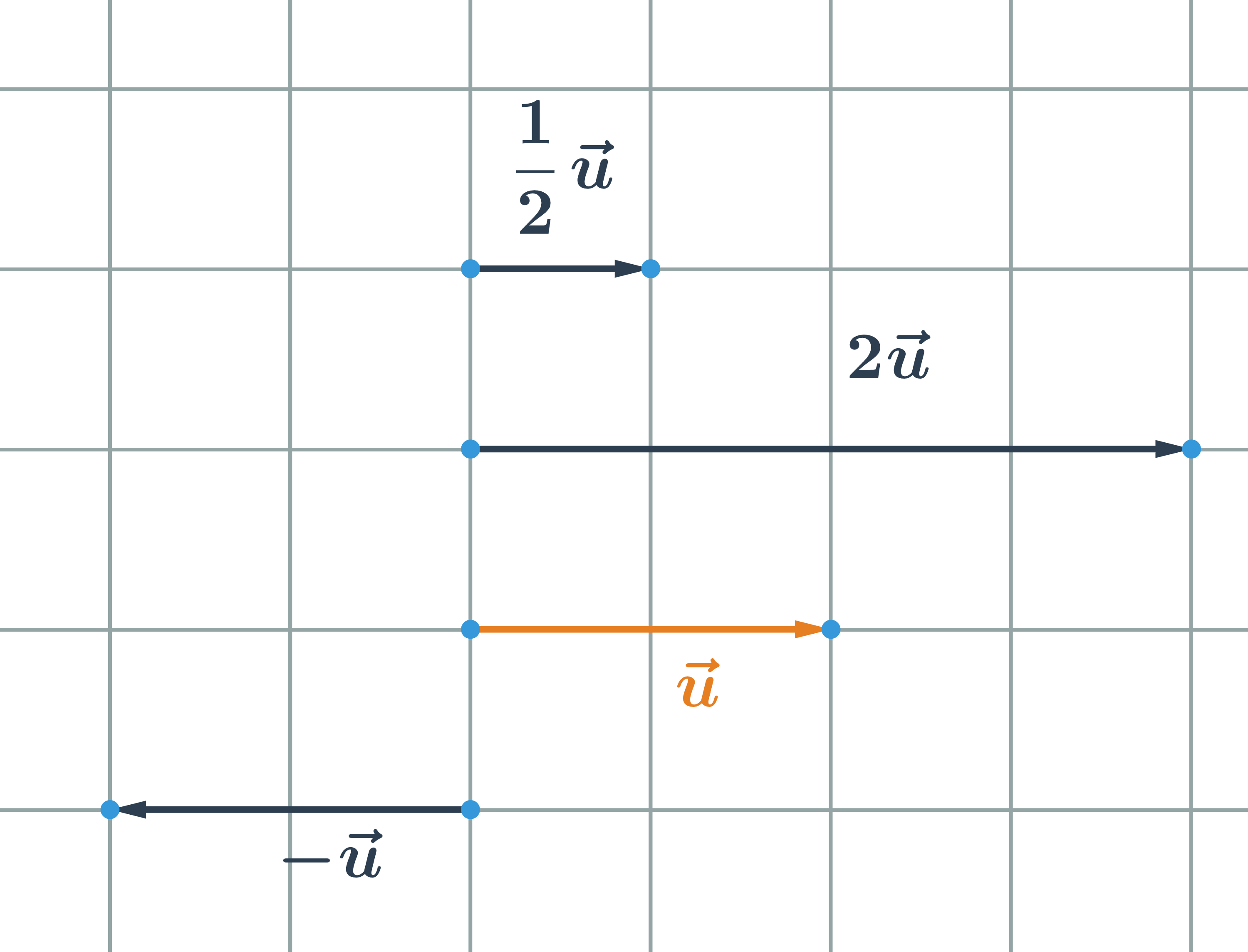
Máme-li souřadnice vektoru \vec{u}=(u_1;u_2), pak jeho násobek \vec{v}=k \cdot \vec{u} má souřadnice \vec{v}=(k \cdot u_1; k\cdot u_2).
Příklad součet a násobek vektoru graficky
Načrtněte vektor \vec{w}=2\vec{a}-\vec{b}+\vec{c}.
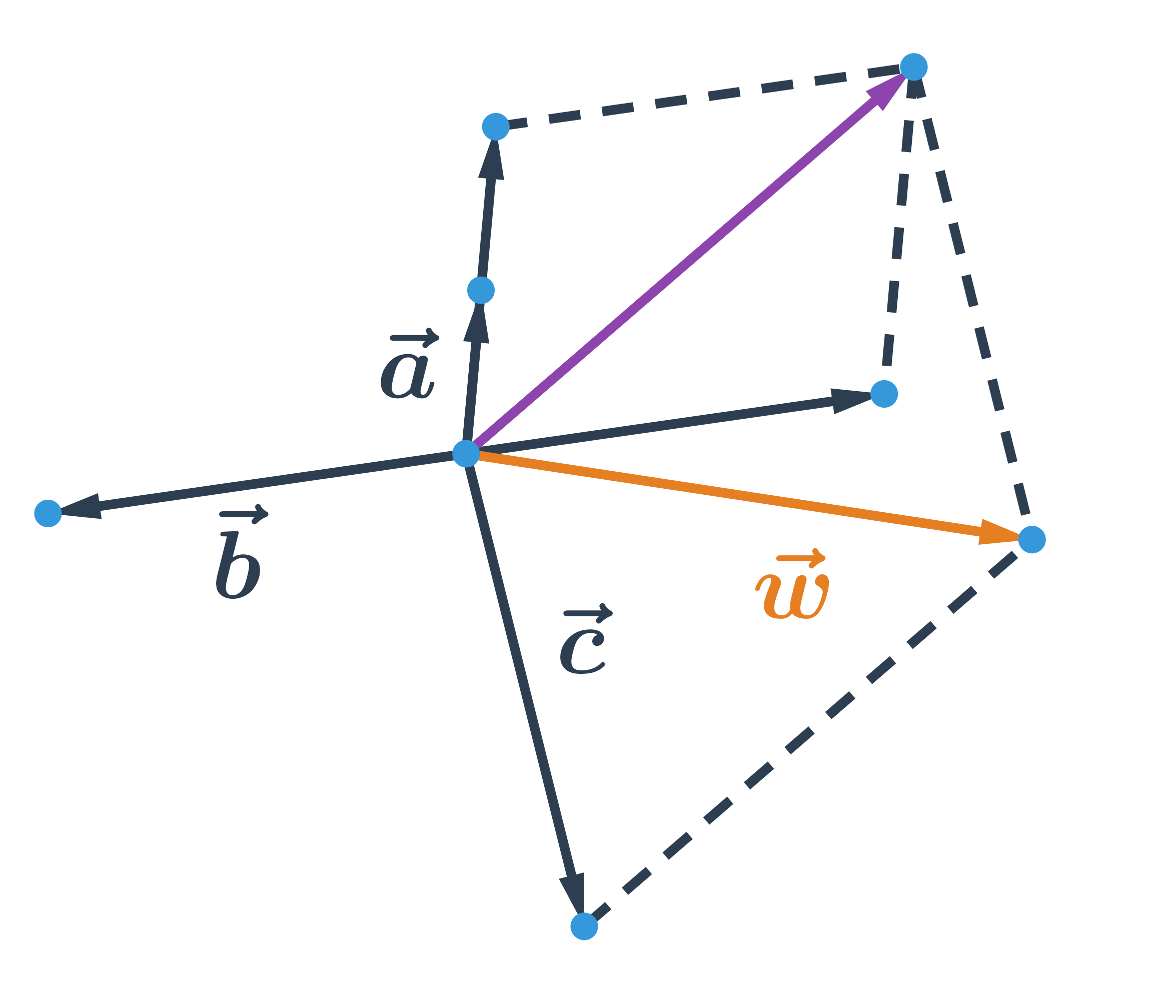
Příklad součet a násobek vektoru v souřadnicích
Jsou dány vektory \vec{u}=(2;-3), \vec{v}=(4;1). Určete souřadnice vektoru \vec{w}=\vec{u}-4\cdot \vec{v}.
- w_1=u_1-4\cdot v_1=2-4\cdot 4=-14
- w_2=u_2-4\cdot v_2=-3-4\cdot 1=-7
Vektory: skalární součin
Skalární součin vektorů \vec{u} a \vec{v} označujeme \vec{u}\cdot \vec{v}. Pro vektory \vec{u}, \vec{v} o velikostech \left| \vec{u} \right| a \left| \vec{v} \right|, které spolu svírají úhel \alpha, je skalární součin definován následovně:
\vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
Vlastnosti skalárního součinu
- Výsledkem skalárního součinu dvou vektorů je číslo (neboli skalár).
- Skalární součin nulového vektoru s libovolným jiným vektorem je vždy roven 0.
- Skalární součin vektorů, které jsou na sebe kolmé, je také roven nule.
Výpočet pomocí souřadnic
Máme-li souřadnice vektorů \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), pak hodnota jejich skalárního součinu je:
u_1\cdot v_1+u_2 \cdot v_2
Poznámka: další typy součinu vektorů
Kromě skalárního součinu existují i jiné typy součinu vektorů (vektorový, smíšený), proto je důležité psát o jaký součin se jedná.Příklad: skalární součin vektorů
Určete skalární součin vektorů, jestliže platí: \left| \vec{u} \right|=4, \left| \vec{v} \right|=3 a vektory svírají úhel 60°.
- Vzoreček: \vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
- Dosadíme známé hodnoty: \vec{u}\cdot \vec{v}=4\cdot3\cdot \cos 60°=4\cdot3\cdot\frac{1}{2}=6
Určení úhlu svíraného dvěma vektory
S využitím vztahu pro skalární součin můžeme určit úhel vektorů: \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}
Příklad: úhel svíraný vektory
Určete úhel vektorů \vec{u}=(3;3) a \vec{v}=(2;0).
- Platí \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}.
- Pomocí známých souřadnic vektorů umíme spočítat skalární součin \vec{u}\cdot\vec{v} a velikosti vektorů \left| \vec{u} \right|, \left| \vec{v} \right|:
- \vec{u}\cdot \vec{v}=u_1\cdot v_1+u_2 \cdot v_2=3\cdot2+3\cdot0=6
- \left| \vec{u} \right|=\sqrt{u_1^2 + u_2^2}=\sqrt{3^2+3^2}=\sqrt{18}
- \left| \vec{v} \right|=\sqrt{v_1^2 + v_2^2}=\sqrt{2^2+0^2}=\sqrt{4}
- Dosadíme tyto hodnoty do vztahu pro výpočet \cos \alpha:
- \cos \alpha =\frac {6}{\sqrt{18}\cdot\sqrt{4}}=\frac{6}{3\sqrt{2}\cdot2}=\frac{1}{\sqrt{2}}
- Úhel vektorů je 45°.
Přímka je jednoznačně určena bodem, který na ní leží a směrovým vektorem, což si můžete prakticky vyzkoušet v kapitole Určení přímky.
V rovině i v prostoru lze zapsat přímku jako množinu bodů, které splňují parametrickou rovnici. V rovině umíme pro danou přímku napsat také obecnou rovnici (ale v prostoru ne).
Máme-li přímku popsanou rovnicí, umíme určit vzájemnou polohu dvou přímek nebo vzájemnou polohu přímky a bodu výpočtem.
NahoruPřímky: pojmy
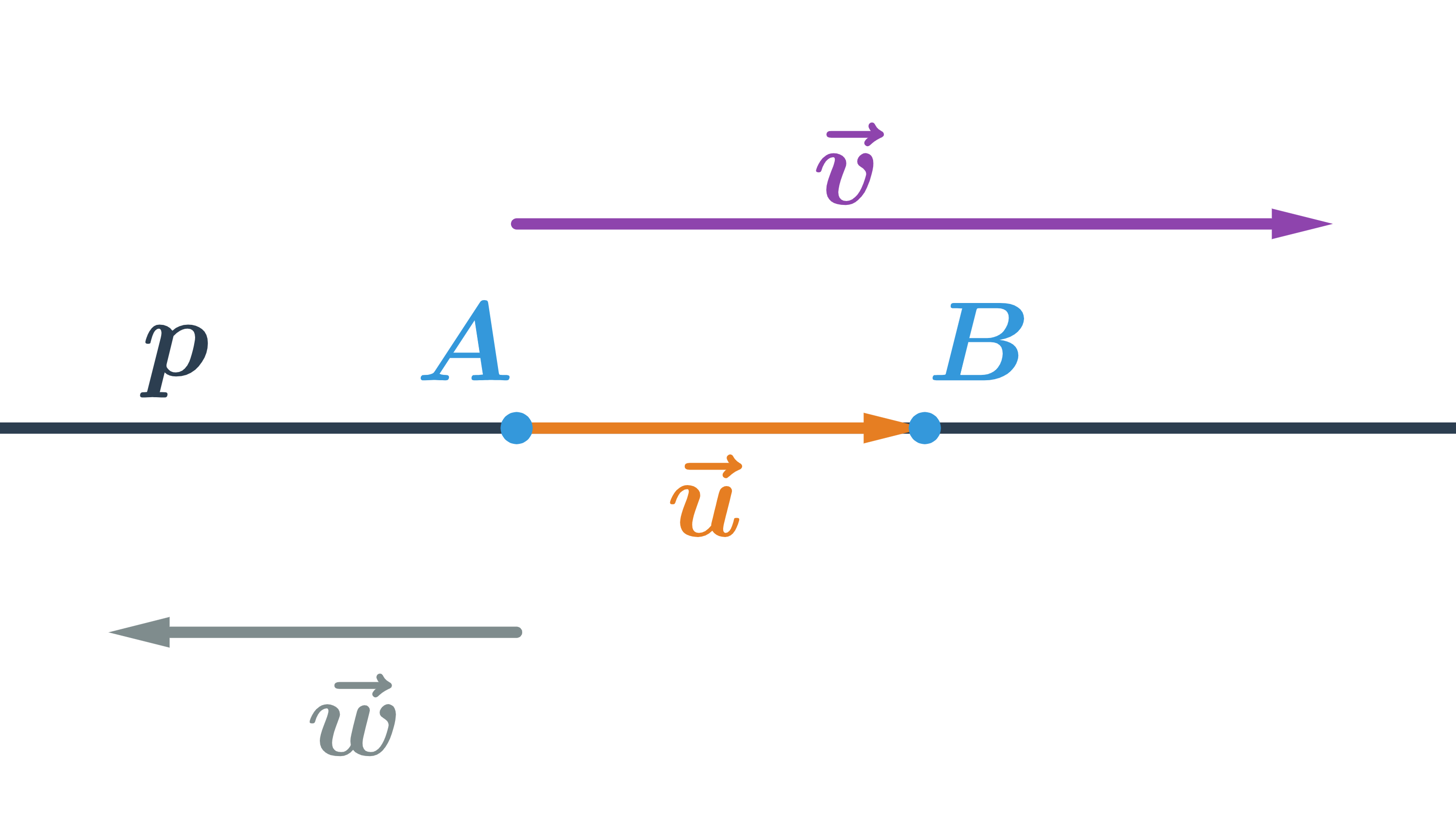
Přímka je jednoznačně určena dvěma body, na obrázku je přímka p určená body A a B. Každý vektor, který je rovnoběžný s vektorem \overrightarrow{AB} se nazývá směrový vektor přímky p. Kterýkoliv z vektorů na obrázku je směrový vektor přímky p. K tomu, abychom určili konkrétní přímku ještě potřebujeme znát jeden bod na přímce (přímka p na obrázku je určena bodem A a kterýmkoliv z vektorů \vec{u}, \vec{v}, \vec{w}).
Parametrické rovnice přímky
Přímka určená bodem A=[a_1;a_2] a vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array} Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr.
Jak souvisí hodnota parametru t s polohou bodu na přímce
- Přímka p je určená bodem A a vektorem \vec{u}=\overrightarrow{AB}, tedy p:X=A+t\vec{u}
- Pro hodnotu t=0 dostaneme: X=A+t\vec{u}=A+0\cdot \vec{u} … bod A
- Pro hodnotu t=1 dostaneme: X=A+t\vec{u}=A+1\cdot \vec {u} … bod B
- Pro hodnotu t=2 dostaneme: X=A+t\vec{u}=A+2\cdot \vec {u} … bod C
- Pro hodnotu t=\frac{1}{2} dostaneme: X=A+t\vec{u}=A+\frac{1}{2}\cdot \vec{u} … bod D (střed úsečky AB)
- Pro hodnotu t=-1 dostaneme: X=A+t\vec{u}=A-1\cdot \vec{u} … bod E
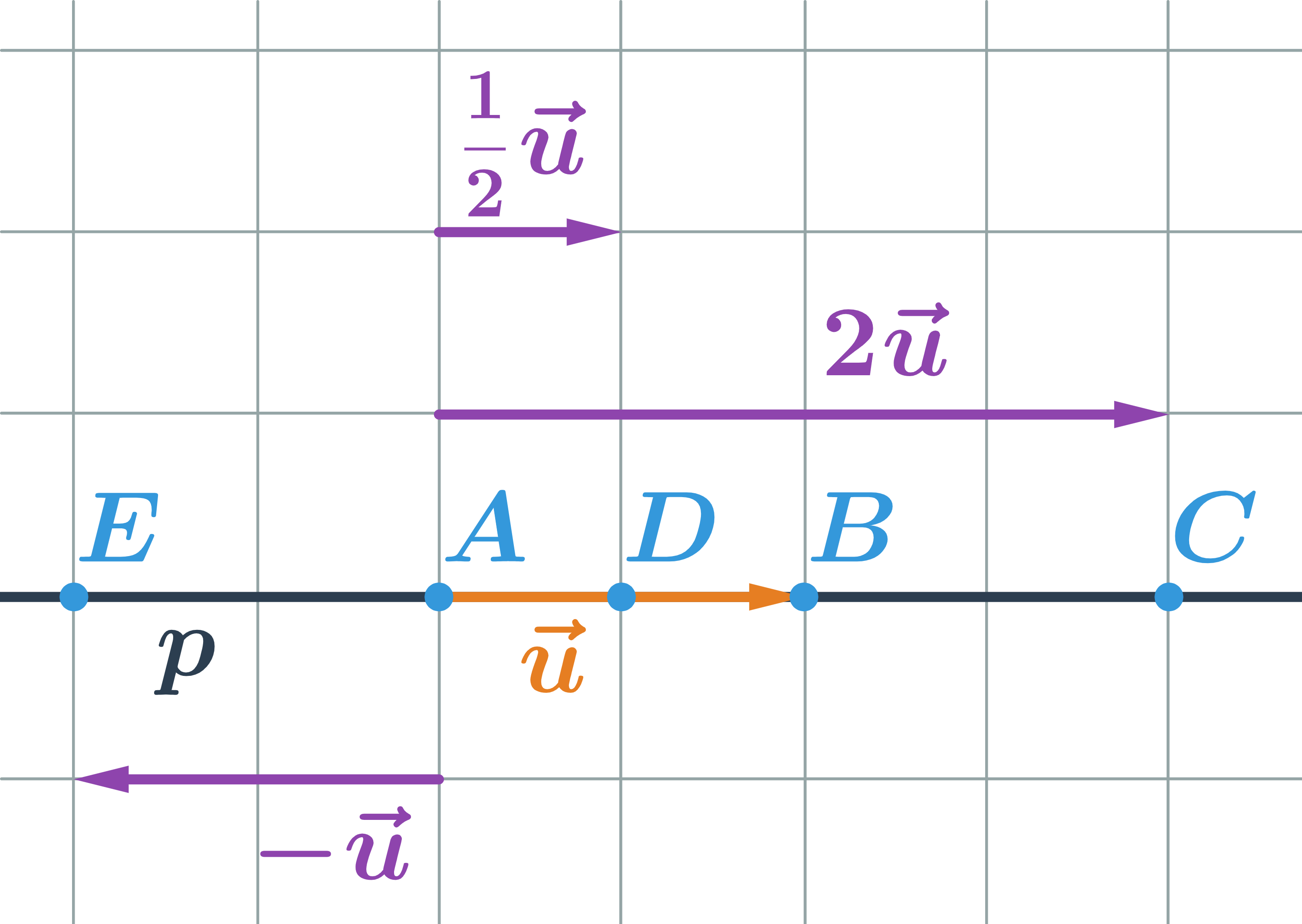
- Každá hodnota parametru určuje jeden bod na přímce, pro určení celé přímky tedy potřebujeme všechna reálná čísla, proto píšeme t\in\mathbb{R}.
- Body, které leží na úsečce AB (tedy body ležící mezi body A a B), vyjádříme parametricky, pokud do rovnice X=A+t\vec{u} dosadíme hodnoty parametru t splňující 0\leq t\leq1.
Obecná rovnice přímky
Každý vektor kolmý k přímce p se nazývá normálový vektor přímky p. Obecná rovnice přímky je rovnice ve tvaru: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.
Souřadnice směrového a normálového vektoru přímky p
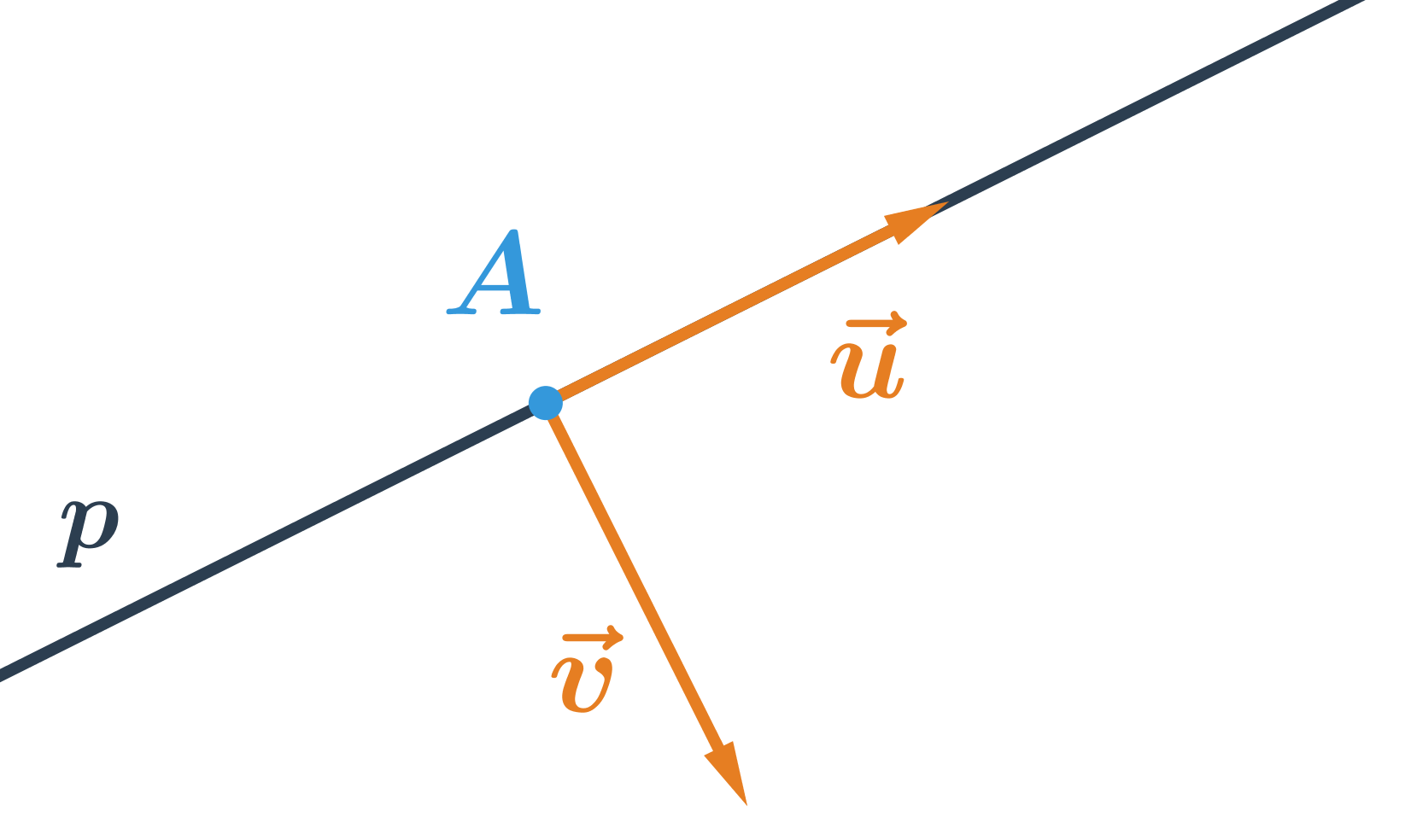
- Pro přímku danou obecnou rovnicí ax+by+c=0:
- \vec{v} je normálový vektor přímky p, jeho souřadnice jsou: \vec{v}=(a;b)
- \vec{u} je směrový vektor přímky p, protože je to vektor kolmý k vektoru \vec{v}=(a;b), jeho souřadnice jsou: \vec{u}=(-b;a)
- Pro přímku danou parametricky: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
- \vec{u} je směrový vektor přímky p, jeho souřadnice jsou: \vec{u}=(u_1;u_2)
- \vec{v} je normálový vektor přímky p, protože je to vektor kolmý k vektoru \vec{u}=(u_1;u_2), jeho souřadnice jsou: \vec{v}=(-u_2;u_1)
Obecná rovnice přímky rovnoběžné s osou x
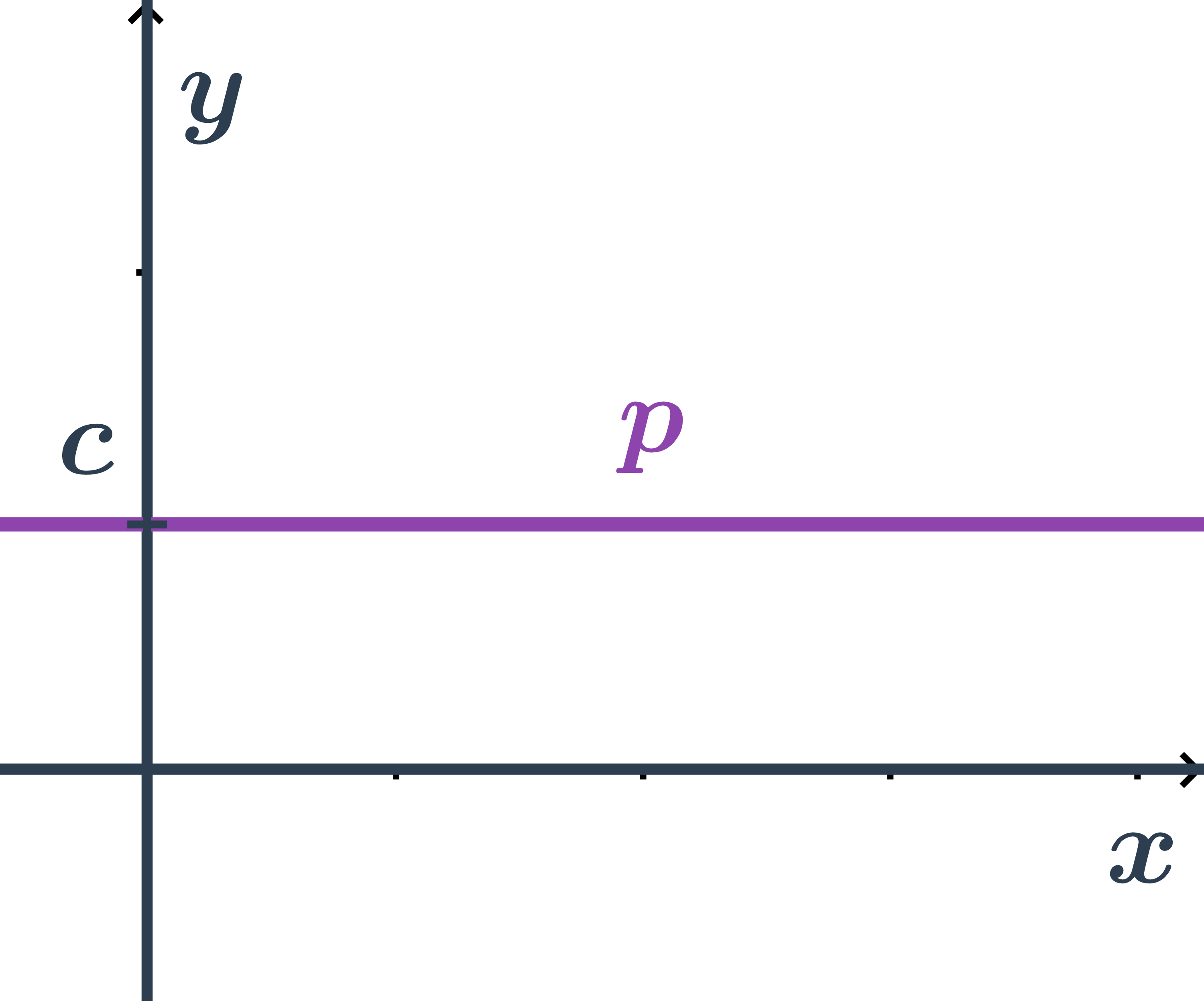
- Pro všechny body ležící na přímce je druhá souřadnice stejná a to: y=c
- Tedy přímka má obecnou rovnici: y-c=0
Obecná rovnice přímky rovnoběžné s osou y
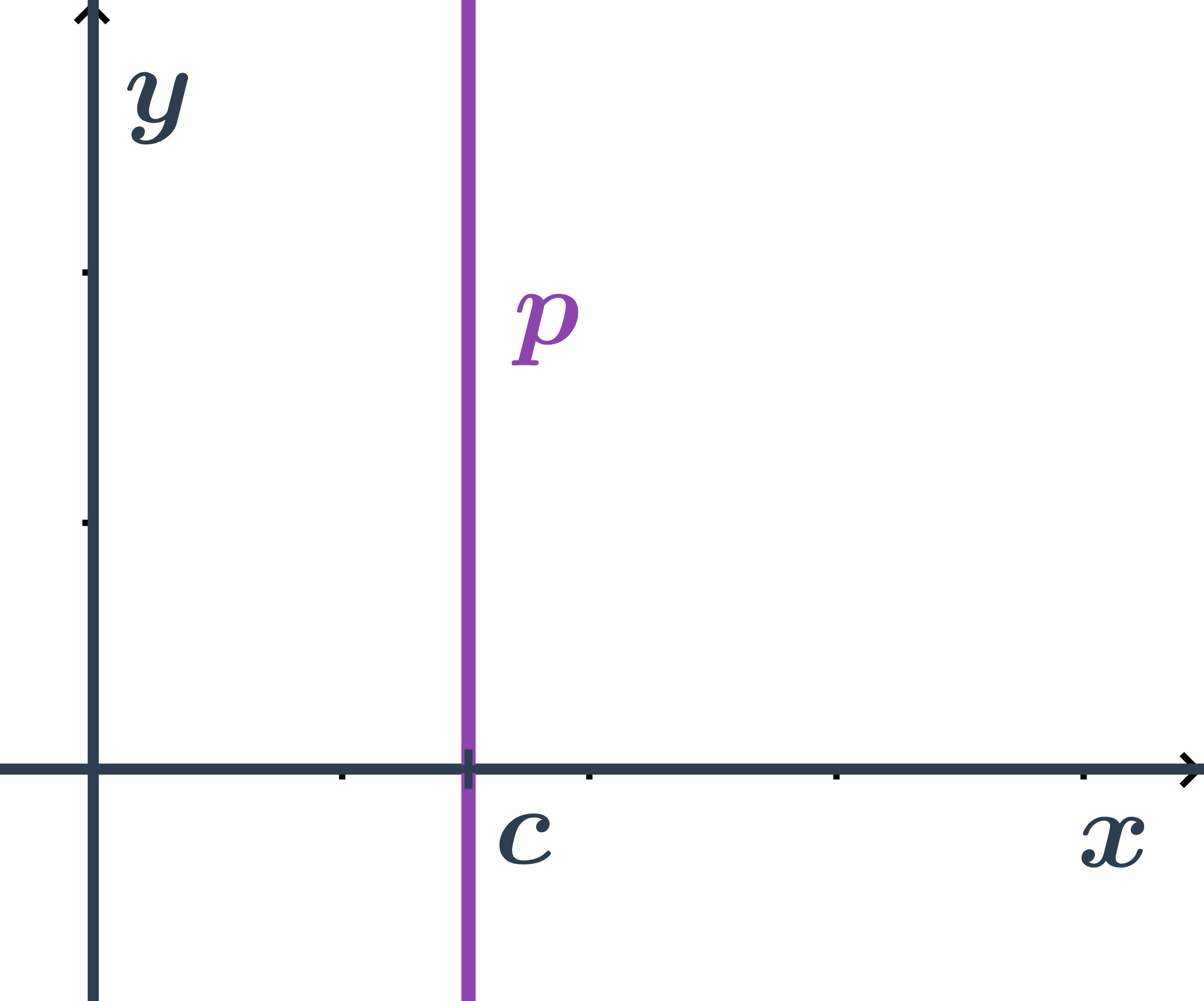
- Pro všechny body ležící na přímce je první souřadnice stejná a to: x=c
- Tedy přímka má obecnou rovnici: x-c=0
Bod a přímka
Bod M=[m_1;m_2] leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky. Pokud je přímka daná obecnou rovnicí ax+by+c=0, pro souřadnice bodu, který leží na přímce platí: a\cdot m_1+b\cdot m_2+c=0 Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t. (Více o vzájemné poloze bodu a přímky.)
Obecná rovnice přímky, která prochází počátkem
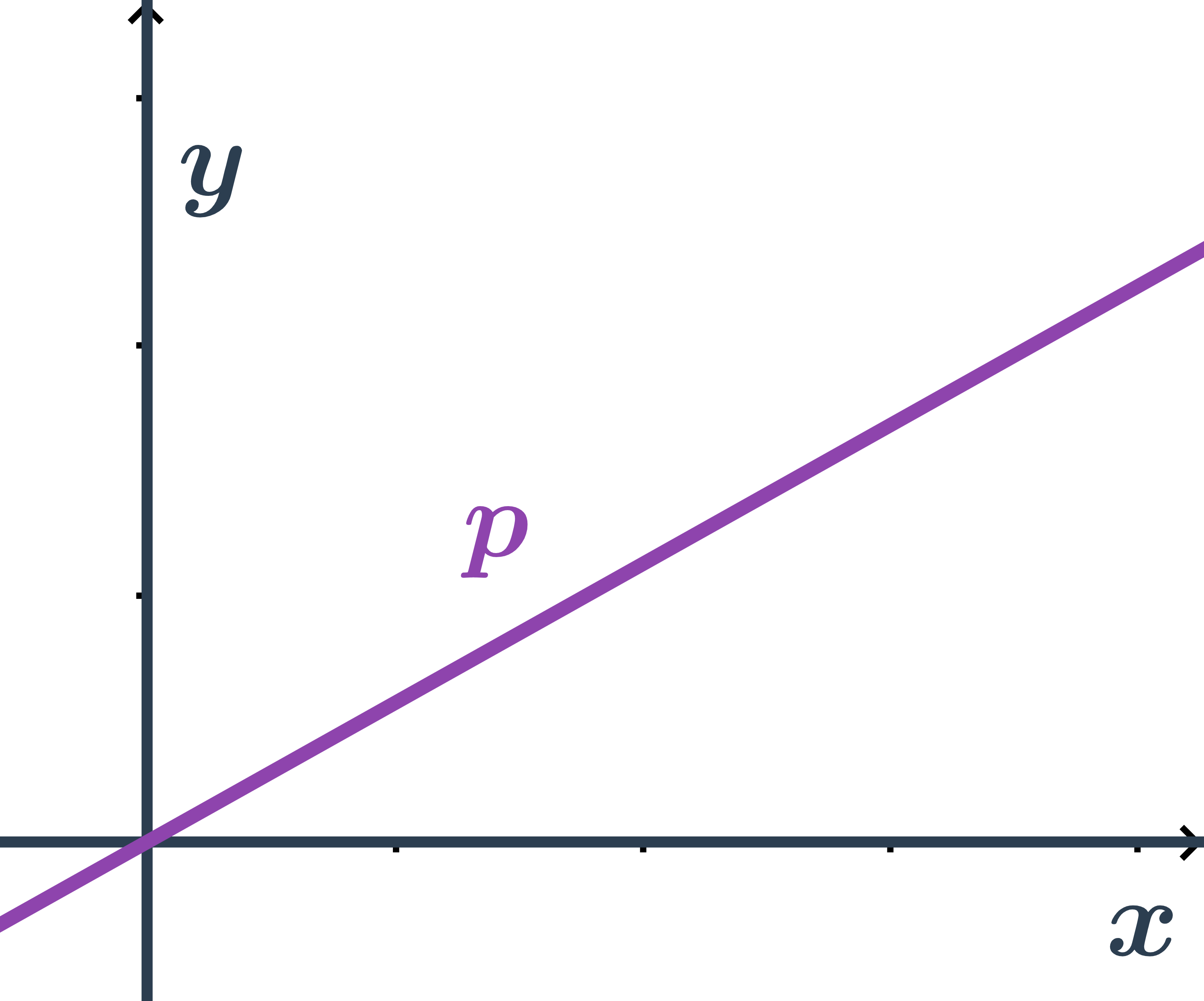
- Přímka prochází bodem O=[0;0], tedy souřadnice počátku splňují její obecnou rovnici ax+by+c=0.
- Dosadíme souřadnice bodu O a zkusíme zjistit nějaké informace o konstantách a,b,c.
- a\cdot0+b\cdot0+c=0\Leftrightarrow c=0
- Proto přímka, která prochází počátkem má obecnou rovnici ax+by=0.
Dvě přímky
Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.
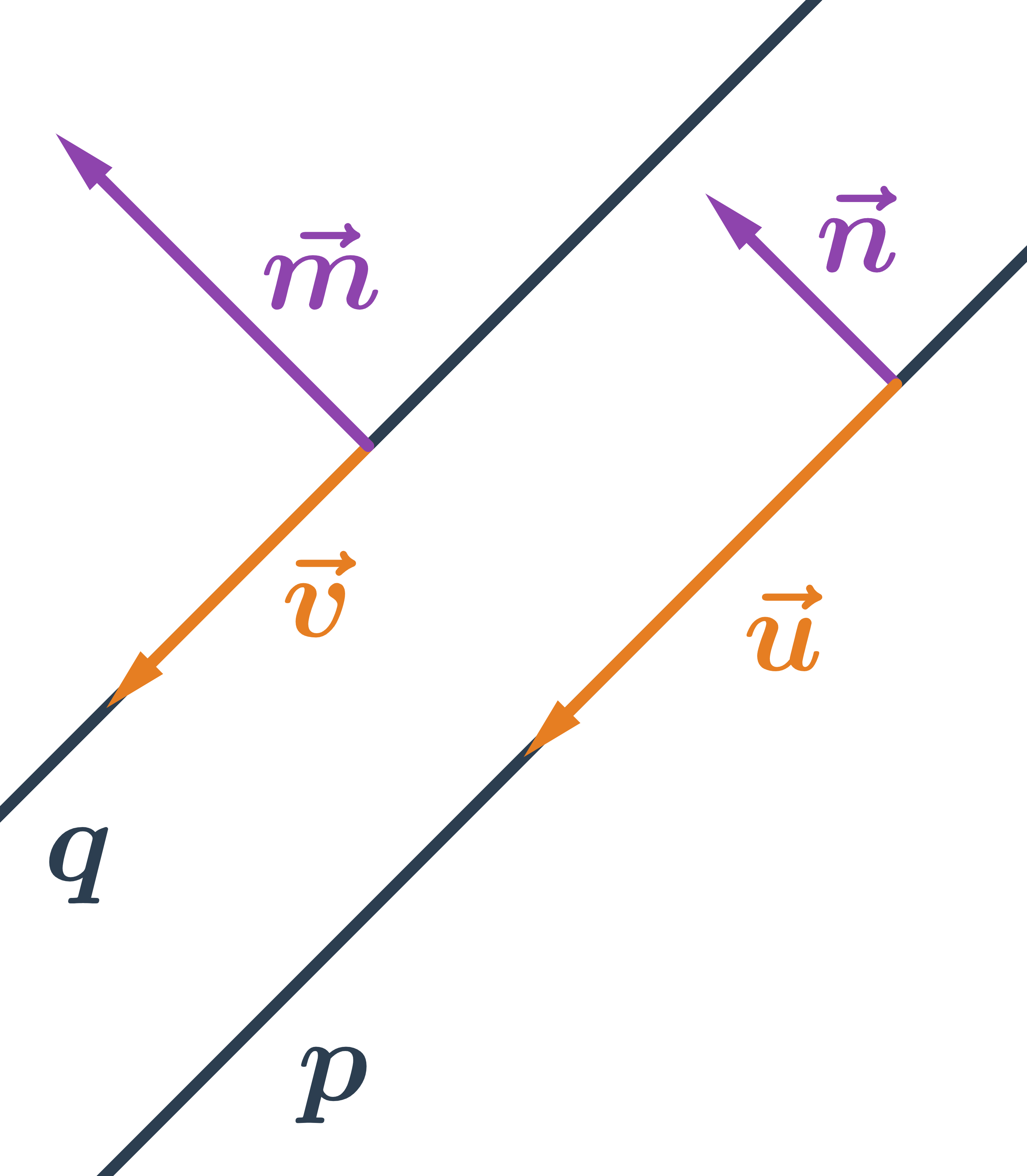
Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
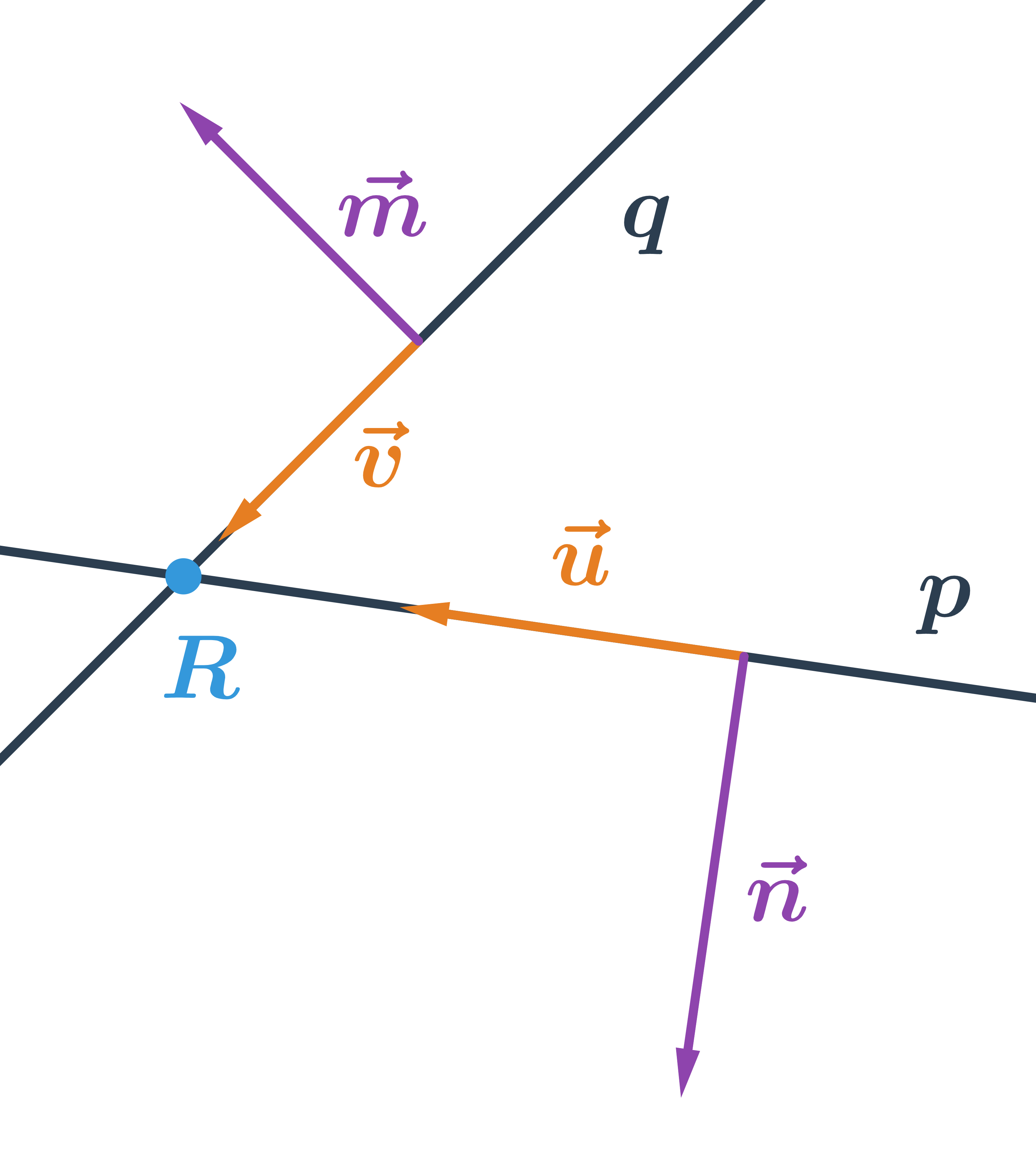
Více o vzájemné poloze dvou přímek.
Přímka v prostoru
Přímku v prostoru nelze vyjádřit obecnou rovnicí. Parametrickou rovnici přímky v prostoru určíme obdobně jako v rovině na základě znalosti souřadnic směrového vektoru a jednoho bodu na přímce.
NahoruUrčení přímky
Přímka je obvykle určena bodem a vektorem, případně dvěma body.
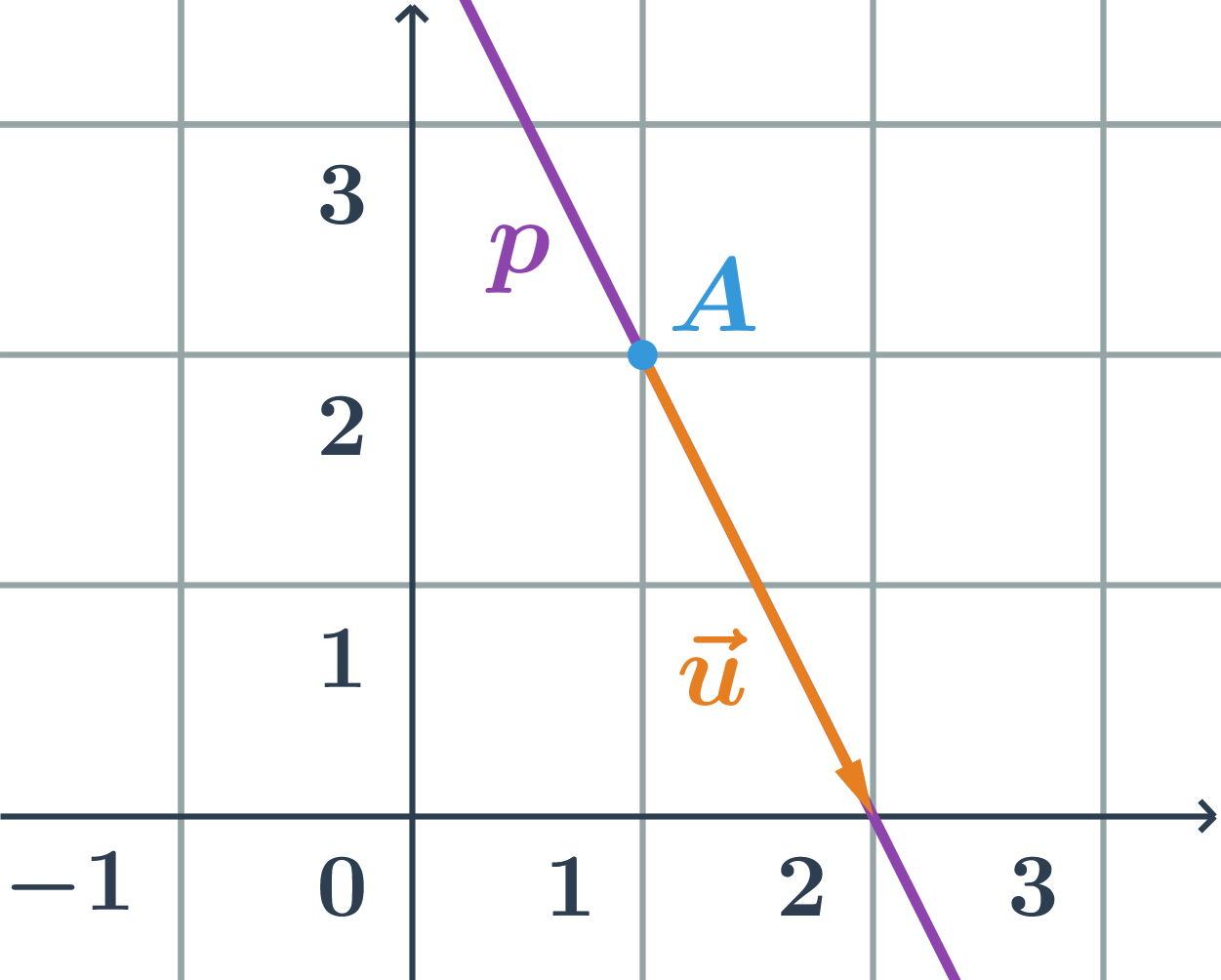
Přímka p na obrázku je určena například:
- bodem A=[1;2], který na ní leží a směrovým vektorem \vec{u}=(1;-2)
- nebo dvěma různými body [1;2] a [2;0], které na ní leží
Parametrické rovnice přímky v rovině
Přímka určená bodem A=[a_1;a_2] a směrovým vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr. Pokud známe dva body A, B ležící na přímce, směrový vektor je například \vec{u}=\overrightarrow{AB}.
Parametrické rovnice přímky p určené body A=[1;2] a B=[3;1]
- přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(2;-1)
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2-t\\&&t\in\mathbb{R}\end{array}
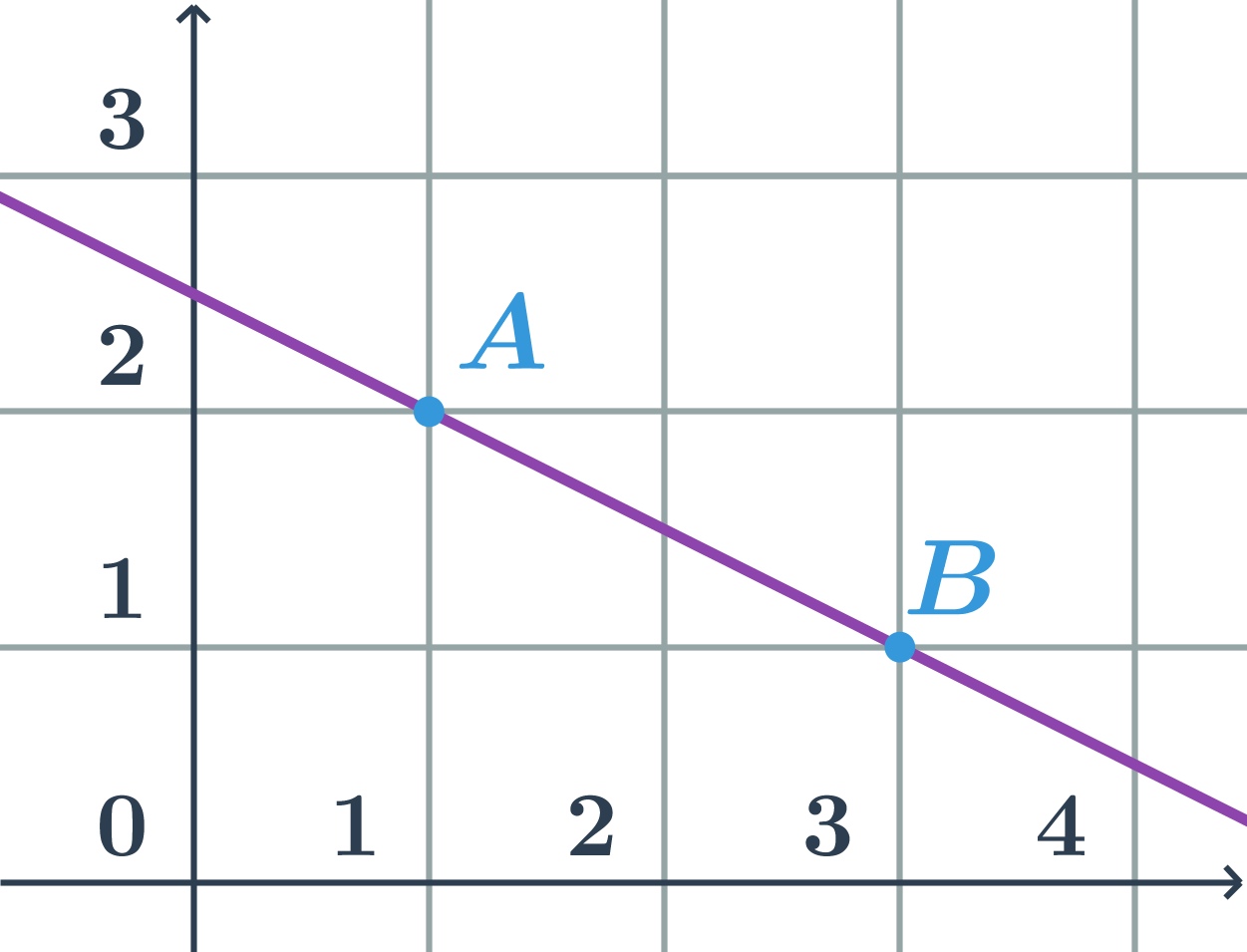
Různé parametrické rovnice přímky na obrázku
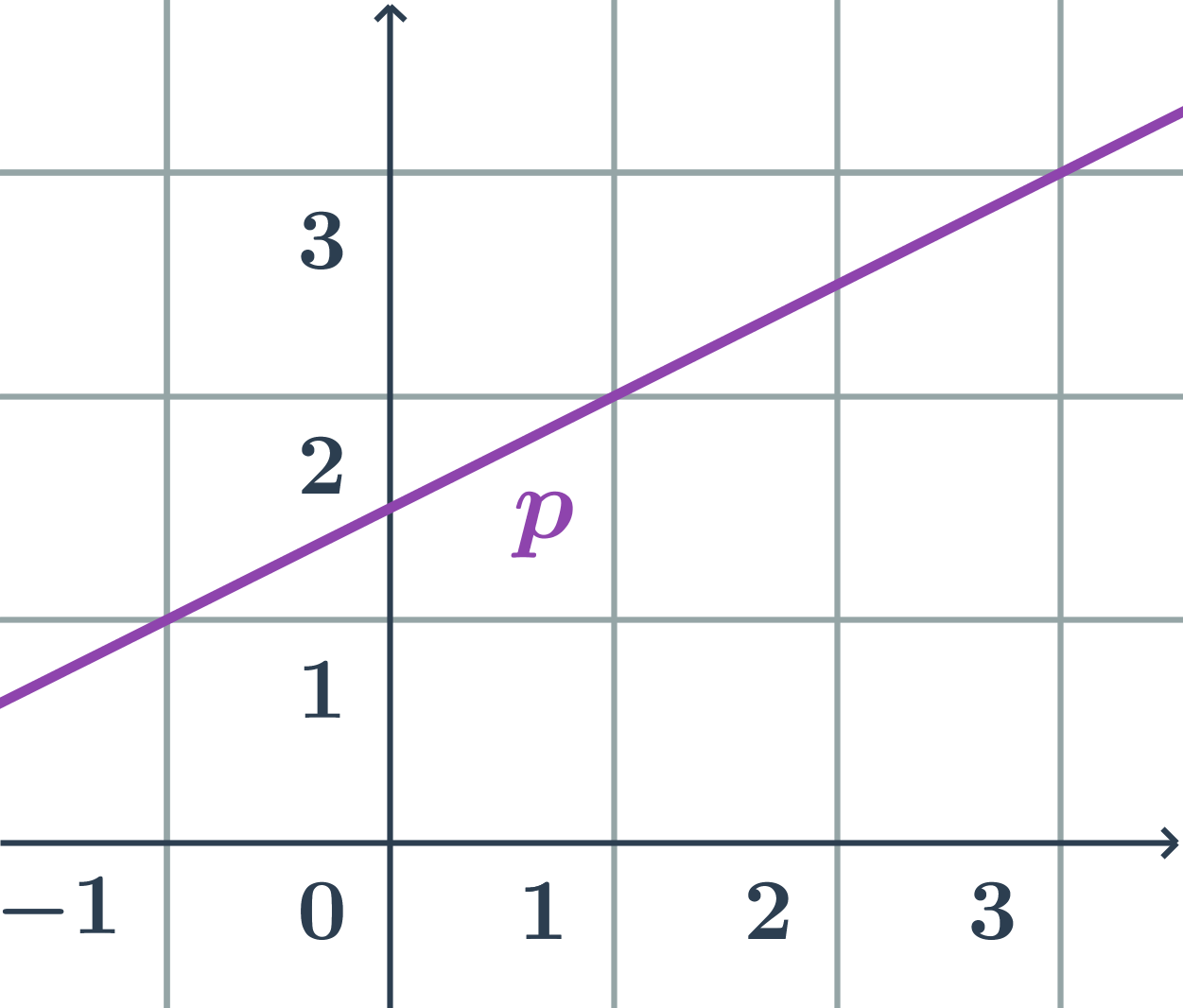
Určíme souřadnice směrového vektoru a jednoho bodu na přímce:
- například: \vec{u}=(2;1), A=[1;2]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2+t\\&&t\in\mathbb{R}\end{array}
Další možnost parametrického vyjádření:
- \vec{v}=(-4;-2), B=[3;3]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&3-4t\\y&=&3-2t\\&&t\in\mathbb{R}\end{array}
Pro určení parametrických rovnic můžeme vybrat kterýkoliv bod ležící na přímce a jakýkoliv zápis souřadnic směrového vektoru, možností jak parametricky vyjádřit danou přímku je tedy nekonečně mnoho.
Obecná rovnice přímky v rovině
Obecná rovnice přímky v rovině má tvar: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo. Normálový vektor \vec{n}=(a;b) je vektor kolmý k dané přímce, tedy i kolmý ke směrovému vektoru přímky.
Obecná rovnice přímky p určené body A=[1;5] a B=[2;3]
- Přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;-2), tedy například vektor \vec{n}=(2;1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 2x+y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7
- Obecná rovnice přímky p je: 2x+y-7=0
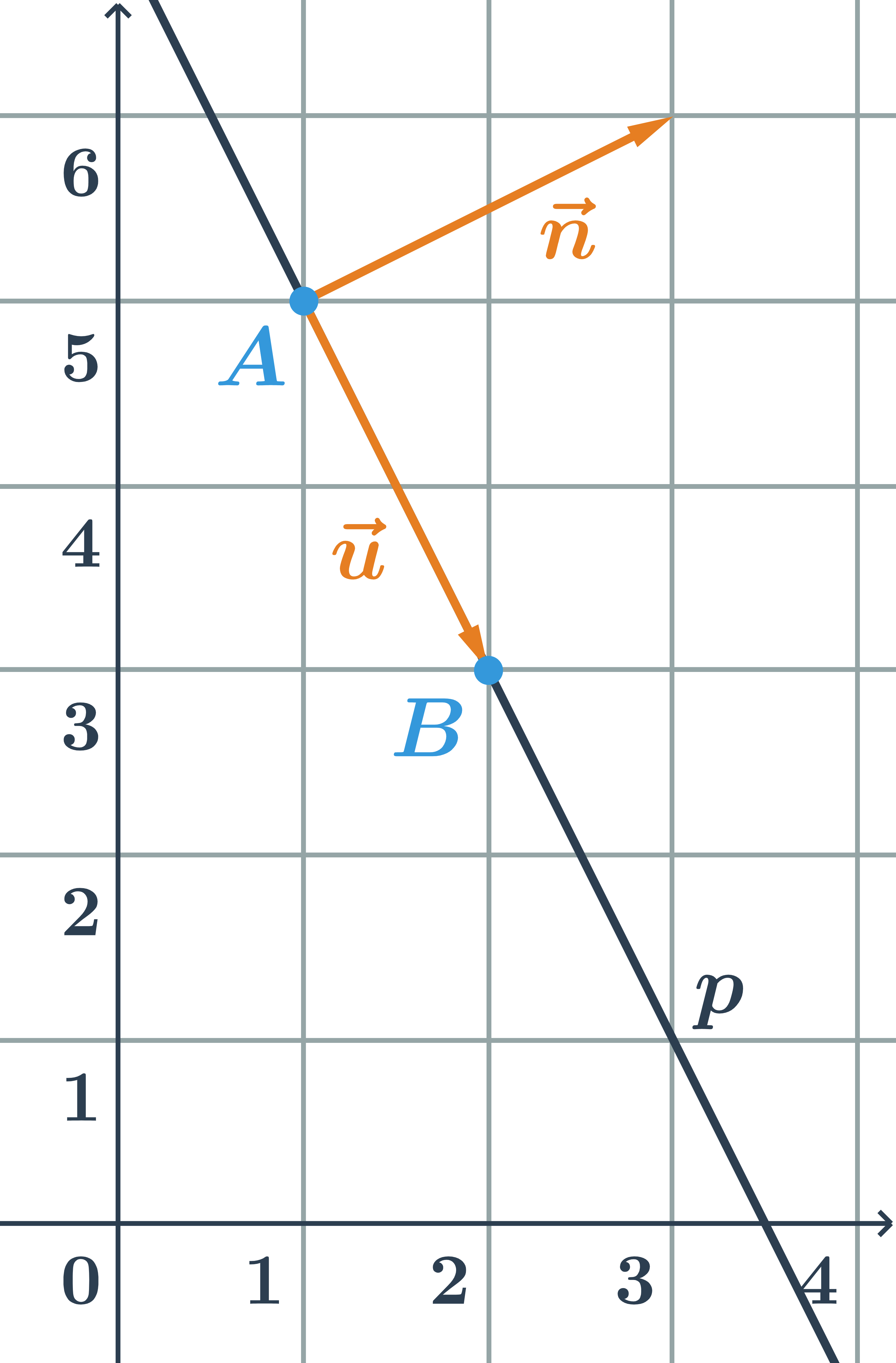
Obecná rovnice přímky dané parametricky
Určete obecnou rovnici přímky p, která je dána následující parametrickou soustavou rovnic: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Přímka p je určená bodem A=[1;4] a směrovým vektorem \vec{u}=(2;6).
- Souřadnice směrového vektoru můžeme upravit na tvar: \vec{u}=(1;3).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;3), tedy například vektor \vec{n}=(3;-1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 3x-y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1
- Obecná rovnice přímky p je: 3x-y+1=0
Parametrické vyjádření přímky dané obecnou rovnicí
Určete parametrické vyjádření přímky p, která má obecnou rovnici: 3x-2y+4=0.
- Přímka p má normálový vektor \vec{n}=(3;-2).
- Směrový vektor je kolmý k vektoru \vec{n}=(3;-2), tedy například vektor \vec{u}=(2;3).
- Určíme jeden bod na přímce p : jednu souřadnici můžeme zvolit, například x=0, druhou souřadnici dopočítáme: 3\cdot0-2y+4=0\Rightarrow y=2
- Z obecné rovnice jsme tedy zjistili, že na přímce leží bod A=[0;2].
- Parametrické vyjádření přímky p je: \begin{array}{rrl}x&=&0+2t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
Směrnicový tvar rovnice přímky
Každou přímku p, která není rovnoběžná s osou y, můžeme vyjádřit ve tvaru: y=kx+q, kde k,q\in\mathbb{R}.
Tento tvar se nazývá směrnicový tvar rovnice přímky.
Konstanta k se nazývá směrnice a její hodnota je tangens úhlu, který svírá přímka p s kladnou částí osy x, tedy: k=\tan \varphi.
Konstanta q určuje průsečík přímky p s osou y, souřadnice průsečíku jsou: P=[0;q]. Pro přímku, která prochází počátkem, je q=0, tedy směrnicový tvar její rovnice je: y=kx.
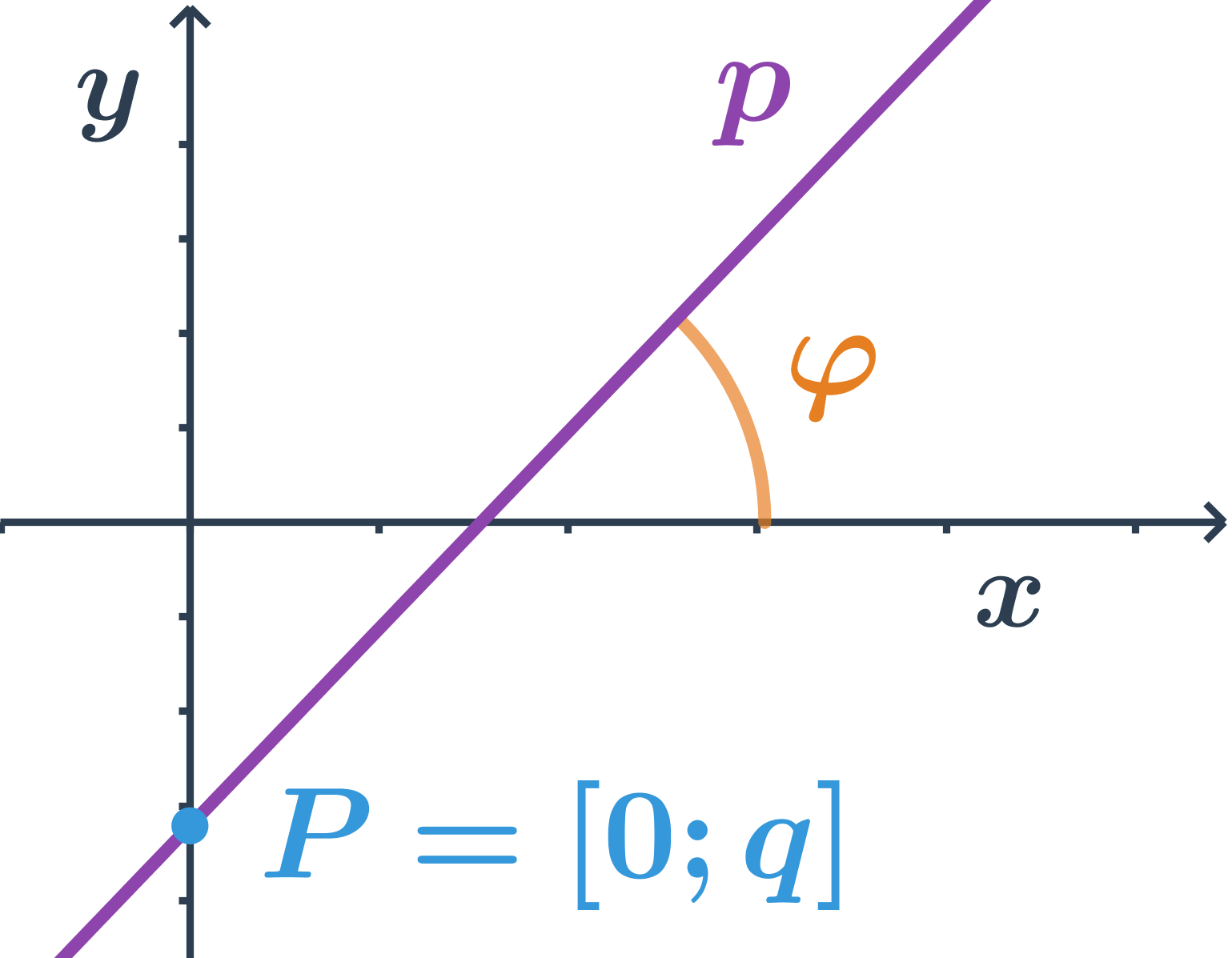
Směrnice přímky, která má směrový vektor \vec{u}=(u_1;u_2), je podíl souřadnic směrového vektoru:
k=\tan \varphi=\frac{u_2}{u_1}
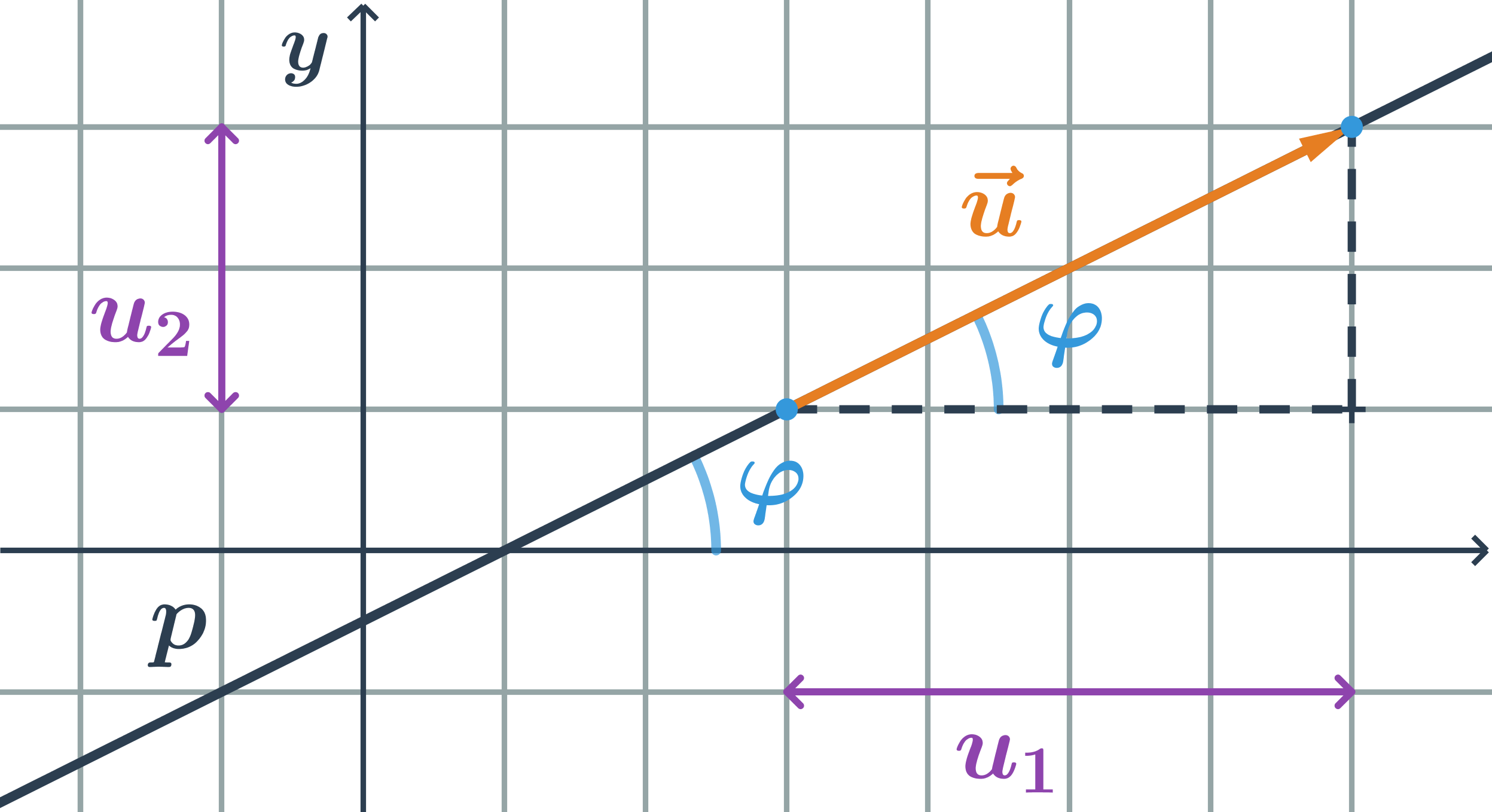
Různé hodnoty směrnice
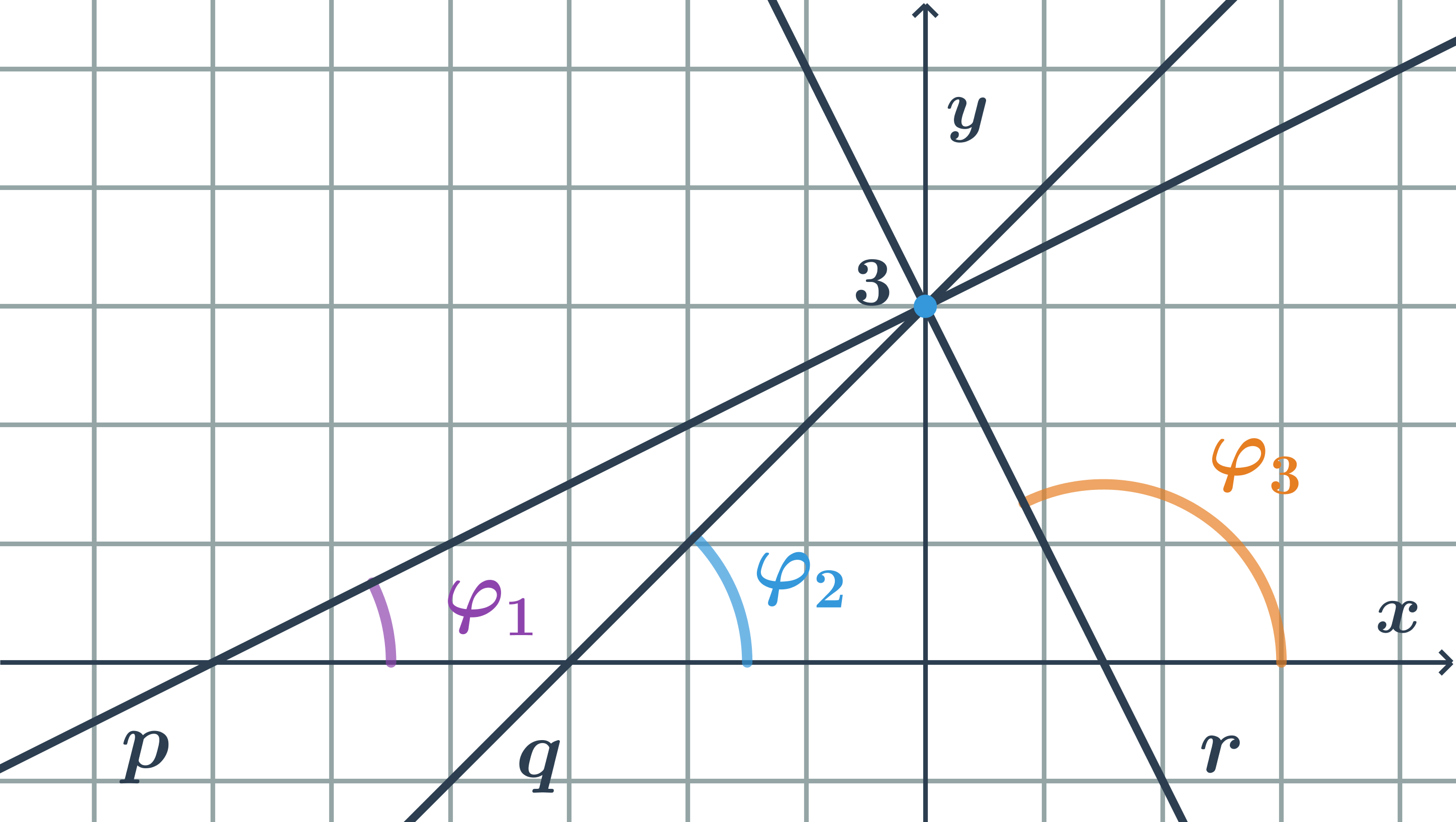
- Směrnice přímky p: k_1=\tan \varphi_1=\frac{1}{2}
- Směrnice přímky q: k_2=\tan \varphi_2=\frac{1}{1}=1
- Směrnice přímky r: k_3=\tan \varphi_3=\frac{2}{1}=2
- Čím větší odchylka od kladné části osy x, tím větší hodnota směrnice k.
- Přímka rovnoběžná s osou x svírá s kladnou částí osy x úhel 0^\circ a tedy její směrnice je \tan 0^\circ=0.
- Přímka rovnoběžná s osou y svírá s kladnou částí osy x úhel 90^\circ a pro tuto hodnotu funkce tangens není definována, proto nemůžeme určit směrnici.
Směrnicový tvar přímky z obrázku
Hledáme směrnicový tvar rovnice přímky: y=kx+q.
- Pro nalezení konstant k a q určíme směrový vektor přímky p a průsečík s osou y.
- směrový vektor přímky: \vec{u}=(1;-2)
- směrnice: k=\tan \varphi=\frac{u_2}{u_1}=\frac{-2}{1}=-2
- průsečík přímky s osou y: P=[0;5]
- konstanta q=y_P=5
- přímka na obrázku má směrnicový tvar y=-2x+5
Dvě přímky
Dvě rovnoběžné přímky svírají s kladnou částí osy x stejný úhel, mají tedy stejnou směrnici.
Pro dvě k sobě kolmé přímky platí:
- přímka p má směrový vektor \vec{u}=(u_1;u_2) a tedy směrnici: k=\frac{u_2}{u_1}
- každá přímka k ní kolmá má směrový vektor (-u_2;u_1) a tedy směrnici: \frac{u_1}{-u_2}=-\frac{1}{k}
Vzájemná poloha přímek v rovině
Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné. Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
Rovnoběžky zadané parametrickými rovnicemi
Určete vzájemnou polohu dvou přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-3+3t\\y&=&\hspace{0.25cm}2+t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&1-3s\\y&=&2-s\\&&s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(3;1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-3;-1)
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[-3;2].
- Ověříme, že tento bod neleží na přímce q dosazením souřadnic bodu A do rovnic přímky q: \begin{array}{rrl}-3&=&1-3s \Rightarrow s=\frac{4}{3}\\2&=&2-\hspace{0.15cm}s\Rightarrow s=0\end{array}
- Vyšly různé hodnoty parametru s, takže bod A neleží na q \Rightarrow přímky nejsou totožné
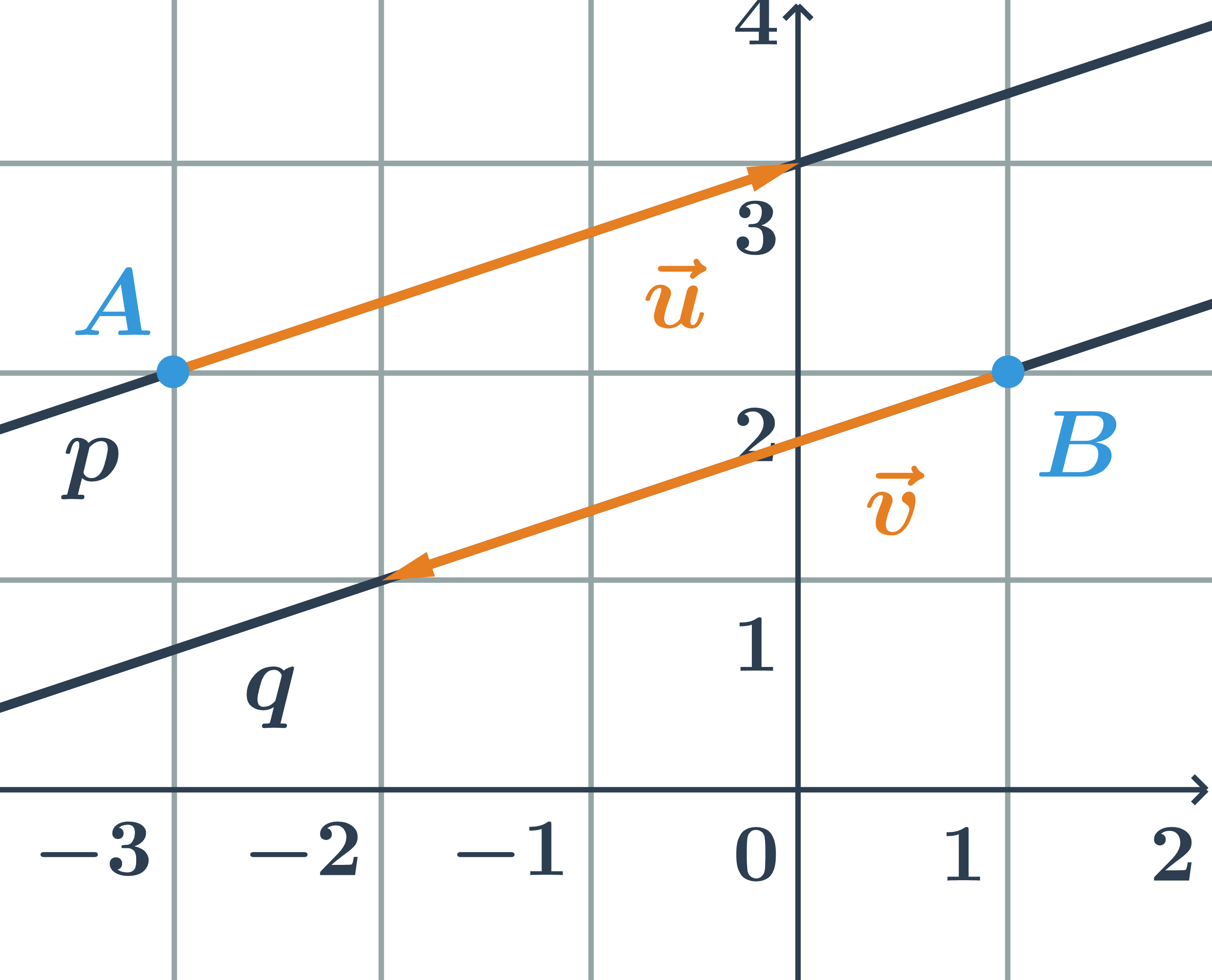
Rovnoběžky zadané obecnými rovnicemi
Určete vzájemnou polohu dvou přímek daných obecnými rovnicemi p: 2x+y-1=0 a q:4x+2y+3=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(4;2)
- Přímky p a q jsou rovnoběžné, protože jejich normálové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[0;1].
- Ověříme, zda A leží na p dosazením souřadnic bodu A do rovnice přímky p: 4\cdot0+2\cdot1+3\neq 0
- A nesplňuje rovnici, takže neleží na přímce q \Rightarrow přímky nejsou totožné
Různoběžky zadané parametrickými rovnicemi
Určete vzájemnou polohu přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-1+t\\y&=&\hspace{0.25cm}3+2t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&-4+s\\y&=&\hspace{0.25cm}3-s\\&&\hspace{0.25cm}s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(1;2)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární.
Průsečík přímek splňuje rovnice obou přímek, tedy každou z jeho souřadnic lze vyjádřit dvěma způsoby, dostáváme následující soustavu rovnic: \begin{array}{lrr}-1+t&=&-4+s\\\hspace{0.25cm}3+2t&=&3-s\end{array}
- Soustavu můžeme vyřešit sečtením obou rovnic: 2+3t=-1\Rightarrow3+3t=0\Rightarrow t=-1
- Výsledný parametr t dosadíme do parametrických rovnic kterékoliv z přímek a dostaneme souřadnice x,y průsečíku.
Průsečík přímek p a q je bod R=[-2;1].
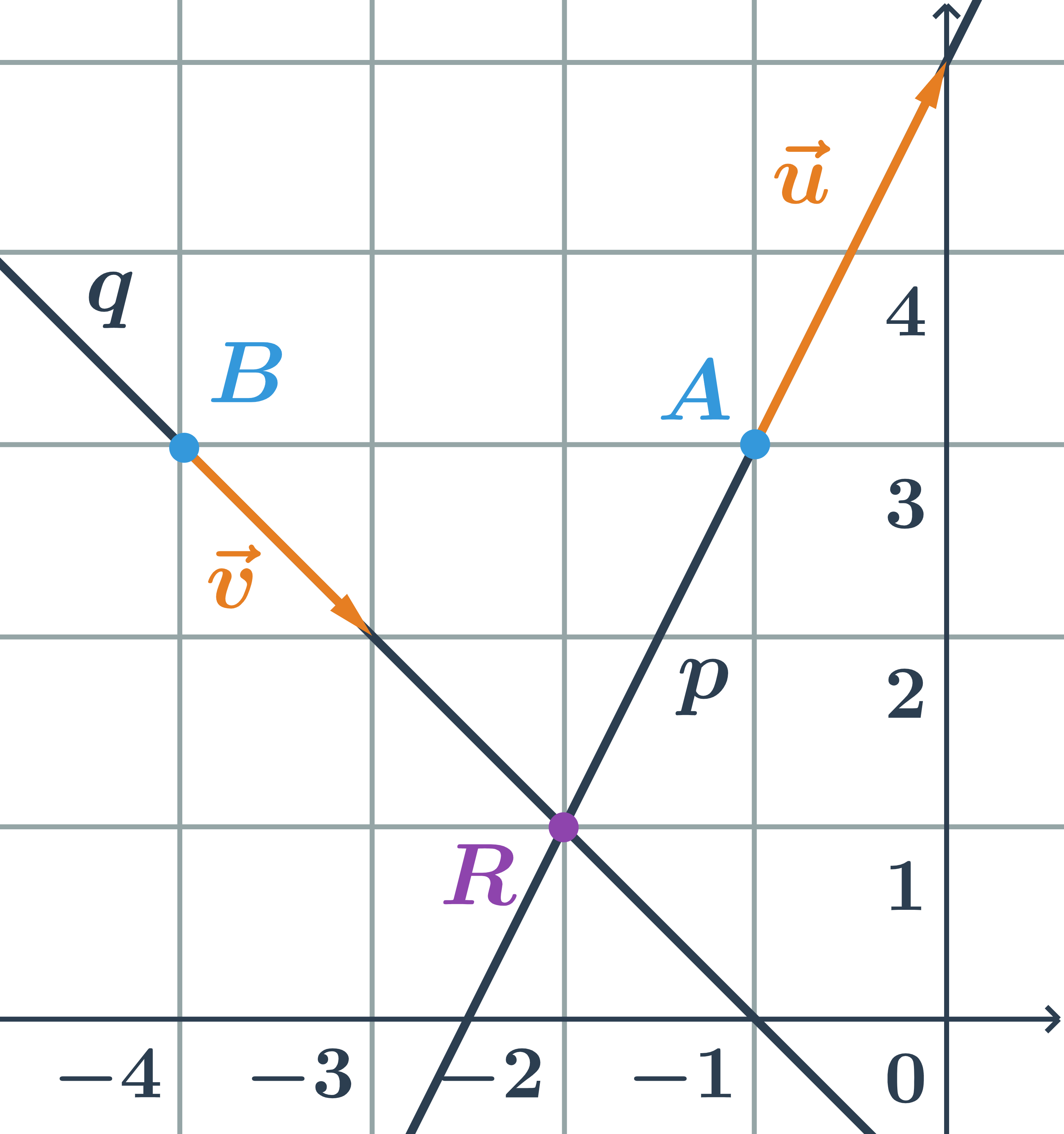
Různoběžky zadané obecnými rovnicemi
Určíme vzájemnou polohu dvou přímek zadaných obecnými rovnicemi p: 2x+y-1=0 a q:x-y+1=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich normálové vektory nejsou kolineární.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice jsou řešením soustavy: \begin{array}{rrr}2x+y-1&=&0\\x-y+1&=&0\end{array}
- Můžeme vyřešit sečtením obou rovnic: 3x=0\Rightarrow x=0
- Průsečík přímek p a q je bod R=[0;1]
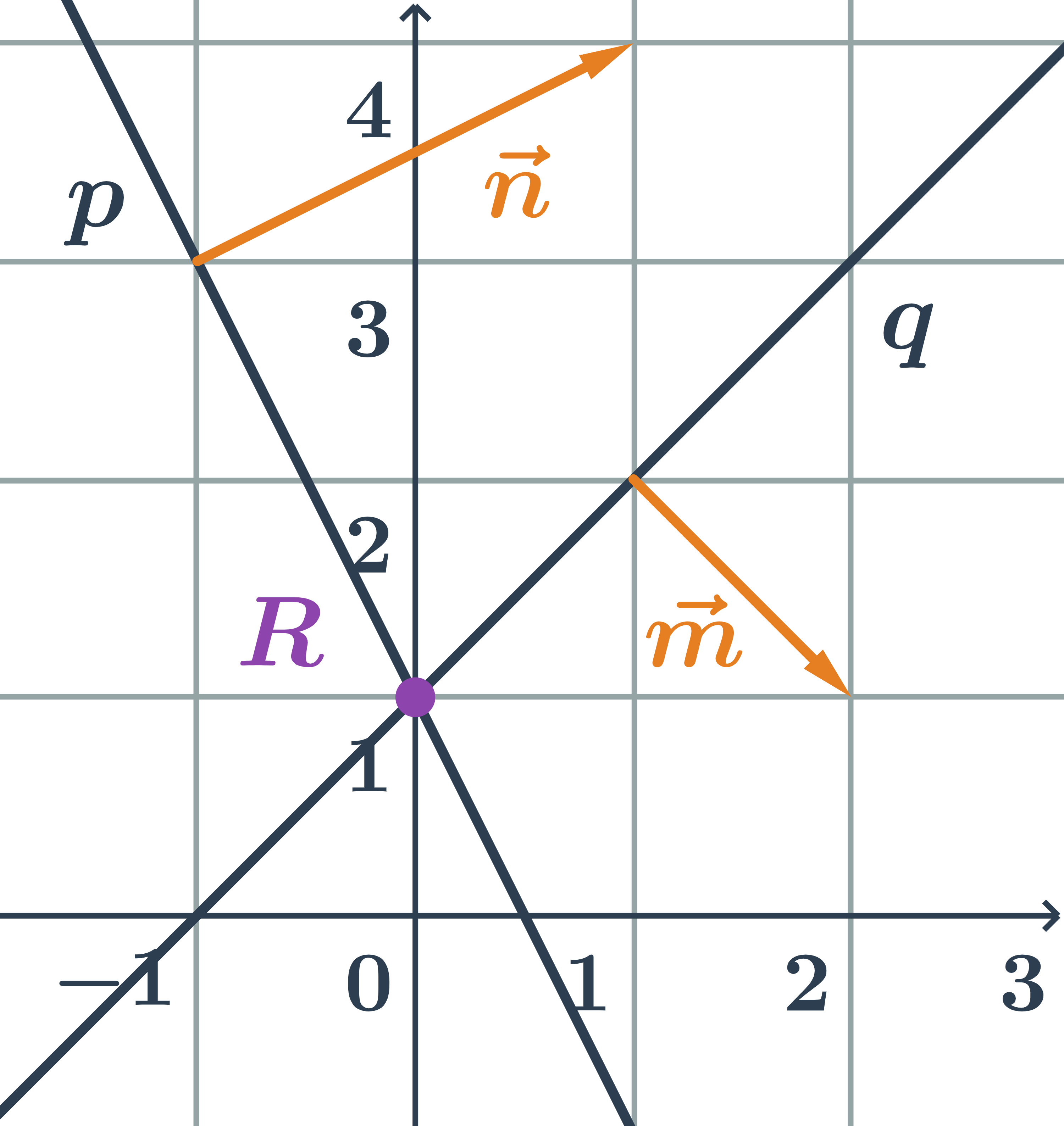
Přímka daná obecnou rovnicí a druhá parametricky – první příklad
Určete vzájemnou polohu přímek p,q zadaných takto:
\hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\\&&t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;-1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-2;-4)
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární. Proto normálový vektor jedné přímky je kolmý ke směrovému vektoru druhé přímky.
- Ověříme, že přímky nejsou totožné: stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce q leží například bod B=[3;2].
- Na přímce p tento bod neleží, což zjistíme dosazením souřadnic bodu B do rovnice přímky: 2\cdot3-2+3\neq 0
- Bod B nesplňuje rovnici, takže neleží na přímce p \Rightarrow přímky nejsou totožné
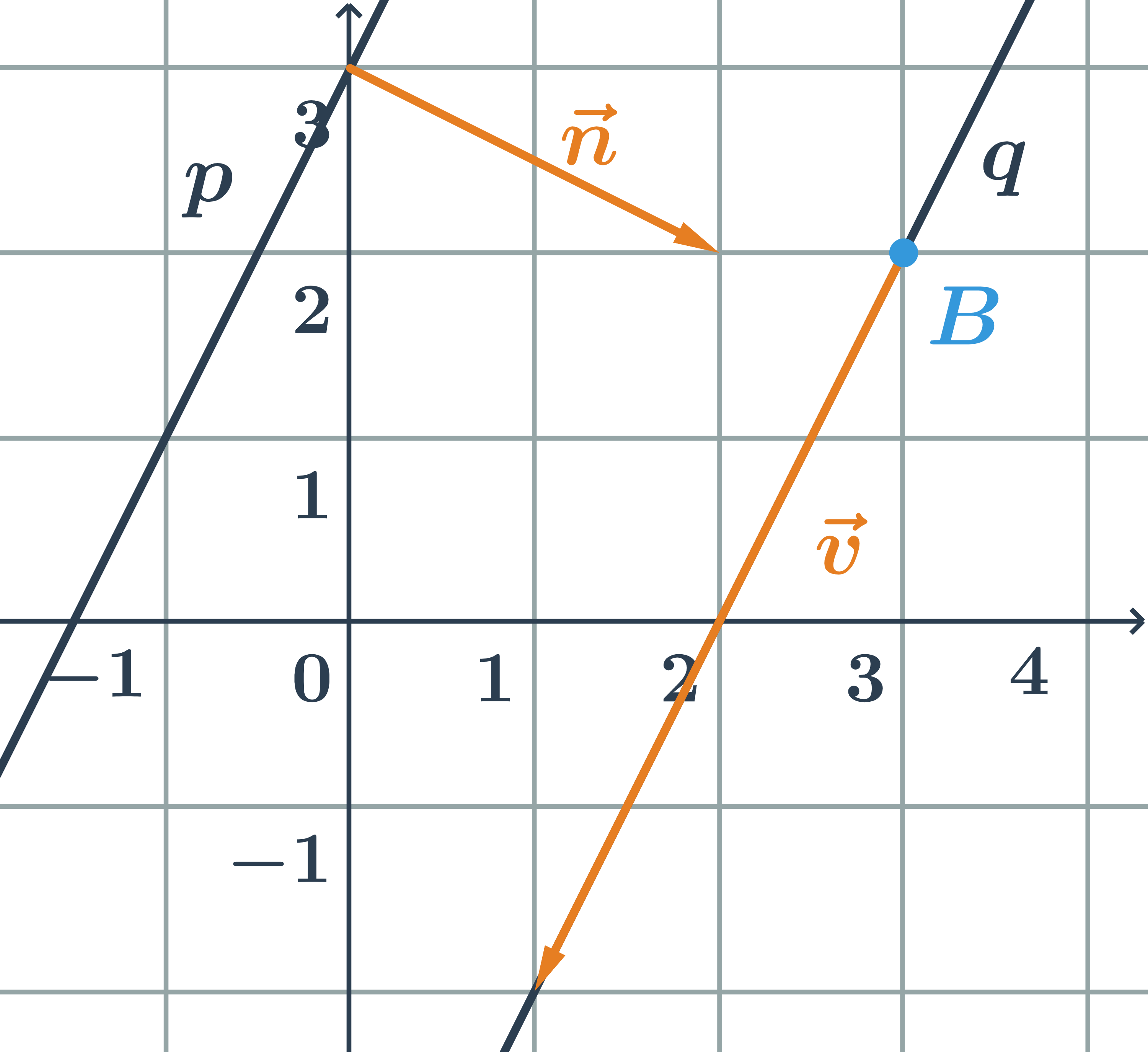
Přímka daná obecnou rovnicí a druhá parametricky – druhý příklad
Určete vzájemnou polohu přímek p,q zadaných:
\hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\\&&\hspace{0.28cm}t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(1;-3)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;2)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární. Vyplývá z toho, že normálový vektor jedné přímky není kolmý ke směrovému vektoru druhé přímky.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice najdeme tak, že parametrické vyjádření přímky q dosadíme do obecné rovnice přímky p: \begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Průsečík přímek p a q je bod R=[3;2]
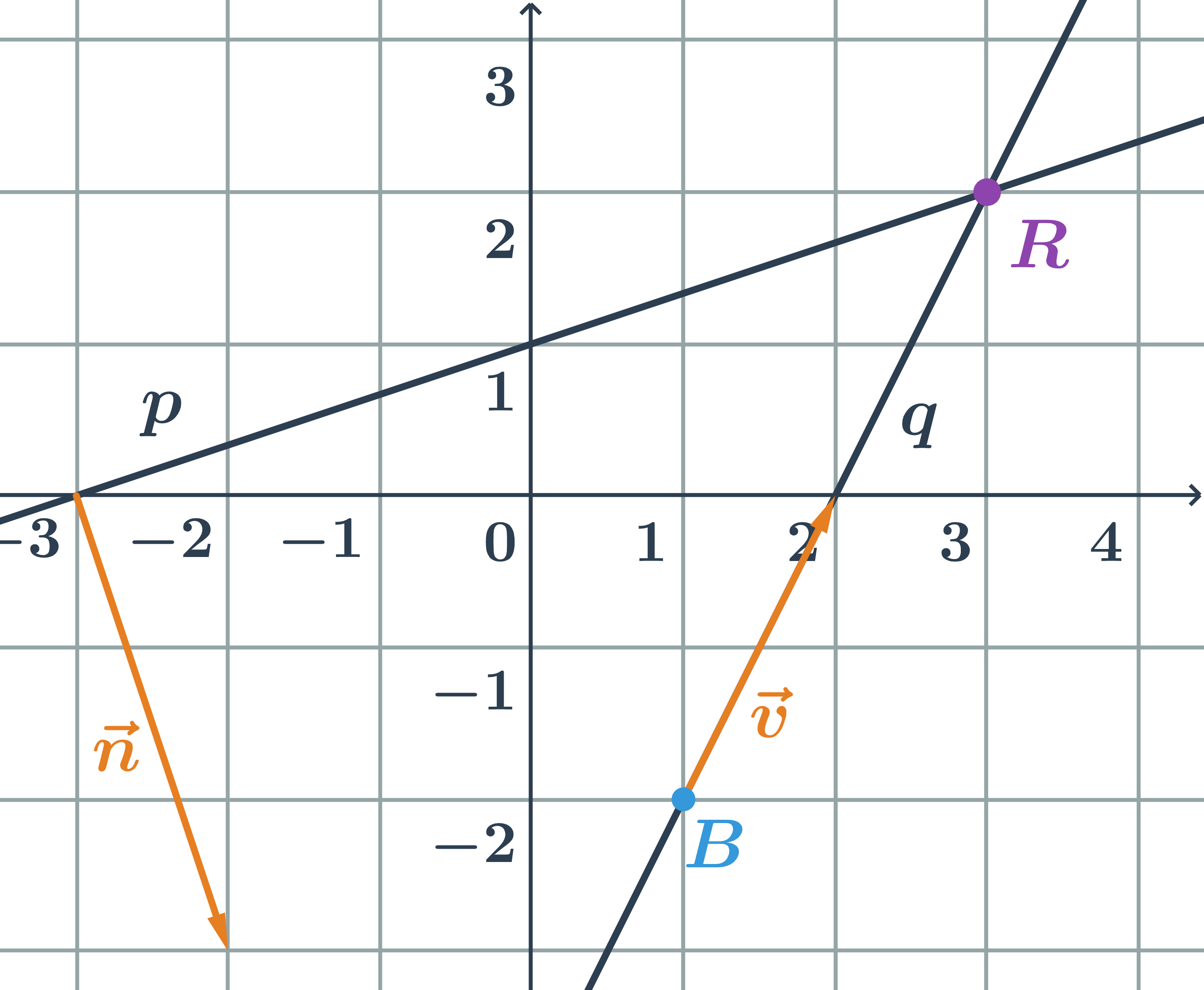
Souvislost počtu společných bodů přímek s počtem řešení soustavy rovnic
Pro určení společného bodu (bodů) dvou přímek, vždy řešíme soustavu rovnic. Tato soustava může mít:
- jedno řešení – přímky jsou různoběžné
- žádné řešení – přímky jsou rovnoběžné
- nekonečně mnoho řešení – přímky jsou totožné
Počet společných bodů – první příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Jedno řešení \Rightarrow různoběžné přímky
Počet společných bodů – druhý příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3-2t)-(2-4t)+3&=&0\\6-4t-2+4t+3&=&0\\7&=&0\end{array}
- Žádné řešení \Rightarrow různé rovnoběžné přímky
Počet společných bodů – třetí příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3+t\\y&=&9+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3+t)-(9+2t)+3&=&0\\6+2t-9-2t+3&=&0\\0&=&0\end{array}
- Nekonečně mnoho řešení \Rightarrow totožné přímky
Vzájemná poloha přímky a bodu v rovině
Bod leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky.
- Pokud je přímka daná obecnou rovnicí, po dosazení souřadnic bodu, který na přímce leží, do rovnice přímky nastane rovnost.
- Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t.
Bod a přímka daná obecnou rovnicí
Určete, zda body A=[2;3] a B=[-1;2] leží na přímce p:2x-3y+5=0.
- Do rovnice přímky dosadíme souřadnice bodu A=[2;3]:
- 2\cdot 2-3\cdot3+5=0 \Rightarrow bod A leží na přímce p
- Do rovnice přímky dosadíme souřadnice bodu B=[-1;2]:
- 2\cdot (-1)-3\cdot2+5=-3 \Rightarrow bod B neleží na přímce p
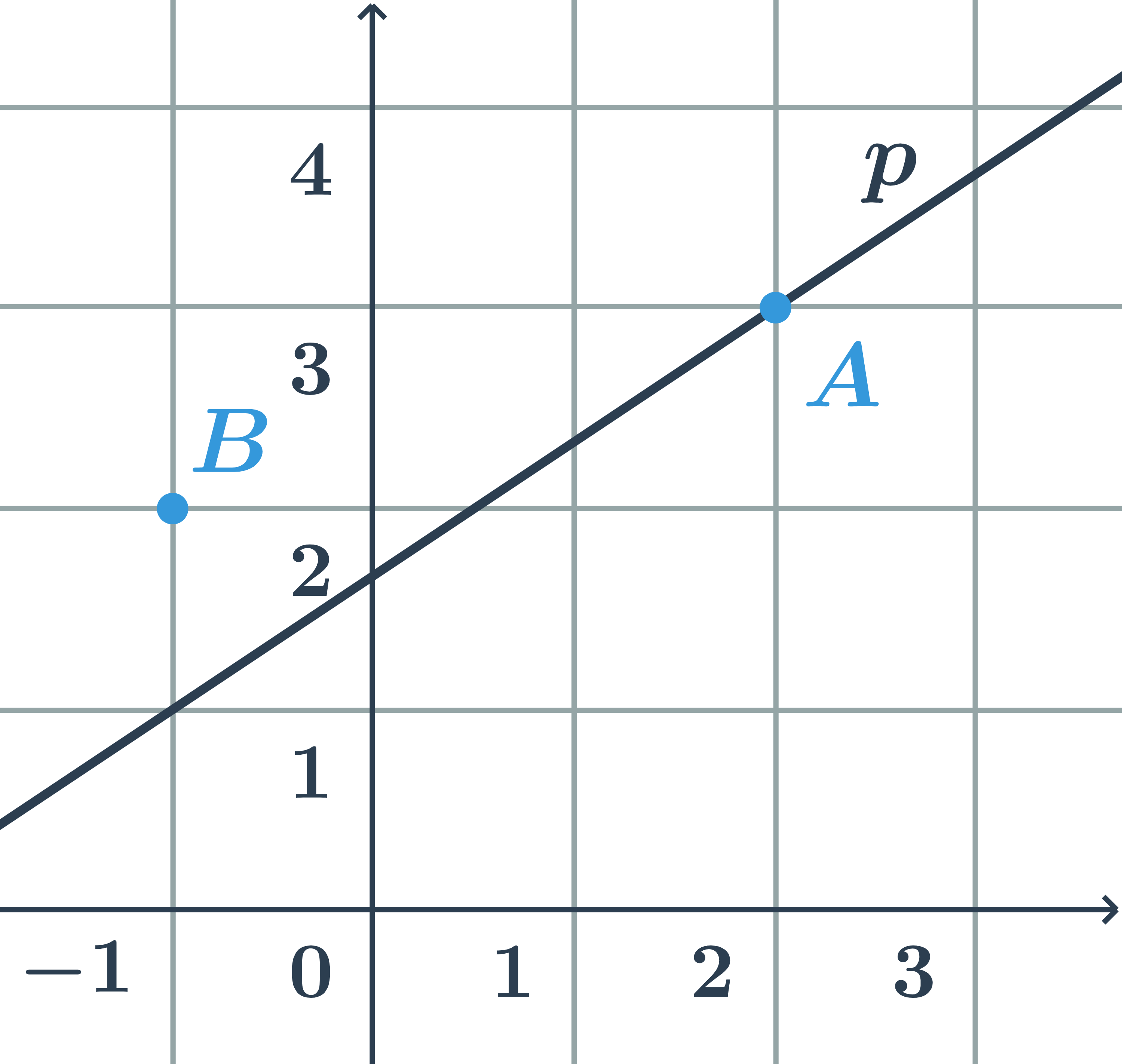
Bod a přímka daná parametricky
Určete, zda body A=[3;1] a B=[4;4] leží na přímce p dané parametricky: \begin{array}{rrl}x&=&2-t\\y&=&3+2t\\&&t\in\mathbb{R}\end{array}
- Do rovnic přímky dosadíme souřadnice bodu A=[3;1]:
\begin{array}{rrrr}3&=&2-t&\Rightarrow t=-1\\1&=&3+2t&\Rightarrow t=-1\end{array} \Rightarrow bod A leží na přímce p
- Do rovnice přímky dosadíme souřadnice bodu B=[4;5]:
\begin{array}{rrrl}4&=&2-t&\Rightarrow t=-2\\5&=&3+2t&\Rightarrow t=1\end{array}\Rightarrow bod B neleží na přímce p
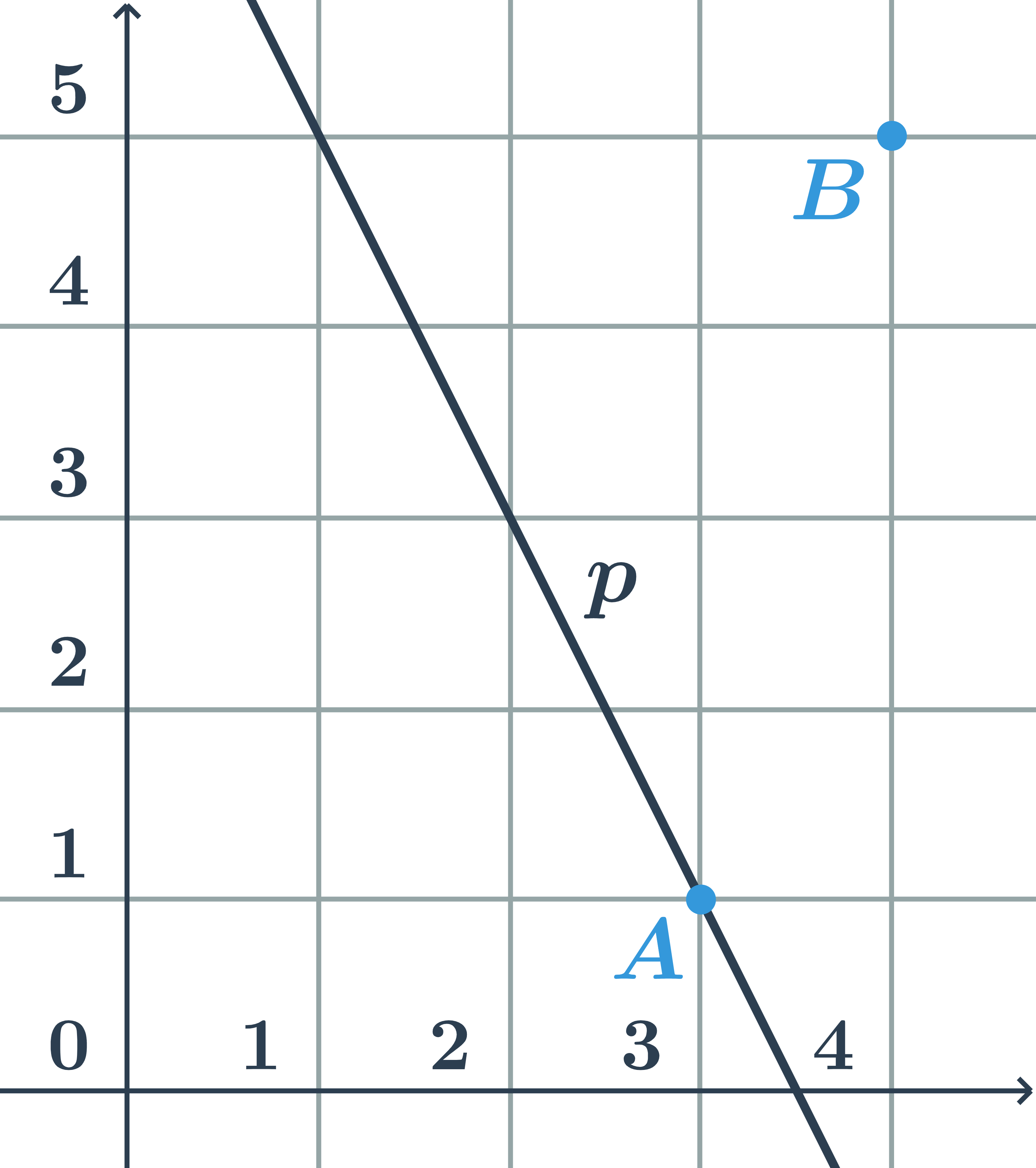
Polohové úlohy
V polohových úlohách řešíme analyticky vzájemnou polohu geometrických útvarů v rovině. Nejčastěji jde o vzájemnou polohu dvou přímek nebo o vzájemnou polohu přímky a bodu.
NahoruMetrické úlohy
V metrických úlohách v analytické geometrii bývá úkolem spočítat konkrétní číselnou hodnotu veličin jako je:
- vzdálenost dvou objektů, např. vzdálenost bodu od přímky,
- odchylka dvou přímek v rovině.
Vzdálenost bodu od přímky
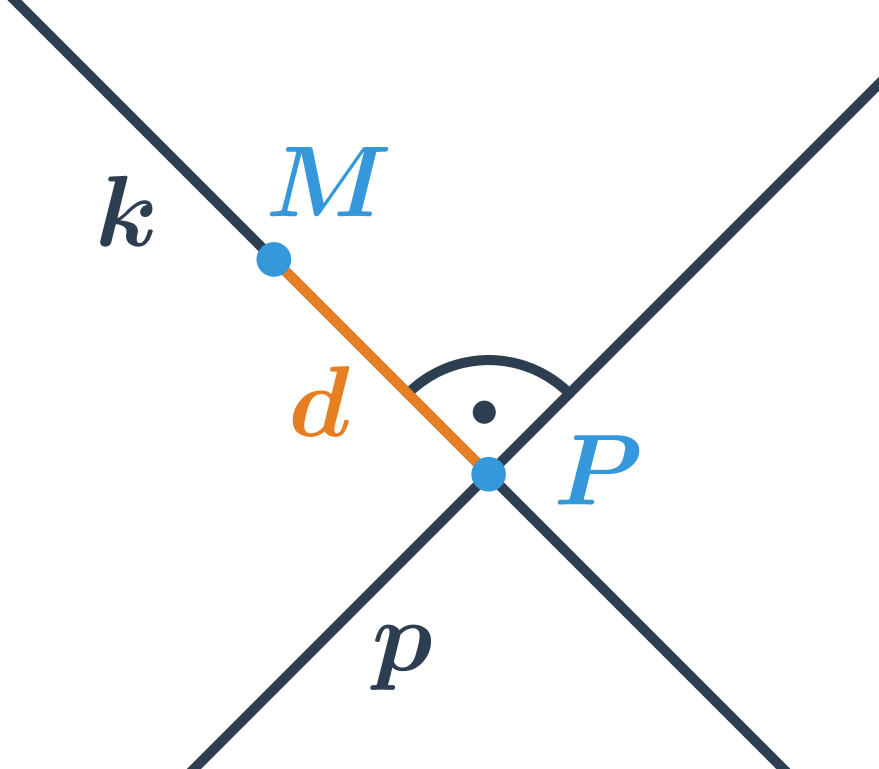
Vzdálenost bodu od přímky je délka nejkratší úsečky určené bodem M a bodem ležícím na přímce p. Jak je vidět z obrázku tato nejkratší úsečka leží na kolmici z bodu M k přímce p. Vzdálenost bodu od přímky tedy můžeme určit takto:
- najdeme přímku k, která prochází bodem M a je kolmá k přímce p
- určíme průsečík P přímky k s přímkou p
- vzdálenost bodu M od přímky p je délka úsečky PM
Příklad: vzdálenost bodu od přímky – pomocí kolmice
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0.
- Přímka k, která prochází bodem M a je kolmá k přímce p má směrový vektor kolineární s normálovým vektorem přímky p.
- Souřadnice směrového vektoru přímky k jsou: \vec{u}=(4;3).
- Přímka k má parametrické vyjádření: p:X=M+t\vec{u}
- p:\begin{array}{rrl}x&=&5+4t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
- Souřadnice průsečíku P přímky k s přímkou p určíme dosazením parametrického vyjádření přímky k do obecné rovnice přímky p.
\begin{array}{rrl}4(5+4t)+3(2+3t)-1&=&0\\20+16t+6+9t-1&=&0\\25+25t&=&0\Rightarrow t=-1\end{array}
- Průsečík přímek k a p je bod P=[1;-1].
- Vzdálenost bodu M od přímky p je délka úsečky PM:
- Vzorec pro délku úsečky: d=\sqrt{(x_M-x_P)^2+(y_M-y_P)^2}
- Dosadíme souřadnice bodů M,P: d=\sqrt{(5-1)^2+(2-(-1))^2}=\sqrt{16+9}=5
Vzorec pro vzdálenost bodu od přímky dané obecnou rovnicí
Vzdálenost bodu M=[m_1;m_2] od přímky p dané obecnou rovnicí ax+by+c=0 je dána vzorcem: d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}}
Příklad: vzdálenost bodu od přímky – pomocí vzorce
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0 s využitím vzorce.
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[5;2] a koeficienty a a b z obecné rovnice přímky.
- Obecná rovnice pro p je 4x+3y-1=0, tedy a=4 a b=3.
- Máme: d=\frac{\left| 4\cdot5+3\cdot2-1\right|}{\sqrt{4^2+3^2}}=\frac{25}{\sqrt{25}}=5
Vzdálenost dvou rovnoběžek
Umíme-li určit vzdálenost bodu od přímky, snadno určíme také vzdálenost dvou rovnoběžek. Stačí si uvědomit, že všechny body ležící na jedné přímce mají od druhé přímky stejnou vzdálenost. Proto je vzdálenost rovnoběžek stejná jako vzdálenost libovolného bodu na jedné přímce od přímky druhé.
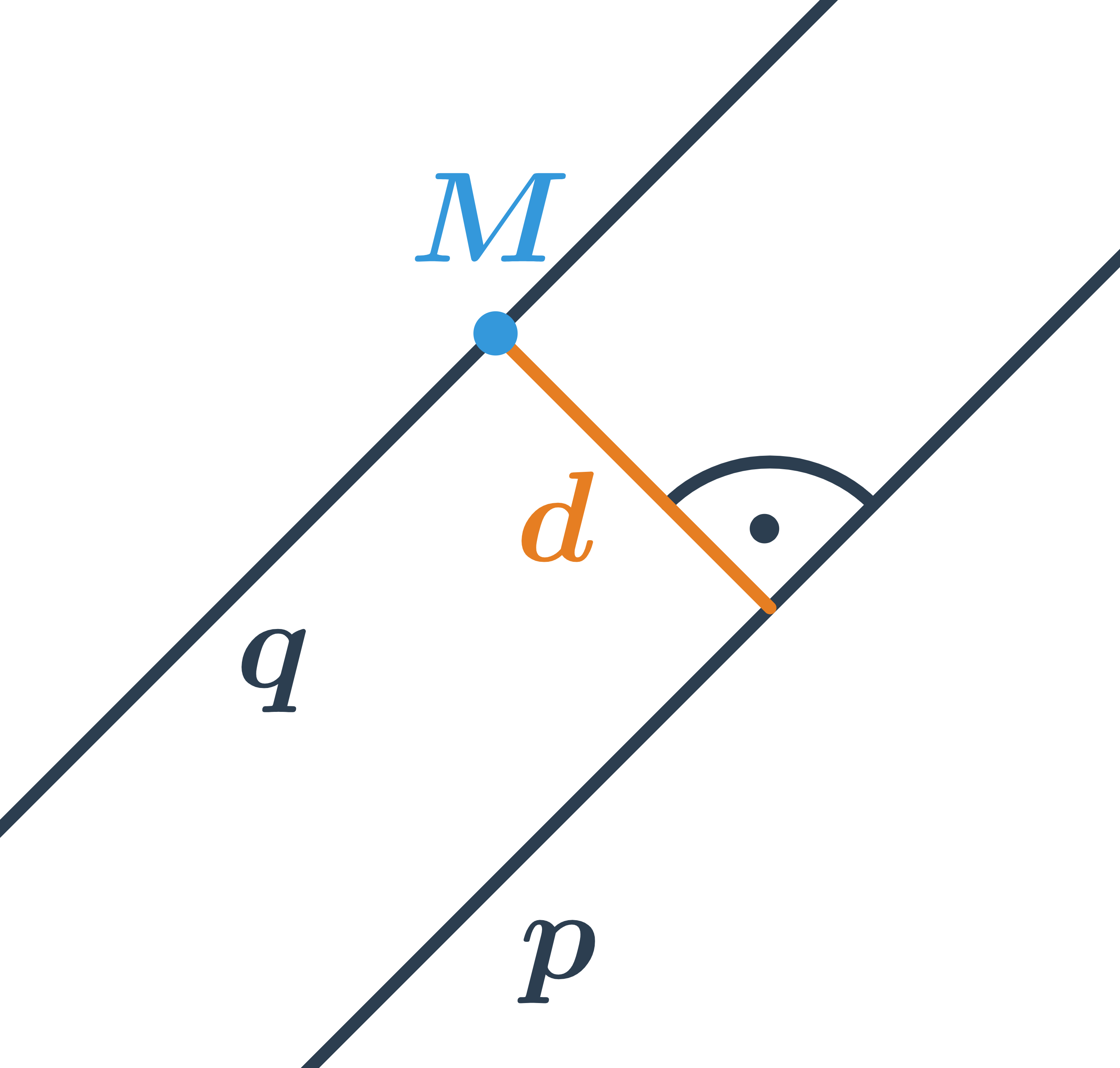
Příklad: vzdálenost rovnoběžek
Určete vzdálenost rovnoběžek p:2x-4y+3=0 a q:x-2y+1=0.
- Určíme souřadnice jednoho bodu (M) na přímce q tak, že jednu souřadnici zvolíme a druhou dopočítáme.
- Zvolíme například souřadnici y=0, pak x-2\cdot0+1=0\Rightarrow x=-1
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[-1;0] a koeficienty a a b z obecné rovnice přímky p.
- Obecná rovnice pro p je 2x-4y+3=0, tedy a=2 a b=-4.
- Máme: d=\frac{\left| 2\cdot(-1)-4\cdot0+3\right|}{\sqrt{2^2+(-4)^2}}=\frac{1}{\sqrt{20}}
- Vzdálenost rovnoběžek p a q je: d=\frac{1}{\sqrt{20}}
Odchylka dvou přímek
Odchylka rovnoběžek je 0^\circ. Odchylka různoběžek je velikost ostrého nebo pravého úhlu, který přímky svírají.
Odchylku různoběžek p a q můžeme vypočítat na základě znalosti směrových nebo normálových vektorů přímek. Vzorec pro výpočet úhlu různoběžek je obdobný jako vzorec pro výpočet úhlu vektorů
Odchylka různoběžek je úhel \alpha, pro který platí: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|} Vektory \vec{u} a \vec{v} uvedené ve vzorci jsou směrové vektory \overrightarrow{s_p} a \overrightarrow{s_q} nebo normálové vektory \overrightarrow{n_p} a \overrightarrow{n_q} přímek p a q.
Pro dvě k sobě kolmé přímky platí, že jejich odchylka \alpha=90^\circ a tedy \cos\alpha=0.
Proč musí být ve vzorci pro výpočet odchylky přímek absolutní hodnota?
- Odchylka přímek p a q na obrázku je ostrý úhel \alpha, nikoliv tupý úhel \beta.
- \alpha a \beta jsou vedlejší úhly, pro které je hodnota funkce \cos opačná, tedy: \cos\alpha=-\cos\beta
- Pro úhel \alpha je \cos\alpha \gt 0, pro \beta je $$
- Absolutní hodnota ve vzorci nám zaručí, že najdeme úhel, kde hodnota funkce \cos je kladná, tedy úhel ostrý, který je odchylkou daných přímek.
Odchylka přímek a úhly v trojúhelníku
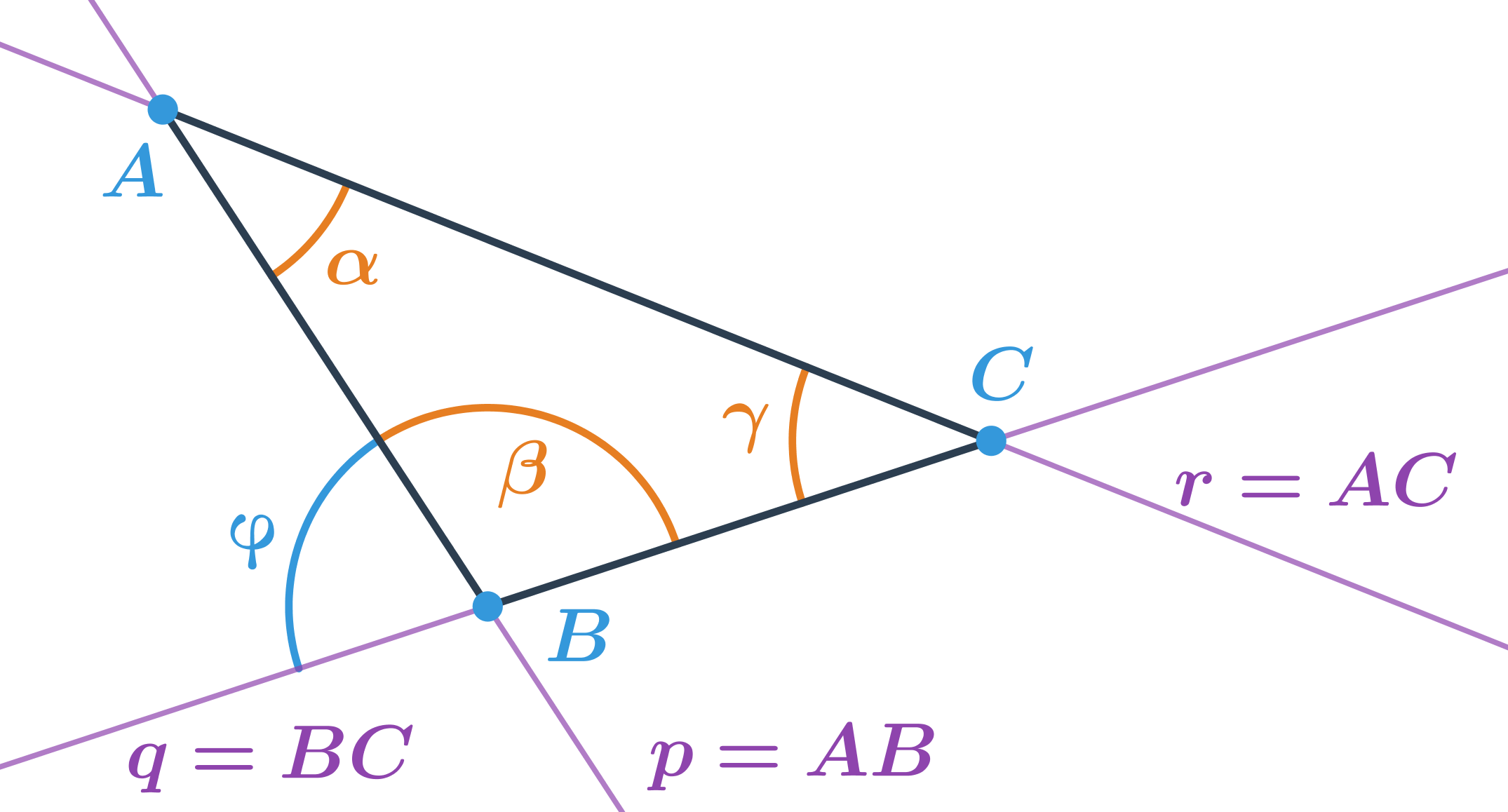
V trojúhelníku na obrázku:
- úhel \alpha je menší než 90^\circ a je to odchylka přímek AB a AC
- úhel \beta je větší než 90^\circ a není to odchylka přímek AB a BC
- úhel \gamma je menší než 90^\circ a je to odchylka přímek BC a AC
Velikost úhlů v trojúhelníku nemusí být stejná jako odchylka přímek, na kterých leží strany trojúhelníku. Úhly v trojúhelníku počítáme jako odchylku vektorů, které určují daný úhel. Tento úhel může být větší než 90^\circ, proto využijeme vzorec pro výpočet odchylky vektorů (ve vzorci nebude absolutní hodnota).
Odchylka přímek
Určete odchylku přímek p:x-2y+3=0 a q:2x-y+1=0
- Přímky jsou dané obecnými rovnicemi, proto pro výpočet jejich odchylky využijeme normálové vektory: \overrightarrow{n_p}=(1;-2) a \overrightarrow{n_q}=(2;-1)
- Dosadíme do vzorce: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|}=\frac{\left| 1\cdot2+(-2) \cdot(-1) \right|}{\sqrt{1^2+(-2)^2}\cdot\sqrt{2^2+(-1)^2}}=\frac{4}{\sqrt{5}\cdot \sqrt{5}}=\frac{4}{5}
- Pomocí funkce cos^{-1} na kalkulačce dopočítáme odchylku: \alpha=36^\circ
Rovina je určena třemi body, které neleží na jedné přímce. Z předchozích kapitol již víme, že dvojice bodů určuje přímku, případně vektor, proto je mnoho dalších způsobů jak určit rovinu:
- bodem a přímkou
- dvěma různoběžnými přímkami
- dvěma rovnoběžnými přímkami
- bodem a dvěma vektory
V prostoru lze zapsat rovinu jako množinu bodů, které splňují parametrickou rovnici nebo obecnou rovnici.
Máme-li rovinu popsanou rovnicí, umíme určit vzájemnou polohu roviny a bodu výpočtem.
NahoruRoviny: pojmy
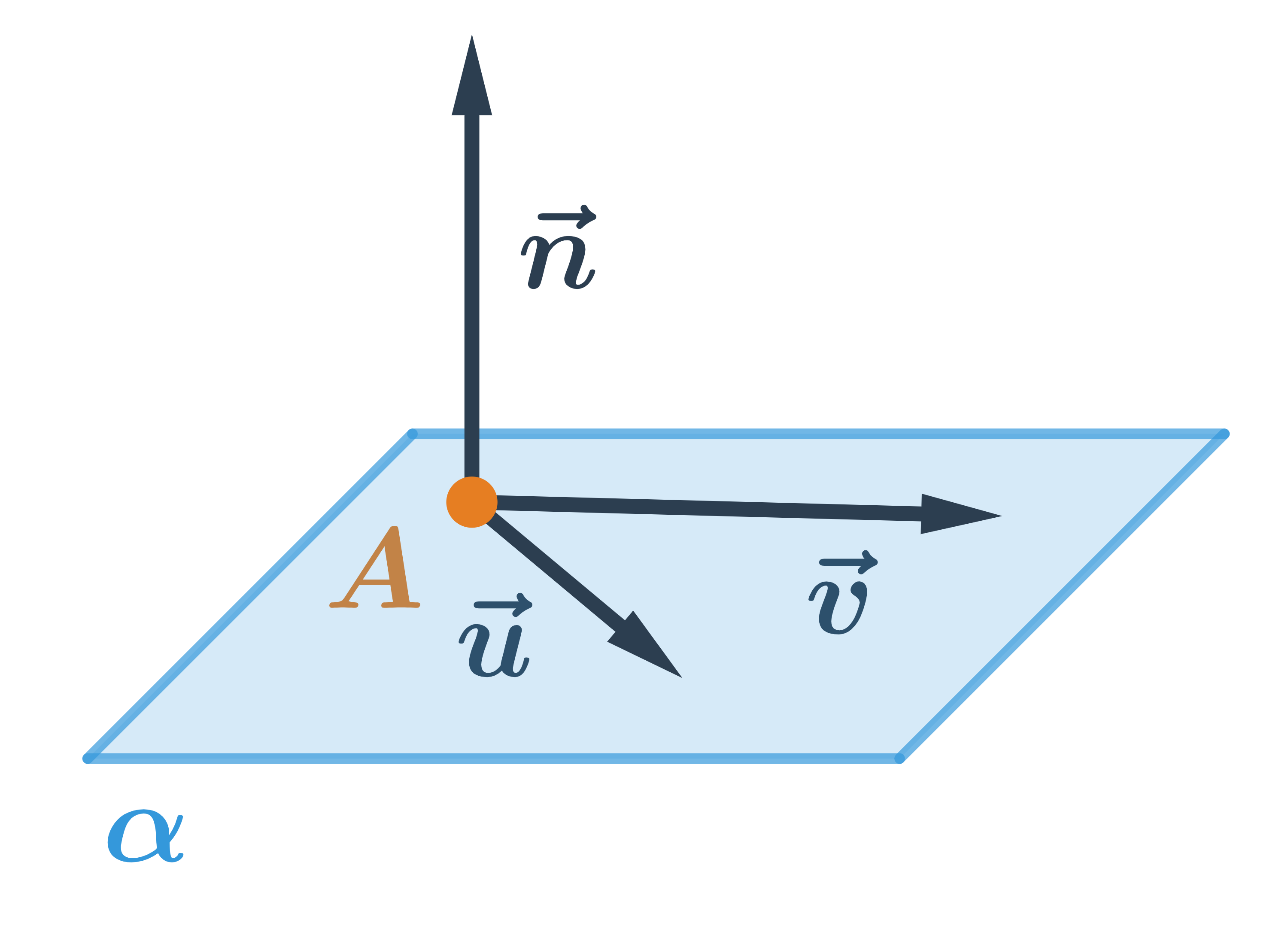
Přímka je jednoznačně určena bodem a dvěma vektory, které nejsou kolineární. Na obrázku je rovina \alpha určená bodem A a vektory \vec{u}, \vec{v}. Každý vektor, který je kolmý k rovině \alpha se nazývá normálový vektor roviny \alpha. Na obrázku je normálový vektor \vec{n}.
Parametrické rovnice roviny
Rovina určená bodem A=[a_1;a_2;a_3] a vektory \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit \alpha:X=A+t\vec{u}+s\vec{v}, kde t, s nazýváme parametry.
Obecná rovnice roviny
Obecná rovnice roviny je ve tvaru ax+by+cz+d=0, kde konstanty a, b, c jsou souřadnice normálového vektoru a d reálné číslo.
Obecná rovnice roviny rovnoběžné s osami x a y
Pro všechny body ležící v rovině je třetí souřadnice stejná, tedy rovina má obecnou rovnici: z+d=0.
Obecná rovnice roviny rovnoběžné s osami x a z
Pro všechny body ležící v rovině je druhá souřadnice stejná, tedy rovina má obecnou rovnici: y+d=0.
Obecná rovnice roviny rovnoběžné s osami y a z
Pro všechny body ležící v rovině je první souřadnice stejná, tedy rovina má obecnou rovnici: z+d=0.
Bod a rovina
Bod M=[m_1;m_2;m_3] leží v rovině, jestliže jeho souřadnice vyhovují rovnici roviny.
- Pokud je rovina daná obecnou rovnicí ax+by+cz+d=0, pro souřadnice bodu, který leží na přímce platí: a\cdot m_1+b\cdot m_2+c\cdot m_3+d=0
- Pokud je rovina daná parametricky, po dosazení souřadnic bodu do parametrických rovnic dostaneme soustavu tří rovnic pro dvě neznámé t, s, která má právě jedno řešení (dvojici reálných čísel).
Obecná rovnice roviny, která prochází počátkem
- Rovina prochází bodem O=[0;0;0], tedy musí platit: a\cdot0+b\cdot0+c\cdot0+d=0\Rightarrow d=0.
- Rovina, která prochází počátkem má obecnou rovnici: ax+by+cz=0.
Dvě rovnoběžné roviny
Normálové vektory dvou rovnoběžných rovin \alpha: a_1x+b_1y+c_1z+d_1=0 a \beta: a_2x+b_2y+c_2z+d_2=0 jsou kolineární, tedy souřadnice jednoho vektoru jsou k-násobek souřadnic druhého vektoru. Pro konstanty v obecných rovnicích musí platit:
\begin{array}{rll}a_2&=&k\cdot a_1\\ b_2&=&k\cdot b_1\\c_2&=&k\cdot c_1\\&&k\in\mathbb{R}\end{array}
Pokud by platilo i d_2=k\cdot d_1 roviny jsou totožné.
NahoruParametrické rovnice roviny
Pro určení parametrických rovnic roviny potřebujeme znát souřadnice jednoho bodu a dvou nekolineárních vektorů v rovině \alpha. Rovina určená bodem A=[a_1;a_2;a_3] a vektory \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit \alpha:X=A+t\vec{u}+s\vec{v}, kde t,s \in \mathbb{R} jsou parametry.
Parametrické rovnice roviny určené třemi body
Určete parametrické rovnice roviny \alpha určené body A=[3;2;1], B=[1;3;4], C=[2;-3;3].
- rovina \alpha je určená bodem A a vektory \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{AC}:
- \vec{u}=\overrightarrow{AB}=B-A=(-2;1;3)
- \vec{v}=\overrightarrow{AC}=C-A=(-1;-5;2)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&3-2t-s\\y&=&2+t-5s\\z&=&1+3t+2s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určené bodem a dvěma vektory
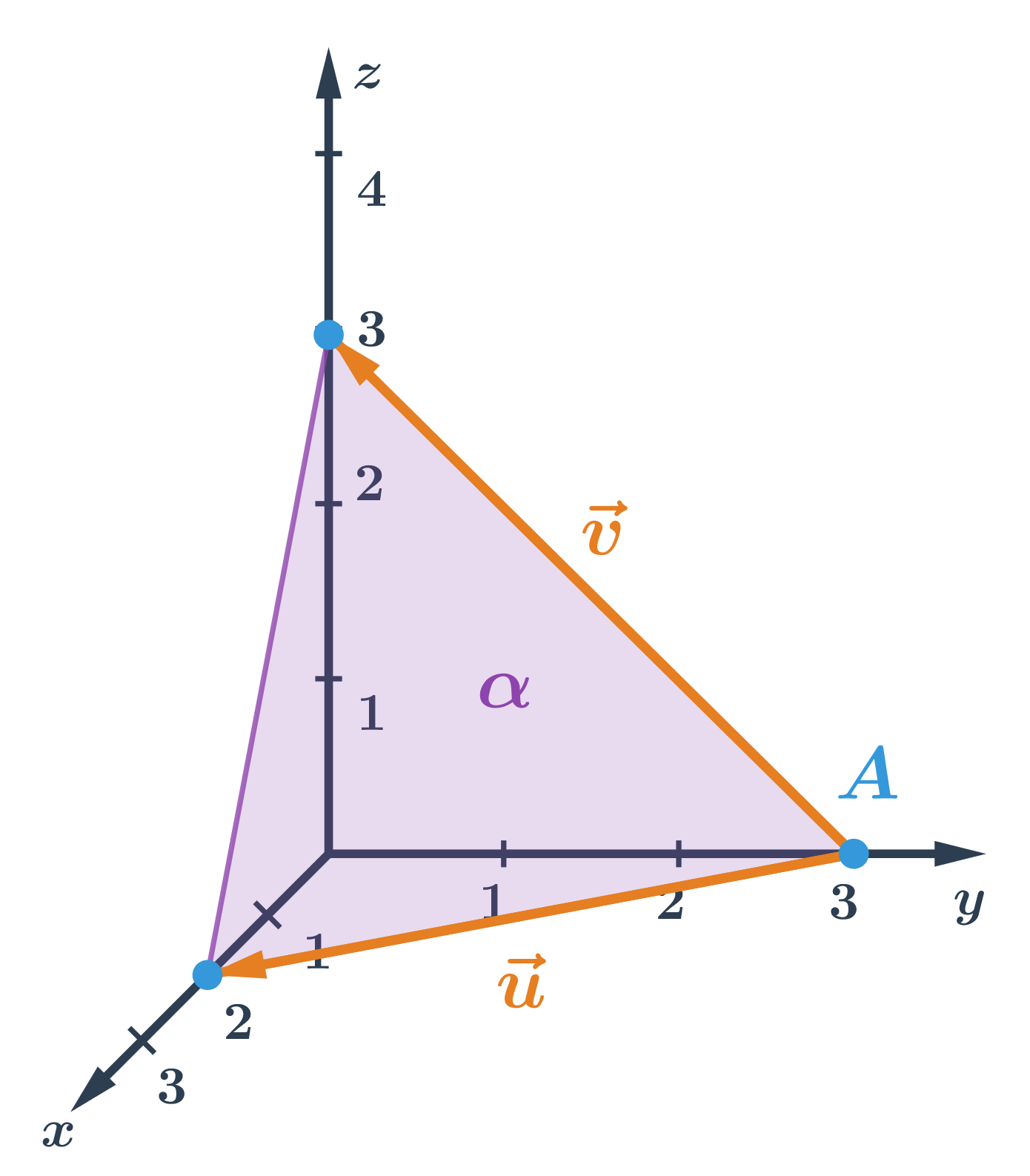
- rovina \alpha je určená bodem A a vektory \vec{u}, \vec{v}
- souřadnice určíme z obrázku:
- A=[0;3;0],
- \vec{u}=(2;-3;0),
- \vec{v}=(0;-3;3)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&2t\\y&=&3-3t-3s\\z&=&3s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určené různoběžkami p a q
Určete parametrické rovnice roviny určené dvěma různoběžkami s následujícími parametrickými rovnicemi:
p:\begin{array}{rrl}x&=&2+3t\\y&=&1+2t\\z&=&4-4t\\&&t\in\mathbb{R}\end{array}, q:\begin{array}{rrl}x&=&2+4s\\y&=&1-2s\\z&=&4-5s\\&&s\in\mathbb{R}\end{array}
- rovina \alpha je určená společným bodem různoběžek a směrovými vektory přímek p a q
- společný bod různoběžek: R=[2;1;4],
- směrový vektor přímky p:\vec{u}=(3;2;4),
- směrový vektor přímky q:\vec{v}=(4;-2;-5)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&2+3t+4s\\y&=&1+2t-2s\\z&=&4-4t-5s\\&&t,s\in\mathbb{R}\end{array}
Obecná rovnice roviny
Obecná rovnice roviny má tvar ax+by+cz+d=0, kde konstanty a, b, c jsou souřadnice normálového vektoru a d reálné číslo. Normálový vektor \vec{n}=(a;b;c) je vektor kolmý k dané rovině.
Obecná rovnice roviny určené bodem a normálovým vektorem
Určete obecnou rovnici roviny \alpha určené bodem A=[-3;1;2] a normálovým vektorem \vec{n}=(2;3;-4).
- Souřadnice normálového vektoru jsou konstanty a, b, c v obecné rovnici roviny, proto obecná rovnice bude mít tvar: 2x+3y-4z+d=0
- Konstantu d určíme dosazením souřadnic bodu A=[-3;1;2] do obecné rovnice: 2\cdot(-3)+3\cdot1-4\cdot 2+d=0\Rightarrow -11+d=0\Rightarrow d=11
- Obecná rovnice roviny \alpha je: 2x+3y-4z+11=0
Obecná rovnice roviny dané bodem a rovnoběžné s jinou rovinou
Obecná rovnice roviny \alpha, která prochází bodem A=[2;3;1] a je rovnoběžná s rovinou \beta:3x+y+4z+1=0.
- Dvě rovnoběžné roviny mají stejný normálový vektor, souřadnice normálového vektoru jsou souřadnice a, b, c v obecné rovnici roviny.
- Proto obecná rovnice hledané roviny \alpha bude mít tvar: 3x+y+4z+d=0
- Konstantu d určíme dosazením souřadnic bodu A=[2;3;1] do obecné rovnice: 3\cdot2+3+4\cdot 1+d=0\Rightarrow 13+d=0\Rightarrow d=-13
- Obecná rovnice roviny \alpha je: 3x+y+4z-13=0
Vzájemná poloha bodu a roviny
Bod leží v rovině, jestliže jeho souřadnice vyhovují rovnici roviny. Pokud je rovina daná obecnou rovnicí, po dosazení souřadnic bodu do rovnice roviny nastane rovnost. Pokud je rovina daná parametricky, po dosazení souřadnic bodu dostaneme soustavu tří rovnic pro dvě neznámé, která má právě jedno řešení.
Bod a rovina daná obecnou rovnicí
Určete, zda body A=[3;4;2] a B=[1;3;0] leží v rovině \alpha dané obecnou rovnicí 2x-y+3z+1=0.
- Do rovnice roviny dosadíme souřadnice bodu A=[3;4;2].
- 2\cdot 3-4+3\cdot2+1=0\Rightarrow9\neq 0, tedy bod A neleží v rovině \alpha.
- Do rovnice roviny dosadíme souřadnice bodu B=[1;3;0].
- 2\cdot 1-3+3\cdot0+1=0\Rightarrow0=0, tedy bod B leží v rovině \alpha.
Bod a rovina daná parametricky
Určete, zda body A=[2;3;4] a B=[0;2;2] leží v rovině \alpha dané parametrickými rovnicemi:
\begin{array}{rrl}x&=&1-t+s\\y&=&2+t+s\\z&=&3-t+s\\&&t,s\in\mathbb{R}\end{array}
- Do rovnic roviny dosadíme souřadnice bodu A=[1;3;4]: \begin{array}{rrrr}2&=&1-t+s\\3&=&2+t+s\\4&=&3-t+s\\\end{array}
- Z prvních dvou rovnic určíme hodnoty t a s, dosazením do třetí rovnice zjistíme, zda nalezené hodnoty jsou řešením soustavy a tedy zda bod leží v rovině:
- první a druhou rovnici sečteme: 5=3+2s\Rightarrow s=1
- hodnotu s=1 dosadíme do první rovnice: 1=1-t+1\Rightarrow t=1
- hodnoty s=1 a t=1 dosadíme do třetí rovnice: 4=3-1+1. Tato rovnost neplatí, tedy bod A neleží v rovině \alpha.
- Do rovnic roviny dosadíme souřadnice bodu B=[0;-3;2]: \begin{array}{rrrr}0&=&1-t+s\\-3&=&2+t+s\\2&=&3-t+s\\\end{array}
- Z prvních dvou rovnic určíme hodnoty t a s, dosazením do třetí rovnice zjistíme, zda nalezené hodnoty jsou řešením soustavy a tedy zda bod leží v rovině:
- první a druhou rovnici sečteme: -3=3+2s\Rightarrow s=-3
- hodnotu s=-3 dosadíme do první rovnice: 0=1-t-3\Rightarrow t=-2
- hodnoty s=-3 a t=-2 dosadíme do třetí rovnice: 2=3-(-2)-3. Tato rovnost platí, tedy bod B leží v rovině \alpha.
Kuželosečky
Jak již název napovídá, mají kuželosečky společný původ. Každá z nich vzikne jako řez rotační kuželové plochy rovinou. 
- Kružnice vznikne jako řez rovinou, která je kolmá na osu kuželové plochy.
- Pokud rovinu řezu trochu nakloníme, vznikne elipsa.
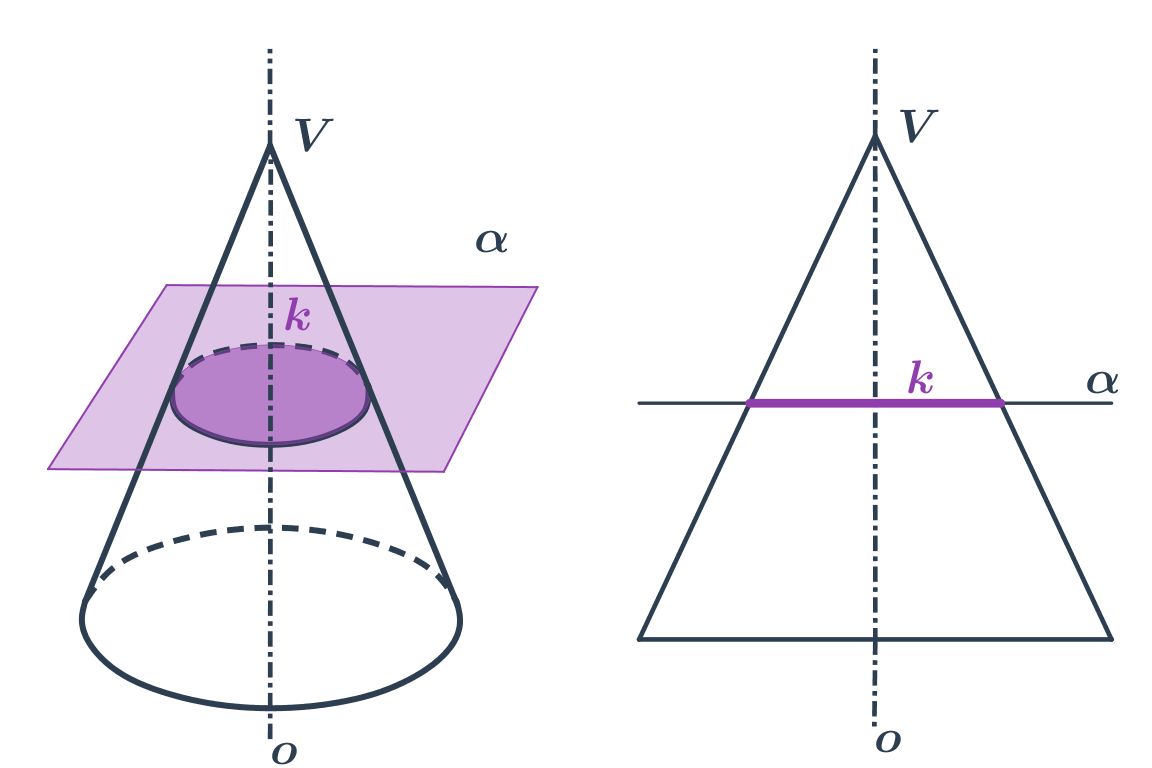
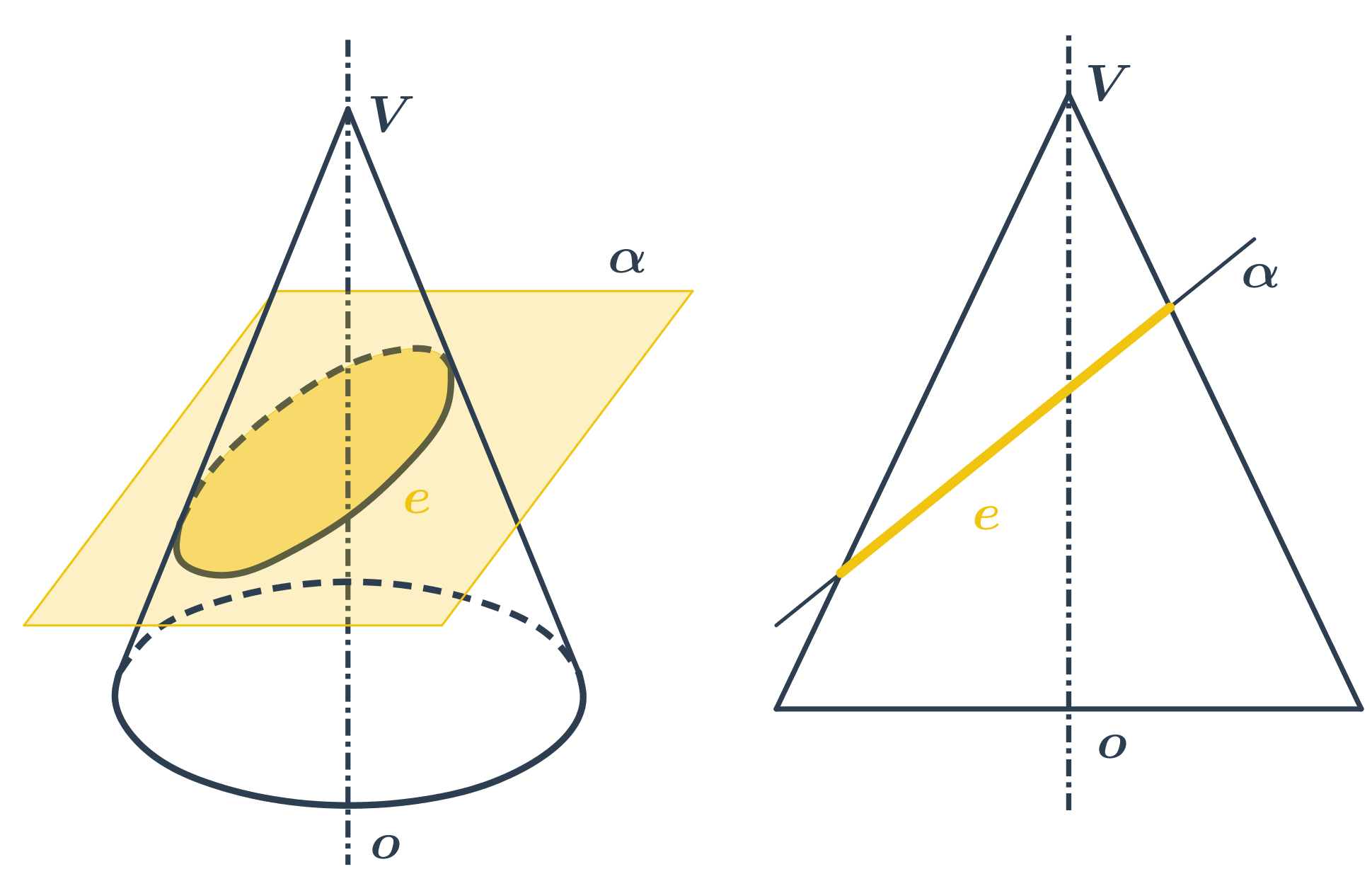
- Pokud rovinu řezu nakloníme tolik, že bude rovnoběžná s některou z přímek na kuželové ploše, vznikne parabola.
- Při dalším naklánění už rovina řezu protne obě části kuželové plochy a vznikne dvoudílná hyperbola.
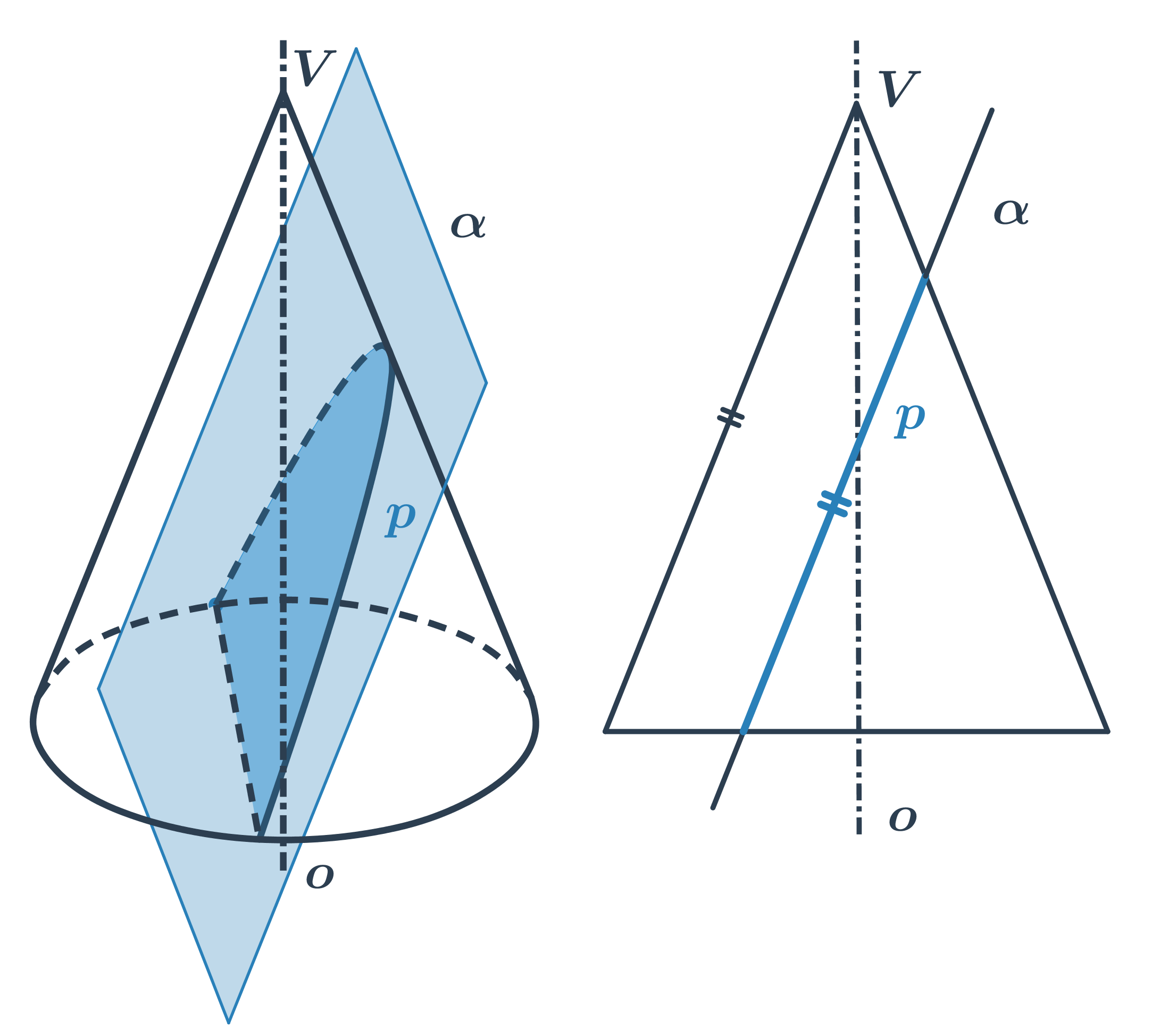
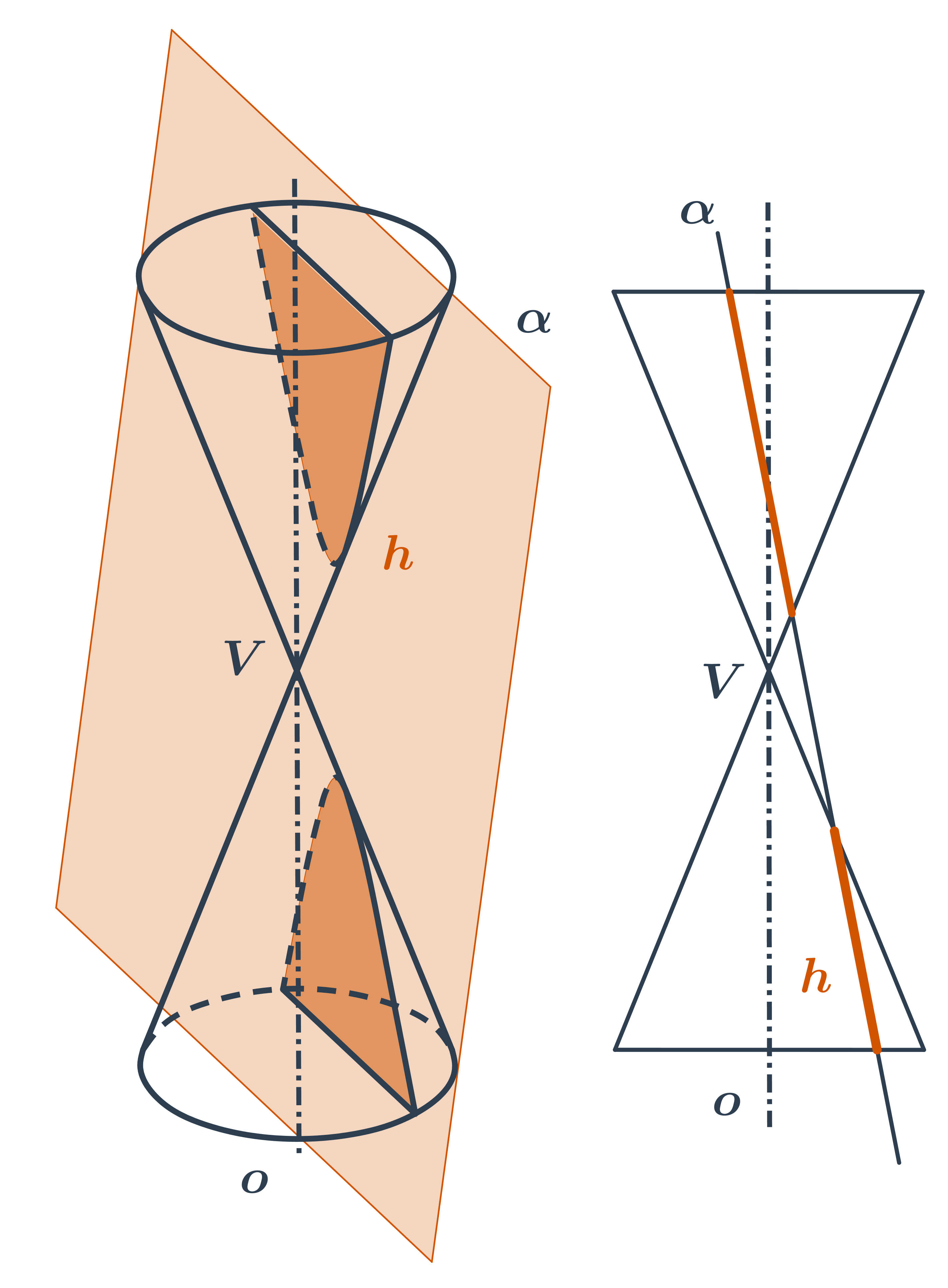
Na kuželosečky můžeme také hledět jako na množiny bodů dané vlastnosti. V analytické geometrii často zapisujeme tyto množiny pomocí rovnic.
NahoruKružnice (kuželosečka)
Kružnice je množina všech bodů v rovině, které mají od daného pevného bodu S stejnou vzdálenost r. Bod S nazýváme střed kružnice, hodnotu r nazveme poloměr kružnice. 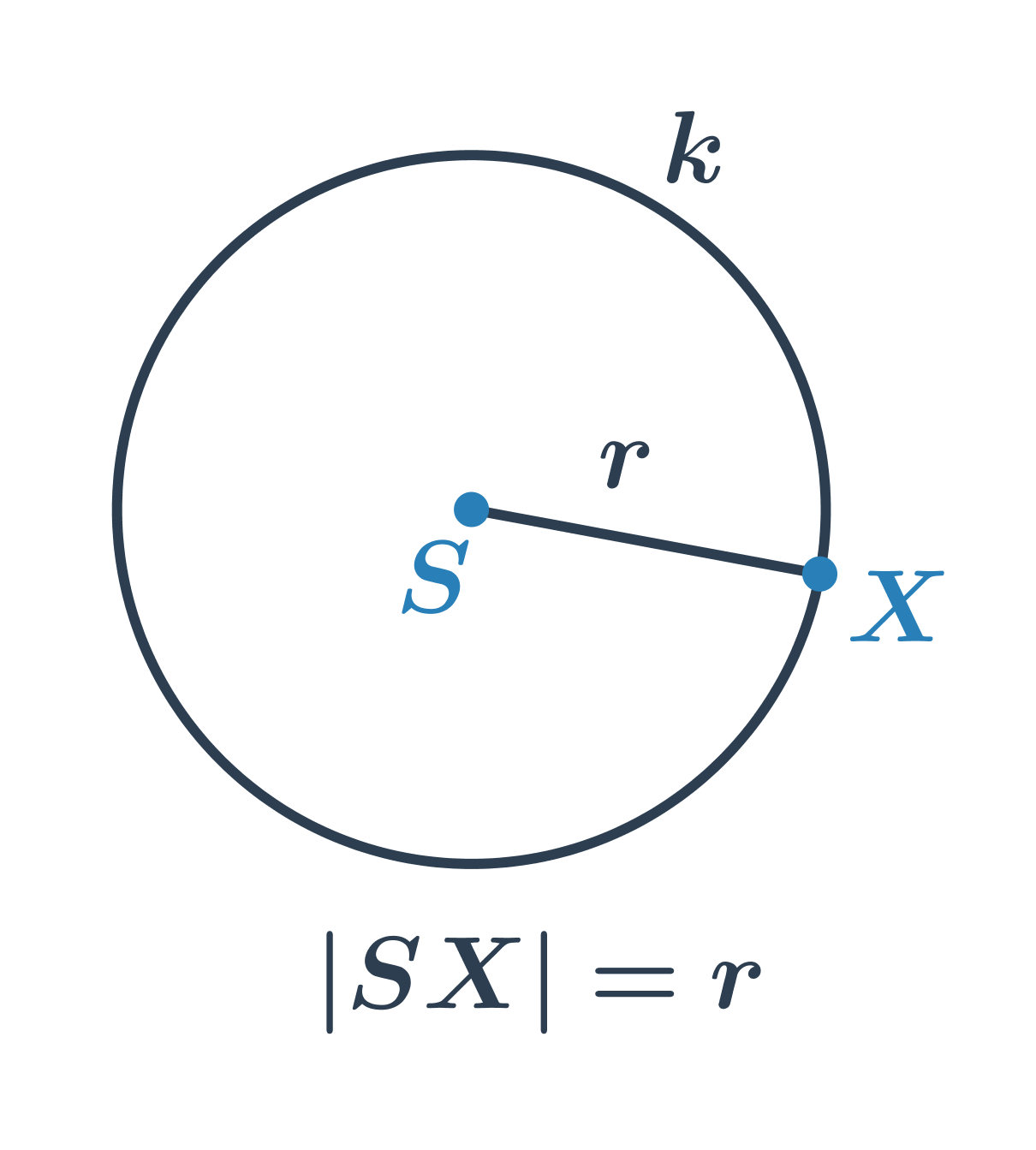
Středová rovnice kružnice
Středová rovnice kružnice o středu S[m;n] a poloměru r je ve tvaru: (x-m)^2 +(y-n)^2=r^2 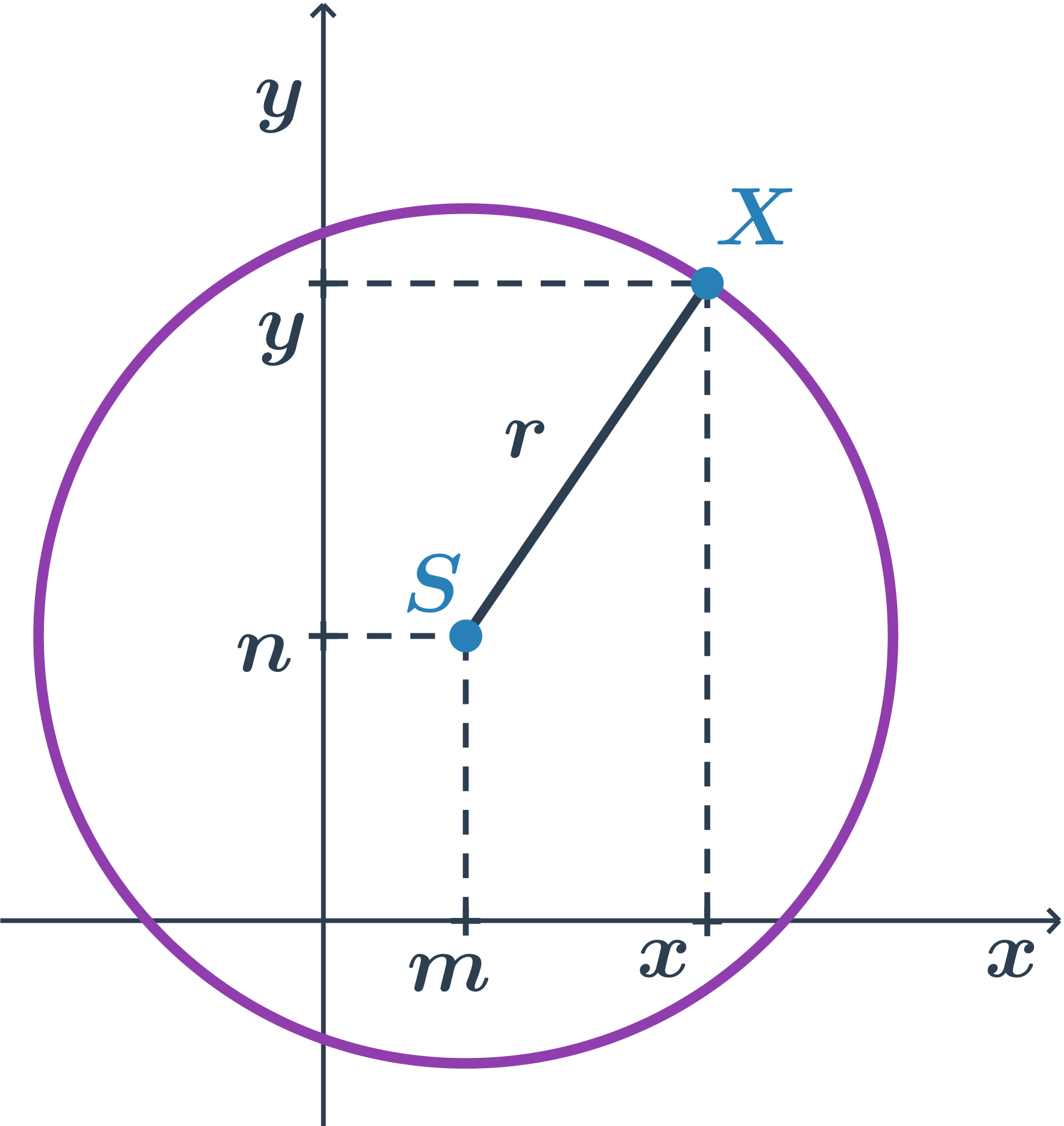
Příklad: Určete středovou rovnici kružnice se středem v bodě S[-1;2] a poloměrem r=3.
- Středová rovnice je ve tvaru: (x-m)^2 +(y-n)^2=r^2
- Dosadíme souřadnice středu a poloměr. Při dosazení si dáme pozor na to, že souřadnice středu ve středové rovnici odečítáme: (x-(-1))^2 +(y-2)^2=3^2
- Po úpravě: (x+1)^2 +(y-2)^2=9
Obecná rovnice kružnice
Podobně jako existuje několik tvarů rovnic přímky, můžeme i rovnici kružnice zapsat různými způsoby. Obecná rovnice kružnice je ve tvaru: x^2 +y^2-2mx-2ny+p=0.
Každá rovnice v tomto tvaru ale nemusí ještě být obecnou rovnicí kružnice. Pro obecnou rovnici kružnice musí platit, že výraz m^2+n^2-p je kladný. Praktické ověření, zda se jedná o kružnici, ale obvykle provádíme převedením na středovou rovnici kružnice.
Příklad: Najděte střed a poloměr kružnice dané obecnou rovnicí x^2+y^2+4x+6y-12=0.
- Nejprve si uspořádáme členy podle proměnných: x^2+4x+y^2-6y-12=0.
- Našim dalším cílem je upravit výraz na levé straně jako součet dvou druhých mocnin (čtverců), podle vzorečků a^2\pm 2ab+b^2=(a\pm b)^2.
- K oběma stranám rovnice přičteme konstanty 4 a 9, abychom součty členů s proměnnými x a y mohli upravit na druhé mocniny (provedeme v obou případech doplnění na čtverec): x^2+4x+4+y^2-6y+9-12=4+9
- A upravíme: (x+2)^2 +(y-3)^2-12=13
- Na závěr ještě převedeme -12 na druhou stranu rovnice: (x+2)^2 +(y-3)^2=25
- Tímto jsme převedli obecnou rovnici kružnice na středovou rovnici kružnice.
- Poloměr kružnice je r=\sqrt{25}=5.
- Souřadnice středu S[m,n] odčítáme ve středové rovnici od proměnných x a y, mají tedy opačná znaménka než konstanty v závorkách ve středové rovnici \Rightarrow S[-2;3].
Kružnice a přímka
- přímka s protíná kružnici ve dvou bodech – sečna kružnice
- přímka t protíná kružnici v jednom bodě – tečna kružnice
- přímka v kružnici neprotíná – vnější přímka kružnice
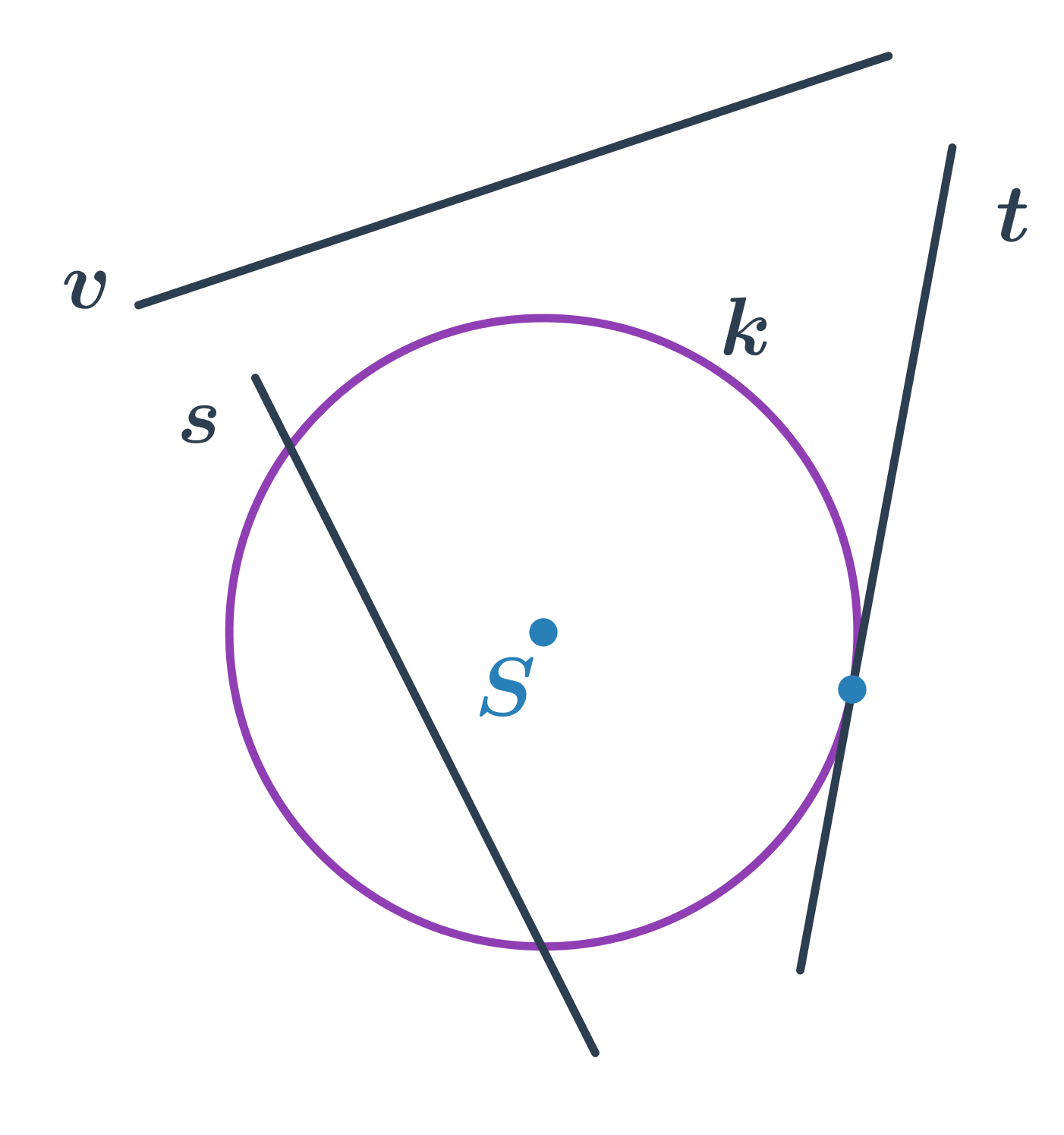
Rovnice tečny kružnice v bodě, který leží na kružnici
Kružnice daná rovnicí (x-m)^2 +(y-n)^2=r^2 má v bodě T[x_0;y_0] tečnu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.Jak si zapamatovat rovnici tečny
- Středová rovnice je ve tvaru (x-m)^2 +(y-n)^2=r^2.
- Závorky rozložíme na součiny dvoučlenů (x-m)(x-m) +(y-n)(y-n)=r^2.
- V každém součinu zaměníme jedno x za x_0 a jedno y za y_0
- Dostaneme rovnici tečny (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Příklad: Určete rovnici tečny kružnice (x-1)^2+(y+2)^2=13 v jejím bodě T[3;1].
- Ověříme, zda bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
- Tečna má rovnici (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
- Dosadíme souřadnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
- Roznásobíme závorky: 2x-2 +3y+6=13
- A dostaneme obecnou rovnici tečny 2x+3y-9=0
Polára kružnice
Z bodu R mimo kružnici můžeme sestrojit dvě tečny k dané kružnici. Přímka určená body dotyku tečen se nazývá polára kružnice vzhledem k bodu R. 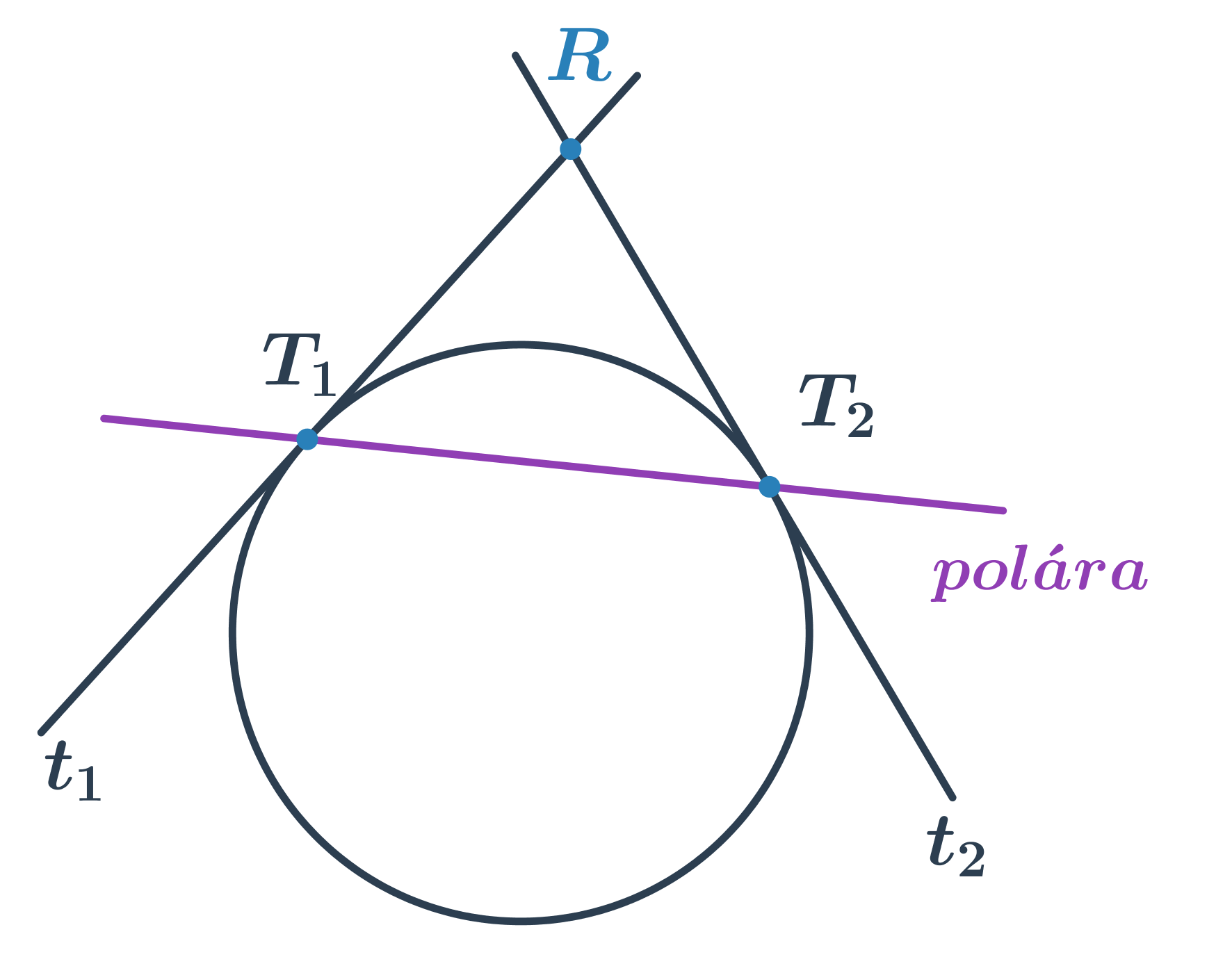
Rovnice poláry kružnice kružnice (x-m)^2 +(y-n)^2=r^2 vzhledem k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.
K čemu poláru použijeme?
- Poláru využíváme ke konstrukci tečen ležících z bodu mimo kružnici.
- Podle vzorce určíme rovnici poláry, tedy přímky.
- Najdeme průsečíky poláry a kružnice – to jsou body dotyku hledaných tečen.
- Když známe body dotyku, určíme podle vztahu pro rovnici tečny v bodě kružnice obecné rovnice obou tečen.
Elipsa je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý součet vzdáleností 2a, který je větší než vzdálenost ohnisek. 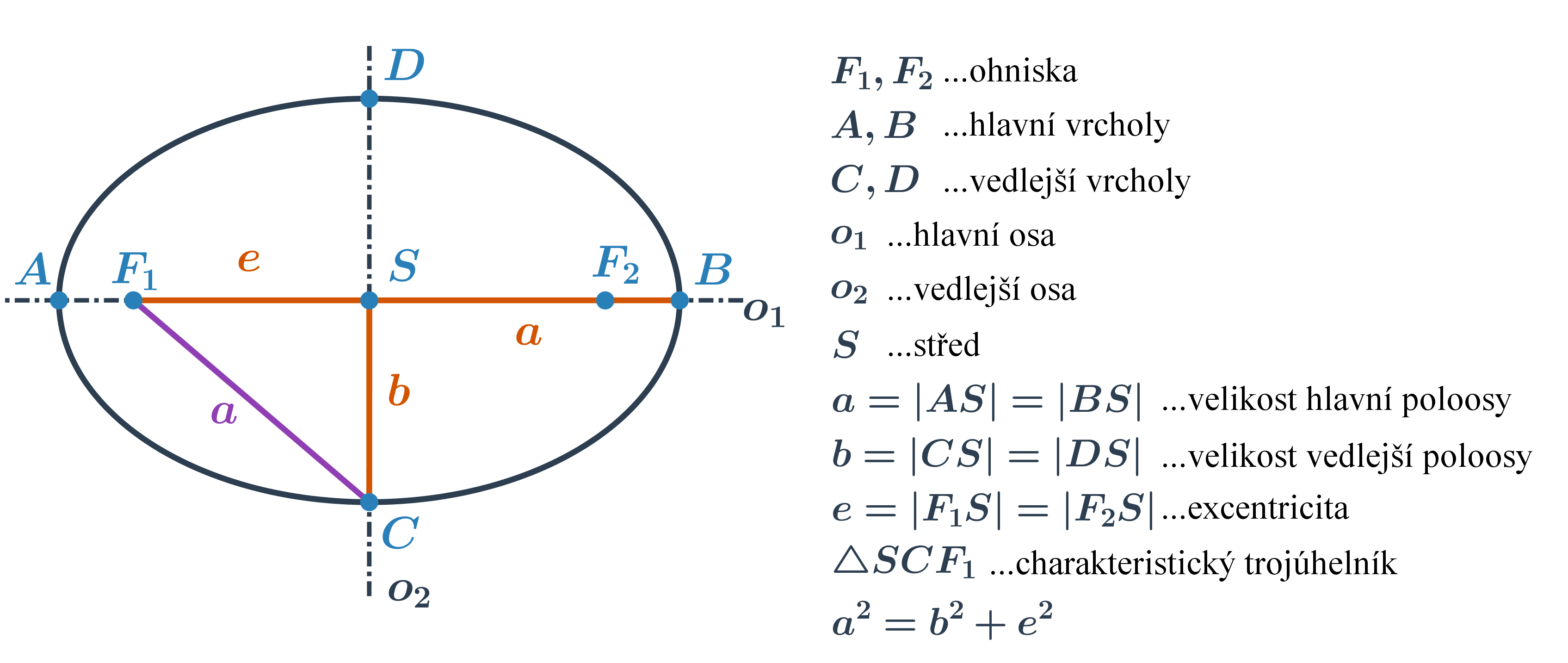
Středová rovnice elipsy
Tvar středové rovnice elipsy o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a a b závisí na poloze hlavní osy:
hlavní osa je rovnoběžná s osou x, rovnice je ve tvaru: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1
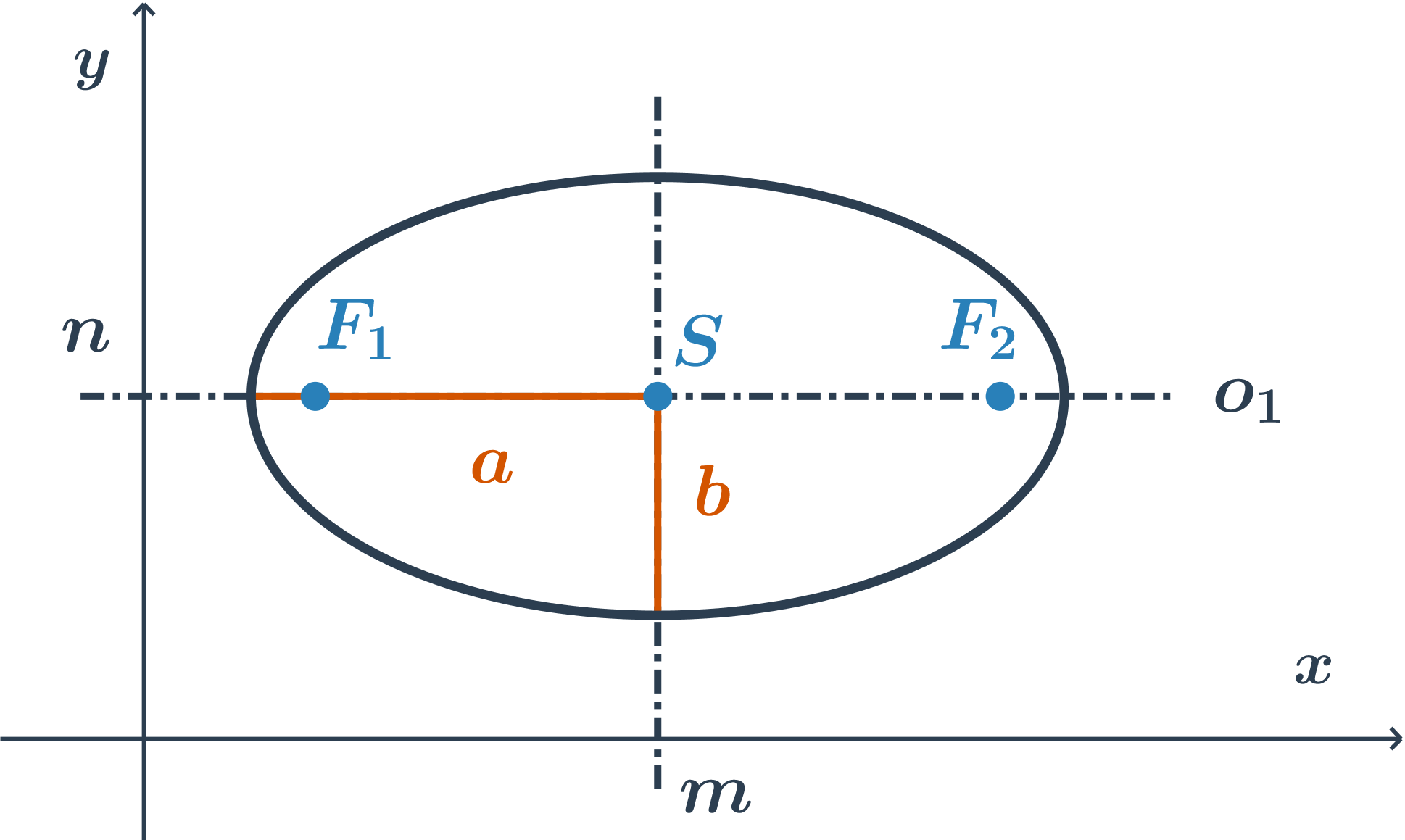
hlavní osa je rovnoběžná s osou y, rovnice je ve tvaru: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1
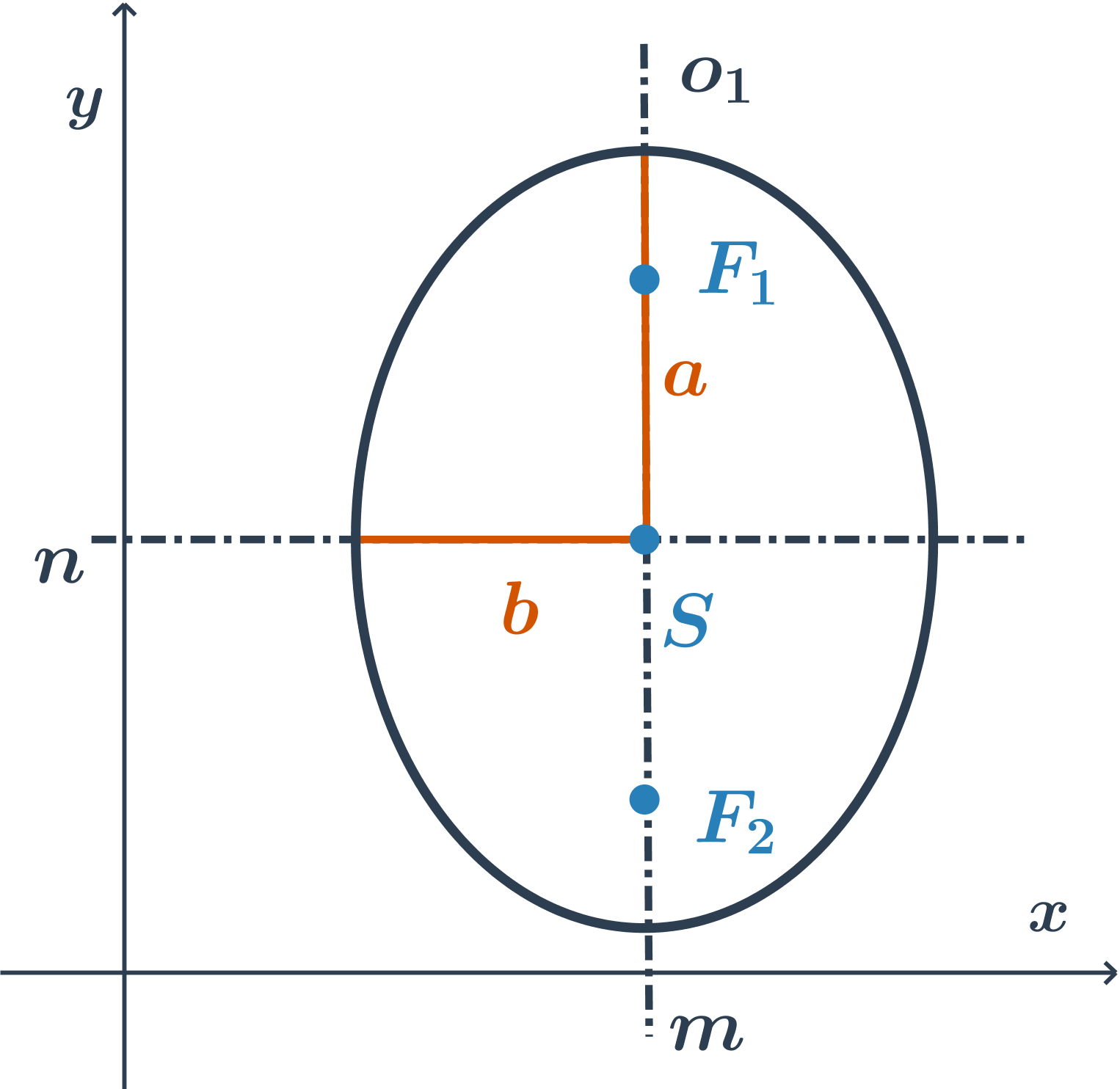
Návod: jak z rovnice poznat, se kterou souřadnou osou je rovnoběžná hlavní osa elipsy
- Podíváme se do jmenovatelů.
- Větší jmenovatel je druhá mocnina velikosti hlavní poloosy (a menší jmenovatel je druhá mocnina velikosti vedlejší poloosy).
- Proměnná v daném čitateli (zlomku s větším jmenovatelem) pak určuje, se kterou osou je hlavní osa elipsy rovnoběžná.
- Stručně řečeno: je‑li větší číslo například ve jmenovateli s proměnnou x, je hlavní osa rovnoběžná s osou x
Příklad: určení středové rovnice elipsy s daným středem, velikostmi poloos a směrem hlavní osy
Určete středovou rovnici elipsy se středem v bodě S[-2;3], je‑li a=3, b=2 a hlavní osa je rovnoběžná s osou y.
- Středová rovnice je ve tvaru \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
- Dosadíme souřadnice středu a velikosti hlavní a vedlejší poloosy. Při dosazení si dáme pozor na to, že souřadnice středu odčítáme: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
- Po úpravě: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1
Obecná rovnice elipsy
Podobně jako existuje několik rovnic přímky, můžeme i rovnici elipsy zapsat jiným způsobem. Obecná rovnice elipsy je ve tvaru:
Ax^2 +By^2+Cx+Dy+E=0, A\ne B, A\cdot B>0.
Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí elipsy. Praktické ověření, zda se jedná o elipsu provádíme převedením na středovou rovnici.
Příklad: určuje daná rovnice elipsu?
Rozhodněte, zda rovnice x^2+3y^2+8x-18y+31=0 určuje elipsu.
- Nejprve si uspořádáme členy: x^2+8x+3y^2-18y+31=0.
- Ze členů s proměnnou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
- K oběma stranám rovnice přičteme konstanty 16 a 27, abychom členy s proměnnými x a y mohli upravit podle vztahu (a\pm b)^2=a^2 \pm 2ab +b^2.
- Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
- A upravíme: (x+4)^2 +3(y-3)^2+31=43
- Převedeme konstantu 31 na druhou stranu rovnice: (x+4)^2 +3(y-3)^2=12
- Na závěr rovnici vydělíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
- Jedná se tedy o elipsu.
Elipsa a přímka
- přímka s protíná elipsu ve dvou bodech – sečna elipsy
- přímka t protíná elipsu v jednom bodě – tečna elipsy
- přímka v elipsu neprotíná – vnější přímka elipsy
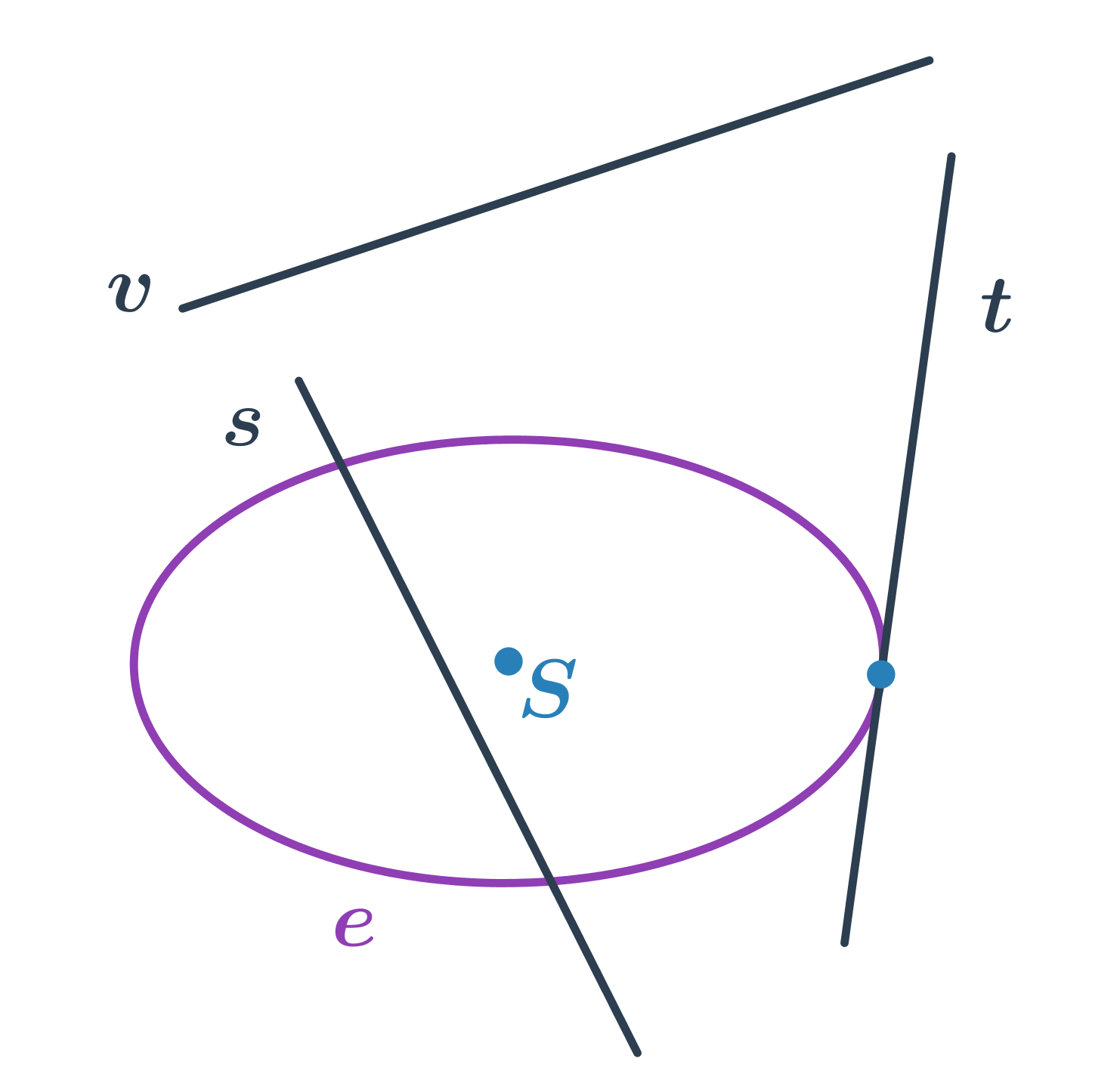
Rovnice tečny elipsy v bodě, který leží na elipse
Elipsa daná rovnicí \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bodě T[x_0;y_0] tečnu určenou rovnicí:
\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1
Podobně můžeme zapsat i rovnici tečny elipsy, která má hlavní osu rovnoběžnou s osou y.
Příklad: určení rovnice tečny elipsy v jejím daném bodě
Určete rovnici tečny elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jejím bodě T[1;-2].
- Ověříme, zda bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
- Tečna má rovnici \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
- Dosadíme souřadnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
- Zbavíme se zlomků: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
- Roznásobíme závorky: -2x+4 -4y+8=18
- A dostaneme obecnou rovnici tečny: x+2y+3=0
Parabola je množina všech bodů roviny, které mají stejnou vzdálenost od daného bodu (ohnisko) a dané přímky (řídicí přímka)
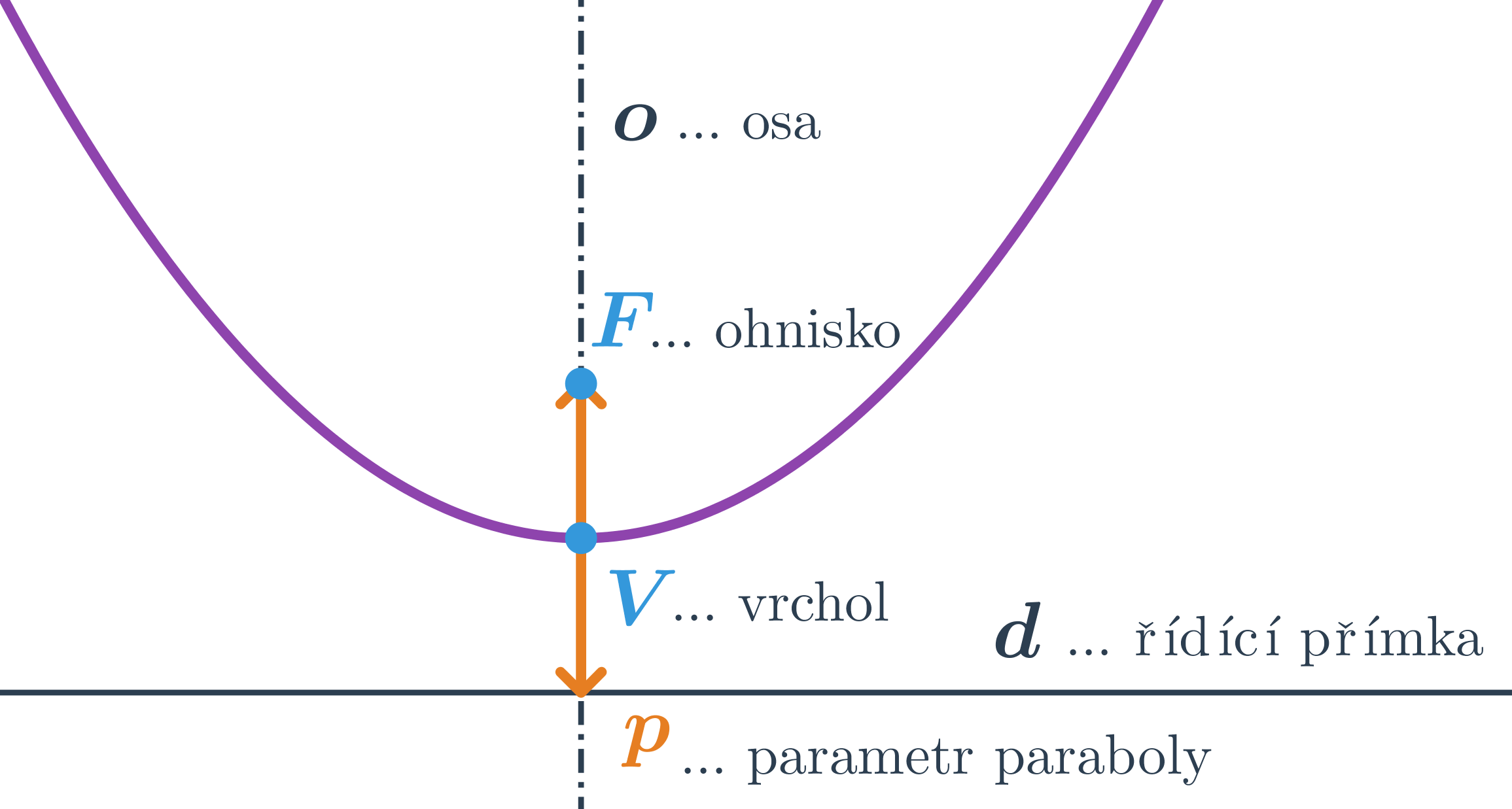
Vrcholová rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly rovnoběžná s osou y, vrcholová rovnice pak má tvar: (x-m)^2=\pm 2p(y-n)
- osa paraboly rovnoběžná s osou x, vrcholová rovnice pak má tvar: (y-n)^2=\pm 2p(x-m)
V rovnici paraboly označují m, n souřadnice vrcholu paraboly, tedy vrchol je bod V=[m;n]. Dále p je parametr paraboly = vzdálenost ohniska od řídicí přímky. Znaménko před parametrem závisí na poloze vrcholu vzhledem k bodům paraboly.
Příklad paraboly s osou rovnoběžnou s osou y
- body paraboly mají y souřadnici alespoň tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= + 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace
- body paraboly mají y souřadnici nejvýše tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= - 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou x
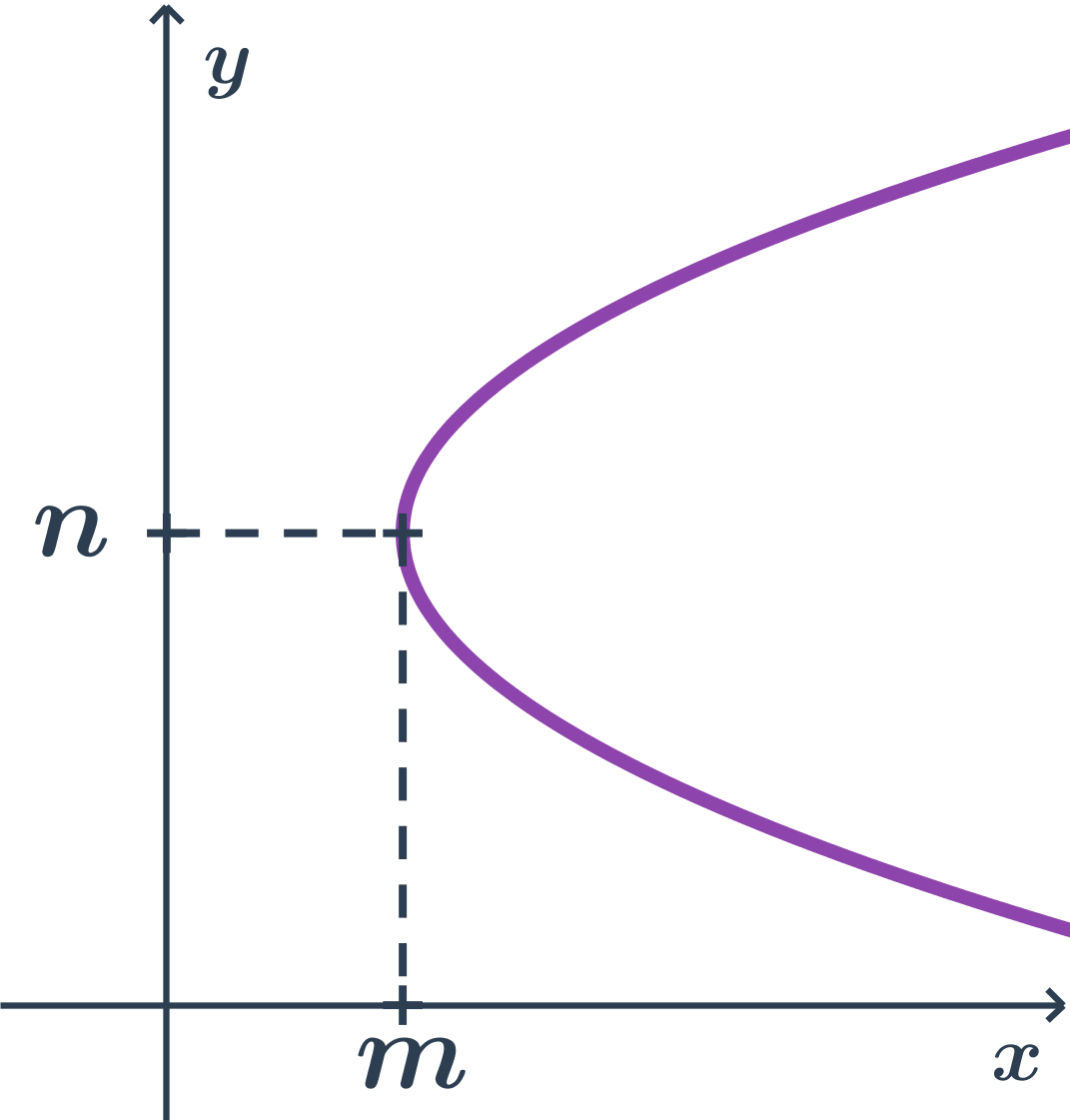
- body paraboly mají x souřadnici alespoň tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= + 2p(x-m)
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace
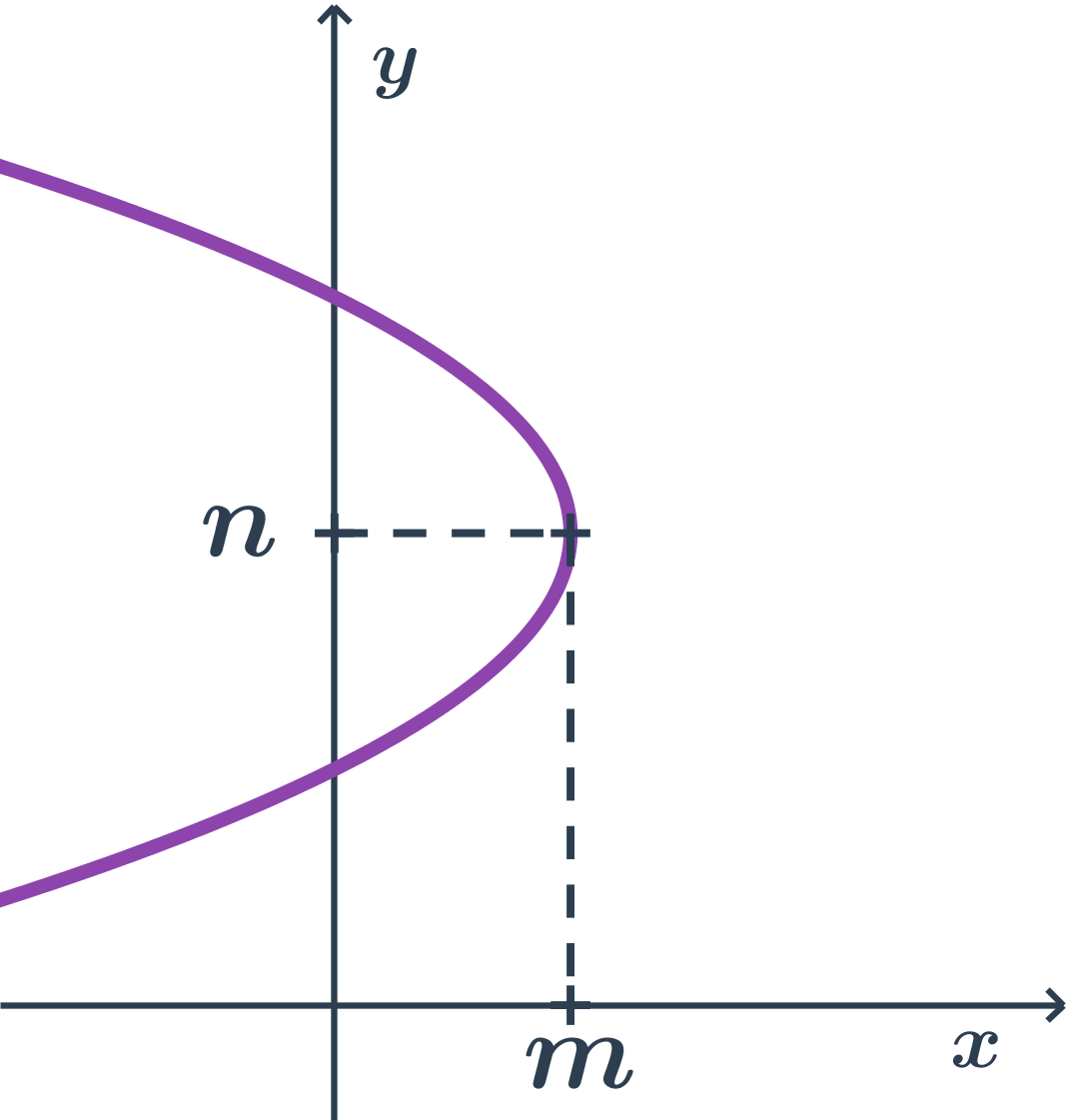
- body paraboly mají x souřadnici nejvýše tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= - 2p(x-m)
Obecná rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly je rovnoběžná s osou y: y=ax^2+bx+c
- osa paraboly je rovnoběžná s osou x: x=ay^2+by+c
Příklad paraboly s osou rovnoběžnou s osou y, obecná rovnice
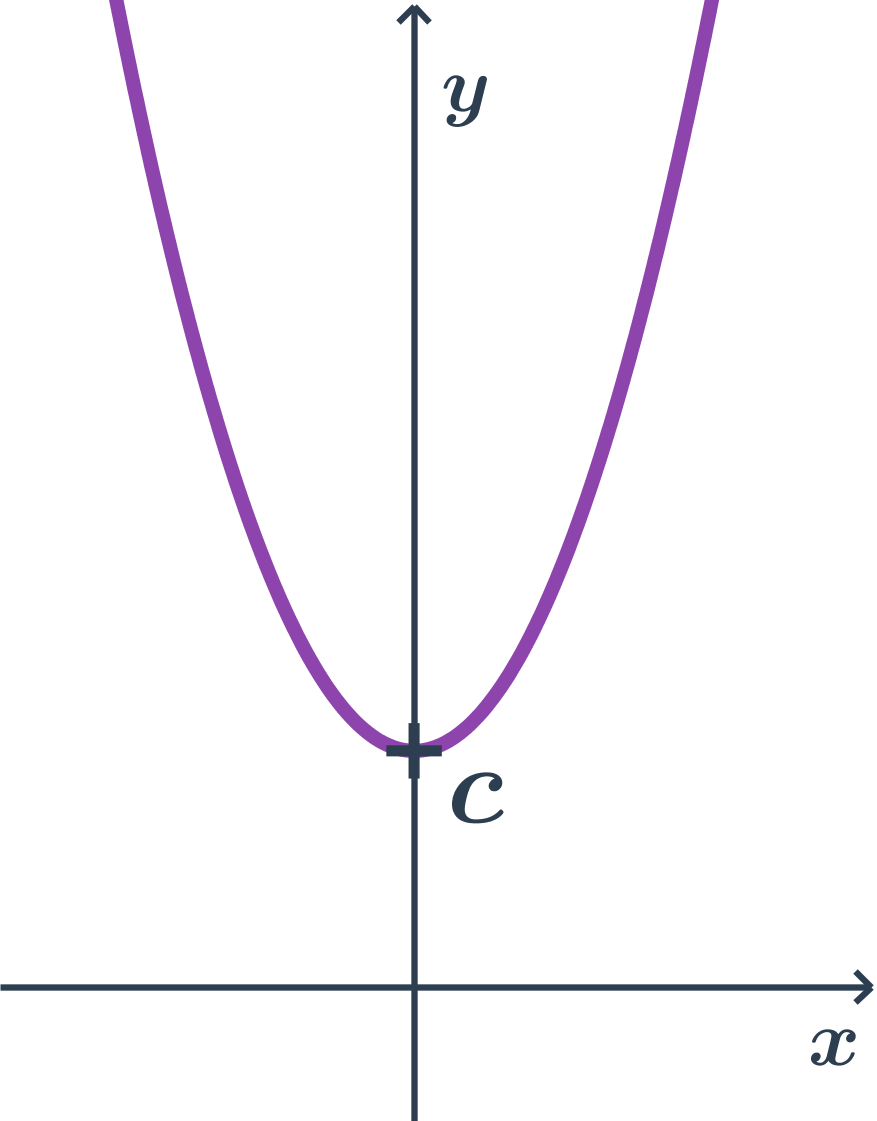
- obecná rovnice: y=ax^2+bx+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace, obecná rovnice
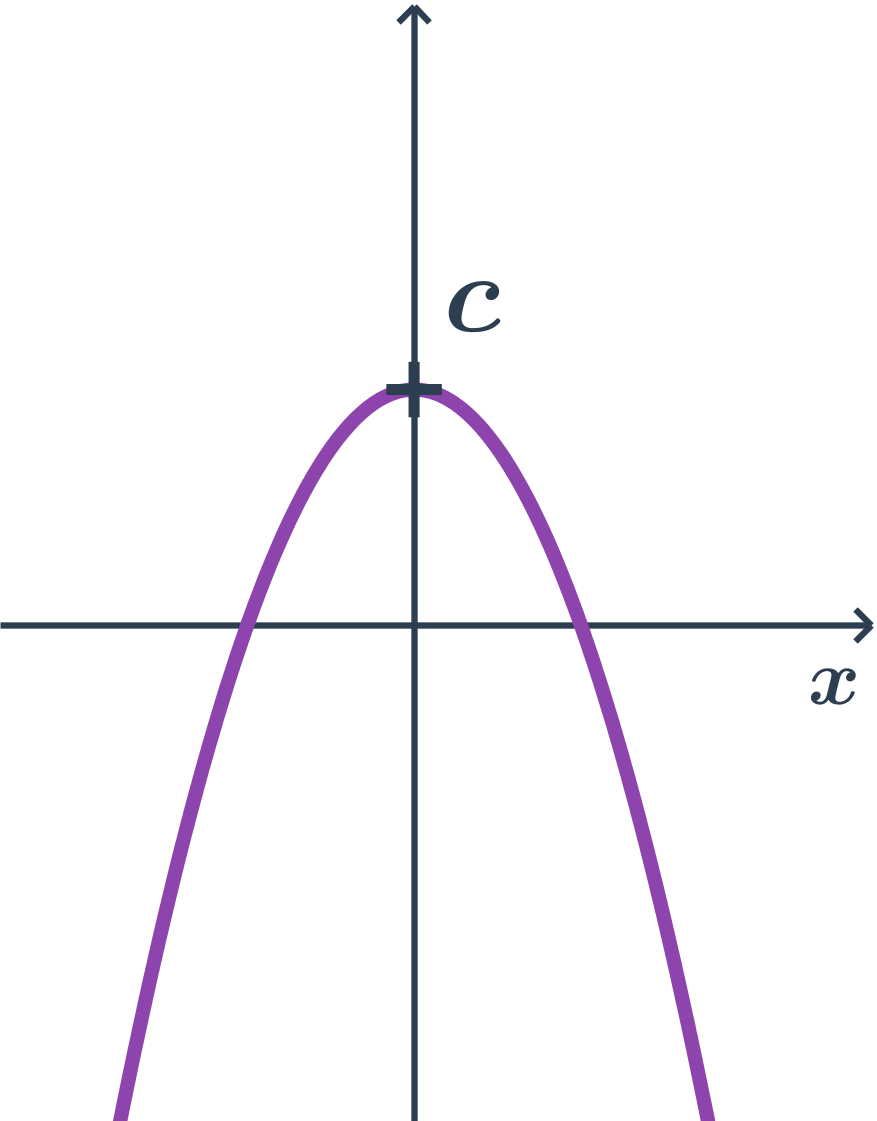
- obecná rovnice: y=ax^2+bx+c
- kde a \lt 0
Příklad paraboly s osou rovnoběžnou s osou x, obecná rovnice
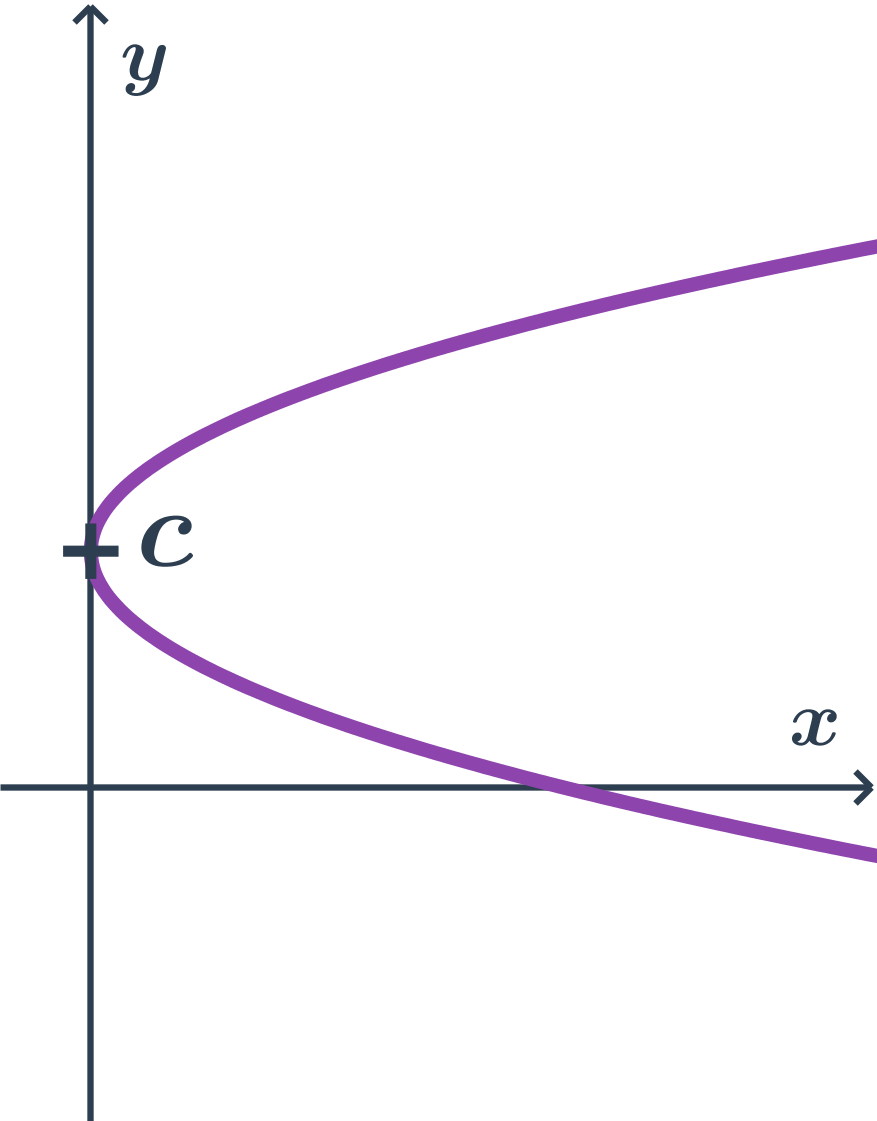
- obecná rovnice: x=ay^2+by+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace, obecná rovnice
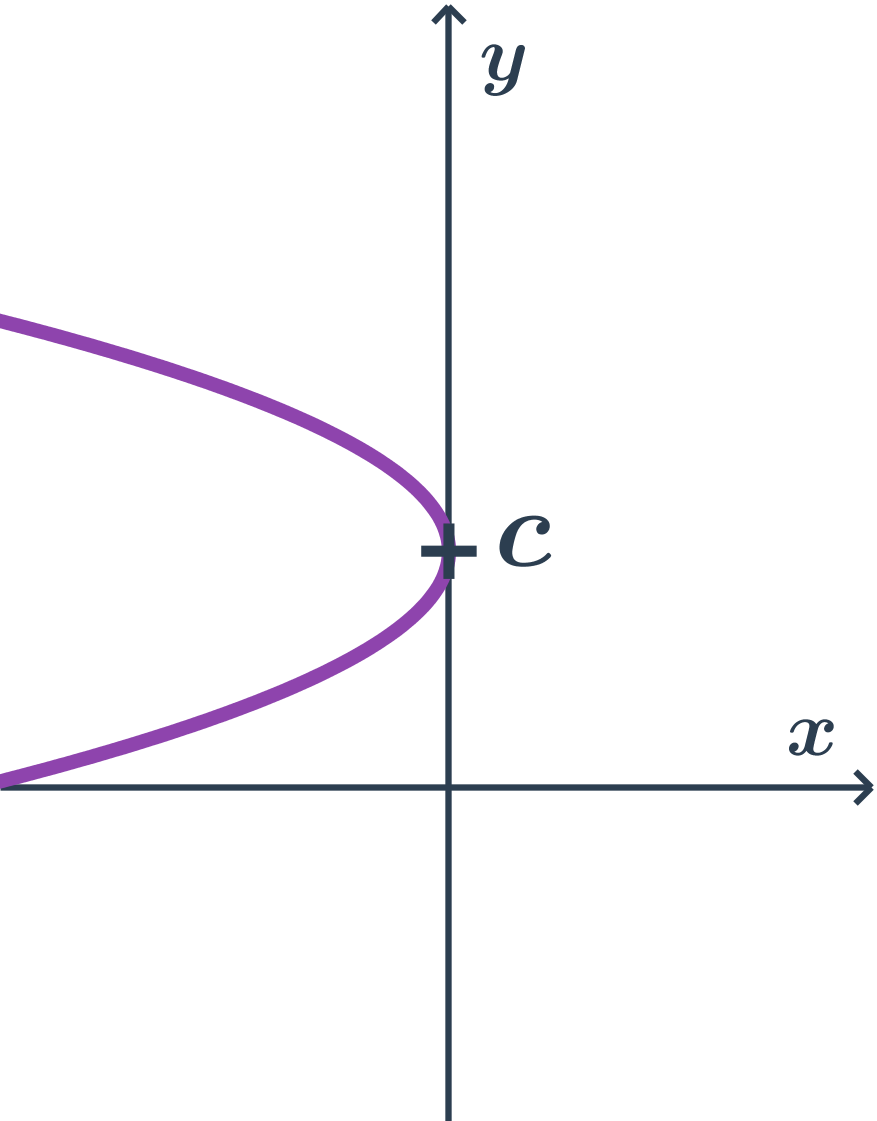
- obecná rovnice: x=ay^2+by+c
- kde a \lt 0
Přímka a parabola
- přímka b protíná parabolu ve dvou bodech – sečna paraboly
- přímka a se dotýká paraboly v jednom bodě – tečna paraboly
- přímka c neprotíná parabolu
Rovnice tečny paraboly v bodě, který leží na parabole
- parabola daná rovnicí (x-m)^2=\pm 2p(y-n) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (x_0 - m)(x - m)=\pm p(y_0 - n) \pm p(y - n)
- parabola daná rovnicí (y-n)^2=\pm 2p(x-m) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (y_0 - n)(y - n)=\pm p(x_0 - m)\pm p(x - m)
Příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2=2(y-1)
- pro tuto parabolu je m=2, n=1, p=1
- na této parabole leží (souřadnice splňují rovnici) například bod T=[4;3]
- tečna dané paraboly v bodě T=[4;3] má rovnici: (4 - 2)(x - 2)= (3 - 1) + (y - 1)
- rovnici tečny můžeme zjednodušit na 2x-4 = y+1, tedy y = 2x-5
Druhý příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2= - 4(y-1)
- pro tuto parabolu je m=2, n=1, p=2, pravá strana je ve formě -2p(y-n)
- na této parabole leží (souřadnice splňují rovnici) například bod T=[6;-3]
- tečna dané paraboly v bodě T=[6;-3] má rovnici: (6-2)(x-2)= -2(-3-1)-2(y-1)
- rovnici tečny můžeme zjednodušit na 4x-8 = 8 -2y+2, tedy y = -2x+9
Speciální poloha přímky a paraboly
Přímka rovnoběžná s osou paraboly je sečna paraboly, přestože se zdá, že má s parabolou jeden společný bod. Druhý společný bod má tato přímka a parabola v nekonečnu.
Hyperbola
Hyperbola je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý rozdíl vzdáleností 2a, který je menší než vzdálenost ohnisek. Hyperbola se skládá ze dvou částí – větví hyperboly. Tyto dvě větve se blíží k přímkám, které nazýváme asymptoty. 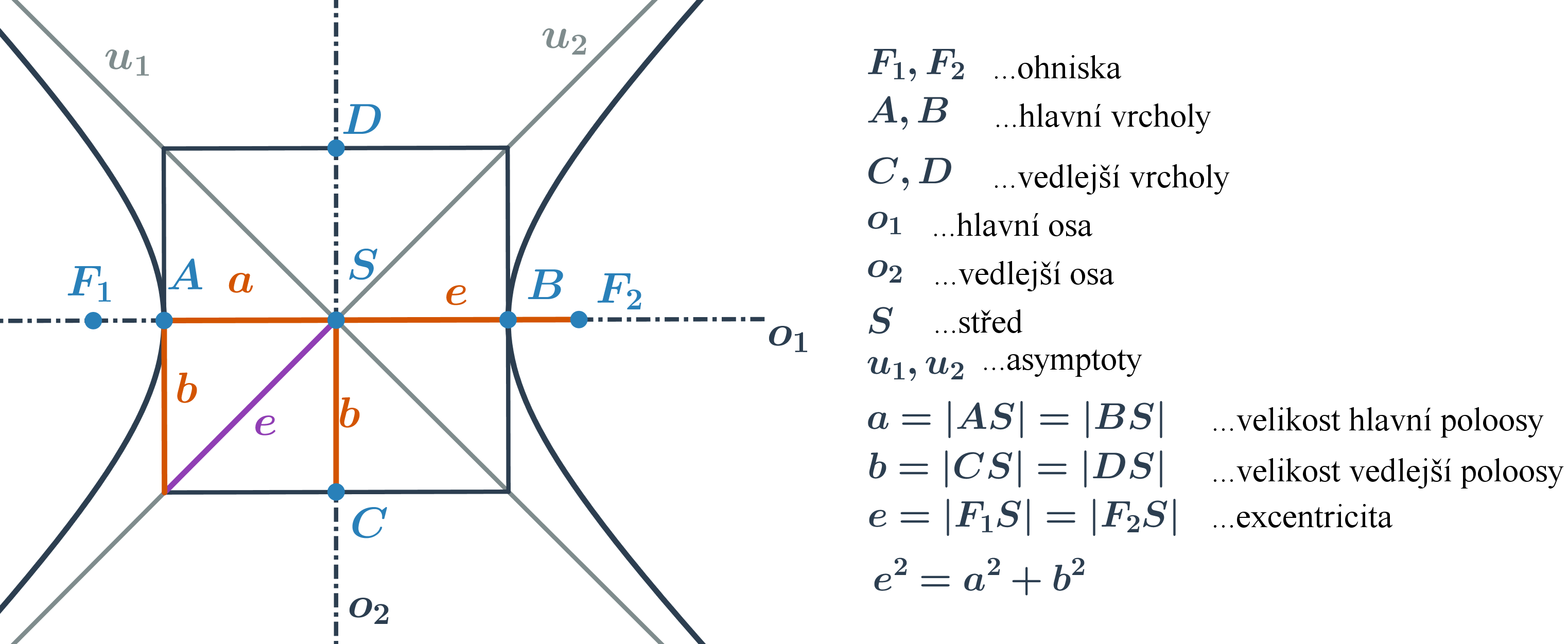
Středová rovnice hyperboly
Tvar středové rovnice hyperboly o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a,b závisí na poloze hlavní osy.
Středová rovnice hyperboly s hlavní osou rovnoběžnou s osou x
Pokud je hlavní osa rovnoběžná s osou x, rovnice je ve tvaru \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1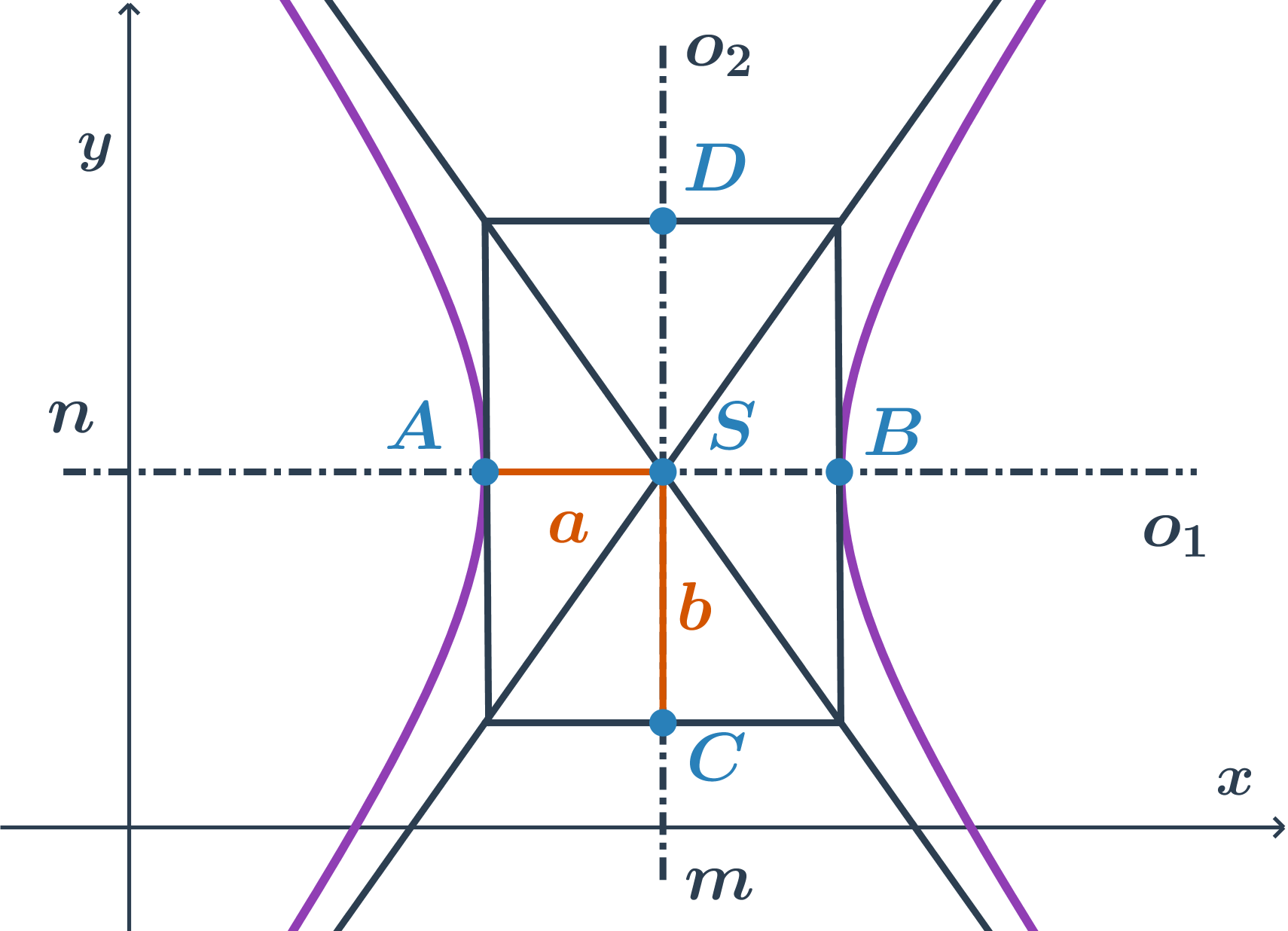
Středová rovnice hyperboly s hlavní osou rovnoběžnou s osou y
Pokud je hlavní osa rovnoběžná s osou y, rovnice je ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1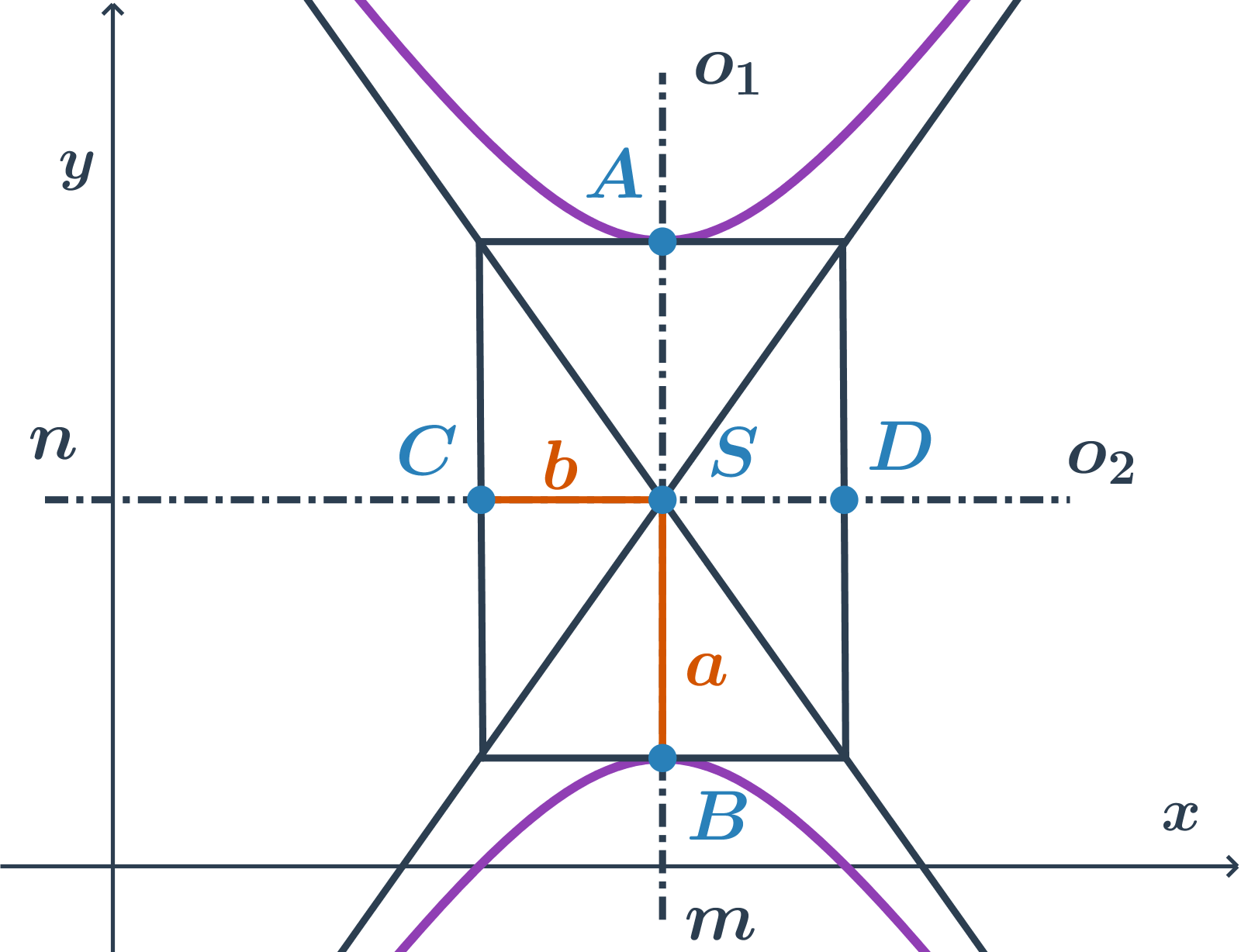
Na rozdíl od elipsy, nemusí být u hyperboly vždy hlavní poloosa a delší než vedlejší poloosa b. Pro rovnoosou hyperbolu dokonce platí a=b.
Jak ze středové rovnice poznat, se kterou souřadnou osou je rovnoběžná hlavní osa hyperboly?
- Podíváme se na znaménka členů s proměnnými x a y.
- Proměnná ve členu, který má před sebou znaménko plus udává, se kterou souřadnou osou je rovnoběžná hlavní osa hyperboly.
- Ve jmenovateli dané proměnné je pak (ve druhé mocnině) velikost hlavní poloosy.
- Stručně řečeno: je-li znaménko plus například u členu s proměnnou x, je hlavní osa rovnoběžná s osou x a ve jmenovateli je druhá mocnina velikosti hlavní poloosy a
Příklad: Určení středové rovnice hyperboly
Určete středovou rovnici hyperboly se středem v bodě S[1;-5], je-li velikost hlavní poloosy 2, velikost vedlejší poloosy 6 a hlavní osa je rovnoběžná s osou y.
- Středová rovnice je ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1. Hlavní poloosa má velikost a, vedlejší b.
- Dosadíme souřadnice středu a velikosti hlavní a vedlejší poloosy. Při dosazení si dáme pozor na to, že souřadnice středu odčítáme: -\frac{(x-1)^2}{6^2} +\frac{(y-(-5))^2}{2^2}=1
- Po úpravě: -\frac{(x-1)^2}{36} +\frac{(y+5)^2}{4}=1
Rovnice asymptot
Už víme, že asymptoty jsou přímky, ke kterým se hyperbola blíží. Pomohou při vykreslení hyperboly. Rovnice asymptot závisí na tvaru středové rovnice hyperboly.
Pro hyperbolu danou rovnicí ve tvaru \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 jsou rovnice asymptot:
y=\pm\frac{b}{a}(x-m)+n
Pro hyperbolu danou rovnicí ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 jsou rovnice asymptot:
y=\pm\frac{a}{b}(x-m)+n
Jak načrtnout hyperbolu?
- Nejprve si vyznačíme střed, hlavní a vedlejší vrcholy.
- Poté sestrojíme charakteristický obdélník hyperboly. To je obdélník, který má strany rovnoběžné s osami a vrcholy hyperboly jsou středy jeho stran. Délky jeho stran jsou tedy 2a a 2b.
- Asymptoty jsou úhlopříčky charakteristického obdélníku.
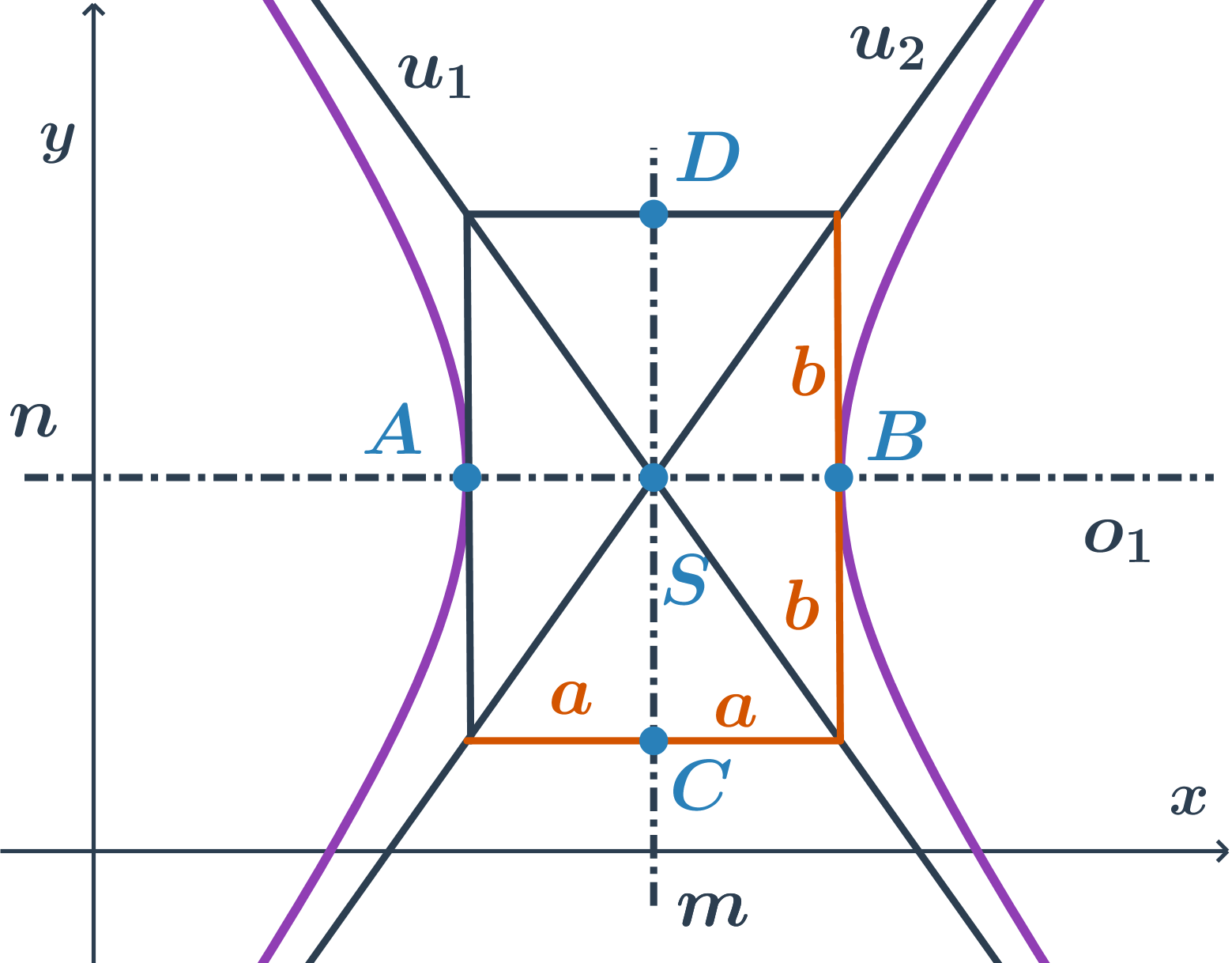
Obecná rovnice hyperboly
Podobně jako existuje několik rovnic elipsy, můžeme i rovnici hyperboly zapsat různými způsoby. Obecná rovnice hyperboly je ve tvaru: Ax^2 +By^2+Cx+Dy+E=0, A\cdot B \lt 0. Podmínka A\cdot B \lt 0 zaručuje, že konstanty A, B mají opačná znaménka. Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí hyperboly. Praktické ověření, zda se jedná o hyperbolu provádíme převedením na středovou rovnici.
Příklad: Určuje daná rovnice hyperbolu?
Rozhodněte, zda rovnice -x^2+2y^2+8x-18y+31=0 určuje hyperbolu.
- Nejprve si uspořádáme členy: -x^2+8x+y^2-18y+40=0.
- Ze členů s proměnnou x vytkneme -1: -(x^2-8x)+y^2-18y+40=0
- K oběma stranám rovnice přičteme konstantu 81 a odečteme konstantu 16, abychom členy s proměnnými x a y mohli upravit podle vztahu pro (a\pm b)^2: -(x^2-8x+16)+y^2-18y+81+40=81-16
- A upravíme: -(x-4)^2 +(y-9)^2+40=65
- Převedeme konstantu 40 na druhou stranu rovnice: -(x-4)^2 +(y-9)^2 =25
- Na závěr rovnici vydělíme 25: -\frac{(x-4)^2}{25} +\frac{(y-9)^2}{25}=1
- Jedná se tedy o hyperbolu. Hlavní osa je rovnoběžná s osou y a a=b=5.
Hyperbola a přímka
- přímka s protíná hyperbolu ve dvou bodech – sečna hyperboly
- přímka t protíná hyperbolu v jednom bodě – tečna hyperboly
- přímka v hyperbolu neprotíná – vnější přímka hyperboly
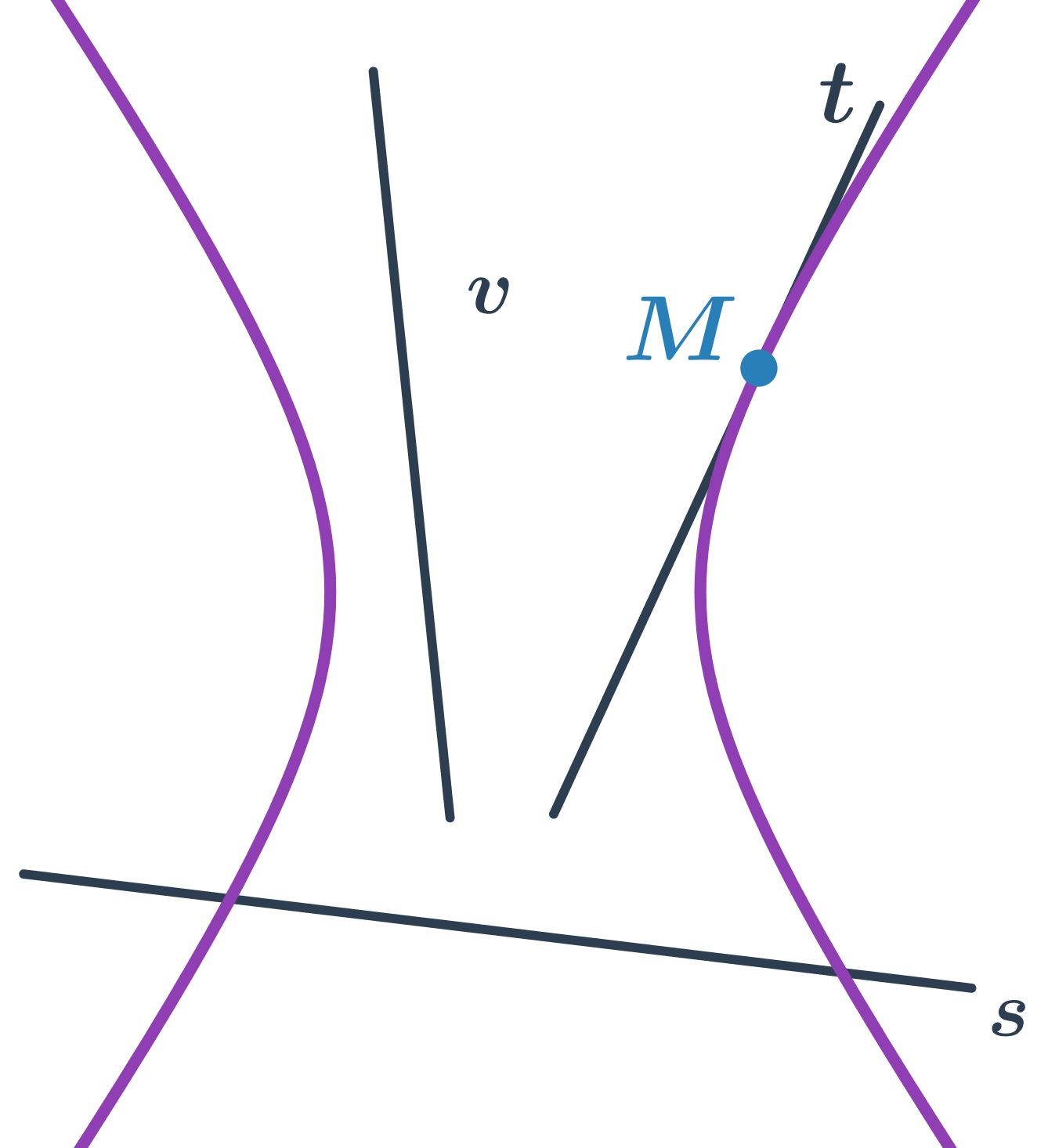
Speciální polohou sečny hyperboly je přímka, která je rovnoběžná s asymptotou. Taková sečna pak protíná hyperbolu v jednom bodě. 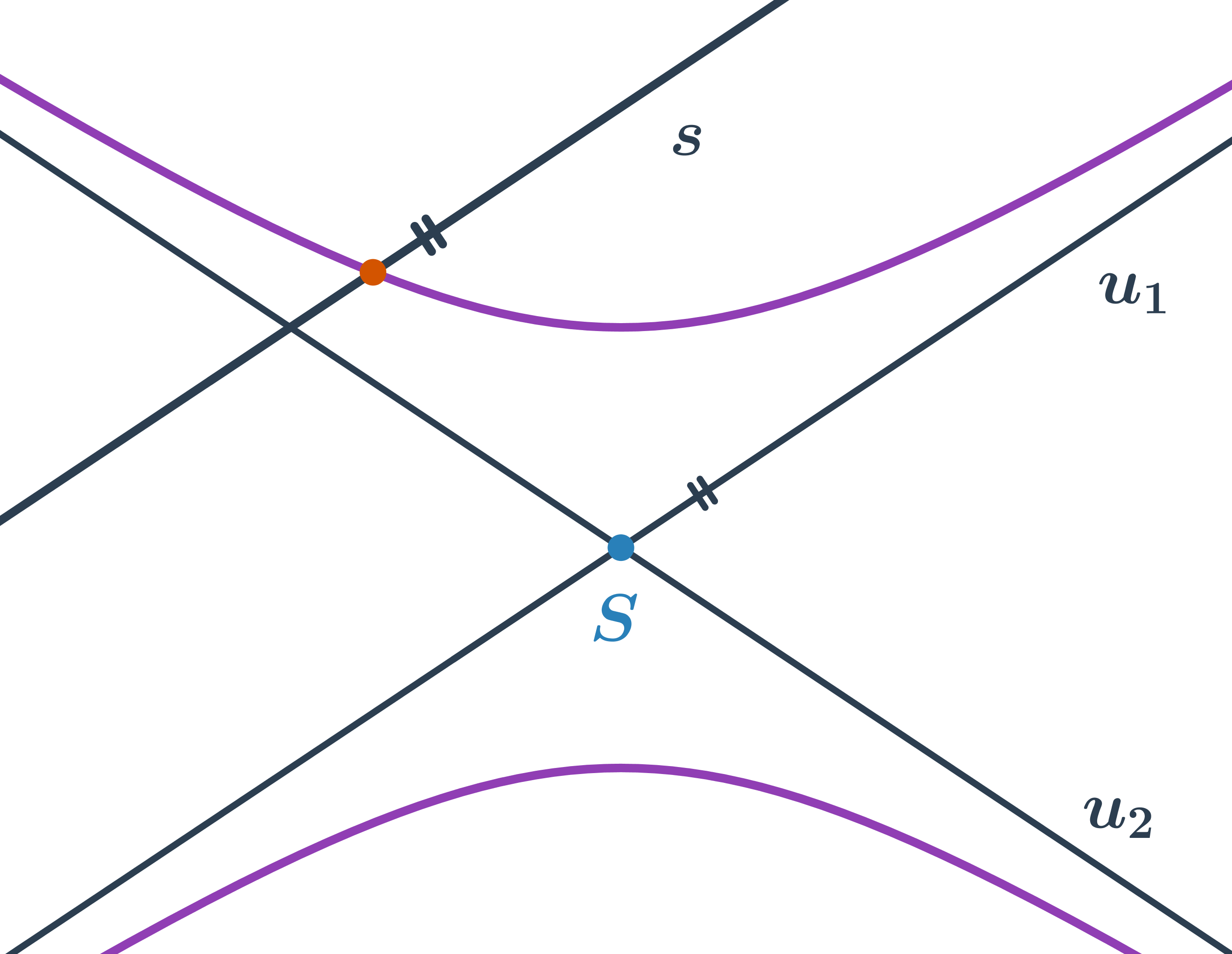
Jak rozlišit, je-li přímka tečna nebo sečna?
- Nejprve určíme vzájemnou polohu přímky a hyperboly.
- Pokud vyjdou dva průsečíky, jedná se o sečnu v obecné poloze.
- Pokud vyjde jeden průsečík, musíme ještě rozhodnout, jestli je přímka rovnoběžná s asymptotou. Pokud ne, jedná se o tečnu. V opačném případě jde o sečnu.
Rovnice tečny hyperboly v bodě, který leží na hyperbole
Hyperbola daná rovnicí \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 má v bodě T[x_0;y_0] tečnu danou rovnicí:
\frac{(x-m)(x_0-m)}{a^2} -\frac{(y-n)(y_0-n)}{b^2}=1.
Podobně můžeme zapsat i rovnici tečny hyperboly, která má hlavní osu rovnoběžnou s osou y.
Nahoru