Parametrické rovnice roviny

GSO

umime.to/GSO

Pro určení parametrických rovnic roviny potřebujeme znát souřadnice jednoho bodu a dvou nekolineárních vektorů v rovině \alpha. Rovina určená bodem A=[a_1;a_2;a_3] a vektory \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:

\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}

Zkráceně můžeme vyjádřit \alpha:X=A+t\vec{u}+s\vec{v}, kde t,s \in \mathbb{R} jsou parametry.

Parametrické rovnice roviny určené třemi body

Určete parametrické rovnice roviny \alpha určené body A=[3;2;1], B=[1;3;4], C=[2;-3;3].

rovina \alpha je určená bodem A a vektory \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{AC}:
\vec{u}=\overrightarrow{AB}=B-A=(-2;1;3)
\vec{v}=\overrightarrow{AC}=C-A=(-1;-5;2)
parametrické rovnice roviny \alpha jsou:

\begin{array}{rrl}x&=&3-2t-s\\y&=&2+t-5s\\z&=&1+3t+2s\\&&t,s\in\mathbb{R}\end{array}

Parametrické rovnice roviny určené bodem a dvěma vektory

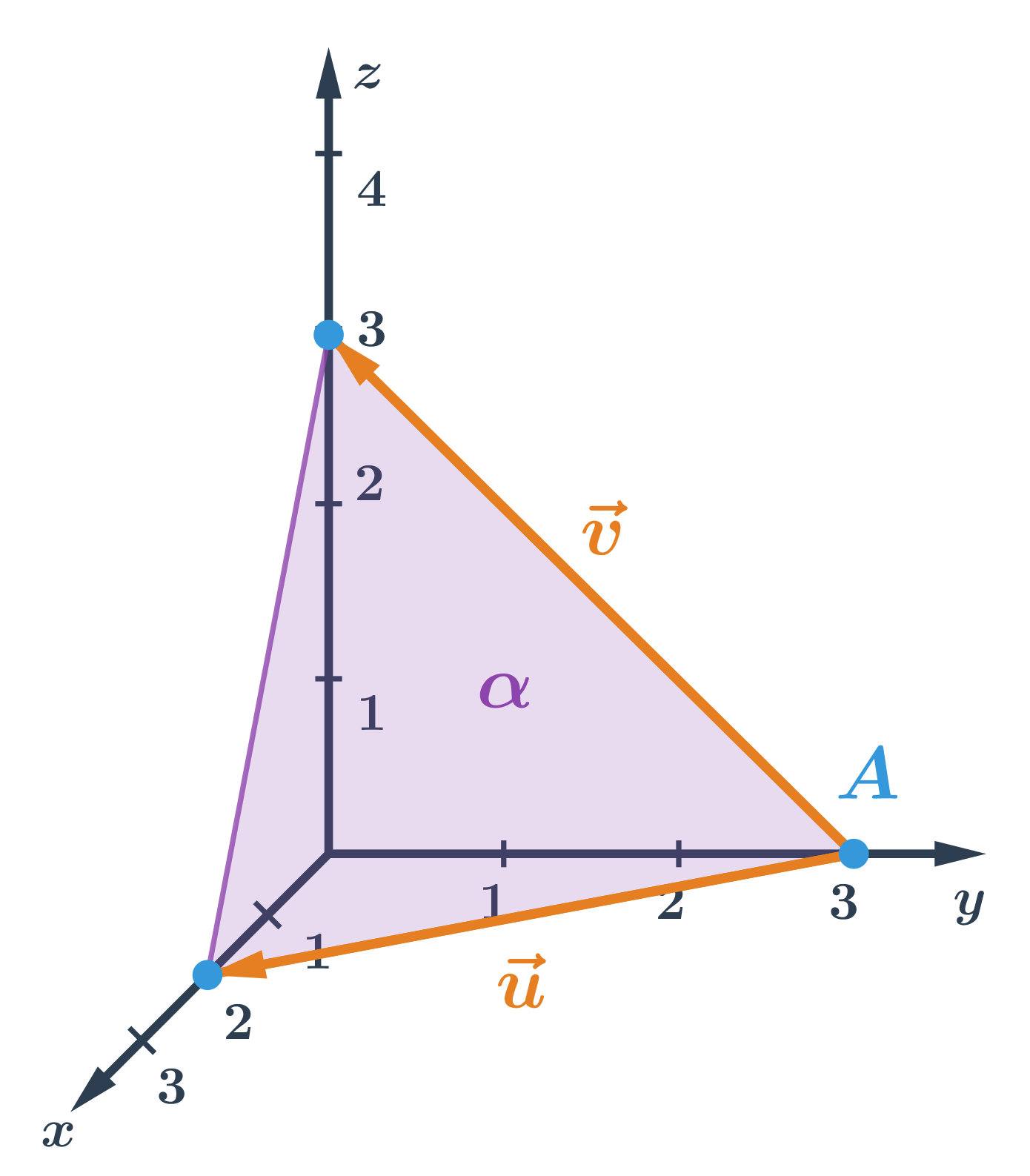
rovina \alpha je určená bodem A a vektory \vec{u}, \vec{v}
souřadnice určíme z obrázku:
- A=[0;3;0],
- \vec{u}=(2;-3;0),
- \vec{v}=(0;-3;3)
parametrické rovnice roviny \alpha jsou:

\begin{array}{rrl}x&=&2t\\y&=&3-3t-3s\\z&=&3s\\&&t,s\in\mathbb{R}\end{array}

Parametrické rovnice roviny určené různoběžkami p a q

Určete parametrické rovnice roviny určené dvěma různoběžkami s následujícími parametrickými rovnicemi:

p:\begin{array}{rrl}x&=&2+3t\\y&=&1+2t\\z&=&4-4t\\&&t\in\mathbb{R}\end{array}, q:\begin{array}{rrl}x&=&2+4s\\y&=&1-2s\\z&=&4-5s\\&&s\in\mathbb{R}\end{array}

rovina \alpha je určená společným bodem různoběžek a směrovými vektory přímek p a q
- společný bod různoběžek: R=[2;1;4],
- směrový vektor přímky p:\vec{u}=(3;2;4),
- směrový vektor přímky q:\vec{v}=(4;-2;-5)
parametrické rovnice roviny \alpha jsou:

\begin{array}{rrl}x&=&2+3t+4s\\y&=&1+2t-2s\\z&=&4-4t-5s\\&&t,s\in\mathbb{R}\end{array}

Souhrn je skryt.

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Parametrické rovnice roviny

Rozhodovačka • těžké

Předcházející

Navazující

Cvičení

Parametrické rovnice roviny

umime.to/GSO

Rozhodovačka