Konstrukce trojúhelníků: známé délky stran

F9P

umime.to/F9P

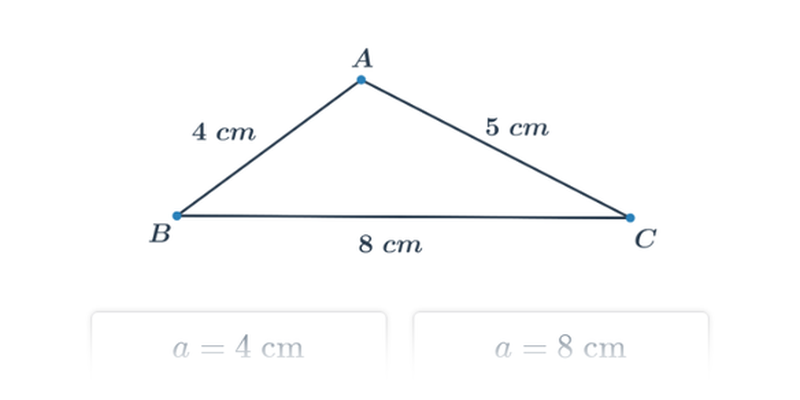
Při konstrukci trojúhelníků můžeme každou stranu označit dvěma způsoby:

přímo – strana a
pomocí vrcholů – strana BC

Při konstrukcích také můžeme zaměňovat označení strany a její délky. Můžeme psát a=|BC|. Je třeba myslet i na pravidlo, že strana je pojmenovaná podle protějšího vrcholu.

Příklad: Je v trojúhelníku na obrázku délka strany a=8 cm?

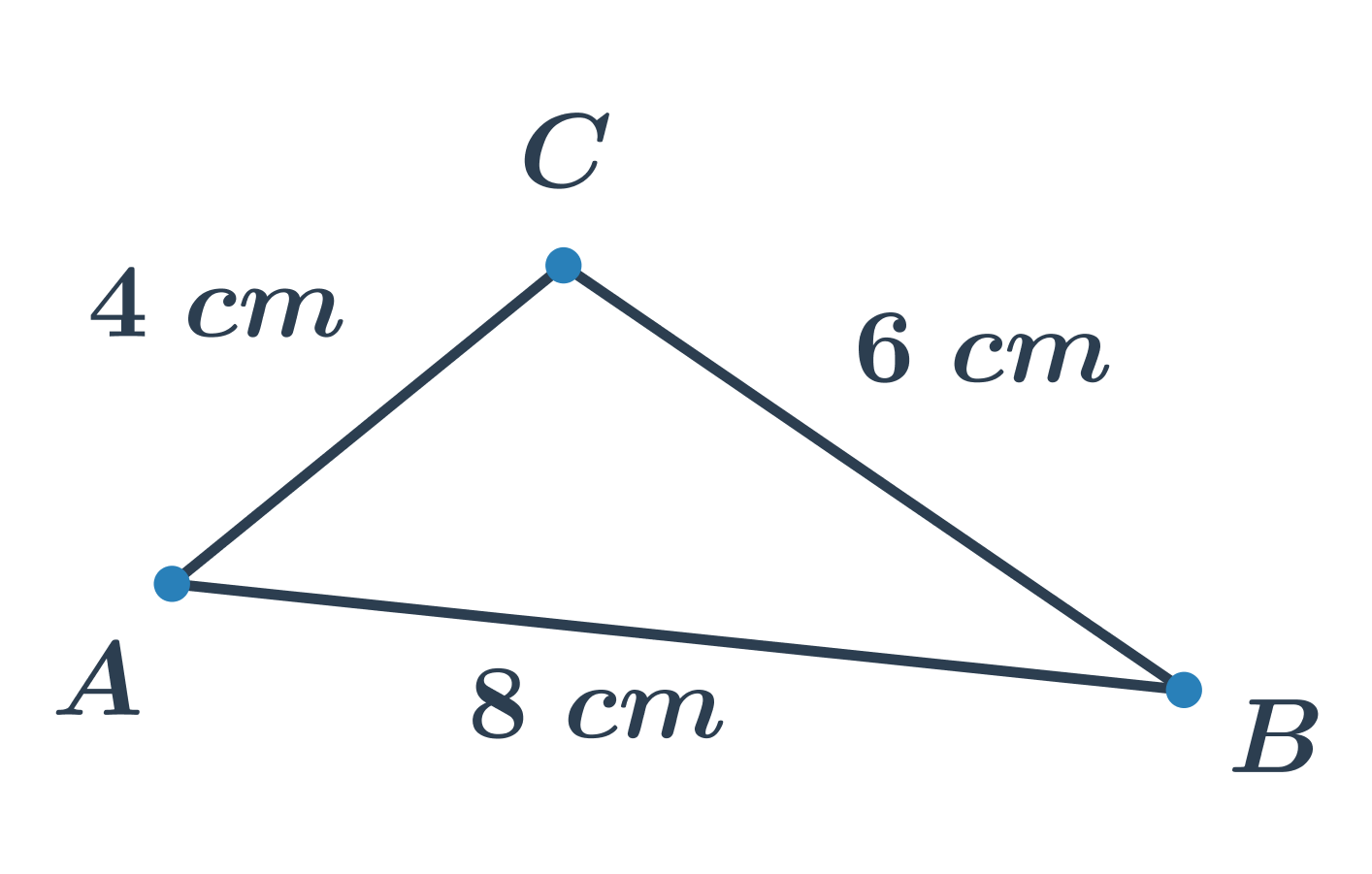
Strana a leží proti vrcholu A. Je to tedy strana BC.
Z obrázku vidíme, že |BC|=6 cm.
Strana a tedy nemá délku 8 cm.
Délku 8 cm má v tomto trojúhelníku strana AB, tedy strana c.

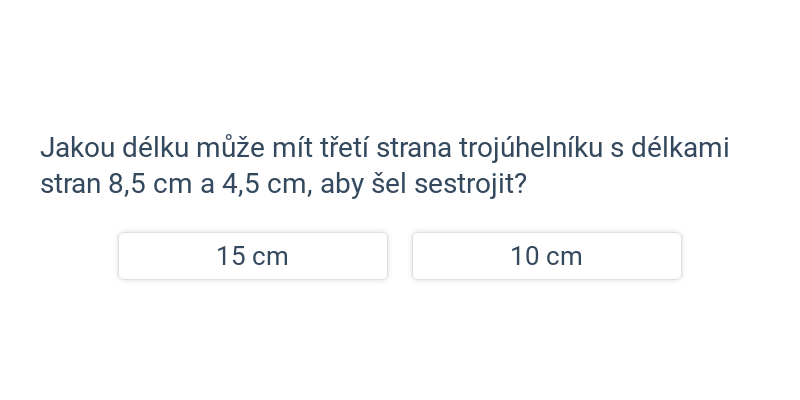
Lze sestrojit trojúhelník se stranami zadané délky?

6\ \text{cm}, 5\ \text{cm}, 4\ \text{cm} - součet dvou nejkratších stran je 4 + 5= 9 \ \text{cm}, to je více než 6\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.
6\ \text{cm}, 5\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 5 = 6\ \text{cm}, to je rovno délce třetí strany, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
5\ \text{cm}, 2\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 2 = 3\ \text{cm}, to je menší než délka třetí strany 5\ \text{cm}, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
7\ \text{cm}, 7\ \text{cm}, 7\ \text{cm} - součet dvou nejkratších stran je 7 + 7= 14\ \text{cm}, to je více než 7\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.

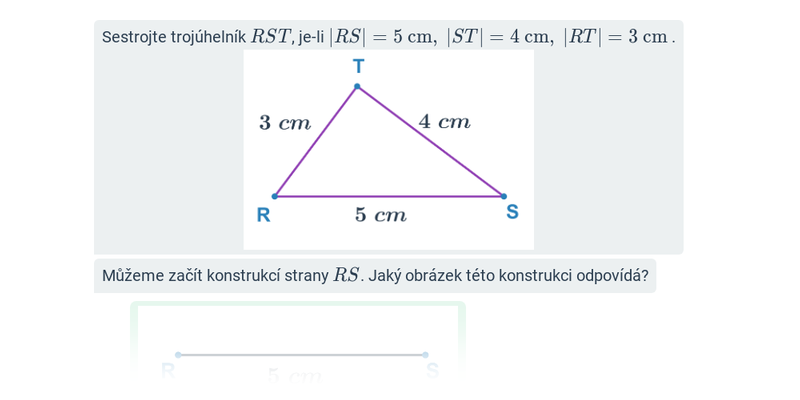
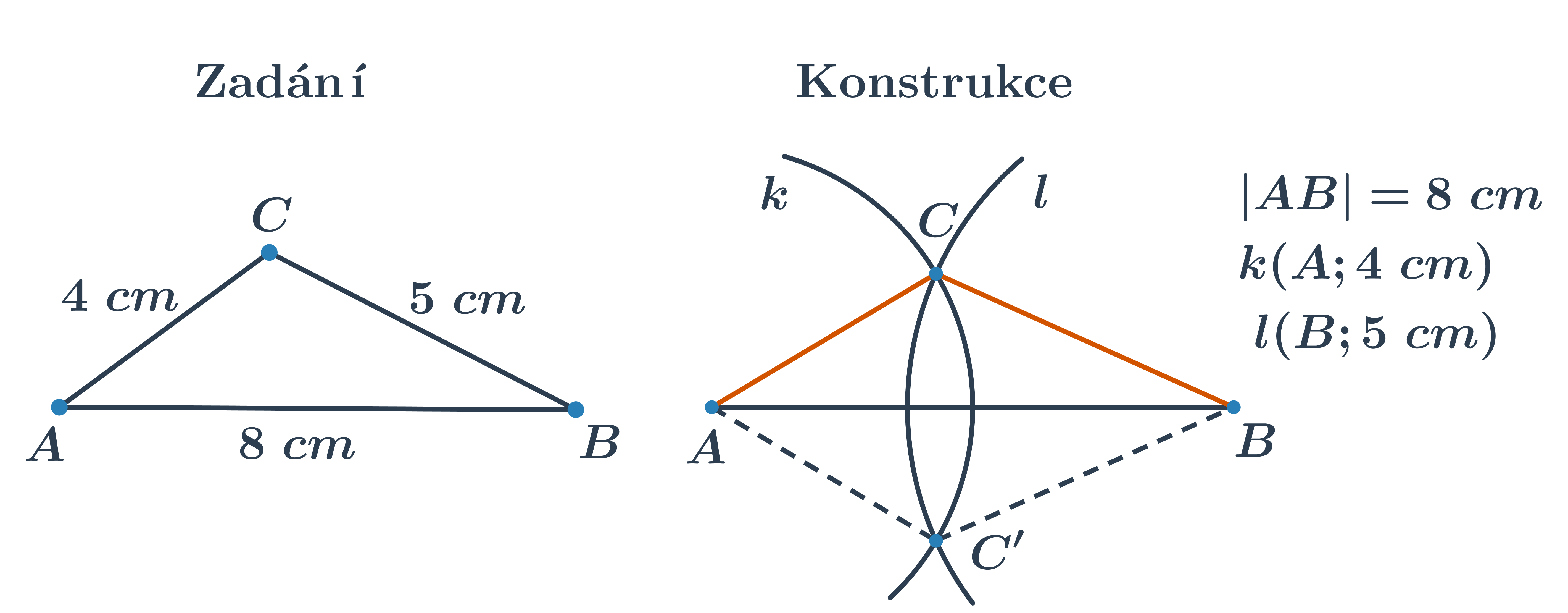
Při konstrukcích trojúhelníků, u kterých známe tři strany, postupujeme tak, že sestrojíme jako první libovolnou stranu, na obrázku například AB. K nalezení posledního vrcholu C použijeme dvě kružnice nebo jejich části. Výsledkem konstrukce jsou dva shodné (stejné) trojúhelníky, proto stačí sestrojit jen jeden.