Čeština
Angličtina
Informatika
Biologie
Umíme to
Němčina
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Cvičení
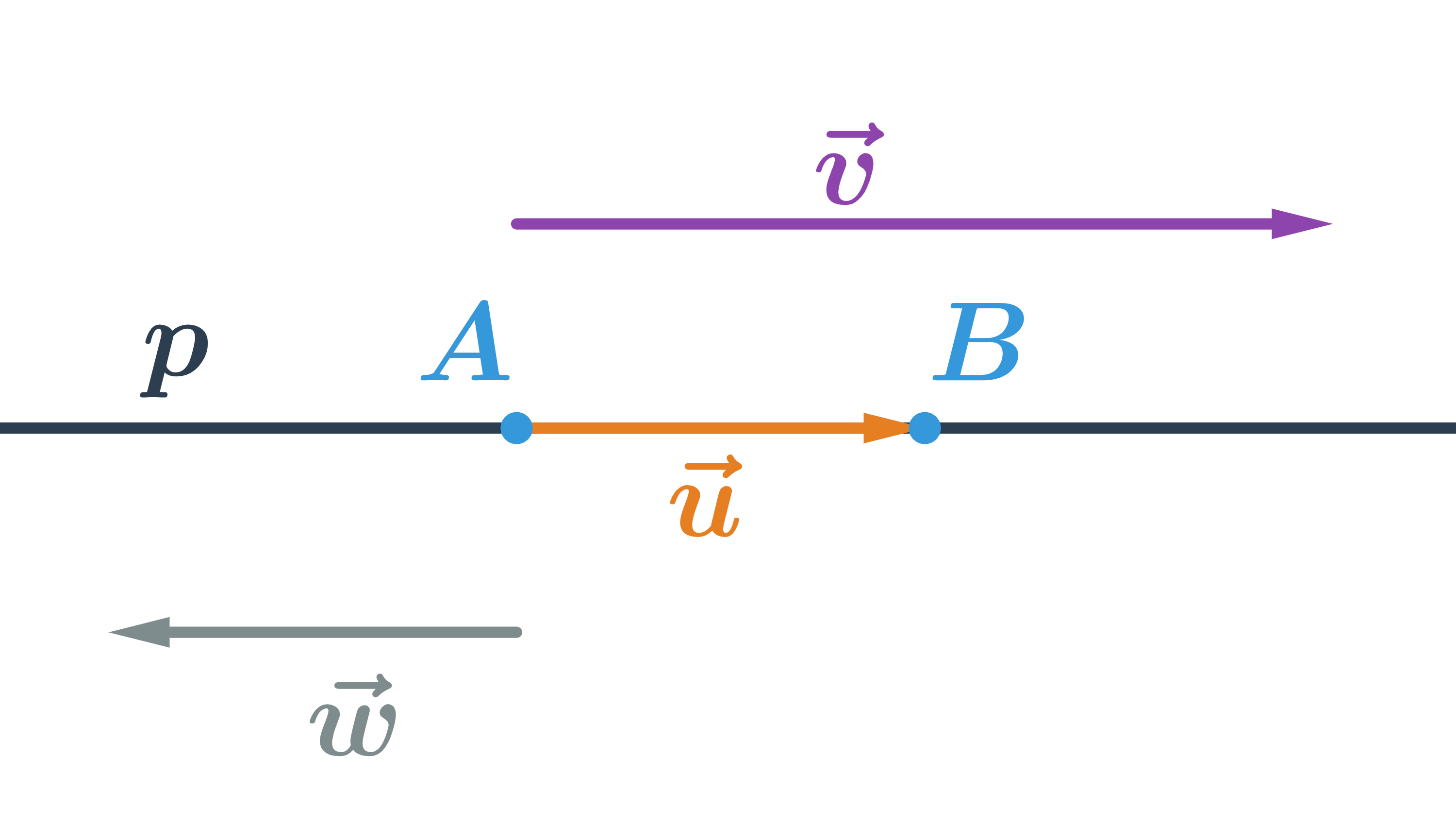
Přímka je jednoznačně určena dvěma body, na obrázku je přímka p určená body A a B. Každý vektor, který je rovnoběžný s vektorem \overrightarrow{AB} se nazývá směrový vektor přímky p. Kterýkoliv z vektorů na obrázku je směrový vektor přímky p. K tomu, abychom určili konkrétní přímku ještě potřebujeme znát jeden bod na přímce (přímka p na obrázku je určena bodem A a kterýmkoliv z vektorů \vec{u}, \vec{v}, \vec{w}).
Parametrické rovnice přímky
Přímka určená bodem A=[a_1;a_2] a vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array} Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr.
Jak souvisí hodnota parametru t s polohou bodu na přímce
- Přímka p je určená bodem A a vektorem \vec{u}=\overrightarrow{AB}, tedy p:X=A+t\vec{u}
- Pro hodnotu t=0 dostaneme: X=A+t\vec{u}=A+0\cdot \vec{u} … bod A
- Pro hodnotu t=1 dostaneme: X=A+t\vec{u}=A+1\cdot \vec {u} … bod B
- Pro hodnotu t=2 dostaneme: X=A+t\vec{u}=A+2\cdot \vec {u} … bod C
- Pro hodnotu t=\frac{1}{2} dostaneme: X=A+t\vec{u}=A+\frac{1}{2}\cdot \vec{u} … bod D (střed úsečky AB)
- Pro hodnotu t=-1 dostaneme: X=A+t\vec{u}=A-1\cdot \vec{u} … bod E
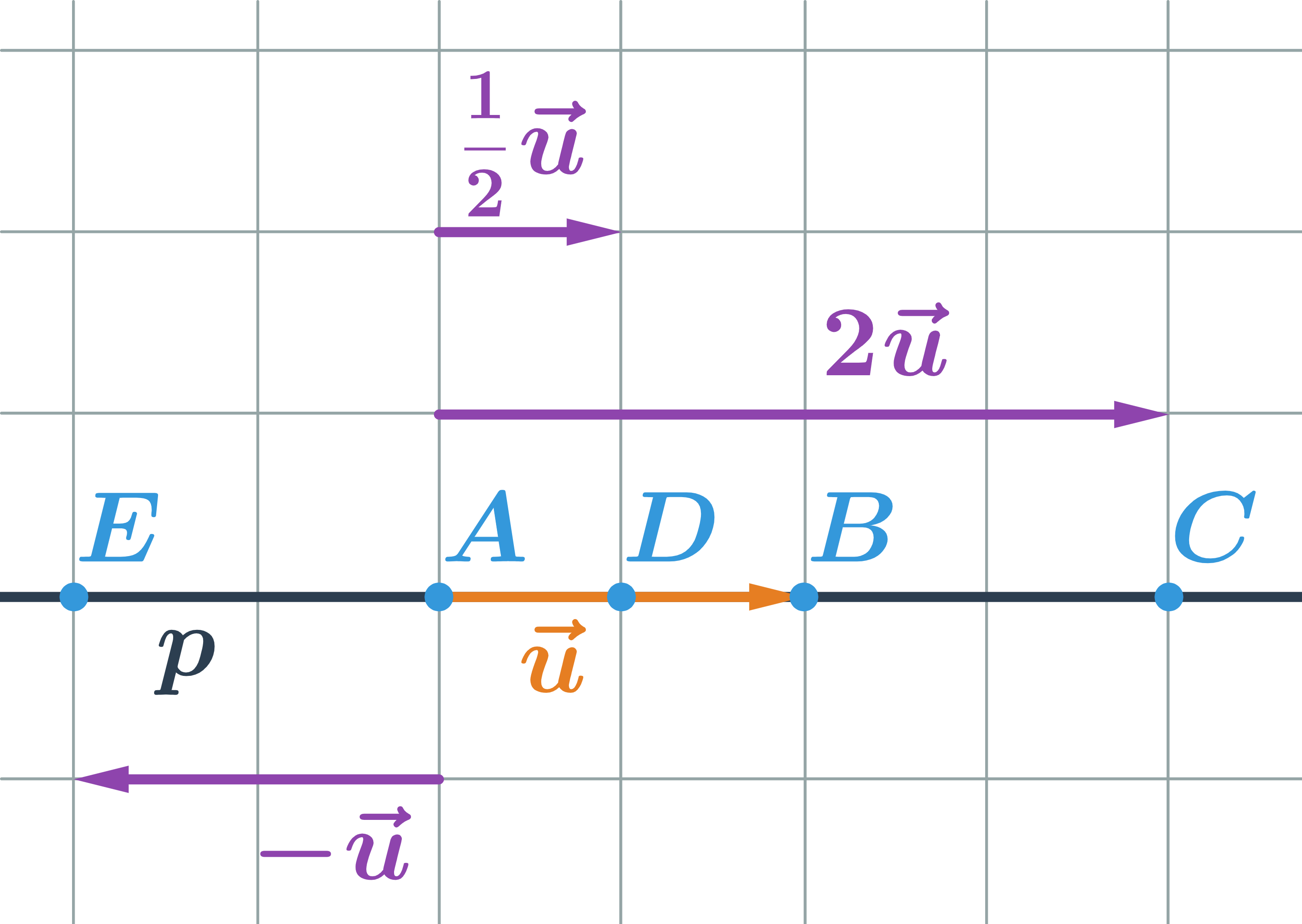
- Každá hodnota parametru určuje jeden bod na přímce, pro určení celé přímky tedy potřebujeme všechna reálná čísla, proto píšeme t\in\mathbb{R}.
- Body, které leží na úsečce AB (tedy body ležící mezi body A a B), vyjádříme parametricky, pokud do rovnice X=A+t\vec{u} dosadíme hodnoty parametru t splňující 0\leq t\leq1.
Obecná rovnice přímky
Každý vektor kolmý k přímce p se nazývá normálový vektor přímky p. Obecná rovnice přímky je rovnice ve tvaru: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.
Souřadnice směrového a normálového vektoru přímky p
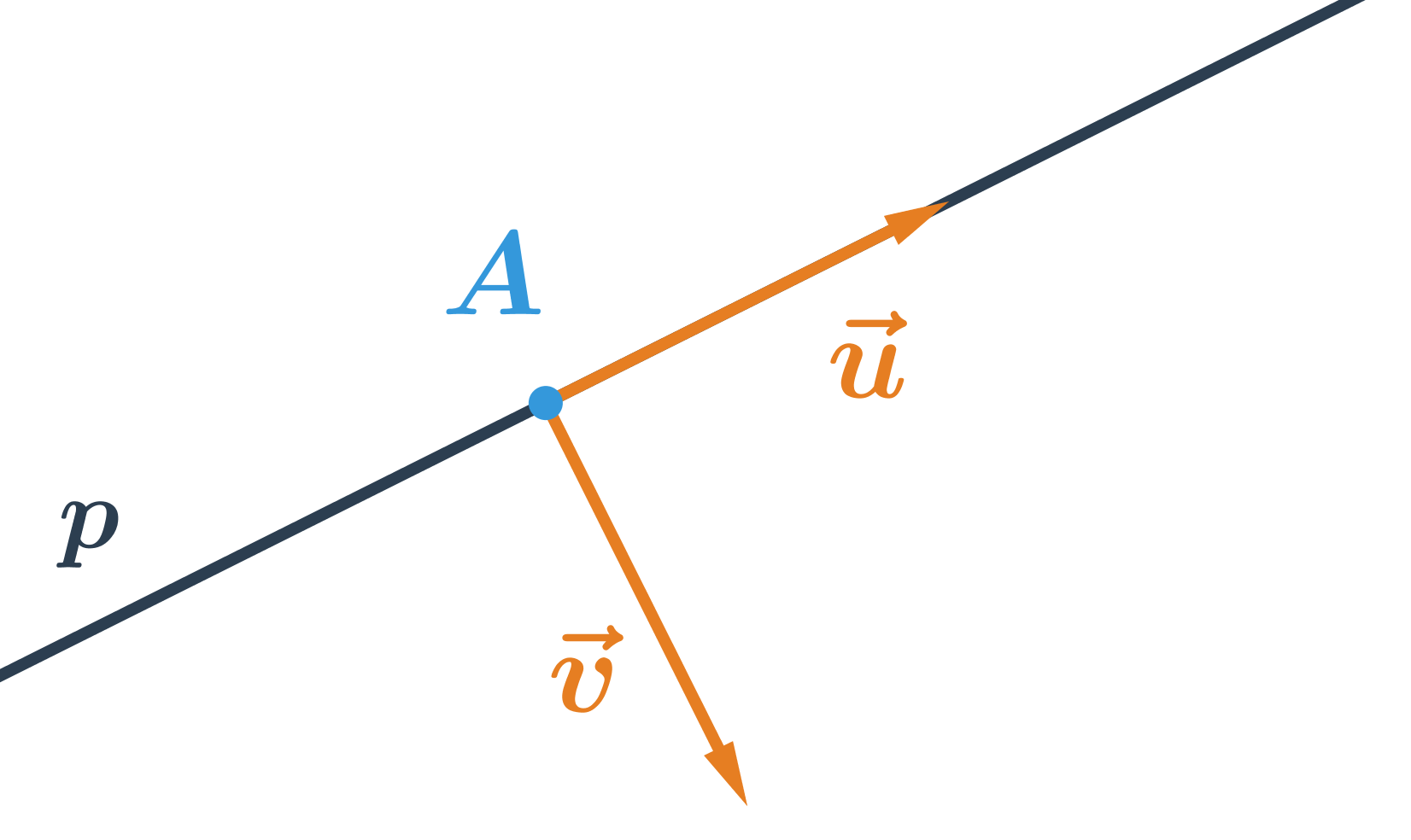
- Pro přímku danou obecnou rovnicí ax+by+c=0:
- \vec{v} je normálový vektor přímky p, jeho souřadnice jsou: \vec{v}=(a;b)
- \vec{u} je směrový vektor přímky p, protože je to vektor kolmý k vektoru \vec{v}=(a;b), jeho souřadnice jsou: \vec{u}=(-b;a)
- Pro přímku danou parametricky: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
- \vec{u} je směrový vektor přímky p, jeho souřadnice jsou: \vec{u}=(u_1;u_2)
- \vec{v} je normálový vektor přímky p, protože je to vektor kolmý k vektoru \vec{u}=(u_1;u_2), jeho souřadnice jsou: \vec{v}=(-u_2;u_1)
Obecná rovnice přímky rovnoběžné s osou x
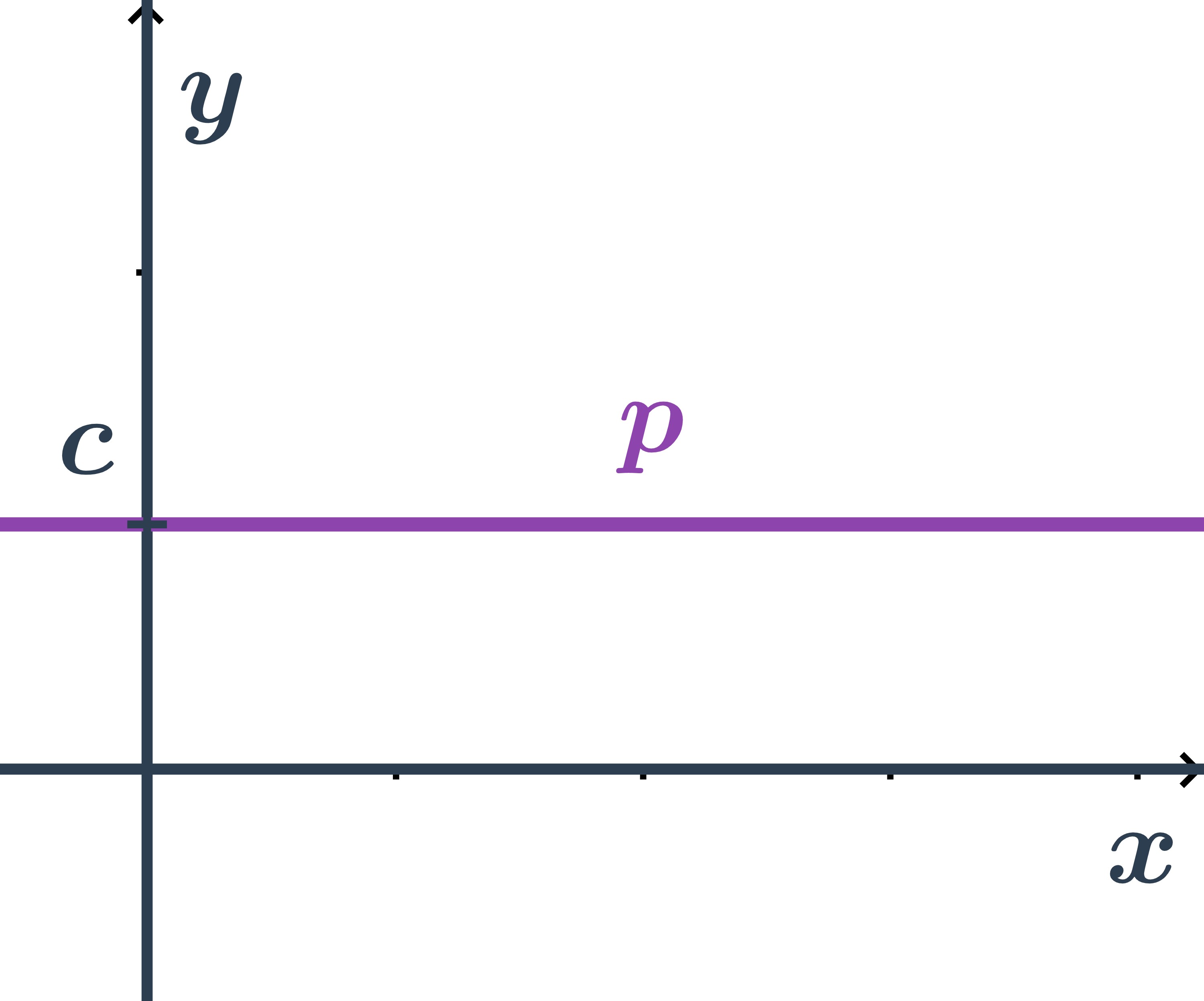
- Pro všechny body ležící na přímce je druhá souřadnice stejná a to: y=c
- Tedy přímka má obecnou rovnici: y-c=0
Obecná rovnice přímky rovnoběžné s osou y
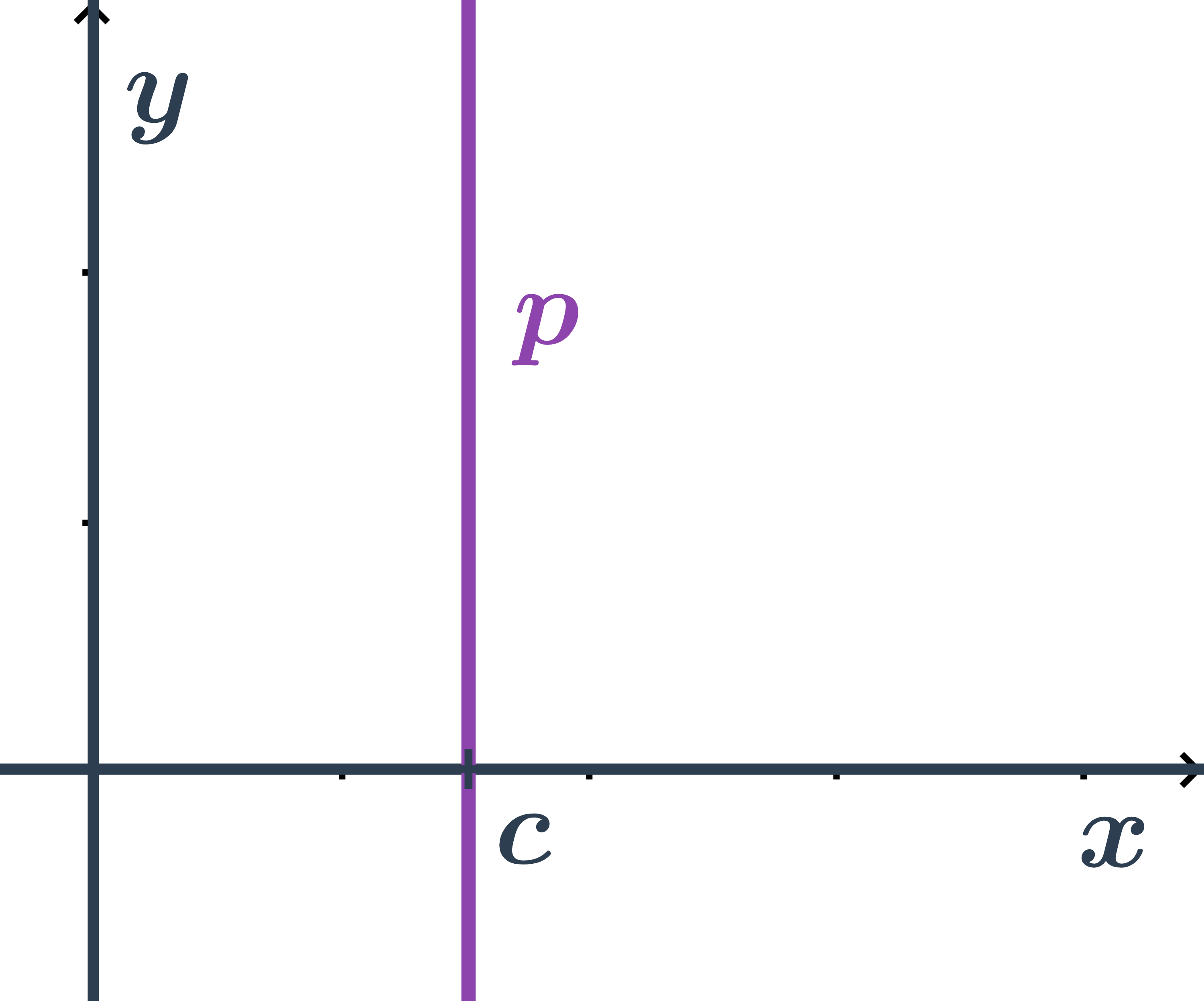
- Pro všechny body ležící na přímce je první souřadnice stejná a to: x=c
- Tedy přímka má obecnou rovnici: x-c=0
Bod a přímka
Bod M=[m_1;m_2] leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky. Pokud je přímka daná obecnou rovnicí ax+by+c=0, pro souřadnice bodu, který leží na přímce platí: a\cdot m_1+b\cdot m_2+c=0 Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t. (Více o vzájemné poloze bodu a přímky.)
Obecná rovnice přímky, která prochází počátkem
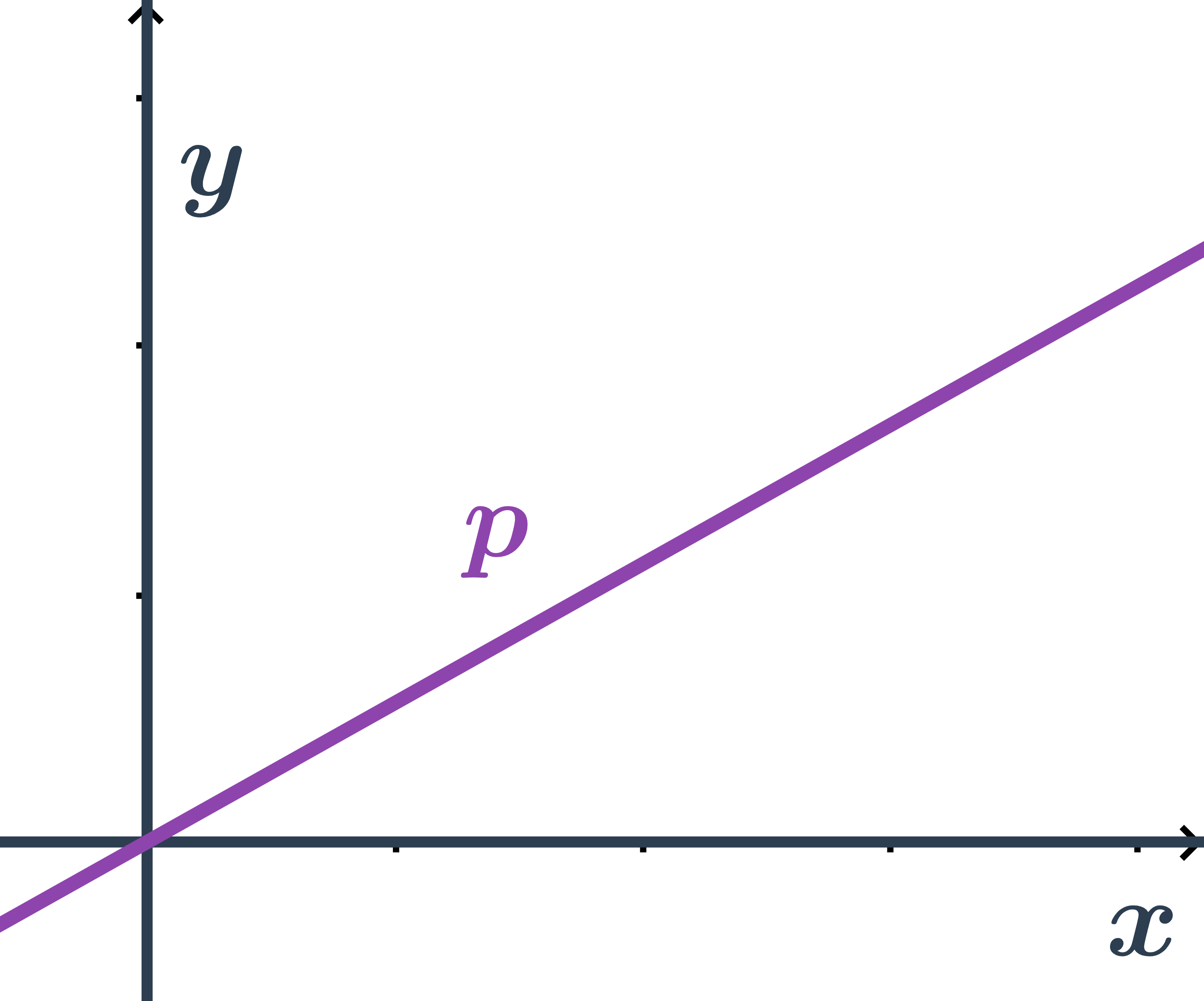
- Přímka prochází bodem O=[0;0], tedy souřadnice počátku splňují její obecnou rovnici ax+by+c=0.
- Dosadíme souřadnice bodu O a zkusíme zjistit nějaké informace o konstantách a,b,c.
- a\cdot0+b\cdot0+c=0\Leftrightarrow c=0
- Proto přímka, která prochází počátkem má obecnou rovnici ax+by=0.
Dvě přímky
Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.
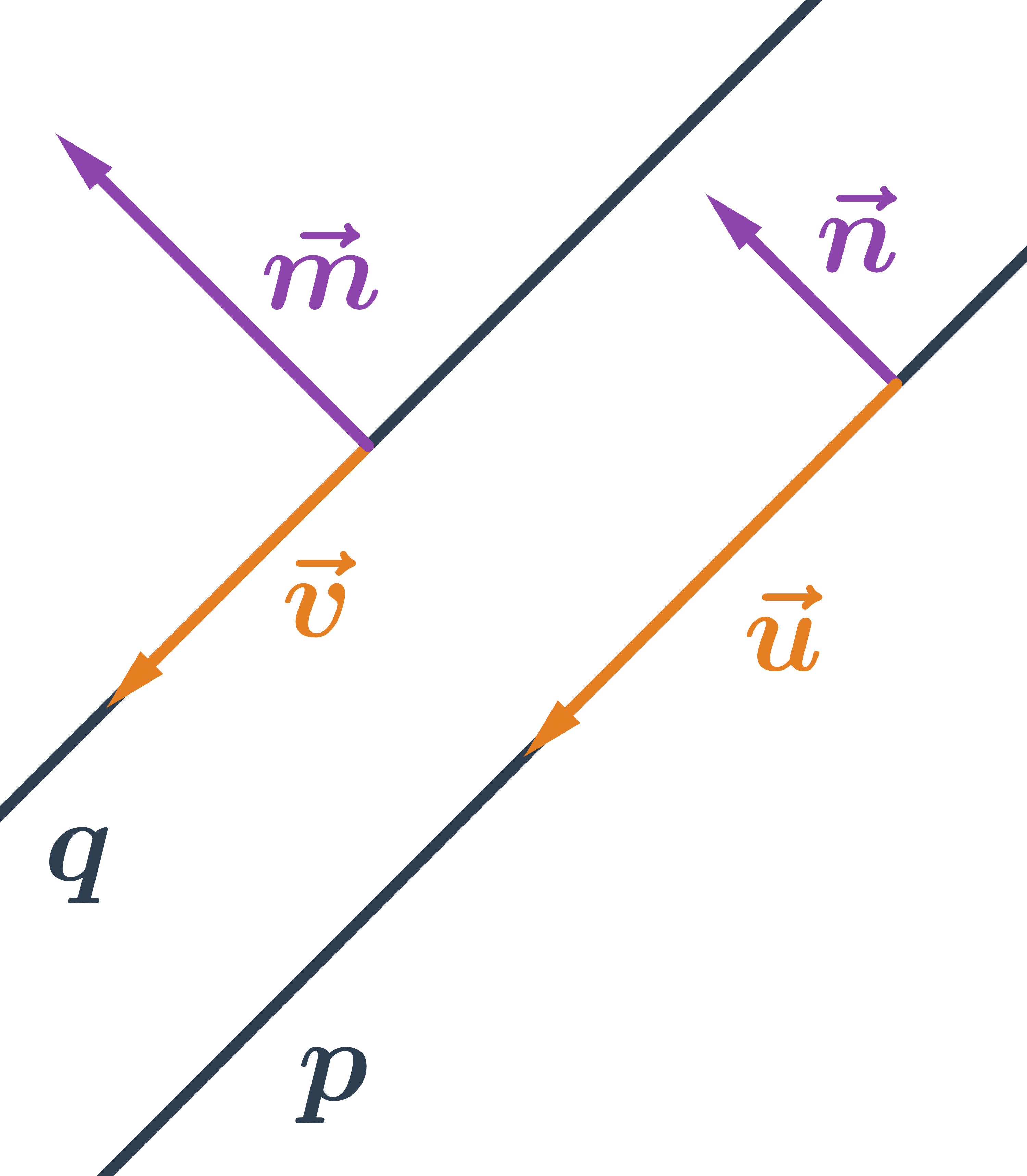
Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
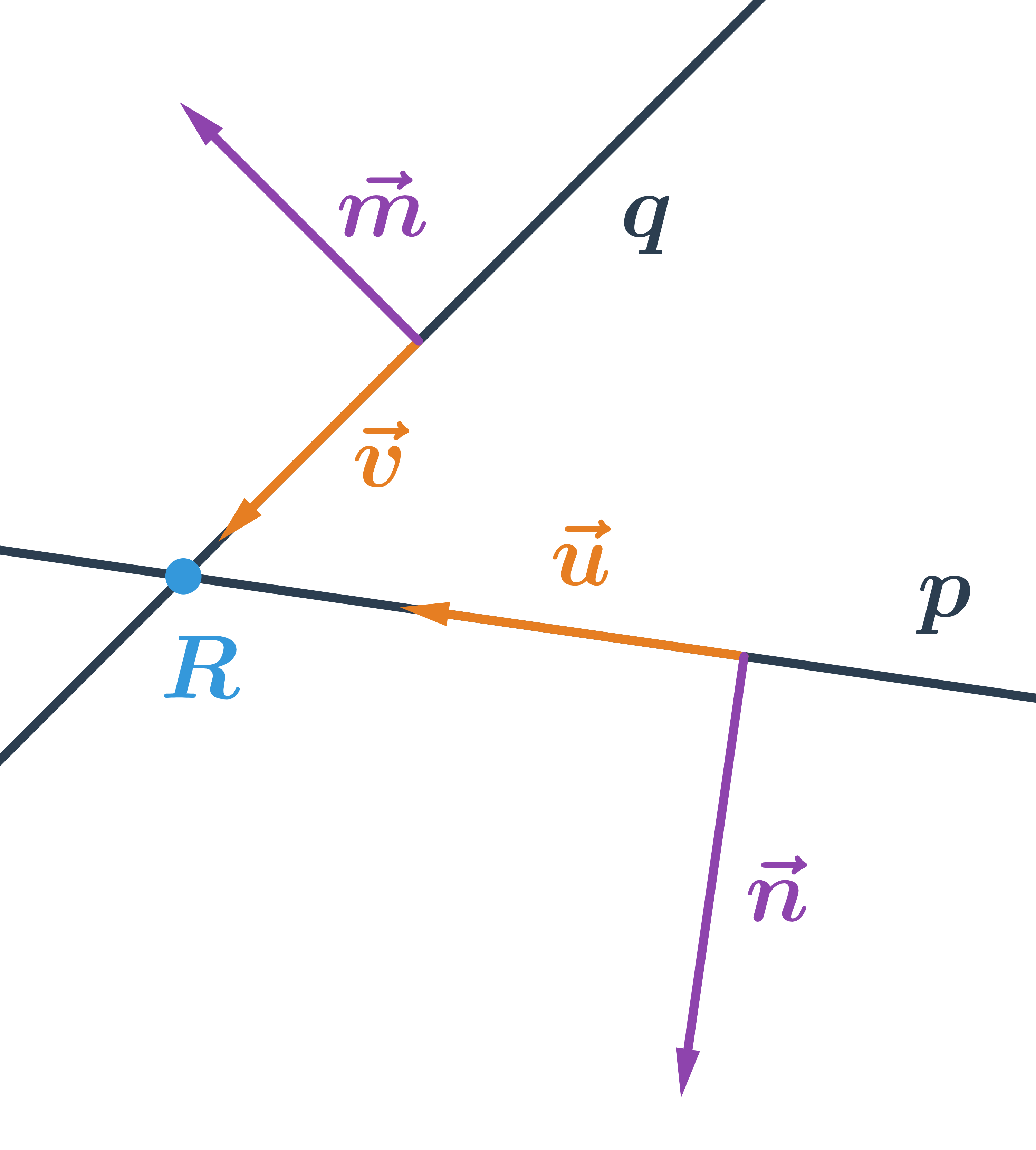
Více o vzájemné poloze dvou přímek.
Přímka v prostoru
Přímku v prostoru nelze vyjádřit obecnou rovnicí. Parametrickou rovnici přímky v prostoru určíme obdobně jako v rovině na základě znalosti souřadnic směrového vektoru a jednoho bodu na přímce.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Přímky: pojmy (střední)
zadání: 32
Typicky zabere: 7 min
