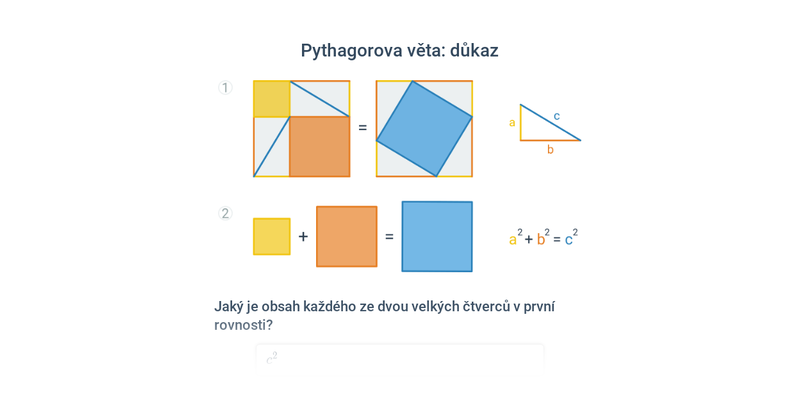
Pythagorova věta má v geometrii velice široké využití, protože mnoho složitějších útvarů můžeme rozložit na pravoúhlé trojúhelníky.
Typickým příkladem aplikace Pythagorovy věty je výpočet délky uhlopříčky čtverce nebo výšky rovnostranného trojúhelníku:
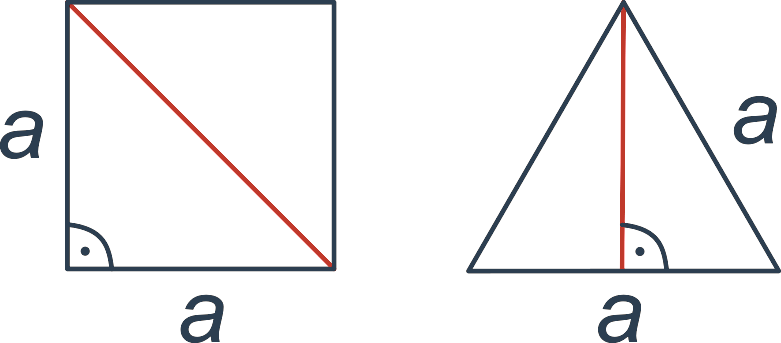
Ve čtverci o straně a tvoří uhlopříčka přeponu pravoúhlého trojúhelníku s odvěsnami délky a. Pro délku uhlopříčky u tedy platí u^2 = a^2 + a^2. Po úpravách: u = \sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}. Například čtverec o straně 10 cm tedy má uhlopříčku délky 10\cdot \sqrt{2} \doteq 14,1 cm.
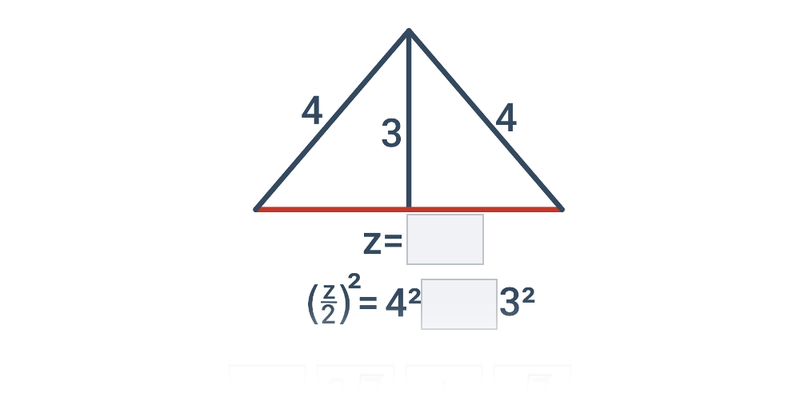
V rovnostranném trojúhelníku o straně a tvoří výška odvěsnu pravoúhlého trojúhelníku s přeponou délky a a odvěsnou délky \frac{a}{2}. Pro délku výšky v tedy platí v^2 + \large(\frac{a}{2}\large)^2 = a^2. Po úpravách dostáváme v^2 = a^2 - \frac{a^2}{2^2} = \frac{3}{4}a^2, v = a\frac{\sqrt{3}}{2}. Například v rovnostranném trojúhelníku o straně 5 metrů má tedy výška délku \frac{\sqrt{3}}{2}\cdot 5 \doteq 4,33 metru.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
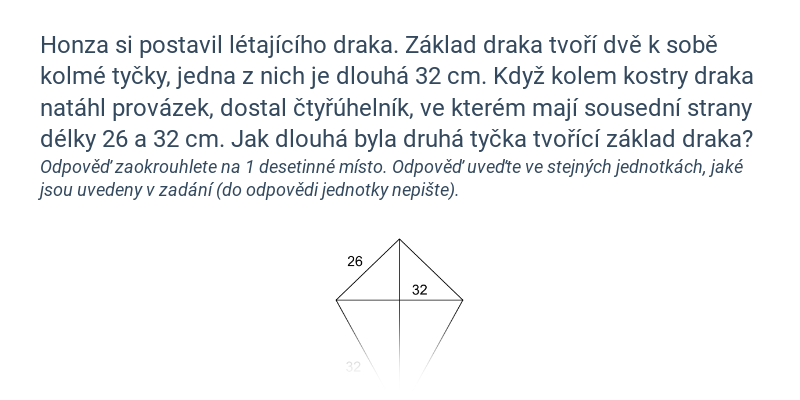
Slovní úlohy
Klasické procvičování slovních úloh, s pestrou nabídkou zadání a vysvětlujícími texty.
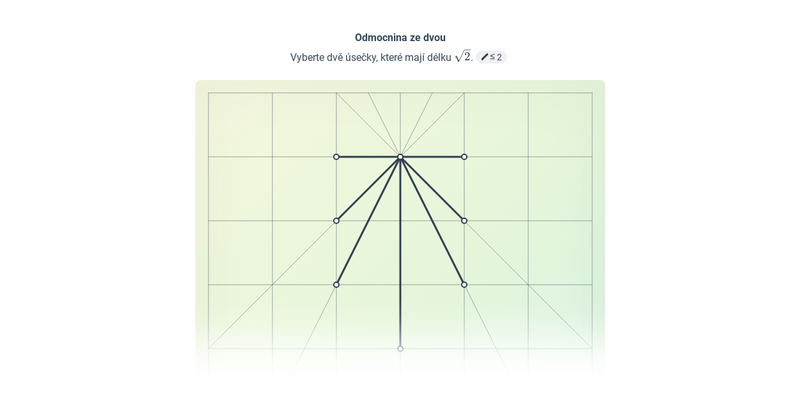
Mřížkovaná
Úloha na procvičení geometrie s jednoduchým ovládáním a zajímavými úlohami.
Pythagorova věta
Porozumění
Čtení textů, odpovídání na otázky testující porozumění textu.