Délka úsečky v prostoru

GMD

umime.to/GMD

Stáhnout QR kód

Délku úsečky v prostoru spočítáme stejně jako vzdálenost bodů v prostoru.

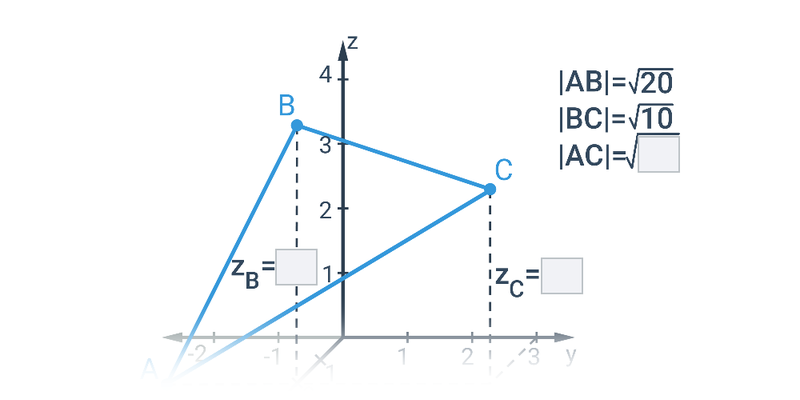
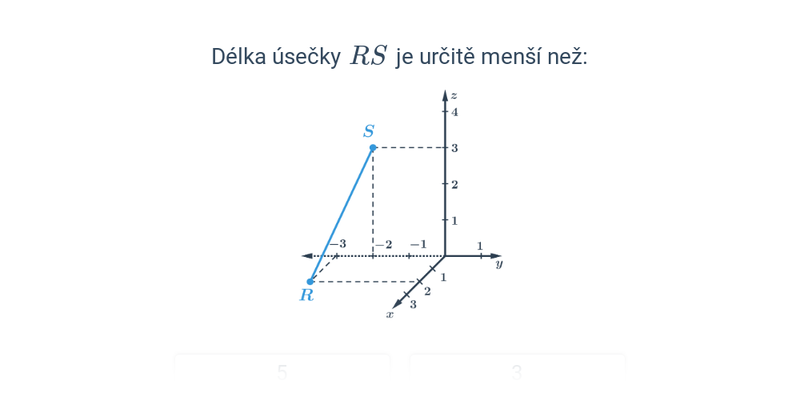
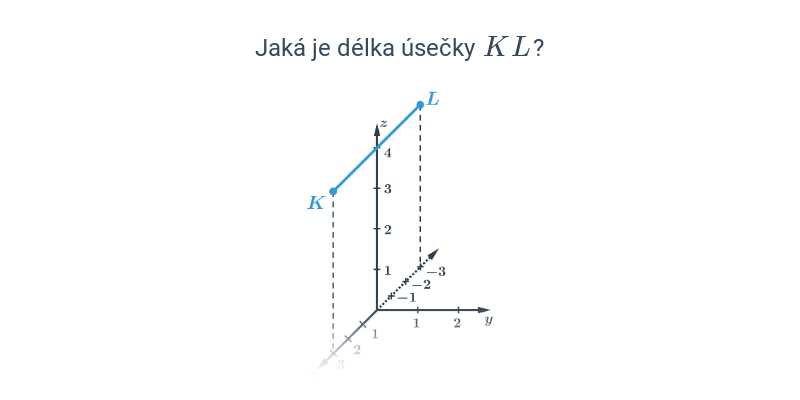
Jsou‑li dány souřadnice A[x_A; y_A;z_A], B[x_B; y_B;z_B], je délka úsečky AB:

|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2+(z_B-z_A)^2}

Příklad: Délka úsečky EF: E[-2;0;1], F[-4;2;0]

|EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2+ (z_F-z_E)^2}
Dosadíme souřadnice bodů EF; E[-2;0;1], F[-4;2;0]:
\sqrt{(-4-(-2))^2 + (2-0)^2+(0-1)^2}=\sqrt{(-2)^2 + 2^2+(-1)^2}=\sqrt{4+4+1}=\sqrt{9}=3
Délka úsečky je: |EF|=3

Souhrn je skryt.

Přesouvání

Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.

Délka úsečky v prostoru

Přesouvání • střední

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Délka úsečky v prostoru

Rozhodovačka • střední

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Délka úsečky v prostoru

Psaná odpověď • střední

Předcházející

Navazující

Cvičení

Délka úsečky v prostoru

umime.to/GMD

Přesouvání