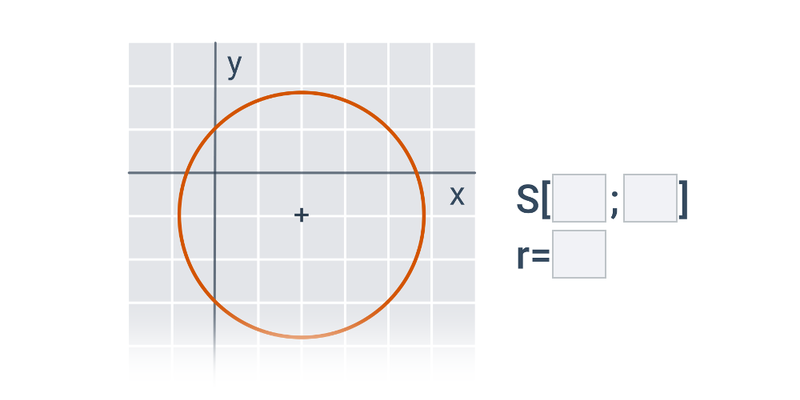Čeština
Angličtina
Informatika
Biologie
Umíme to
Němčina
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Pexeso
Grafař
Porozumění
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Předcházející
Navazující
Kružnice je množina všech bodů v rovině, které mají od daného pevného bodu S stejnou vzdálenost r. Bod S nazýváme střed kružnice, hodnotu r nazveme poloměr kružnice.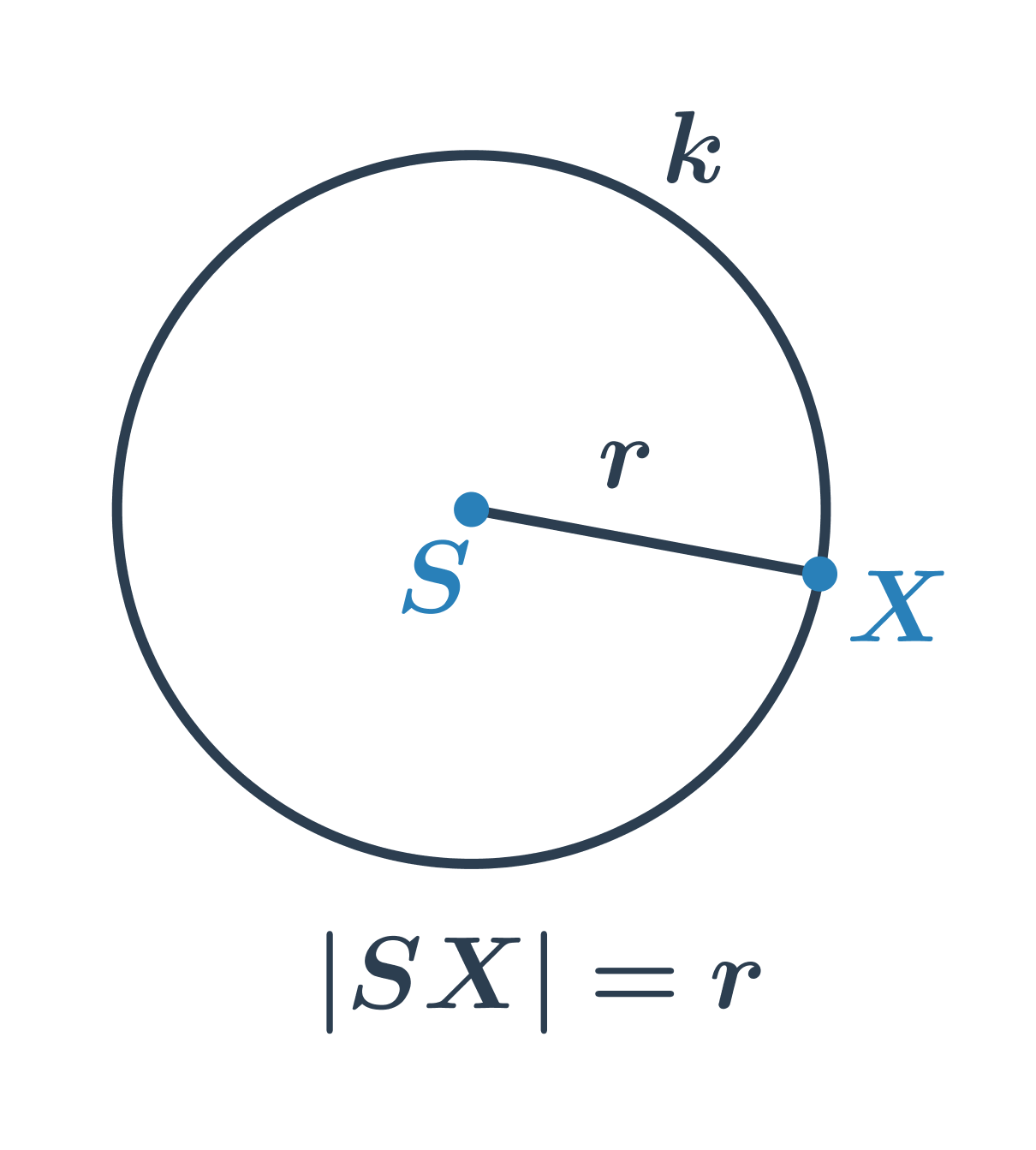 
Středová rovnice kružnice
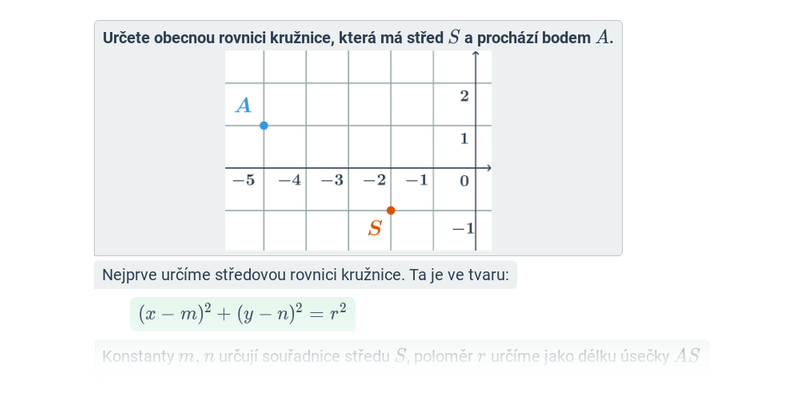
Středová rovnice kružnice o středu S[m;n] a poloměru r je ve tvaru: (x-m)^2 +(y-n)^2=r^2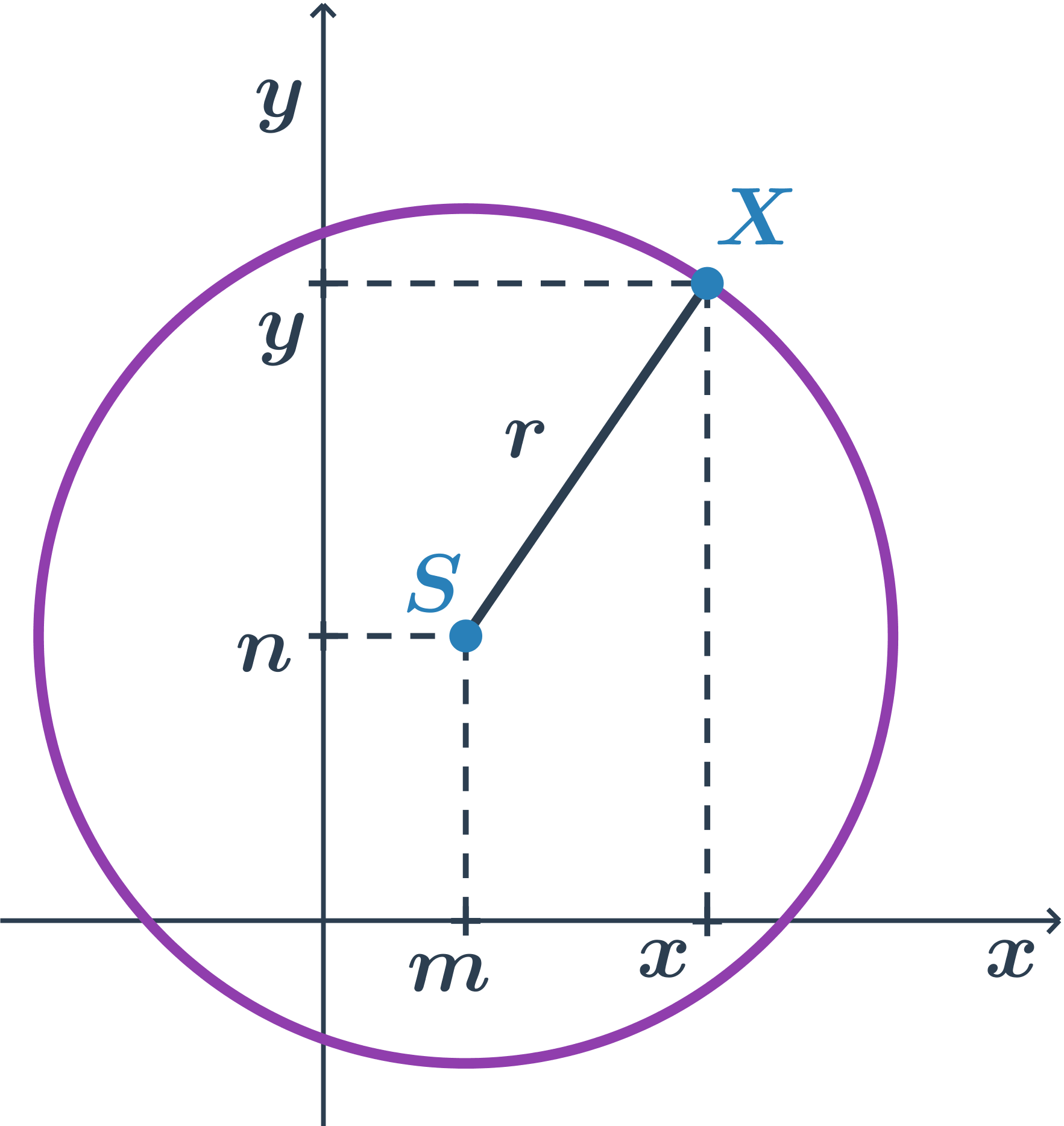 
Příklad: Určete středovou rovnici kružnice se středem v bodě S[-1;2] a poloměrem r=3.
- Středová rovnice je ve tvaru: (x-m)^2 +(y-n)^2=r^2
- Dosadíme souřadnice středu a poloměr. Při dosazení si dáme pozor na to, že souřadnice středu ve středové rovnici odečítáme: (x-(-1))^2 +(y-2)^2=3^2
- Po úpravě: (x+1)^2 +(y-2)^2=9
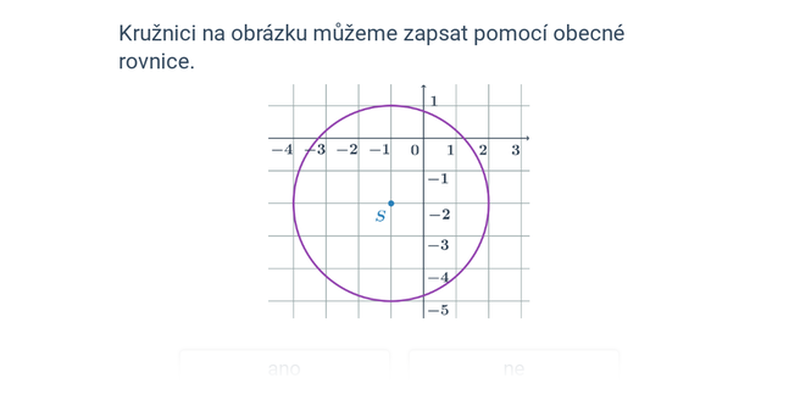
Obecná rovnice kružnice
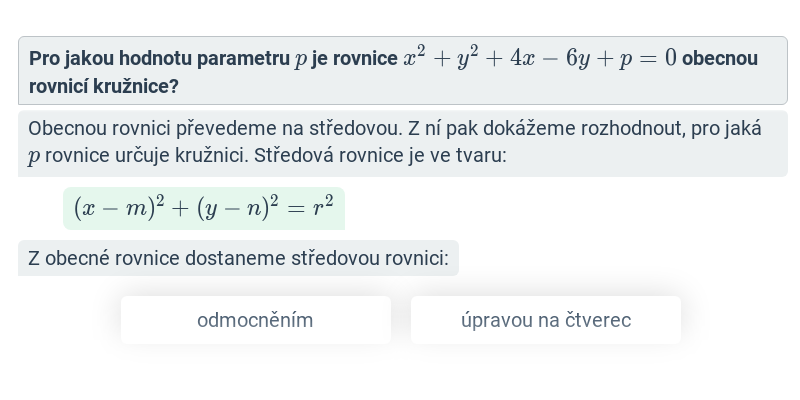
Podobně jako existuje několik tvarů rovnic přímky, můžeme i rovnici kružnice zapsat různými způsoby. Obecná rovnice kružnice je ve tvaru: x^2 +y^2-2mx-2ny+p=0.
Každá rovnice v tomto tvaru ale nemusí ještě být obecnou rovnicí kružnice. Pro obecnou rovnici kružnice musí platit, že výraz m^2+n^2-p je kladný. Praktické ověření, zda se jedná o kružnici, ale obvykle provádíme převedením na středovou rovnici kružnice.
Příklad: Najděte střed a poloměr kružnice dané obecnou rovnicí x^2+y^2+4x+6y-12=0.
- Nejprve si uspořádáme členy podle proměnných: x^2+4x+y^2-6y-12=0.
- Našim dalším cílem je upravit výraz na levé straně jako součet dvou druhých mocnin (čtverců), podle vzorečků a^2\pm 2ab+b^2=(a\pm b)^2.
- K oběma stranám rovnice přičteme konstanty 4 a 9, abychom součty členů s proměnnými x a y mohli upravit na druhé mocniny (provedeme v obou případech doplnění na čtverec): x^2+4x+4+y^2-6y+9-12=4+9
- A upravíme: (x+2)^2 +(y-3)^2-12=13
- Na závěr ještě převedeme -12 na druhou stranu rovnice: (x+2)^2 +(y-3)^2=25
- Tímto jsme převedli obecnou rovnici kružnice na středovou rovnici kružnice.
- Poloměr kružnice je r=\sqrt{25}=5.
- Souřadnice středu S[m,n] odčítáme ve středové rovnici od proměnných x a y, mají tedy opačná znaménka než konstanty v závorkách ve středové rovnici \Rightarrow S[-2;3].
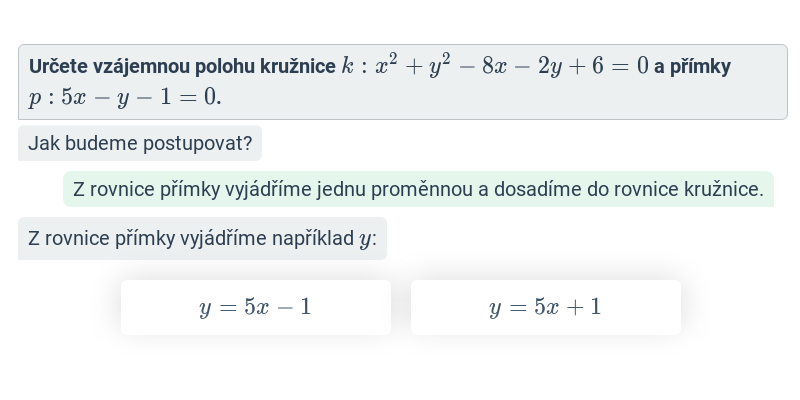
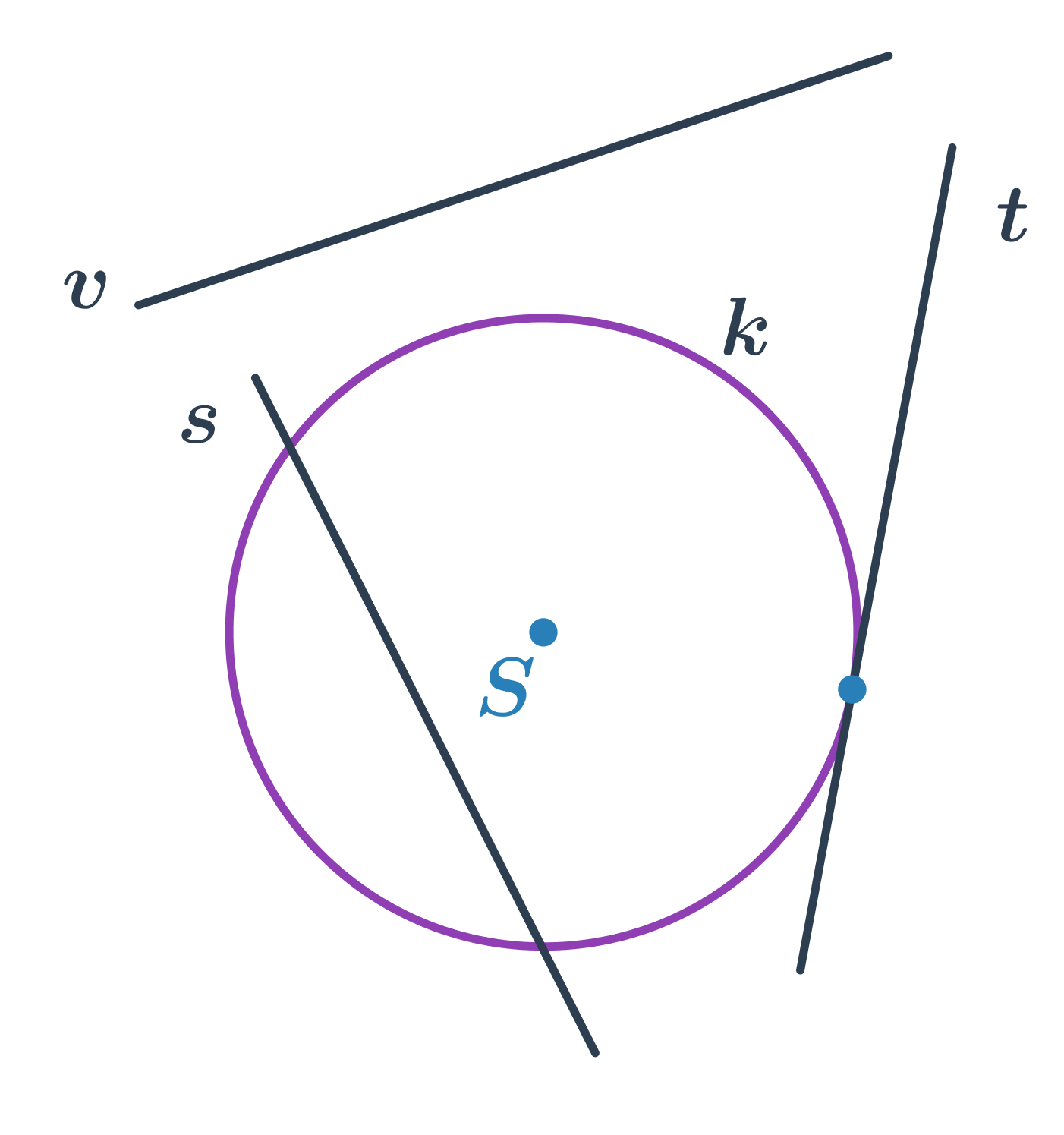
Kružnice a přímka
- přímka s protíná kružnici ve dvou bodech – sečna kružnice
- přímka t protíná kružnici v jednom bodě – tečna kružnice
- přímka v kružnici neprotíná – vnější přímka kružnice
Rovnice tečny kružnice v bodě, který leží na kružnici
Kružnice daná rovnicí (x-m)^2 +(y-n)^2=r^2 má v bodě T[x_0;y_0] tečnu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.Jak si zapamatovat rovnici tečny
- Středová rovnice je ve tvaru (x-m)^2 +(y-n)^2=r^2.
- Závorky rozložíme na součiny dvoučlenů (x-m)(x-m) +(y-n)(y-n)=r^2.
- V každém součinu zaměníme jedno x za x_0 a jedno y za y_0
- Dostaneme rovnici tečny (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Příklad: Určete rovnici tečny kružnice (x-1)^2+(y+2)^2=13 v jejím bodě T[3;1].
- Ověříme, zda bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
- Tečna má rovnici (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
- Dosadíme souřadnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
- Roznásobíme závorky: 2x-2 +3y+6=13
- A dostaneme obecnou rovnici tečny 2x+3y-9=0
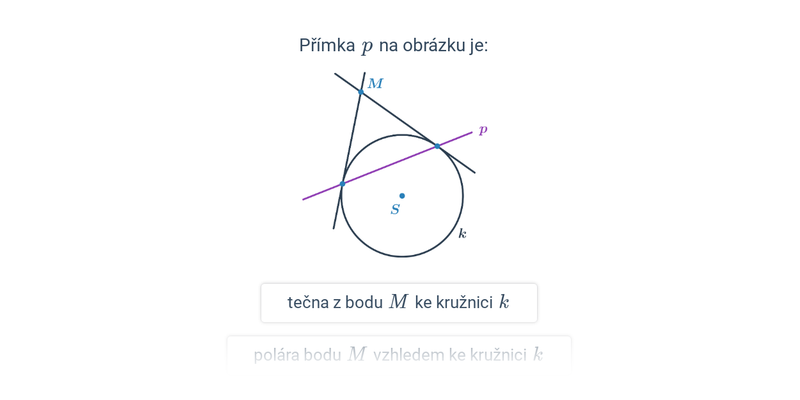
Polára kružnice
Z bodu R mimo kružnici můžeme sestrojit dvě tečny k dané kružnici. Přímka určená body dotyku tečen se nazývá polára kružnice vzhledem k bodu R.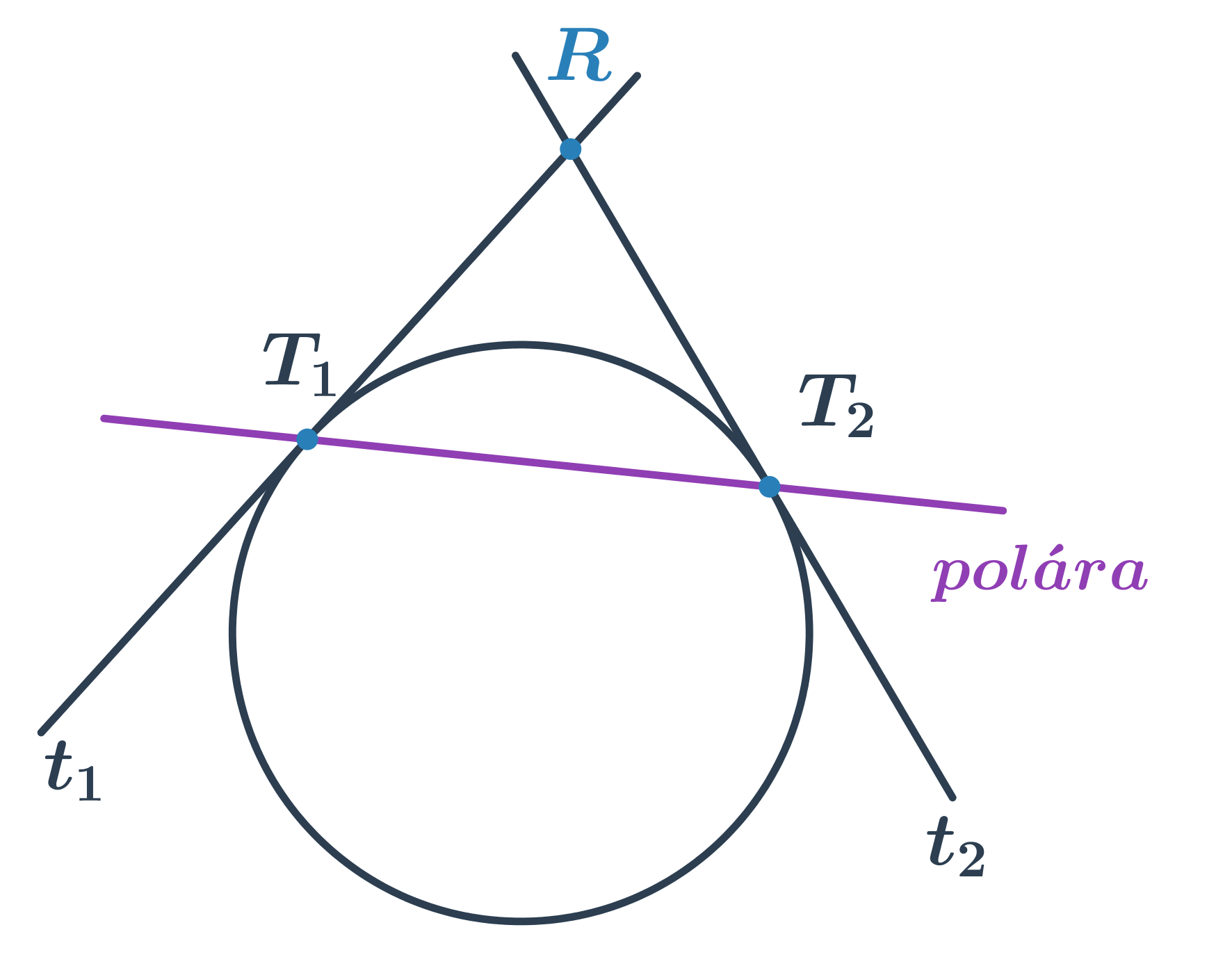 
Rovnice poláry kružnice kružnice (x-m)^2 +(y-n)^2=r^2 vzhledem k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.
K čemu poláru použijeme?
- Poláru využíváme ke konstrukci tečen ležících z bodu mimo kružnici.
- Podle vzorce určíme rovnici poláry, tedy přímky.
- Najdeme průsečíky poláry a kružnice – to jsou body dotyku hledaných tečen.
- Když známe body dotyku, určíme podle vztahu pro rovnici tečny v bodě kružnice obecné rovnice obou tečen.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Kružnice: středová rovnice (střední)
zadání: 12
Typicky zabere: 4 min
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Kružnice: obecná rovnice (střední)
zadání: 30
Typicky zabere: 4 min
Kružnice: vzájemná poloha přímky a kružnice (střední)
zadání: 31
Typicky zabere: 4 min
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Kružnice: středová rovnice (střední)
zadání: 14
Typicky zabere: 6 min
Kružnice: obecná rovnice (střední)
zadání: 13
Typicky zabere: 6 min
Kružnice: obecná rovnice (těžké)
zadání: 14
Typicky zabere: 8 min
Kružnice: vzájemná poloha přímky a kružnice (střední)
zadání: 15
Typicky zabere: 12 min
Kružnice: vzájemná poloha přímky a kružnice (těžké)
zadání: 15
Typicky zabere: 9 min
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Kružnice: středová rovnice (střední)
zadání: 30
Typicky zabere: 4 min
