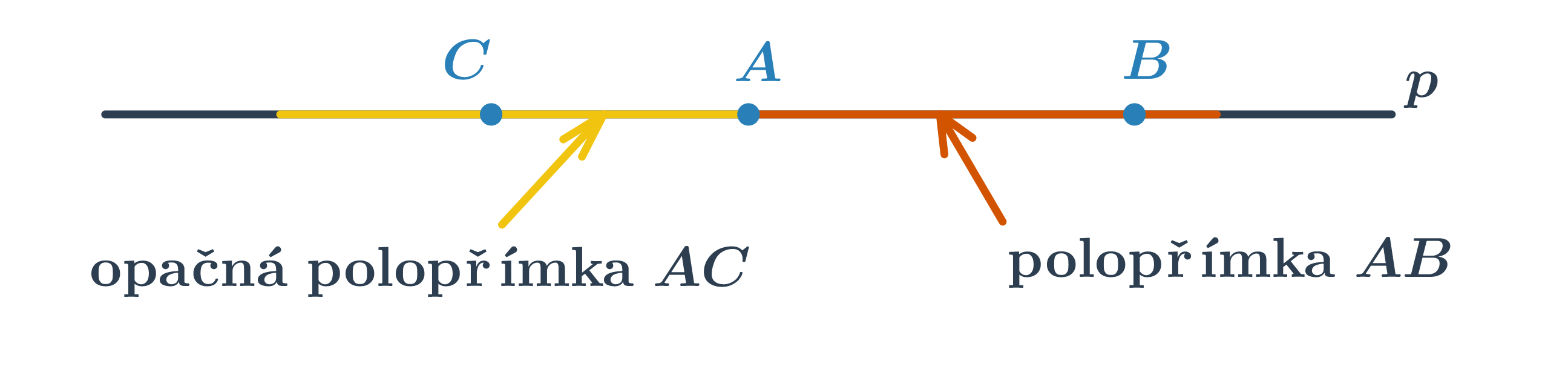
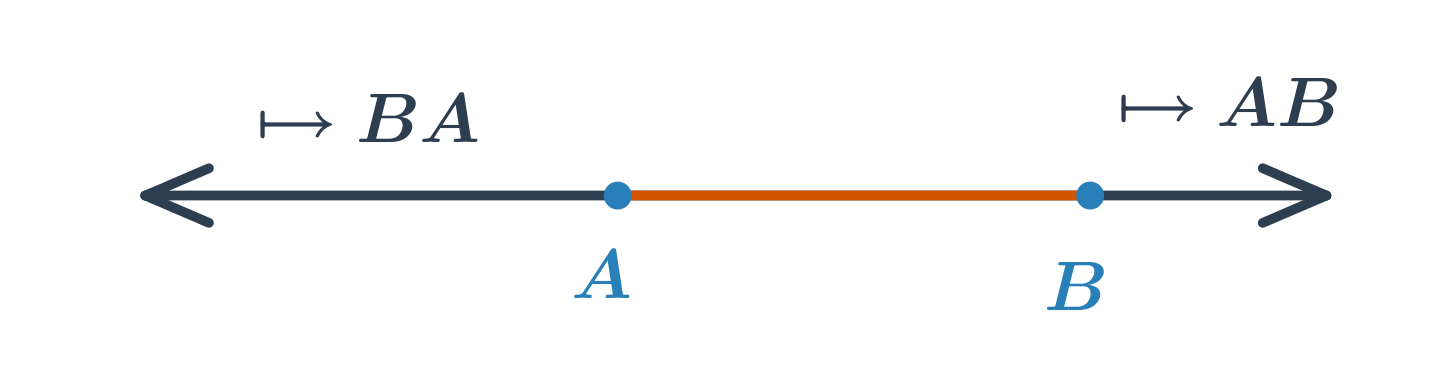
Polopřímky a poloroviny

Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem. Tento bod se nazývá počáteční. Polopřímku s počátečním bodem A procházející bodem B značíme \mapsto AB. Každý bod rozděluje přímku na dvě opačné polopřímky se společným počátečním bodem.

Základní vlastnosti polopřímek:

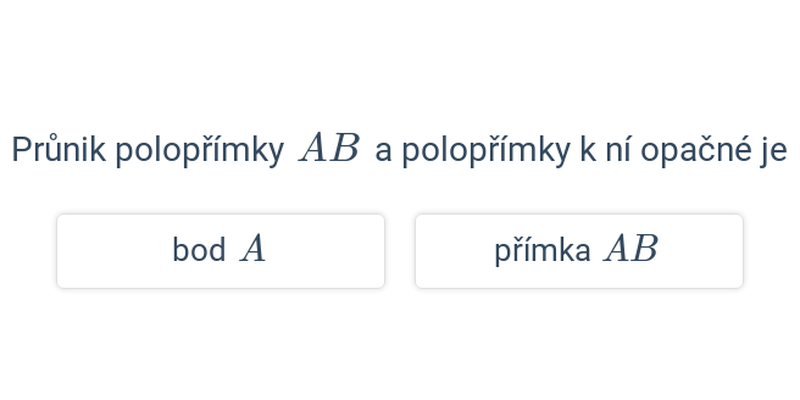
• Sjednocením dvou opačných polopřímek je přímka.
• Průnikem dvou opačných polopřímek je bod.
• Průnikem polopřímek \mapsto AB a \mapsto BA je úsečka AB.

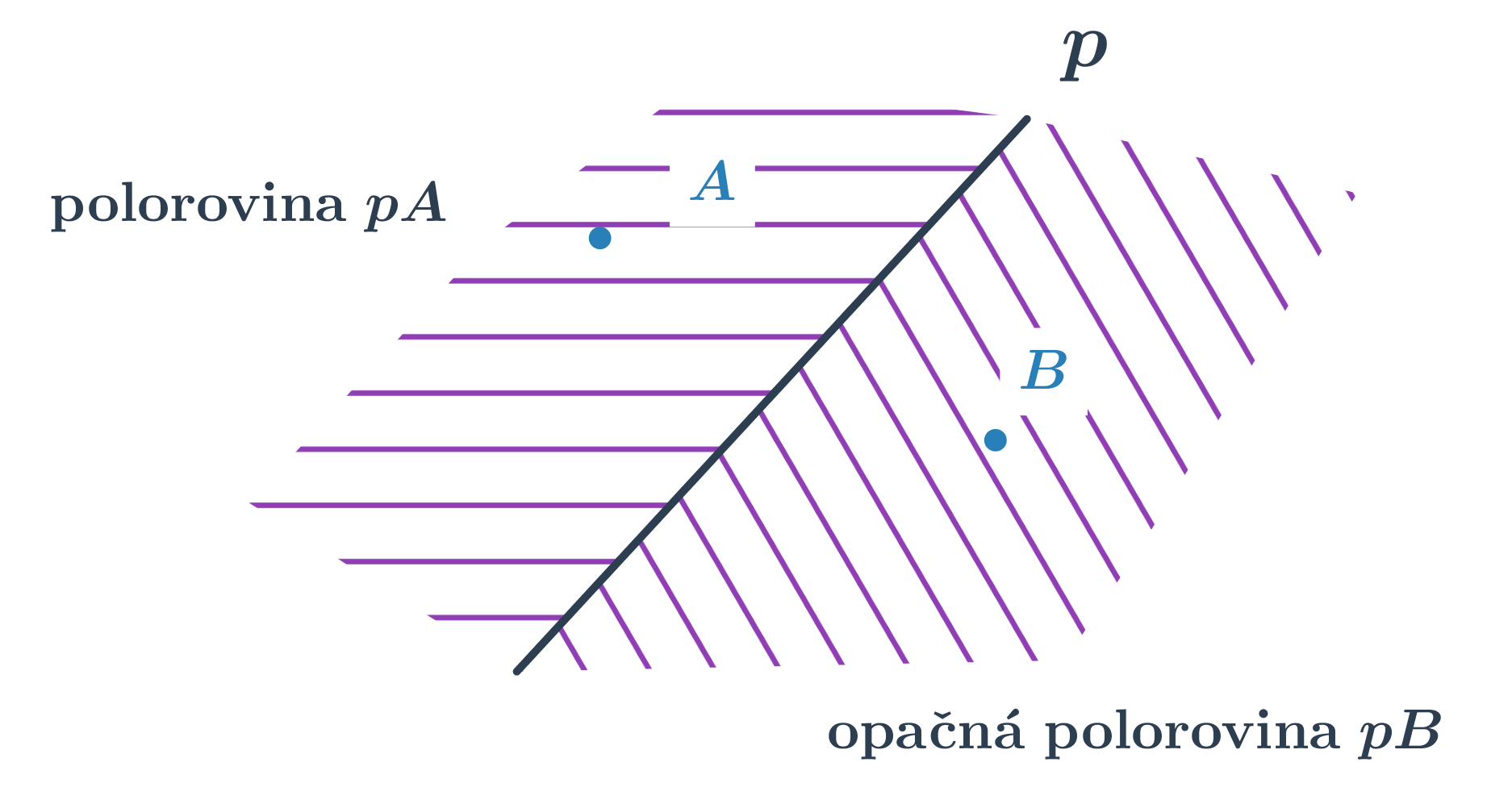
Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme \mapsto pK. Je-li přímka p určena body A, B, můžeme také psát \mapsto ABK. Každá přímka rozděluje rovinu na dvě opačné poloroviny se společnou hraniční přímkou.

Základní vlastnosti polorovin:

• Sjednocením dvou opačných polorovin je rovina.
• Průnikem dvou opačných polorovin je hraniční přímka.
• Průnikem dvou polorovin s rovnoběžnými hraničními přímkami je pás rovnoběžek.

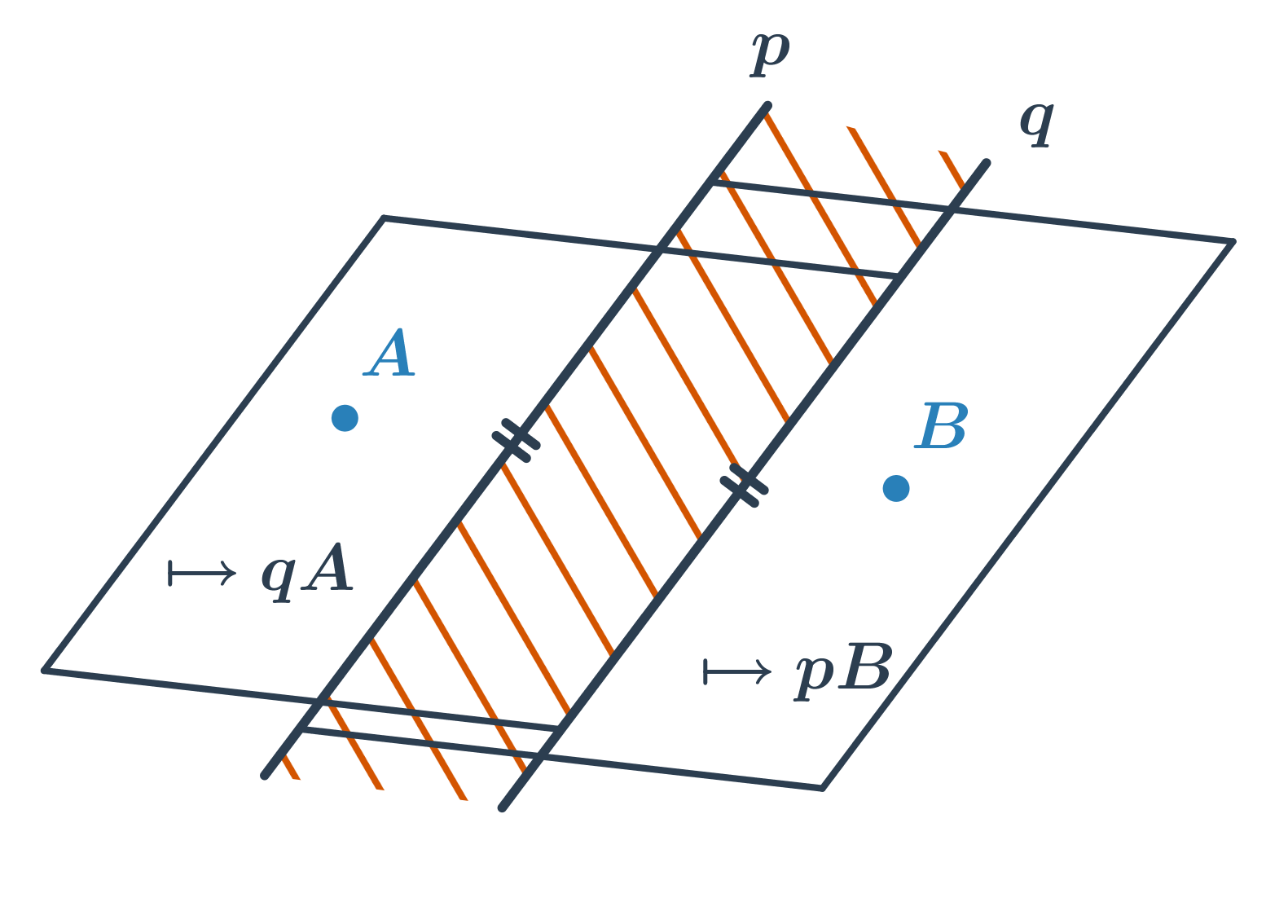
Pro zápis geometrických konstrukcí používáme množinové operace, především průnik (\cap) a sjednocení (\cup).

Příklad: Rozhodněte, co je průnikem polopřímky CA a poloroviny ABC.

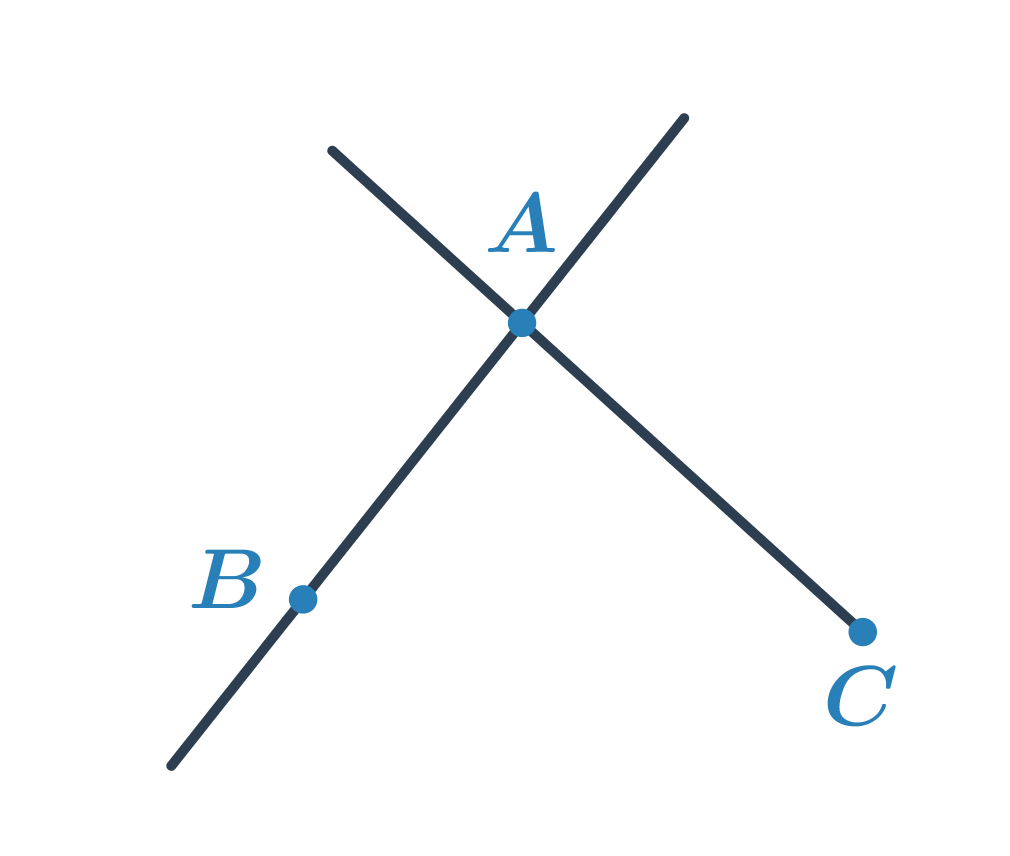
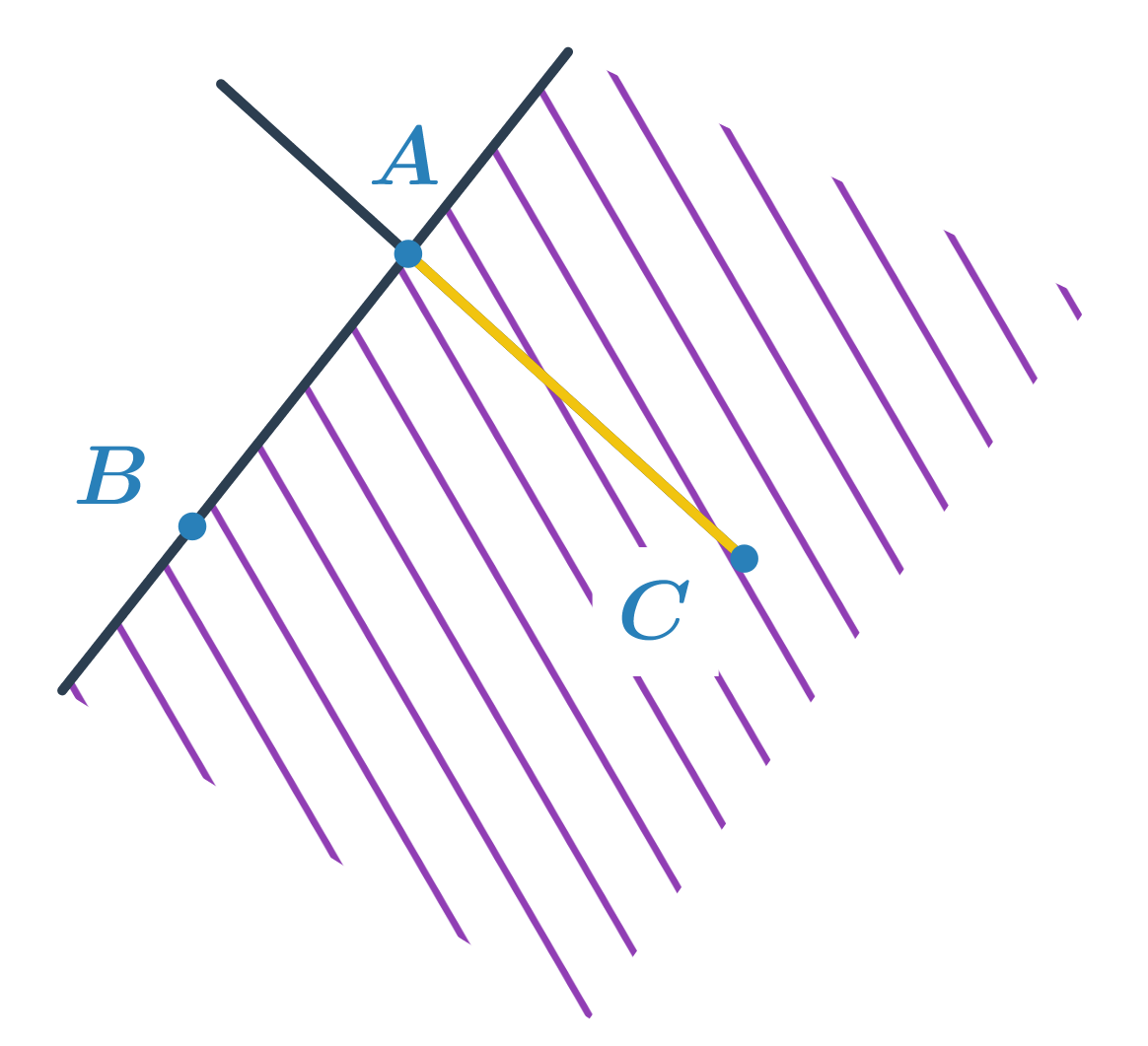
Polorovina ABC je určena hraniční přímkou AB a bodem C. Polopřímka CA má počáteční bod C a prochází bodem A. Průnikem je pak úsečka AC. Matematicky bychom úlohu zapsali: AC = \mapsto ABC \cap \mapsto CA.