Vzájemná poloha přímky a bodu v rovině

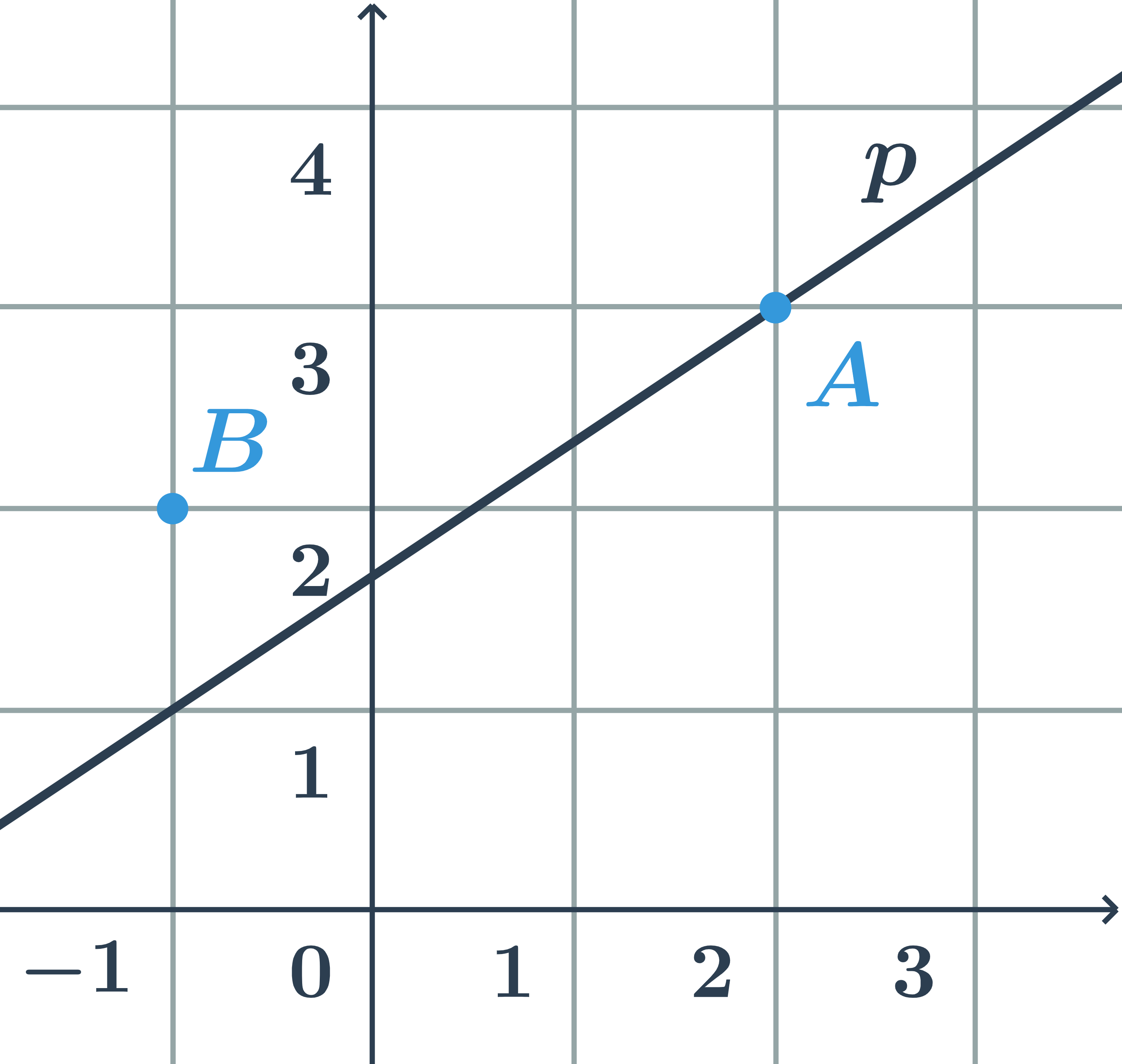
Určete, zda body A=[2;3] a B=[-1;2] leží na přímce p:2x-3y+5=0.

• Do rovnice přímky dosadíme souřadnice bodu A=[2;3]:
• 2\cdot 2-3\cdot3+5=0\Rightarrow bod A leží na přímce p
• Do rovnice přímky dosadíme souřadnice bodu B=[-1;2]:
• 2\cdot (-1)-3\cdot2+5=-3\Rightarrow bod B neleží na přímce p

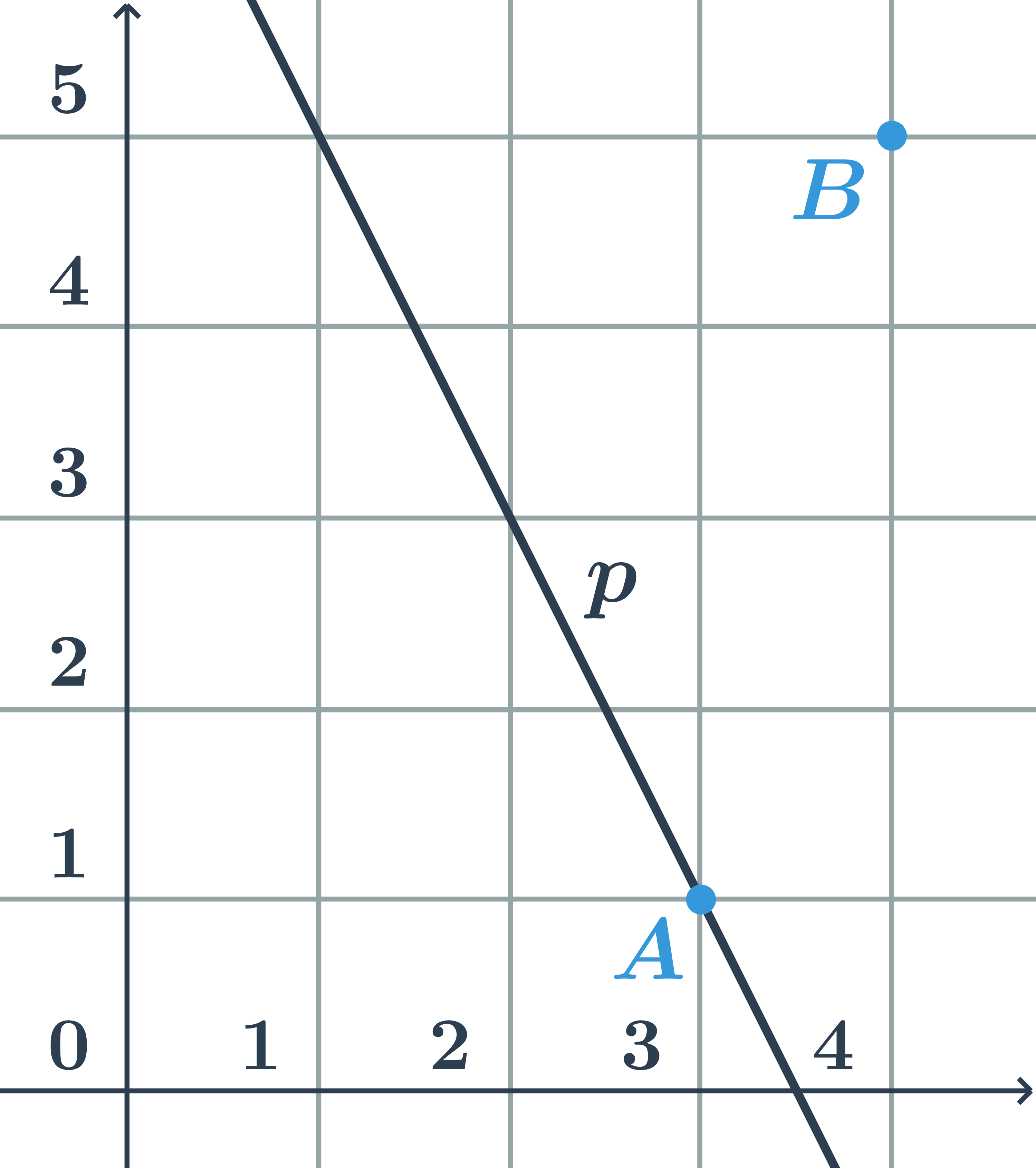
Určete, zda body A=[3;1] a B=[4;4] leží na přímce p dané parametricky: \begin{array}{rrl}x&=&2-t\\y&=&3+2t\\&&t\in\mathbb{R}\end{array}

• Do rovnic přímky dosadíme souřadnice bodu A=[3;1]:

\begin{array}{rrrr}3&=&2-t&\Rightarrow t=-1\\1&=&3+2t&\Rightarrow t=-1\end{array} \Rightarrow bod A leží na přímce p

• Do rovnice přímky dosadíme souřadnice bodu B=[4;5]:

\begin{array}{rrrl}4&=&2-t&\Rightarrow t=-2\\5&=&3+2t&\Rightarrow t=1\end{array}\Rightarrow bod B neleží na přímce p