Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
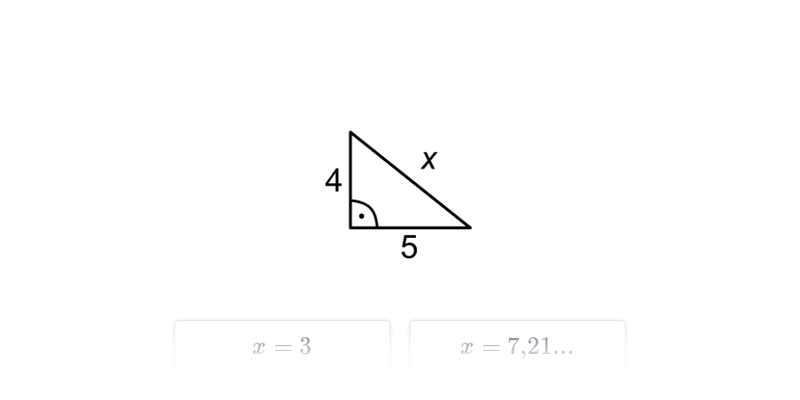
Délka přepony c = \sqrt{a^2 + b^2}. Pokud má pravoúhlý trojúhelník odvěsny délky 3 metry a 6 metrů, přepona má délku \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6{,}41 metrů.
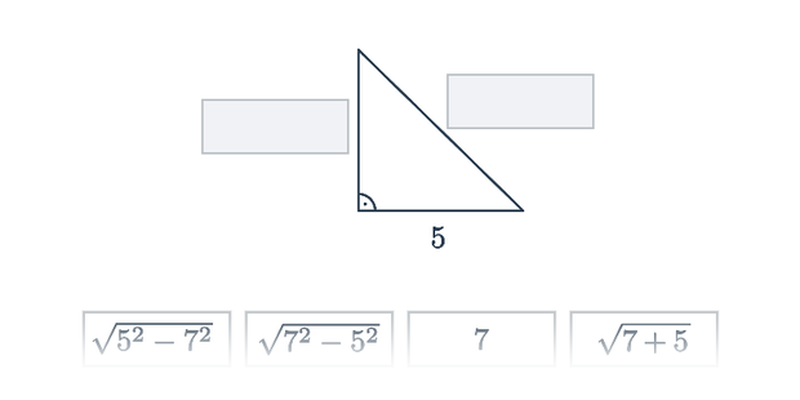
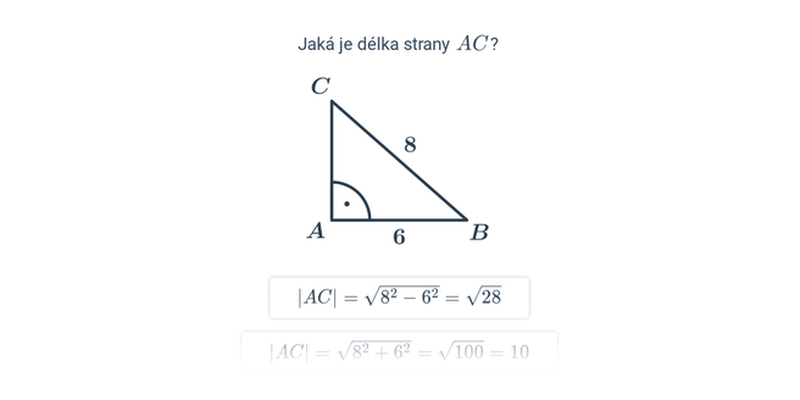
Délka odvěsny a = \sqrt{c^2-b^2}. Pokud má trojúhelník přeponu délky 8 metrů a jedna z odvěsen má délku 4 metry, druhá odvěsna má délku \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6{,}93 metrů.
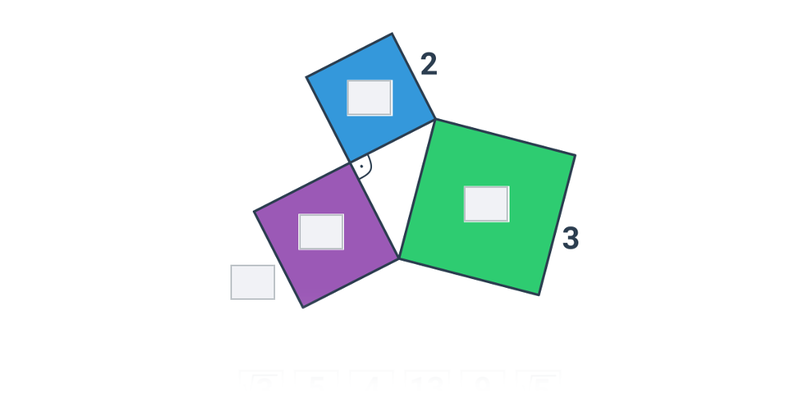
Pythagorejské trojice jsou trojice celých čísel, které splňují a^2+b^2=c^2, tj. trojúhelník s příslušnými délkami stran je pravoúhlý. Typickým příkladem Pythagorejské trojice je (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.
Další příklady Pythagorejských trojic: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). Mezi Pythagorejské trojice patří také všechny násobky těchto trojic, např. (6, 8, 10); (9, 12, 15); (10, 24, 26). Pokud si zapamatujeme některé základní Pythagorejské trojice, především nejjednodušší trojici (3, 4, 5), tak nám to může usnadnit výpočty.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
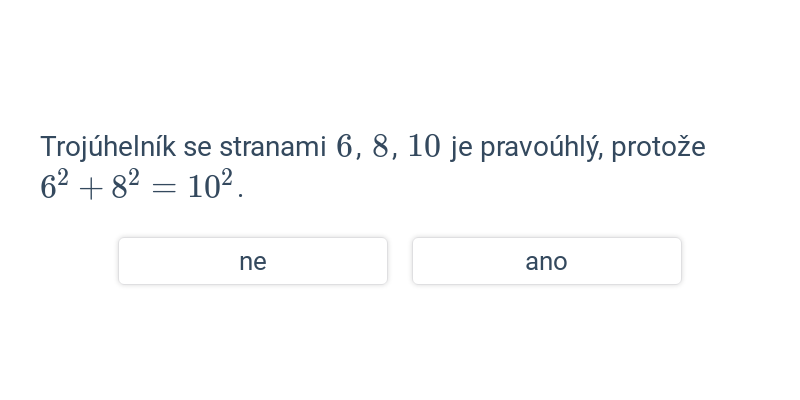
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
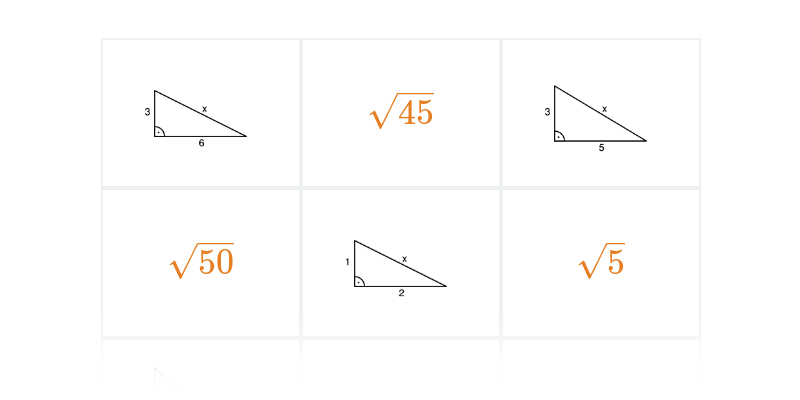
Pexeso
Hledání dvojic, které k sobě patří.
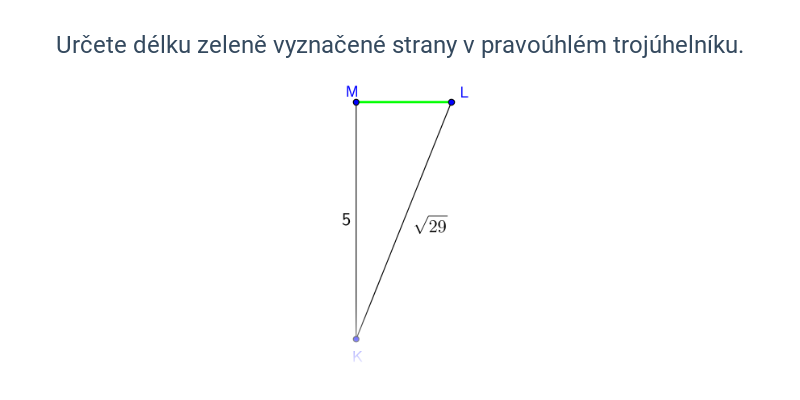
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.