Úhly a mnohoúhelníky – 3. střední škola

F2A

umime.to/F2A

Součet vnitřních úhlů v obecném mnohoúhelníku s n stranami (tedy n-úhelníku) je 180^\circ\cdot(n-2). Například v pětiúhelníku je součet vnitřních úhlů 180^\circ(5-2)=540^\circ. Každý vnitřní úhel pak může mít jinou velikost.

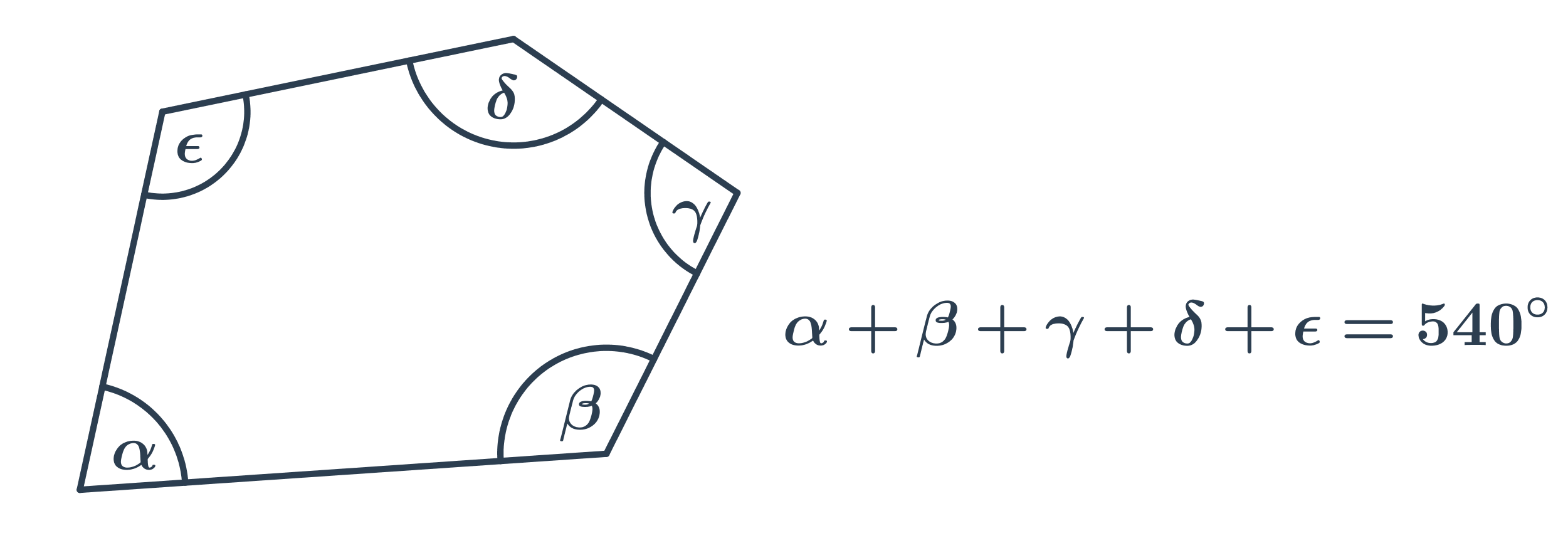
Pravidelné mnohoúhelníky

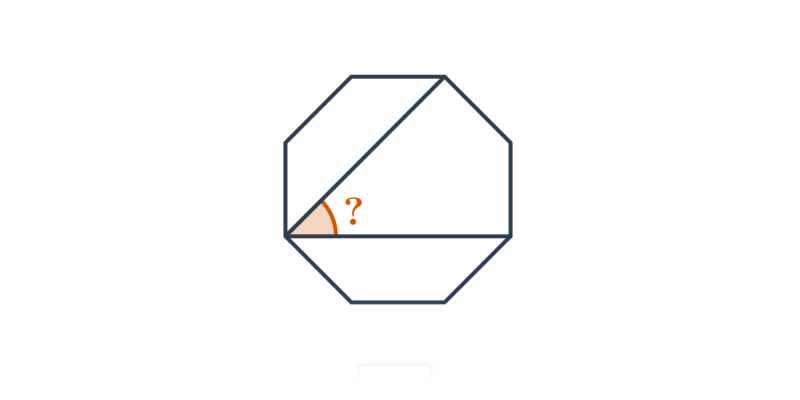
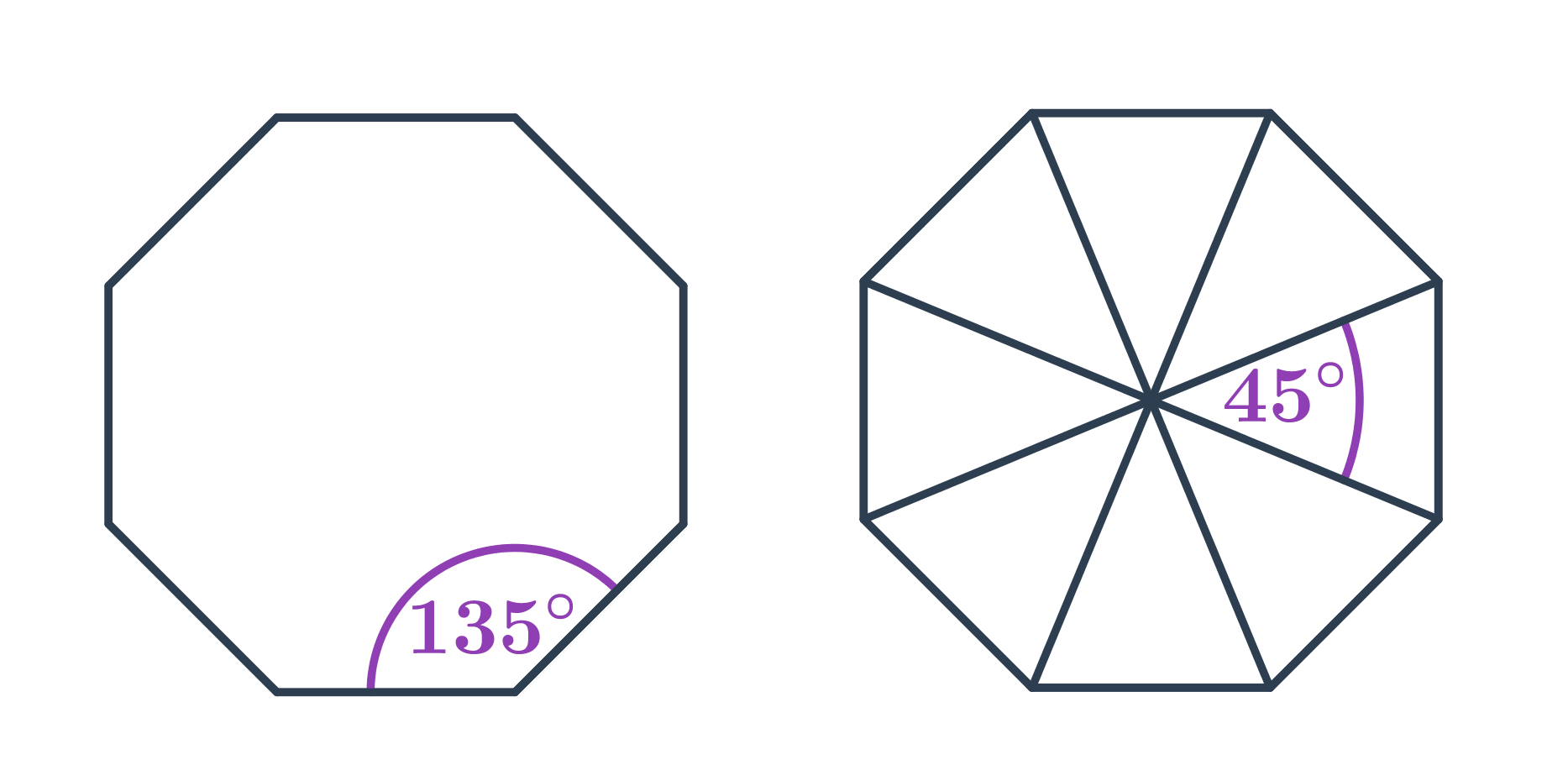
Každý vnitřní úhel v pravidelném mnohoúhelníku s n vrcholy má velikost 180^\circ\cdot\frac{n-2}{n}. Například v pravidelném osmiúhelníku má každý vnitřní úhel velikost 180^\circ\cdot\frac{8-2}{6}=135^\circ.
Velikost středového úhlu pravidelného n-úhelníku je \frac{360^\circ}{n}. Například v pravidelném osmiúhelníku má každý středový úhel velikost \frac{360^\circ}{8}=45^\circ.

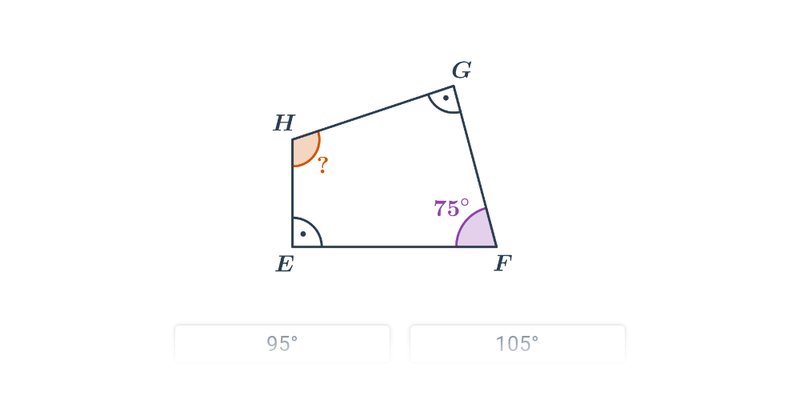
Při výpočtu neznámého úhlu v mnohoúhelníku lze využít i vrcholových a vedlejších úhlů.

Příklad: Určete velikost úhlu

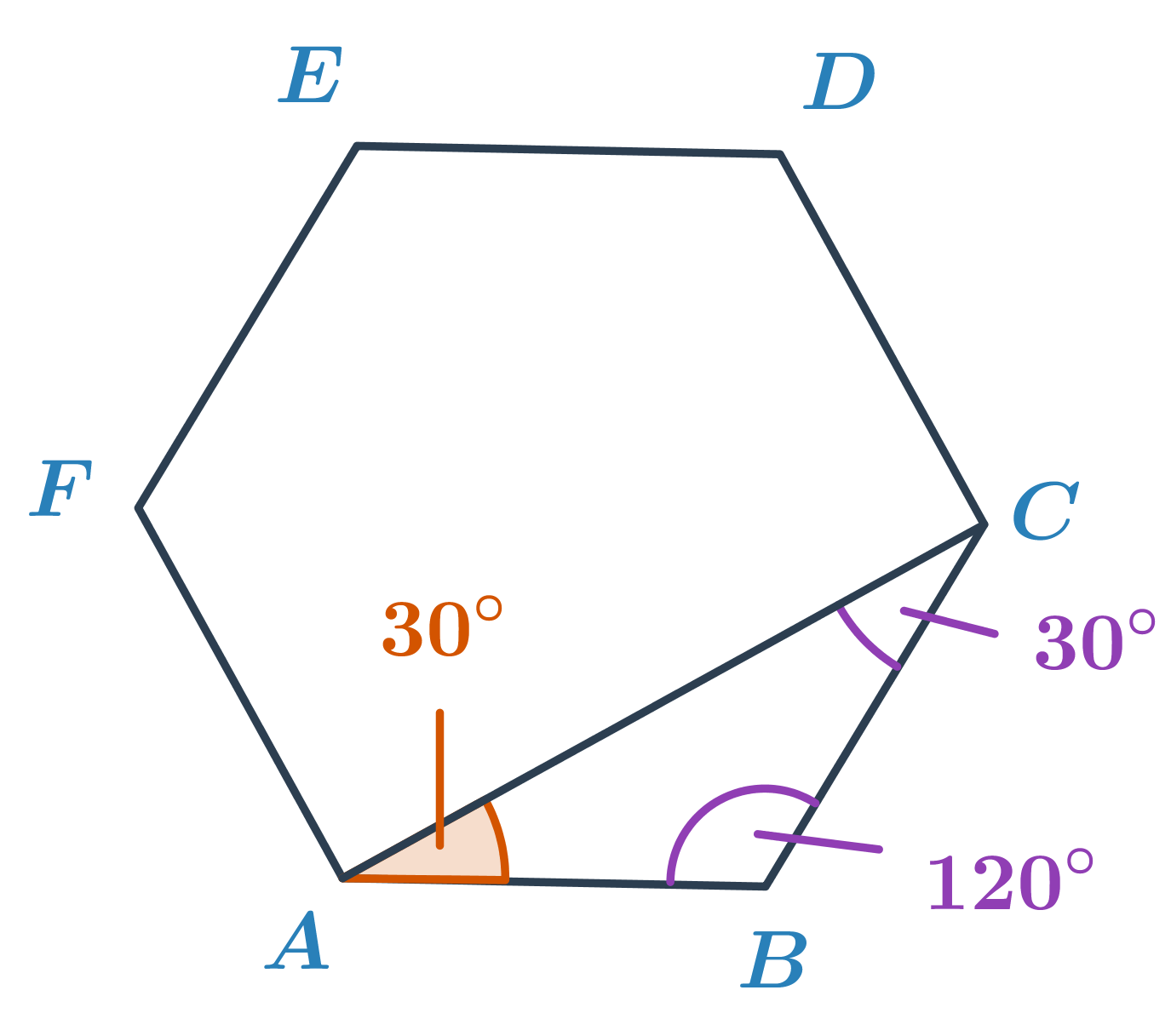
Určete velikost oranžového úhlu v pravidelném šestiúhelníku ABCDEF.

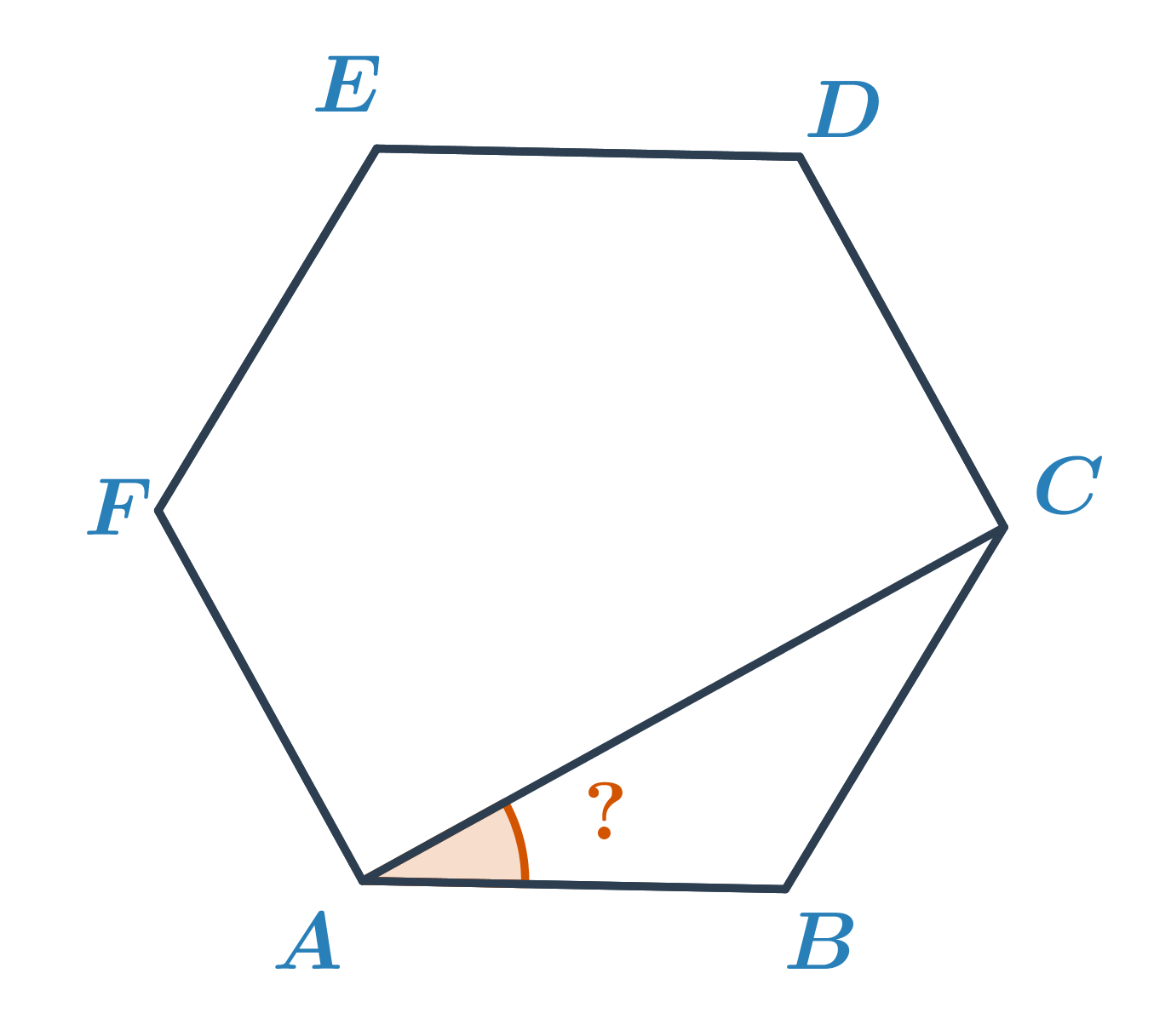
V pravidelném šestiúhelníku má každý úhel stejnou velikost, a to 180^\circ\cdot\frac{6-2}{6}=120^\circ. Úhel ABC má tedy velikost 120^\circ. Trojúhelník ABC je rovnoramenný, úhly u vrcholů A a C jsou pak shodné. Jejich velikost je (180^\circ-120^\circ):2=30^\circ.

Souhrn je skryt.

Pro toto téma zatím není dostupné žádné procvičování.

Předcházející

Úhly a mnohoúhelníky – 3. střední škola

umime.to/F2A

Pravidelné mnohoúhelníky

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?