Délka úsečky v rovině

GMC

umime.to/GMC

Stáhnout QR kód

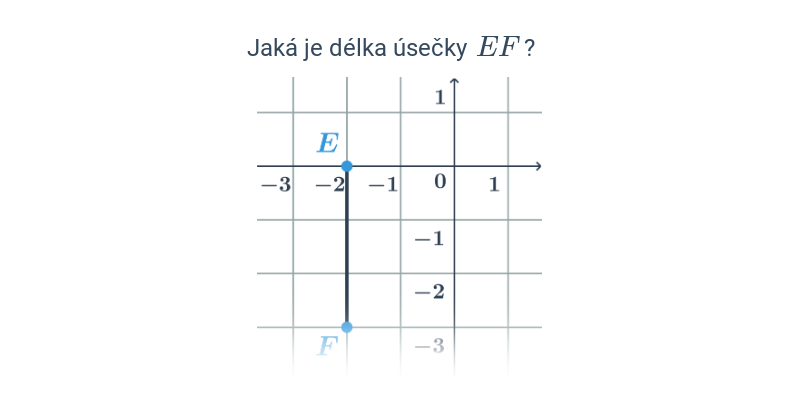
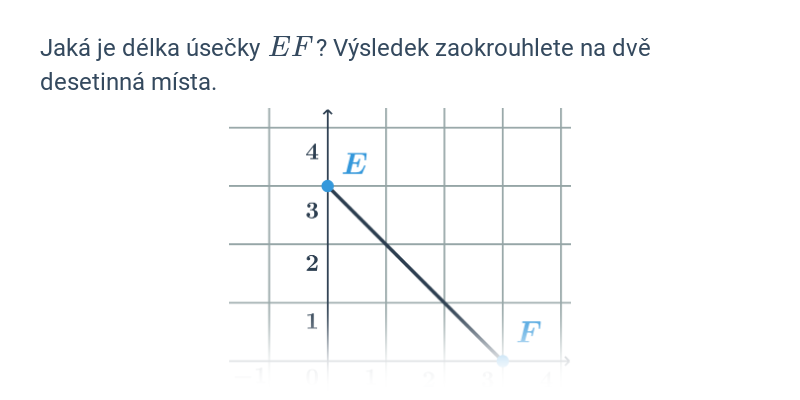
Délku úsečky v rovině spočítáme stejně jako vzdálenost bodů v rovině.

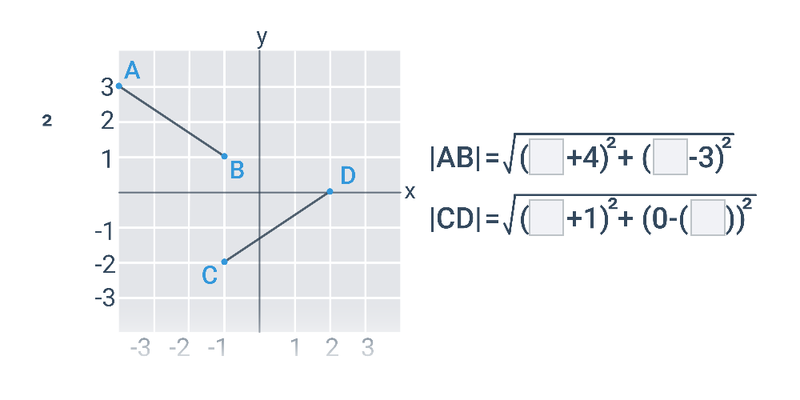
Jsou‑li dány souřadnice A[x_A; y_A], B[x_B; y_B], je délka úsečky AB:

|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}

Vzoreček vychází z Pythagorovy věty.

Je nutné počítat rozdíl souřadnic v pořadí „druhý bod mínus první“?

Není. Výrazy x_B-x_A a x_A-x_B nejsou stejné. Ale jsou opačné a ve vzorci počítáme jejich druhé mocniny, které se rovnají.
Navíc geometricky, délka úsečky AB je stejná jako délka úsečky BA.
Důvodem zápisu právě v tomto tvaru je fakt, že délka úsečky je rovna velikosti vektoru \overrightarrow{AB} a u vektoru se jeho velikost vždy počítá „koncový bod mínus počáteční“.

Příklad: Délka úsečky EF: E[0;-1], F[-4;2]

|EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
Dosadíme souřadnice bodů E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
Délka úsečky je: |EF|=5

Souhrn je skryt.

Přesouvání

Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.

Délka úsečky v rovině

Přesouvání • střední

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Délka úsečky v rovině

Rozhodovačka • lehké

Pexeso

Hledání dvojic, které k sobě patří.

Délka úsečky v rovině

Délka úsečky

Pexeso • střední

Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Délka úsečky v rovině

Krok po kroku • lehké

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Délka úsečky v rovině

Psaná odpověď • střední

Předcházející

Navazující

Cvičení

Délka úsečky v rovině

umime.to/GMC

Přesouvání