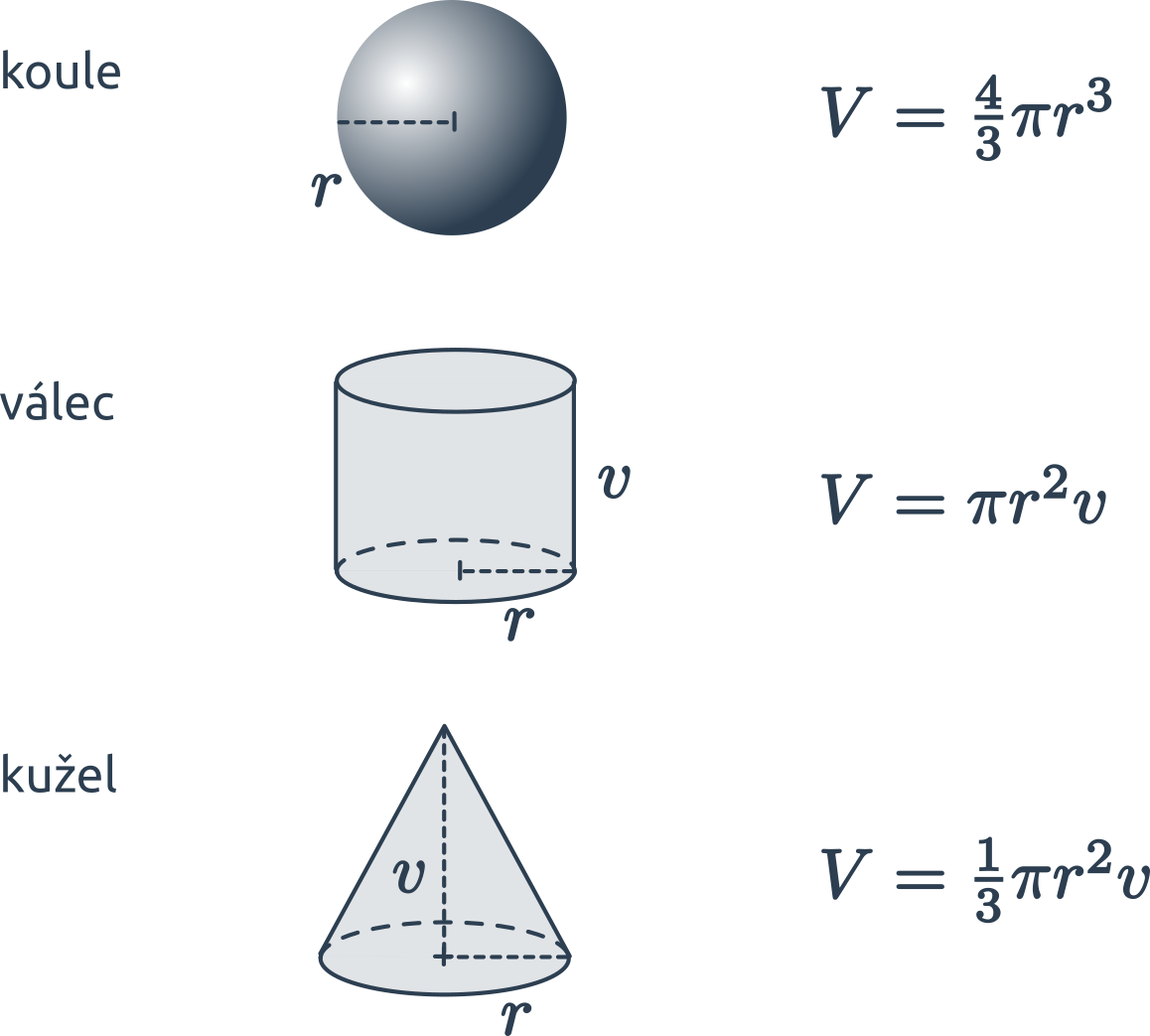
Objem „kulatých“ těles vypočítáme za využití konstanty \pi \approx 3{,}14 159 265. Ve vzorcích označuje r poloměr (koule či podstavy) a v výšku válce.
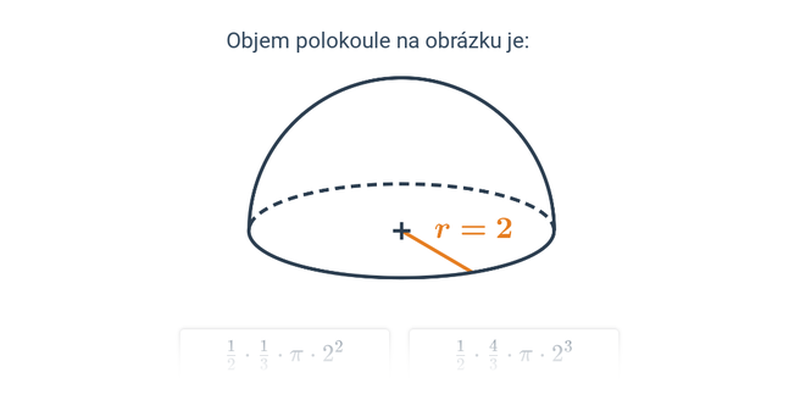
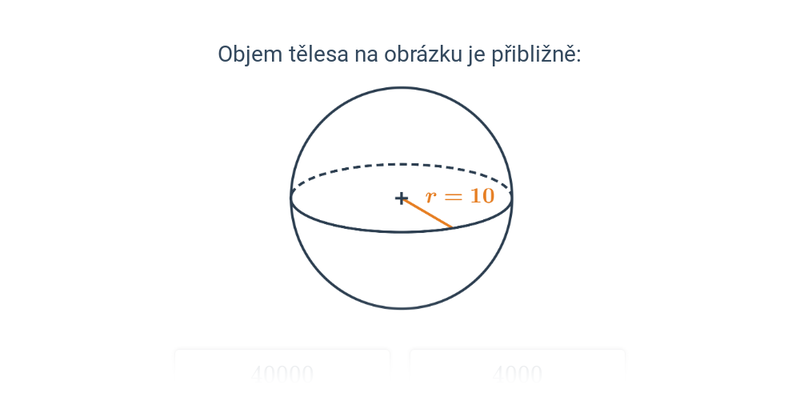
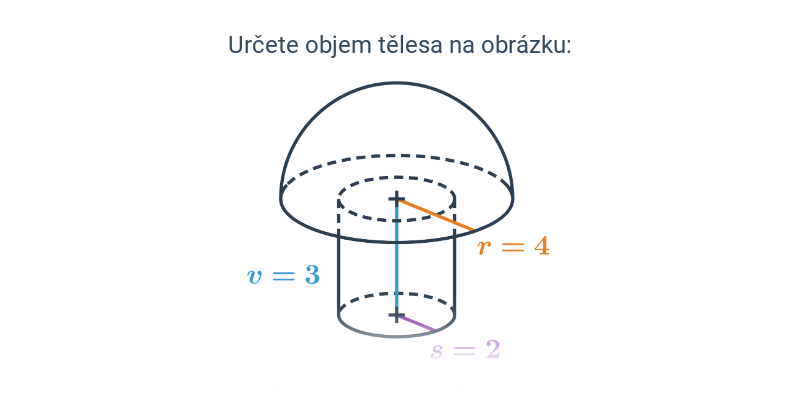
- Objem koule je V = \frac43 \pi r^3.
- Objem válce je obsah (kruhové) podstavy vynásobený výškou, tedy V = S_p \cdot v = \pi r^2 v.
- Objem kužele je jedna třetina obsahu podstavy vynásobeného výškou, tedy V = \frac13 S_p \cdot v = \frac13 \pi r^2 v.
Příklad: objem koule s daným poloměrem
Určete objem koule o poloměru 3 m.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Dosadíme za r známou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 3^3 m³ = 36 \pi m³ \doteq 113 m³
Velikost poloměru je zadaná v metrech, proto je výsledný objem koule v metrech krychlových.
Příklad: objem koule s daným průměrem
Určete objem koule o průměru 4 dm.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Známe průměr, proto umíme určit poloměr koule jako polovinu průměru r=\frac42=2 dm
- Dosadíme za r spočítanou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 2^3 dm³ = \frac{32}{3} \pi dm³ \doteq 33{,}5 dm³
Velikost průměru je zadaná v decimetrech, proto je výsledný objem koule v decimetrech krychlových.
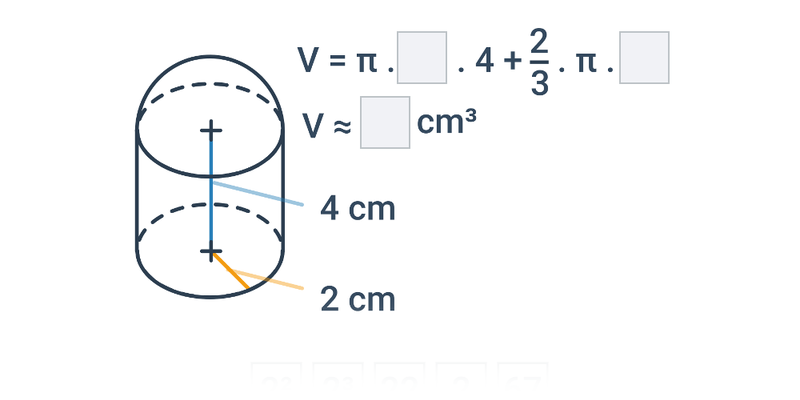
Příklad: objem válce
Určete objem válce o poloměru podstavy 5 mm a výšce 0{,}1 cm.
- Poloměr podstavy a výšku máme v různých jednotkách. Převedeme velikost výšky na milimetry, abychom měli všechny údaje v mm.
- r=5 mm, v=0{,}1 cm = 1 mm
- Objem válce se známým poloměrem podstavy r a výškou v spočítáme jako: V = \pi r^2 v
- Dosadíme za r a v známé hodnoty v mm.
- Daný válec má objem: V = \pi \cdot 5^2 \cdot 1 mm³ = 25 \pi mm³ \doteq 78{,}5 mm³
Výpočty provádíme s velikostí poloměru i výšky v milimetrech, proto je výsledný objem válce v milimetrech krychlových.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.