Výpis souhrnů
Rovinné útvary
Podtémata
- Rovinné útvary
- Trojúhelník
- Obsah trojúhelníku
- Obvod trojúhelníku
- Pythagorova věta
- Pythagorova věta: základní použití
- Pythagorova věta: aplikace
- Euklidovy věty
- Pojmy související s trojúhelníkem
- Úhly v trojúhelníku
- Konstrukční úlohy: trojúhelníky
- Konstrukce trojúhelníků: známé délky stran
- Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
- Konstrukce trojúhelníků: věty sss, sus, usu, Ssu
- Konstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
- Čtverec a obdélník
- Konstrukce čtyřúhelníků: čtverce a obdélníky
- Obvod čtverce a obdélníku
- Obsah čtverce a obdélníku
- Rovnoběžník
- Konstrukce čtyřúhelníků: rovnoběžníky
- Obvod rovnoběžníku
- Obsah rovnoběžníku
- Lichoběžník
- Konstrukce čtyřúhelníků: lichoběžníky
- Obvod lichoběžníku
- Obsah lichoběžníku
- Kruh a kružnice
- Pojmy související s kružnicí
- Obvod kruhu, délka kružnice
- Obsah kruhu
- Úhly a kružnice
- Obsah kruhové výseče
- Délka oblouku
Rovinné útvary
Rovinné útvary jsou množiny bodů v rovině, tedy jde o dvourozměrné útvary. Nejznámější rovinné útvary jsou například čtverec, obdélník, trojúhelník, kružnice, kruh, rovnoběžník, lichoběžník, pravidelný nebo nepravidelný mnohoúhelník.
U některých rovinných útvarů umíme jednoduše spočítat jejich obvod a obsah.
NahoruTrojúhelník
Trojúhelník je základní geometrický útvar, který má tři vrcholy a tři strany. Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi.
Značení stran a úhlů v trojúhelníku:
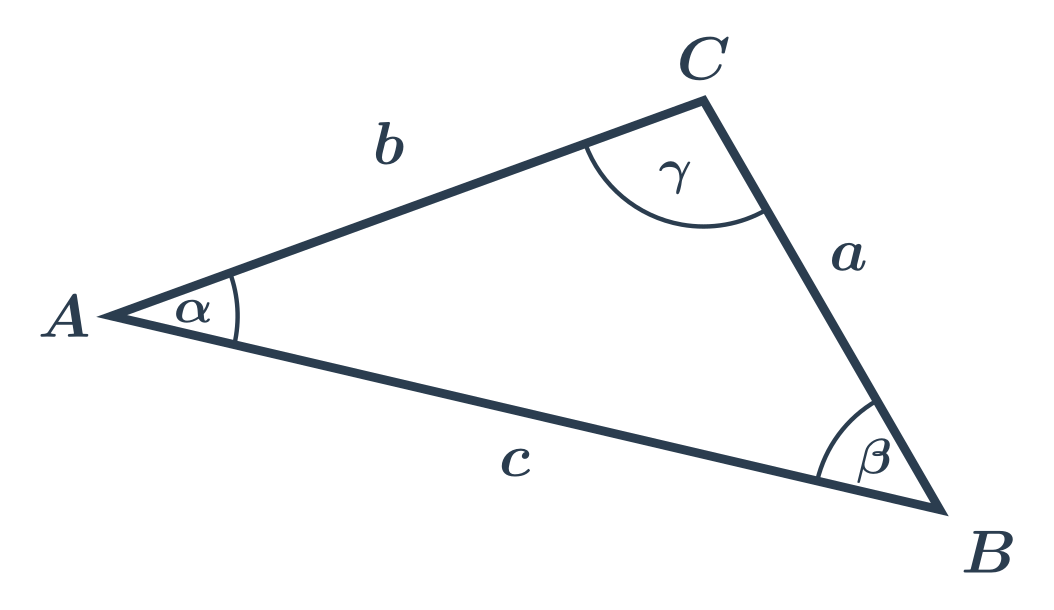
Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
Výšky příslušné stranám v trojúhelníku:
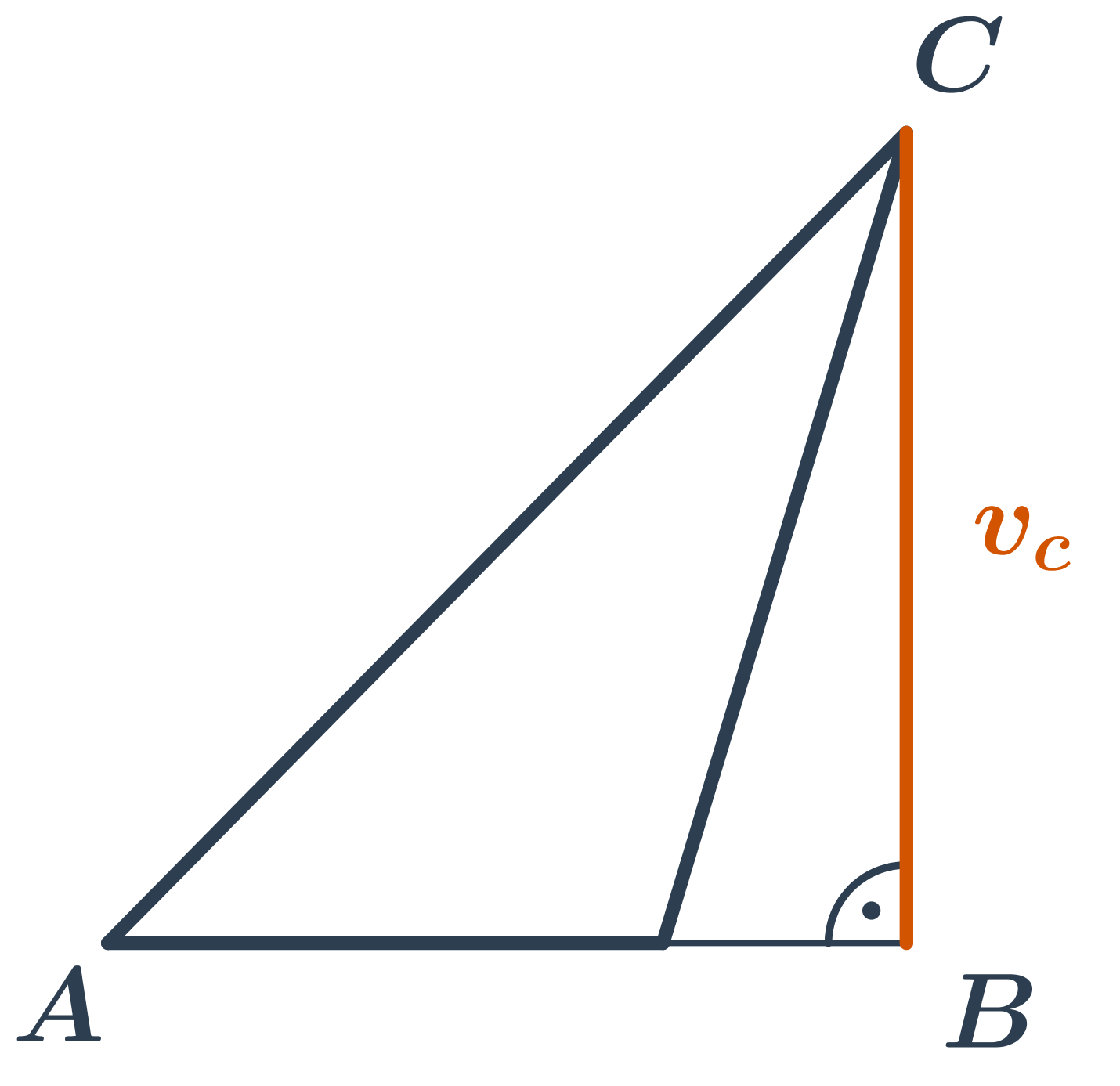
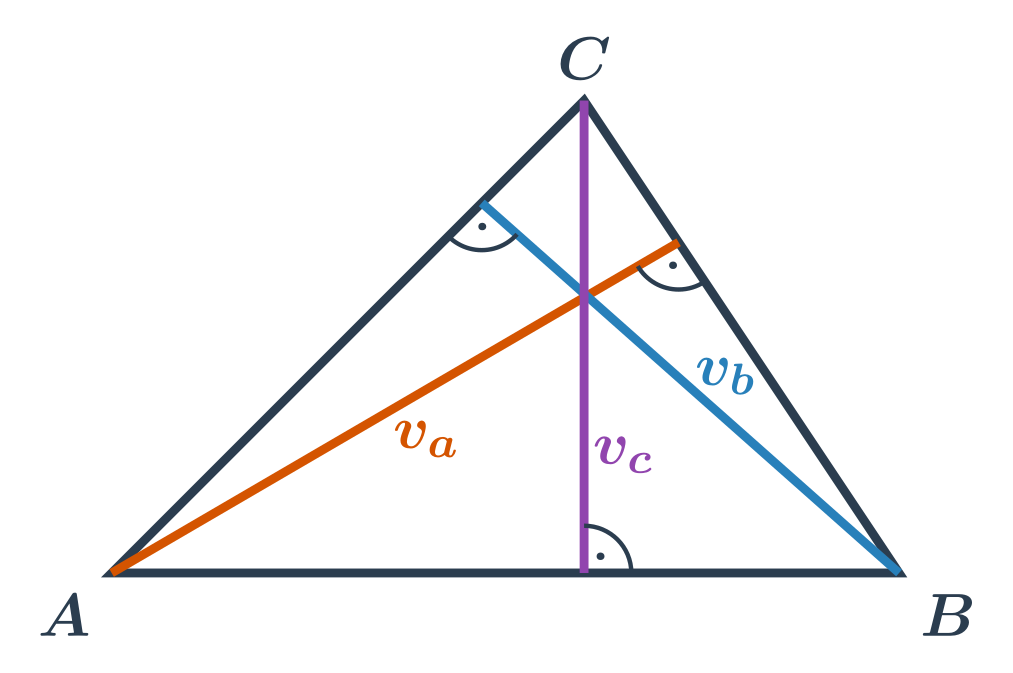 Výška v_a je vzdálenost bodu A od přímky, na které leží strana a. Tedy je to vzdálenost bodu A od paty kolmice na přímku BC vedené bodem A. Tato pata kolmice může a nemusí ležet přímo na straně a.
Výška v_a je vzdálenost bodu A od přímky, na které leží strana a. Tedy je to vzdálenost bodu A od paty kolmice na přímku BC vedené bodem A. Tato pata kolmice může a nemusí ležet přímo na straně a.
Témata související s trojúhelníkem:
- Pojmy související s trojúhelníkem – rovnoramenný, rovnostranný, výška, tečna, kružnice opsaná
- Obvod trojúhelníku, Obsah trojúhelníku – výpočty na základě zadaných údajů o trojúhelníku
- Úhly v trojúhelníku – součet úhlů, výpočty úhlů
- Konstrukční úlohy s trojúhelníky – narýsování trojúhelníku na základě zadaných údajů, např. za využití vět sss, sus, usu
- Pythagorova věta, Euklidovy věty, Goniometrické funkce – témata související s pravoúhlými trojúhelníky
Obsah trojúhelníku
Obsah trojúhelníku spočítáme jako součin délky libovolné strany trojúhelníka a výšky příslušné k této straně, takže: S_{\triangle} = \frac12 \cdot a \cdot v_a = \frac12 \cdot b \cdot v_b = \frac12 \cdot c \cdot v_c
Což si můžeme představit jako polovinu obsahu obdélníku, ve kterém je náš trojúhelník takto vepsán:
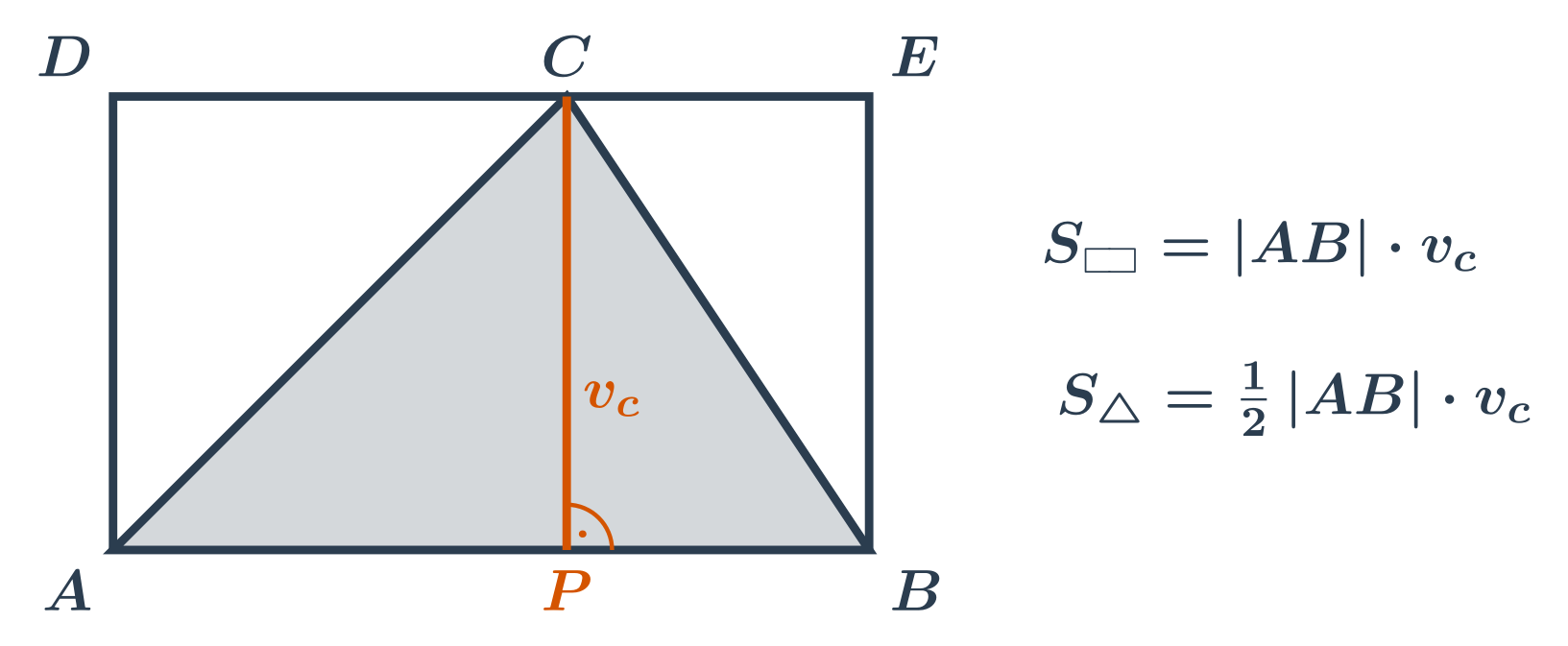
Příklady: obsah ostroúhlých trojúhelníků
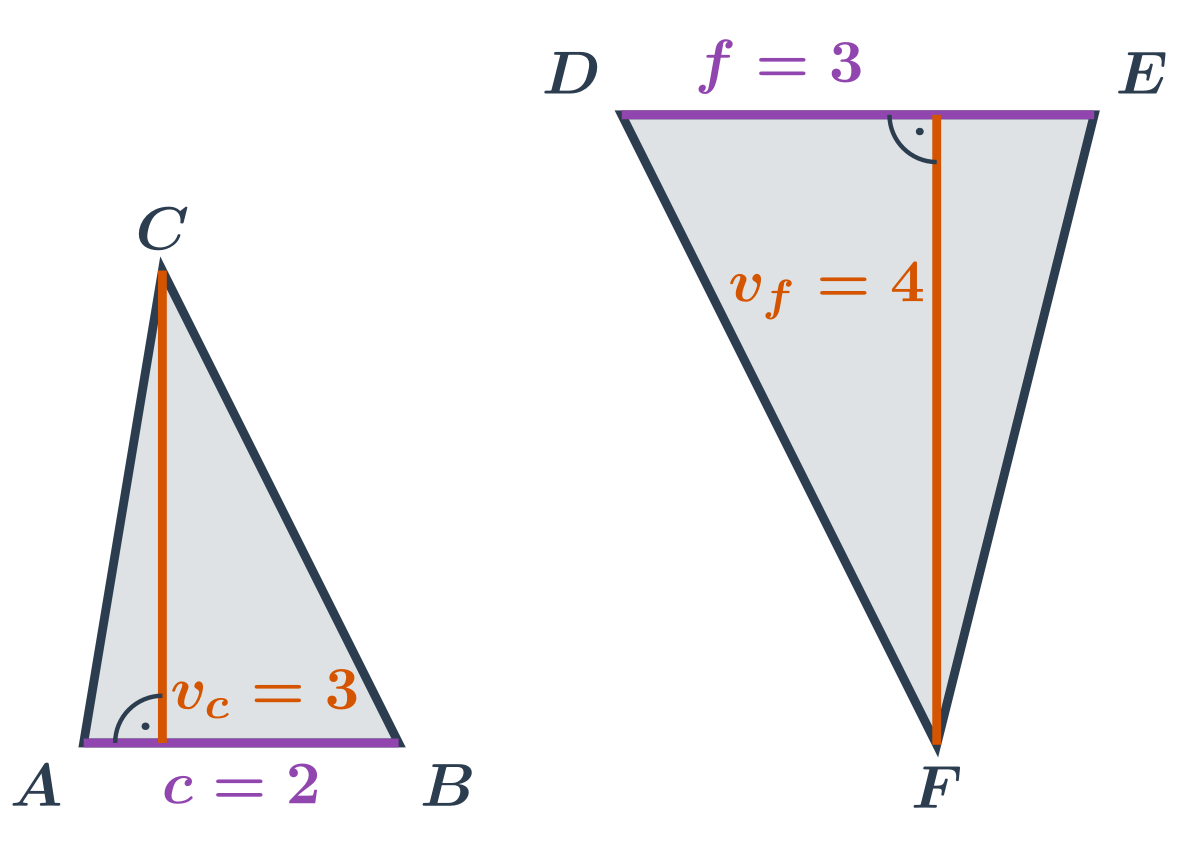
- Trojúhelník ABC: Délka strany \left| AB \right| je 2. Velikost k ní příslušné výšky v_c je 3. Obsah trojúhelníku ABC je roven \frac12 \cdot 2 \cdot 3 = 3.
- Trojúhelník DEF: Nevadí nám, že trojúhelník na náčrtku vypadá zvláštně natočený. Známe délku strany \left| DE \right|, což je 3. Velikost k ní příslušné výšky v_f je 4. Obsah trojúhelníku DEF je roven \frac12 \cdot 3 \cdot 4 = 6.
Příklady: obsah tupoúhlého a pravoúhlého trojúhelníku
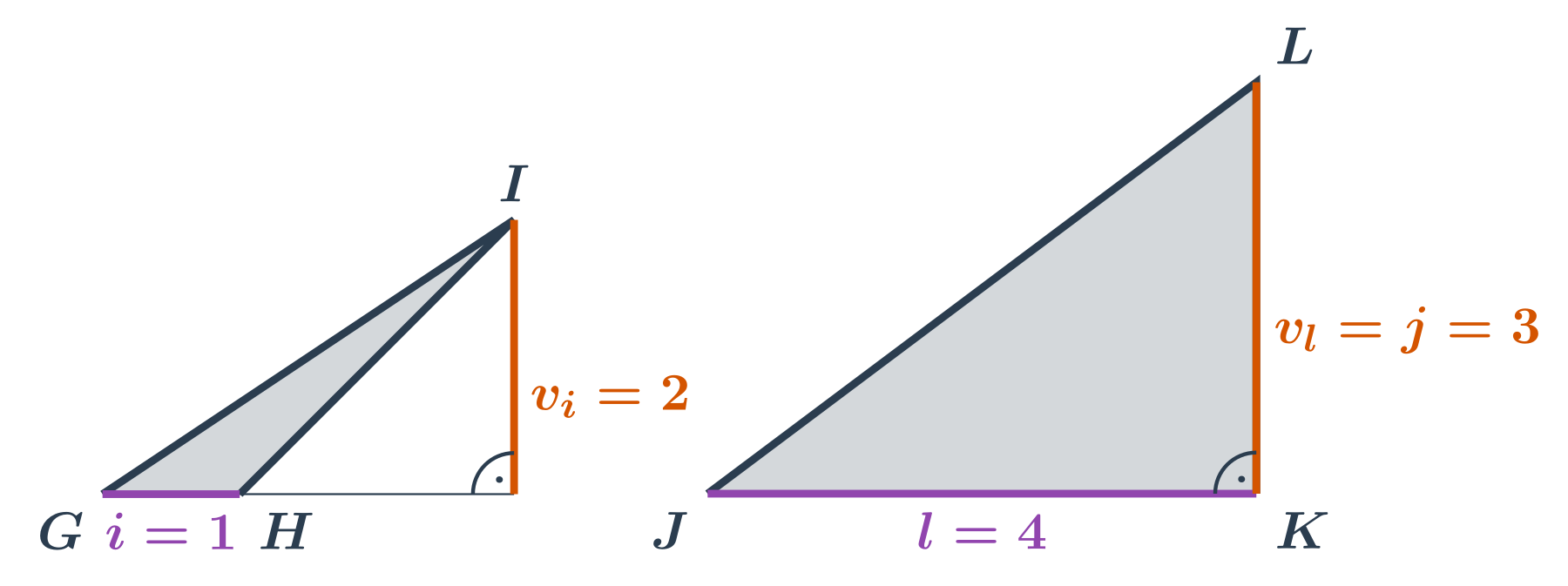
- Trojúhelník GHI: Nevadí nám ani když je pata kolmice, na které leží výška, mimo stranu trojúhelníka. Délka strany \left| GH \right| je 1. Velikost k ní příslušné výšky v_i je 2. Obsah trojúhelníku GHI je \frac12 \cdot 2 \cdot 1 = 1.
- Trojúhelník JKL: S pravoúhlým trojúhelníkem si také poradíme. Délka strany \left| JK \right| je 4. Velikost k ní příslušné výšky v_l je 3 (a je to zároveň i délka strany KL našeho trojúhelníku). Obsah trojúhelníku JKL je \frac12 \cdot 4 \cdot 3 = 6.
Obvod trojúhelníku
Obvod trojúhelníku spočítáme jako součet délek jeho stran: o=a+b+c
Příklad: obvod trojúhelníku
Trojúhelník na obrázku má délky stran a=10, b=8, c=14, takže jeho obvod je o=a+b+c=10+8+14=32.
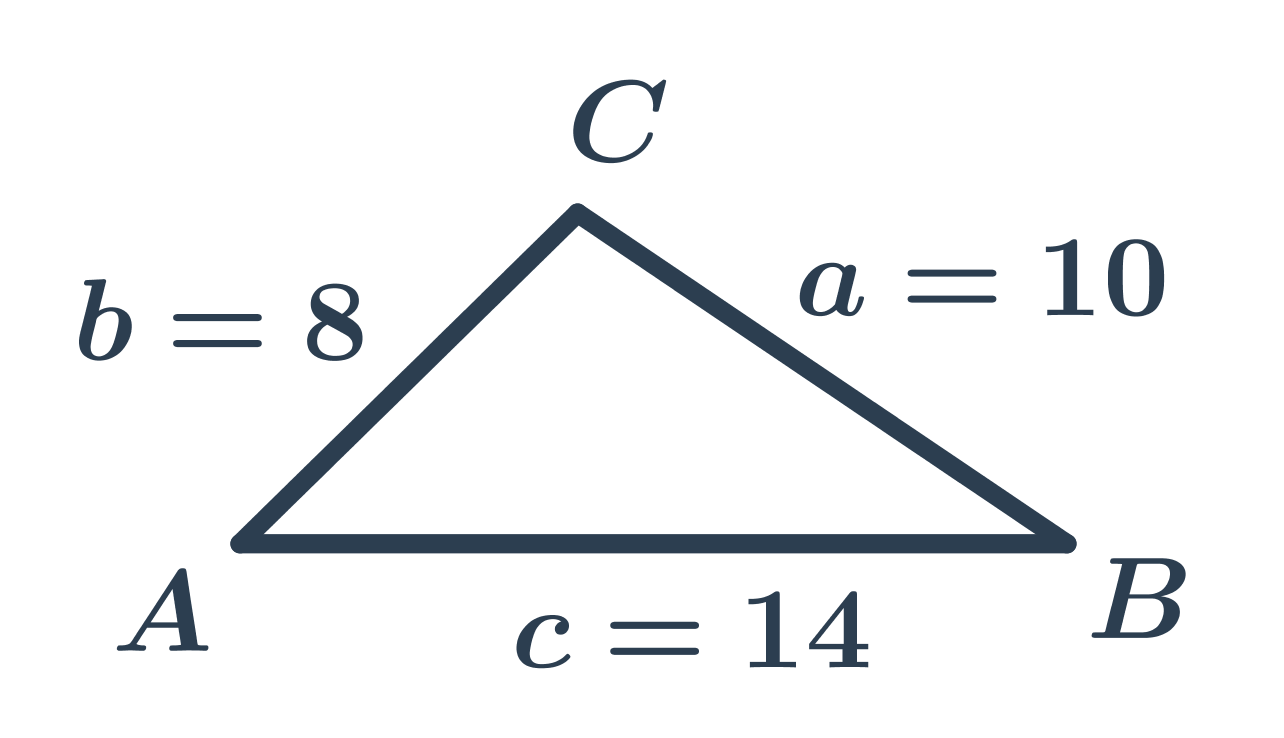
Pythagorova věta
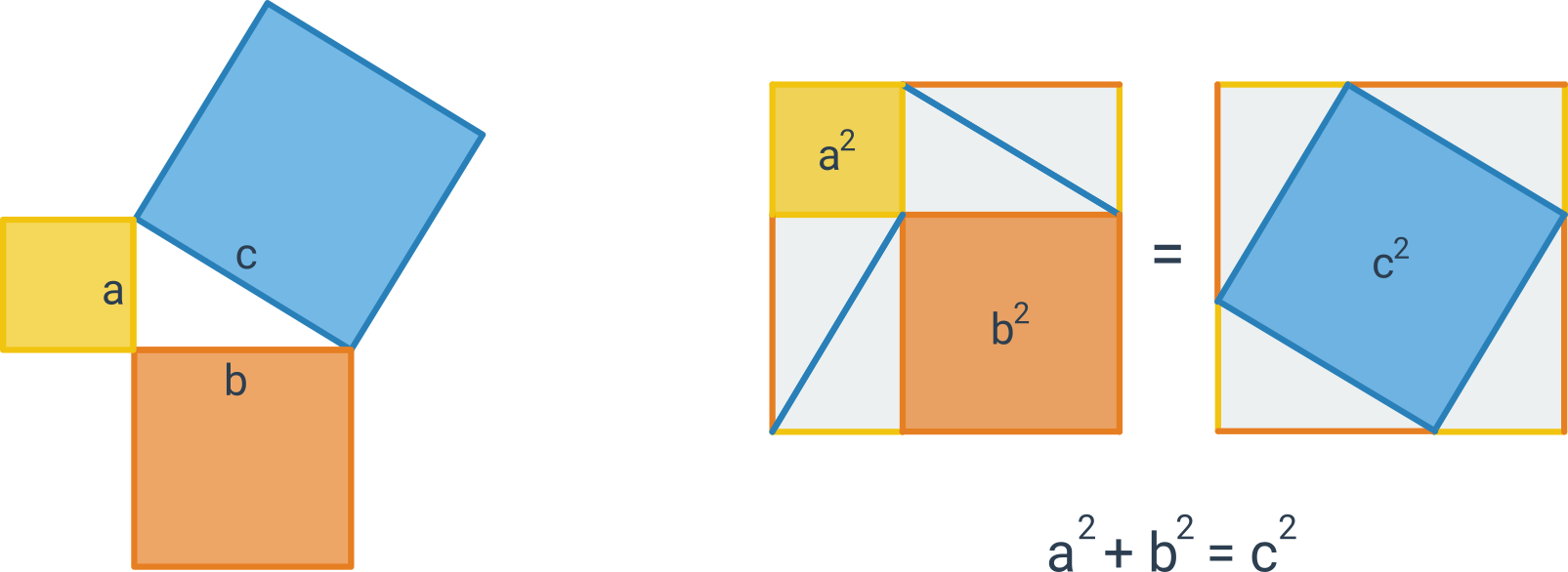
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Pythagorovu větu můžeme zapsat vztahem c^2 = a^2 + b^2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b. Platí i opačný směr: Pokud má trojúhelník strany délek a, b, c, které splňují rovnost c^2 = a^2 + b^2, pak musí jít o pravoúhlý trojúhelník s přeponou c.
Následující obrázek znázorňuje graficky znění věty a také „obrázkový důkaz“ této věty:
Procvičování Pythagorovy věty máme rozdělené do dvou podtémat:
- Základní použití – základní aplikace vzorce a^2+b^2=c^2, výpočty délky strany pravoúhlého trojúhelníku při znalosti zbylých dvou stran
- Aplikace – využití Pythagorovy věty v různých geometrických případech (např. výška trojúhelníku, uhlopříčka kvádru) a slovních úlohách
Komiks pro zpestření
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
Délka přepony c = \sqrt{a^2 + b^2}. Pokud má pravoúhlý trojúhelník odvěsny délky 3 metry a 6 metrů, přepona má délku \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6{,}41 metrů.
Délka odvěsny a = \sqrt{c^2-b^2}. Pokud má trojúhelník přeponu délky 8 metrů a jedna z odvěsen má délku 4 metry, druhá odvěsna má délku \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6{,}93 metrů.
Pythagorejské trojice jsou trojice celých čísel, které splňují a^2+b^2=c^2, tj. trojúhelník s příslušnými délkami stran je pravoúhlý. Typickým příkladem Pythagorejské trojice je (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.
Další příklady Pythagorejských trojic: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). Mezi Pythagorejské trojice patří také všechny násobky těchto trojic, např. (6, 8, 10); (9, 12, 15); (10, 24, 26). Pokud si zapamatujeme některé základní Pythagorejské trojice, především nejjednodušší trojici (3, 4, 5), tak nám to může usnadnit výpočty.
NahoruPythagorova věta: aplikace
Pythagorova věta má v geometrii velice široké využití, protože mnoho složitějších útvarů můžeme rozložit na pravoúhlé trojúhelníky.
Typickým příkladem aplikace Pythagorovy věty je výpočet délky uhlopříčky čtverce nebo výšky rovnostranného trojúhelníku:
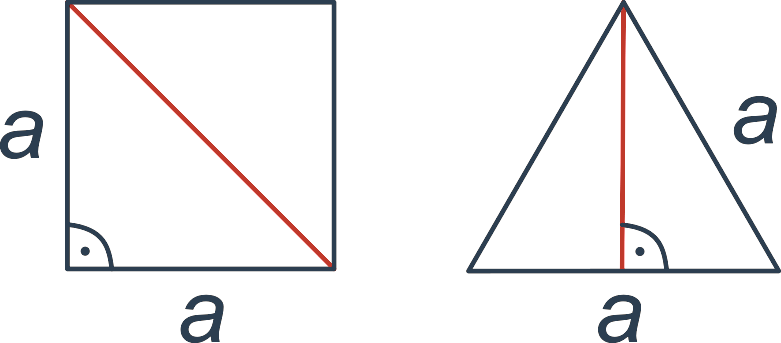
Ve čtverci o straně a tvoří uhlopříčka přeponu pravoúhlého trojúhelníku s odvěsnami délky a. Pro délku uhlopříčky u tedy platí u^2 = a^2 + a^2. Po úpravách: u = \sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}. Například čtverec o straně 10 cm tedy má uhlopříčku délky 10\cdot \sqrt{2} \doteq 14,1 cm.
V rovnostranném trojúhelníku o straně a tvoří výška odvěsnu pravoúhlého trojúhelníku s přeponou délky a a odvěsnou délky \frac{a}{2}. Pro délku výšky v tedy platí v^2 + \large(\frac{a}{2}\large)^2 = a^2. Po úpravách dostáváme v^2 = a^2 - \frac{a^2}{2^2} = \frac{3}{4}a^2, v = a\frac{\sqrt{3}}{2}. Například v rovnostranném trojúhelníku o straně 5 metrů má tedy výška délku \frac{\sqrt{3}}{2}\cdot 5 \doteq 4,33 metru.
NahoruEuklidovy věty
Euklidovy věty jsou dvě tvrzení o vlastnostech pravoúhlého trojúhelníku.
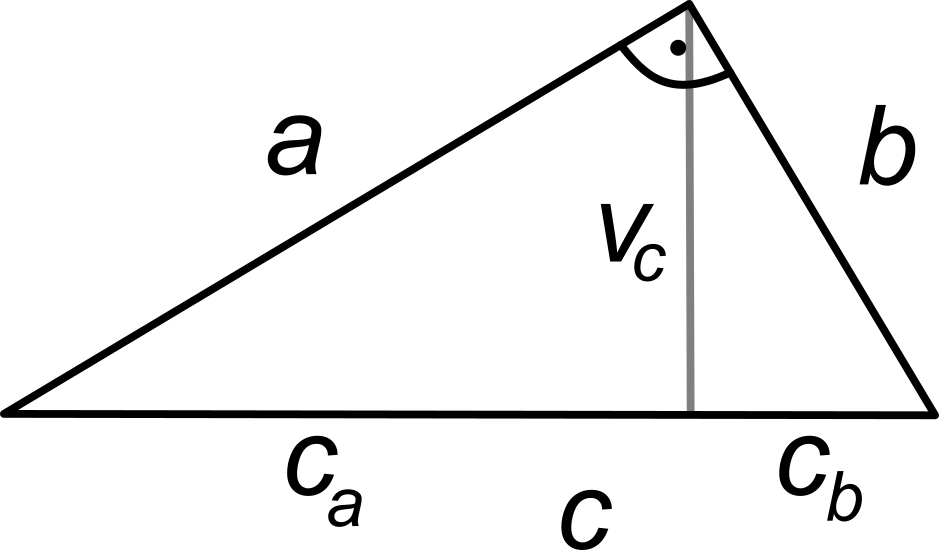
Euklidova věta o výšce
Obsah čtverce sestrojeného nad výškou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z obou úseků přepony:
v_c^2 = c_a\cdot c_b
Euklidova věta o odvěsně
Obsah čtverce sestrojeného nad odvěsnou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z přepony a úseku přepony k této odvěsně přilehlého.
- a^2 = c\cdot c_a
- b^2 = c\cdot c_b
Pojmy související s trojúhelníkem
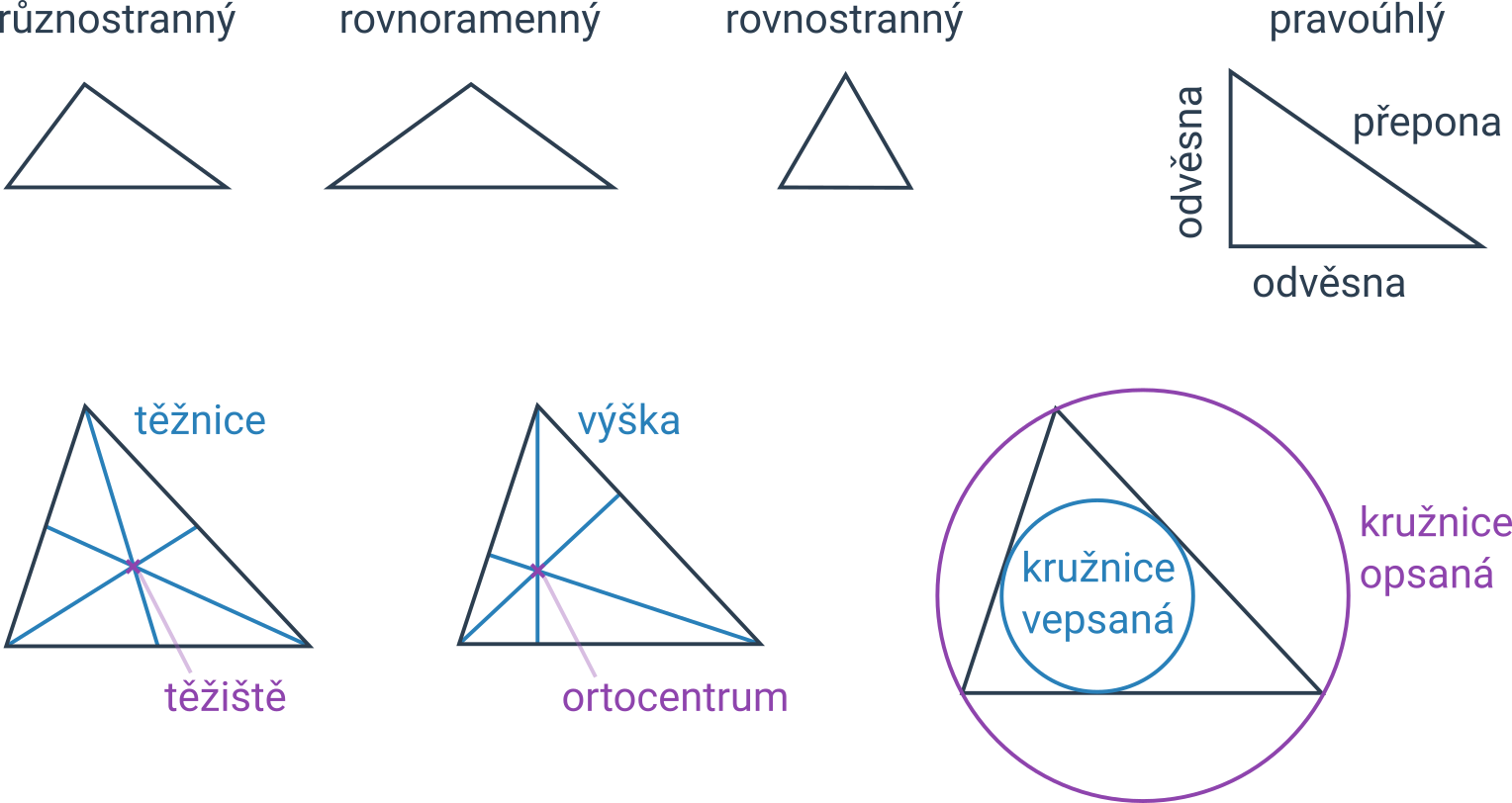
| obecný (různostranný) trojúhelník | trojúhelník, ve kterém žádné dvě strany nejsou shodné |
| rovnoramenný trojúhelník | trojúhelník, který má dvě strany shodné |
| rovnostranný trojúhelník | trojúhelník, který má všechny tři strany shodné |
| pravoúhlý trojúhelník | trojúhelník, který má jeden úhel pravý |
| odvěsna | strana sousedící s pravým úhlem v pravoúhlém trojúhelníku |
| přepona | strana protilehlá k pravému úhlu v pravoúhlém trojúhelníku |
| těžnice | úsečka spojující střed strany a protilehlý vrchol trojúhelníku |
| těžiště | průsečík těžnic |
| výška | úsečka spojující vrchol trojúhelníku a patu kolmice vedené tímto vrcholem na protější stranu |
| ortocentrum | průsečík výšek |
| kružnice opsaná | kružnice, která prochází všemi vrcholy trojúhelníku |
| kružnice vepsaná | kružnice, která se dotýká všech stran trojúhelníku |
| střed kružnice opsané | průsečík os stran |
| střed kružnice vepsané | průsečík os úhlů |
Pozn. Přesné definice rovnoramenného trojúhelníku se liší: někteří autoři vyžadují „alespoň“ dvě strany shodné, jiní „právě“ dvě strany shodné. Rozdíl je v tom, zda rovnostranné trojúhelníky považujeme za rovnoramenné.
NahoruÚhly v trojúhelníku
Při výpočtu velikosti neznámého úhlu v trojúhelníku využíváme základní vlastnosti, že součet vnitřních úhlů v trojúhelníku je 180°.
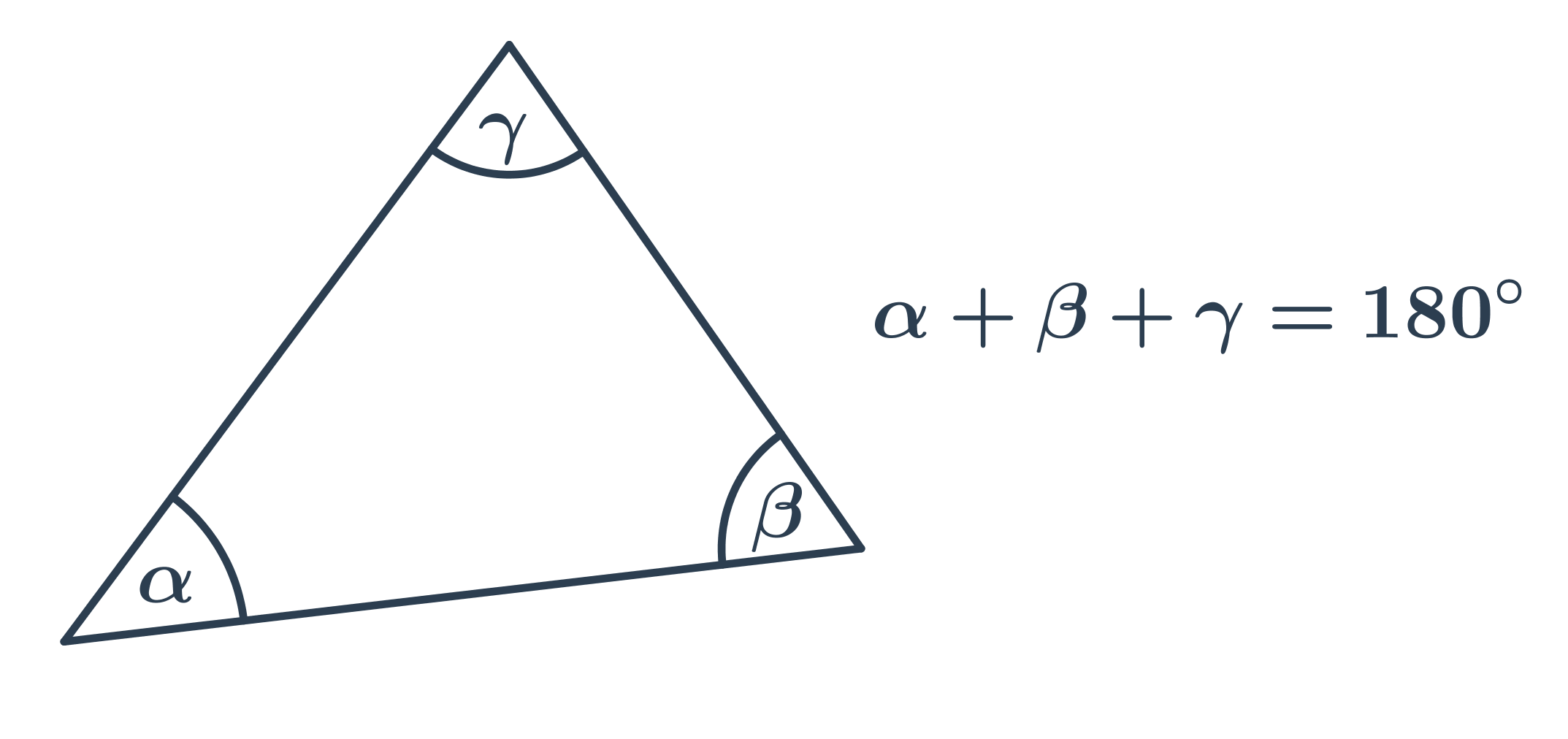
Speciální případy:
- V rovnostranném trojúhelníku mají všechny vnitřní úhly velikost 60°.
- V rovnoramenném trojúhelníku jsou oba úhly u základny stejné.
- V pravoúhlém trojúhelníku je velikost jednoho úhlu 90°, součet velikostí zbývajících dvou úhlů je také 90°.
Při výpočtu lze využít i vrcholových a vedlejších úhlů.
Příklad: výpočet velikosti úhlu
Určete velikost oranžového úhlu:
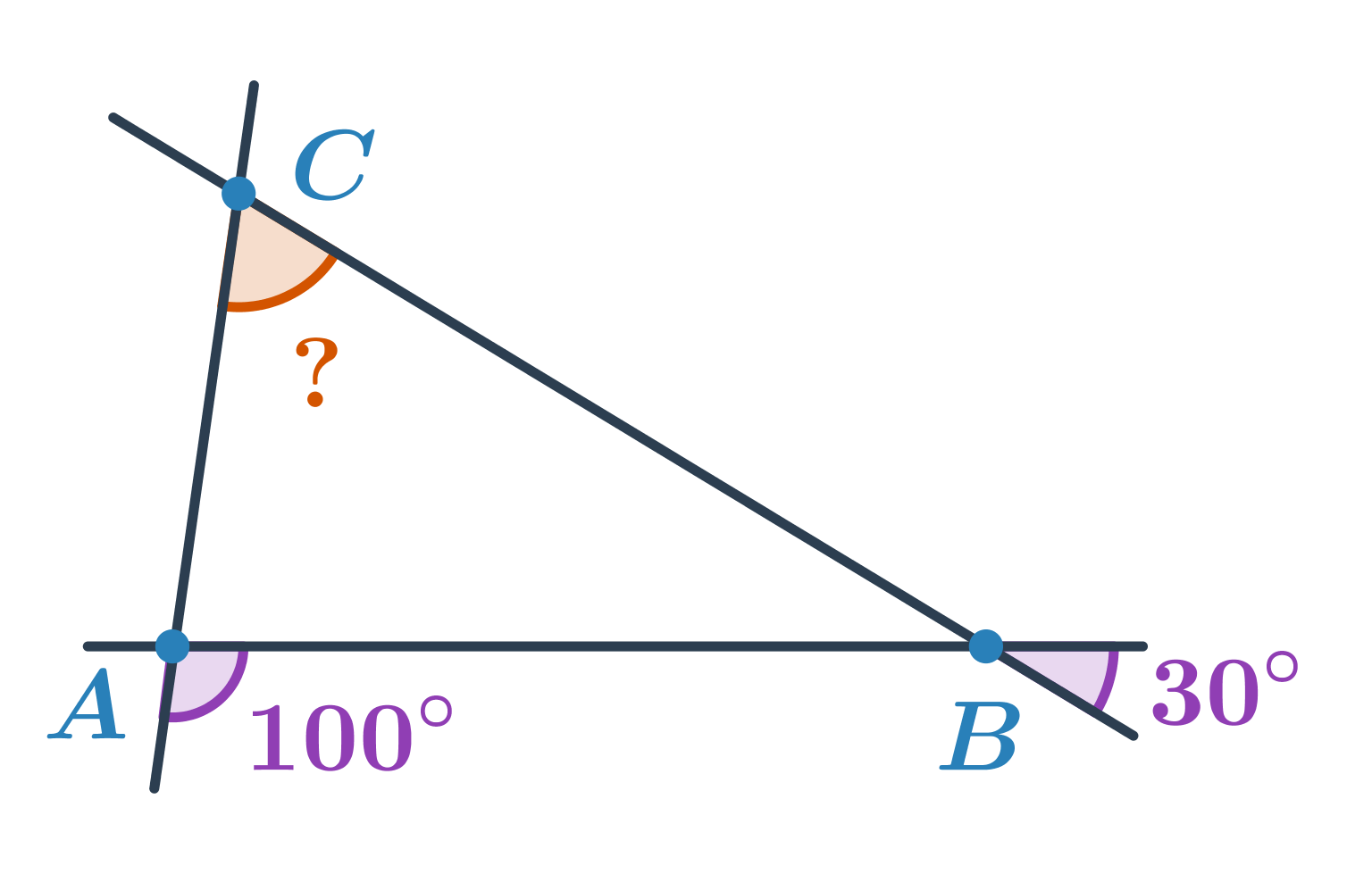
- Úhel u vrcholu B tvoří s úhlem o velikosti 30° dvojici vrcholových úhlů. Jeho velikost je tedy 30°.
- Úhel u vrcholu A tvoří s úhlem o velikosti 100° dvojici vedlejších úhlů. Jeho velikost je tedy 180°-100°=80°.
- Pro velikost neznámého úhlu u vrcholu C pak platí: 180°-80°-30°=70°
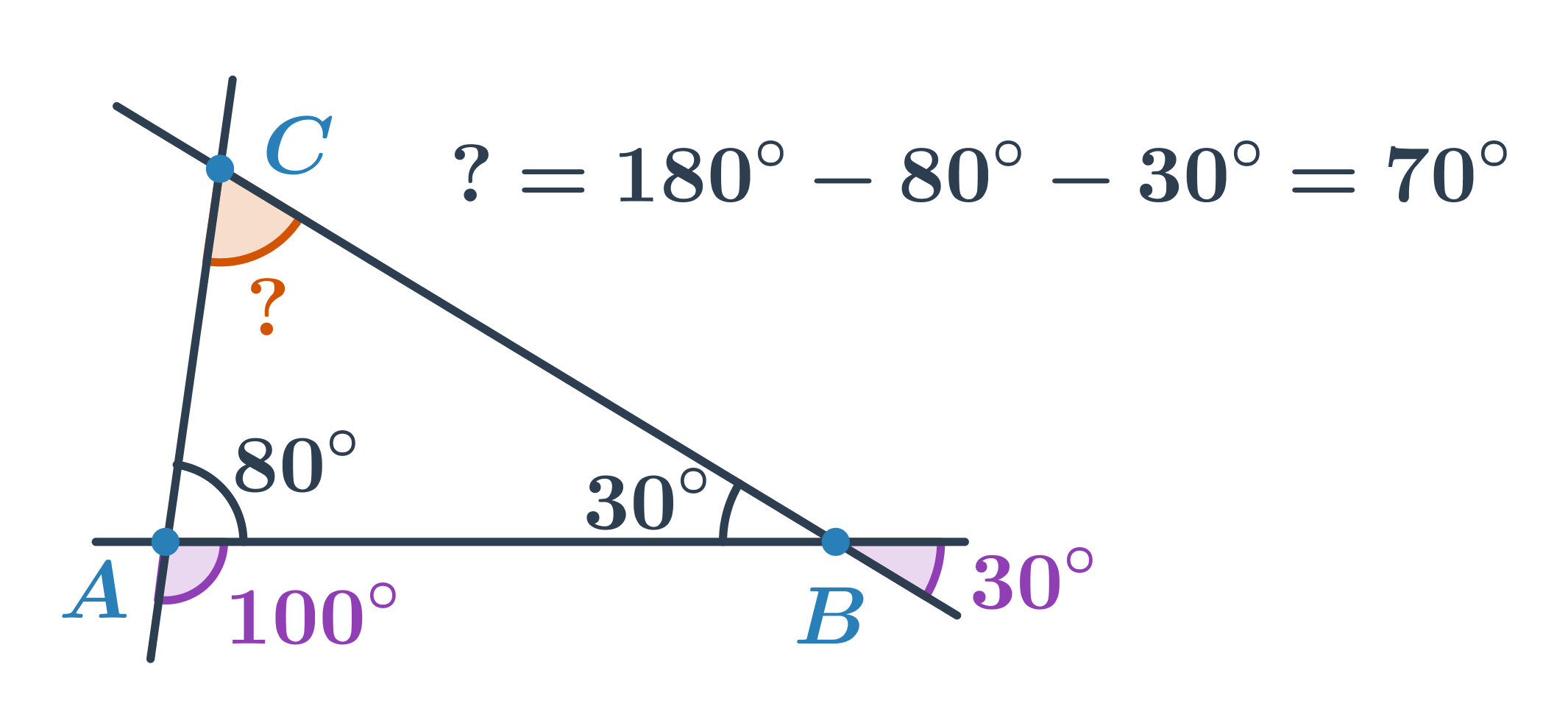
Konstrukční úlohy: trojúhelníky
Při řešení jednodušších úloh provádíme konstrukce trojúhelníků se známými délkami stran. Nesmíme přitom zapomínat, že platí tzv. trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, jedině pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
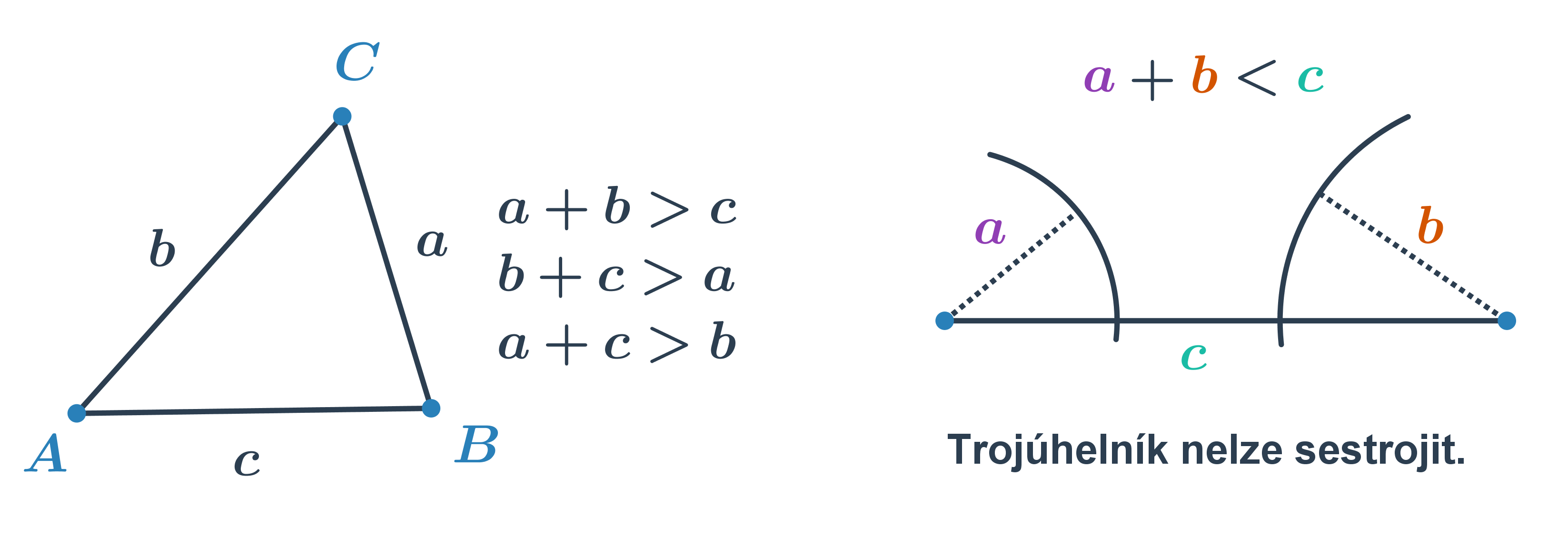
Občas má některý trojúhelník zajímavou vlastnost, která nám pomůže odvodit si potřebné informace k jeho sestrojení — může jít např. o konstrukci rovnoramenného nebo rovnostranného trojúhelníku.
Při řešení složitějších příkladů provádíme konstrukci trojúhelníků podle vět sss, sus, usu, Ssu, využíváme přitom známé věty o sestrojitelnosti trojúhelníků.
U nejtěžších příkladů, jako je konstrukce trojúhelníků, kdy známé údaje zahrnují těžnice, výšky, opsanou nebo vepsanou kružnici trojúhelníka využíváme při konstrukci další pojmy související s trojúhelníkem, či množiny bodů daných vlastností.
NahoruKonstrukce trojúhelníků: známé délky stran
Při konstrukci trojúhelníků můžeme každou stranu označit dvěma způsoby:
- přímo – strana a
- pomocí vrcholů – strana BC
Při konstrukcích také můžeme zaměňovat označení strany a její délky. Můžeme psát a=|BC|. Je třeba myslet i na pravidlo, že strana je pojmenovaná podle protějšího vrcholu.
Příklad: Je v trojúhelníku na obrázku délka strany a=8 cm?
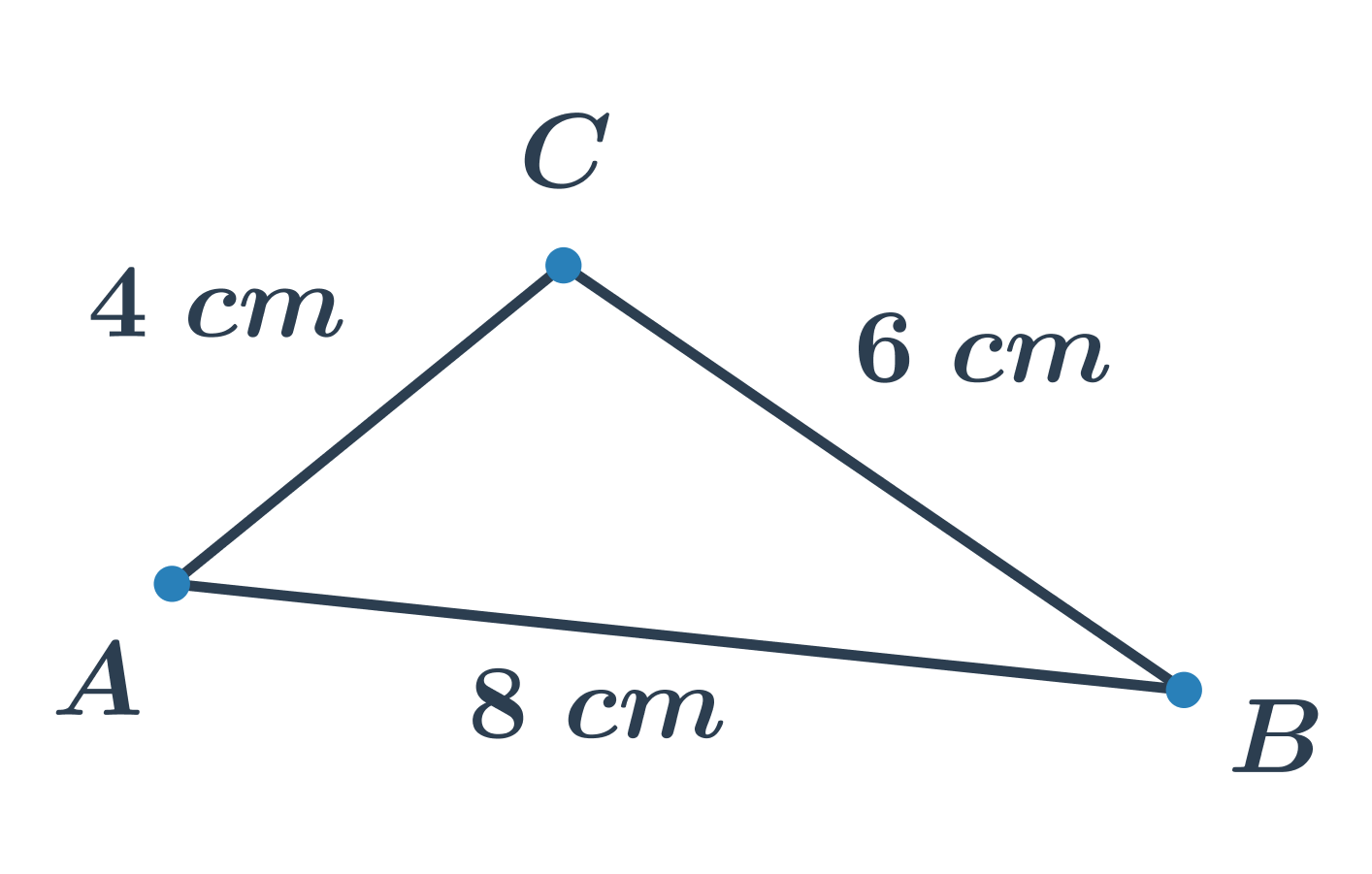
- Strana a leží proti vrcholu A. Je to tedy strana BC.
- Z obrázku vidíme, že |BC|=6 cm.
- Strana a tedy nemá délku 8 cm.
- Délku 8 cm má v tomto trojúhelníku strana AB, tedy strana c.
Lze sestrojit trojúhelník se stranami zadané délky?
- 6\ \text{cm}, 5\ \text{cm}, 4\ \text{cm} - součet dvou nejkratších stran je 4 + 5= 9 \ \text{cm}, to je více než 6\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.
- 6\ \text{cm}, 5\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 5 = 6\ \text{cm}, to je rovno délce třetí strany, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
- 5\ \text{cm}, 2\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 2 = 3\ \text{cm}, to je menší než délka třetí strany 5\ \text{cm}, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
- 7\ \text{cm}, 7\ \text{cm}, 7\ \text{cm} - součet dvou nejkratších stran je 7 + 7= 14\ \text{cm}, to je více než 7\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.
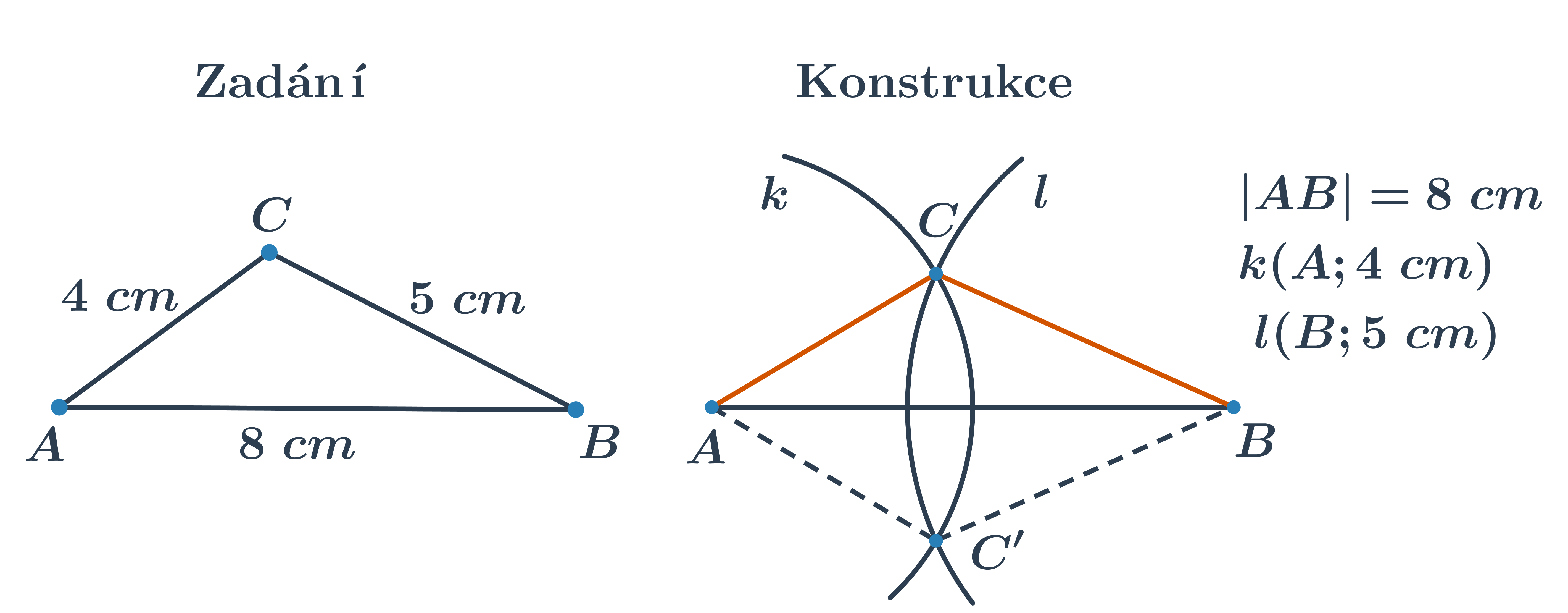
Při konstrukcích trojúhelníků, u kterých známe tři strany, postupujeme tak, že sestrojíme jako první libovolnou stranu, na obrázku například AB. K nalezení posledního vrcholu C použijeme dvě kružnice nebo jejich části. Výsledkem konstrukce jsou dva shodné (stejné) trojúhelníky, proto stačí sestrojit jen jeden.
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
Při konstrukci rovnoramenného trojúhelníku využíváme jeho základní vlastnosti:
- Má dvě strany (ramena) shodné. Vrchol proti základně tedy leží na ose základny.
- Shodné (stejně velké) jsou i vnitřní úhly při základně.
- Výška kolmá na základnu leží na ose základny a dělí rovnoramenný trojúhelník na dva shodné trojúhelníky.
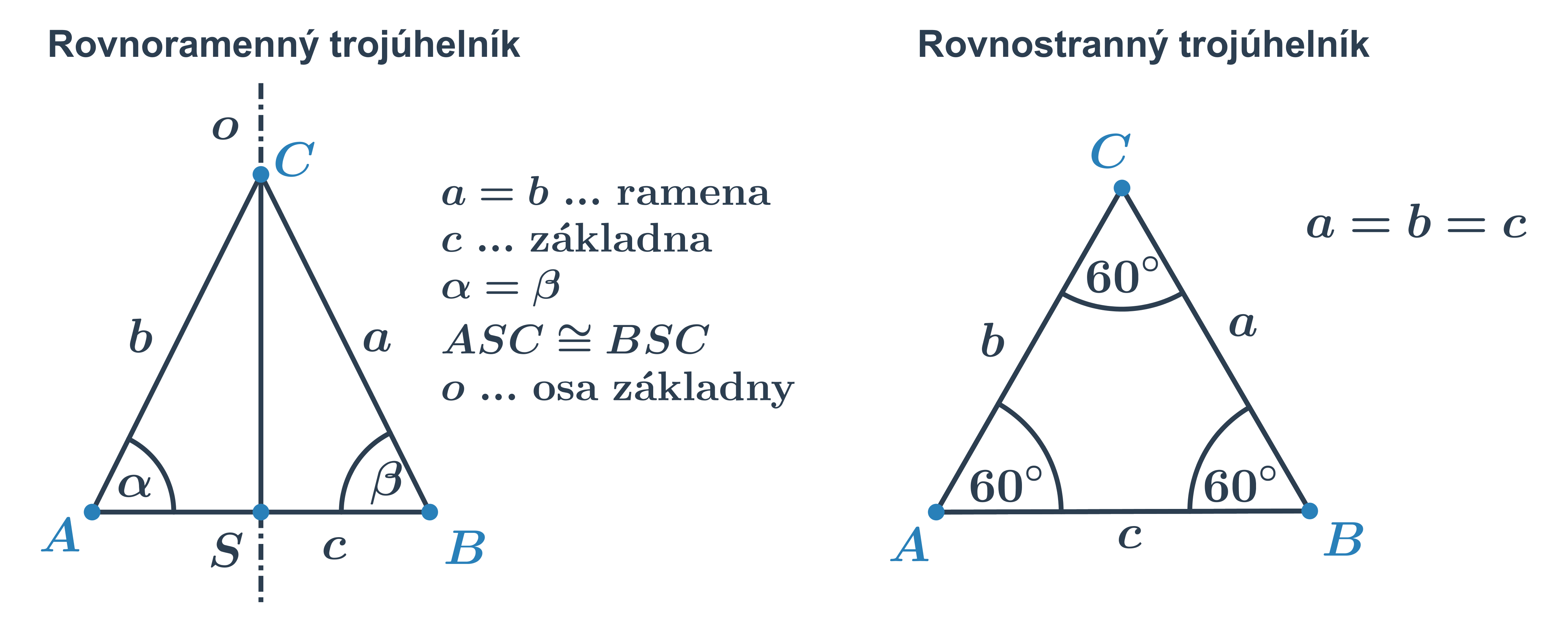
Rovnostranný trojúhelník můžeme chápat jako speciální případ rovnoramenného trojúhelníka. Má všechny strany stejně dlouhé a velikost všech jeho vnitřních úhlů je 60°.
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: věty sss, sus, usu, Ssu
Při složitějších příkladech využíváme věty o sestrojitelnosti trojúhelníků (kde s značí stranu a u úhel):
- Věta sss — v trojúhelníku jsou dány délky všech stran, pro které platí trojúhelníková nerovnost.
- Věta sus— v trojúhelníku jsou dány délky dvou stran a velikost úhlu, který svírají (menší než 180°).
- Věta usu — v trojúhelníku je dána délka jedné strany a velikosti 2 úhly k ní přiléhající (součet velikostí daných úhlů je menší než 180°).
- Věta Ssu — známe velikosti dvou stran trojúhelníka a velikost úhlu proti větší z těchto stran (velikost zadaného úhlu je menší než 180°).
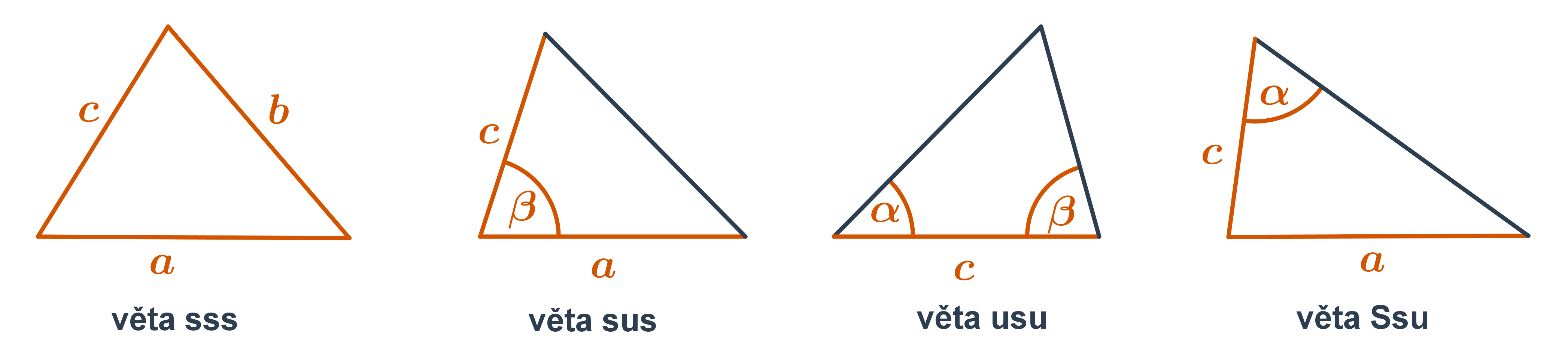
Tyto věty také používáme při určení shodnosti trojúhelníků.
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
Při řešení složitějších příkladů použijeme další pojmy související s trojúhelníkem, například výška, těžnice, střední příčka, kružnice opsaná či vepsaná.
Těžnice je úsečka, která spojuje vrchol trojúhelníku se středem protější strany. Každý trojúhelník má tři těžnice a jejich průsečík tvoří těžiště trojúhelníku. Těžiště rozděluje každou těžnici v poměru 2 : 1. Delší část těžnice je úsečka mezi vrcholem a těžištěm.
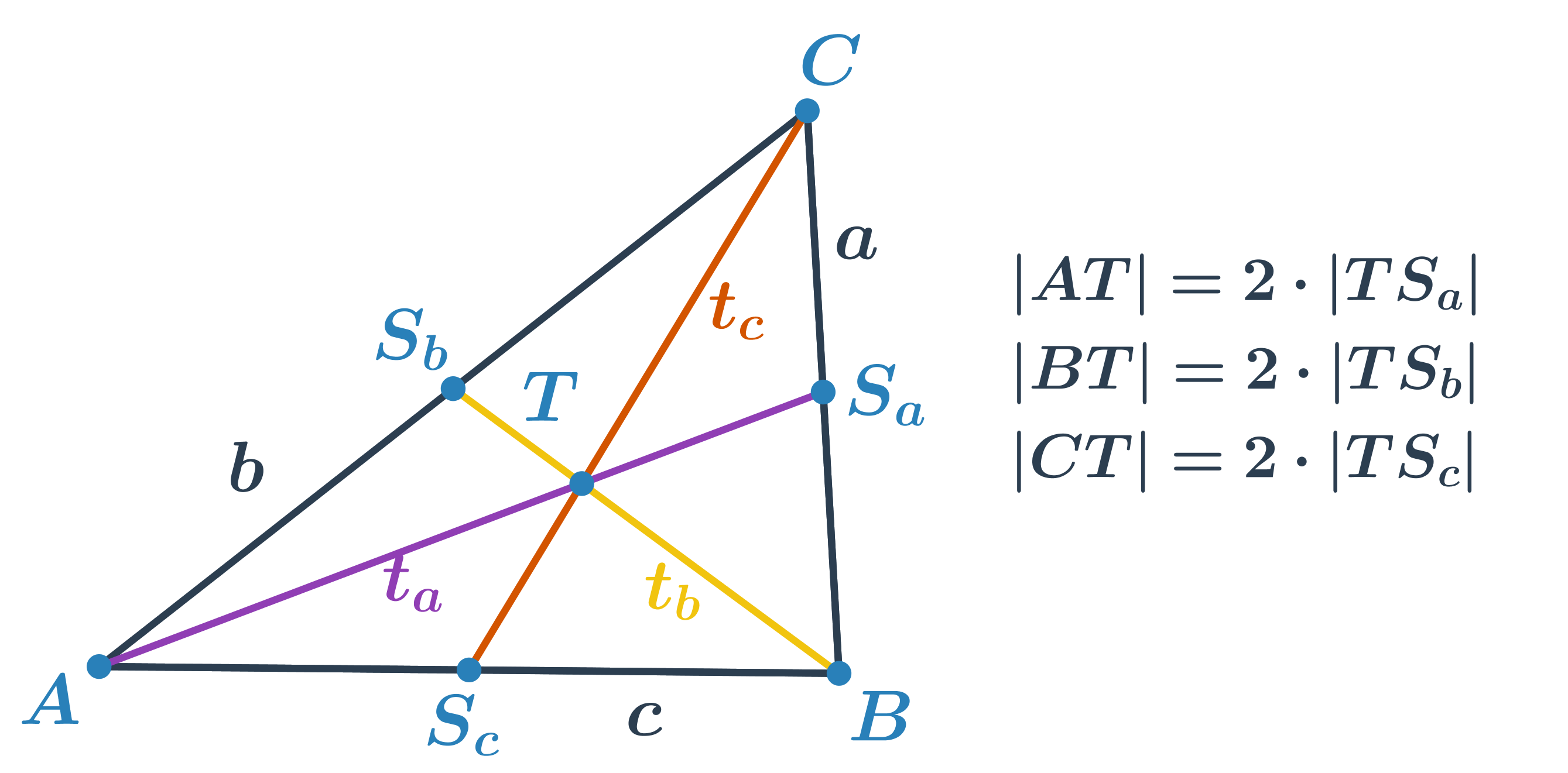
Střední příčka trojúhelníku je úsečka, která spojuje středy dvou stran v trojúhelníku. Je rovnoběžná se stranou, jejíž střed nespojuje a její délka je rovna polovině délky této strany.
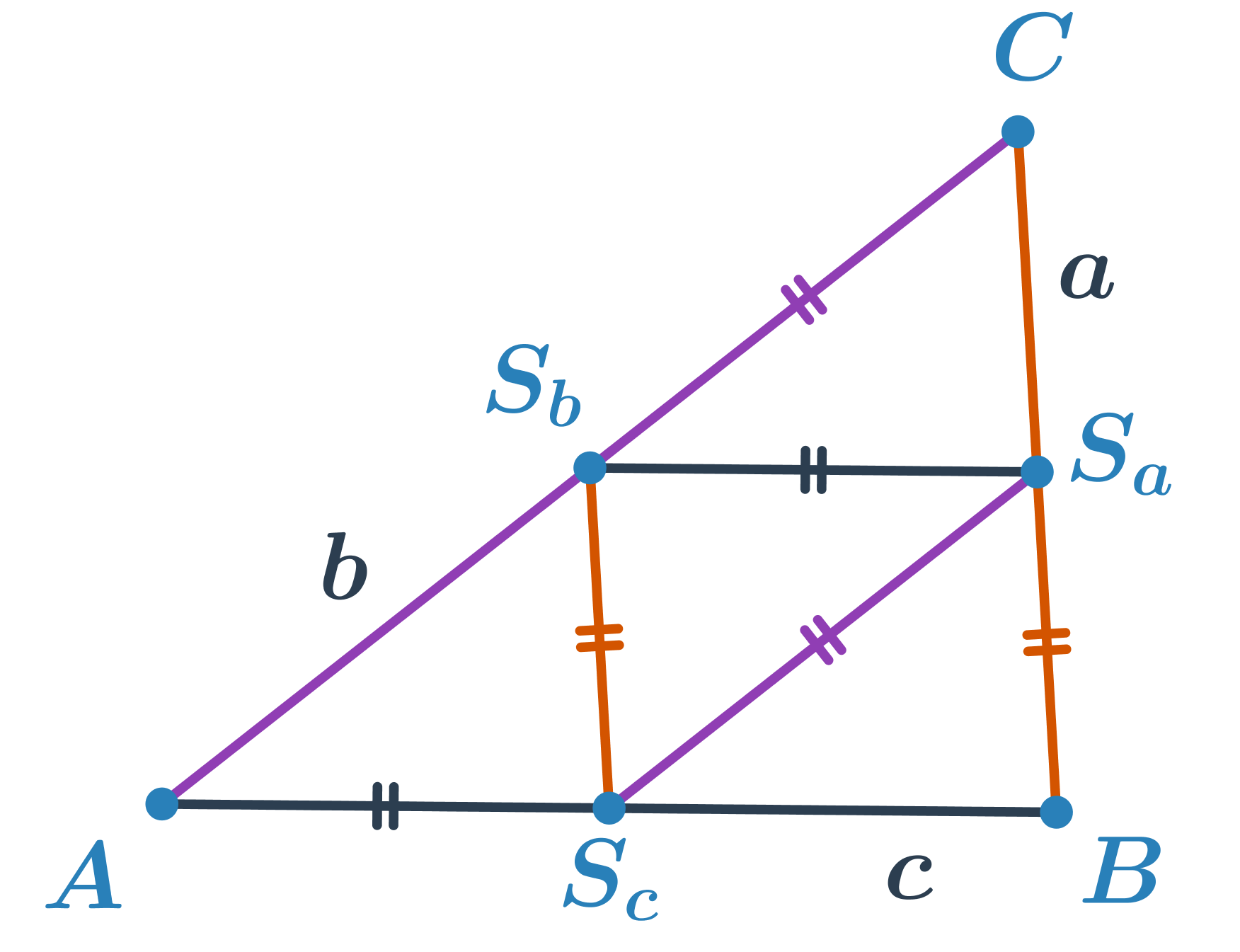
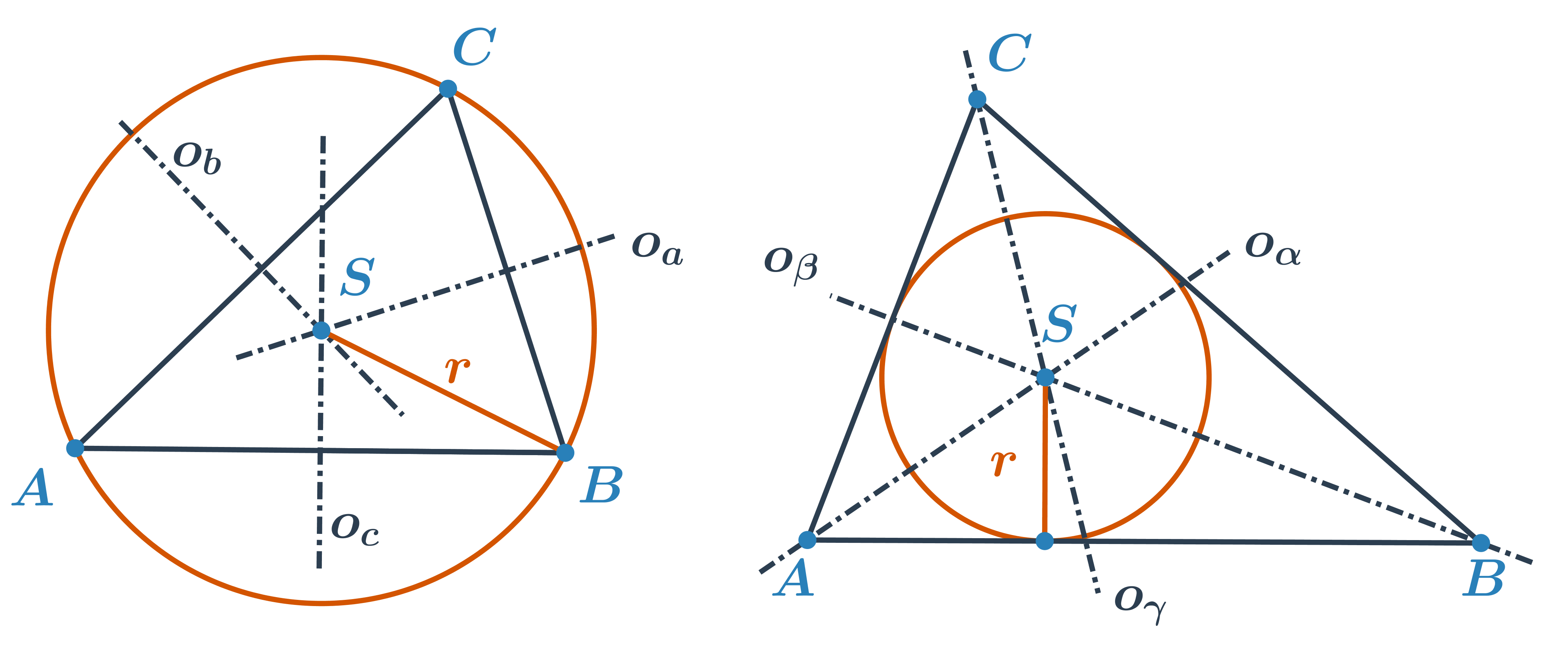
Kružnice opsaná je kružnice, která prochází všemi vrcholy trojúhelníka. Její střed leží v průsečíku os stran. To znamená, že střed kružnice opsané je stejně vzdálen od všech vrcholů trojúhelníku.
Kružnice vepsaná je kružnice, která se dotýká všech stran trojúhelníku. Její střed leží v průsečíku os vnitřních úhlů trojúhelníku. To znamená, že střed kružnice vepsané je stejně vzdálen od všech tří přímek, na kterých leží strany trojúhelníku.
Kromě níže uvedených interaktivních cvičení jsou k dispozici také pracovní listy k vytištění a rýsování na papíře:
NahoruČtverec a obdélník
Obdélník patří mezi čtyřúhelníky. Je to rovnoběžník, který má všechny vnitřní úhly pravé.
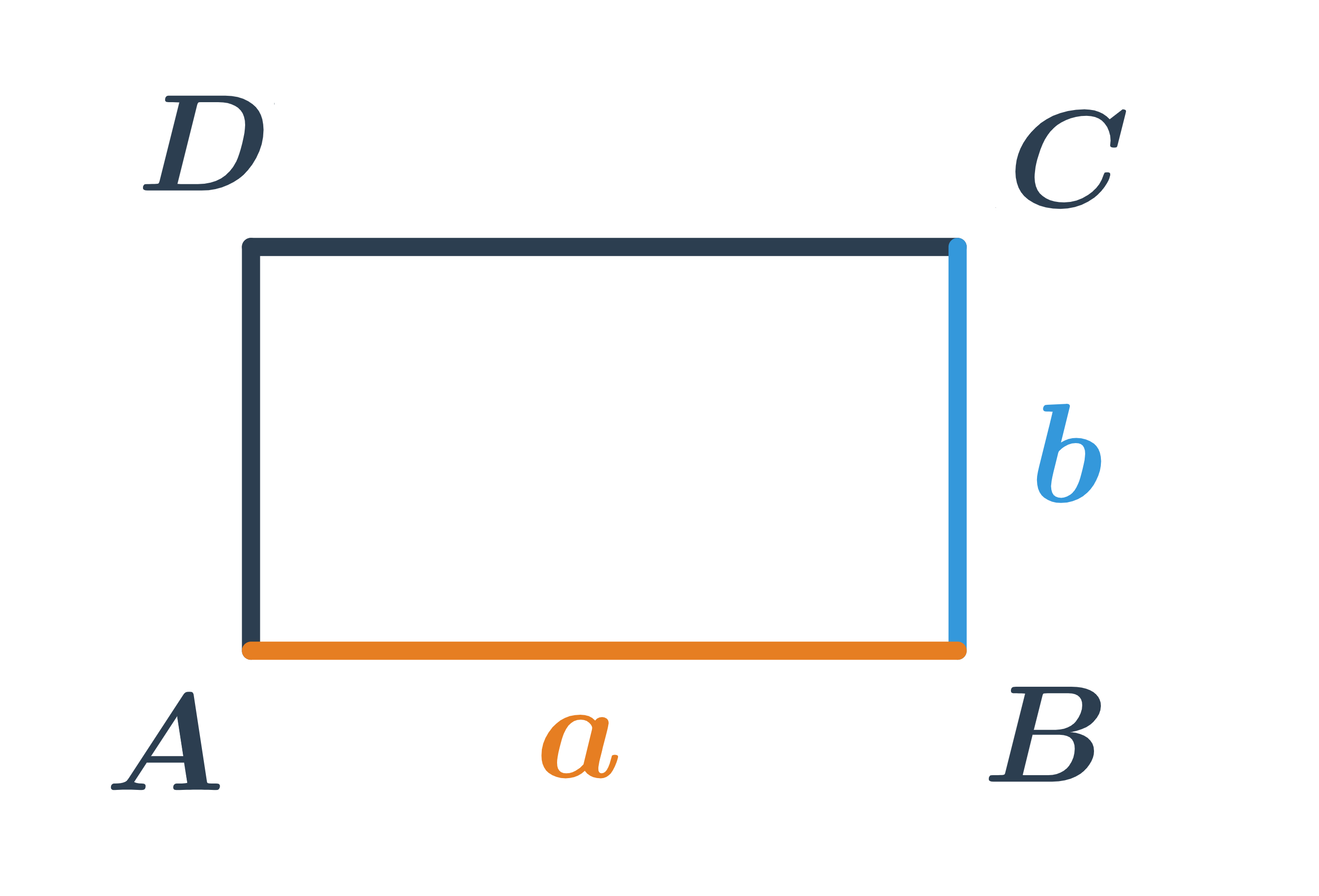
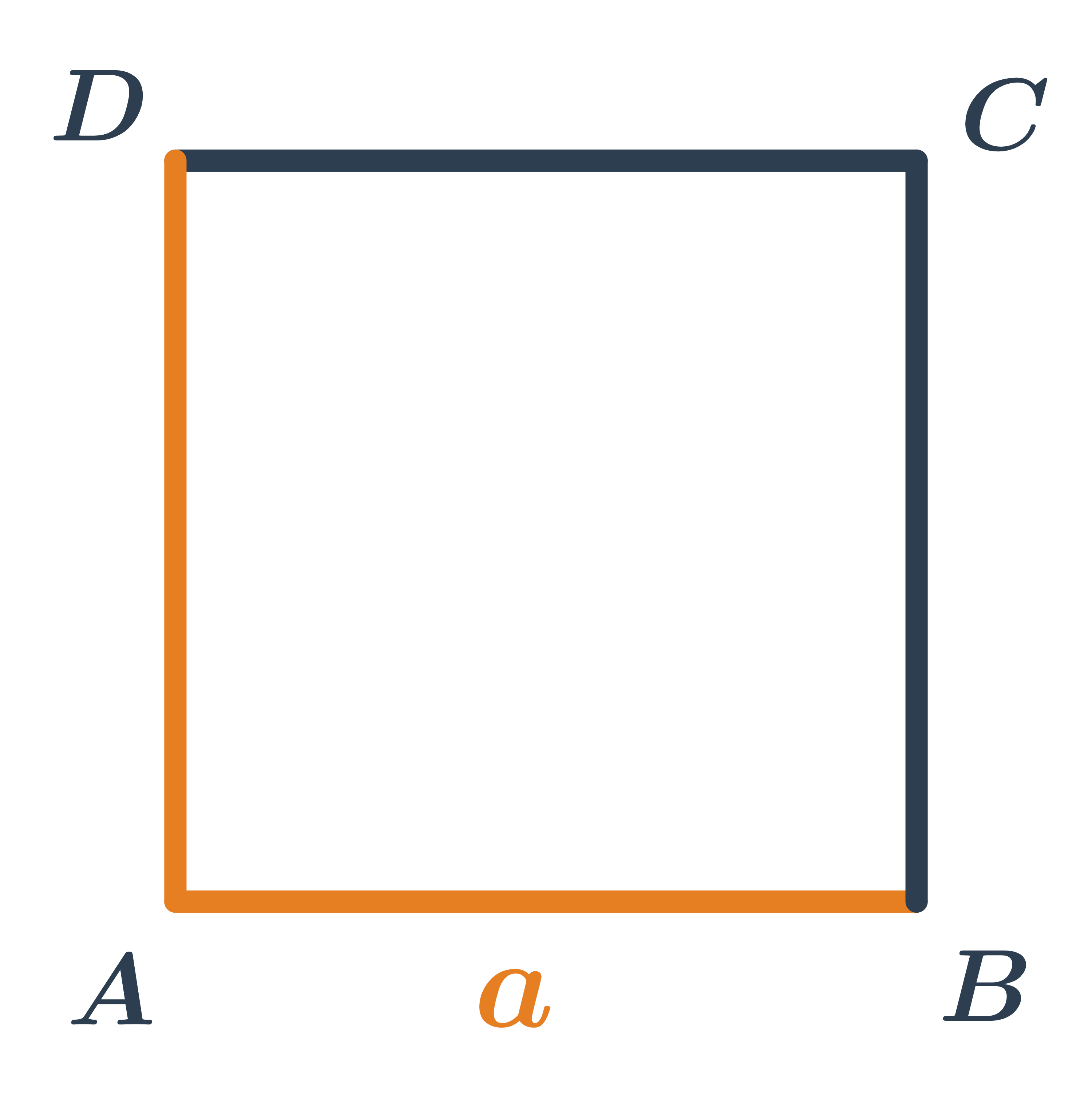
Čtverec je zvláštní případ obdélníku, který má všechny strany stejně dlouhé.
Konstrukce čtyřúhelníků: čtverce a obdélníky
Konstrukce obdélníků
Při řešení konstrukčních úloh s obdélníky využíváme jejich následující vlastnosti:
- Všechny vnitřní úhly obdélníku jsou pravé, sousední strany jsou tedy na sebe kolmé.
- Protější strany jsou rovnoběžné.
- Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
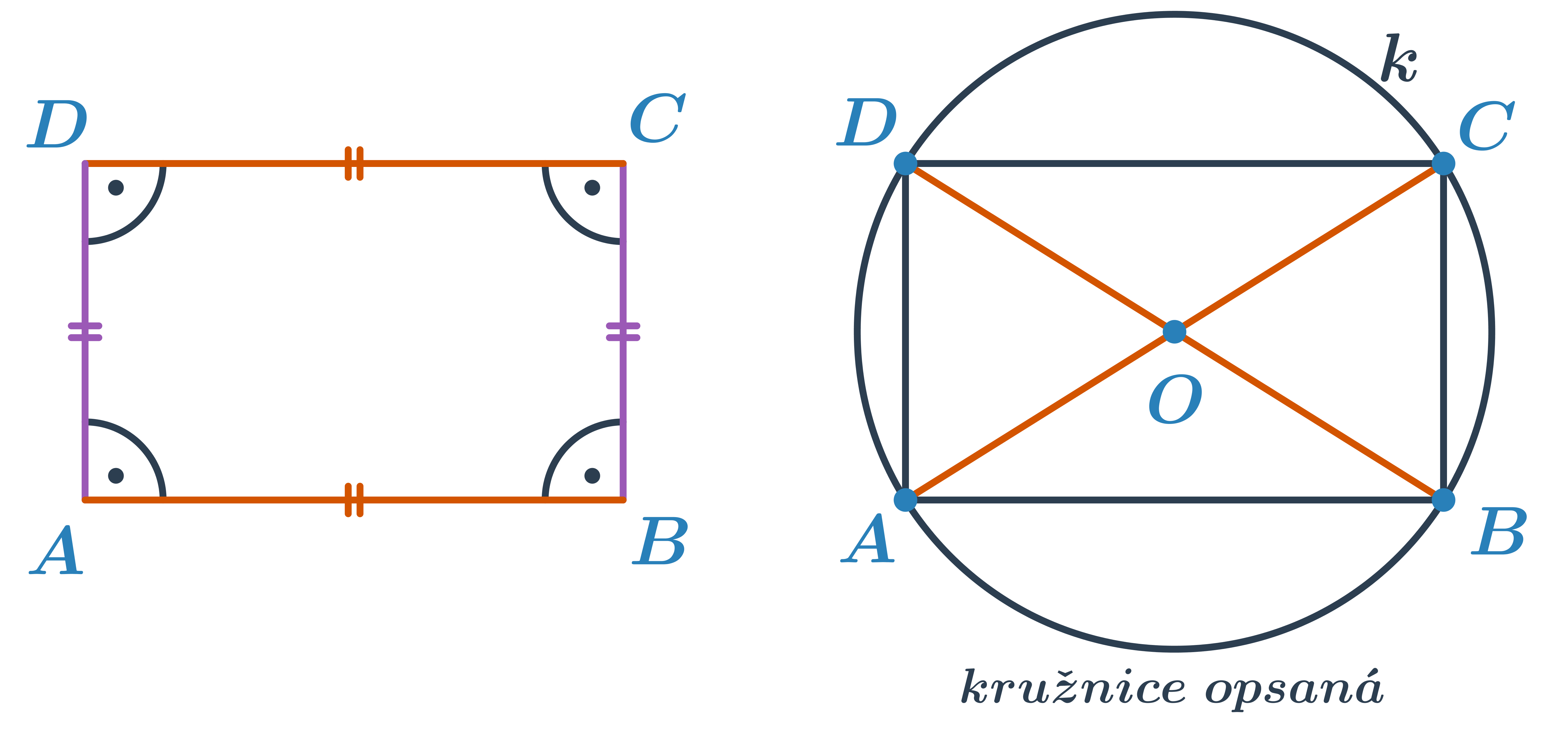
- Úhlopříčky obdélníku jsou stejně dlouhé a navzájem se půlí.
- Každému obdélníku lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy obdélníku a má střed v průsečíku úhlopříček.
Konstrukce čtverců
Čtverec můžeme považovat za zvláštní případ obdélníku (nebo rovnostranného rovnoběžníku). Stejně jako obdélník má všechny vnitřní úhly pravé, sousední strany jsou na sebe kolmé a protější strany čtverce jsou rovnoběžné. Úhlopříčky čtverce se protínají v bodě, který nazýváme střed čtverce. Čtverce mají všechny pěkné vlastnosti obdélníků a ještě některé speciální navíc:
- Všechny strany čtverce jsou stejně dlouhé.
- Úhlopříčky čtverce jsou stejně dlouhé, jsou na sebe kolmé, procházejí středem čtverce a navzájem se půlí.
- Každému čtverci lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy čtverce a má střed ve středu čtverce.
- Každému čtverci lze také vepsat kružnici. Nazýváme ji kružnice vepsaná, dotýká se stran čtverce a má střed ve středu čtverce.
Kromě interaktivního procvičování níže jsou k dispozici ještě pracovní listy k vytištění a rýsování na papíře:
NahoruObvod čtverce a obdélníku
Obvod čtverce o straně délky a je o=a+ a+a+a= 4a.
Obvod obdélníku se stranami o délkách a,b je roven o=a + b + a + b = 2\cdot (a+b).
NahoruObsah čtverce a obdélníku
Obsah čtverce o straně délky a je S=a\cdot a=a^2.
Obsah obdélníku se stranami o délkách a,b je roven S=a\cdot b.
NahoruRovnoběžník
Rovnoběžník je čtyřúhelník, jehož protilehlé strany jsou rovnoběžné. Dříve se označoval také jako kosodélník.
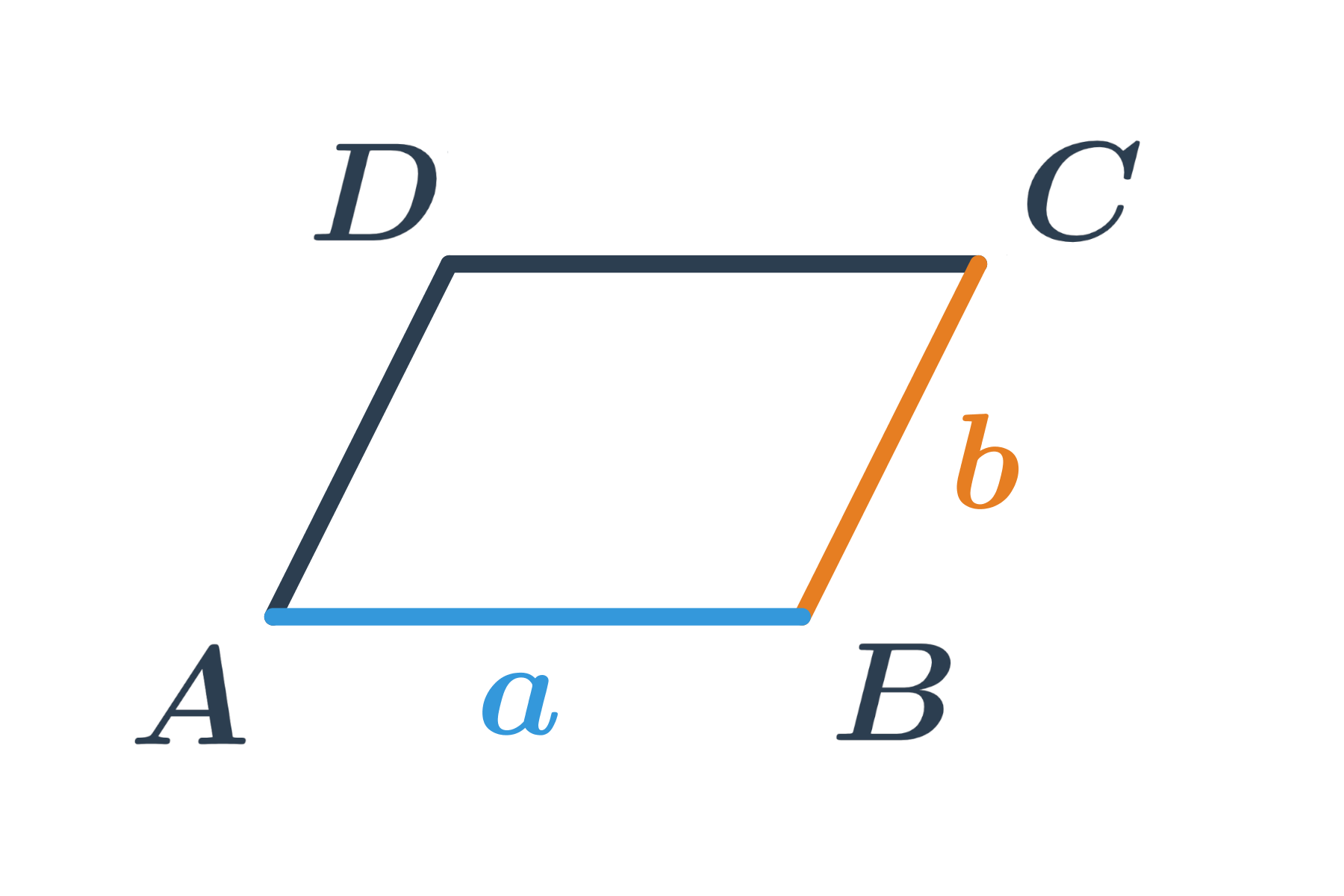
Speciální případy rovnoběžníku:
- Kosočtverec má všechny strany stejně dlouhé.
- Obdélník má vnitřní úhly pravé.
- Čtverec má vnitřní úhly pravé a všechny strany stejně dlouhé.
Konstrukce čtyřúhelníků: rovnoběžníky
Konstrukce rovnoběžníků
Rovnoběžník je speciální případ čtyřúhelníku, jehož protilehlé strany jsou rovnoběžné. Při řešení konstrukčních úloh využíváme následují vlastnosti rovnoběžníků:
- Protější strany jsou rovnoběžné.
- Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
- Úhlopříčky rovnoběžníku nejsou stejně dlouhé, ale navzájem se půlí a protínají se ve středu rovnoběžníku.
- Každé dva protější úhly jsou stejné.
- Součet vnitřních úhlů u jedné strany je 180°.
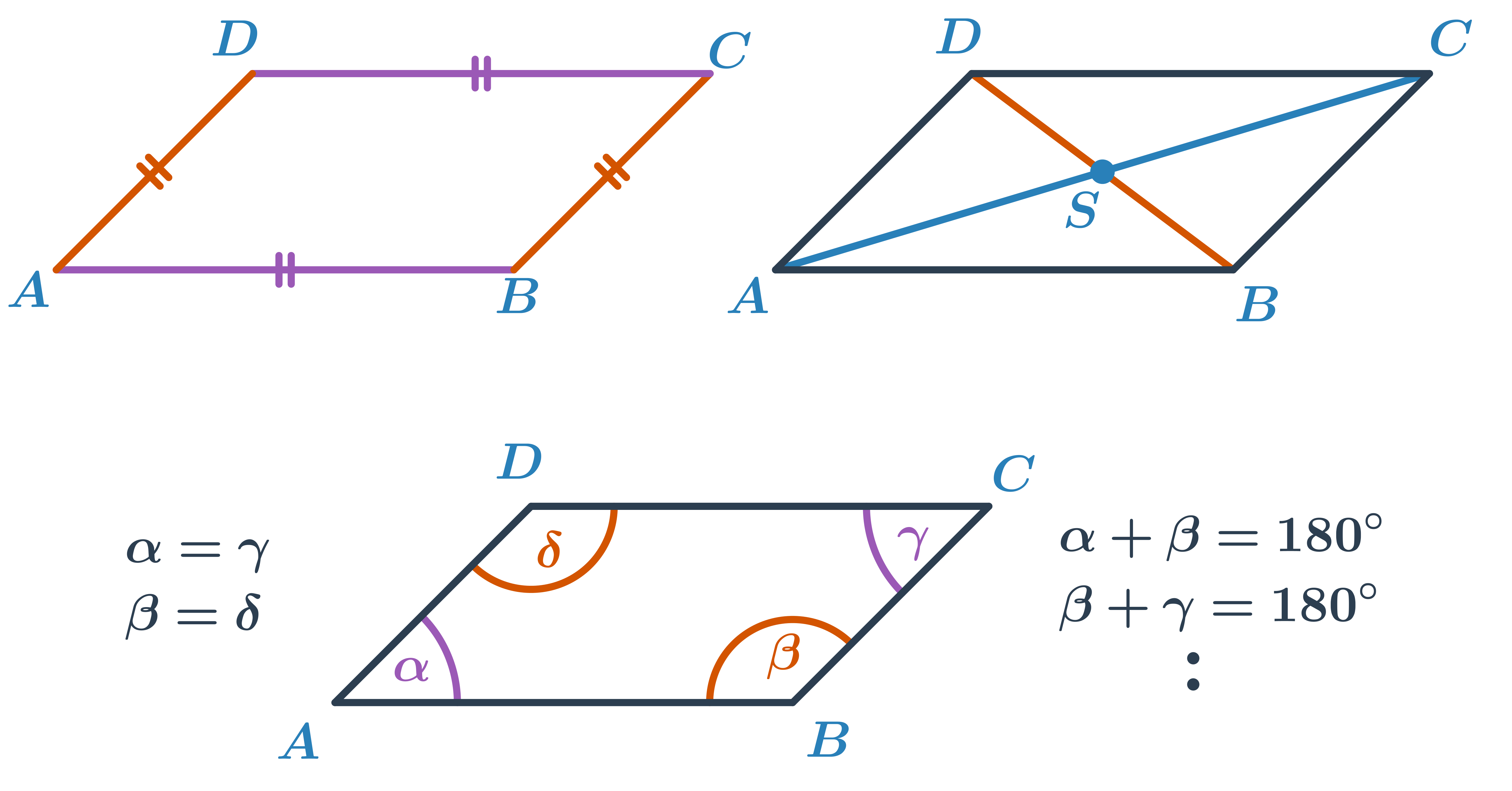
Při konstrukci rovnoběžníku potřebujeme znát tři údaje, ze kterých jsem často schopni sestrojit některý trojúhelník určený podle vět s vrcholy ve trojici vrcholů rovnoběžníku. Zbývající vrchol rovnoběžníku pak najdeme pomocí rovnoběžek nebo shodnosti protějších stran.
Příklad: Sestrojte rovnoběžník ABCD, je-li dáno a=8 cm, b=5 cm, \beta=110^\circ.
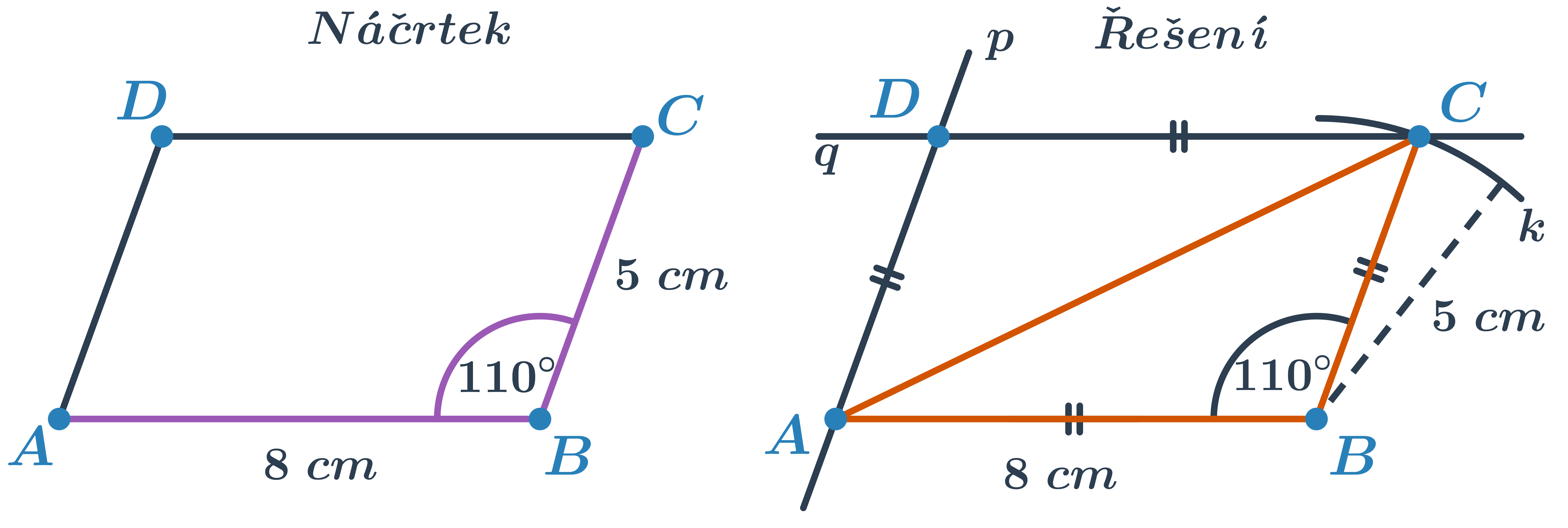
- Nejprve sestrojíme trojúhelník ABC určený podle věty sus.
- Pro konstrukci bodu D sestrojíme postupně ve vrcholech A a C rovnoběžky se stranami BC a AB.
Konstrukce kosočtverců
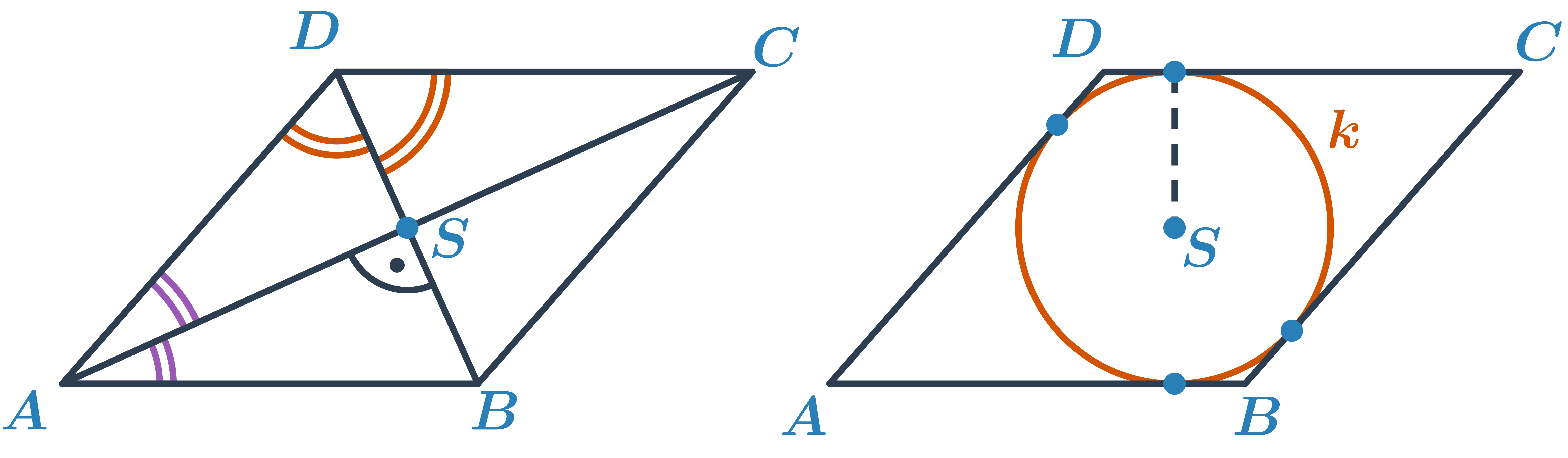
Kosočtverec je speciální případ rovnoběžníku. Má všechny strany stejně dlouhé. Proti obecnému rovnoběžníku mají jeho úhlopříčky navíc dvě speciální vlastnosti – jsou na sebe kolmé a půlí vnitřní úhly. Kosočtverci lze (stejně jako čtverci) vepsat kružnici.
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
NahoruObvod rovnoběžníku
Obvod rovnoběžníku se stranami o délkách a,b je roven S=a + b + a + b = 2\cdot (a+b).
NahoruObsah rovnoběžníku
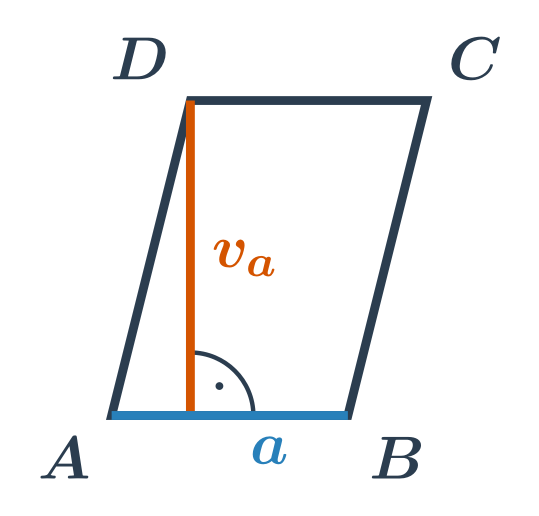
Obsah rovnoběžníku je roven součinu délky strany a k ní příslušné výšky. Tedy obsah rovnoběžníku ABCD, ve kterém ke straně o délce a přísluší výška v_a spočítáme jako S= a\cdot v_a.
Lichoběžník
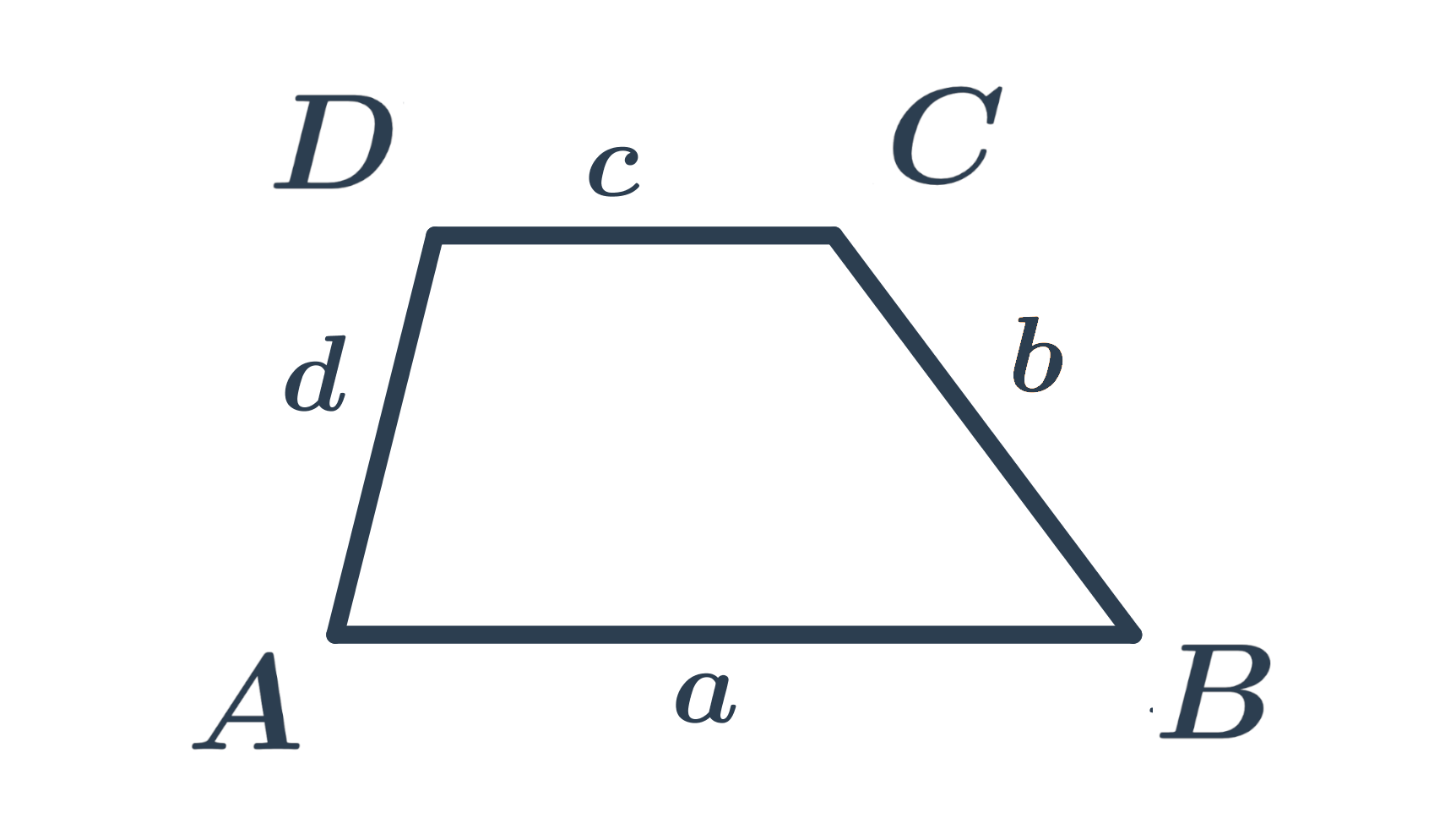
Lichoběžník je čtyřúhelník, jehož dvě protější strany jsou rovnoběžné (říkáme jim základny) a zbývající dvě protější strany jsou různoběžné.
Pravoúhlý lichoběžník má dva z vnitřních úhlů pravé (základny lichoběžníku jsou rovnoběžné, je‑li jeden vnitřní úhel pravý, musí být jeho doplněk do 180° u druhé základny také pravý).
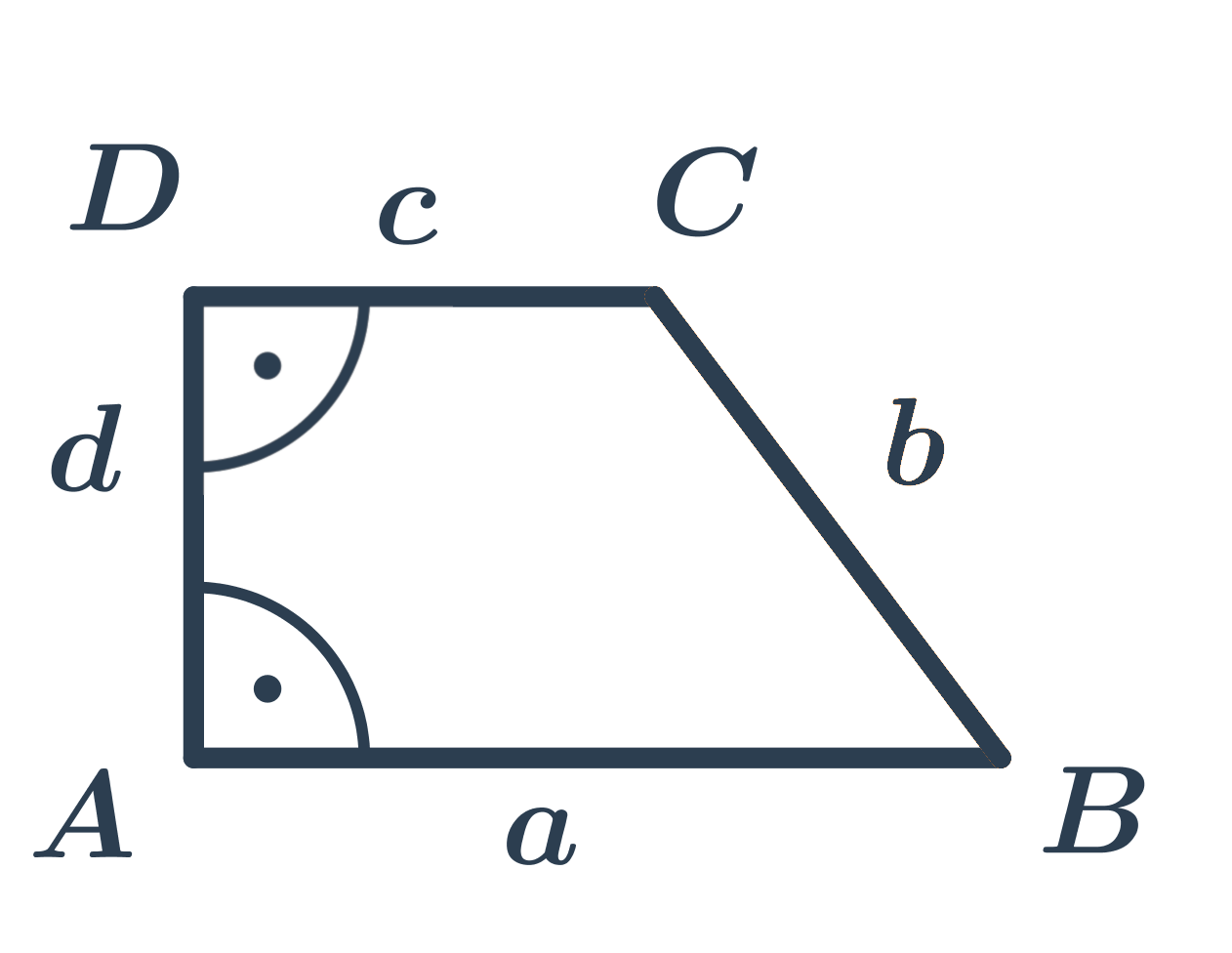
Rovnoramenný lichoběžník má ramena stejné délky.
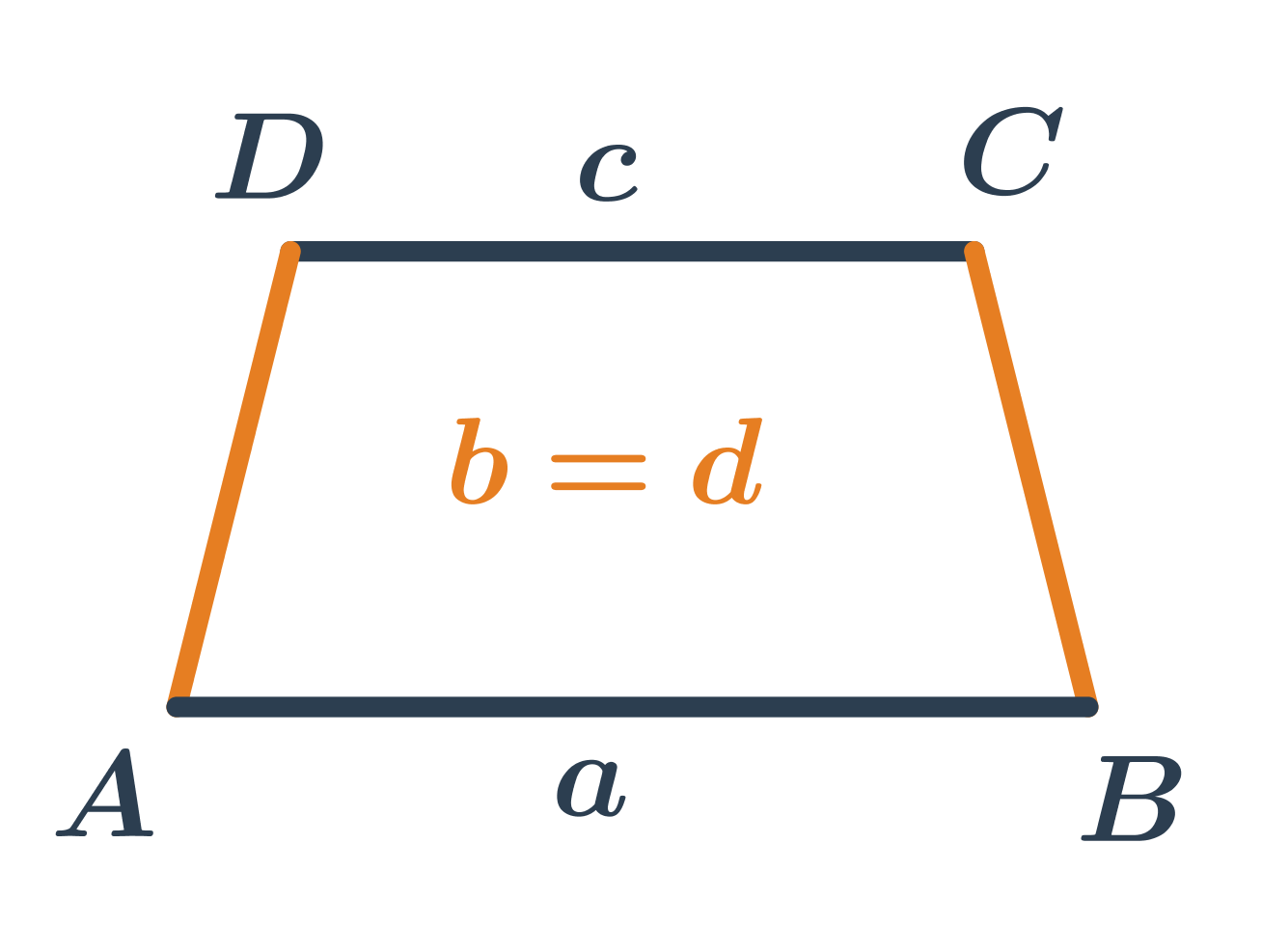
Konstrukce čtyřúhelníků: lichoběžníky
Konstrukce lichoběžníků
Lichoběžník je čtyřúhelník, který má dvě rovnoběžné strany – ty se nazývají základny a dvě různoběžné strany – ramena. Vzdálenost základen se nazývá výška. Při konstrukcích budeme využívat následující vlastnosti:
- Základny jsou rovnoběžné.
- Úsečka spojující středy ramen se nazývá střední příčka a je rovnoběžná se základnami.
- Součet vnitřních úhlů u každého ramene je 180°.

Při konstrukci lichoběžníku potřebujeme znát čtyři údaje, ze kterých často dokážeme sestrojit trojúhelník určený podle vět s vrcholy ve třech vrcholech lichoběžníku. Zbývající vrchol lichoběžníku pak najdeme pomocí posledního údaje a rovnoběžnosti základen.
Příklad: konstrukce lichoběžníku, známé délky tří stran a úhlopříčky
Sestrojte lichoběžník ABCD, je-li dáno a=8 cm, b=6 cm, c=5 cm, |AC|=8 cm.
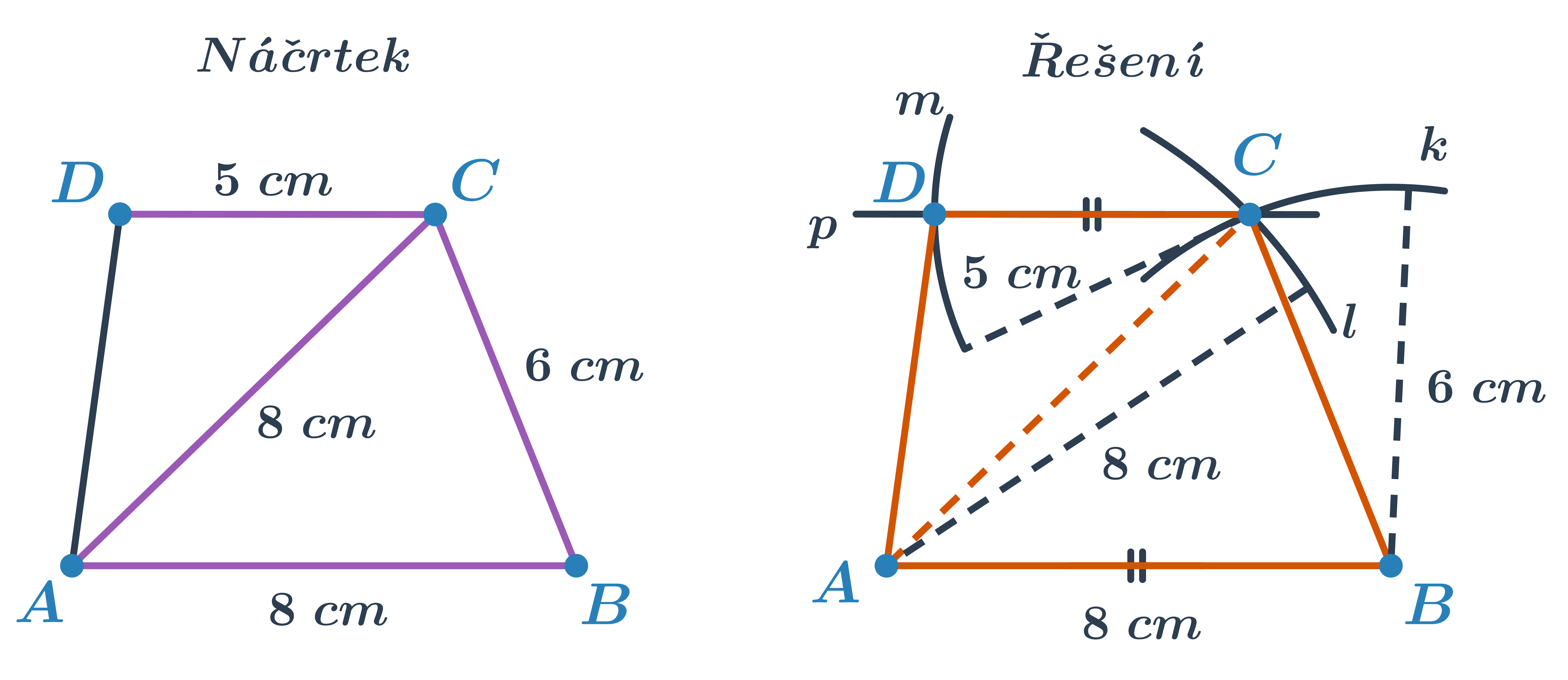
- Nejprve sestrojíme trojúhelník ABC určený podle věty sss.
- Základna CD je rovnoběžná se základnou AB. Bodem C tedy sestrojíme rovnoběžku p se stranou AB.
- Na tuto rovnoběžku pak naneseme délku strany c – poslední známý údaj.
Konstrukce rovnoramenných lichoběžníků
V rovnoramenném lichoběžníku mají obě ramena stejnou délku. Odpovídající vnitřní úhly u těchto ramen jsou pak stejné (dva stejné úhly \alpha = \beta u jedné základny a dva stejné úhly \gamma=\delta=180^\circ - \alpha u druhé základny). Úhlopříčky rovnoramenného lichoběžníku jsou stejně dlouhé. Narozdíl od obecného lichoběžníku mu lze opsat kružnici. Střed této opsané kružnice ale neleží v průsečíku úhlopříček.
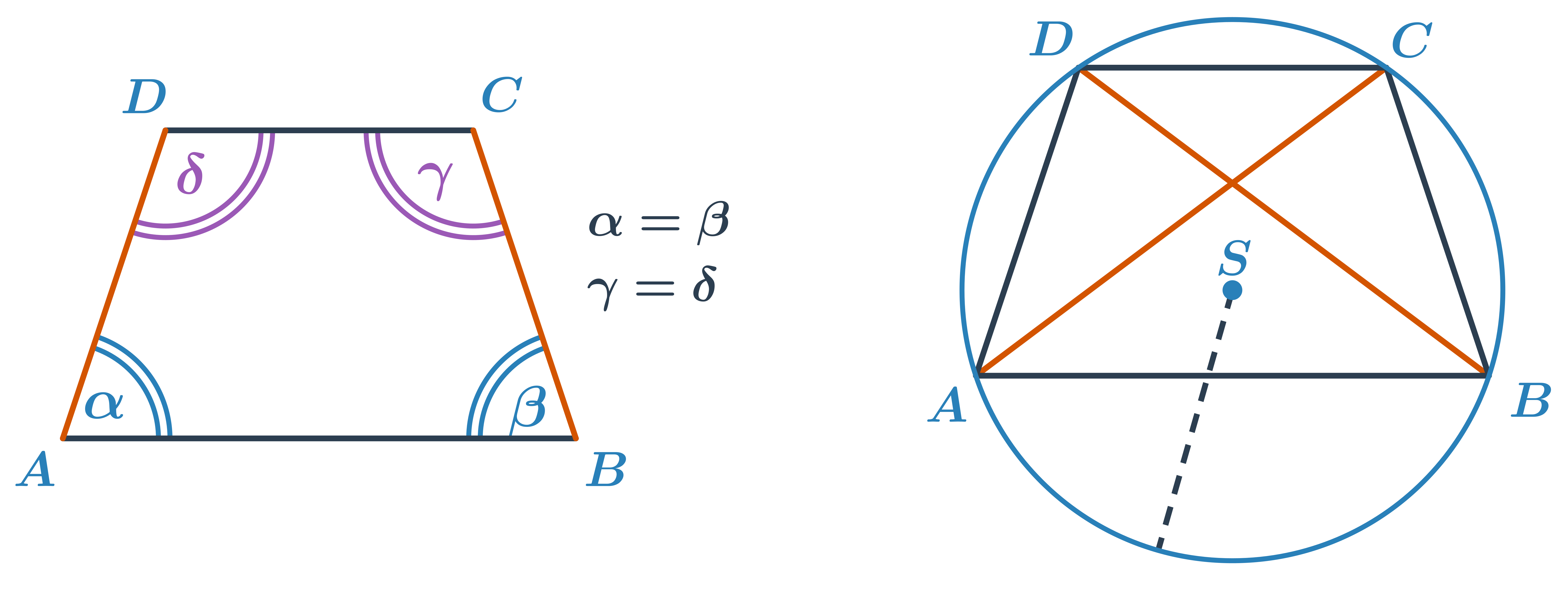
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
NahoruObvod lichoběžníku
Obvod lichoběžníku je součet délek jeho stran. Tedy obvod lichoběžníku ABCD se stranami o délkách a,b,c,d vypočítáme podle vzorečku o=a+b+c+d.

Obsah lichoběžníku
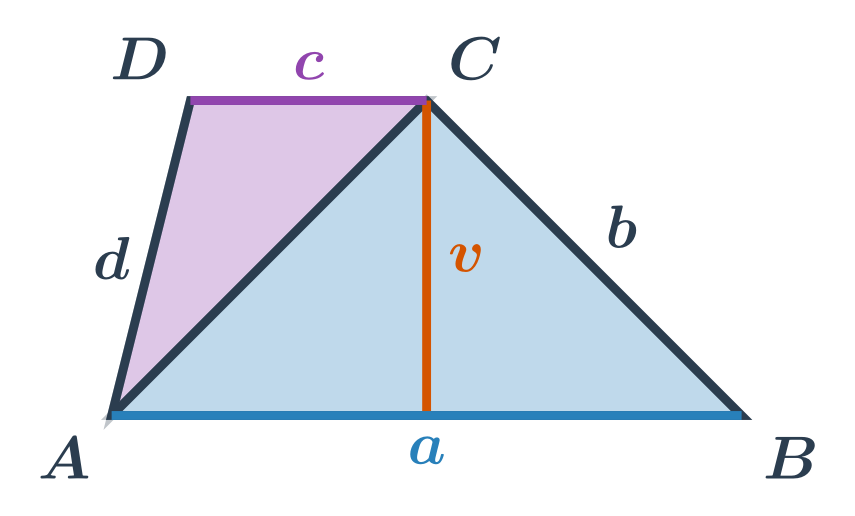
Obsah lichoběžníku se základnami o délkách a,c a výškou v spočítáme podle vzorečku S=\frac{1}{2} \cdot (a+c) \cdot v.
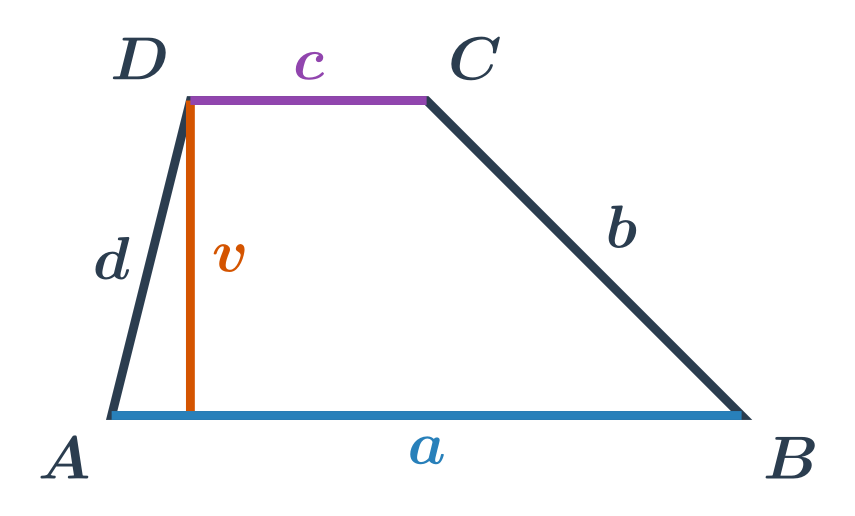
Intuice za tímto vzorečkem je vidět na následujícím obrázku. Obsah lichoběžníku je roven součtu obsahů dvou trojúhelníků.
- První trojúhelník má výšku v příslušnou ke straně délky a. Jeho obsah je S_{ABC}=\frac{1}{2} \cdot a \cdot v.
- Druhý trojúhelník má výšku v příslušnou ke straně délky c. Jeho obsah je S_{ACD}=\frac{1}{2} \cdot c \cdot v.
Součet obsahů těchto dvou trojúhelníků je S = S_{ABC} + S_{ACD} = \frac{1}{2} \cdot a \cdot v + \frac{1}{2} \cdot c \cdot v = \frac{1}{2} \cdot (a+c) \cdot v
Kruh a kružnice
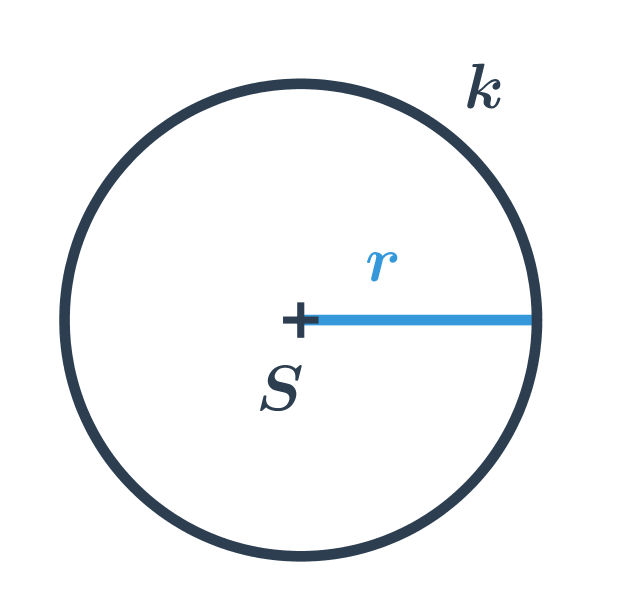
Kružnice s daným středem S a poloměrem r je tvořena všemi body v rovině, které jsou od středu vzdáleny přesně o r. U každého bodu v rovině pak můžeme určit, kde leží:
- na kružnici (jejich vzdálenost od S je rovna r)
- ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici)
- ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)
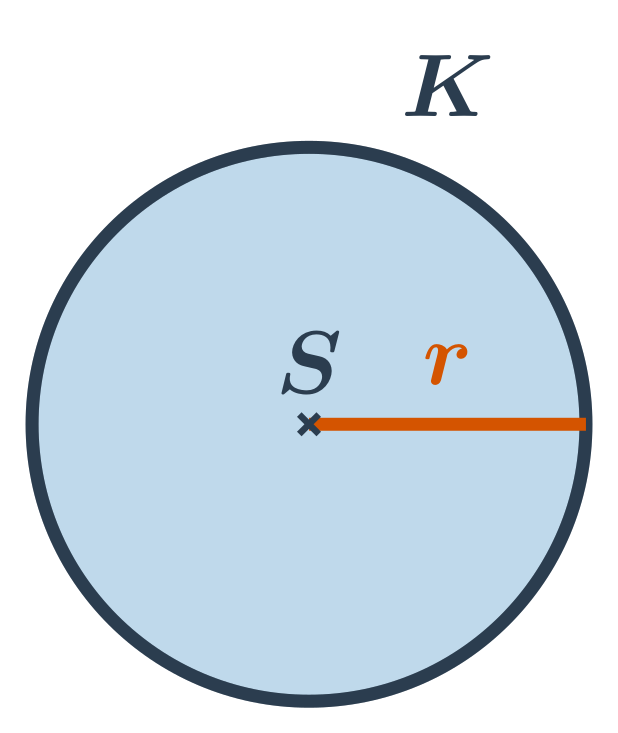
Kruh s daným středem S a poloměrem r je tvořen všemi body v rovině, které jsou od středu vzdáleny nejvýše o r. Kruh s daným středem a poloměrem je tedy sjednocení kružnice se stejným středem a poloměrem a její vnitřní oblasti. Střed S kruhu je bod, který patří do kruhu. (Zatímco střed kružnice neleží na kružnici, ale v její vnitřní oblasti.)
Pojmy související s kružnicí
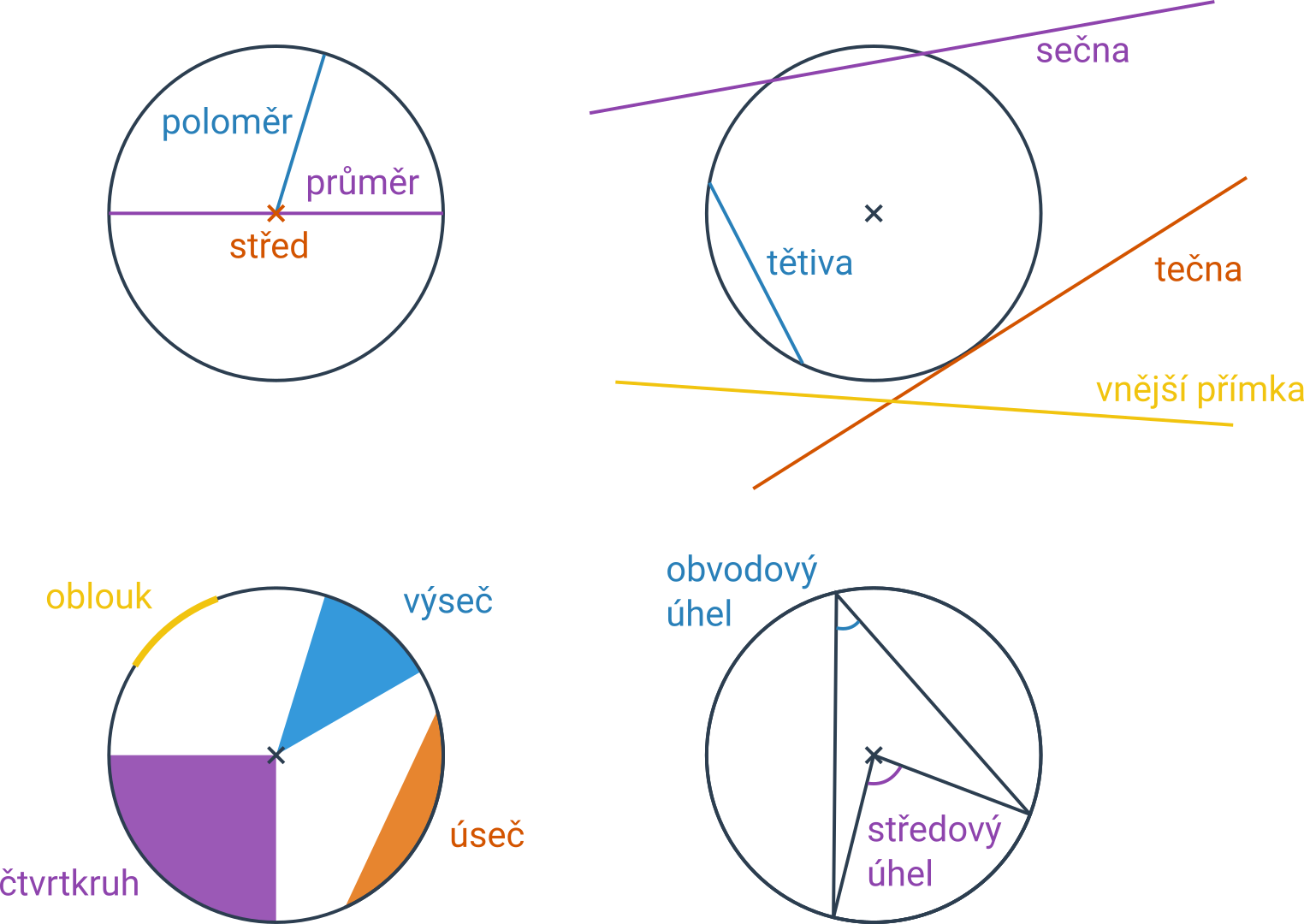
| poloměr | jejíž jeden koncový bod leží na kružnici a druhý koncový bod ve středu kružnice |
| průměr | úsečka, která prochází středem kružnice a jejíž oba krajní body leží na této kružnici |
| tečna | přímka, která se kružnice dotýká právě v jednom bodě |
| sečna | přímka, která kružnici protíná ve dvou bodech |
| vnější přímka | přímka, která kružnici neprotíná |
| tětiva | úsečka spojující dva body na kružnici |
| kruhová výseč | část kruhu příslušná středovému úhlu |
| mezikruží | plocha mezi dvěma soustřednými kružnicemi |
| půlkruh | výseč příslušná přímému úhlu (180°) |
| čtvrtkruh | výseč příslušná pravému úhlu (90°) |
| úseč | část kruhu vymezená tětivou a kruhovým obloukem vzniklá rozdělením kruhu sečnou |
| středový úhel | úhel, jehož vrcholem je střed kružnice a jehož ramena procházejí krajními body oblouku |
| obvodový úhel | úhel, jehož vrchol leží na kružnici a ramena procházejí krajními body oblouku |
Komiks pro zpestření

Obvod kruhu, délka kružnice
Vzorec pro obvod kruhu
Obvod kruhu (i kružnice) o poloměru r je o=2\pi r. Pro průměr d platí o = \pi d.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obvodu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru r nebo průměru d = 2r. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obvodu kruhu přibližuje níže uvedený obrázek. Obvod oranžového čtverce je 8\cdot r. Obvod kruhu je „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Příklady: obvod kruhu
- Mějme kruh o poloměru 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Kružnice o průměru 2 cm má délku \pi \cdot 2 \approx 6,3 cm.
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud jej chceme obejít po jeho okrajové čáře, ujdeme 2 \pi \cdot 9{,}1 \approx 57 metrů.
Obsah kruhu
Vzorec pro obsah kruhu
Obsah kruhu o poloměru r je S=\pi r^2. Pro průměr d platí S = \frac{1}{4} \pi d^2.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obsahu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru nebo průměru. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obsahu kruhu přibližuje níže uvedený obrázek. Žluté čtverce mají obsah r^2. Oranžový čtverec se skládá ze čtyř žlutých čtverců, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový čtverec, což odpovídá tomu, že obsah kruhu je přibližně 3{,}14 \cdot r^2.

Příklady
- Mějme kruh o poloměru 3 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Uvažujme kružnici o průměru 2 cm. Její vnitřní oblast má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud bychom chtěli veškerou trávu v kruhu nabarvit na růžovo, museli bychom nabarvit \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Komiks pro zpestření
Úhly a kružnice
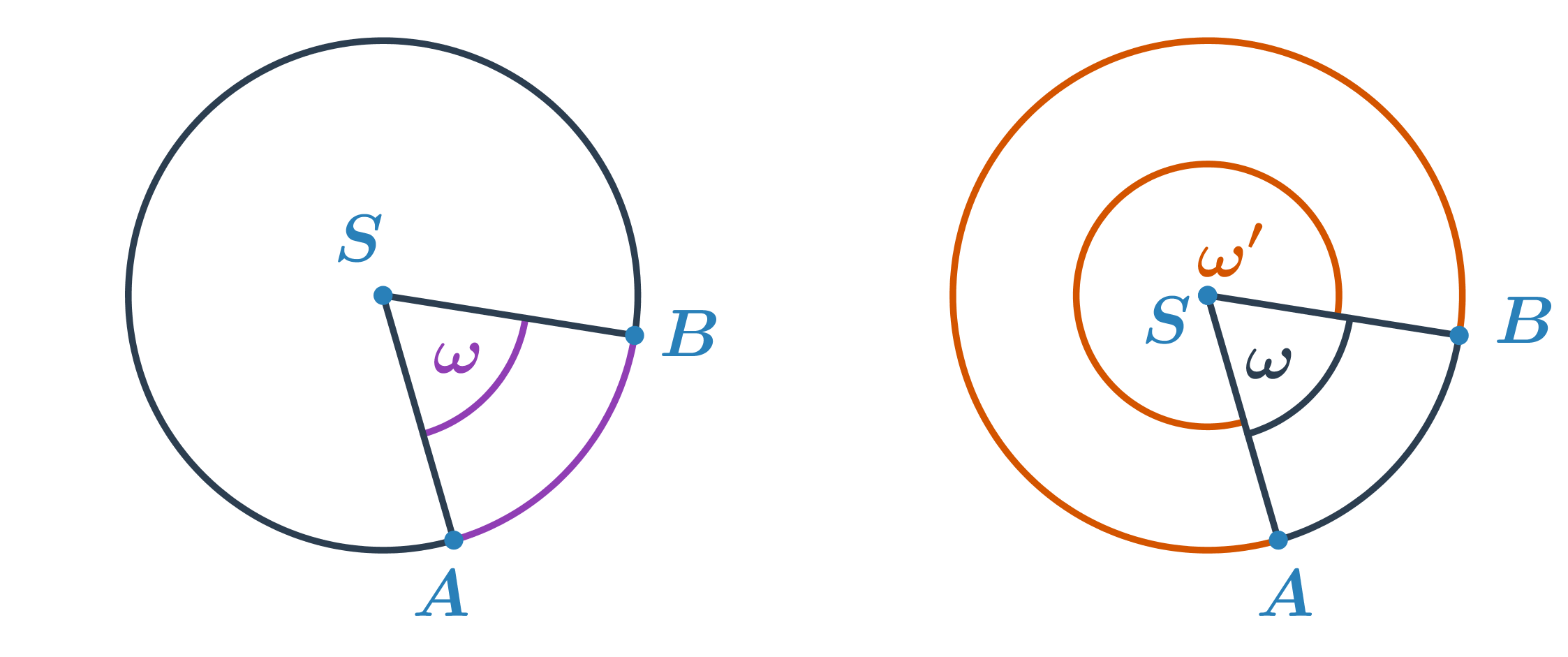
Středový úhel
- Úhel s vrcholem ve středu S kružnice k, jehož ramena procházejí krajními body A, B oblouku kružnice k.
- Pro každé dva body na kružnici lze určit dva středové úhly. Každý přísluší tomu oblouku, který v daném úhlu leží.
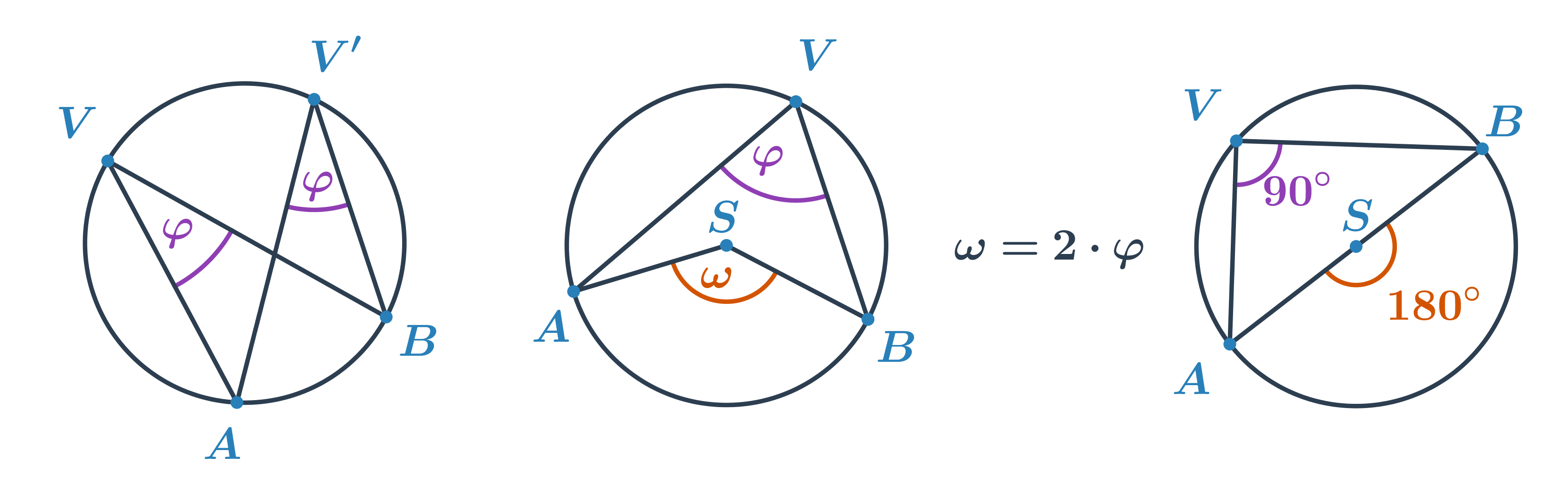
Obvodový úhel
- Úhel, jehož vrchol V leží na kružnici k a jeho ramena procházejí body A, B oblouku kružnice k (A \neq V \neq B)
- Všechny obvodové úhly příslušné oblouku AB s vrcholem V, který na oblouku neleží, mají stejnou velikost.
- Velikost středového úhlu \omega se rovná dvojnásobku velikosti obvodového úhlu \varphi příslušného ke stejnému oblouku, \omega = 2\cdot\varphi.
- Thaletova věta: Obvodový úhel nad průměrem kružnice je pravý.
Úsekový úhel
- Úhel, jenž svírá tětiva AB kružnice k s tečnou t kružnice v bodě A nebo B.
- Velikost úsekového úhlu je stejná jako velikost obvodového úhlu nad obloukem AB.
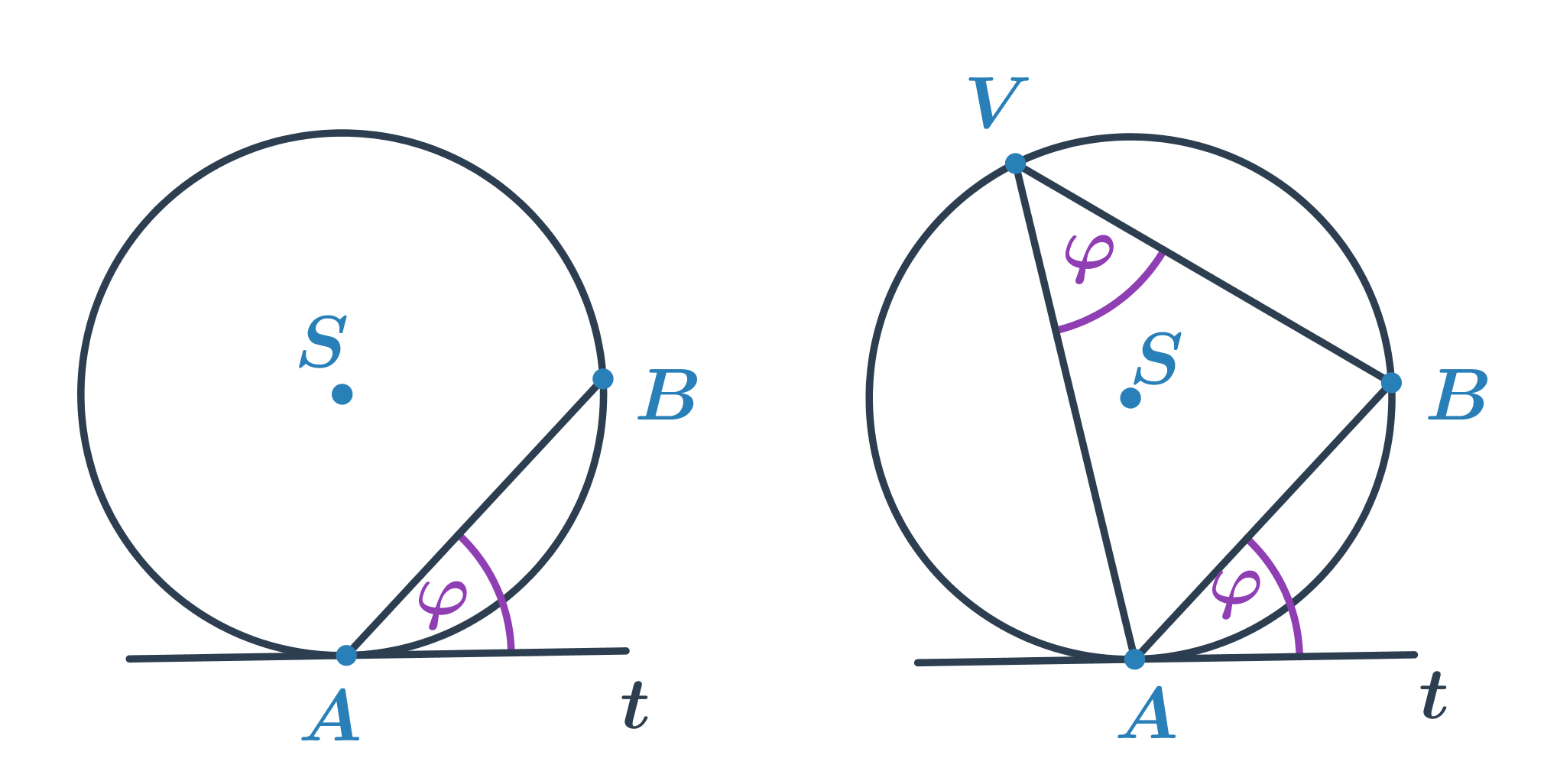
Příklad 1: Určete velikost úhlu
Určete velikost oranžového úhlu.
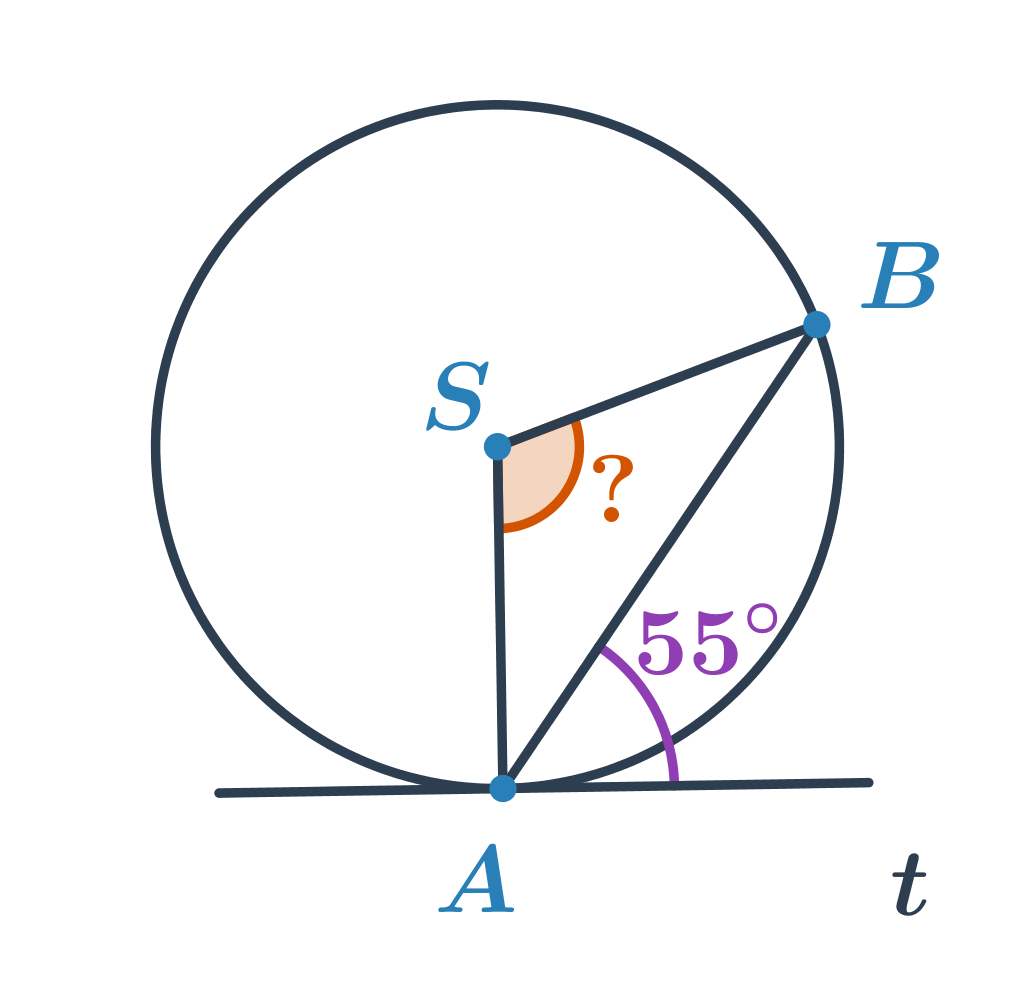
Úhel o velikosti 55^\circ je úsekový úhel příslušný tětivě AB. Víme, že velikosti úsekového a příslušného obvodového úhlu jsou stejné, tedy 55^\circ. Neznámý úhel je středový úhel příslušný menšímu oblouku AB. Jeho velikost je dvojnásobkem velikosti obvodového úhlu, tedy 2\cdot55^\circ=110^\circ.
Příklad 2: Určete velikost úhlu
Určete velikost oranžového úhlu.
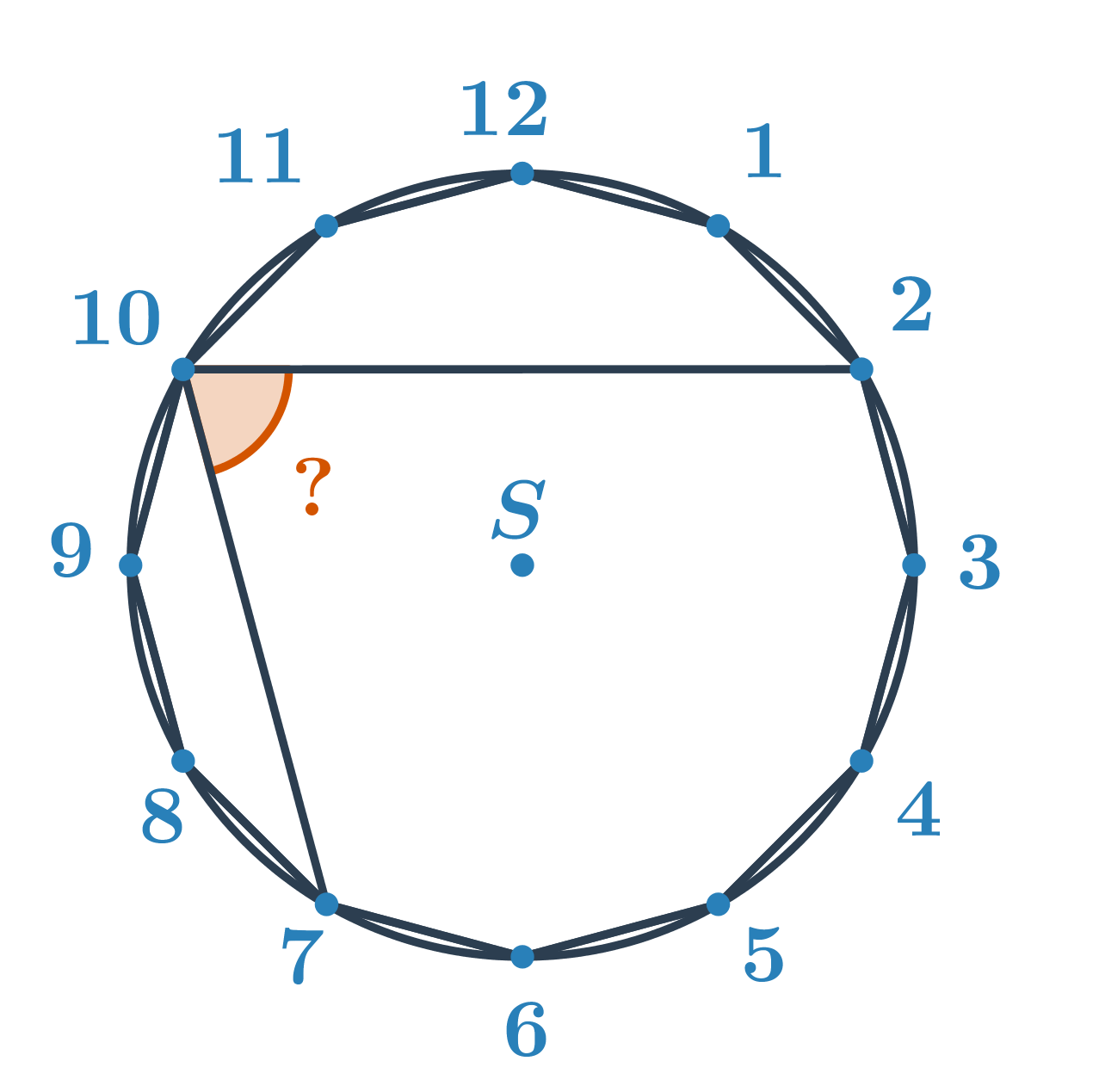
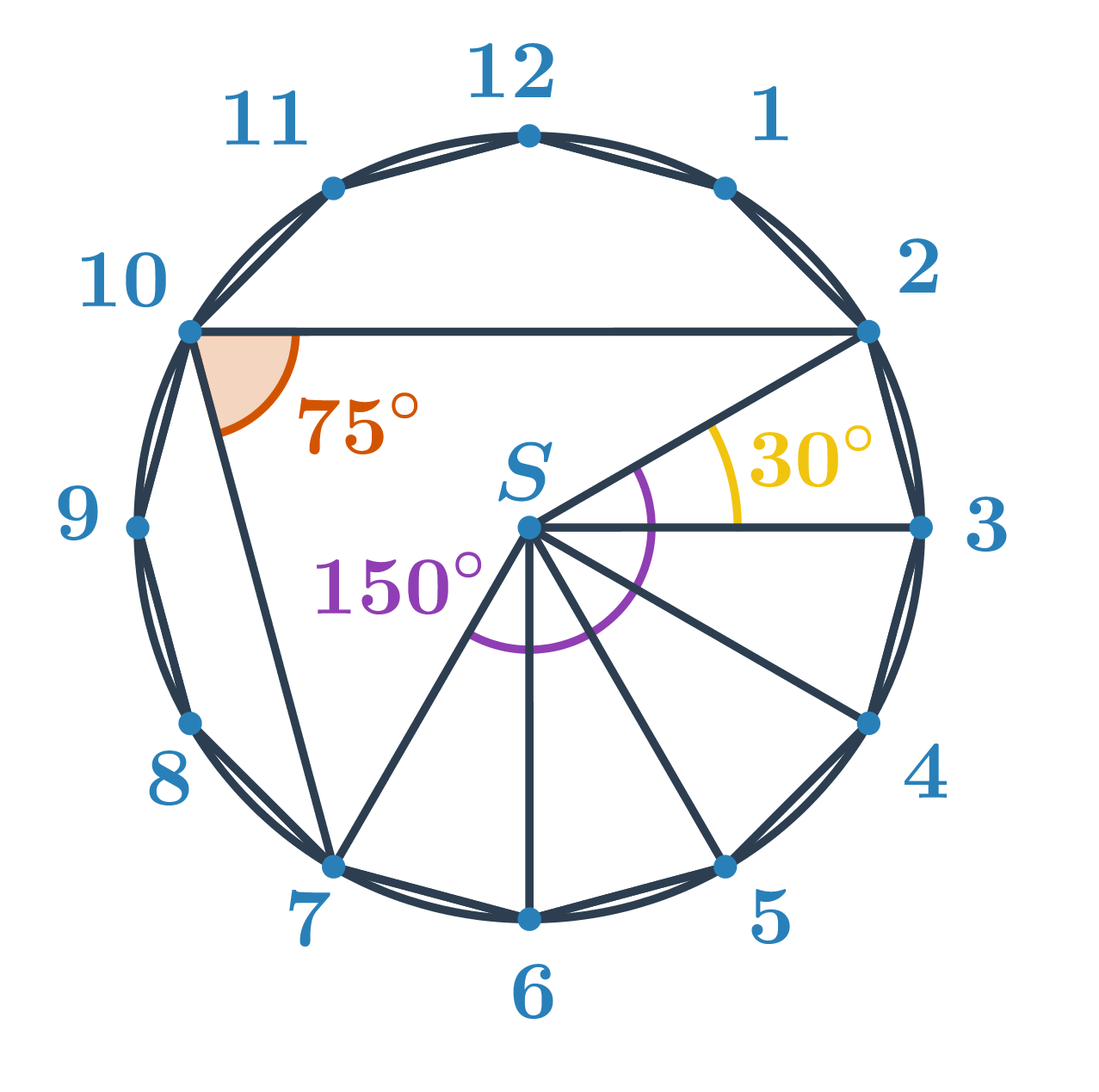
Neznámý úhel je obvodovým úhlem nad menším obloukem s koncovými body 2 a 7. Určíme velikost příslušného středového úhlu. Z kapitoly úhly a mnohoúhelníky víme, že velikost středového úhlu pravidelného n-úhelníku je \frac{360^\circ}{n}. Pro pravidelný dvanáctiúhelník je tedy úhel mezi spojnicemi dvou vedlejších vrcholů a středu \frac{360^\circ}{12}=30^\circ. Středový úhel příslušný oblouku 2 a 7 je pak 5\cdot30^\circ=150^\circ. Hledaný obvodový úhel má poloviční velikost, tedy 150^\circ:2=75^\circ.
Obsah kruhové výseče
Obsah kruhové výseče
Obsah kruhové výseče se středovým úhlem \alpha a poloměrem r spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Příklady
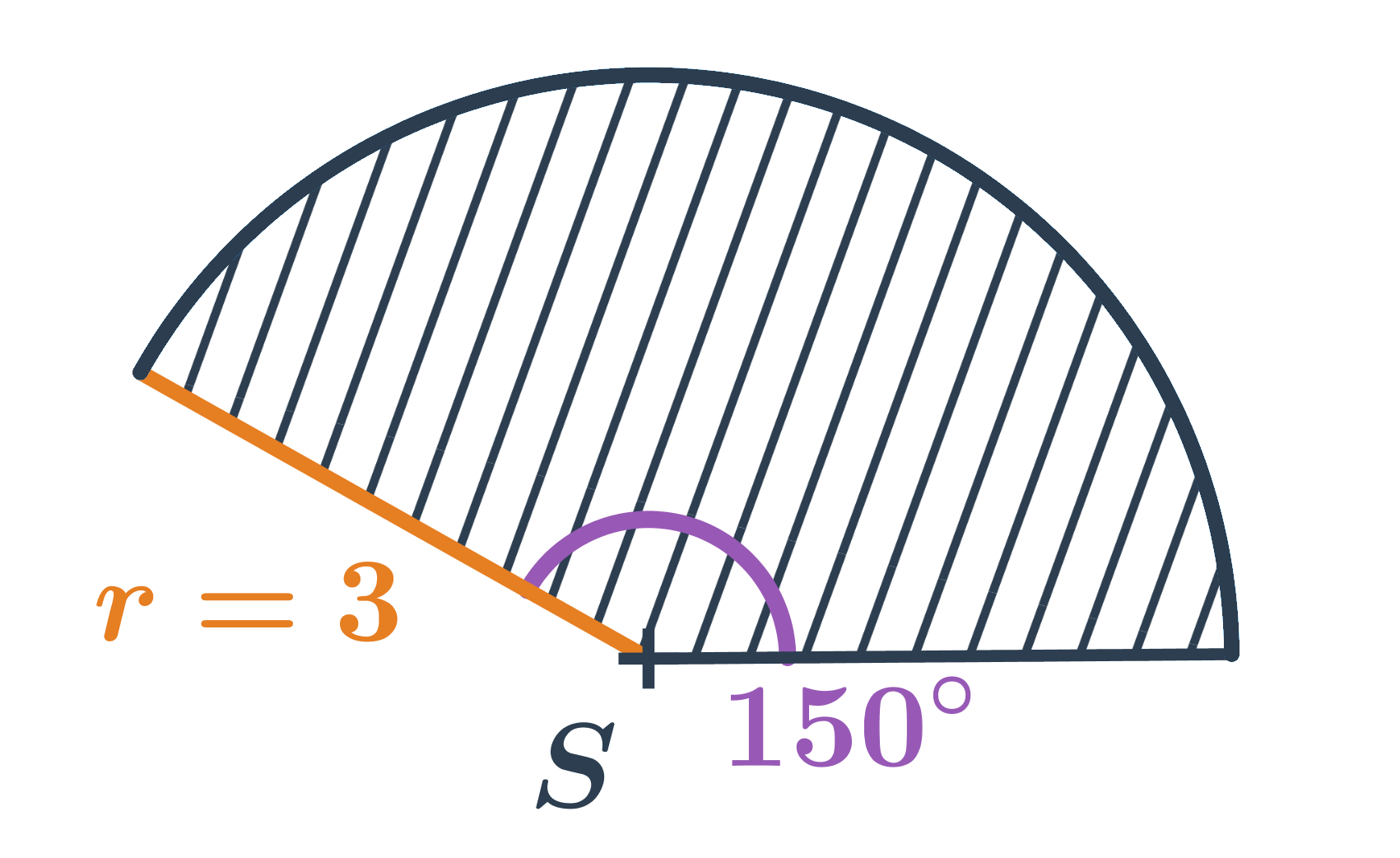
- Kruhová výseč na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
- Obsah celého kruhu (výseče se středovým úhlem 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2
Délka oblouku
Délku oblouku, který na kružnici o poloměru r odpovídá středovému úhlu \alpha spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Příklad – délka oblouku odpovídajícího 90^{\circ}
Délka oblouku na obrázku je:
\frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
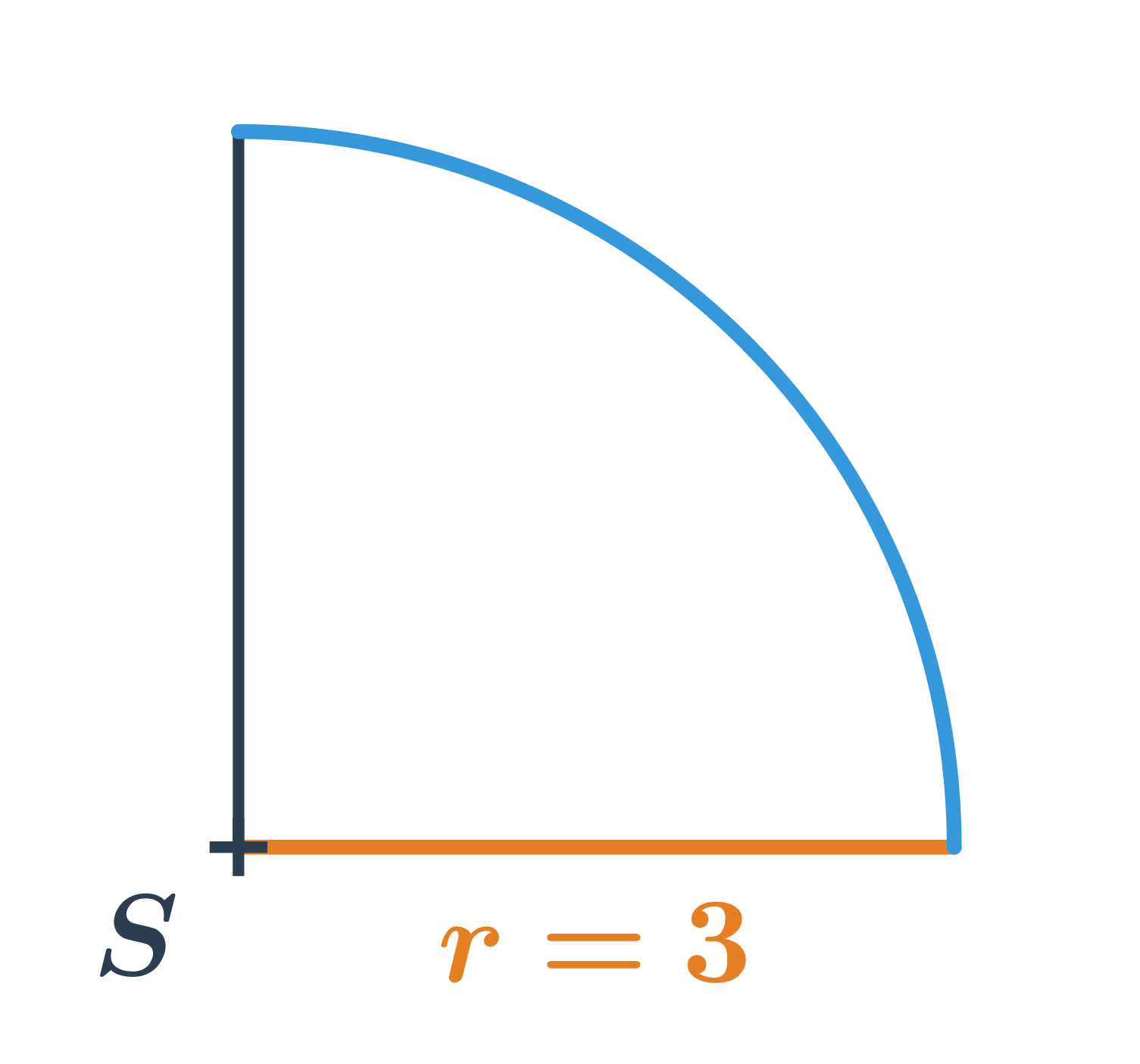 Jedná se o čtvrtinu délky kružnice.
Jedná se o čtvrtinu délky kružnice.
Příklad – délka oblouku odpovídajícího 360^{\circ}
Délka celé kružnice (tedy pro celých 360^{\circ}) je:
\frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r

