Výpis souhrnů
Úsečky
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Úsečka je část přímky mezi dvěma krajními body (včetně těchto bodů). Úsečka je v rovině i v prostoru jednoznačně zadaná svými krajními body.
NahoruDélka úsečky v rovině
Délku úsečky v rovině spočítáme stejně jako vzdálenost bodů v rovině.
Jsou‑li dány souřadnice A[x_A; y_A], B[x_B; y_B], je délka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}
Vzoreček vychází z Pythagorovy věty.
Je nutné počítat rozdíl souřadnic v pořadí „druhý bod mínus první“?
- Není. Výrazy x_B-x_A a x_A-x_B nejsou stejné. Ale jsou opačné a ve vzorci počítáme jejich druhé mocniny, které se rovnají.
- Navíc geometricky, délka úsečky AB je stejná jako délka úsečky BA.
- Důvodem zápisu právě v tomto tvaru je fakt, že délka úsečky je rovna velikosti vektoru \overrightarrow{AB} a u vektoru se jeho velikost vždy počítá „koncový bod mínus počáteční“.
Příklad: Délka úsečky EF: E[0;-1], F[-4;2]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
- Dosadíme souřadnice bodů E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
- Délka úsečky je: |EF|=5
Střed úsečky v rovině
Střed úsečky dělí úsečku na dvě stejné části. Pokud leží krajní body úsečky AB na číselné ose a jejich polohám odpovídají hodnoty a a b, potom jejímu středu S odpovídá číslo s=\frac{a+b}{2}. Střed úsečky je „průměrem“ jejích krajních bodů.
Pro úsečku v rovině bude situace následující.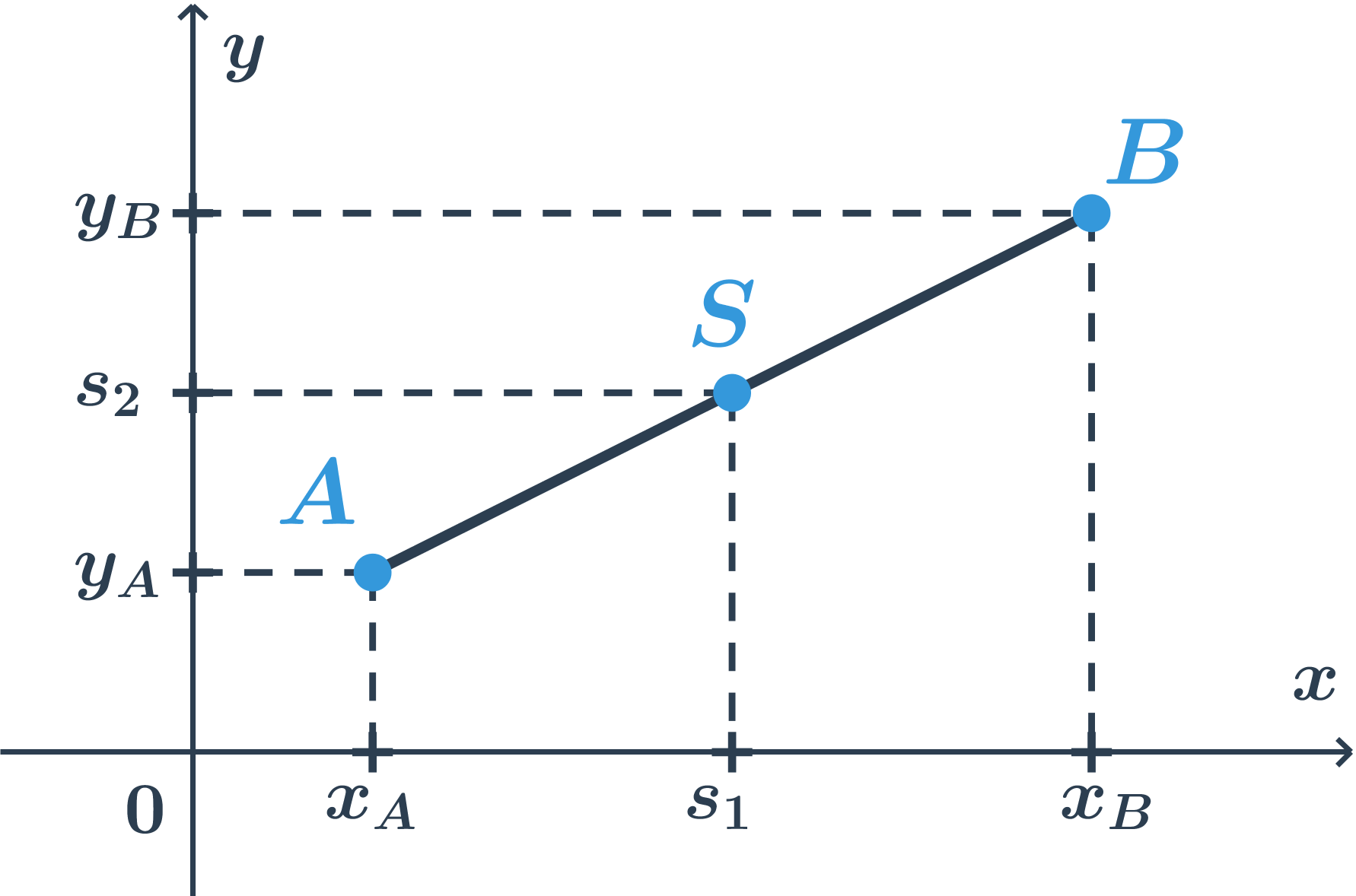 
Situace na obou souřadných osách je stejná jako předtím. Spočítáme obě souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Pro střed S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Příklad: určení středu úsečky
Najděte střed úsečky AB: A[6;-1], B[2;3]
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Střed úsečky AB je bod S[4;1]
Příklad: určení druhého krajního bodu úsečky
Určete souřadnice druhého krajního bodu úsečky AB, je‑li dán bod A[-3;0] a její střed S[1;3].
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Dopočítáme neznámé x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Bod B má souřadnice [5;6].
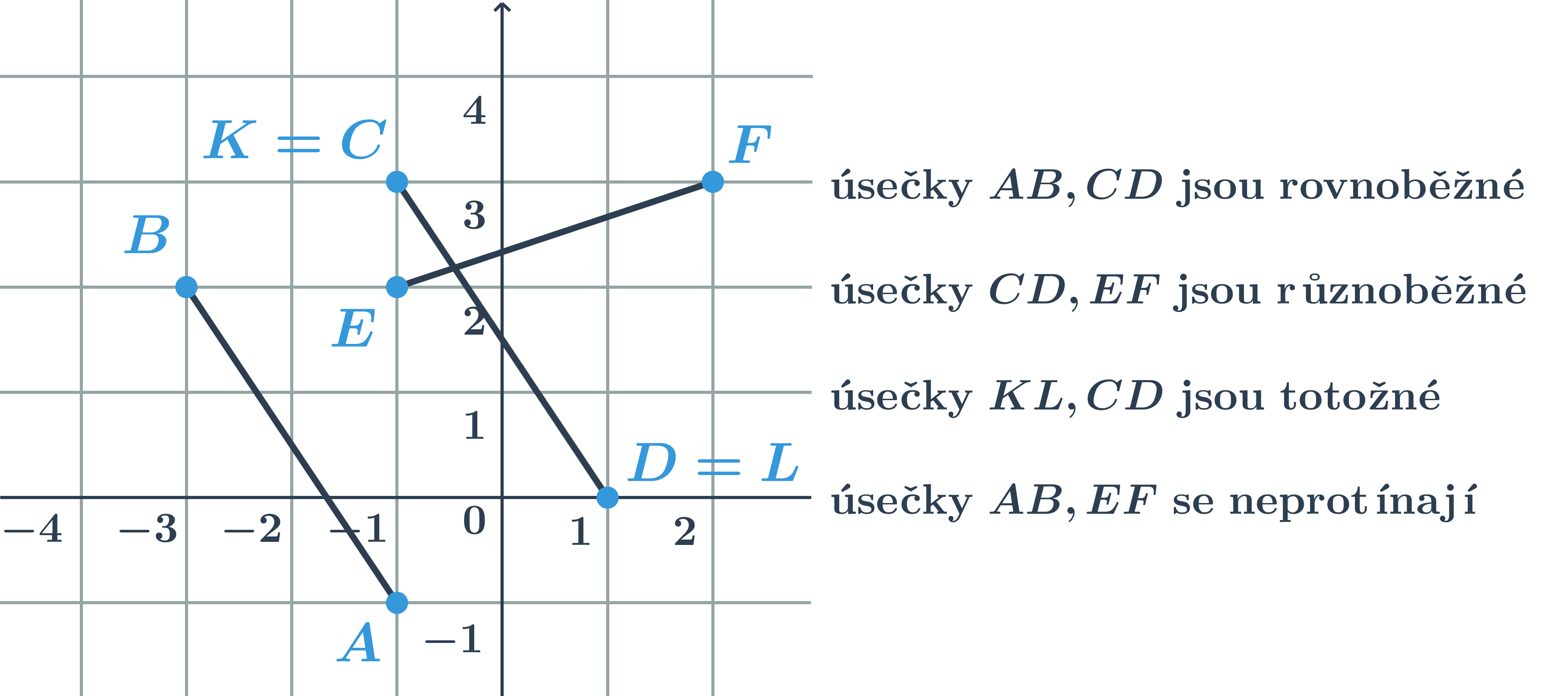
Vzájemná poloha úseček v rovině
Dvě úsečky v rovině mohou mít společné krajní body, pak říkáme, že jsou totožné. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou různoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.
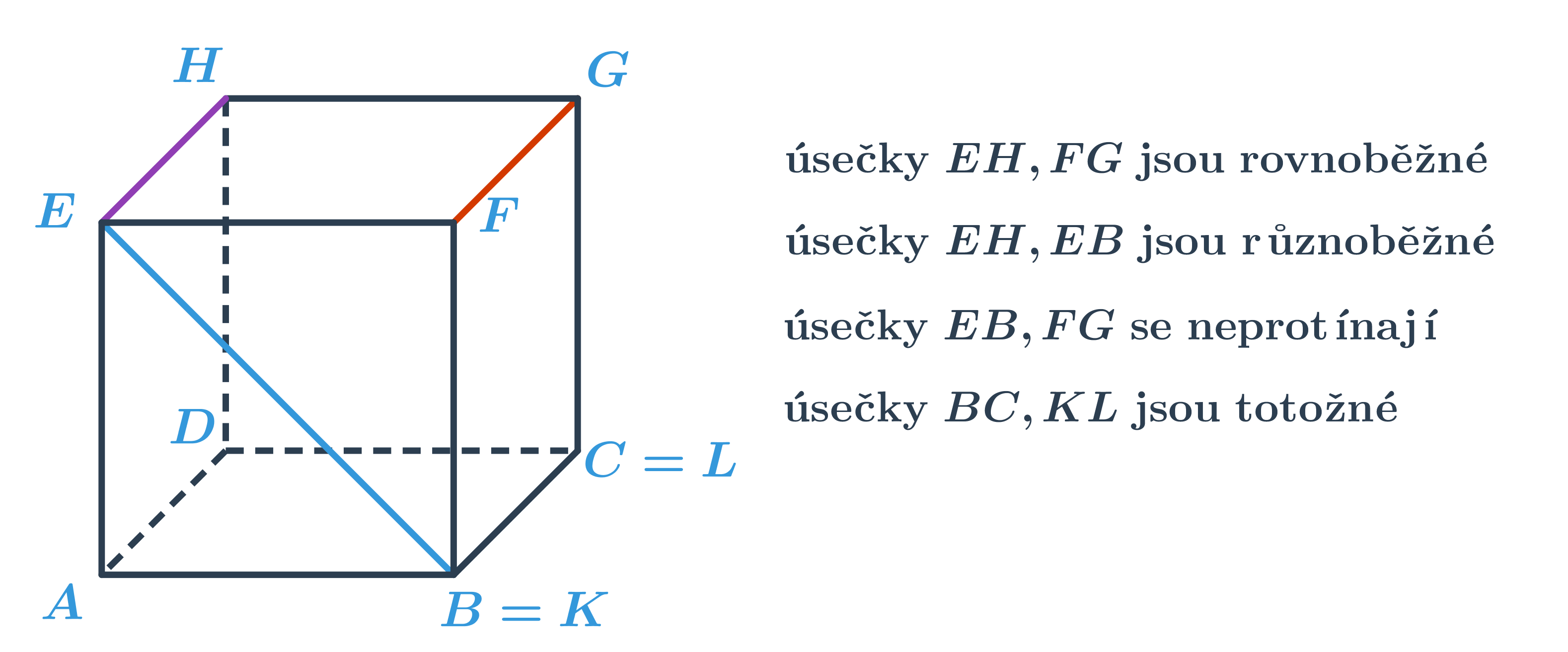
Délka úsečky v prostoru
Délku úsečky v prostoru spočítáme stejně jako vzdálenost bodů v prostoru.
Jsou‑li dány souřadnice A[x_A; y_A;z_A], B[x_B; y_B;z_B], je délka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2+(z_B-z_A)^2}
Příklad: Délka úsečky EF: E[-2;0;1], F[-4;2;0]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2+ (z_F-z_E)^2}
- Dosadíme souřadnice bodů EF; E[-2;0;1], F[-4;2;0]:
\sqrt{(-4-(-2))^2 + (2-0)^2+(0-1)^2}=\sqrt{(-2)^2 + 2^2+(-1)^2}=\sqrt{4+4+1}=\sqrt{9}=3 - Délka úsečky je: |EF|=3
Střed úsečky v prostoru
Střed úsečky v prostoru spočítáme podobně jako střed úsečky v rovině. Spočítáme všechny souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Pro střed S[s_1;s_2;s_3] úsečky AB, kde A[x_A; y_A;z_A], B[x_B; y_B;z_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2} , s_3 = \frac{z_A+z_B}{2}
Příklad: určení středu úsečky
Najděte střed úsečky AB: A[2;1;-3], B[2;-3;3]
Pro souřadnice středu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme souřadnice bodů A[2;1;-3], B[2;-3;3].
- s_1 = \frac{2+2}{2}=2, s_2 = \frac{1-3}{2}=-1, s_3 = \frac{-3+3}{2}=0
Střed úsečky AB je bod S[2;-1;0]
Příklad: určení druhého krajního bodu úsečky
Určete souřadnice druhého krajního bodu úsečky AB, je-li dán bod A[1;2;4] a její střed S[1;-3;0].
- Pro souřadnice středu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme souřadnice bodů A[1;2;4], S[1;-3;0].
- 1 = \frac{1+x_B}{2}, -3 = \frac{2+y_B}{2}, 0 = \frac{4+z_B}{2}
- Dopočítáme neznámé x_B, y_B, z_B:
\begin{array}{rclcrcr} 2&=&1+x_B &\Rightarrow& x_B&=&1\\ -6&=&2+y_B &\Rightarrow& y_B&=&-8\\ 0&=&4+z_B &\Rightarrow& z_B&=&-4 \end{array}
- Bod B má souřadnice [2;-8;-4].
Vzájemná poloha úseček v prostoru
Podobně jako v rovině mohou mít dvě úsečky společné krajní body, pak říkáme, že jsou totožné. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou různoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.
Tyto vzájemné polohy si dobře můžeme ilustrovat na krychli.
