Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Výpis souhrnů
Roviny
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Rovina je určena třemi body, které neleží na jedné přímce. Z předchozích kapitol již víme, že dvojice bodů určuje přímku, případně vektor, proto je mnoho dalších způsobů jak určit rovinu:
- bodem a přímkou
- dvěma různoběžnými přímkami
- dvěma rovnoběžnými přímkami
- bodem a dvěma vektory
V prostoru lze zapsat rovinu jako množinu bodů, které splňují parametrickou rovnici nebo obecnou rovnici.
Máme-li rovinu popsanou rovnicí, umíme určit vzájemnou polohu roviny a bodu výpočtem.
NahoruRoviny: pojmy
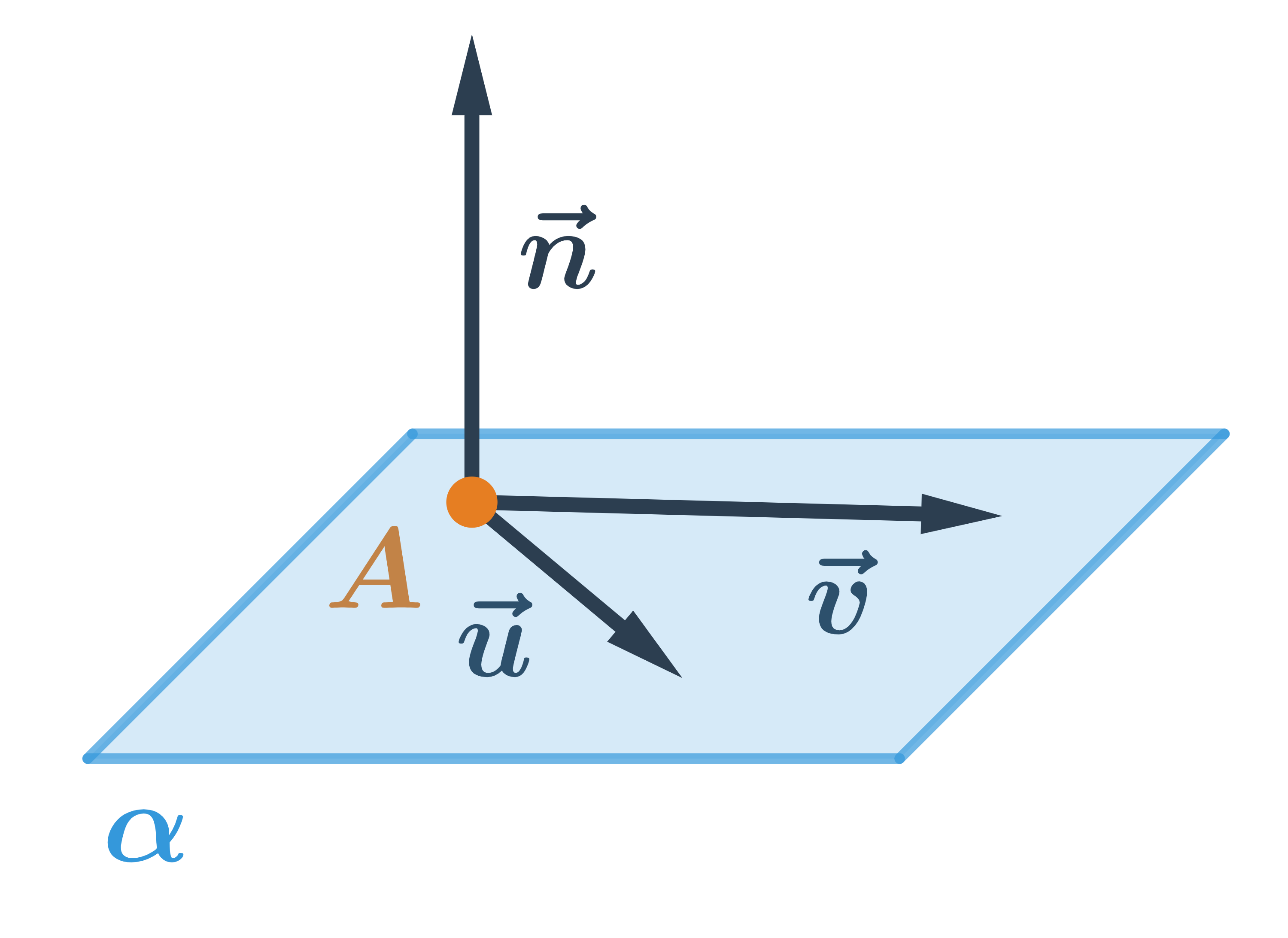
Přímka je jednoznačně určena bodem a dvěma vektory, které nejsou kolineární. Na obrázku je rovina \alpha určená bodem A a vektory \vec{u}, \vec{v}. Každý vektor, který je kolmý k rovině \alpha se nazývá normálový vektor roviny \alpha. Na obrázku je normálový vektor \vec{n}.
Parametrické rovnice roviny
Rovina určená bodem A=[a_1;a_2;a_3] a vektory \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit \alpha:X=A+t\vec{u}+s\vec{v}, kde t, s nazýváme parametry.
Obecná rovnice roviny
Obecná rovnice roviny je ve tvaru ax+by+cz+d=0, kde konstanty a, b, c jsou souřadnice normálového vektoru a d reálné číslo.
Obecná rovnice roviny rovnoběžné s osami x a y
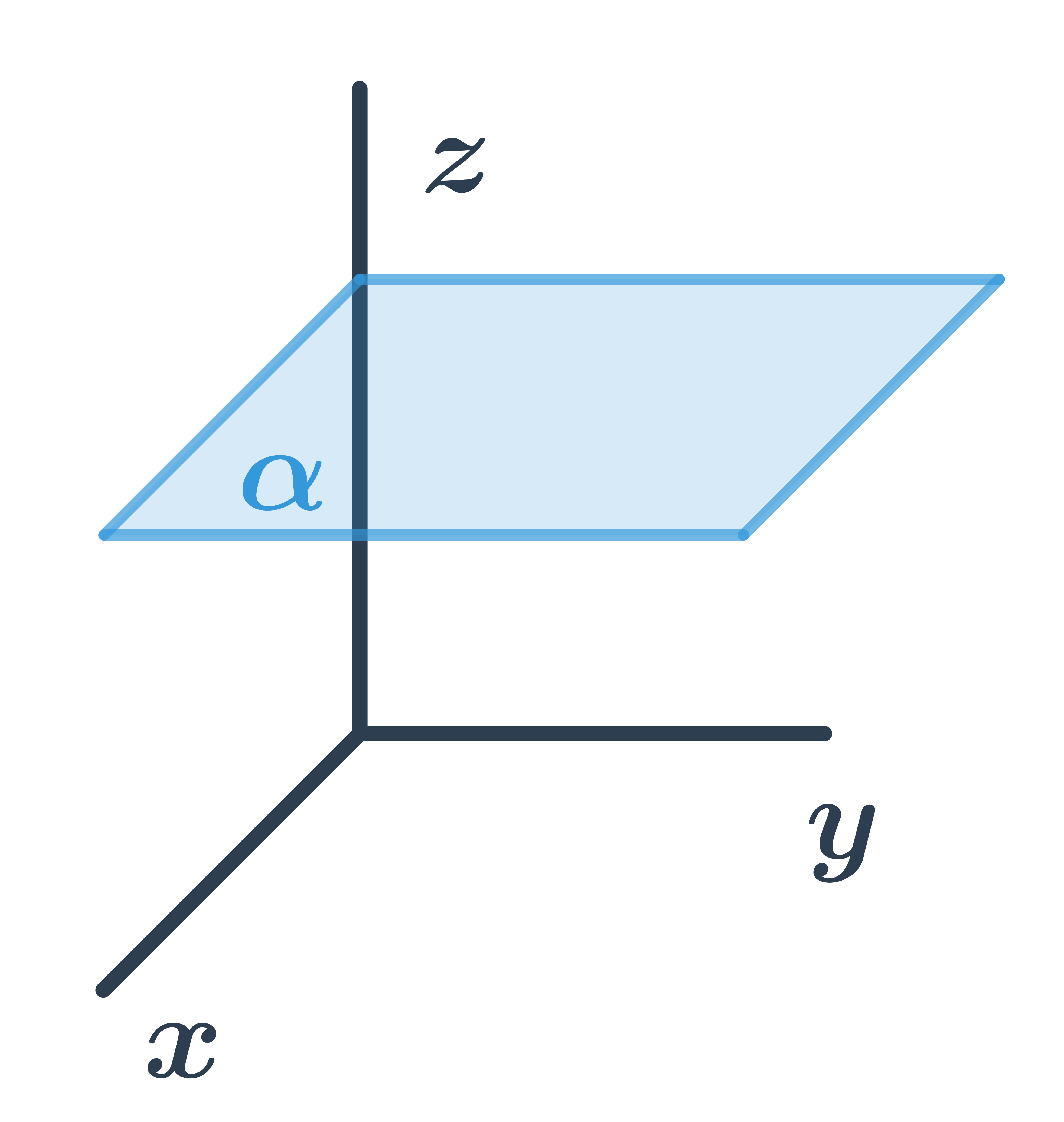
Pro všechny body ležící v rovině je třetí souřadnice stejná, tedy rovina má obecnou rovnici: z+d=0.
Obecná rovnice roviny rovnoběžné s osami x a z
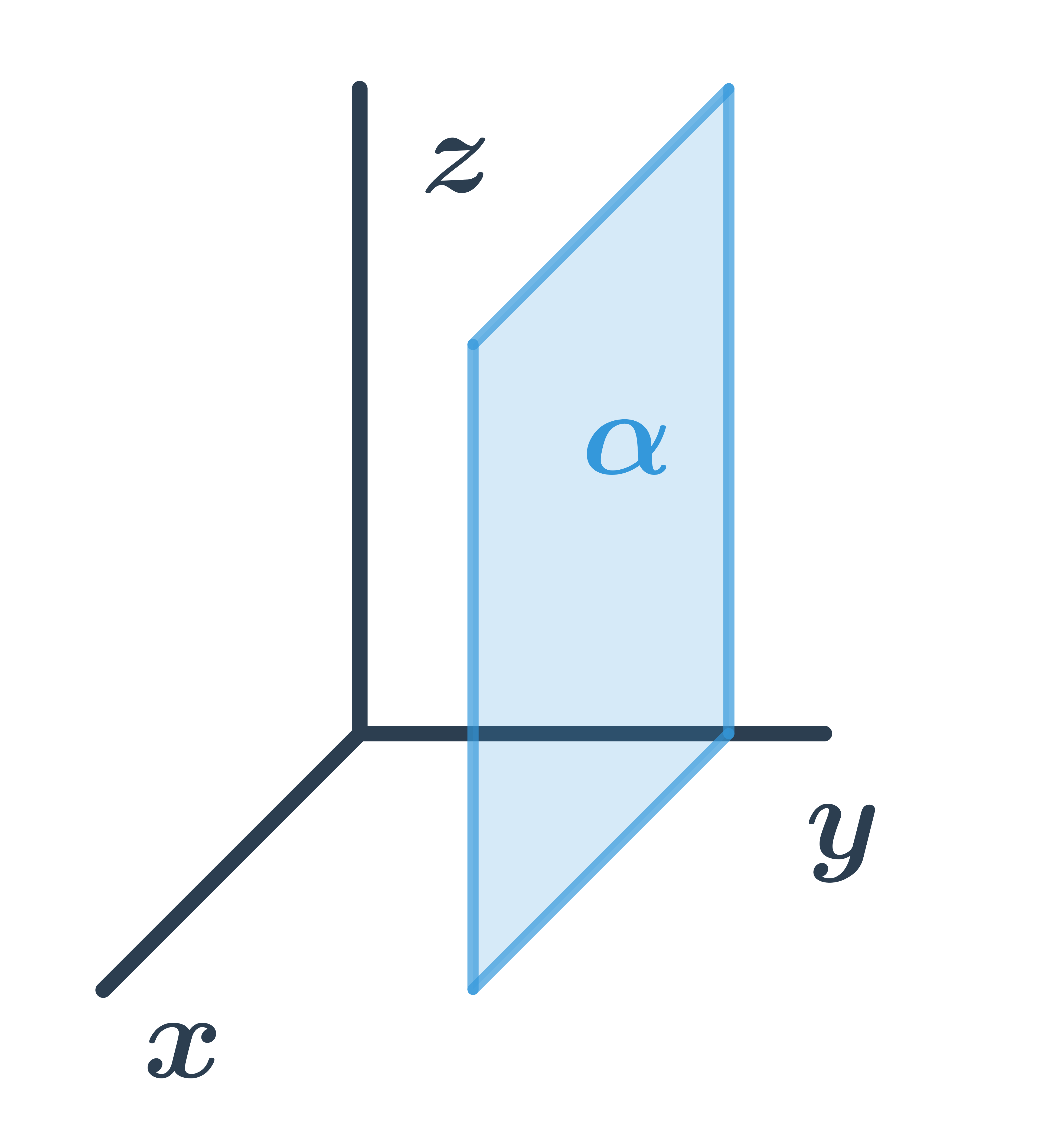
Pro všechny body ležící v rovině je druhá souřadnice stejná, tedy rovina má obecnou rovnici: y+d=0.
Obecná rovnice roviny rovnoběžné s osami y a z
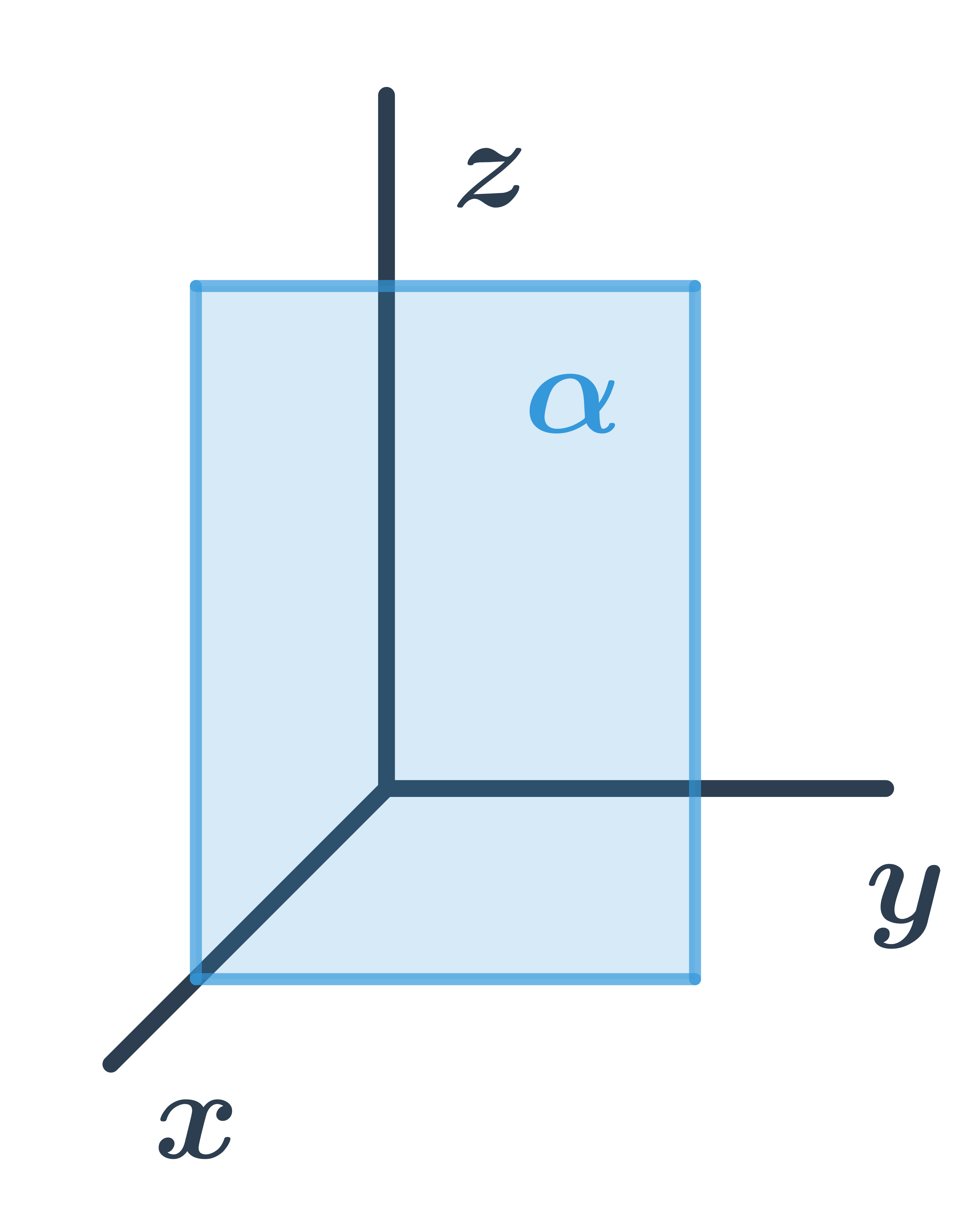
Pro všechny body ležící v rovině je první souřadnice stejná, tedy rovina má obecnou rovnici: z+d=0.
Bod a rovina
Bod M=[m_1;m_2;m_3] leží v rovině, jestliže jeho souřadnice vyhovují rovnici roviny.
- Pokud je rovina daná obecnou rovnicí ax+by+cz+d=0, pro souřadnice bodu, který leží na přímce platí: a\cdot m_1+b\cdot m_2+c\cdot m_3+d=0
- Pokud je rovina daná parametricky, po dosazení souřadnic bodu do parametrických rovnic dostaneme soustavu tří rovnic pro dvě neznámé t, s, která má právě jedno řešení (dvojici reálných čísel).
Obecná rovnice roviny, která prochází počátkem
- Rovina prochází bodem O=[0;0;0], tedy musí platit: a\cdot0+b\cdot0+c\cdot0+d=0\Rightarrow d=0.
- Rovina, která prochází počátkem má obecnou rovnici: ax+by+cz=0.
Dvě rovnoběžné roviny
Normálové vektory dvou rovnoběžných rovin \alpha: a_1x+b_1y+c_1z+d_1=0 a \beta: a_2x+b_2y+c_2z+d_2=0 jsou kolineární, tedy souřadnice jednoho vektoru jsou k-násobek souřadnic druhého vektoru. Pro konstanty v obecných rovnicích musí platit:
\begin{array}{rll}a_2&=&k\cdot a_1\\ b_2&=&k\cdot b_1\\c_2&=&k\cdot c_1\\&&k\in\mathbb{R}\end{array}
Pokud by platilo i d_2=k\cdot d_1 roviny jsou totožné.
NahoruParametrické rovnice roviny
Pro určení parametrických rovnic roviny potřebujeme znát souřadnice jednoho bodu a dvou nekolineárních vektorů v rovině \alpha. Rovina určená bodem A=[a_1;a_2;a_3] a vektory \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit \alpha:X=A+t\vec{u}+s\vec{v}, kde t,s \in \mathbb{R} jsou parametry.
Parametrické rovnice roviny určené třemi body
Určete parametrické rovnice roviny \alpha určené body A=[3;2;1], B=[1;3;4], C=[2;-3;3].
- rovina \alpha je určená bodem A a vektory \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{AC}:
- \vec{u}=\overrightarrow{AB}=B-A=(-2;1;3)
- \vec{v}=\overrightarrow{AC}=C-A=(-1;-5;2)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&3-2t-s\\y&=&2+t-5s\\z&=&1+3t+2s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určené bodem a dvěma vektory
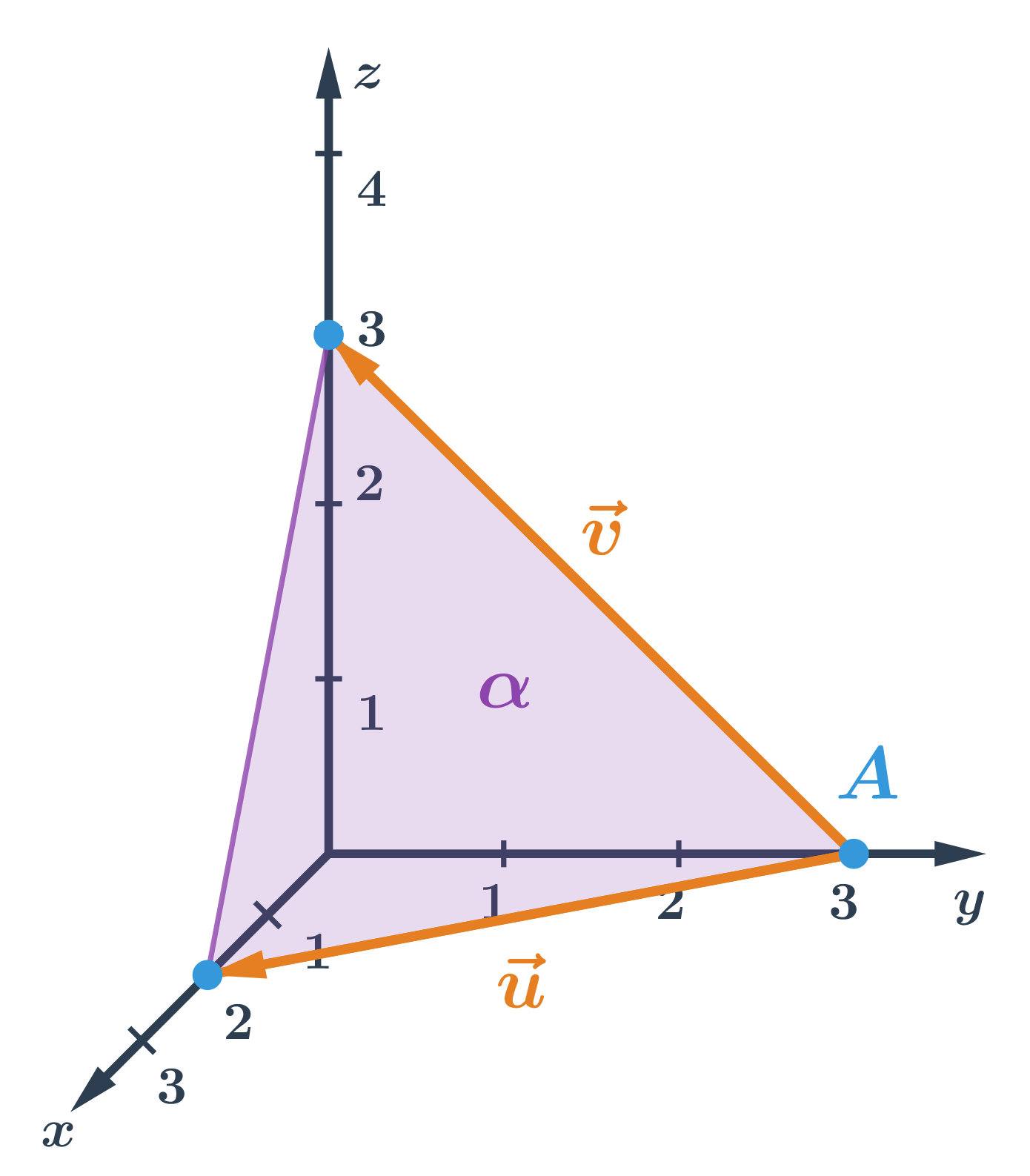
- rovina \alpha je určená bodem A a vektory \vec{u}, \vec{v}
- souřadnice určíme z obrázku:
- A=[0;3;0],
- \vec{u}=(2;-3;0),
- \vec{v}=(0;-3;3)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&2t\\y&=&3-3t-3s\\z&=&3s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určené různoběžkami p a q
Určete parametrické rovnice roviny určené dvěma různoběžkami s následujícími parametrickými rovnicemi:
p:\begin{array}{rrl}x&=&2+3t\\y&=&1+2t\\z&=&4-4t\\&&t\in\mathbb{R}\end{array}, q:\begin{array}{rrl}x&=&2+4s\\y&=&1-2s\\z&=&4-5s\\&&s\in\mathbb{R}\end{array}
- rovina \alpha je určená společným bodem různoběžek a směrovými vektory přímek p a q
- společný bod různoběžek: R=[2;1;4],
- směrový vektor přímky p:\vec{u}=(3;2;4),
- směrový vektor přímky q:\vec{v}=(4;-2;-5)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&2+3t+4s\\y&=&1+2t-2s\\z&=&4-4t-5s\\&&t,s\in\mathbb{R}\end{array}
Obecná rovnice roviny
Obecná rovnice roviny má tvar ax+by+cz+d=0, kde konstanty a, b, c jsou souřadnice normálového vektoru a d reálné číslo. Normálový vektor \vec{n}=(a;b;c) je vektor kolmý k dané rovině.
Obecná rovnice roviny určené bodem a normálovým vektorem
Určete obecnou rovnici roviny \alpha určené bodem A=[-3;1;2] a normálovým vektorem \vec{n}=(2;3;-4).
- Souřadnice normálového vektoru jsou konstanty a, b, c v obecné rovnici roviny, proto obecná rovnice bude mít tvar: 2x+3y-4z+d=0
- Konstantu d určíme dosazením souřadnic bodu A=[-3;1;2] do obecné rovnice: 2\cdot(-3)+3\cdot1-4\cdot 2+d=0\Rightarrow -11+d=0\Rightarrow d=11
- Obecná rovnice roviny \alpha je: 2x+3y-4z+11=0
Obecná rovnice roviny dané bodem a rovnoběžné s jinou rovinou
Obecná rovnice roviny \alpha, která prochází bodem A=[2;3;1] a je rovnoběžná s rovinou \beta:3x+y+4z+1=0.
- Dvě rovnoběžné roviny mají stejný normálový vektor, souřadnice normálového vektoru jsou souřadnice a, b, c v obecné rovnici roviny.
- Proto obecná rovnice hledané roviny \alpha bude mít tvar: 3x+y+4z+d=0
- Konstantu d určíme dosazením souřadnic bodu A=[2;3;1] do obecné rovnice: 3\cdot2+3+4\cdot 1+d=0\Rightarrow 13+d=0\Rightarrow d=-13
- Obecná rovnice roviny \alpha je: 3x+y+4z-13=0
Vzájemná poloha bodu a roviny
Bod leží v rovině, jestliže jeho souřadnice vyhovují rovnici roviny. Pokud je rovina daná obecnou rovnicí, po dosazení souřadnic bodu do rovnice roviny nastane rovnost. Pokud je rovina daná parametricky, po dosazení souřadnic bodu dostaneme soustavu tří rovnic pro dvě neznámé, která má právě jedno řešení.
Bod a rovina daná obecnou rovnicí
Určete, zda body A=[3;4;2] a B=[1;3;0] leží v rovině \alpha dané obecnou rovnicí 2x-y+3z+1=0.
- Do rovnice roviny dosadíme souřadnice bodu A=[3;4;2].
- 2\cdot 3-4+3\cdot2+1=0\Rightarrow9\neq 0, tedy bod A neleží v rovině \alpha.
- Do rovnice roviny dosadíme souřadnice bodu B=[1;3;0].
- 2\cdot 1-3+3\cdot0+1=0\Rightarrow0=0, tedy bod B leží v rovině \alpha.
Bod a rovina daná parametricky
Určete, zda body A=[2;3;4] a B=[0;2;2] leží v rovině \alpha dané parametrickými rovnicemi:
\begin{array}{rrl}x&=&1-t+s\\y&=&2+t+s\\z&=&3-t+s\\&&t,s\in\mathbb{R}\end{array}
- Do rovnic roviny dosadíme souřadnice bodu A=[1;3;4]: \begin{array}{rrrr}2&=&1-t+s\\3&=&2+t+s\\4&=&3-t+s\\\end{array}
- Z prvních dvou rovnic určíme hodnoty t a s, dosazením do třetí rovnice zjistíme, zda nalezené hodnoty jsou řešením soustavy a tedy zda bod leží v rovině:
- první a druhou rovnici sečteme: 5=3+2s\Rightarrow s=1
- hodnotu s=1 dosadíme do první rovnice: 1=1-t+1\Rightarrow t=1
- hodnoty s=1 a t=1 dosadíme do třetí rovnice: 4=3-1+1. Tato rovnost neplatí, tedy bod A neleží v rovině \alpha.
- Do rovnic roviny dosadíme souřadnice bodu B=[0;-3;2]: \begin{array}{rrrr}0&=&1-t+s\\-3&=&2+t+s\\2&=&3-t+s\\\end{array}
- Z prvních dvou rovnic určíme hodnoty t a s, dosazením do třetí rovnice zjistíme, zda nalezené hodnoty jsou řešením soustavy a tedy zda bod leží v rovině:
- první a druhou rovnici sečteme: -3=3+2s\Rightarrow s=-3
- hodnotu s=-3 dosadíme do první rovnice: 0=1-t-3\Rightarrow t=-2
- hodnoty s=-3 a t=-2 dosadíme do třetí rovnice: 2=3-(-2)-3. Tato rovnost platí, tedy bod B leží v rovině \alpha.
