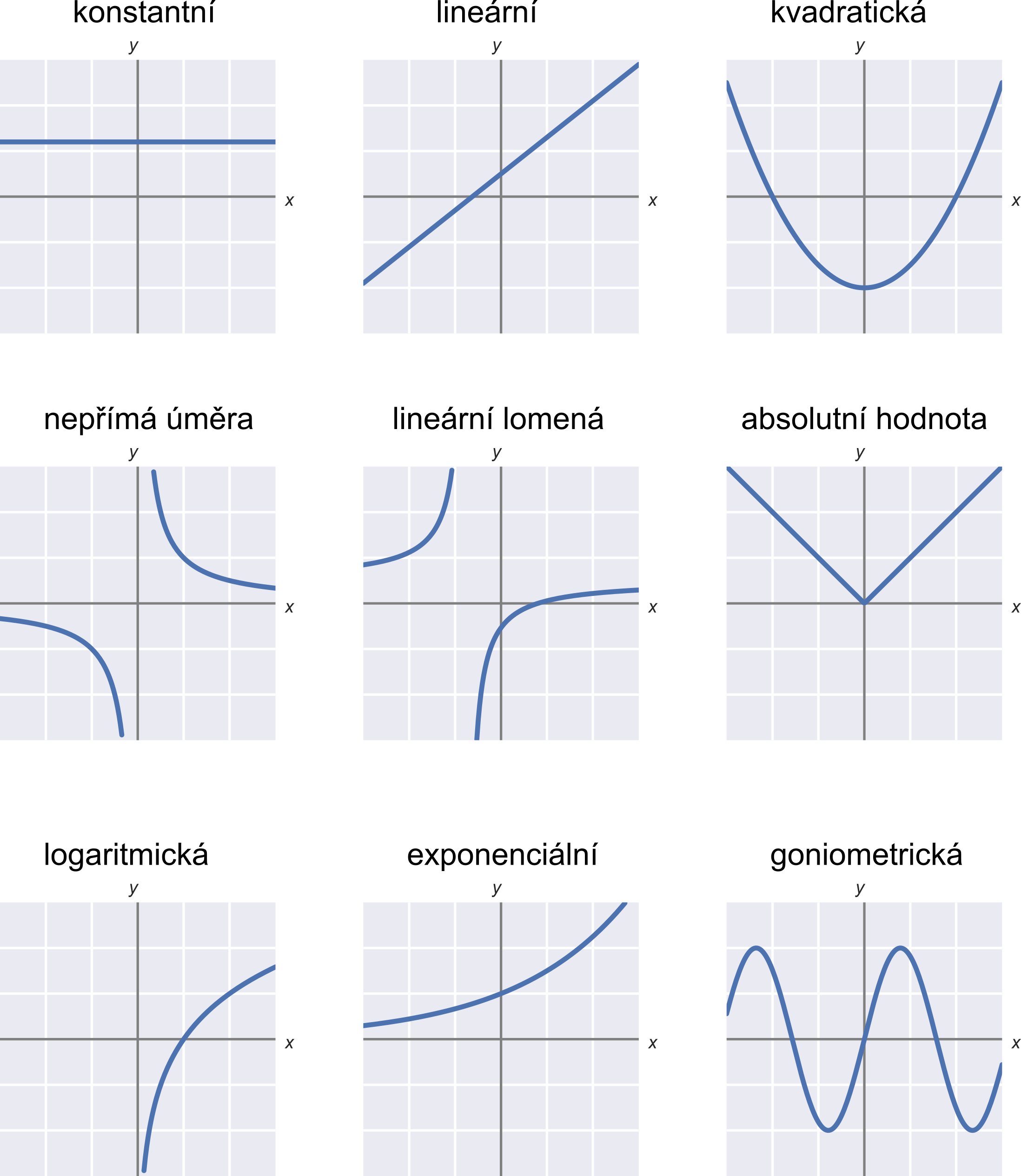
Výpis souhrnů
Funkce
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
- Funkce
- Funkce: základy
- Základní typy funkcí
- Vlastnosti funkcí
- Grafy funkcí
- Grafy lineárních funkcí
- Grafy kvadratických funkcí
- Grafy funkcí s absolutní hodnotou
- Grafy lineárních lomených funkcí
- Grafy mocninných funkcí
- Grafy goniometrických funkcí
- Grafy exponenciálních funkcí
- Grafy logaritmických funkcí
- Grafy lineárních nerovnic
- Souřadnice bodů v rovině
- Lineární funkce
- Vlastnosti lineární funkce
- Základní rovnice s jednou neznámou
- Lineární lomené funkce
- Vlastnosti lineární lomené funkce
- Kvadratické funkce
- Vlastnosti kvadratické funkce
- Kvadratické rovnice
- Goniometrické funkce
- Goniometrické funkce a pravoúhlý trojúhelník
- Hodnoty goniometrických funkcí
- Goniometrické funkce: vztahy a vzorce
- Vlastnosti goniometrických funkcí
- Mocninné funkce
- Exponenciální funkce
- Vlastnosti exponenciálních funkcí
- Logaritmické funkce
- Vlastnosti logaritmických funkcí
Funkce je speciální typ závislosti, při které je každé hodnotě z jedné množiny (definičního oboru funkce) přiřazena právě jedna hodnota z druhé množiny (oboru hodnot).
V matematice obvykle pracujeme s funkcemi nad množinami čísel, kde vztah mezi x a y popisuje matematický výraz, píšeme ve tvaru y=f(x). Definiční obor je množina všech hodnot x, které uvažujeme (např. množina všech x pro která má výraz f(x) smysl), označujeme D(f). Obor hodnot je množina všech funkčních hodnot y, označujeme H(f).
Procvičit si Co je funkce? lze v tématu Funkce: základy.
Mezi základní typy funkcí, se kterými se v matematice setkáme, patří:
| Typ | Příklad |
|---|---|
| Lineární funkce | f(x) = 3x + 1 |
| Lineární lomené funkce | f(x) = \frac{2x -4}{x+3} |
| Kvadratické funkce | f(x) = x^2 - 4x + 3 |
| Goniometrické funkce | f(x) = \sin x |
| Mocninné funkce | f(x) = x^3, f(x) = \sqrt{x} |
| Exponenciální a logaritmické funkce | f(x) = 2^x, f(x) = \log x |
Téma typy a vlastnosti funkcí se zabývá podrobnějším rozlišováním mezi jednotlivými typy funkcí a jejich vlastnostmi, jako jsou periodičnost či omezenost.
Funkce pro lepší pochopení často zakreslujeme graficky, což nám umožňuje lépe vidět vztah mezi x a f(x). Téma grafy funkcí zastřešuje procvičování v tomto ztvárnění.
Příklad: graf funkce
Každému číslu x v definičním oboru funkce odpovídá právě jedna funkční hodnota y=f(x).
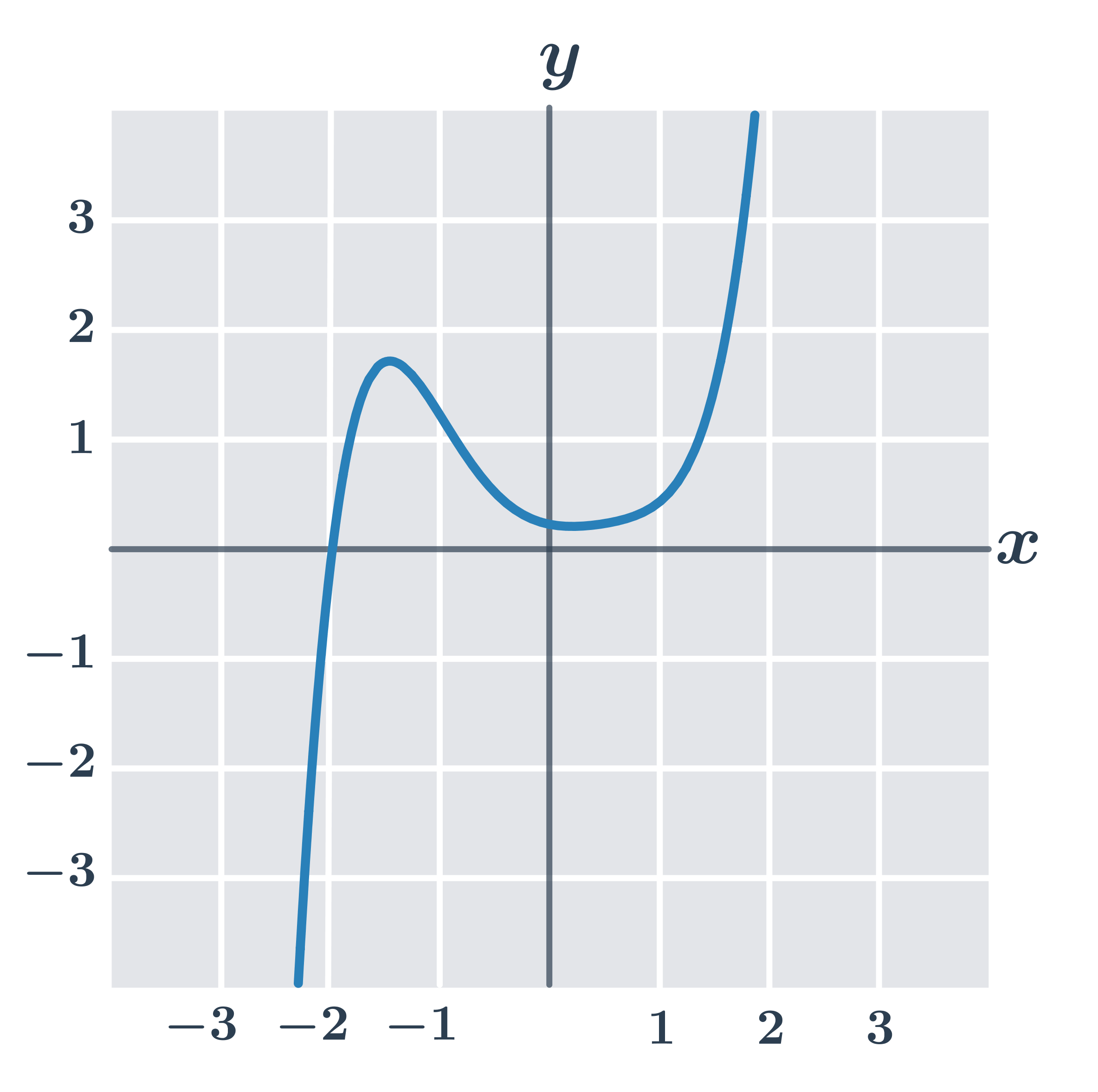
Příklad: toto není graf funkce
Na následujícím obrázku není graf funkce:
Například pro x=1 bychom neměli jednoznačně danou hodnotu y=f(x) (máme dva oranžově zvýrazněné body s x=1, ale dvěma různými souřadnicemi y).
Funkce: základy
Pro snadnější pochopení pojmu funkce uvedeme příklad: Děti ve třídě mají napsat měsíc svého narození. Každému dítěti je tak daným pravidlem přiřazen měsíc.
Funkce je zde předpis, který každému x (dítě) z nějaké množiny D (všechny děti ze třídy) přiřazuje právě jednu funkční hodnotu y (měsíc, ve kterém se dané dítě narodilo). Daný předpis je funkce, protože každému x je přiřazena právě jedna hodnota y – každé dítě má právě jeden měsíc, ve kterém se narodilo.
Přitom ale nemusí každému y odpovídat právě jedna hodnota x. Dva různé prvky z množiny D mohou mít stejnou funkční hodnotu – dvě děti mohou mít stejný měsíc narození.
Souvislost s informatikou
Funkci můžeme chápat také jako vztah, který přiřazuje každému vstupu právě jeden výstup. Jako intuitivní příklad funkce může posloužit „obarvovač na modro“ – na vstup bere kostku, na výstup dává kostku obarvenou na modro.
Takové pojetí funkcí najdeme v informatice, kde funkce pomáhají definovat různé operace a jsou počítány pomocí algoritmů.
Vlastnosti funkcí
Pro zjednodušení popisu uvažujeme v tomto shrnutí pouze funkce, jejichž definiční obor tvoří všechna reálná čísla.
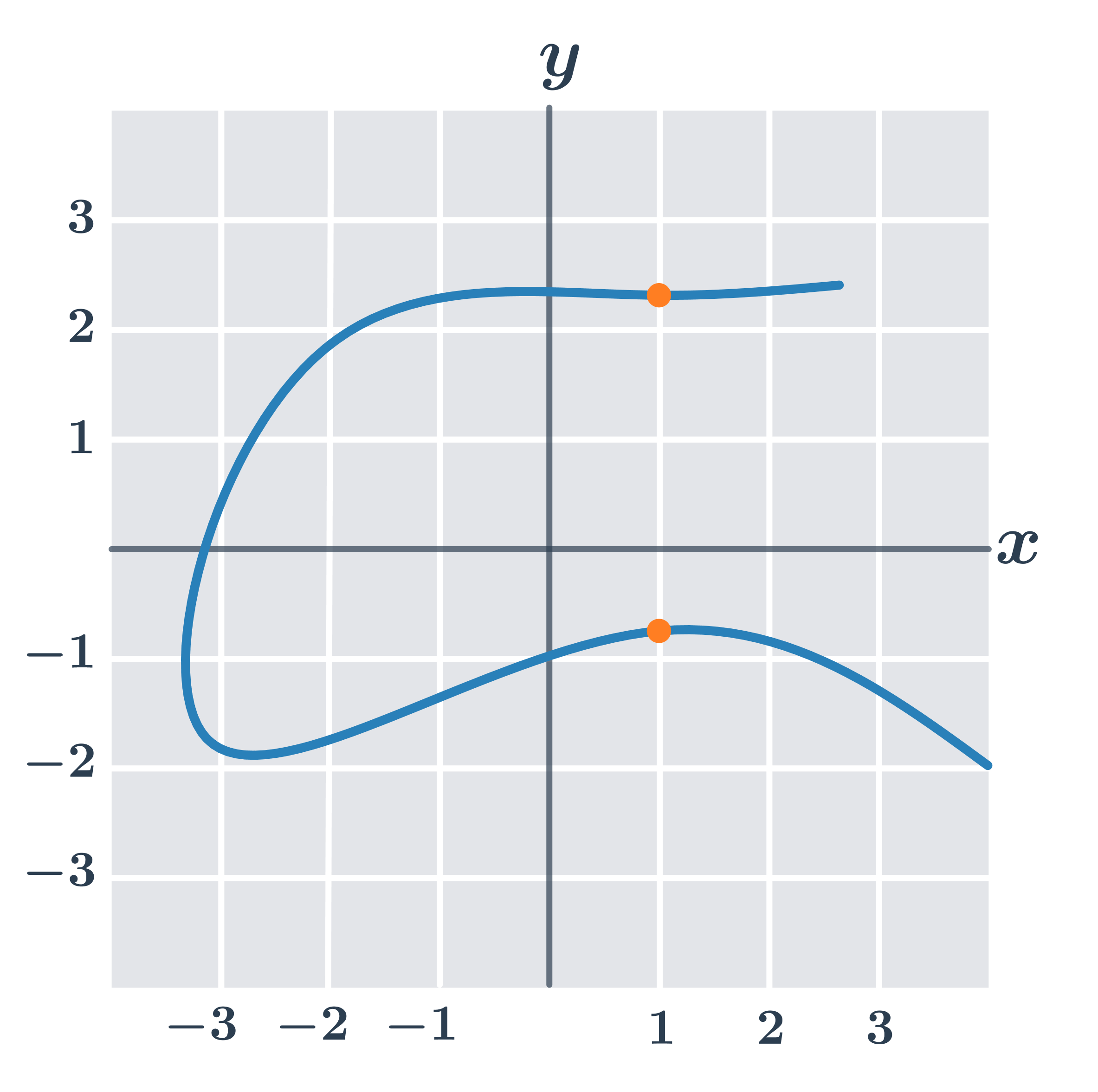
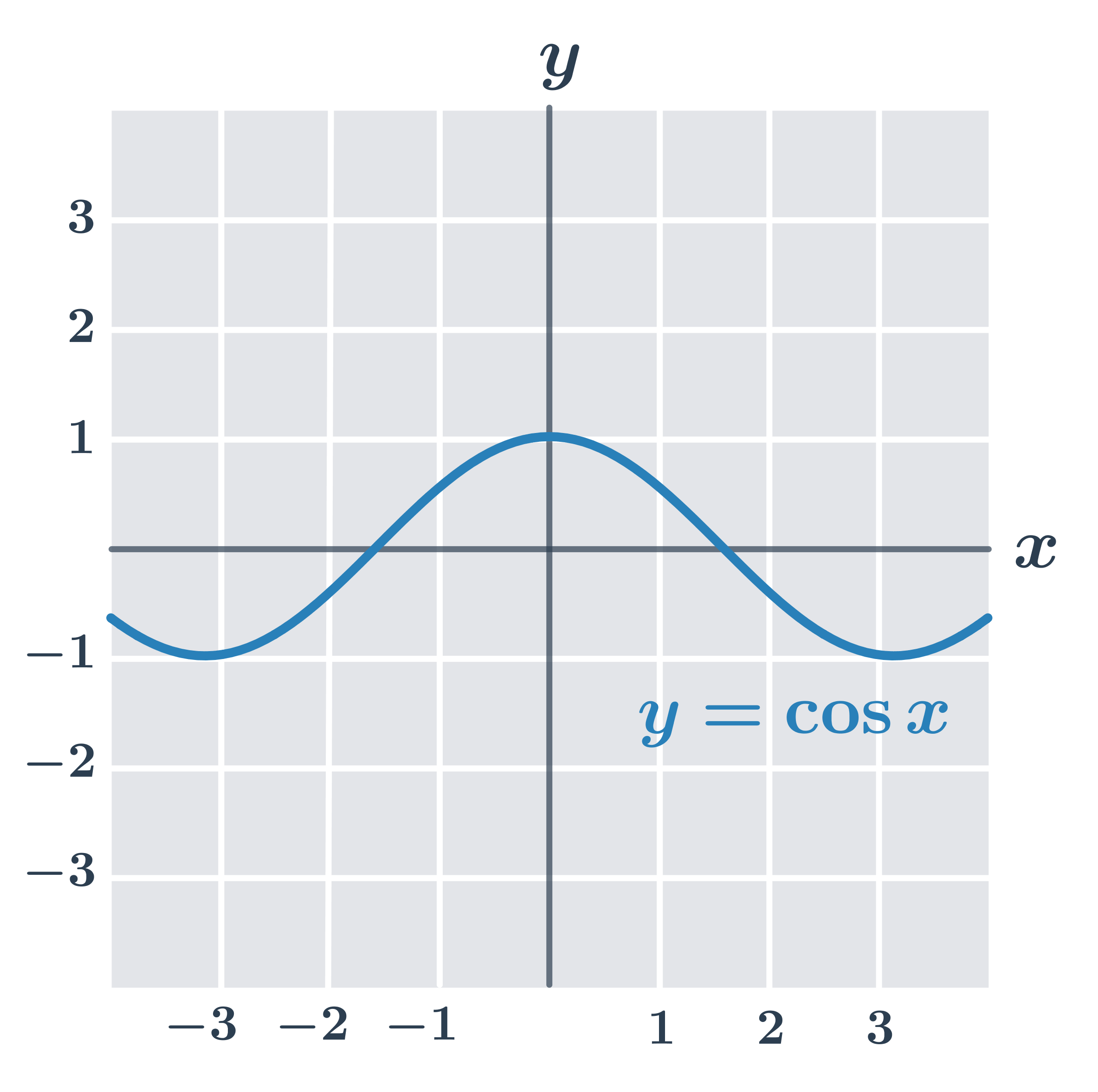
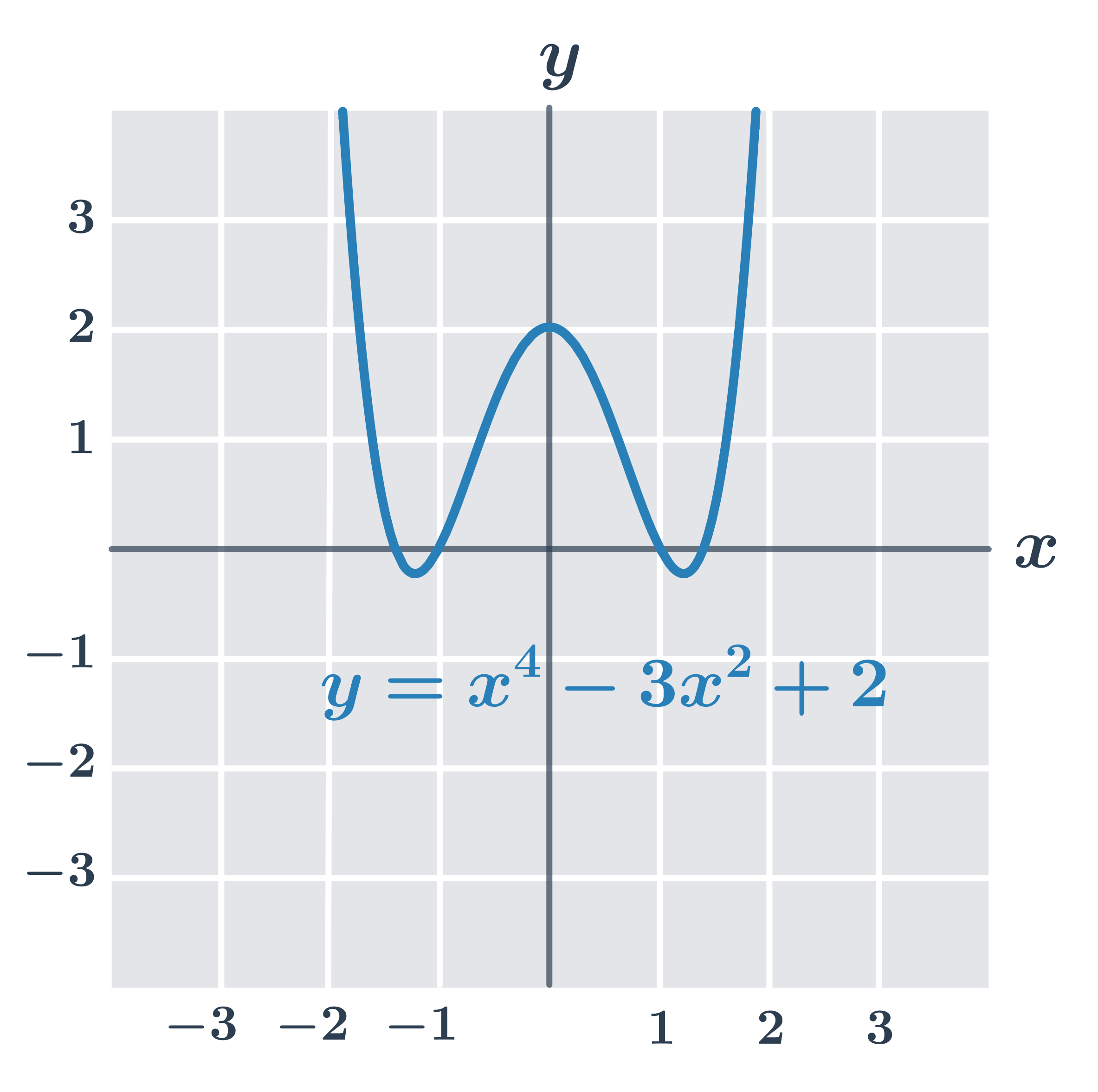
Funkce f se nazývá sudá, právě když pro každé x je f(-x) = f(x). Graf sudé funkce je souměrný podle osy y.
Příklady sudých funkcí
- f_1(x) = x^2
- f_2(x) = \cos x
- f_3(x) = x^4-3x^2+2
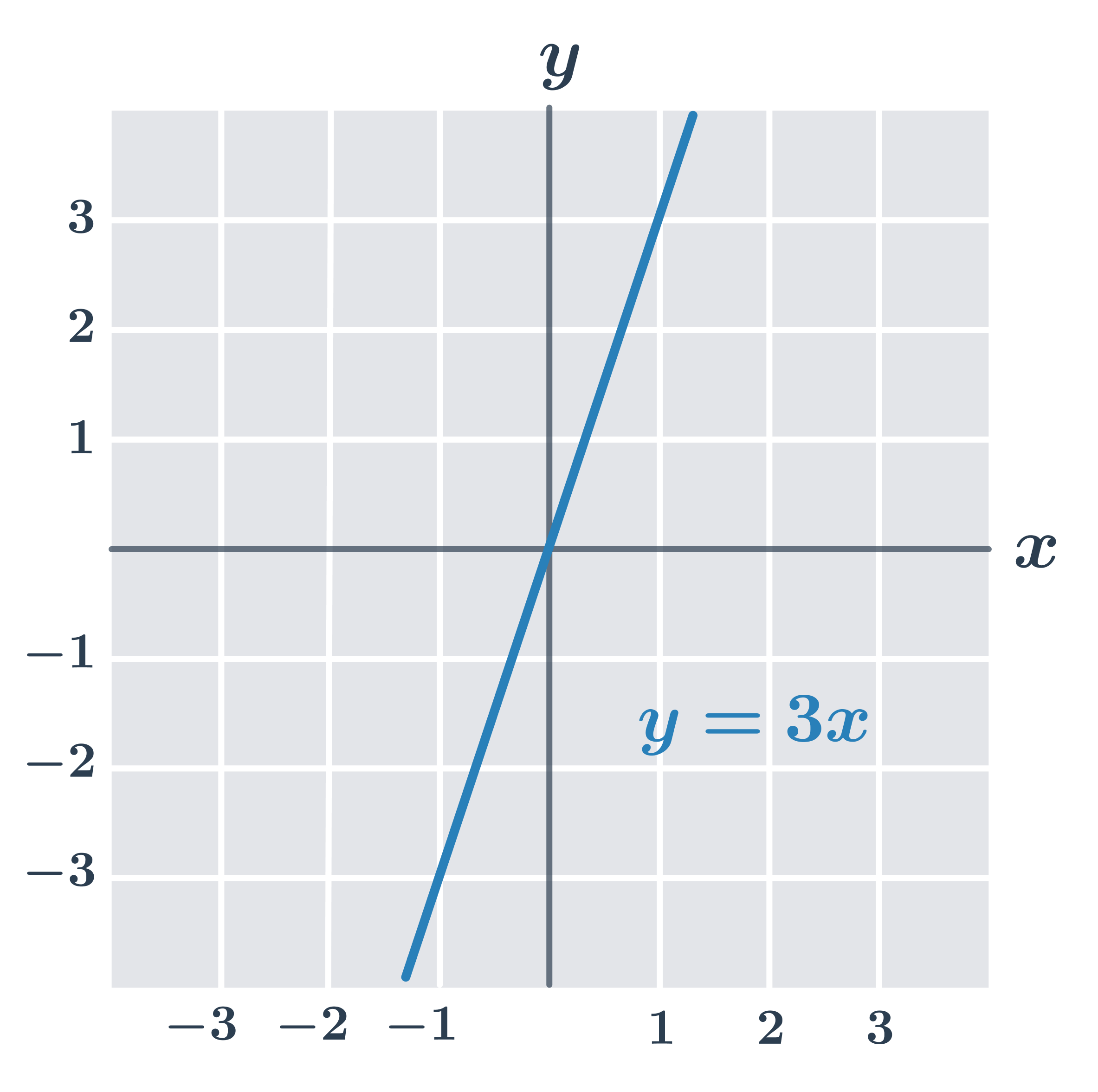
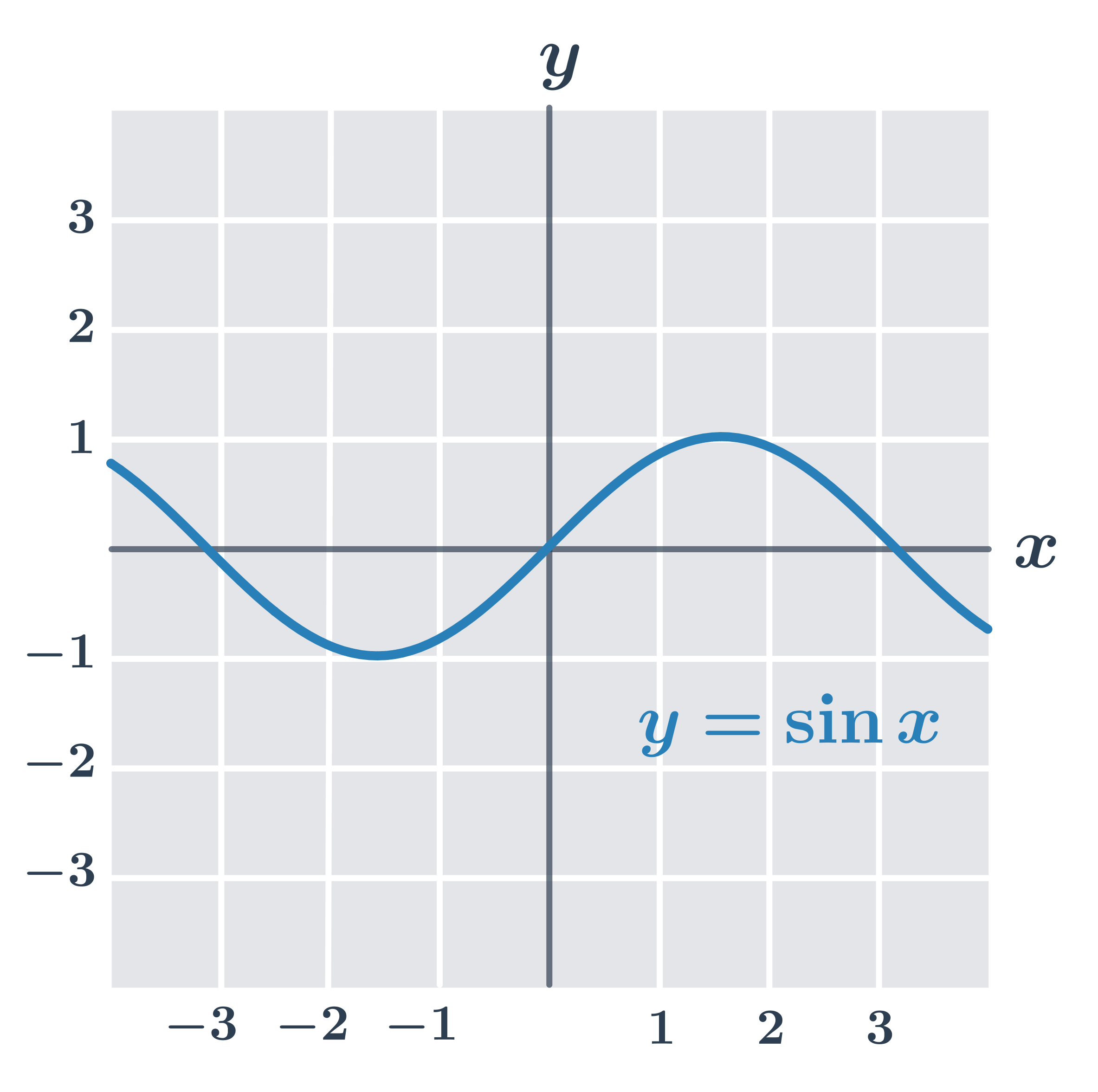
Funkce f se nazývá lichá, právě když pro každé x je f(-x) = -f(x). Graf liché funkce je středově souměrný podle počátku soustavy souřadnic.
Příklady lichých funkcí
- f_1(x) = 3x
- f_2(x) = \sin x
- f_3(x) = x^3-2x
Funkce f se nazývá periodická, právě když existuje číslo p \neq 0 (perioda funkce) takové, že pro každé x platí f(x+p)=f(x). Typickými příklady periodických funkcí jsou funkce goniometrické. Naopak třeba polynomy periodické nejsou (s výjimkou konstantní funkce).
Funkce f se nazývá zdola omezená, právě když existuje takové číslo k, že pro každé x platí f(x) \geq k. Funkce f se nazývá shora omezená, právě když existuje takové číslo k, že pro každé x platí f(x) \leq k. Funkce f se nazývá omezená, pokud je současně omezená shora i zdola.
Příklady (ne)omezených funkcí
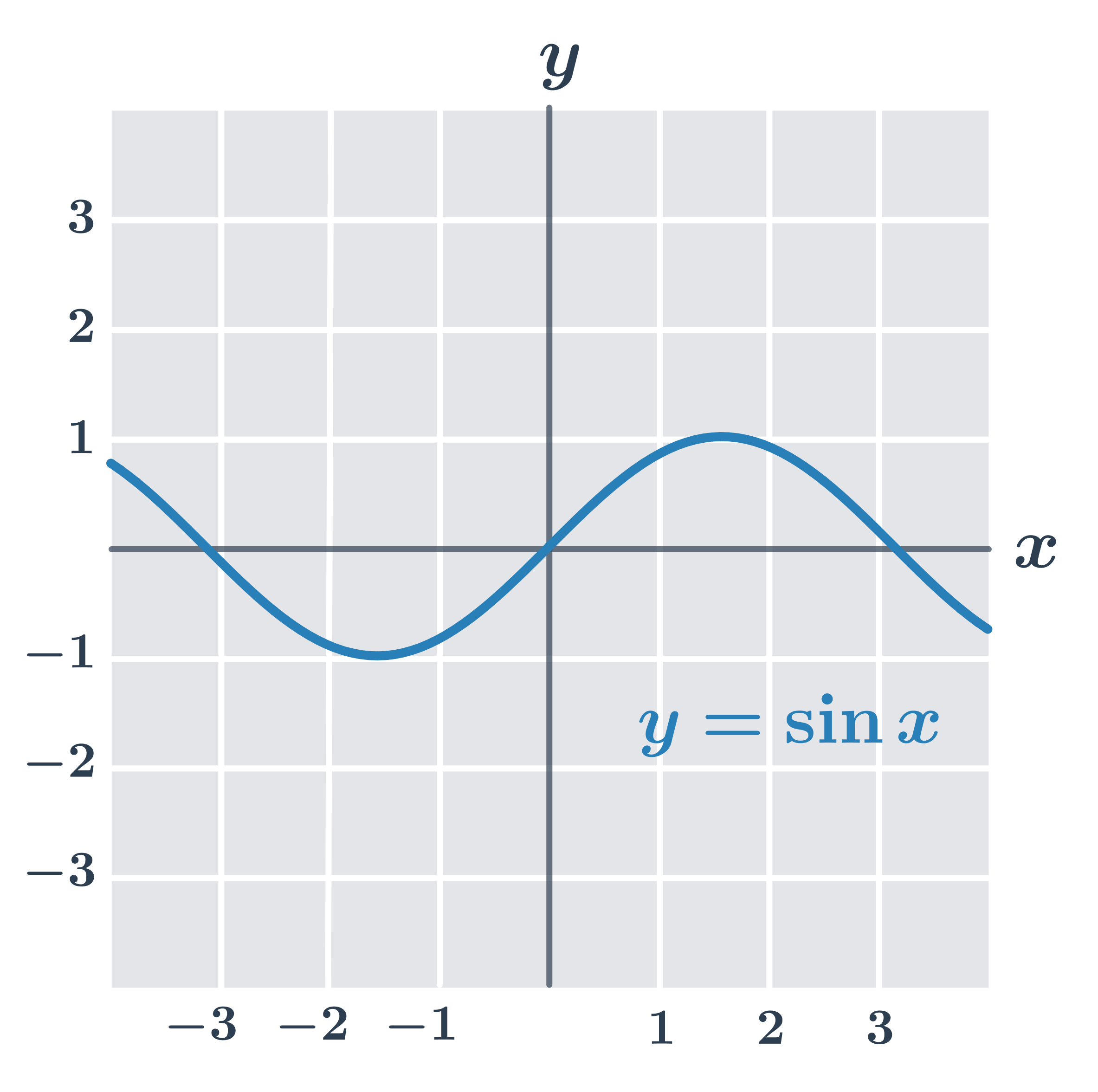
- Funkce f(x) = \sin x je omezená.
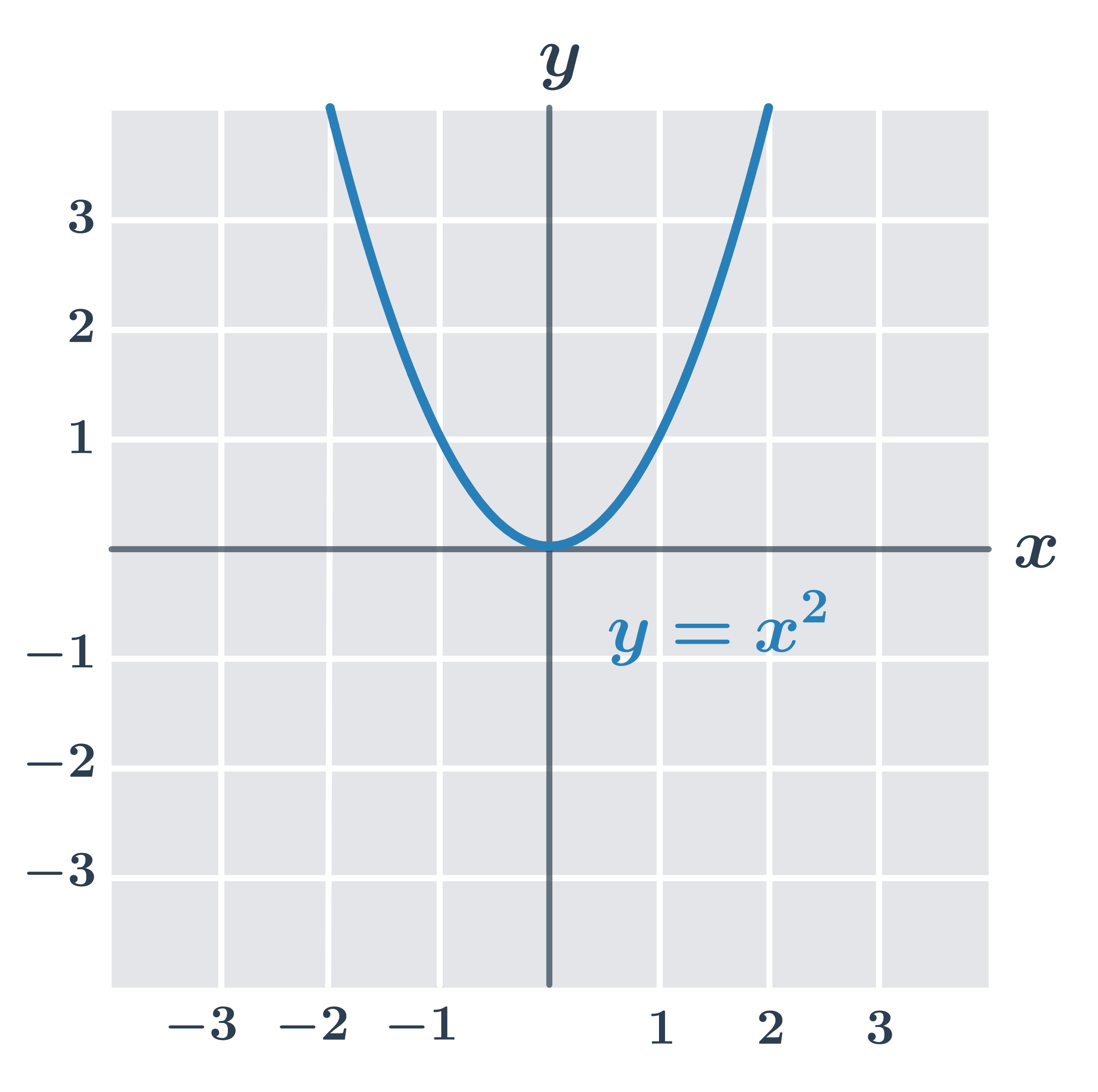
- Funkce f(x) = x^2 je omezená zdola (protože \forall x: f(x) \geq 0), ale není omezená shora.
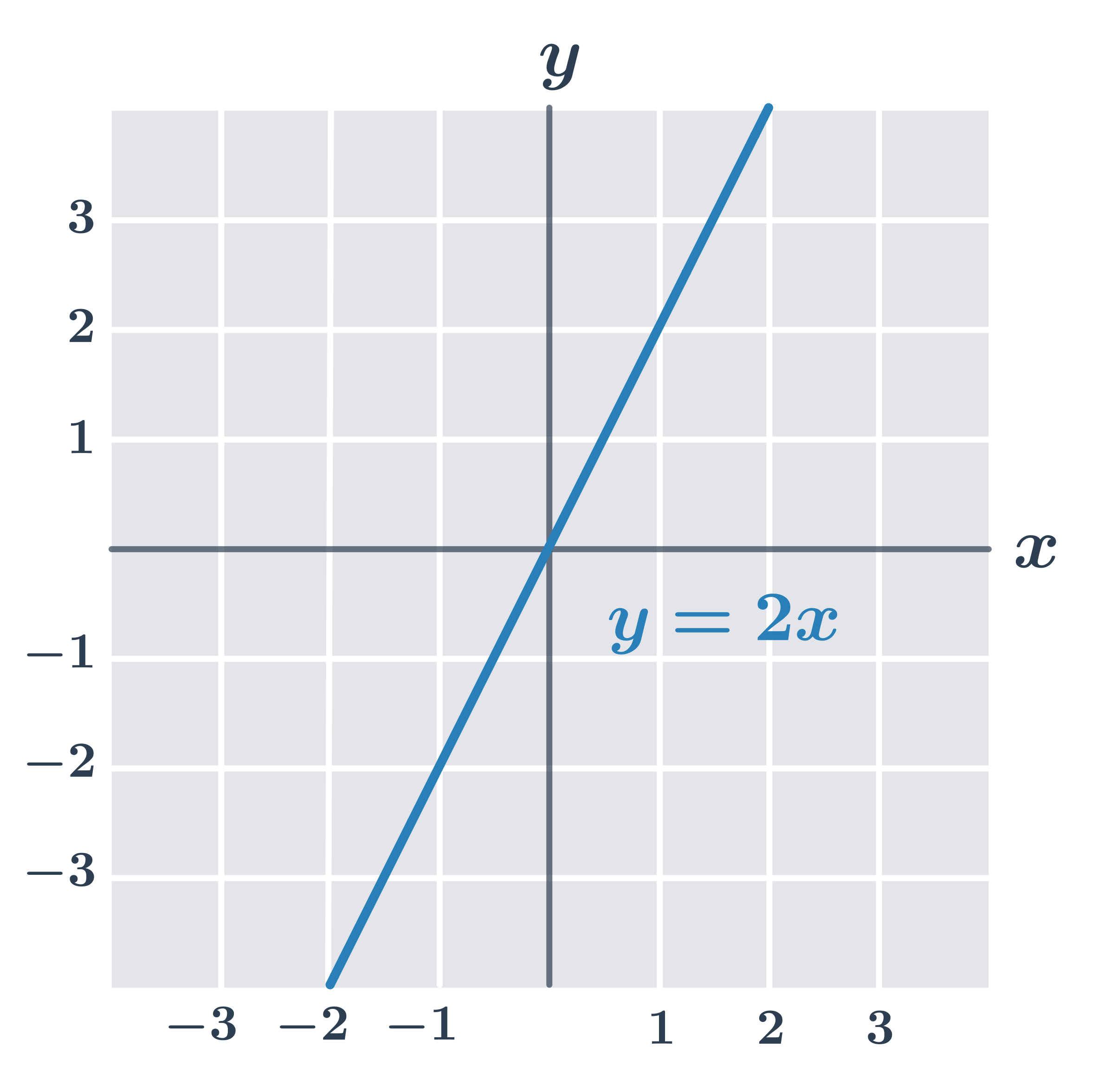
- Funkce f(x) = 2x není omezená ani shora, ani zdola.
Funkce f se nazývá prostá, právě když pro každou dvojici x_1 \neq x_2 platí f(x_1) \neq f(x_2).
Funkce f se nazývá rostoucí, právě když pro každou dvojici x_1 \lt x_2 platí f(x_1) \lt f(x_2).
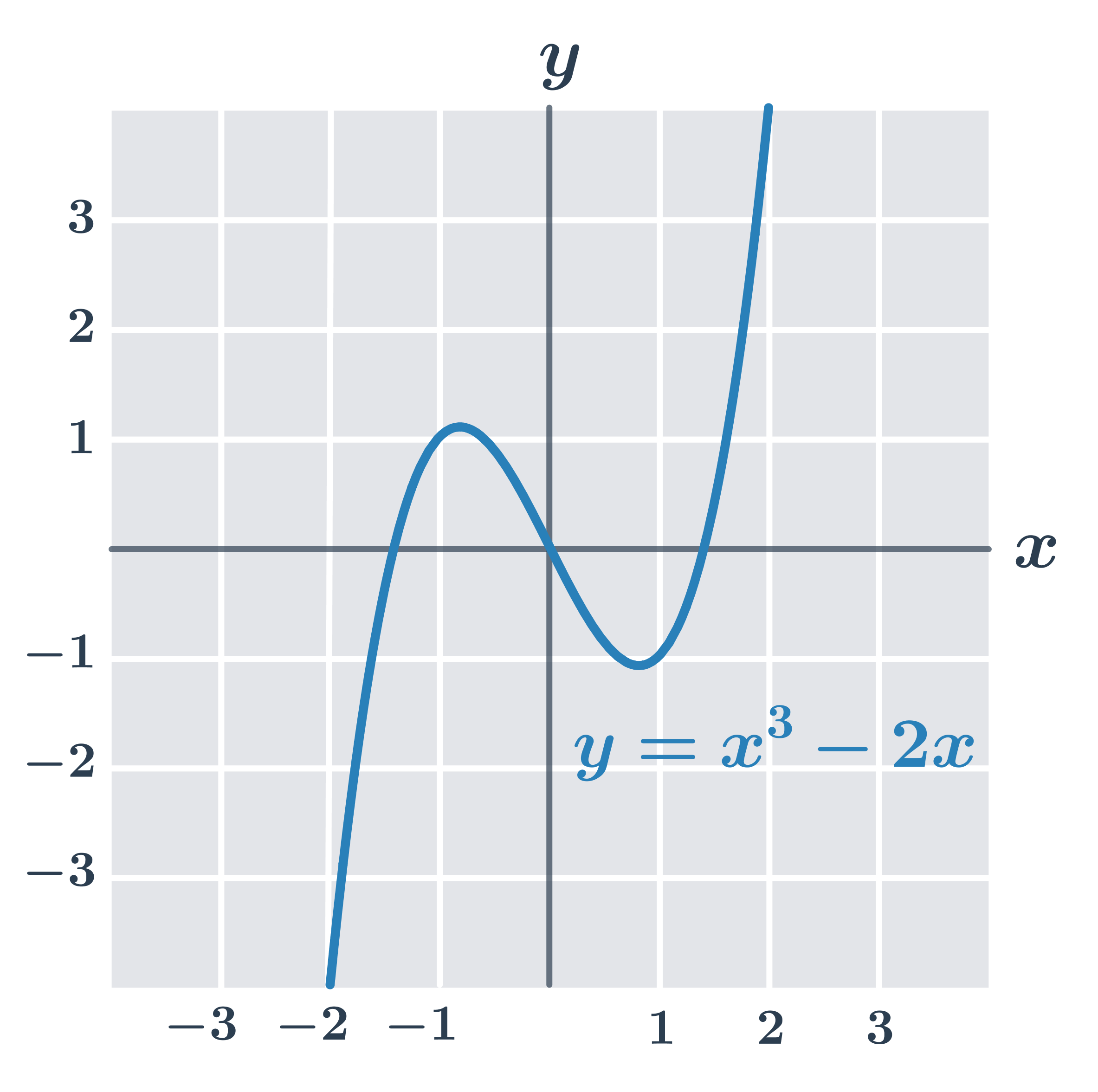
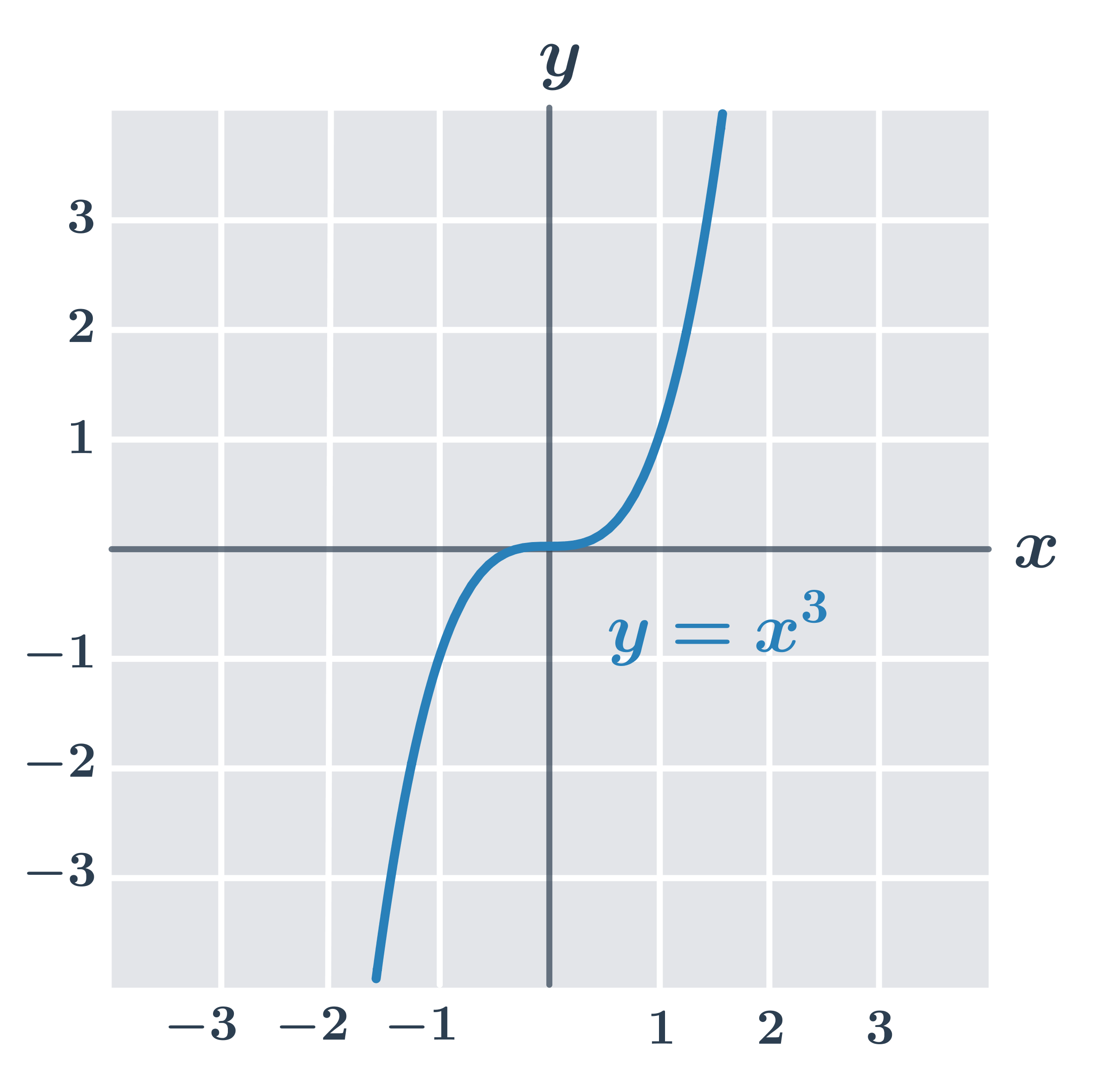
Příklad: funkce f(x) = x^3
Funkce f(x)=x^3 s definičním oborem D(f) = \mathbb{R} je prostá a rostoucí.
Funkce f se nazývá klesající, právě když pro každou dvojici x_1 \lt x_2 platí f(x_1) \gt f(x_2).
Příklad: funkce f(x) = \frac{1}{x}
Funkce f(x)= \frac{1}{x} s definičním oborem D(f) = (-\infty,0) \cup (0,\infty):
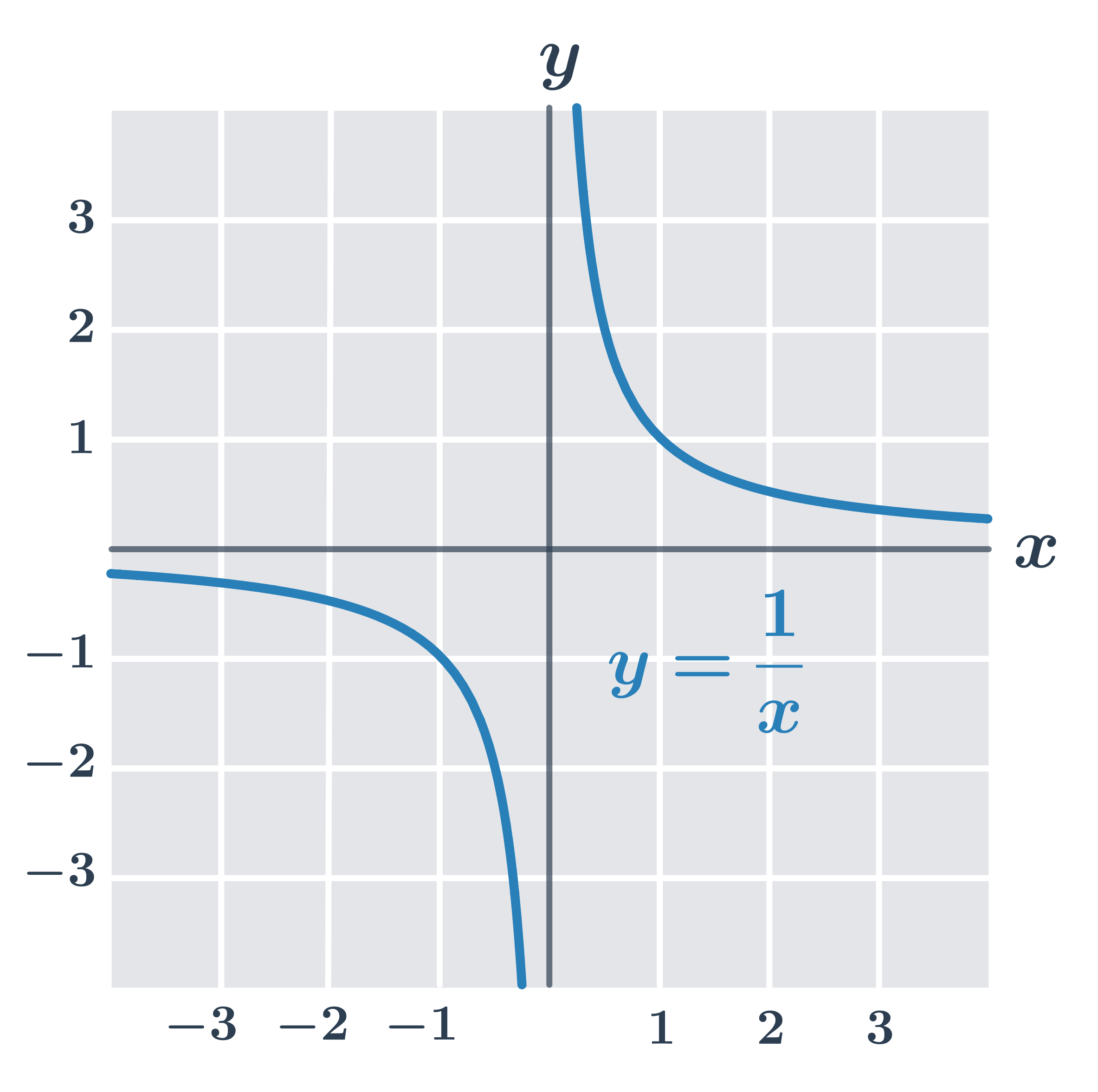
- funkce klesá na intervalu (-\infty,0)
- funkce také klesá na intervalu (0,\infty)
- ale funkce není klesající na celém D(f), např. -1 \lt 1, ale f(-1) \lt f(1)
Funkce f má v bodě x_0 maximum, jestliže pro každé x \in D(f) je f(x) \leq f(x_0). Maximum je tedy bod, ve kterém je funkční hodnota maximální (takových bodů může být i víc než jeden, např. u funkce sinus).
Funkce f má v bodě x_0 minimum, jestliže pro každé x \in D(f) je f(x) \geq f(x_0). Minimum je tedy bod, ve kterém je funkční hodnota minimální (takových bodů opět může být i více než jeden).
Maximum a minimum se nazývají extrémy funkce.
Příklad: maximum funkce f(x)=1-x^2
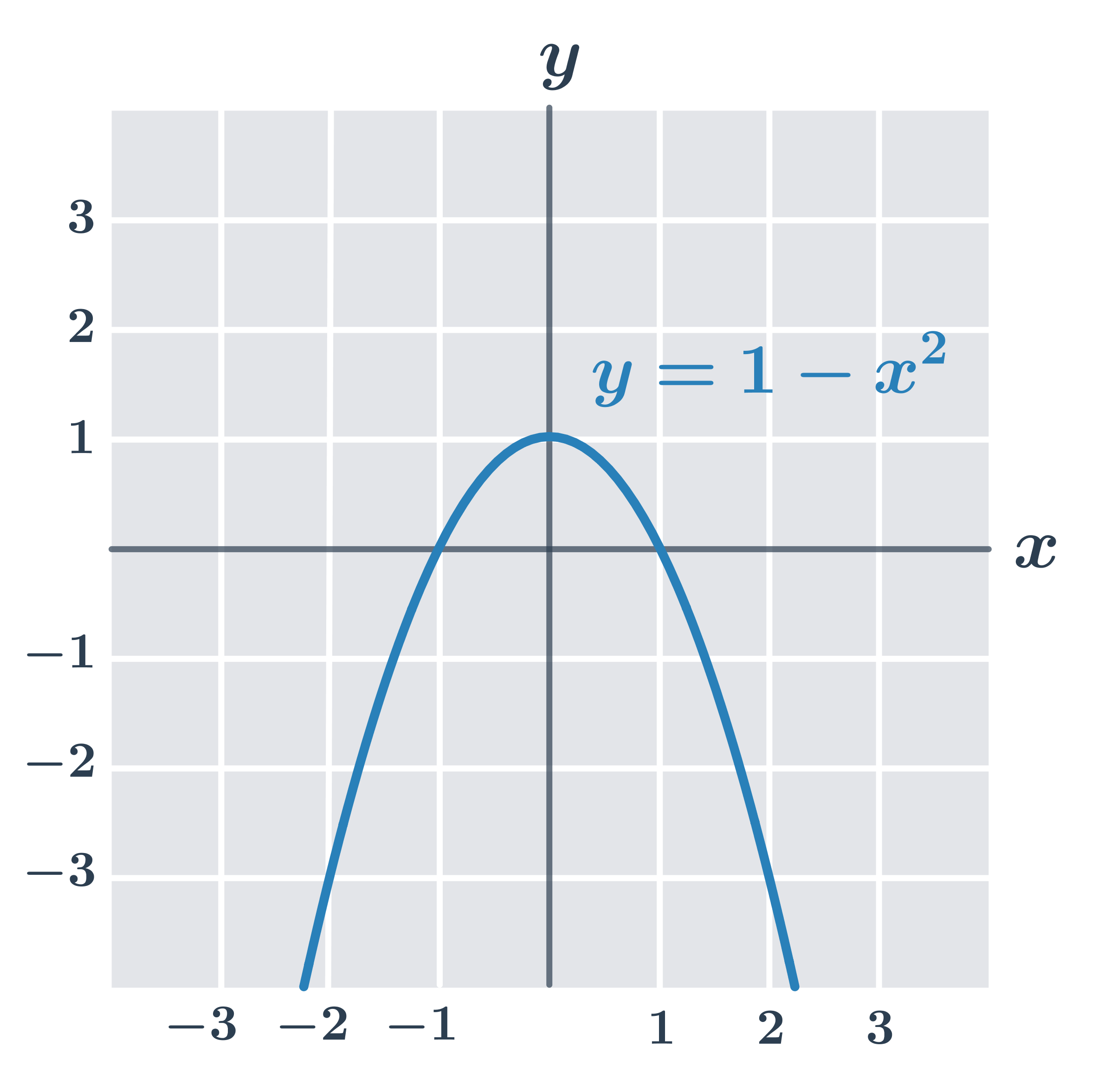
- Funkce f:y=1-x^2 má ze všech reálných čísel nejvyšší hodnotu v bodě x=0, je f(0)=1 a pro libovolné reálné číslo x je f(x) \leq 1.
- Funkce tedy nabývá maxima pro x=0. Minimum tato funkce nemá.
Příklad: minimum funkce f(x)=(x-1)^2
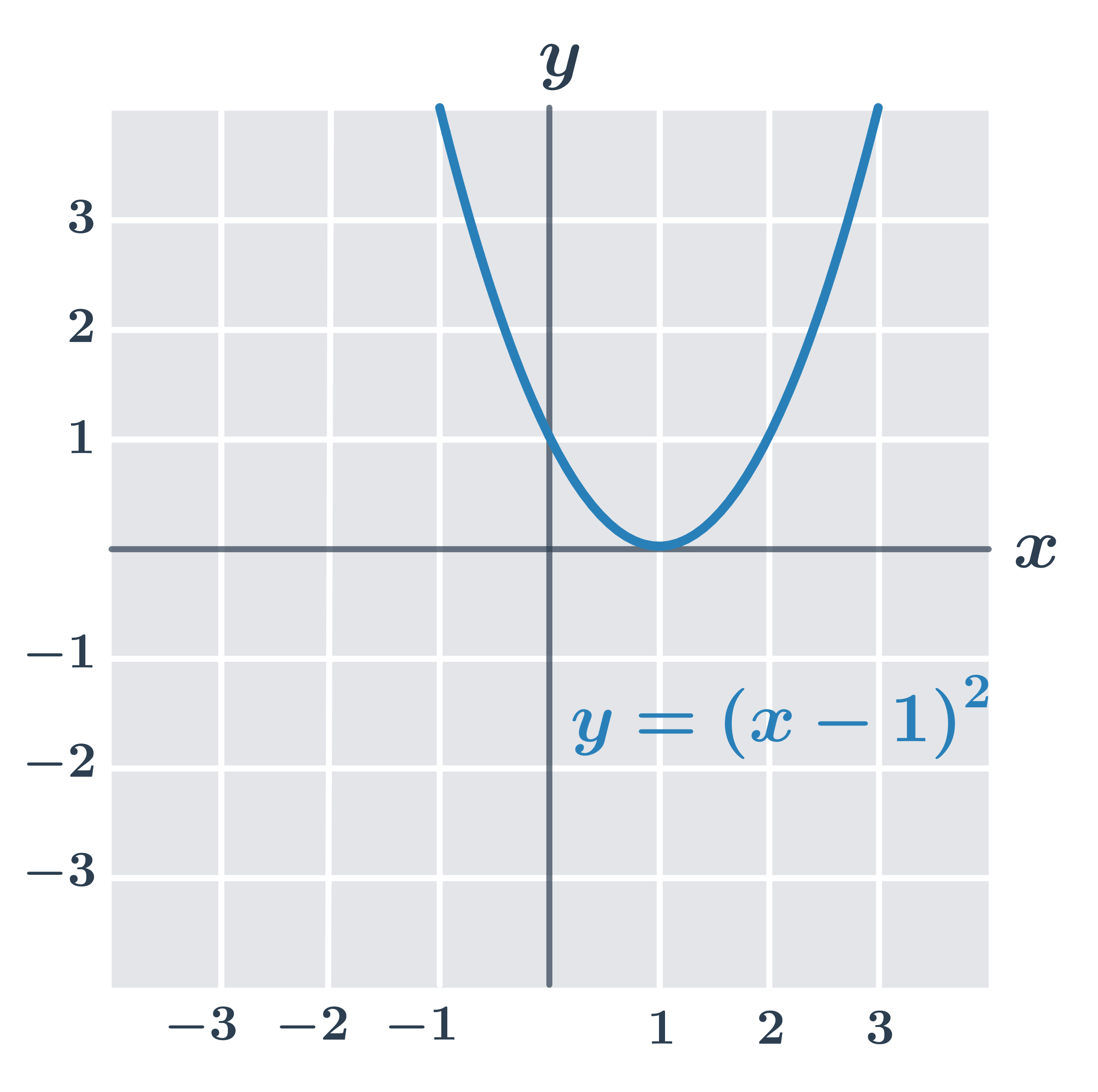
- Funkce f:y=(x-1)^2 má nejnižší hodnotu v bodě x=1, máme f(1) = 0 a pro libovolné reálné číslo x je f(x) \geq 0.
- Funkce tedy má v bodě x=1 minimum. Maximum tato funkce nemá.
Grafy funkcí
Graf funkce f zadané předpisem y=f(x) pro všechna x z množiny D(f) je množina bodů v rovině, jejichž kartézské souřadnice x, y splňují následující podmínky:
- souřadnice x je v definičním oboru funkce f (neboli x \in D(f))
- závislost souřadnice y na x je popsaná funkčním předpisem y=f(x) (pro každé x z D(f) je v grafu právě jeden bod, jeho souřadnice jsou x a f(x))
Příklad: graf, definiční obor, obor hodnot funkce
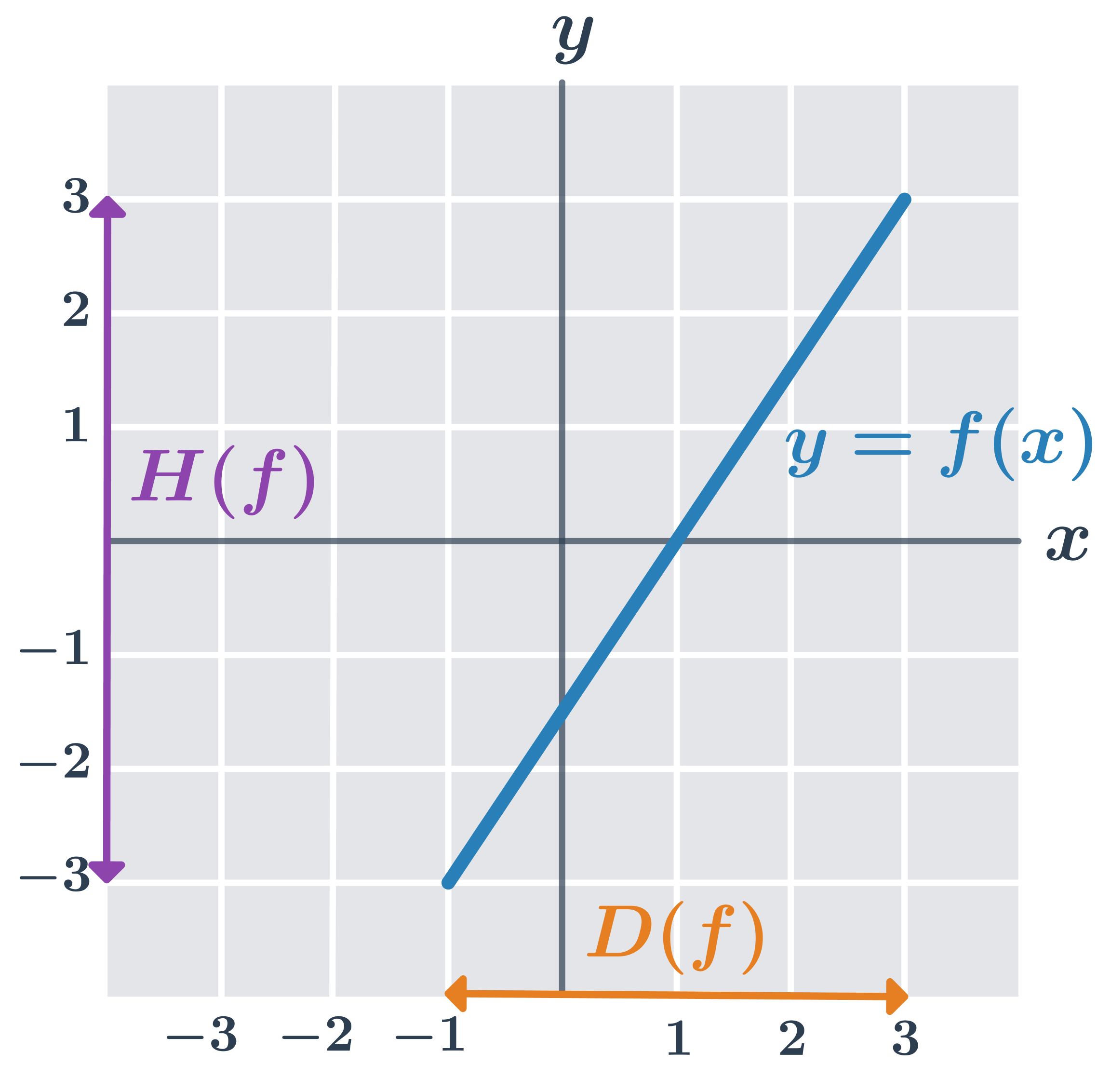
Na obrázku je graf funkce y=2x-1 pro x\in \langle -1;3\rangle. Definiční obor je vyznačen na ose x, obor hodnot na ose y.
Grafy lineárních funkcí
Lineární funkci můžeme vždy zapsat ve tvaru f(x)= a \cdot x + b, kde a a b jsou konstanty. Číslo a je směrnice (též nazývaná sklon), konstanta b je absolutní člen. Grafem lineární funkce je přímka, kterou snadno sestrojíme pomocí dvou bodů.
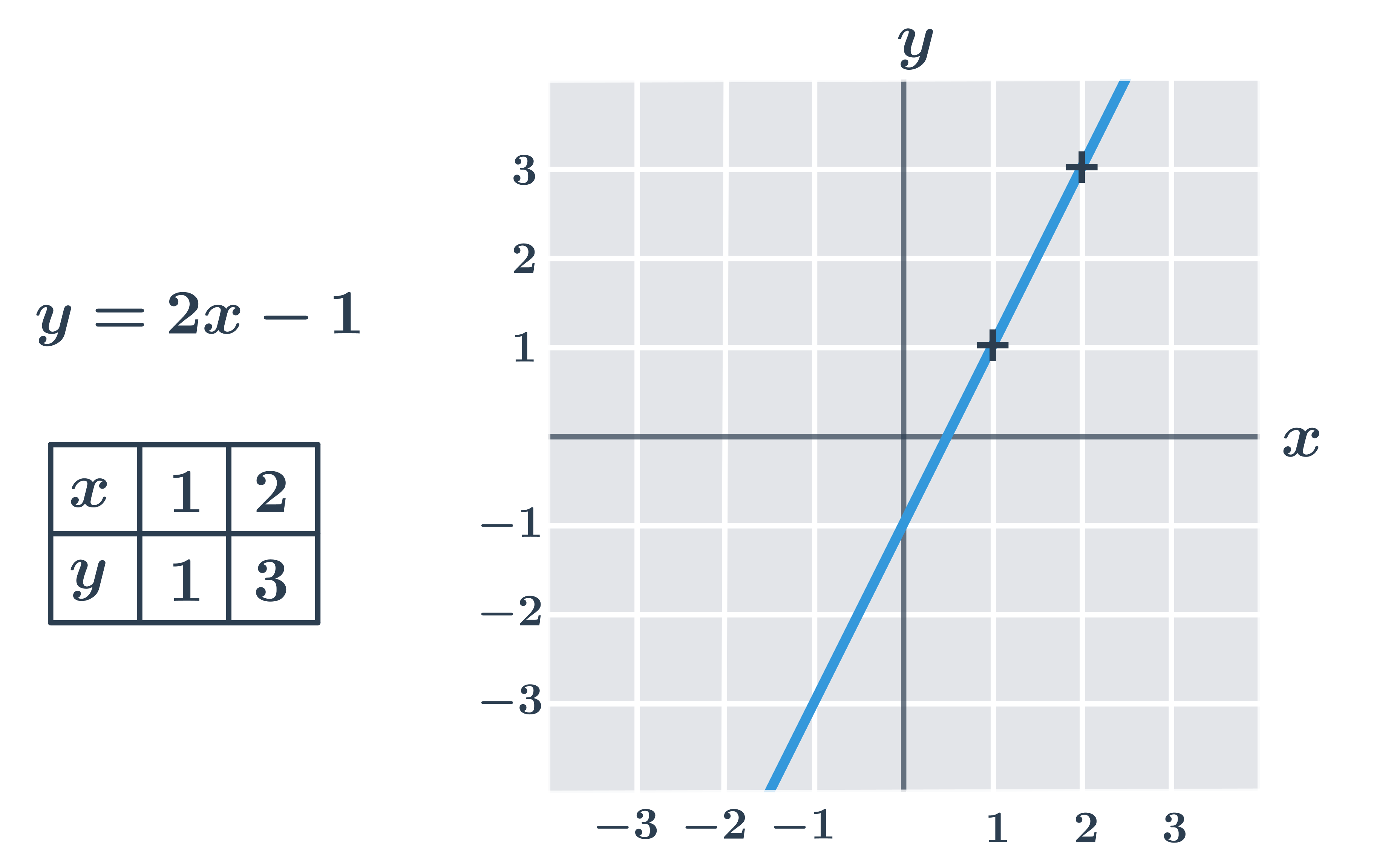
Příklad: graf funkce y=-0{,}5x+1.
- Zvolíme si dvě libovolné hodnoty proměnné x. Vhodnou volbou je x=0, tím zároveň určíme i průsečík s osou y.
- Pro x=0 dopočítáme hodnotu y, tedy: y=-0{,}5\cdot 0+2=0+1=1
- Dále zvolíme například x=2 a dosadíme: y=-0{,}5\cdot 2+1=-1+1=0
- Graf funkce y=-0{,}5x+1 pak prochází body [0;1] a [2;0].
Přímku, která je grafem funkce f(x)=a\cdot x+b můžeme sestrojit také pomocí konstant a a b, přičemž platí:
- Absolutní člen b udává „svislý posun“. Je to průsečík přímky s osou y. V uvedených příkladech je vyznačen oranžovou barvou.
- Směrnice a udává sklon přímky, což můžeme vyjádřit jako „o kolik jednotek na ose y se po dané přímce posuneme, když se posuneme o jednu jednotku na ose x“. V uvedených příkladech je směrnice vyznačena žlutou barvou.
Důležitá jsou znamínka (naznačená v obrázcích šipkami). Kladný absolutní člen znamená posun nahoru, záporný absolutní člen znamená posun dolů. Kladná směrnice znamená stoupající přímku, záporná směrnice znamená klesající přímku.
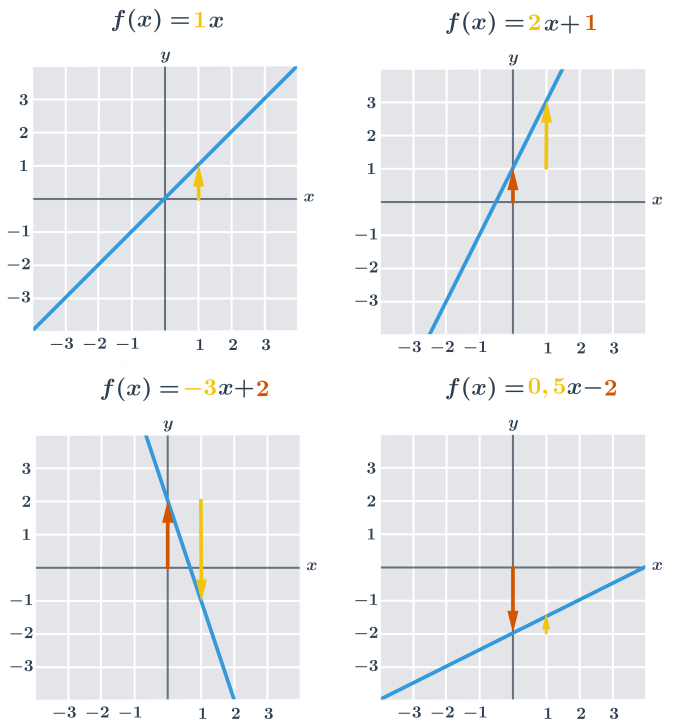
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
NahoruGrafy kvadratických funkcí
Kvadratickou funkci lze vyjádřit ve tvaru f(x) = ax^2 + bx + c, kde a\neq 0. Grafem kvadratické funkce je parabola. Tento graf zobrazuje funkci 0{,}5 x^2 + x - 4:
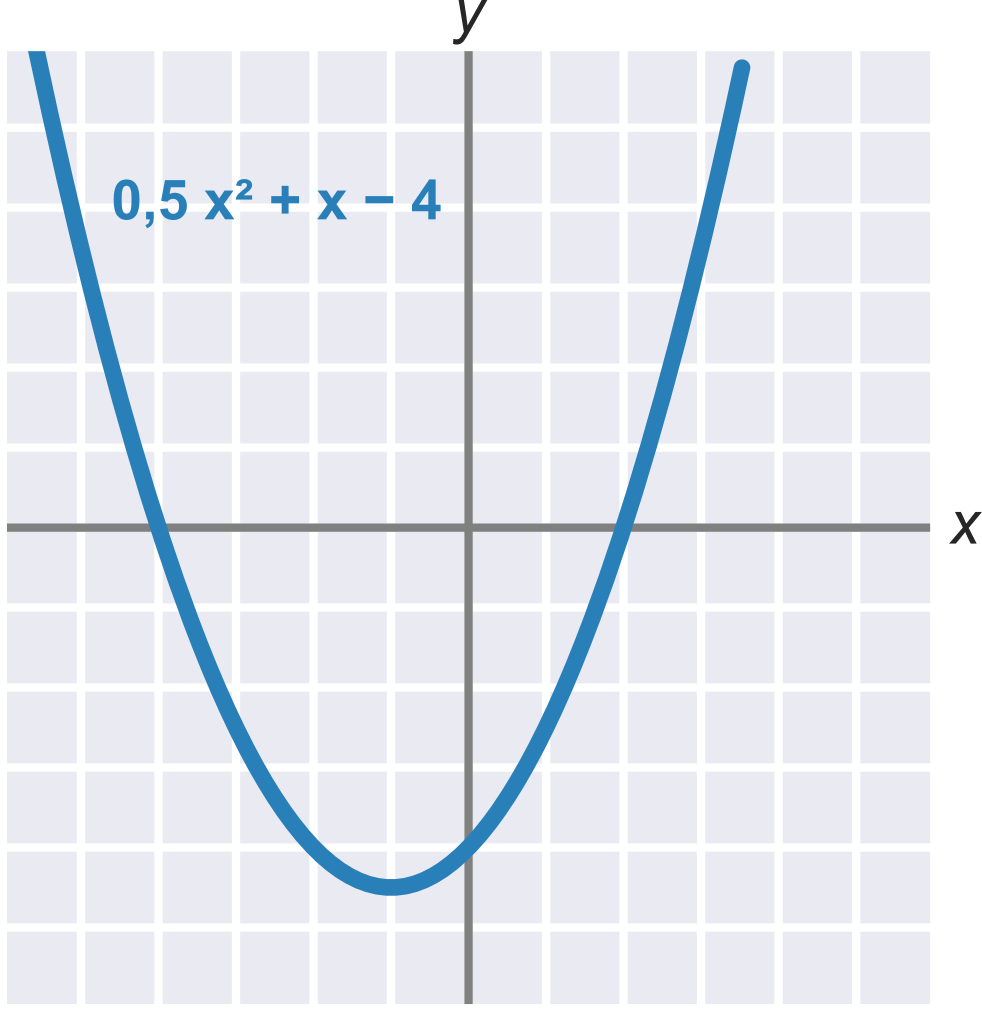
Průsečíky s osou x jsou řešení kvadratické rovnice ax^2 + bx + c = 0. Pro výše uvedený příklad 0{,}5 x^2 + x - 4 jsou těmito řešeními x_1 = -4 a x_2 = 2.
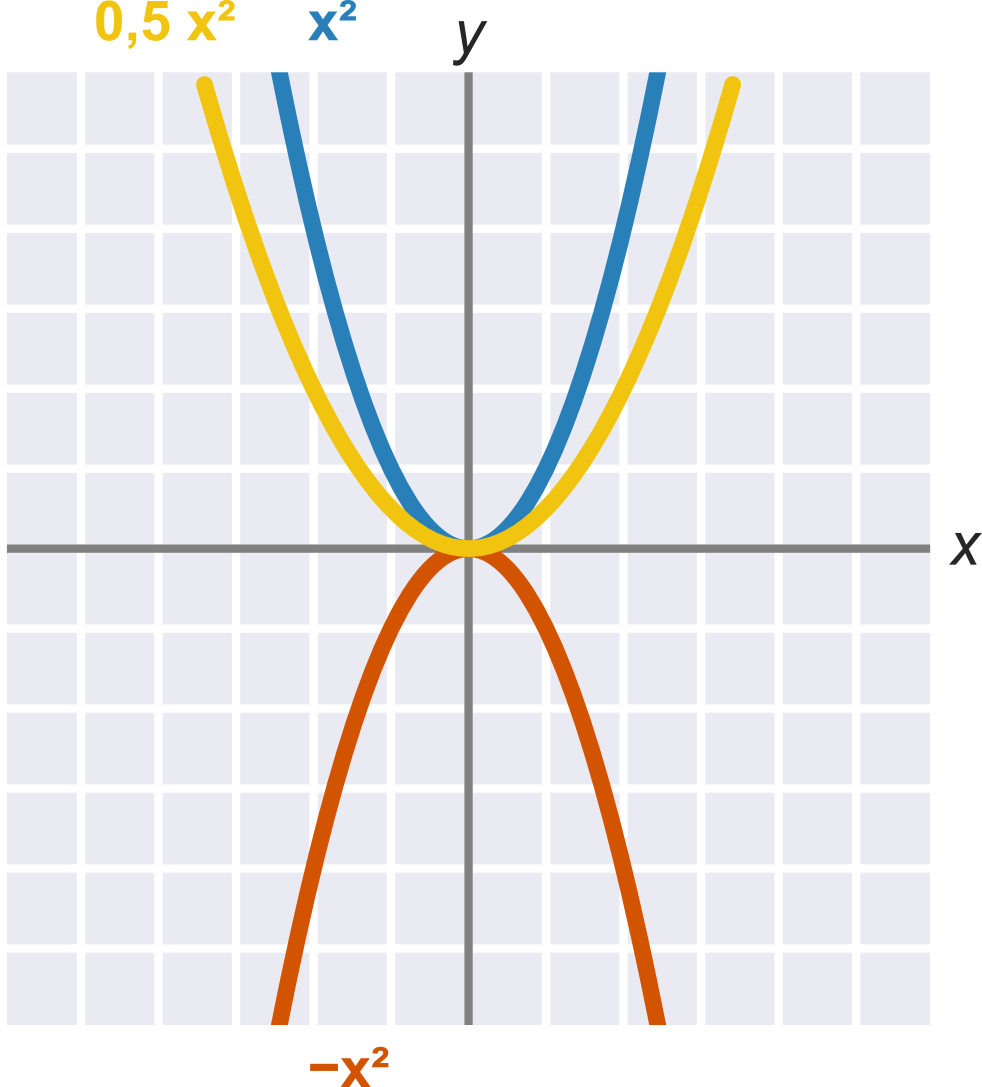
Vliv koeficientů a a c na tvar grafu kvadratické funkce
Kvadratický koeficient a ovlivňuje základní podobu paraboly:
- Pokud je a \gt 0, „směřuje parabola nahoru“ (přesněji: je to zdola omezená, konvexní funkce).
- Pokud je a \lt 0, „směřuje parabola dolů“ (přesněji: je to shora omezená, konkávní funkce).
- Velikost kvadratického koeficientu a ovlivňuje, jak je parabola „široká“.
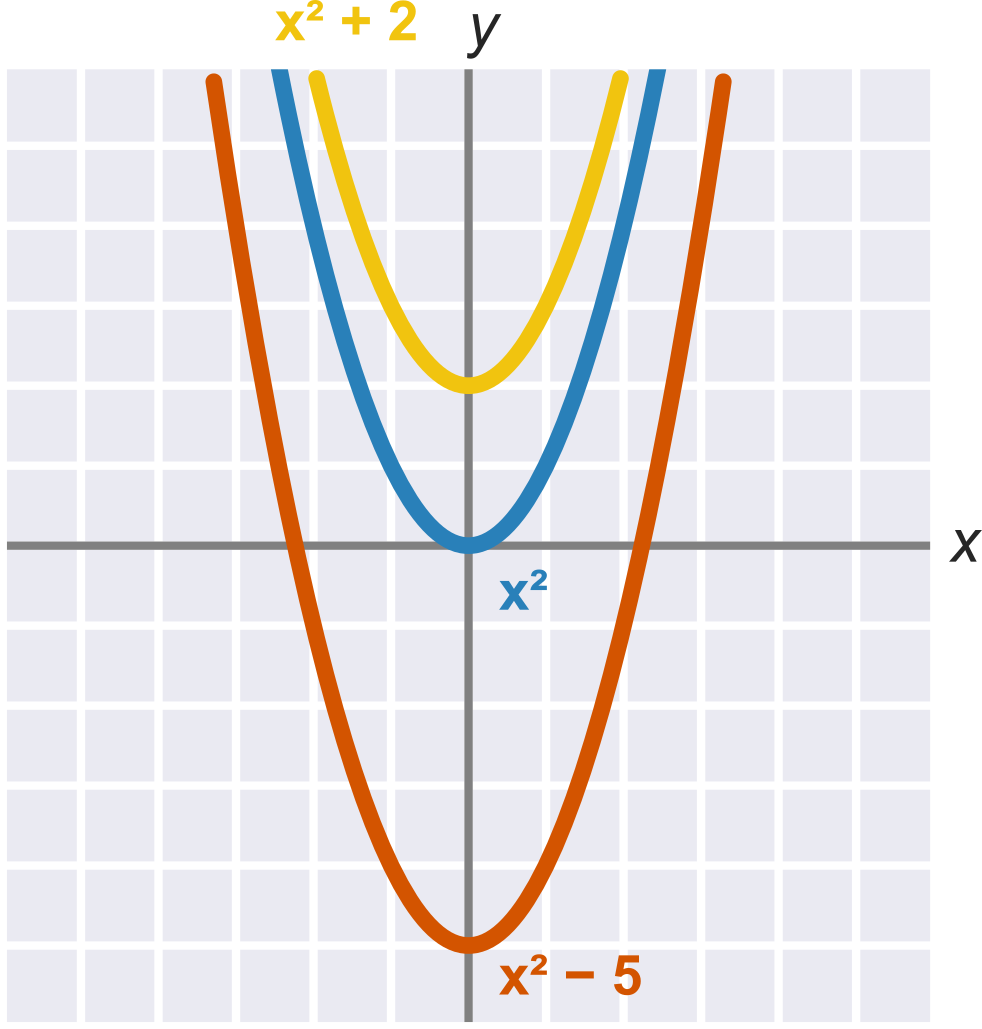
Konstantní člen c ovlivňuje posun paraboly – udává průsečík s osou y.
Určení vrcholu paraboly pomocí úpravy na čtverec
Funkční předpis upravíme tak, aby člen s proměnnou x byl ve tvaru (x-m)^2 (tzv. úprava na čtverec). Souřadnice x vrcholu paraboly je rovna číslu m, souřadnici y získáme jako funkční hodnotu zadané kvadratické funkce v bodě m.
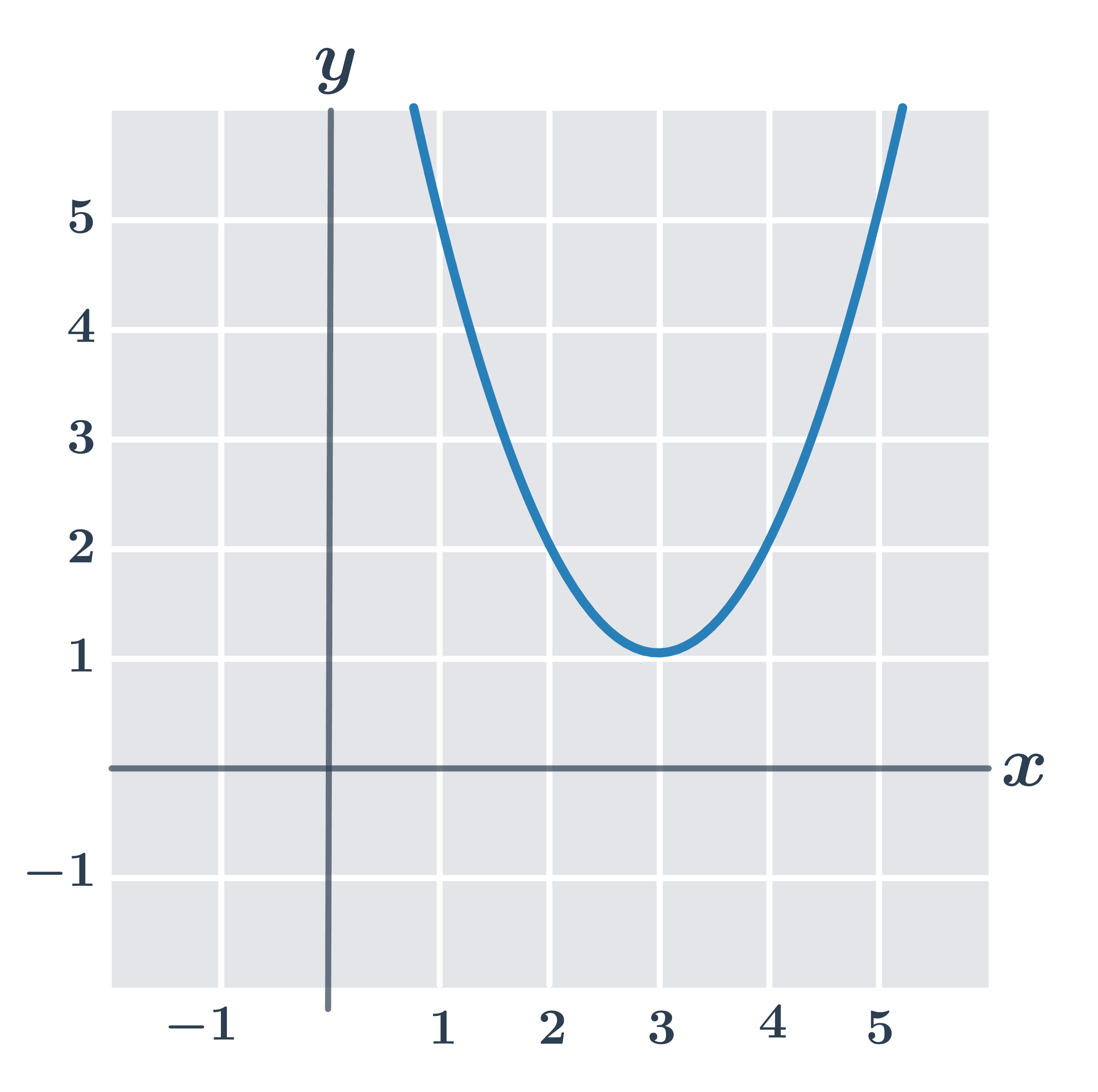
Příklad: určení vrcholu paraboly úpravou na čtverec
Určete vrchol paraboly, která je grafem kvadratické funkce dané předpisem: y=x^2-6x+10
\begin{array}{rrl}y&=&x^2-6x+10\\y&=&x^2-6x+9+1\\y&=&(x-3)^2+1\end{array}
Máme tedy souřadnice vrcholu paraboly x=3 a y=(3-3)^2+1=1.
Zajímavost z analytické geometrie: Převedením konstanty na levou stranu rovnice y=(x-3)^2+1 dostaneme vrcholovou rovnici paraboly y-1=(x-3)^2.
Parabola, která je grafem funkce, má vrchol v bodě [3,1].
Komiks pro zpestření
Grafy funkcí s absolutní hodnotou
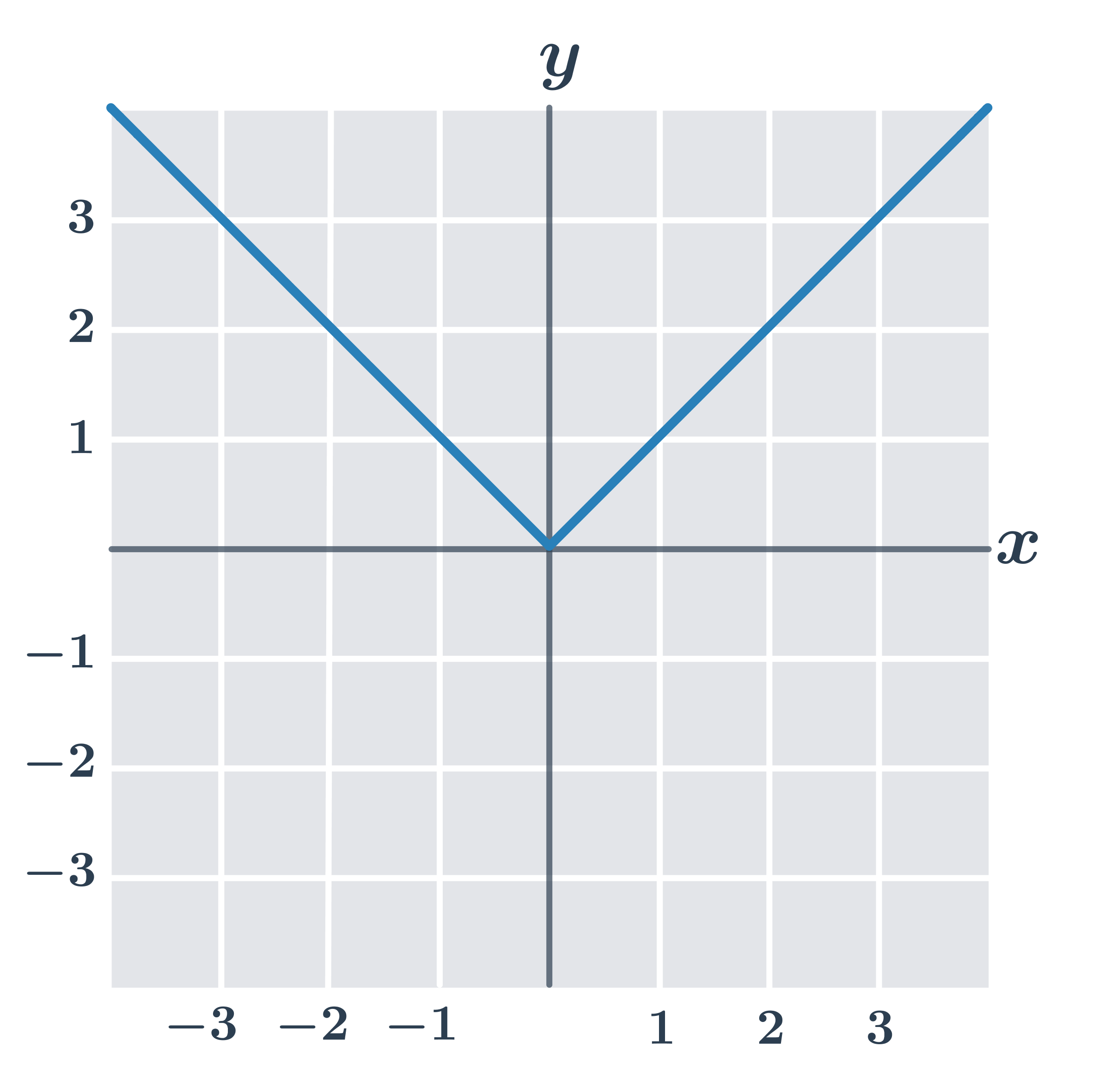
Na obrázku je graf funkce y=|x|. Tento graf tvoří dvě polopřímky s počátkem v bodě [0;0], protože pro absolutní hodnotu platí:
- absolutní hodnota kladného čísla je rovna tomuto číslu: |x|=x
- absolutní hodnota záporného čísla je rovna opačnému číslu: |x|=-x
- absolutní hodnota čísla nula je rovna nule: |0|=0
| x \gt 0 | Grafem funkce y=|x| je polopřímka s počátkem v bodě [0;0] daná rovnicí y=x. |
| x \lt 0 | Grafem funkce y=|x| je polopřímka s počátkem v bodě [0;0] s rovnicí y=-x. |
| x = 0 | Bod [0;0] je počátek polopřímek, které vytvoří graf funkce y=|x|. |
Pokud chceme nakreslit graf funkce y=|f(x)| postupujeme tak, že nakreslíme graf y=f(x) a potom záporné funkční hodnoty nahradíme opačnými. V oblasti, kde jsou funkční hodnoty záporné, se tedy graf překlopí kolem osy x.
Příklad 1: graf funkce y=|x-1|
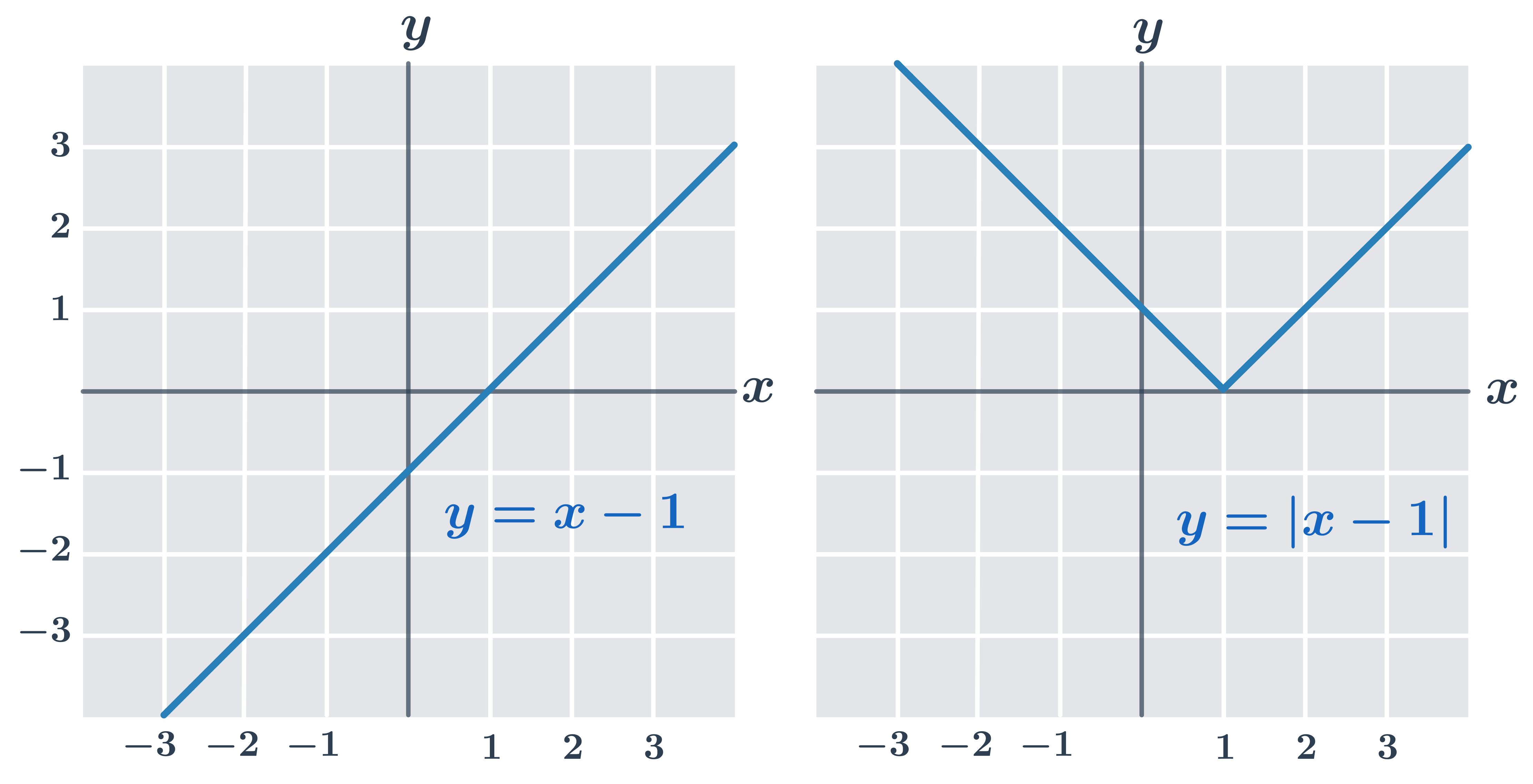
| Pro čísla x \lt 1 má funkce y=x-1 záporné funkční hodnoty. |
| Funkce y=|x-1| má v intervalu (-\infty;1) opačné hodnoty než funkce y=x-1 (graf y=|x-1| je vůči grafu y=x-1 v tomto intervalu překlopený podle osy x). |
| V intervalu (1;\infty) jsou grafy funkcí y=x-1 a y=|x-1| stejné. |
Příklad 2: graf funkce y=|x^2-4|
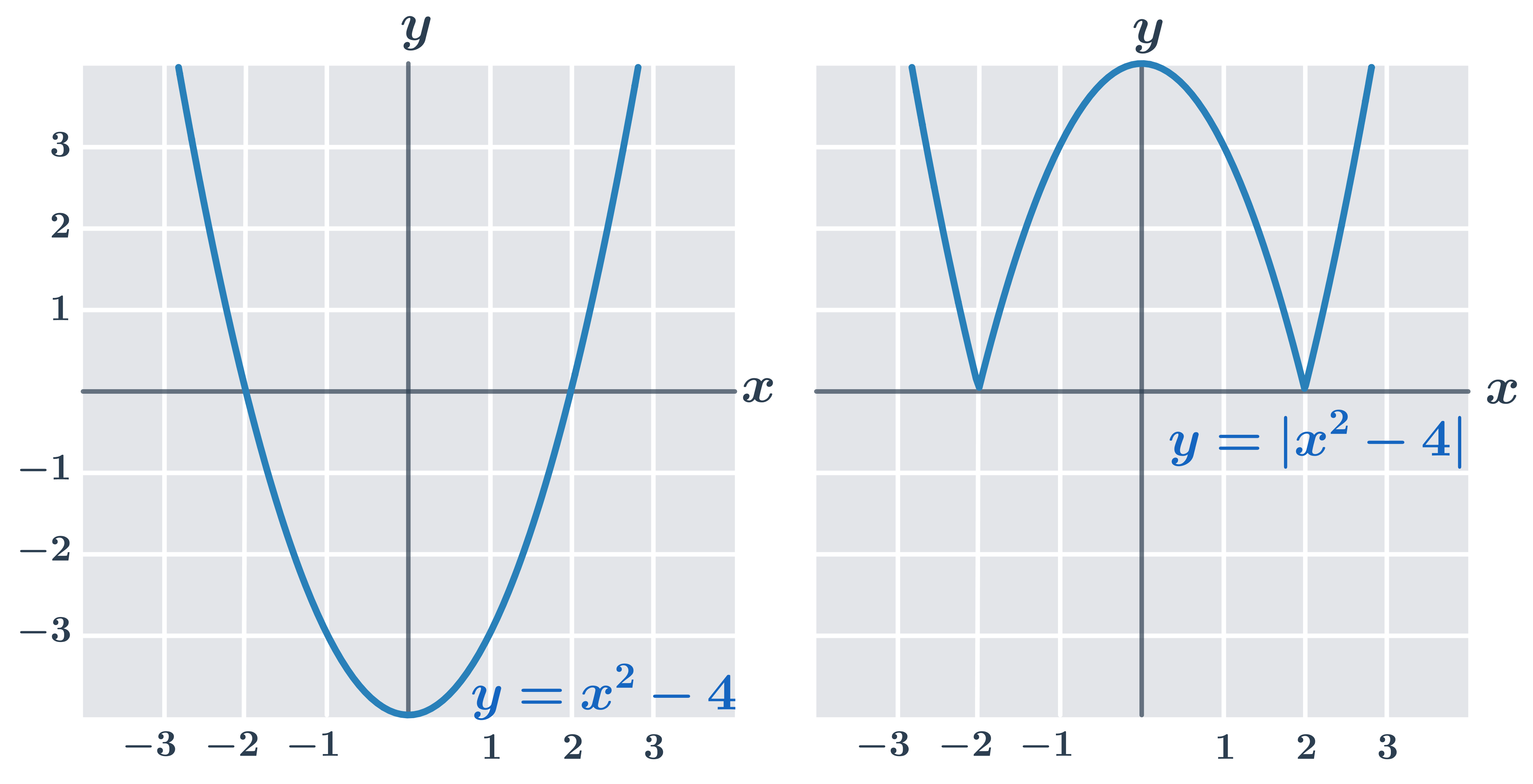
| V intervalu (-2;2) má funkce y=x^2-4 záporné funkční hodnoty. |
| Funkce y=|x^2-4| má v intervalu (-2;2) opačné hodnoty než funkce y=x^2-4 (graf je překlopený podle osy x). |
| V intervalech (-\infty;-2) a (2;\infty) jsou grafy funkcí y=x^2-4 a y=|x^2-4| stejné. |
Grafy lineárních lomených funkcí
Grafem lineární lomené funkce je hyperbola, která má asymptoty rovnoběžné se souřadnými osami x a y.
Asymptota rovnoběžná s osou y prochází bodem, který nepatří do definičního oboru a má tedy rovnici: x =-\frac{d}{c}.
Pro nalezení rovnice asymptoty rovnoběžné s osou x vydělíme čitatele a jmenovatele a funkční předpis y =\frac{ax+b}{cx+d} upravíme na tvar y =\frac{a}{c}+\frac{n}{ax+b}. Asymptota rovnoběžná s osou x má rovnici: y =\frac{a}{c}.
Průsečík grafu s osou x je bod, pro který ax+b=0. V tomto bodě je hodnota funkce nulová, tedy čitatel zlomku \frac{ax+b}{cx+d} je nulový.
Průsečík grafu s osou y je bod, který dostaneme dosazením hodnoty x=0 do funkčního předpisu.
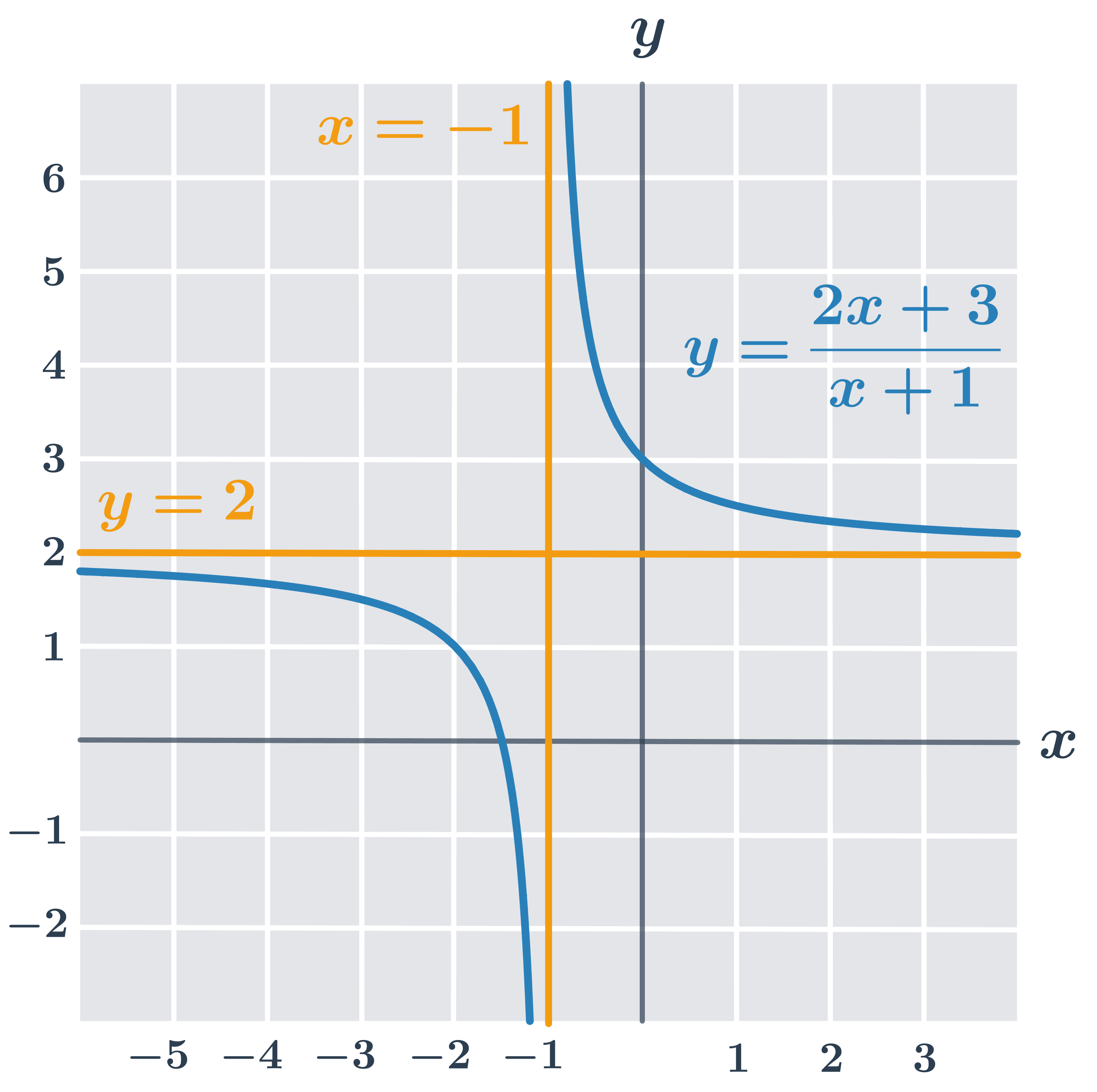
Příklad – funkce y =\frac{2x+3}{x+1}
Rozeberme si graf funkce z obrázku výše:
- definiční obor D(f)=\R - \{-1\}, protože x+1\neq0
- asymptota rovnoběžná s osou y má rovnici x =-1 (pro x=-1 není funkce definovaná, toto číslo neleží v jejím definičním oboru)
- asymptota rovnoběžná s osou x má rovnici y =2, což zjistíme úpravou funkčního předpisu: y =\frac{2x+3}{x+1}=2+\frac{1}{x+1}
- průsečík grafu s osou x je bod [0;-\frac{3}{2}] (řešení rovnice: 2x+3=0)
- průsečík grafu s osou y je bod [3;0], dosazením hodnoty x=0 do y =\frac{2x+3}{x+1}
Grafy mocninných funkcí
Grafy základních mocninných funkcí y= x^n
pro n sudé – graf je souměrný podle osy y, D(f)=\R, H(f)=\langle0, \infty)
pro n liché – graf je souměrný podle počátku, D(f)=\R, H(f)=\R
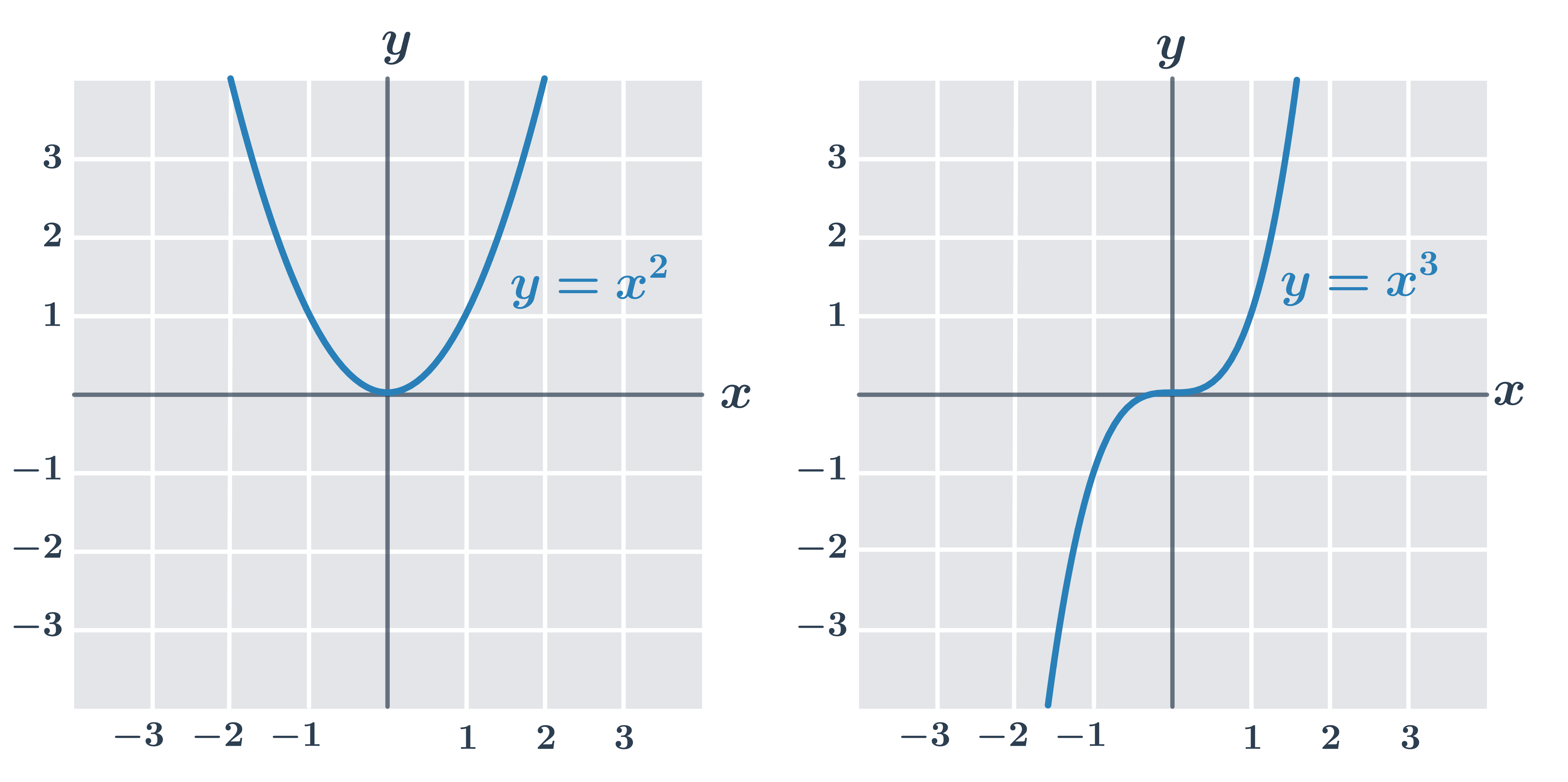
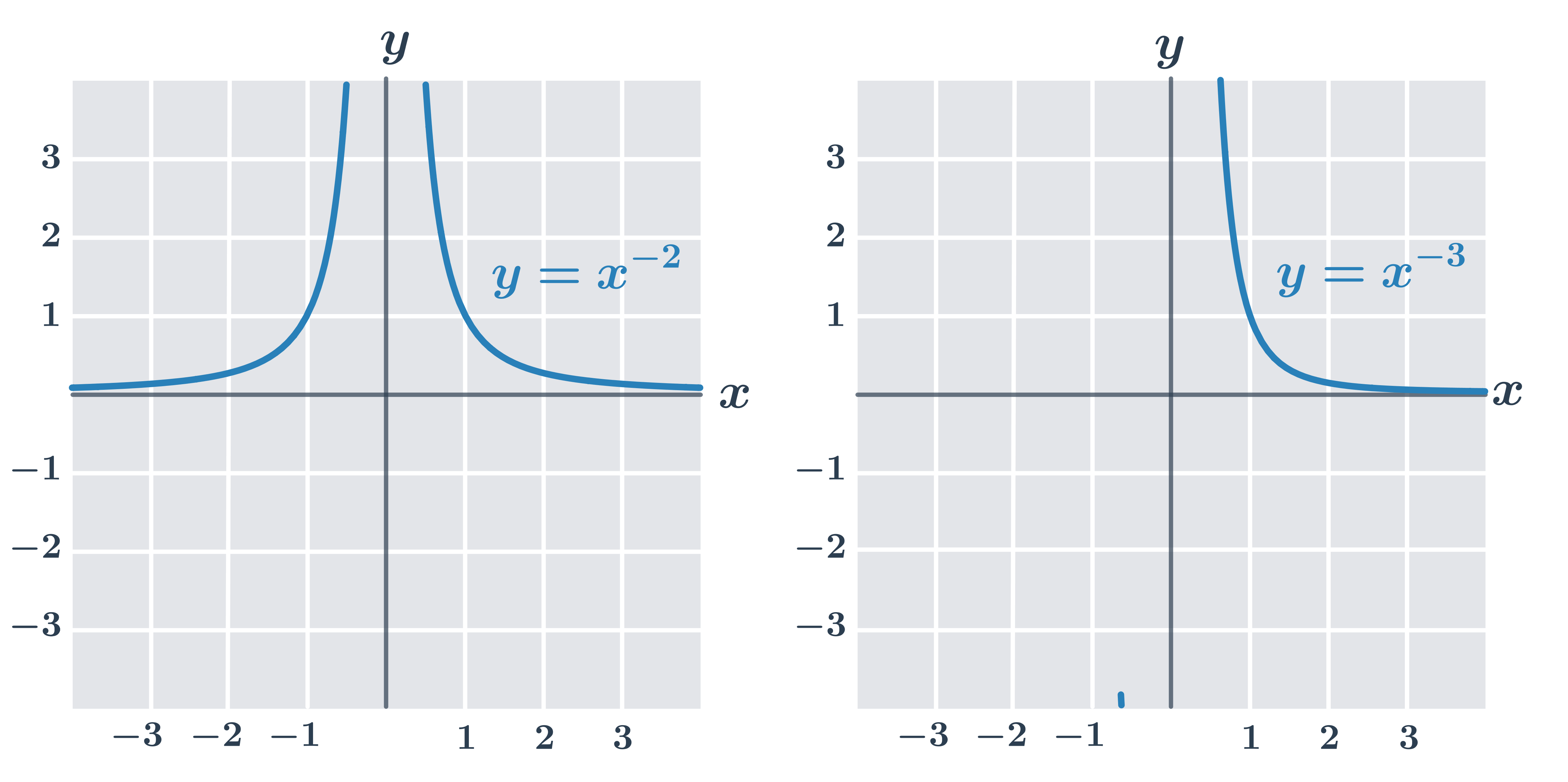
Grafy mocninných funkcí se záporným exponentem y= x^{-n}
pro n sudé – graf souměrný podle osy y, D(f)=\R- \{0\}, H(f)=\langle0, \infty)
pro n liché – graf souměrný podle počátku, D(f)=\R - \{0\}, H(f)=\R - \{0\}
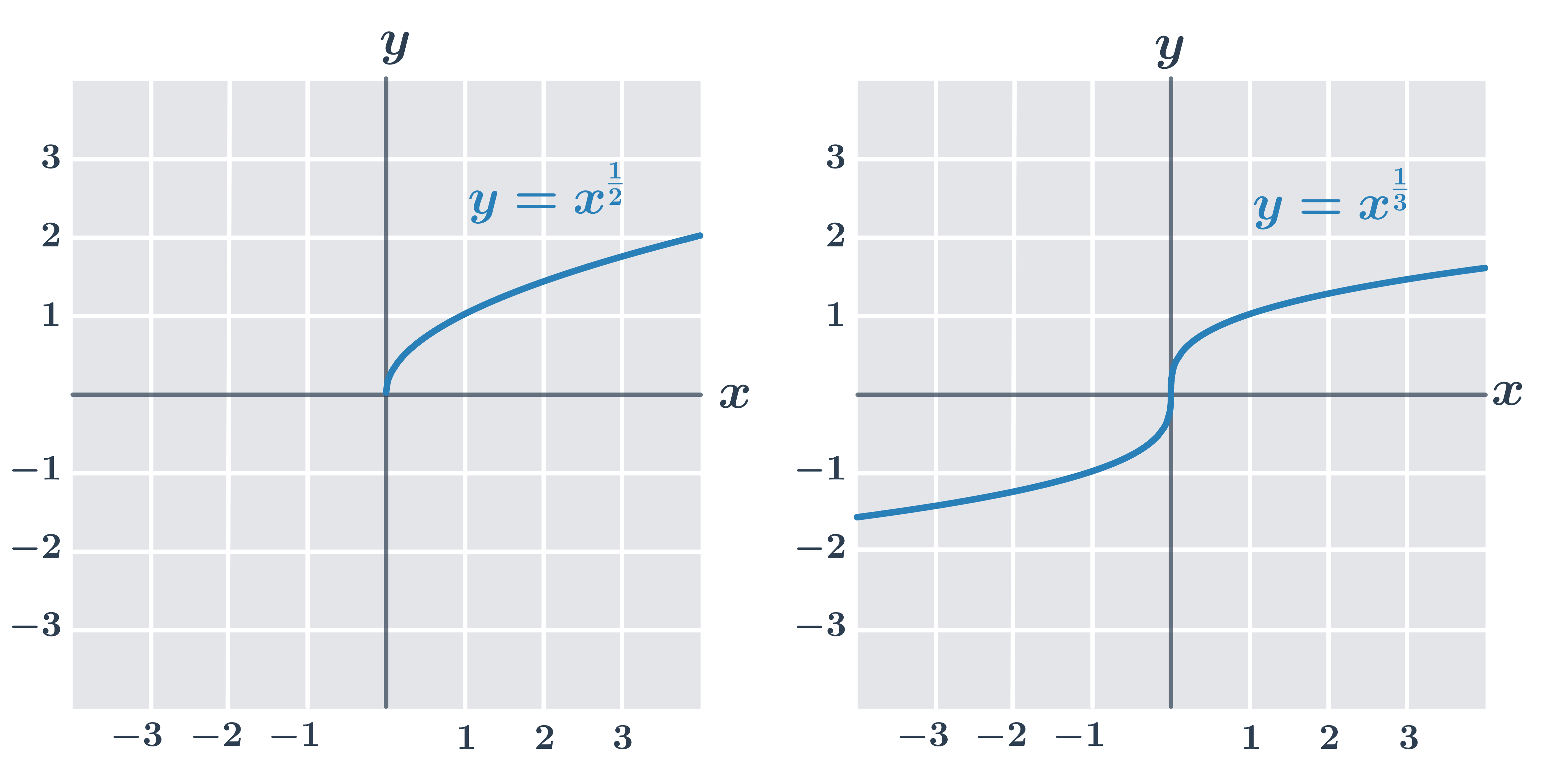
Grafy funkcí y= x^{\frac{1}{n}}:
pro sudé n – funkce y= x^{\frac{1}{n}} definována na kladných číslech, D(f)=\langle0, \infty), H(f)=\langle0, \infty)
pro liché n – funkce y=x^n je prostá, proto bychom mohli definovat n-tou odmocninu i pro záporná čísla, ale často se (např. jako příprava pro práci s mocninnými funkcemi s obecnějšími racionálními exponenty) všechny n-té odmocniny pro sudá i lichá n definují pro jednoduchost jen na intervalu [0,\infty).
Poznámka: výpočty s mocninami a odmocninami
Při výpočtech s mocninami a odmocninami musíme být obezřetní, hodně pravidel platí pro nezáporný základ (pokud počítáme s odmocninami), případně kladný základ (nulu můžeme odmocňovat, ale nesmíme dělit nulou). Příklady:
součin odmocnin je odmocnina součinu: pro nezáporná čísla jako základy odmocnin pravidlo platí, pokud bychom chtěli použít pro záporný základ, nemusí nám v oboru reálných čísel vycházet smysluplné věci: \sqrt{-2} není definovaná, ale \sqrt{(-2)\cdot(-2)} je \sqrt{4} = 2
racionální exponenty: mělo by x^{\frac{2}{6}} být totéž jako x^{\frac{1}{3}}? Exponent je „stejné racionální číslo“, ale pro záporná x by vycházely u těchto dvou předpisů jiné funkční hodnoty (6. odmocnina ze záporného x není definovaná, 6. odmocnina z druhé mocniny záporného čísla je kladná, a 3. odmocnina z x by pro záporná x byla záporná).
racionální exponenty konkrétněji: čemu by se mělo rovnat (-8)^{\frac{2}{6}}? Máme (-8)^{\frac{1}{3}}=-2, ale zároveň \sqrt[6]{(-8)^2} = \sqrt[6]{64} = 2. Můžeme se dostat do potíží, když budeme pravidla, která platí pro mocniny a odmocniny kladných a nezáporných čísel, zkoušet používat i pro záporné základy.
Vliv úprav funkčního předpisu na graf mocninné funkce
Obrázek ukazuje několik úprav funkce y= x^3:
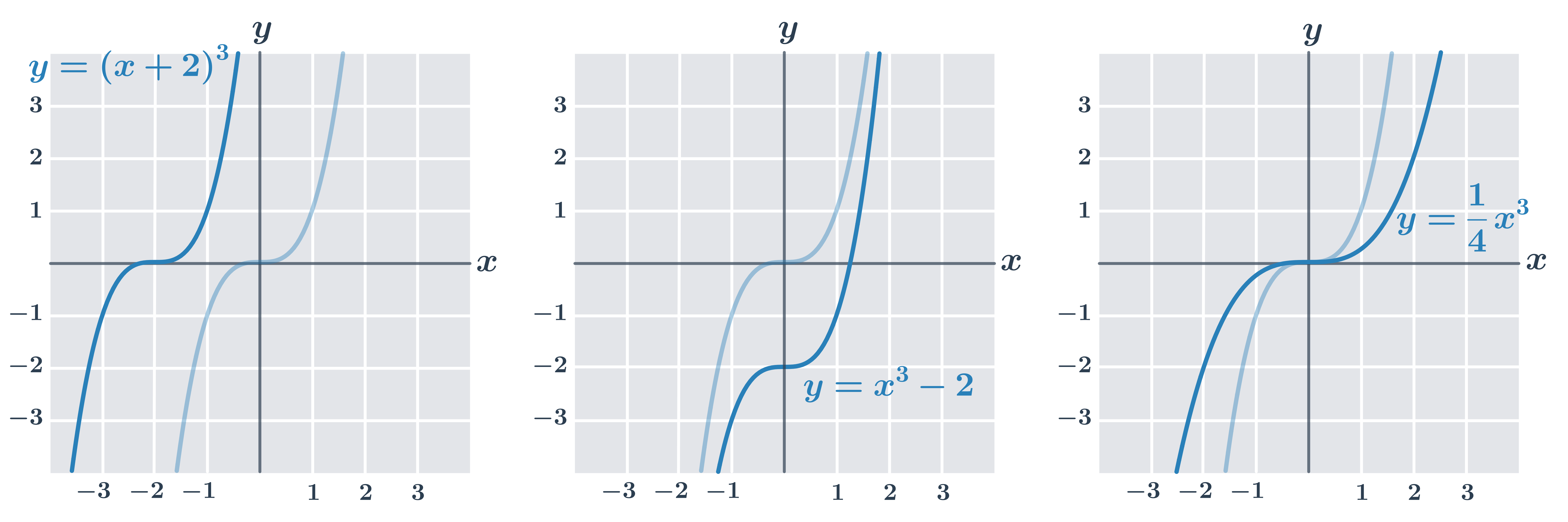
| y= (x+2)^3 | graf je posunutý ve směru osy x |
| y=x^3-2 | graf je posunutý ve směru osy y |
| y=\frac{1}{4} x^3 | graf bude natažený nebo smrštěný ve směru osy y (v uvedeném grafu se funkční hodnoty zmenší na čtvrtinu, například pro x=2 je hodnota funkce y=\frac{1}{4} \cdot 2^3=2) |
Grafy goniometrických funkcí
Grafy základních goniometrických funkcí intuitivně

Všimněte si
- graf které funkce protíná osu y v bodě x=0, y=0? (\sin, \tan)
- graf které funkce protíná osu y v bodě x=0, y=1? (\cos)
- která funkce je definovaná pro všechna x \in \mathbb{R}? (\sin, \cos)
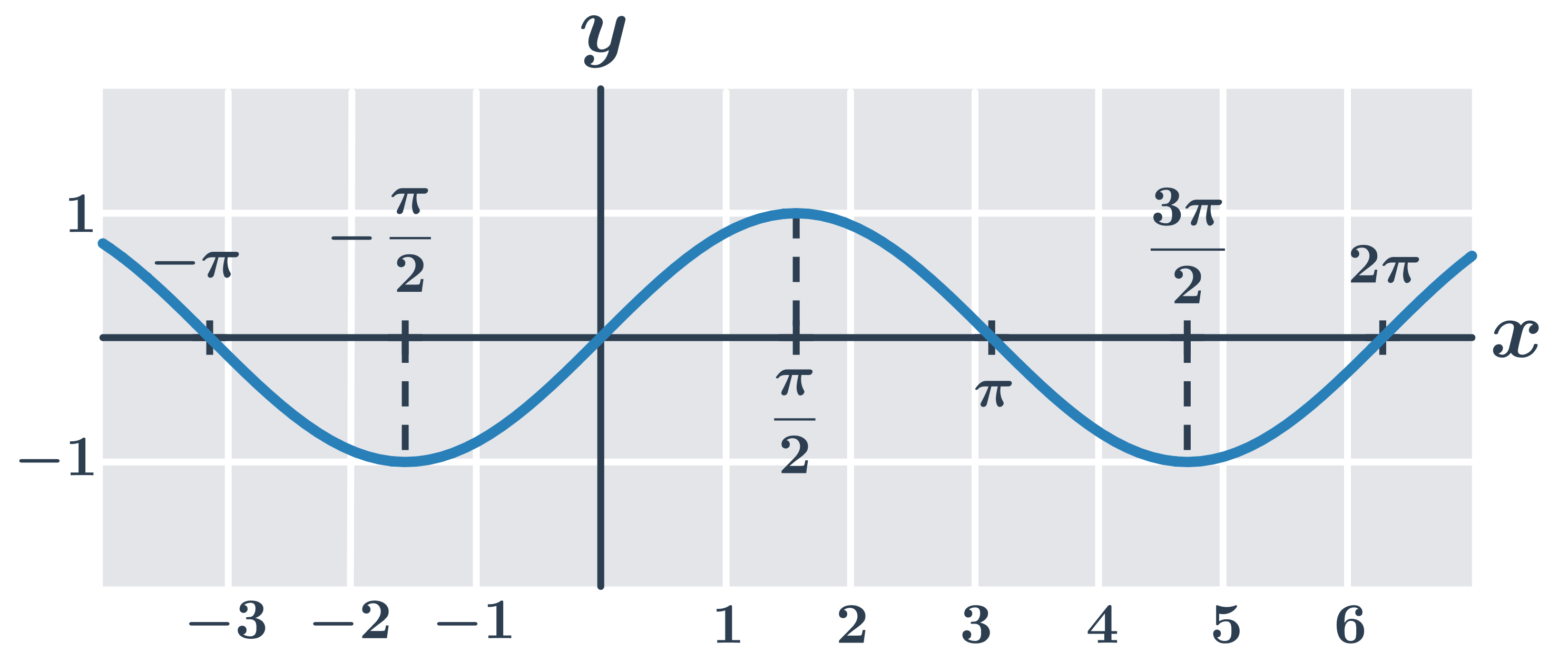
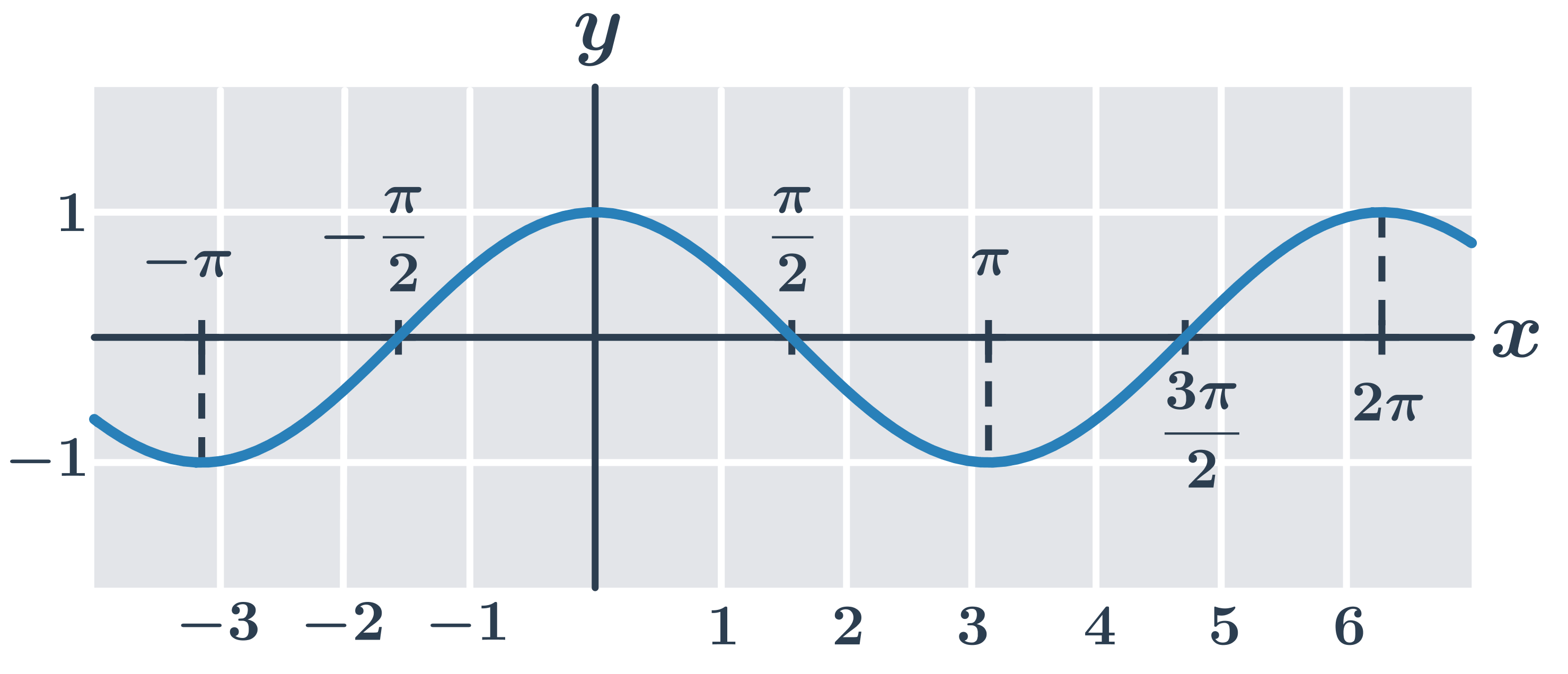
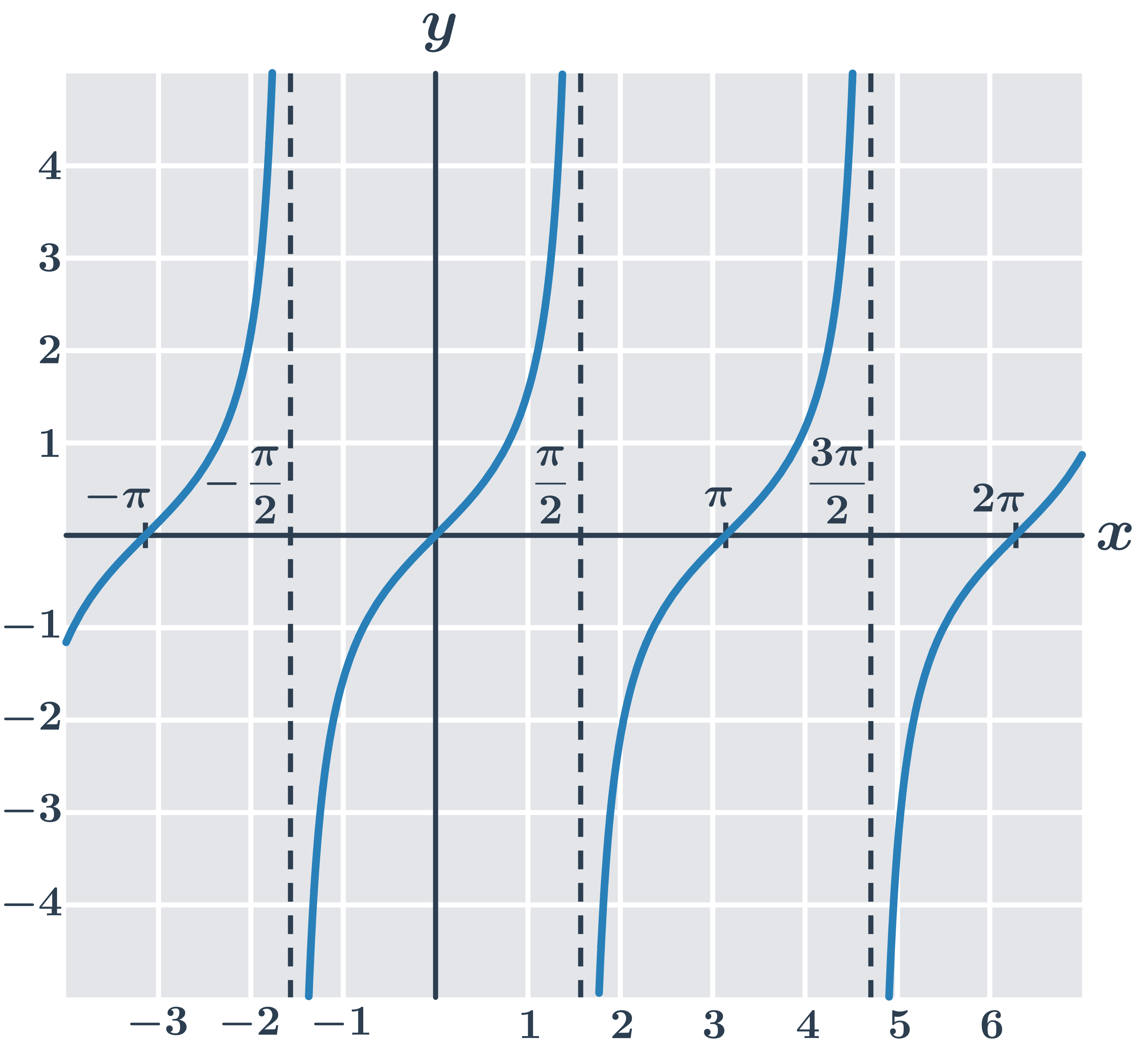
Grafy goniometrických funkcí s popsanými osami
Funkce sinus y=\sin x:
Funkce cosinus y=\cos x:
Funkce tangens y=\tan x:
Funkce kotangens y=\cot x:
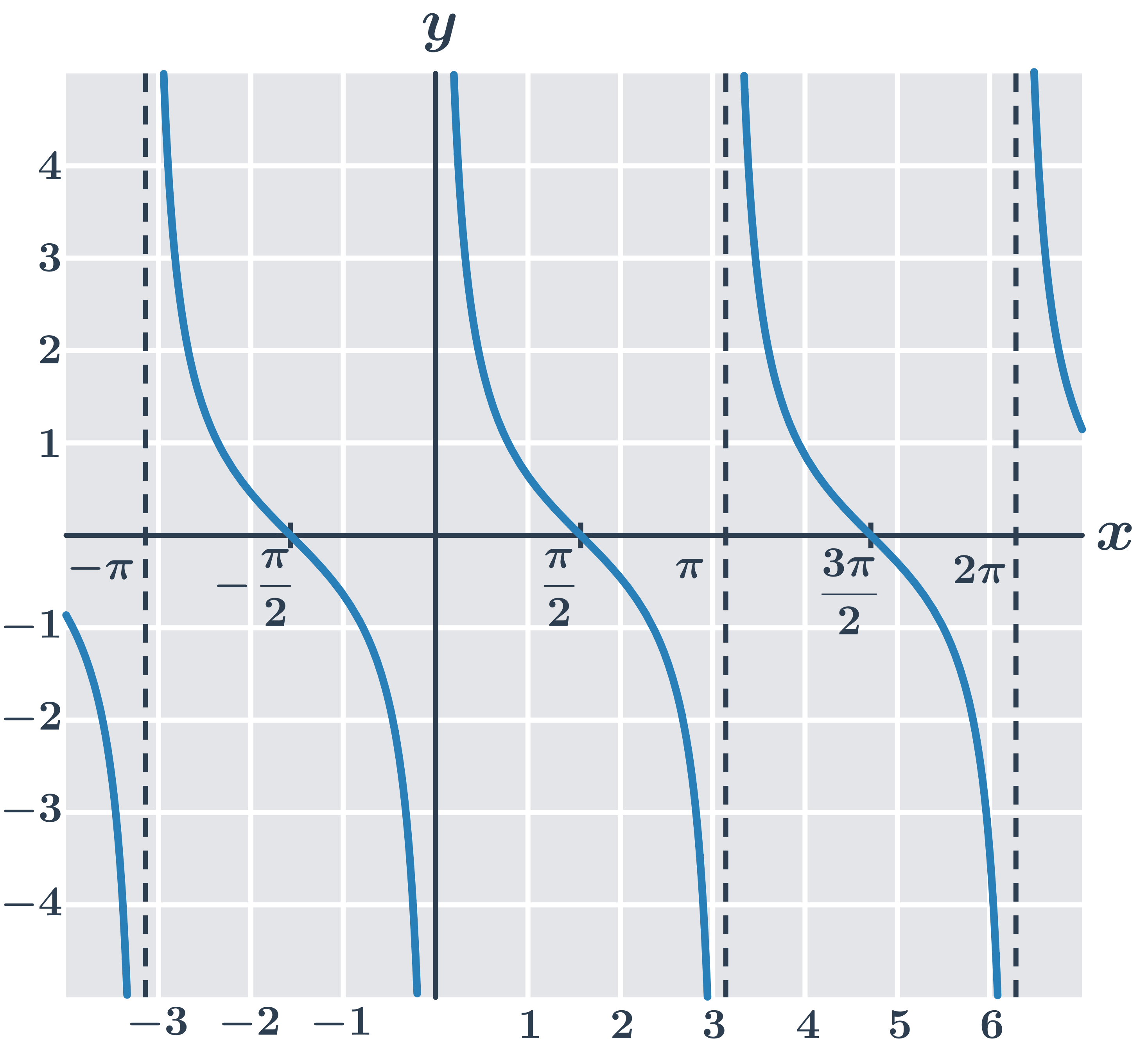
Dopad úprav funkce na graf

Obrázek ukazuje grafy několika úprav funkce \sin x.
| \sin(x+1) | posun grafu ve směru osy x |
| \sin(x)+1 | graf je posunutý ve směru osy y |
| \sin 2x | funkce má změněnou délku periody (v uvedeném příkladu je graf „zmáčknutý“ ve směru osy x, funkce má poloviční délku periody oproti \sin x) |
| 2\sin x | změní se maximální a minimální funkční hodnota (v uvedeném příkladu je graf „roztažený“ ve směru osy y na dvojnásobnou výšku) |
Zajímavost: fyzikální popis některých úprav
| \sin(x+1) | graf má posunutou fázi |
| 2\sin x | změnila se velikost amplitudy |
Grafy exponenciálních funkcí
Grafem exponenciální funkce je křivka jménem exponenciála. Na obrázku jsou grafy exponenciálních funkcí se základy 2 a e = 2{,}7 182 818 284\ldots. Vidíme také, že grafy funkcí e^x a e^{-x} jsou spolu souměrné podle osy y.
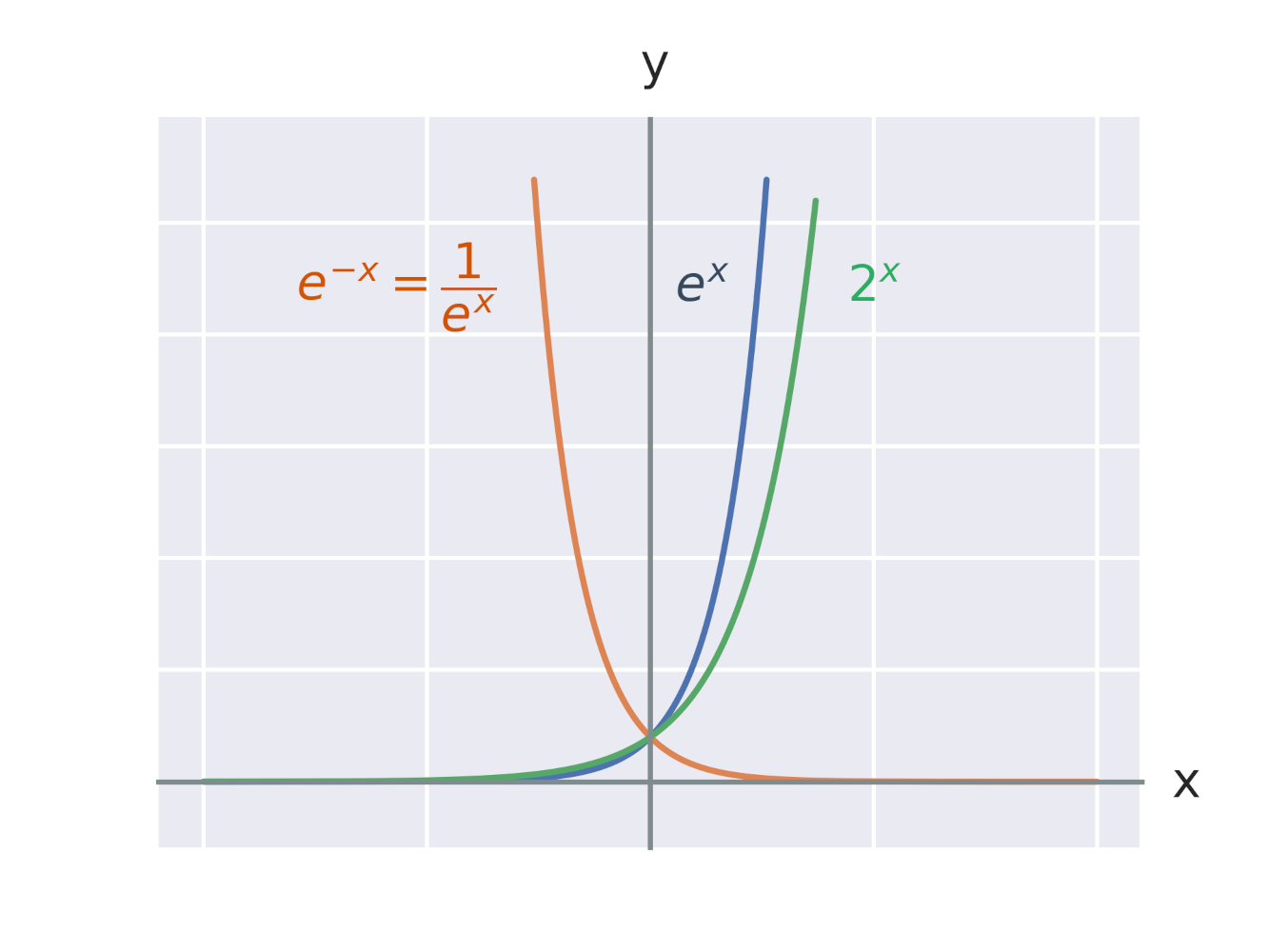
Graf každé exponenciální funkce tvaru f:y =a^x prochází bodem [0,1], protože pro libovolnou konstantu a platí: a^0=1.
Efekt přičtení konstanty k exponenciální funkci
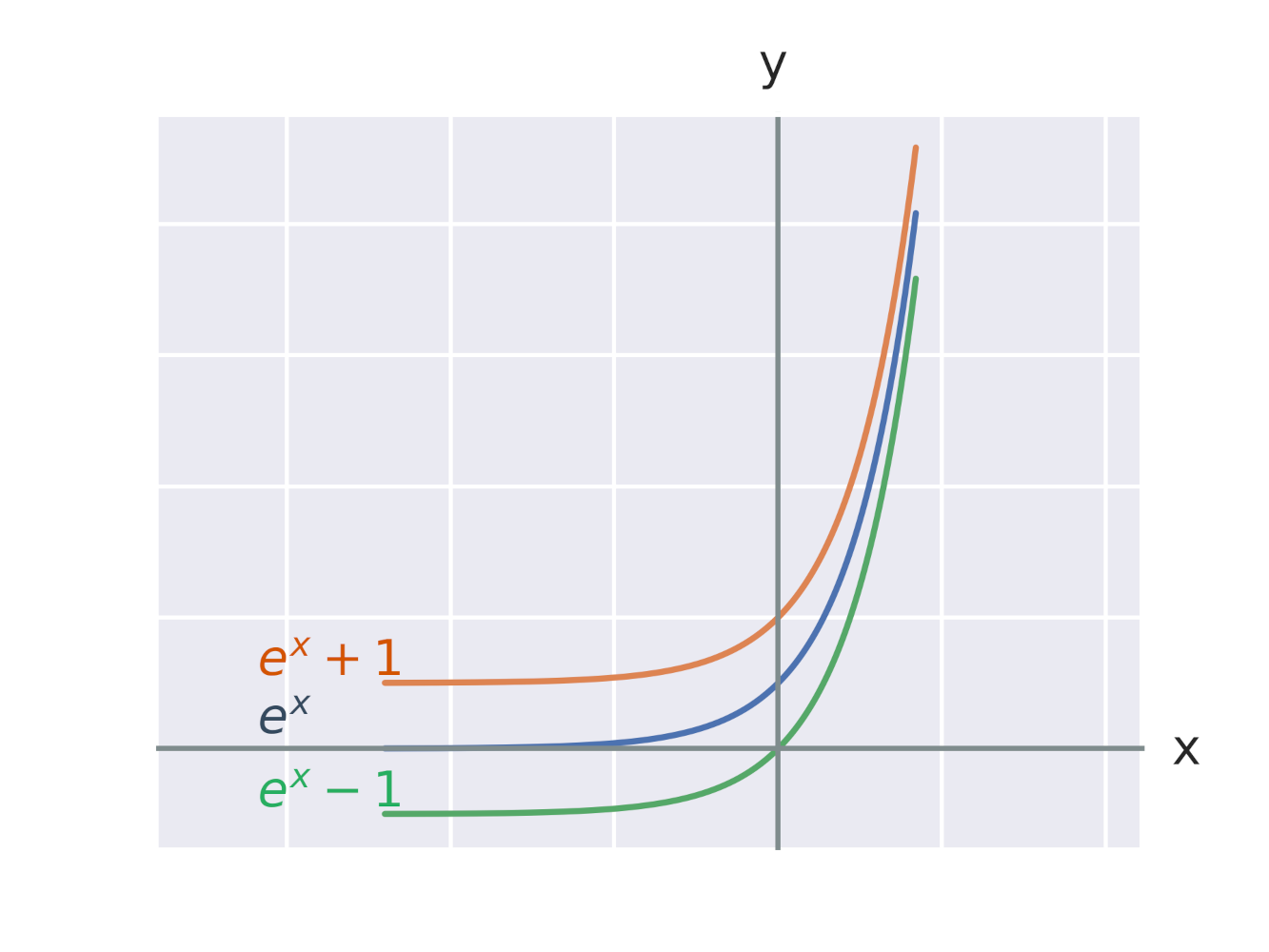
Efekt přičtení konstanty k exponentu
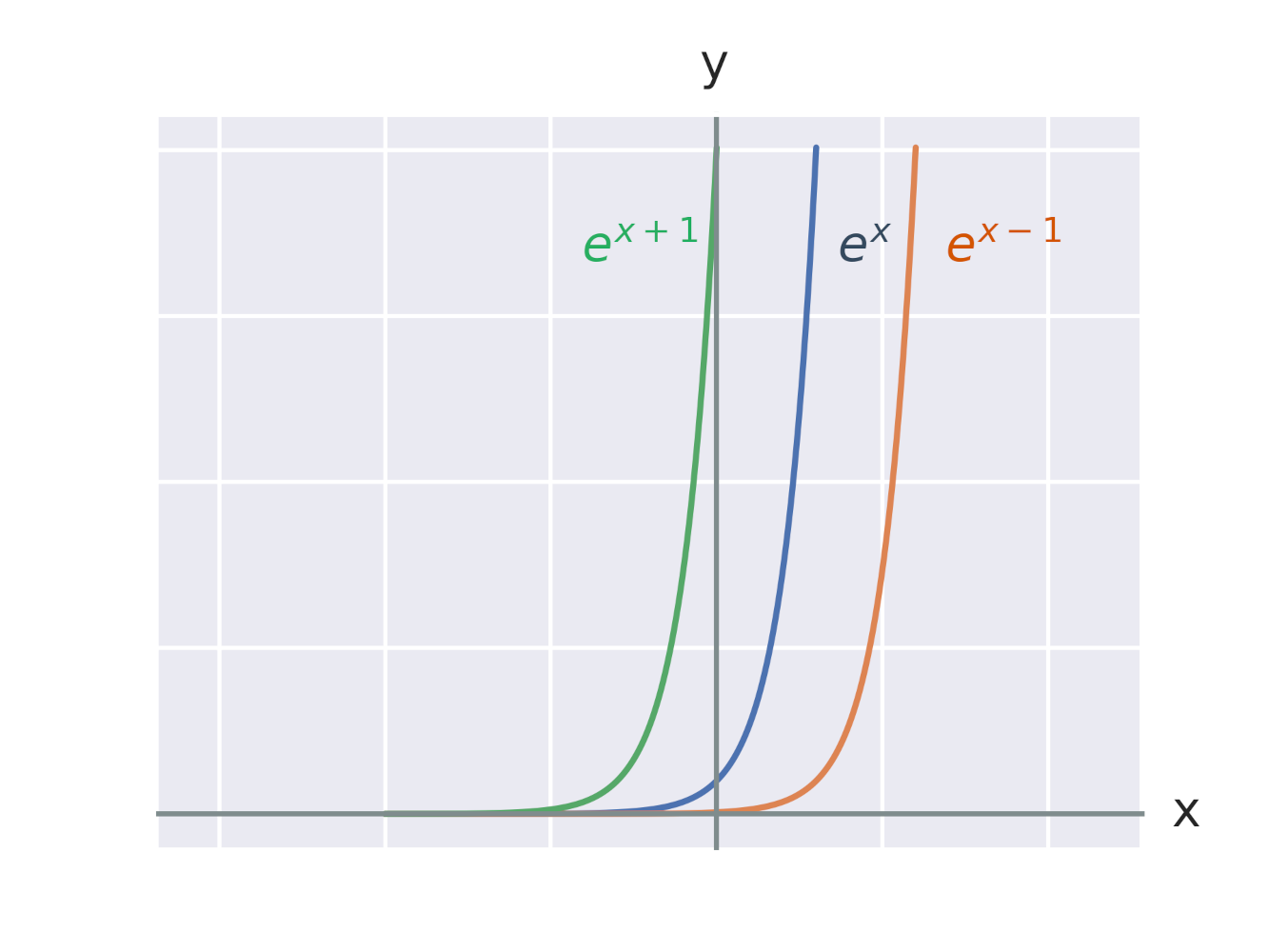
Efekt vynásobení exponenciální funkce konstantou
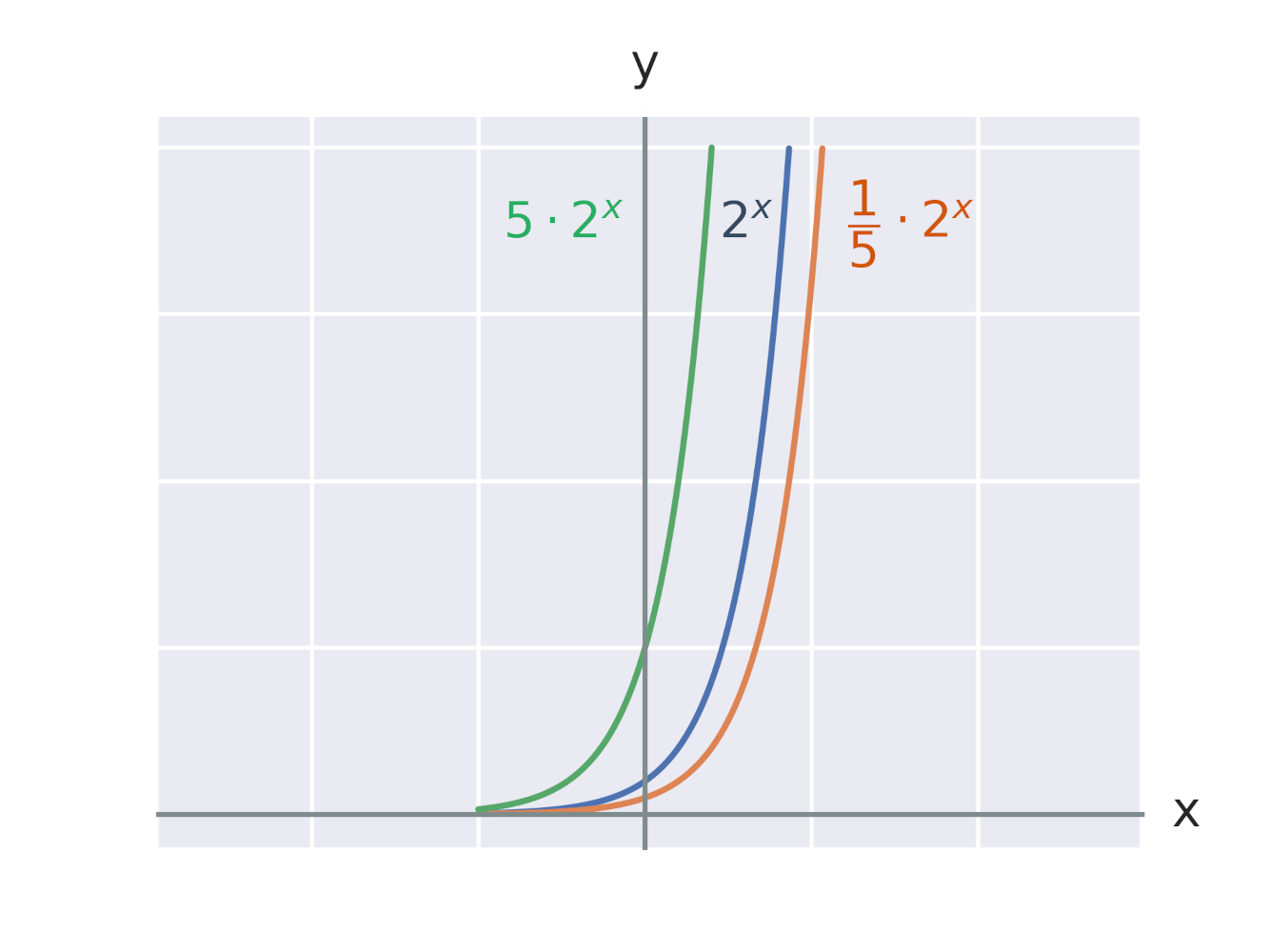
Efekt vynásobení exponentu konstantou
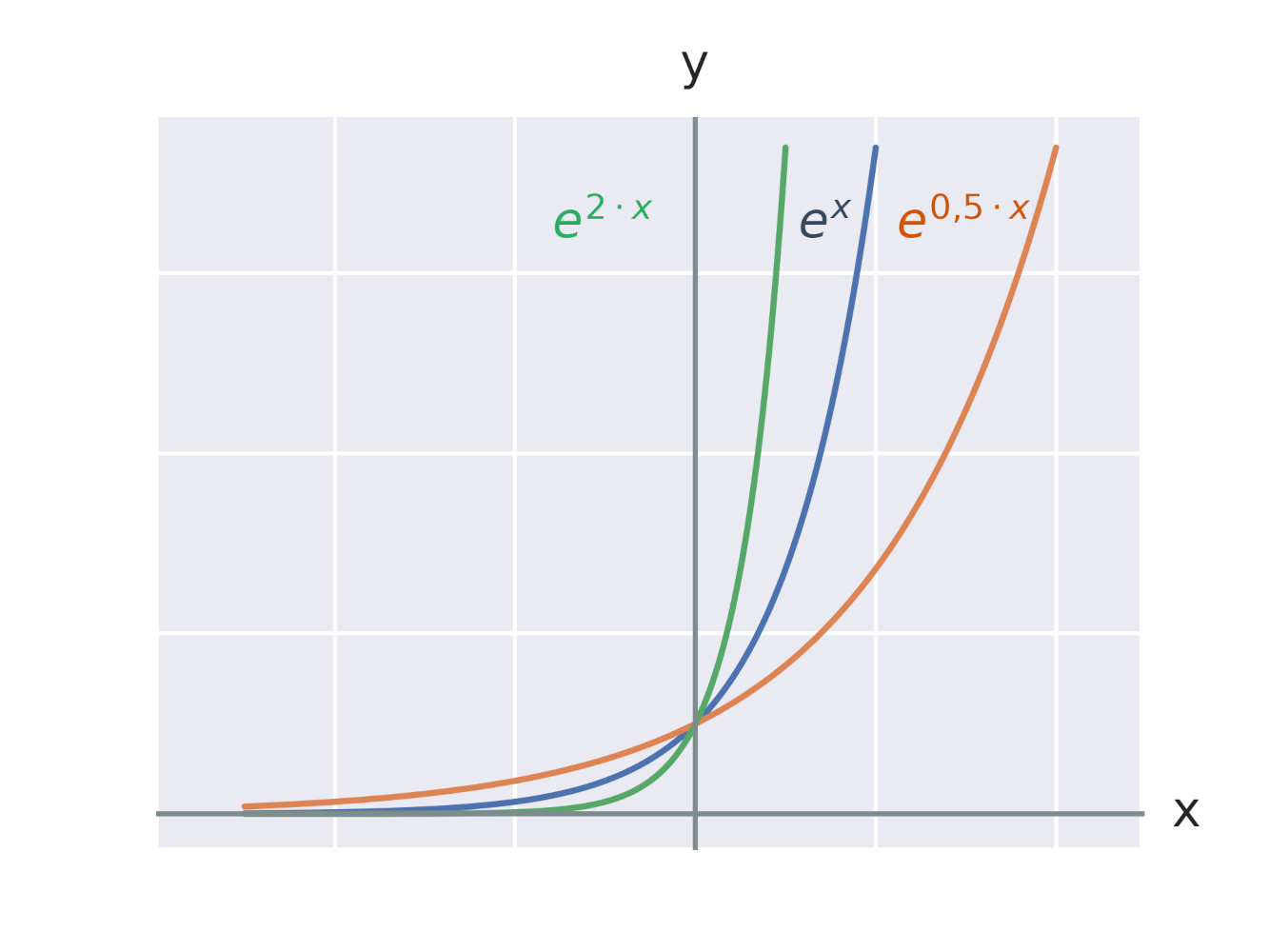
Grafy logaritmických funkcí
Logaritmická funkce je inverzní k exponenciální funkci o stejném základu. Grafy dvou navzájem inverzních funkcí jsou osově souměrné podle osy prvního kvadrantu (tj. přímky splňující x=y).
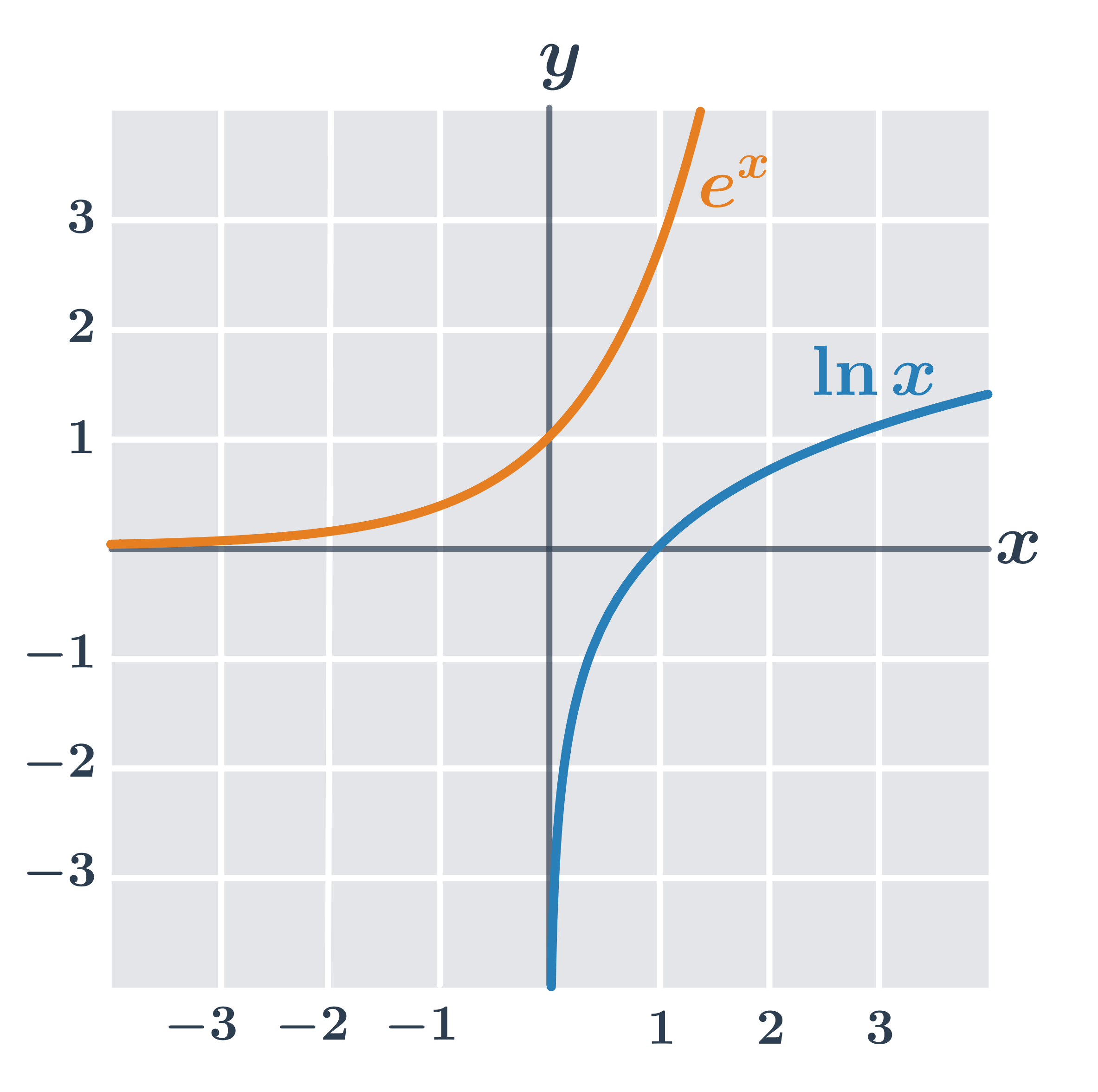
Graf každé logaritmické funkce tvaru y=\log_a x prochází bodem [1,0], protože pro libovolnou konstantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcí s různými základy 2, e, 10.
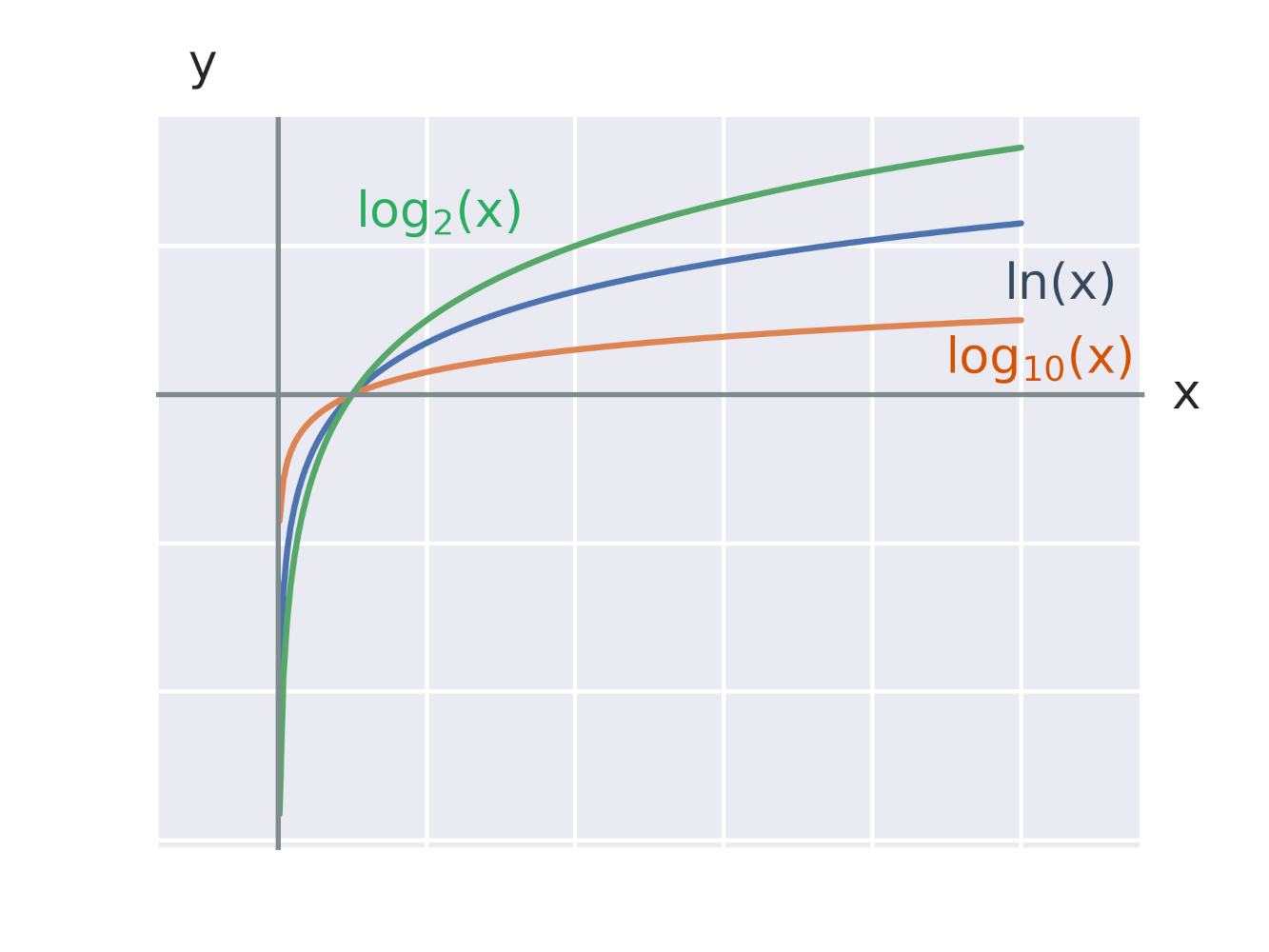
Značení některých význačných logaritmických funkcí:
| funkce | popis | další možná značení |
|---|---|---|
| \log_a x | obecně logaritmus x o základu a pro nějaké a >0, a\neq 1 | |
| \ln x | přirozený logaritmus x, tj. logaritmus x o základu e | v angl. textech někdy \log x |
| \log x | dekadický logaritmus x, tj. logaritmus x o základu 10 | \log_{10}x |
| \log_2 x | binární logaritmus x, tj. logaritmus x o základu 2 | někdy se objevuje \mathrm{lb}\;x |
Efekt přičtení konstanty k logaritmické funkci
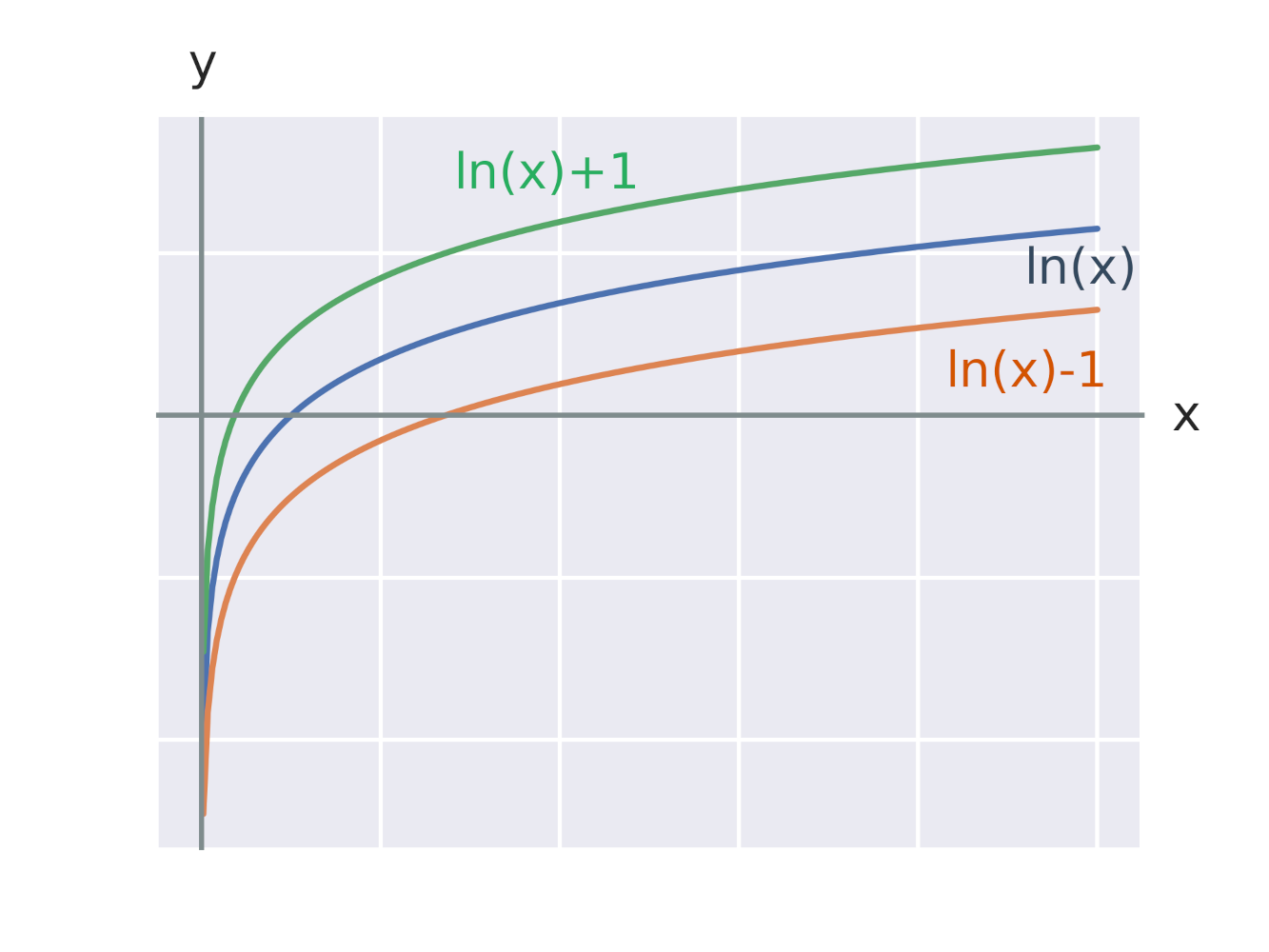
Efekt přičtení konstanty k argumentu logaritmické funkce
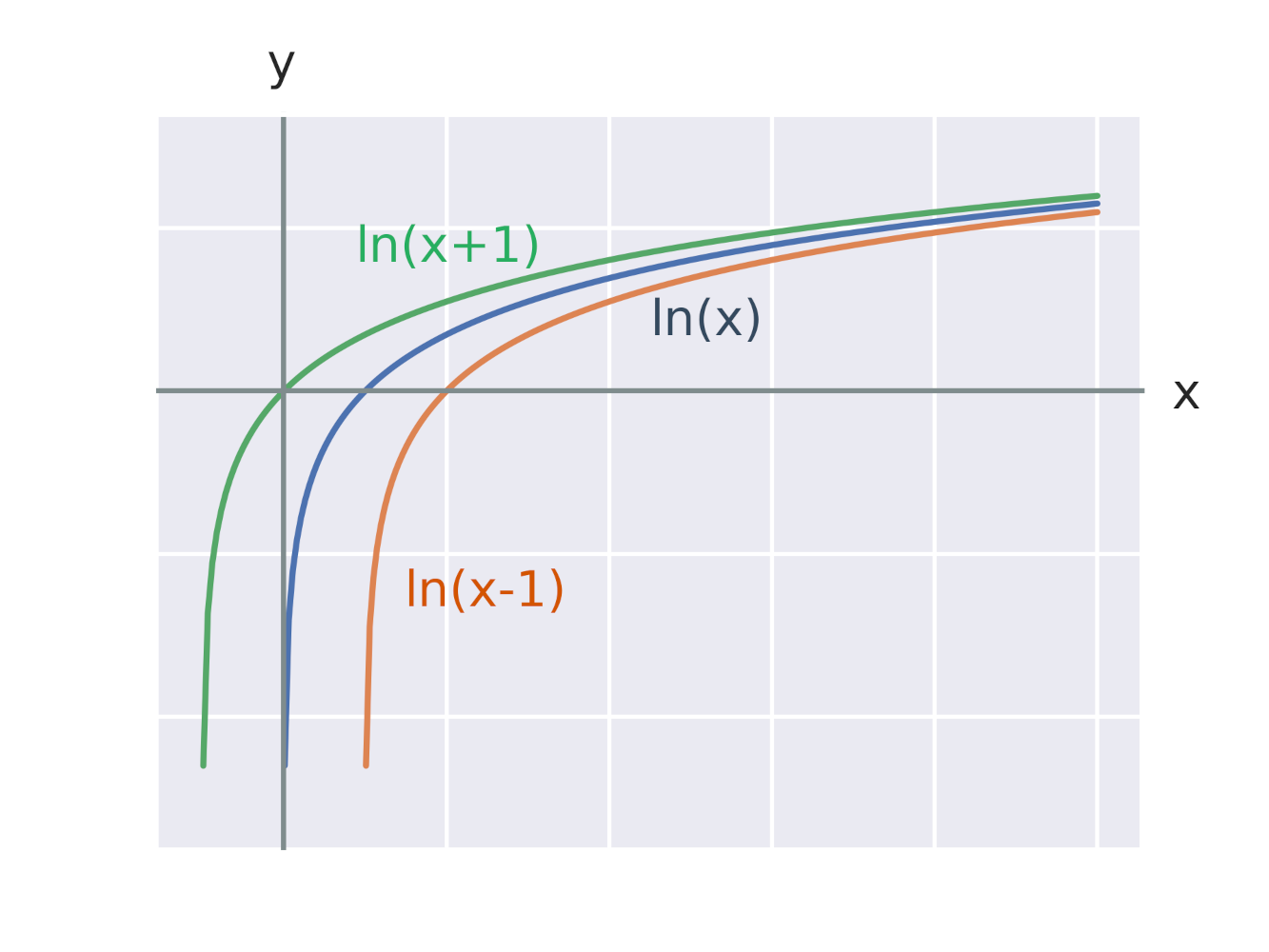
Efekt vynásobení logaritmické funkce konstantou
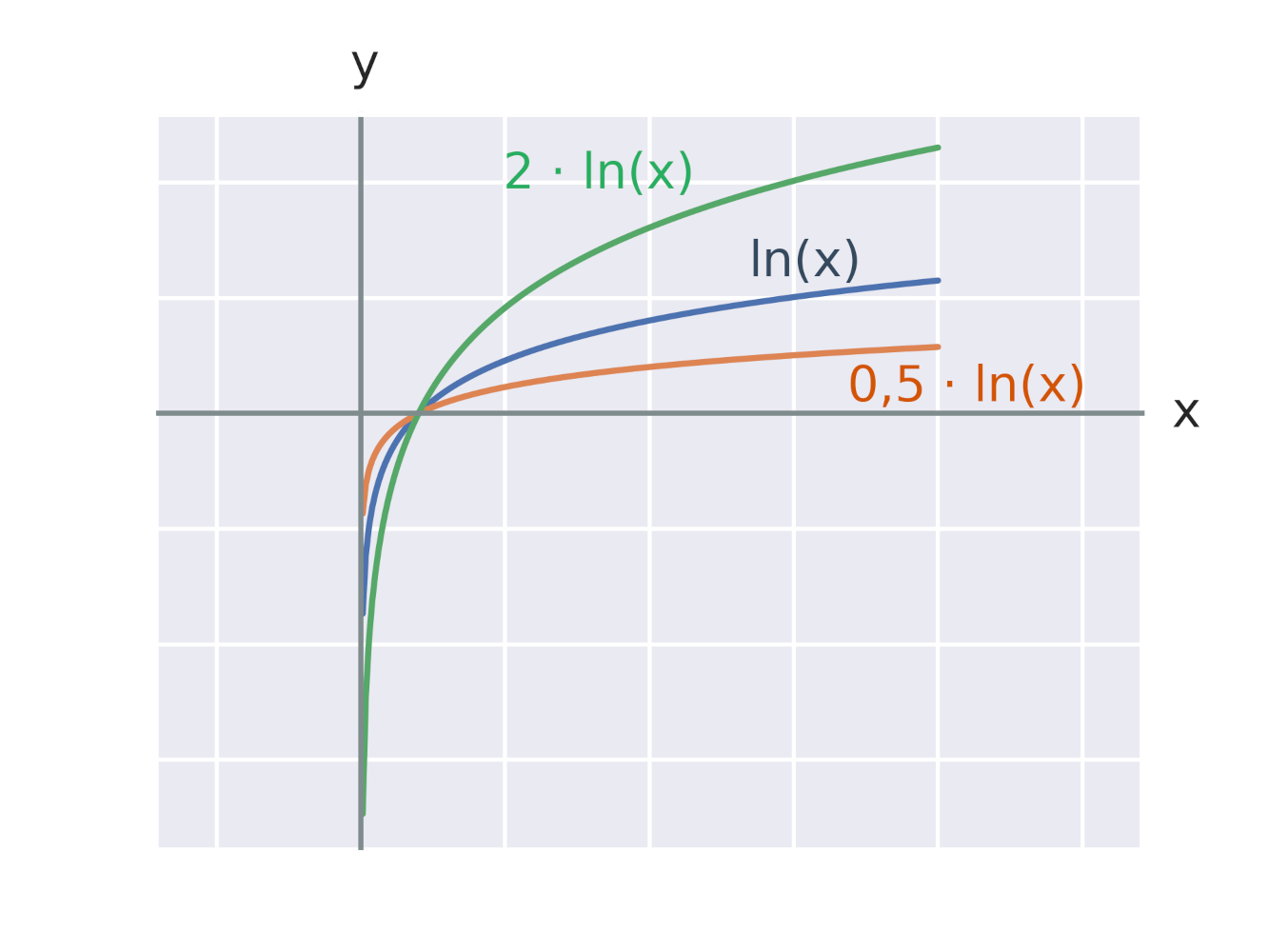
Efekt vynásobení argumentu logaritmické funkce konstantou
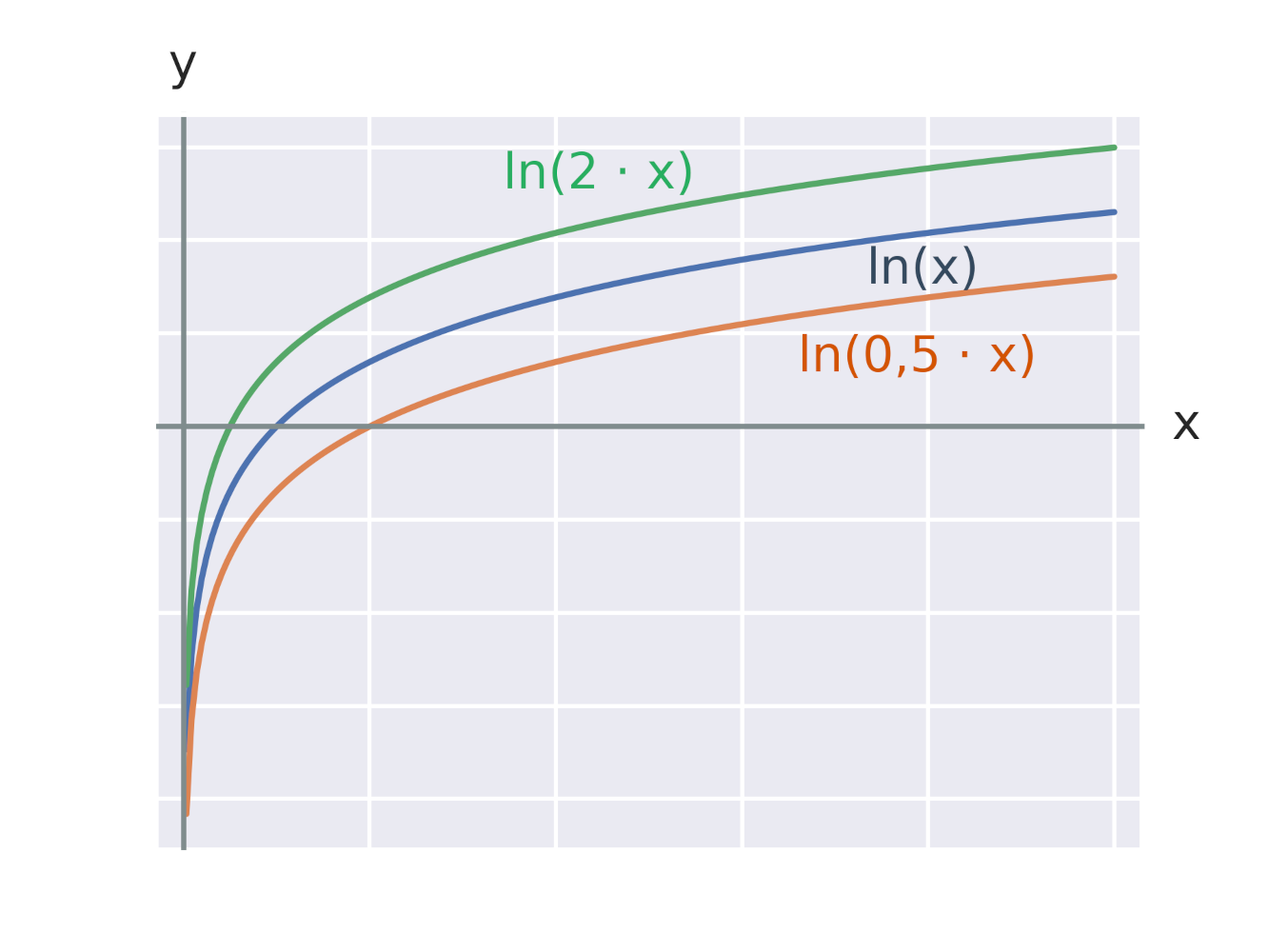
Grafy lineárních nerovnic
Grafem funkce dané předpisem y= ax+b je přímka. Množinou řešení lineární nerovnice budou všechny body [x,y] ležící v polorovině s hraniční přímkou y= ax+b. Může nastat jedna ze čtyř možností:
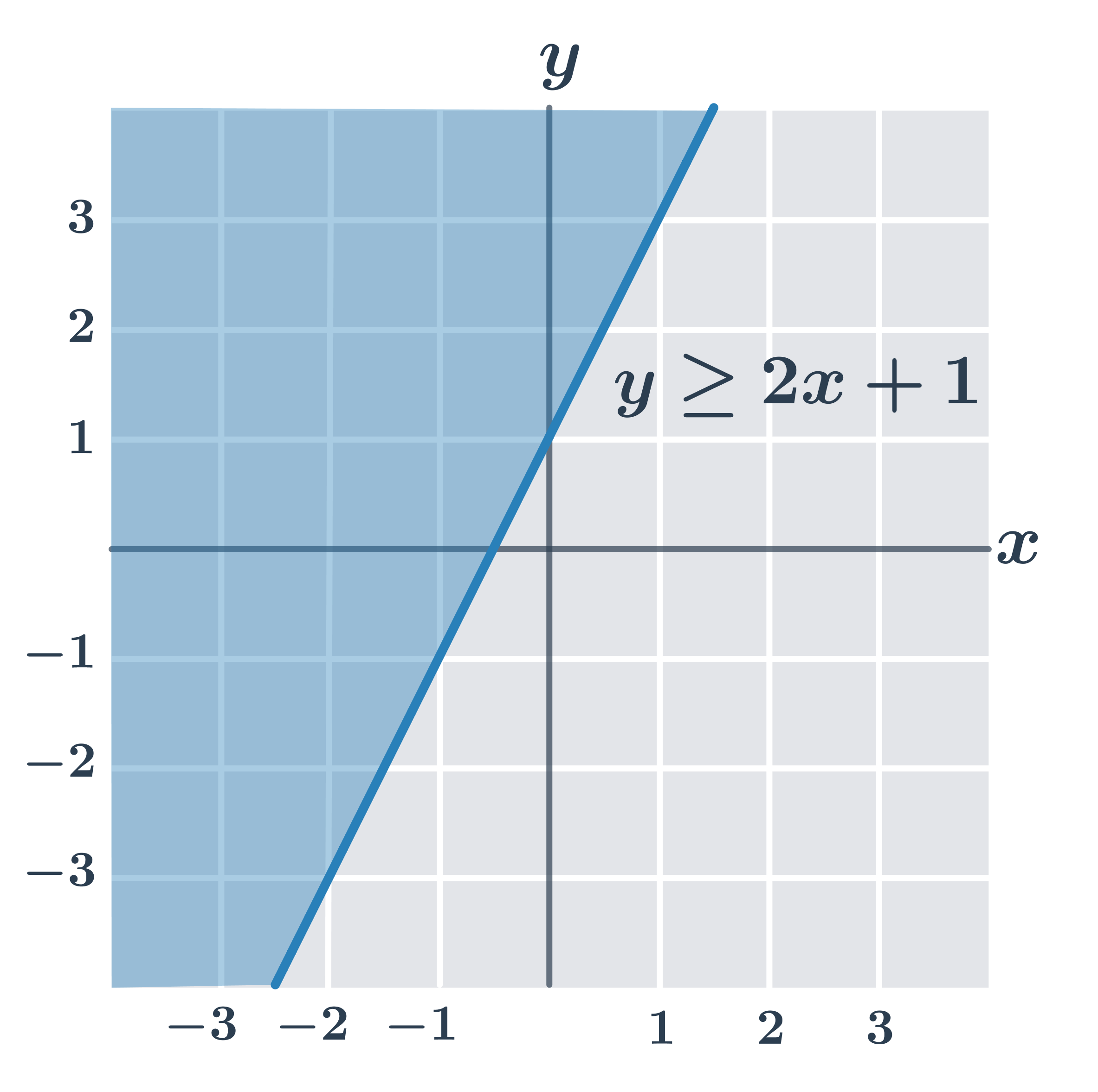
| y\geq ax+b | Nerovnost splňují všechny body v rovině, které leží přímo na přímce dané rovnicí y=ax+b nebo “nad” touto přímkou (se souřadnicí y větší než ax+b). |
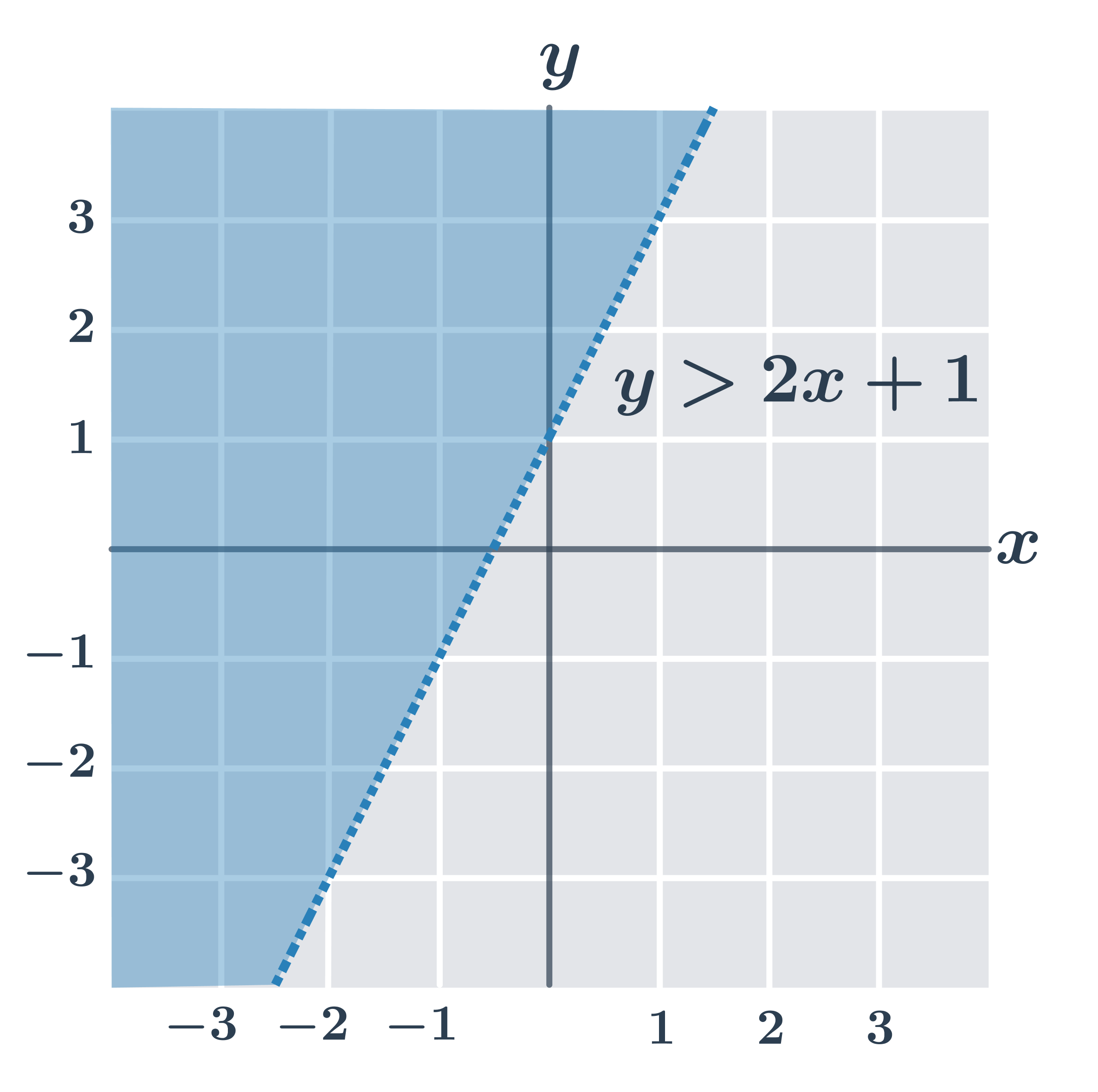
| y \gt ax+b | Nerovnost splňují všechny body v rovině, které leží “nad” přímkou o rovnici y=ax+b. |
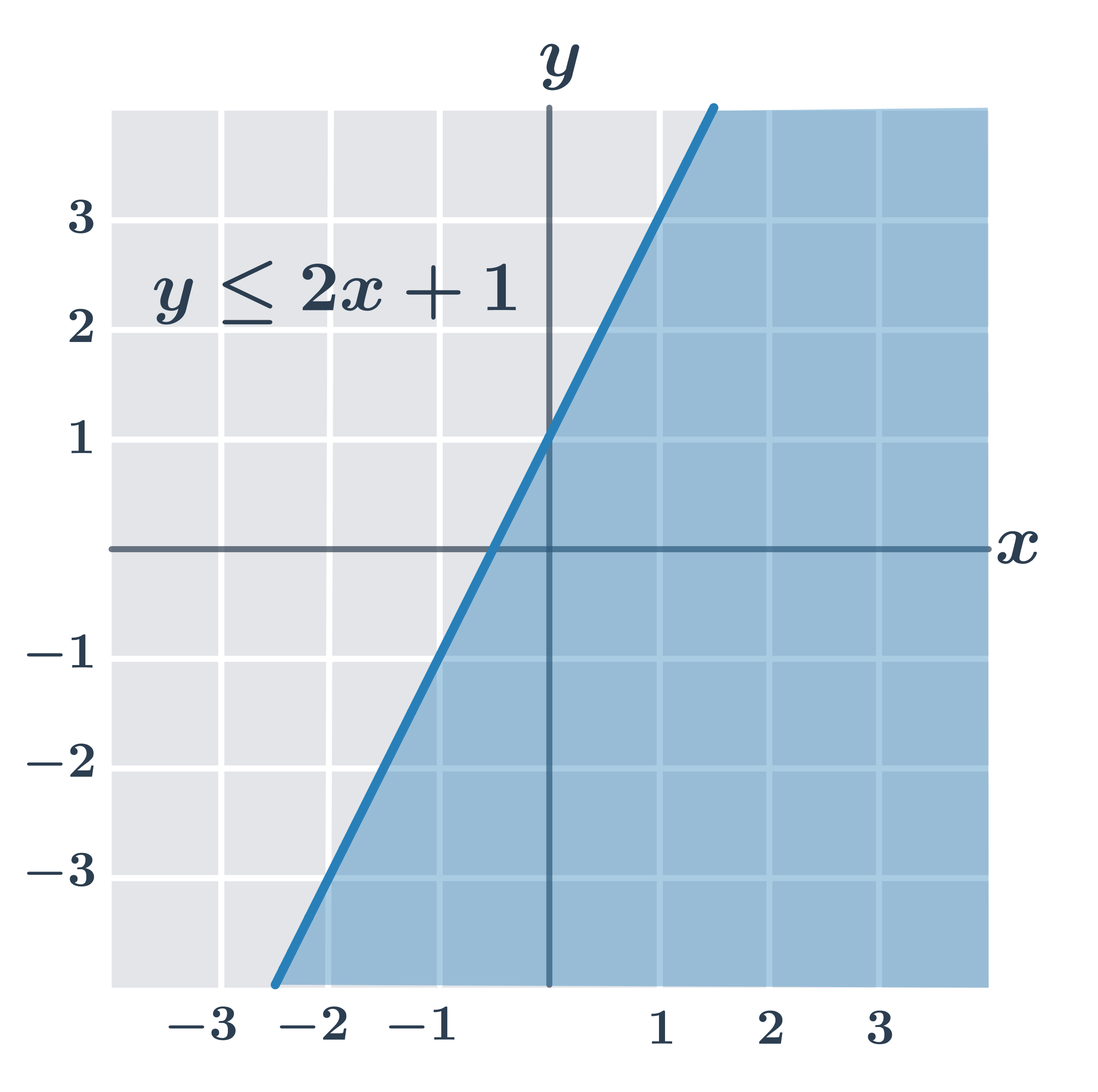
| y\leq ax+b | Nerovnost splňují všechny body v rovině, které leží na přímce o rovnici y=ax+b nebo “pod” touto přímkou (se souřadnicí y menší než ax+b). |
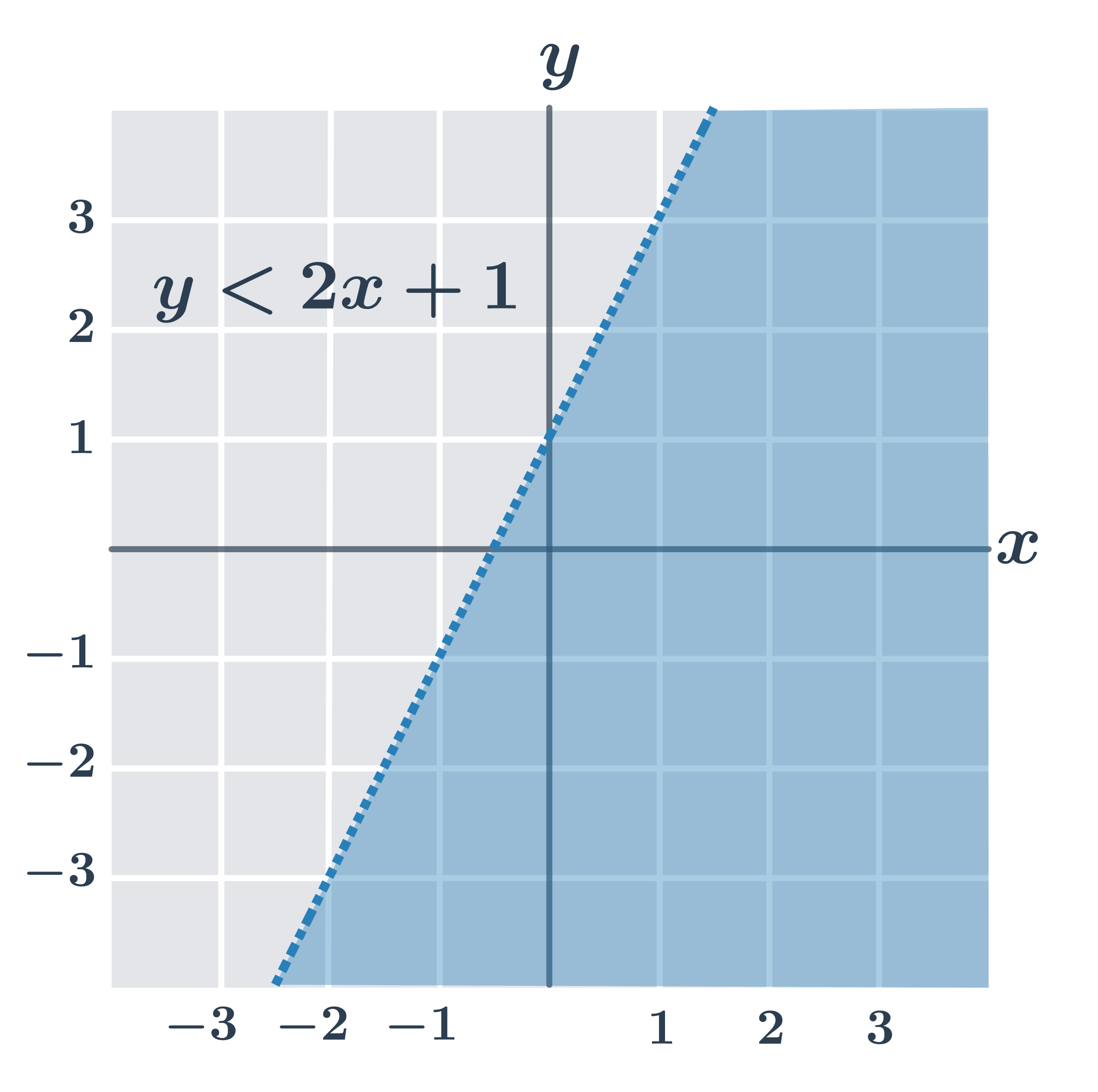
| y \lt ax+b | Nerovnost splňují všechny body v rovině, které leží “pod” přímkou o rovnici y=ax+b. |
Na obrázcích jsou řešení všech typů lineárních nerovnic (všimněte si, že pokud je v nerovnici jen znaménko \gt nebo \lt, body přímo na hraniční přímce lineární nerovnici nesplňují).
- y\geq 2x+1
- y \gt 2x+1
- y\leq 2x+1
- y \lt 2x+1
Souřadnice bodů v rovině
Souřadnice bodů většinou zapisujeme pomocí kartézské soustavy souřadnic v rovině, která má jako osy dvě kolmé přímky. Vodorovná přímka se tradičně označuje x a souřadnice podél této osy se zapisuje první. Svislá přímka se tradičně označuje y a souřadnice podle této osy se zapisuje druhá. Přímky x, y se protínají v bodě [0;0].
Přímky x a y jsou souřadné osy, bod [0;0] je počátek soustavy souřadnic.
Příklad: Souřadnice bodu A
Bod A na obrázku je v dané soustavě souřadnic určen jako x=1, y=2, což můžeme zapsat jako A[1;2].
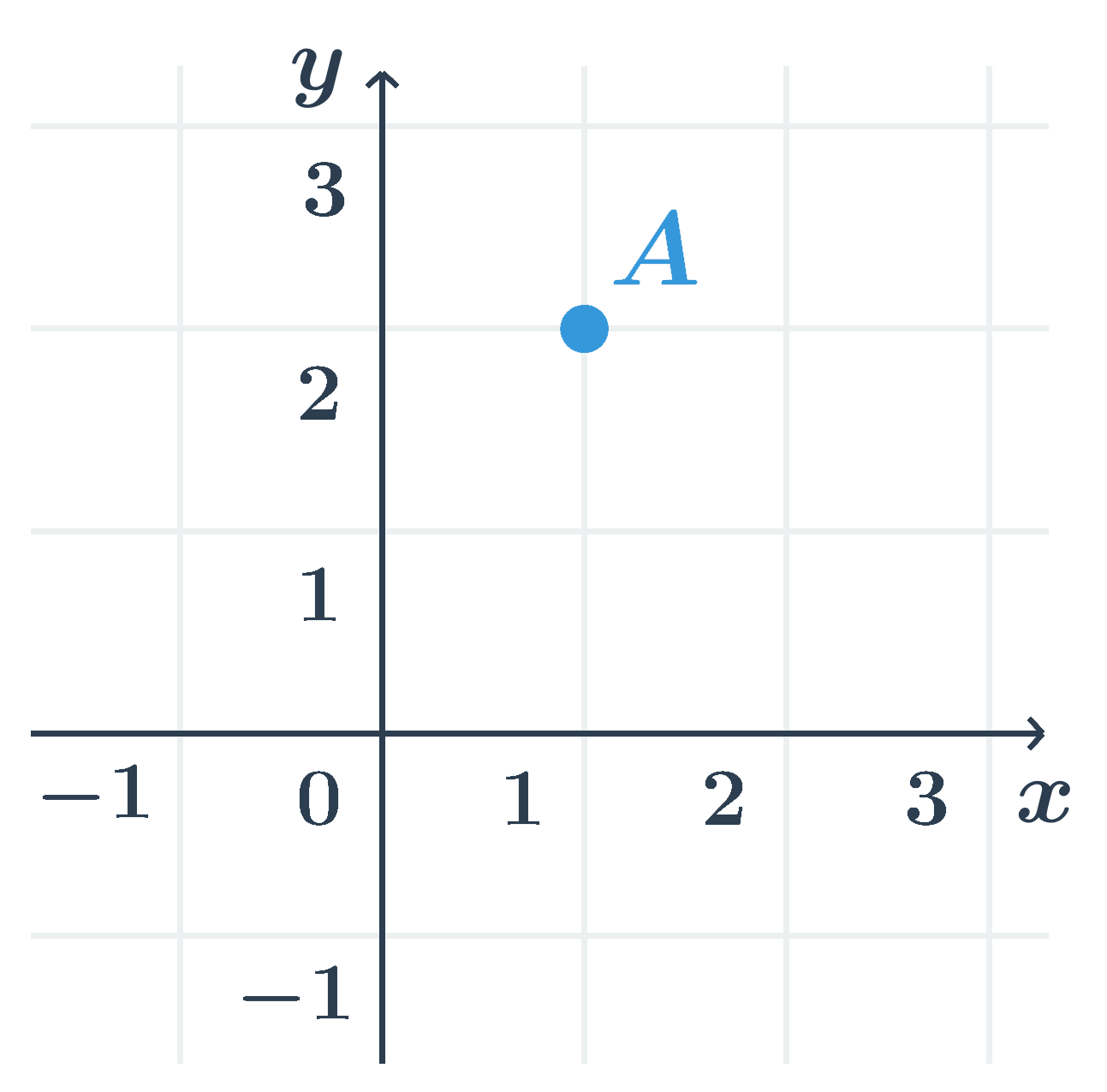
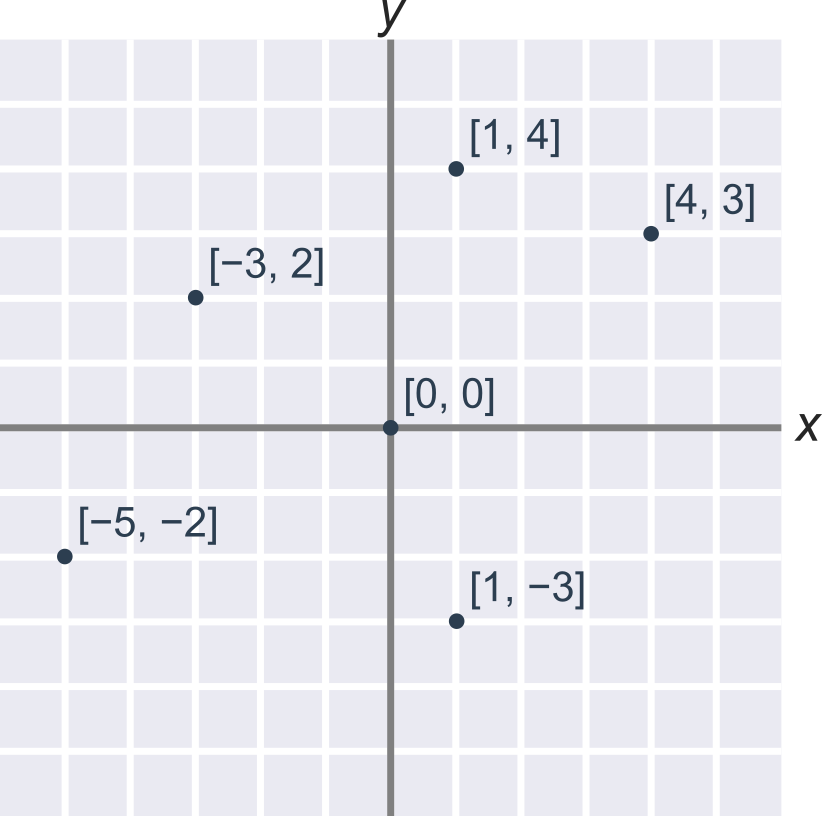
Další příklady souřadnic bodů
Lineární funkce
Funkce f je lineární, pokud ji lze vyjádřit ve tvaru f(x) = a\cdot x + b, kde a a b jsou konstanty. Grafem lineární funkce je přímka. Parametr a je směrnice (též nazývaná sklon), parametr b určuje její svislý posun (též nazývaný absolutní člen).
Příklady lineárních funkcí
- f(x) = 2x
- f(x) = -4x+8
- f(x) = \frac13 x + 1{,}2
Aby byla funkce lineární, nemusí být nutně přímo zapsána ve tvaru f(x) = a\cdot x + b. Stačí, když jde na tento tvar upravit.
Příklady lineárních funkcí v jiném tvaru
- f(x) = 2-x můžeme přepsat jako f(x)= -1x + 2, což je lineární funkce se směrnicí −1 a absolutním členem 2.
- f(x) = 5(3-x) můžeme přepsat jako f(x)= -5x + 15, což je lineární funkce se směrnicí −5 a absolutním členem 15.
- f(x) = x^2 + 7 - x(x-1) vypadá na první pohled jako kvadratická funkce, ale můžeme ji upravit na f(x)= x + 7 (kvadratický člen se vyruší), takže jde o lineární funkci.
S lineárními funkcemi souvisí následující dílčí témata:
- Grafy lineárních funkcí – grafický význam směrnice a absolutního členu, zakreslení grafu podle funkčního předpisu, odvození funkčního předpisu podle grafu
- Vlastnosti lineární funkce – ujasnění obecných vlastností funkcí (např. definiční obor, obor hodnot, rostoucí a klesající funkce) v případě lineární funkce
- Základní rovnice s jednou neznámou – základní rovnice s jednou neznámou odpovídají rovnosti lineárních funkcí a můžeme je ztvárnit graficky pomocí přímek, které představují grafy těchto funkcí
Vlastnosti lineární funkce
Funkce f je lineární, pokud ji lze vyjádřit ve tvaru f(x) = a\cdot x + b, kde a a b jsou konstanty. Definiční obor lineární funkce je celá množina reálných čísel.
Speciálním případem lineární funkce je funkce konstantní. Tu dostáváme v případě, že a=0.
Pokud a \neq 0, pak pro lineární funkci platí:
- je prostá,
- není shora ani zdola omezená,
- nemá maximum ani minimum,
- není periodická,
- obor hodnot je množina reálných čísel.
Pro a \gt 0 je funkce f rostoucí, pro a \lt 0 je funkce f klesající.
Pro b=0 je funkce f lichá.
Grafem lineární funkce je přímka. Průsečík grafu s osou y je v bodě [0, b]. Průsečík grafu s osou x je v bodě [-\frac{b}{a}, 0].
NahoruZákladní rovnice s jednou neznámou
Nejjednodušší rovnice obsahují pouze lineární výrazy, tj. vyskytují se v nich pouze konstanty a násobky proměnné x. Rovnici upravujeme pomocí ekvivalentních úprav: přičítání a odčítání stejného výrazu k oběma stranám rovnice, úpravy výrazů na levé a pravé straně. Pomocí takových úprav ji převedeme do tvaru x = a, kde a je řešení.
Řešený příklad: 3x-1=2x+5
| Od obou stran rovnice odečteme 2x. | 3x-1-2x=2x+5-2x |
| x-1=5 | |
| K oběma stranám rovnice přičteme 1. | x-1+1=5+1 |
| x=6 | |
| Řešení rovnice je x=6. |
Řešený příklad: 2x-7 = 5-4x
| K oběma stranám rovnice přičteme 4x. | 2x - 7 + 4x = 5 - 4x + 4x |
| 6x - 7 = 5 | |
| K oběma stranám rovnice přičteme 7. | 6x - 7 + 7 = 5 + 7 |
| 6x = 12 | |
| Obě strany rovnice vydělíme číslem 6. | 6x : 6 = 12 : 6 |
| x = 2 | |
| Řešení rovnice je x=2. |
Počet řešení
U základních lineárních rovnic mohou nastat tři případy:
- Rovnice nemá žádné řešení, např. x+2=x+3.
- Rovnice má nekonečně mnoho řešení, např. u rovnice x+1+x = 2x+1 je řešením rovnice je libovolné číslo.
- Rovnice má právě jedno řešení, např. výše uvedená rovnice 2x-7 = 5-4x má jediné řešení x=2.
Časté chyby
Mezi časté chyby při řešení rovnic patří:
- provedení úpravy (přičtení čísla, vydělení čísel) pouze na jedné straně rovnice,
- chybné zkombinování konstant a výrazů s proměnnou x, např. úprava 3x + 2 na 5x,
- špatné znaménko u výrazu při převádění z jedné strany rovnice na druhou.
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Komiks pro zpestření

Lineární lomené funkce
Lineární lomenou funkci můžeme vyjádřit jako podíl dvou lineárních funkcí, tedy ve tvaru
f:y =\frac{ax+b}{cx+d},
kde a,b,c,d jsou konstanty.
Definičním oborem lineární lomené funkce je množina všech reálných čísel kromě hodnoty, ve které by jmenovatel zlomku \frac{ax+b}{cx+d} byl nulový:
D(f)=\mathbb{R} - \{-\frac{d}{c}\}
Úpravou podmínky pro nenulovost jmenovatele zlomku dostaneme vyjádření definičního oboru pomocí nerovnice: cx+d\neq0\Rightarrow x\neq -\frac{d}{c}
Kdy je funkce nelineární a nekonstantní (a graf je hyperbola, nikoliv přímka)
K tomu, aby f:y=\frac{ax+b}{cx+d} nebyla lineární ani konstantní funkce, musí být splněno několik podmínek. Pro konstanty a,b,c,d musí platit: c\neq0 a bc-ad\neq0.
- pro c=0 bychom měli lineární funkci danou rovnicí y =\frac{a}{d}\cdot x+\frac{b}{d}
- pro bc-ad=0 bychom měli konstantní funkci y =\frac{a}{c}
Vysvětlení podmínky bc-ad\neq0
| Pro lineární lomenou funkci danou předpisem \frac{ax+b}{cx+d} provedeme dělení čitatele zlomku \frac{ax+b}{cx+d} jeho jmenovatelem: |
| \begin{array}{lrrrr} \hspace{0.3cm}(\hspace{0.4cm}ax+\hspace{0.47cm}b)&:&(cx+d)&=&\frac{a}{c}\\\underline{-( \frac{a}{c}\cdot cx+\frac{a}{c}\cdot d)\hspace{0.5cm}}& \\ \hspace{1.05cm}0+b-\frac{a}{c}\cdot d\\ \end{array} |
| Vyšel nám tedy podíl \frac{a}{c} a zbytek b-\frac{a}{c}\cdot d. |
| Pokud by platilo b-\frac{a}{c}\cdot d=0, mohli bychom funkci y =\frac{ax+b}{cx+d} zapsat zjednodušeně ve tvaru y =\frac{a}{c} a to není lineární lomená funkce, ale funkce konstantní. |
| Abychom měli lineární lomenou funkci, musí tedy platit b-\frac{a}{c}\cdot d\neq0. Tuto podmínku můžeme vynásobením obou stran hodnotou c upravit na tvar: bc-ad\neq0 |
Speciálním případem lineární lomené funkce je nepřímá úměrnost vyjádřená ve tvaru y =\frac{k}{x}.
NahoruVlastnosti lineární lomené funkce
Lineární lomená funkce f:y =\frac{ax+b}{cx+d} má definiční obor D(f)=\R - \{-\frac{d}{c}\}, což můžeme také zapsat jako sjednocení dvou intervalů: D(f)=(-\infty, -\frac{d}{c}) \cup (-\frac{d}{c}, \infty)
Pokud c\neq0 a bc-ad\neq0, pak pro lineární lomenou funkci platí:
- je prostá
- není periodická
- nemá maximum ani minimum
- není shora ani zdola omezená
Další vlastnosti závisí na hodnotách koeficientů a, b, c, d:
- pro bc-ad \gt 0 je lineární lomená funkce klesající na intervalu (-\infty, -\frac{d}{c}) a také klesající na intervalu (-\frac{d}{c}, \infty)
- pro bc-ad \lt 0 je lineární lomená funkce rostoucí na intervalu (-\infty, -\frac{d}{c}) a také je rostoucí na intervalu (-\frac{d}{c}, \infty)
- pro a=0 a d=0 má lineární lomená funkce tvar: f:y =\frac{b}{cx} a je to lichá funkce (f(x) = - f(-x))
Příklad: vlastnosti funkce f:y =\frac{3x+1}{4x+2}
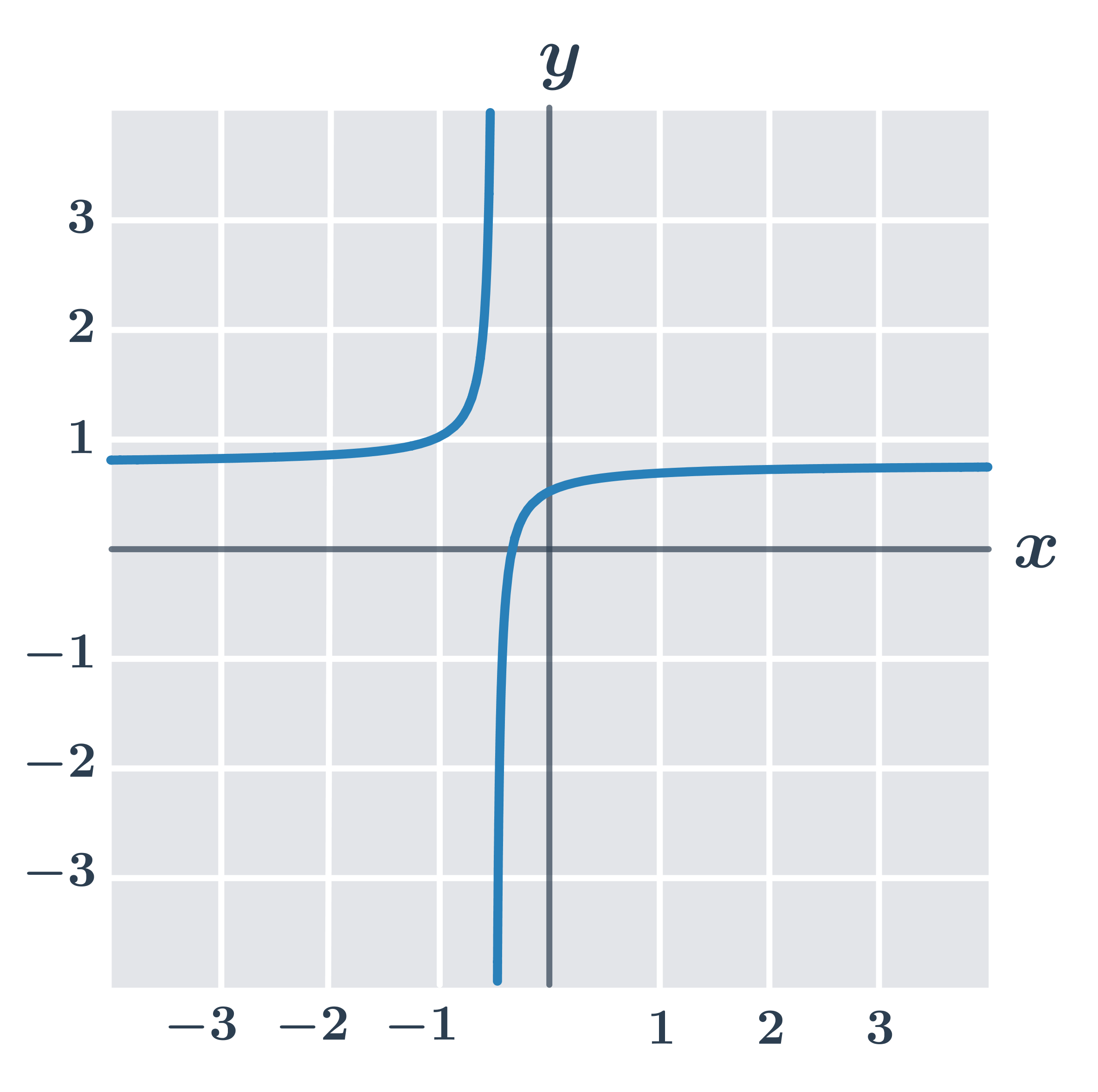
- Definiční obor D(f)=\R - \{-\frac{1}{2}\}.
- Funkce je prostá.
- Funkce je rostoucí na intervalu (-\infty,-\frac{1}{2}) a také je rostoucí na intervalu (-\frac{1}{2},\infty) – snadno poznáme z grafu, ale zároveň můžeme ověřit splnění podmínky bc-ad \lt 0: pro danou funkci bc-ad=1\cdot4-3\cdot2=-2.
Příklad: vlastnosti funkce f:y =\frac{3}{2x}
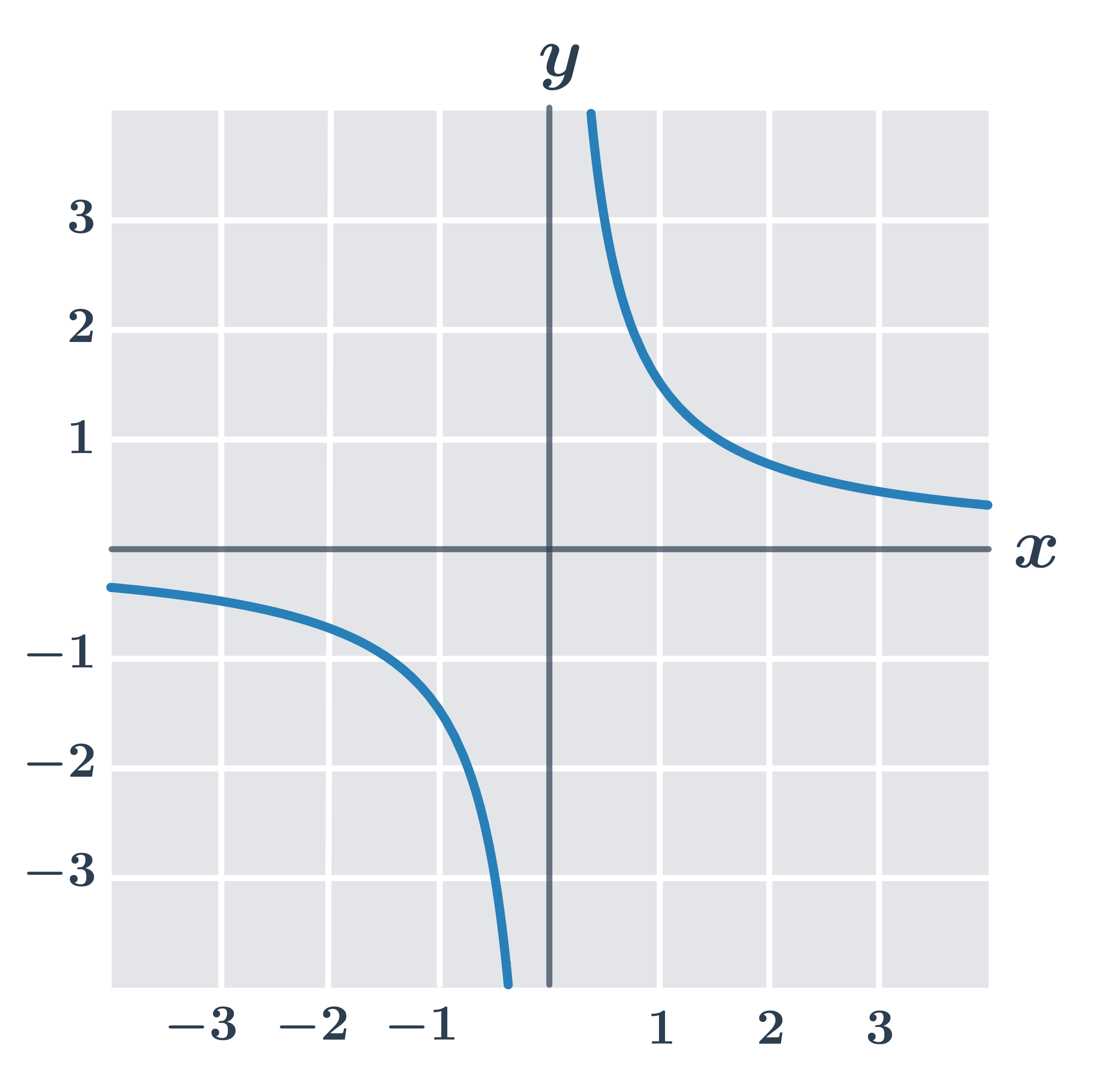
- Definiční obor D(f)=\R - \{0\}.
- Funkce je prostá.
- Funkce je klesající na intervalu (-\infty,0) a také je klesající na intervalu (0,\infty).
- Funkce je lichá – graf je souměrný podle počátku (pro lineární lomené funkce, kde a=0 a d=0).
Poznámka: omezenost lineární lomené funkce
- Definiční obor lineární lomené funkce tvoří vždy dva intervaly.
- Pokud si budeme všímat vlastností funkce jen na jednom z těchto intervalů, jedná se o funkci omezenou zdola nebo shora. Například funkce na obrázku f:y =\frac{2x+3}{x+1}:

- Definiční obor D(f)=\R - \{-1\}, tedy intervaly (-\infty;-1) a (-1;\infty).
- Na intervalu (-\infty;-1) je funkce shora omezená a na intervalu (-1;\infty) zdola omezená.
Kvadratické funkce
Funkce je kvadratická, pokud ji lze vyjádřit ve tvaru f(x) = ax^2 + bx + c, kde a\neq 0. Funkce je ryze kvadratická, pokud nemá lineární člen (tj. b=0). Grafem kvadratické funkce je parabola. Kvadratická funkce je speciální příklad polynomu.
Příklady kvadratických funkcí
- f(x) = x^2
- f(x) = (x+1)^2 = x^2 + 2x + 1
- f(x) = -3x^2 + 2x -8
S kvadratickými funkcemi souvisí následující dílčí témata:
- Grafy kvadratických funkcí – znázornění kvadratické funkce pomocí paraboly, zakreslení grafu podle funkčního předpisu, odvození funkčního předpisu podle grafu
- Vlastnosti kvadratické funkce – ujasnění obecných vlastností funkcí (např. definiční obor, obor hodnot, omezenost, periodičnost) v případě kvadratické funkce
- Kvadratické rovnice – hledání řešení kvadratické rovnice úzce souvisí s hledáním kořenů kvadratické funkce
Vlastnosti kvadratické funkce
Funkce je kvadratická, pokud ji lze vyjádřit ve tvaru f(x) = ax^2 + bx + c, kde a\neq 0.
Definiční obor kvadratické funkce je celá množina reálných čísel.
Kvadratická funkce nemá žádnou z následujících vlastností: prostá, periodická, rostoucí, klesající.
Další vlastnosti závisí na tom, zda je kvadratický člen kladný či záporný:
- Pro a \gt 0 je funkce zdola omezená, není shora omezená. V bodě -\frac{b}{2a} má minimum.
- Pro a \lt 0 je funkce shora omezená, není zdola omezená. V bodě -\frac{b}{2a} má maximum.
Nulové body kvadratické funkce f(x) = ax^2 + bx + c (hodnoty x, pro které je f(x)=0) odpovídají kořenům kvadratické rovnice ax^2 + bx + c=0.
NahoruKvadratické rovnice
Pojmy
Kvadratická rovnice je rovnice, ve které se vyskytuje jedna neznámá ve druhé mocnině. Základní tvar kvadratické rovnice je: ax^2+bx+c=0, kde a, b, c jsou reálná čísla a a\neq 0. Pro kvadratické rovnice používáme následující názvosloví:
- ax^2 je kvadratický člen,
- bx je lineární člen,
- c je absolutní člen.
Příklad: 2x^2+6x-20 = 0
| kvadratický člen | 2x^2 |
| lineární člen | 6x |
| absolutní člen | -20 |
| řešení rovnice | x=2 a x=-5 |
Speciální typy kvadratických rovnic:
- Pokud je b=0 nazýváme rovnici ryze kvadratickou: ax^2+c=0.
- Pokud je c=0 mluvíme o rovnici bez absolutního členu: ax^2+bx=0.
Řešení kvadratické rovnice
Každou kvadratickou rovnici lze řešit pomocí výpočtu diskriminantu D. Pro něj platí: D=b^2-4\cdot a\cdot c. Mohou nastat 3 situace:
- D \lt 0 – rovnice nemá v reálných číslech řešení.
- D = 0 – rovnice má jeden dvojnásobný kořen.
- D \gt 0 – rovnice má dva různé reálné kořeny.
Pro kořeny rovnice platí:
- x_1=\frac{-b+\sqrt{D}}{2a}
- x_2=\frac{-b-\sqrt{D}}{2a}
Řešený příklad: x^2+2x-3=0
- Pro tuto rovnici a=1, b=2, c=-3.
- Diskriminant D=b^2-4ac = 2^2-4\cdot 1\cdot(-3) = 4+12=16.
- D>0, rovnice má tedy dvě řešení.
- x_1 = \frac{-b+\sqrt{D}}{2a} = \frac{-2+\sqrt{16}}{2\cdot 1} = 1
- x_2 = \frac{-b-\sqrt{D}}{2a} = \frac{-2-\sqrt{16}}{2\cdot 1} = -3
- Řešení rovnice jsou tedy hodnoty 1 a -3.
Vietovy vzorce
Kvadratické rovnice můžeme řešit i bez počítání diskriminantu za využití Vietových vzorců. Pro kořeny rovnice platí: x_1+x_2=-\frac{b}{a}, x_1\cdot x_2=\frac{c}{a}. V případě a=1: x_1+x_2=-b, x_1\cdot x_2=c.
NahoruGoniometrické funkce
Goniometrické funkce (nebo též trigonometrické funkce) jsou skupinou funkcí, které dávají do vztahu úhel v pravoúhlém trojúhelníku a poměr dvou jeho stran. Mají široké využití v geometrii a mnoho praktických aplikací – například v navigaci, nebeské mechanice nebo geodézii. Tyto funkce se vyskytují i v dalších oblastech matematiky, jako jsou komplexní čísla nebo nekonečné řady.
Základními goniometrickými funkcemi jsou sinus, kosinus a tangens. Méně často pak můžeme narazit také na sekans, kosekans a kotangens. Inverzní funkce ke goniometrickým funkcím se nazývají cyklometrické (například arkus sinus a arkus tangens).
Podrobněji se goniometrickými funkcemi zabývají tato podtémata:
- Goniometrické funkce a pravoúhlý trojúhelník – základní vztah mezi úhlem a poměrem stran v pravoúhlém trojúhelníku
- Hodnoty goniometrických funkcí – často používané hodnoty základních goniometrických funkcí pro základní úhly (např. 0°, 30°, 45°, 60°, 90°)
- Goniometrické funkce: vztahy a vzorce – klíčové vztahy mezi jednotlivými goniometrickými funkcemi a využití těchto vztahů
- Vlastnosti goniometrických funkcí – vlastnosti goniometrických funkcí, jako jsou periodičnost, symetrie
- Grafy goniometrických funkcí – grafické znázornění goniometrických funkcí
K dispozici je také pomůcka k vytištění Goniometrické funkce: přehled.
NahoruGoniometrické funkce a pravoúhlý trojúhelník
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
- Sinus (\sin) úhlu \alpha je poměr délky odvěsny protilehlé úhlu \alpha a délky přepony.
- Kosinus (\cos) úhlu \alpha je poměr délky odvěsny přilehlé úhlu \alpha a délky přepony.
- Tangens (\tan) úhlu \alpha je poměr délky odvěsny protilehlé úhlu \alpha a délky odvěsny přilehlé úhlu \alpha.
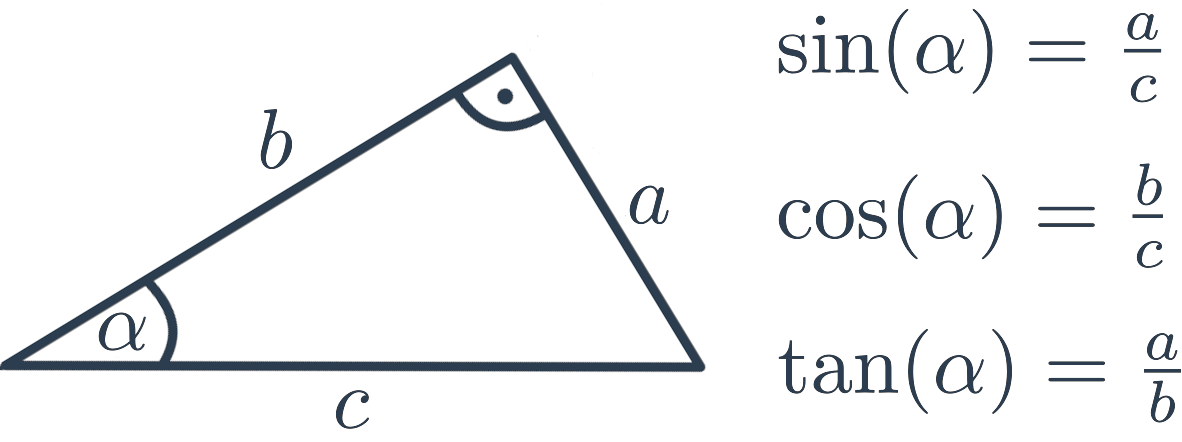
Pokud si pamatujeme význačné hodnoty goniometrických funkcí (jako např. \sin 30^{\circ}=\frac{1}{2}), nebo aspoň máme k dispozici kalkulačku nebo matematické tabulky, znamená pro nás znát hodnotu \sin, \cos nebo \tan některého úhlu v pravoúhlém trojúhelníku totéž jako znát velikost samotného úhlu.
Příklad: známe strany pravoúhlého trojúhelníku, dopočítáme úhly
Pravoúhlý trojúhelník ABC má délky stran a=24, b=10, c=26. Jaké jsou velikosti jeho vnitřních úhlů?
- Pokud je trojúhelník pravoúhlý, je velikost úhlu \gamma naproti nejdelší straně c rovna 90^{\circ}.
- Víme, že \sin \alpha je podíl protilehlé strany a přepony, tedy \sin \alpha=\frac{a}{c}.
- Dosadíme známé velikosti stran: \sin \alpha = \frac{24}{26}\doteq 0{,}923
- Příslušná velikost úhlu je: \alpha \doteq 67^{\circ}
- Z \alpha+\beta+\gamma=180^{\circ} dopočítáme, že \beta je zhruba 23^{\circ}.
Kontrola:
- Víme, že \cos \beta je podíl strany přilehlé k úhlu \beta a přepony, tedy \cos \beta = \frac{a}{c}.
- Dosadíme známé velikosti stran: \cos \beta = \frac{24}{26}\doteq 0{,}923
- Příslušná velikost úhlu je: \beta \doteq 23^{\circ}
Příklad: známe úhel, dopočítáme délku strany pomocí \sin
Mějme pravoúhlý trojúhelník ABC s pravým úhlem u vrcholu C, ve kterém platí \sin \alpha = \frac{1}{2} a délka přepony je c=10. Jaká je délka strany a?
- Víme, že hodnotu \sin \alpha spočítáme jako podíl délky strany protilehlé k úhlu \alpha a délky přepony, tedy \sin \alpha = \frac{a}{c}.
- Dosadíme do této rovnosti za \sin \alpha a za c.
- \frac{1}{2} = \frac{a}{10} \Rightarrow a=5
- Délka strany a je 5.
Příklad: známe úhel, dopočítáme délku strany pomocí \cos
Mějme pravoúhlý trojúhelník ABC s pravým úhlem u vrcholu C, ve kterém platí \cos \alpha = \frac{3}{5} a délka přepony je c=15. Jaká je délka strany a?
- Víme, že hodnotu \cos \alpha spočítáme jako podíl délky strany přilehlé k úhlu \alpha a délky přepony, tedy \cos \alpha = \frac{b}{c}.
- Dosadíme do této rovnosti za \cos \alpha a za c.
- \frac{3}{5} = \frac{b}{15} \Rightarrow b=9
- Délka strany b je 9. Chtěli jsme spočítat délku strany a, což zvládneme ze známých hodnot b,c jednoduše pomocí Pythagorovy věty.
- a^2 = c^2-b^2=255-81=144 \Rightarrow a=12
- Délka strany a je 12.
Příklad: známe úhel, dopočítáme délku strany pomocí \tan
Mějme pravoúhlý trojúhelník ABC s úhlem \alpha = 60^{\circ} a s délkou delší odvěsny 6. Jaká je délka druhé odvěsny?
- Víme, že v pravoúhlém trojúhelníku ABC jsou vnitřní úhly 60^{\circ}, 90^{\circ}, dopočítáme zbývající úhel.
- \beta=180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}
- Vidíme, že \beta \lt \alpha.
- Delší odvěsna bude v trojúhelníku proti většímu úhlu, takže máme a=6.
- \tan \alpha je podíl odvěsny protilehlé úhlu \alpha a odvěsny přilehlé, tedy \tan \alpha = \frac{a}{b}.
- Dosadíme za \tan \alpha hodnotu \tan 60^{\circ} = \sqrt{3} (zjistíme z tabulek nebo z kalkulačky), dosadíme také b=6.
- \sqrt{3} = \frac{6}{b} \Rightarrow b= \frac{6}{\sqrt{3}} = 2\sqrt{3}
- Délka kratší odvěsny je b=2\sqrt{3}.
Hodnoty goniometrických funkcí
Často používané hodnoty goniometrických funkcí ilustruje tento obrázek jednotkové kružnice:
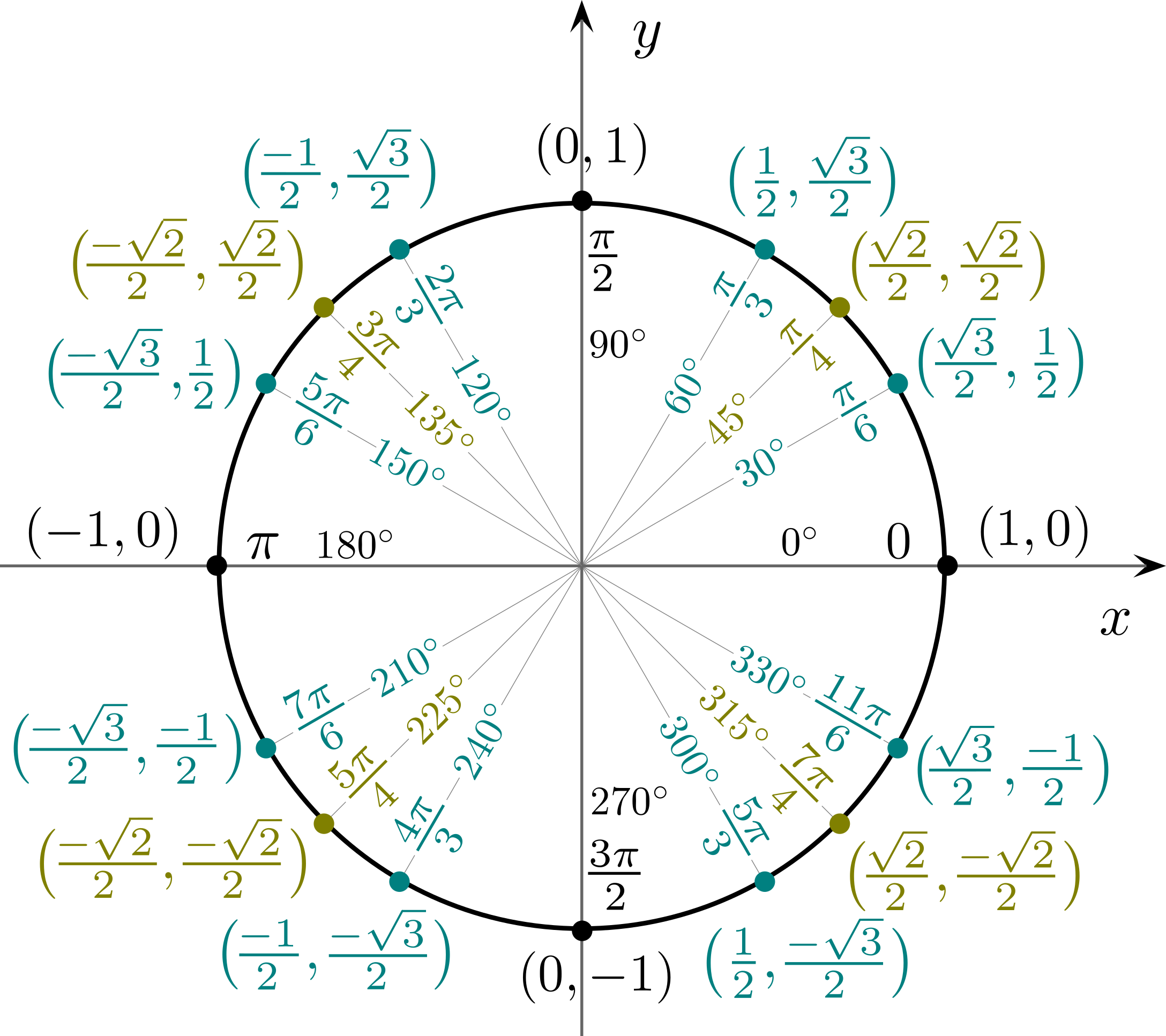
Polopřímka, která svírá úhel \alpha s kladnou částí osy x a začíná v počátku souřadnic, protíná jednotkovou kružnici v bodě se souřadnicemi [\cos \alpha; \sin \alpha], neboli:
- x-ová souřadnice bodu odpovídá hodnotě \cos daného úhlu,
- y-ová souřadnice bodu odpovídá hodnotě \sin daného úhlu.
Příklad: sinus a kosinus úhlu 30°
Polopřímka, která svírá s kladnou částí osy x úhel 30° (to je \frac{\pi}{6} radiánů), protíná jednotkovou kružnici v bodě [\frac{\sqrt{3}}{2}; \frac12]. Takže máme:
- \cos 30^{\circ} = \frac{\sqrt{3}}{2}
- \sin 30^{\circ} = \frac12
Příklad: tangens úhlu 150°
Polopřímka, která svírá s kladnou částí osy x úhel 150° (to je \frac{5\pi}{6} radiánů), protíná jednotkovou kružnici v bodě [-\frac{\sqrt{3}}{2}; \frac12]. Takže máme:
- \cos 150^{\circ} = -\frac{\sqrt{3}}{2}
- \sin 150^{\circ} = \frac12
- spočítáme \tan 150^{\circ} jako podíl \frac{\sin 150^{\circ}}{\cos 150^{\circ} }
- \tan 150^{\circ} = \frac12 : \left(-\frac{\sqrt{3}}{2}\right) = \frac12 \cdot \left(-\frac{2}{\sqrt{3}}\right) = -\frac{1}{\sqrt{3}} = -\frac{\sqrt{3}}{3}
Goniometrické funkce: vztahy a vzorce
Pro goniometrické funkce platí celá řada vztahů a vzorců. Výběr těch základních:
Pro záporné hodnoty úhlů
| \sin(-x) = -\sin x (lichá funkce) |
| \cos(-x) = \cos x (sudá funkce) |
| \tan(-x) = -\tan x (lichá funkce) |
Vztahy mezi funkcemi a posuny
| \sin^2 x + \cos^2 x = 1 |
| \tan x = \frac{\sin x}{\cos x} |
| \sin(x+\frac{\pi}{2}) = \cos x |
| \sin(x+2\pi) = \sin x (perioda 2\pi) |
| \sin(x+\pi) = -\sin x |
Vzorce pro goniometrické funkce součtu argumentů
| \sin(x+y) = \sin x \cos y+\cos x \sin y |
| \sin(x-y) = \sin x \cos y - \cos x \sin y |
| \cos(x+y) = \cos x \cos y - \sin x \sin y |
| \cos(x-y) = \cos x \cos y + \sin x \sin y |
Vzorce pro součet hodnot goniometrických funkcí
| \sin x + \sin y = 2 \sin(\frac{x+y}{2})\cos(\frac{x-y}{2}) |
| \sin x - \sin y = 2\cos(\frac{x+y}{2})\sin(\frac{x-y}{2}) |
| \cos x + \cos y = 2\cos(\frac{x+y}{2})\cos(\frac{x-y}{2}) |
| \cos x - \cos y = -2 \sin(\frac{x+y}{2})\sin(\frac{x-y}{2}) |
Dvojnásobný argument
| \sin 2x = 2\sin x \cos x |
| \cos 2x = \cos^2 x - \sin^2 x |
| \tan 2x = \frac{2\tan x}{1-\tan^2 x} |
Vlastnosti goniometrických funkcí
Pro obě funkce \sin x a \cos x platí:
- definiční obor je množina reálných čísel,
- obor hodnot je interval \langle -1, 1 \rangle,
- funkce je omezená,
- funkce je periodická s periodou 2\pi,
- funkce není prostá.
Pro funkci \sin x platí:
- je lichá,
- hodnoty nula nabývá v bodech x=k\pi.
Pro funkci \cos x platí:
- je sudá,
- hodnoty nula nabývá v bodech x=(2k+1)\frac{\pi}{2}.
Pro funkci \tan x platí:
- definiční obor je \{x \in \mathbb{R}: x \neq (2k+1)\frac{\pi}{2} \},
- obor hodnot je množina reálných čísel,
- funkce je lichá,
- funkce je periodická s periodou \pi,
- funkce je neomezená,
- hodnoty nula nabývá v bodech x=k\pi.
Mocninné funkce
Funkce je mocninná, pokud ji lze vyjádřit ve tvaru y= x^k, kde k je konstanta. Definiční obor i vlastnosti funkce jsou dány hodnotou konstanty k.
Mezi nejčastější typy mocninných funkcí (pro koeficient n\in \N) patří:
- y= x^n … například: y= x^2, y= x^3
- y= x^{-n} … například: y=x^{-2} (můžeme psát také ve tvaru: y= \frac{1}{x^2})
- y= x^{\frac{1}{n}} … například: y= x^{\frac{1}{3}} (můžeme psát také ve tvaru: y= \sqrt [3]{x})
Exponenciální funkce
Funkce je exponenciální, pokud ji lze vyjádřit ve tvaru y= a^x, kde a je konstanta. Konstanta a se nazývá základ a může to být jakékoliv kladné reálné číslo kromě hodnoty 1, tedy a\in (0,1)\cup (1,\infty). Výraz x je exponent. Definičním oborem exponenciální funkce je množina všech reálných čísel, oborem hodnot je množina všech kladných reálných čísel. V běžné řeči používáme pojem exponenciální růst, pokud chceme říct, že něco velmi rychle roste, například počty nemocných při epidemii.
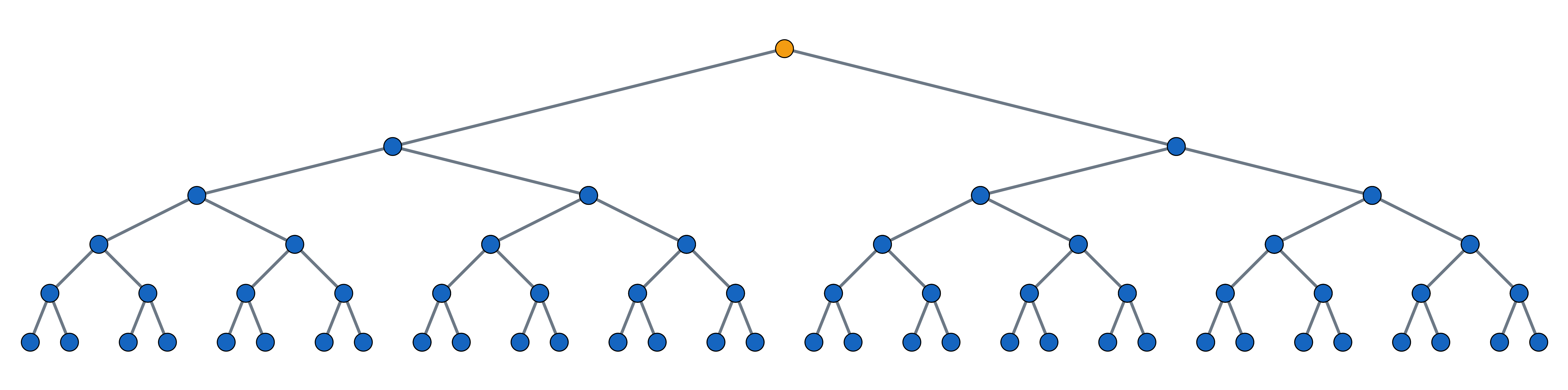
Příklad: exponenciální růst
Nakažlivá nemoc se šíří exponenciálně. Budeme-li uvažovat exponenciální funkci se základem a=2, znamená to, že každý nemocný nakazí další dva lidi. Šíření nemoci se dá dobře znázornit obrázkem:
Vlastnosti exponenciálních funkcí
Pro exponenciální funkci f:y =a^x platí:
- definiční obor D(f)=\R
- obor hodnot H(f)=(0, \infty)
- je prostá
- není periodická
- není sudá ani lichá
- nemá maximum ani minimum
- je zdola omezená
Další vlastnosti závisí na hodnotě koeficientu a:
- pro a>1 je exponenciální funkce rostoucí
- pro a\in (0,1) je exponenciální funkce klesající
Příklad: vlastnosti funkce f\!: y =3^x
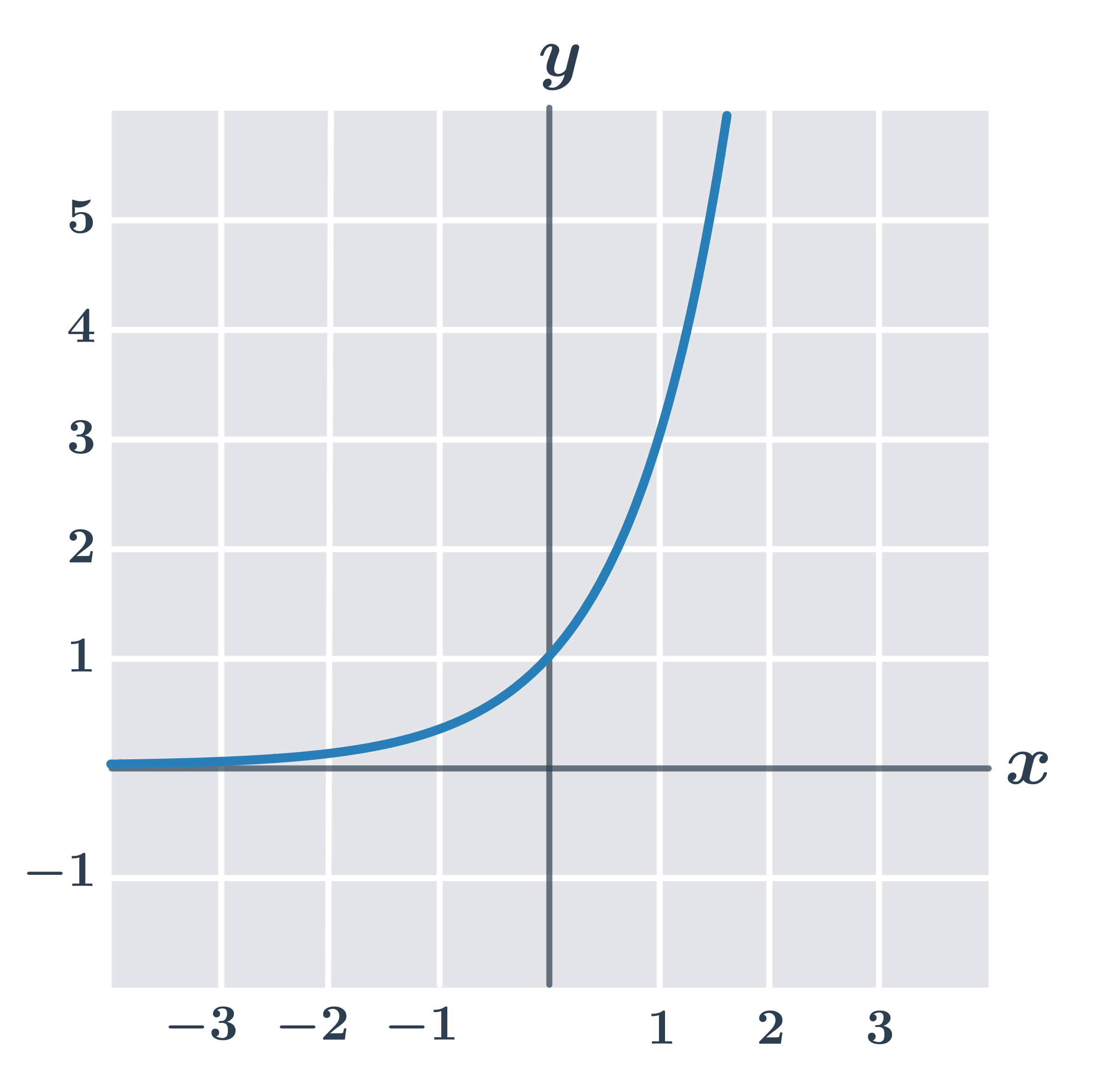
- definiční obor D(f)=\R
- obor hodnot H(f)=(0, \infty)
- je prostá
- je zdola omezená
- je rostoucí
Příklad: vlastnosti funkce f\!: y=\left (\frac{1}{2}\right)^x
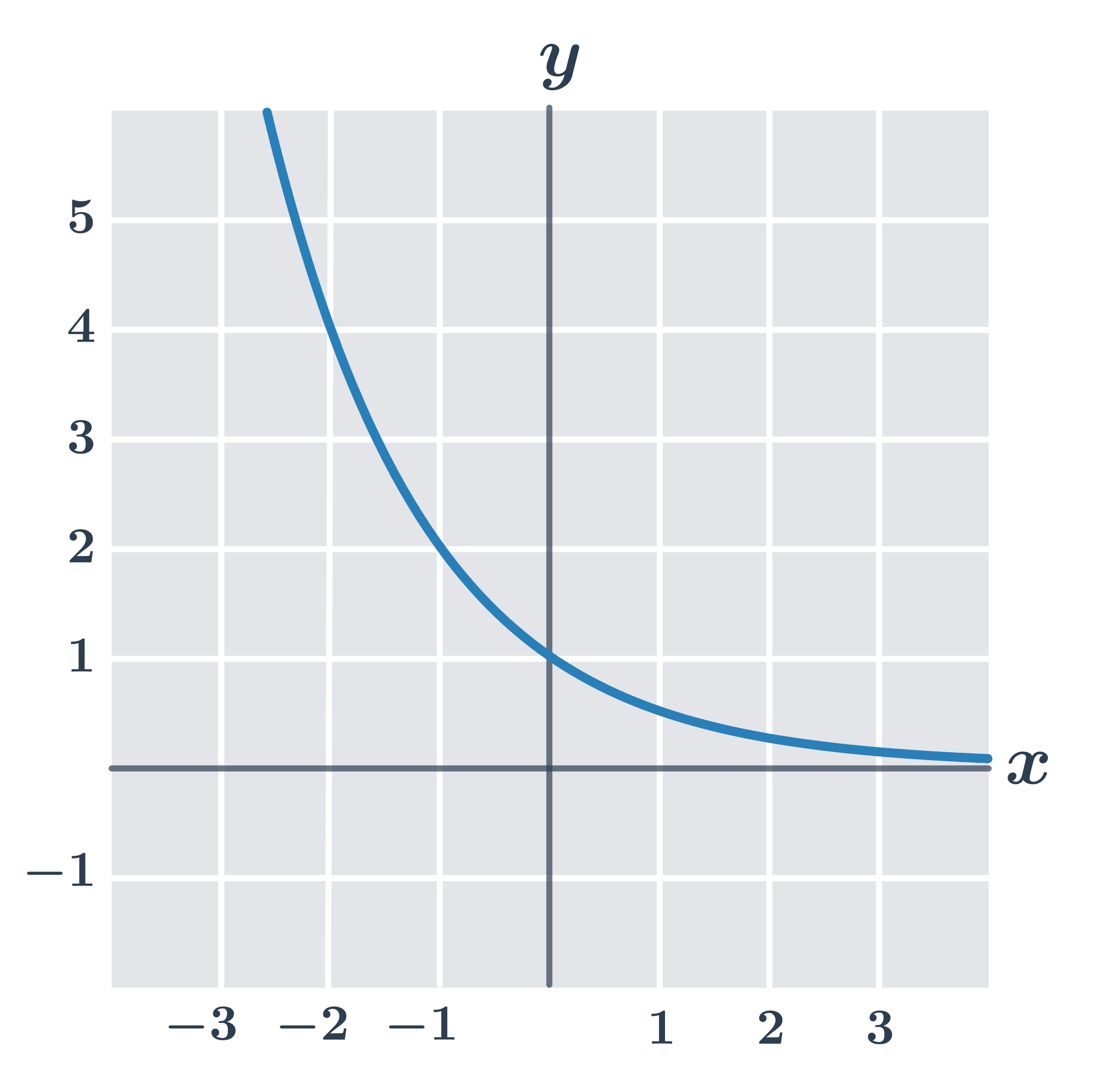
- definiční obor D(f)=\R
- obor hodnot H(f)=(0, \infty)
- je prostá
- je zdola omezená
- je klesající
Logaritmické funkce
Funkce je logaritmická, pokud ji lze vyjádřit ve tvaru y=\log_a x, kde a je konstanta. Konstanta a se nazývá základ a může to být jakékoliv kladné reálné číslo kromě hodnoty 1, tedy a\in (0,1)\cup (1,\infty). Výraz x je argument.
Definičním oborem logaritmické funkce je množina všech kladných reálných čísel, oborem hodnot je množina všech reálných čísel.
NahoruVlastnosti logaritmických funkcí
Pro logaritmickou funkci y=\log_ax platí:
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- není periodická
- není sudá ani lichá
- nemá maximum ani minimum
- není omezená
Další vlastnosti závisí na hodnotě koeficientu a:
- pro a>1 je logaritmická funkce rostoucí
- pro a\in (0,1) je logaritmická funkce klesající
Příklad: vlastnosti funkce y=\log_2 x
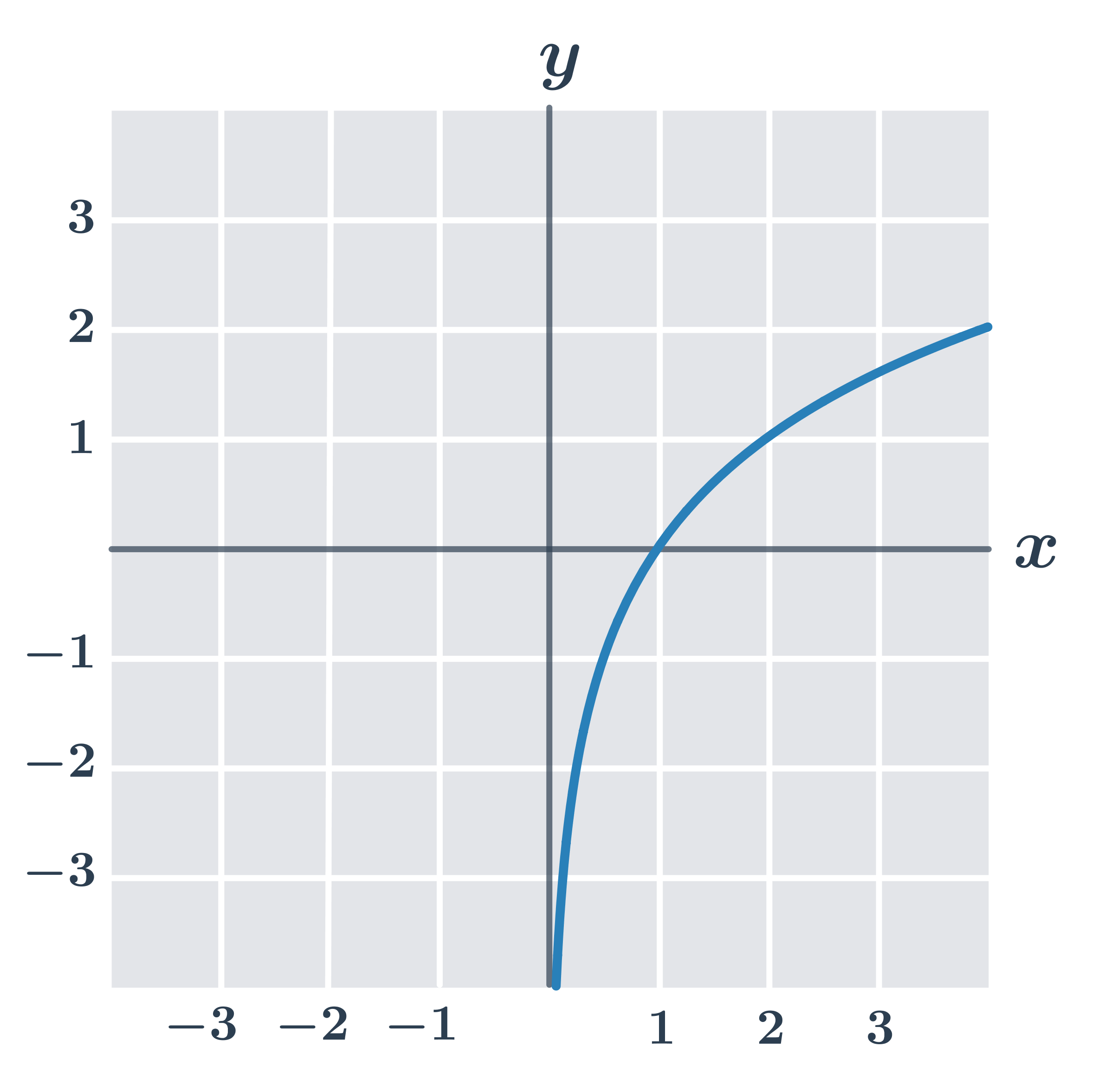
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- je rostoucí
Příklad: vlastnosti funkce y=\log_{\frac{1}{2}} x
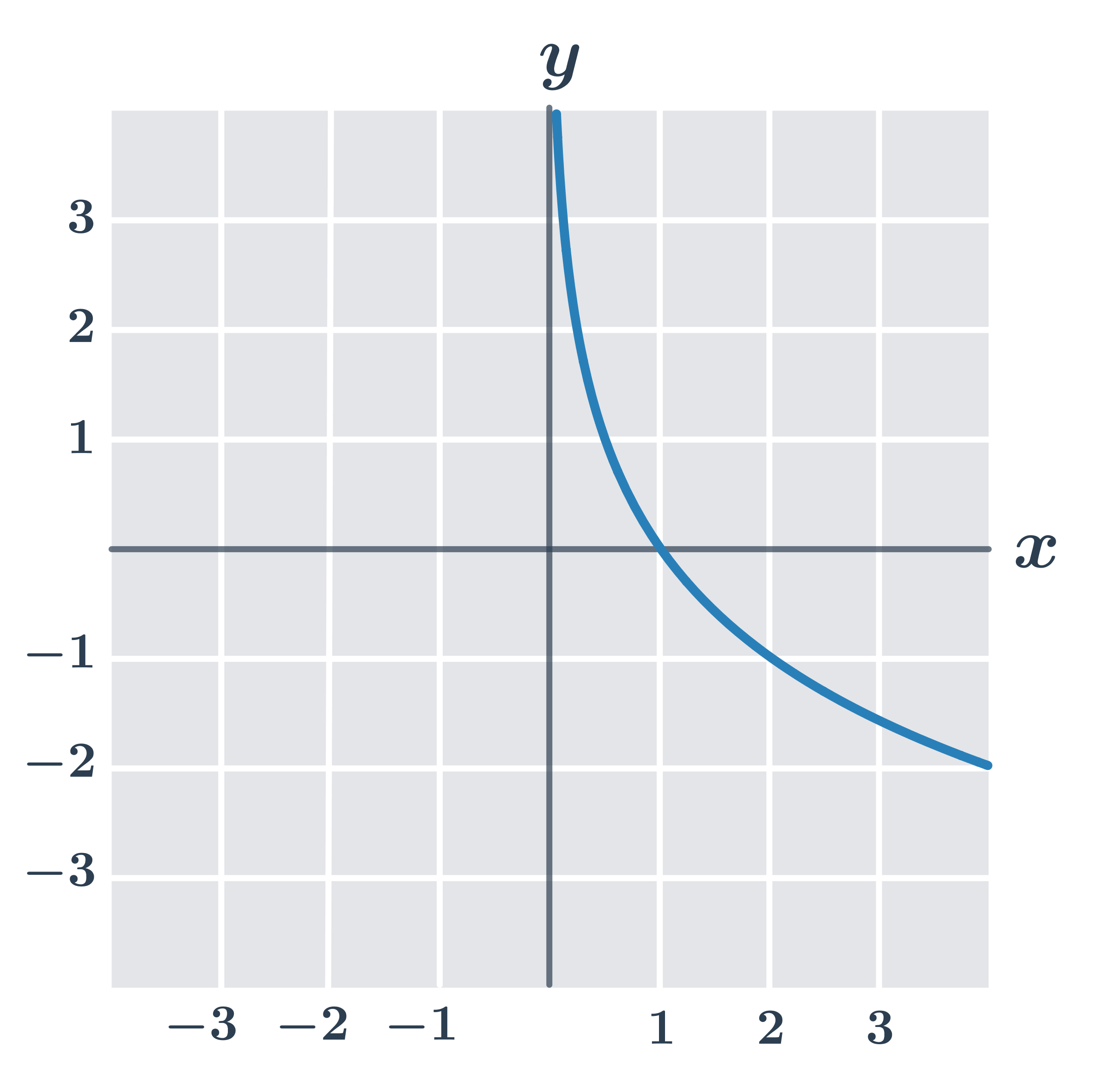
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- je klesající
Příklad: vlastnosti funkce y=\log_3 (x+2)
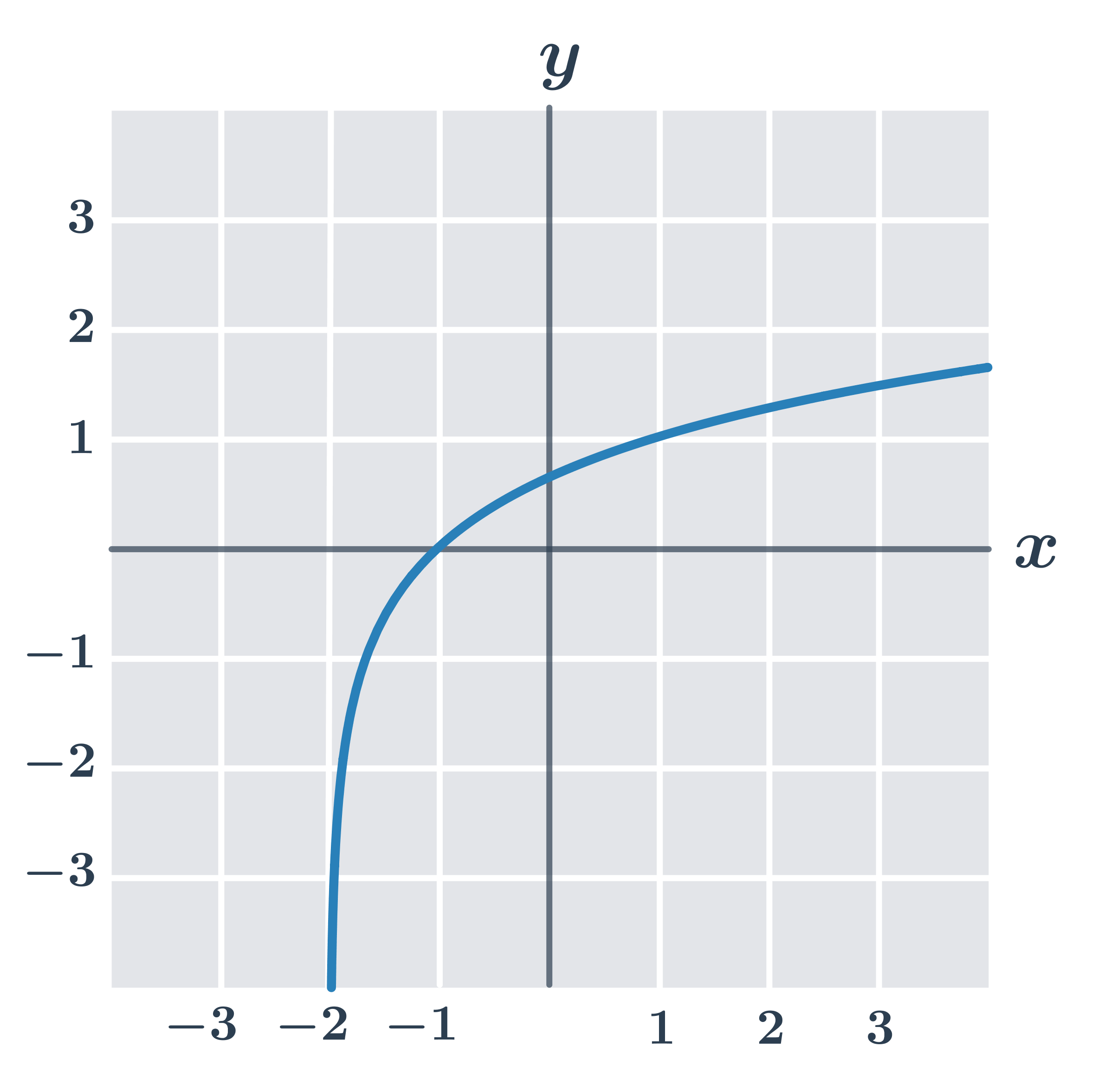
- definiční obor: D(f)=(-2, \infty) … výraz v logaritmu musí být kladný, tedy musí platit: x+2>0\Rightarrow x>-2
- obor hodnot H(f)=\R
- je prostá
- je rostoucí
- průsečík grafu s osou x je bod [-1,0] … najdeme jako řešení logaritmické rovnice: 0=\log_3(x+2). Podle pravidel pro počítání s logaritmy musí platit: 3^0=x+2\Rightarrow 1=x+2\Rightarrow x=-1