Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Krok po kroku
Psaná odpověď
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Cvičení
Grafy základních goniometrických funkcí intuitivně
Všimněte si
- graf které funkce protíná osu y v bodě x=0, y=0? (\sin, \tan)
- graf které funkce protíná osu y v bodě x=0, y=1? (\cos)
- která funkce je definovaná pro všechna x \in \mathbb{R}? (\sin, \cos)
Grafy goniometrických funkcí s popsanými osami
Funkce sinus y=\sin x:
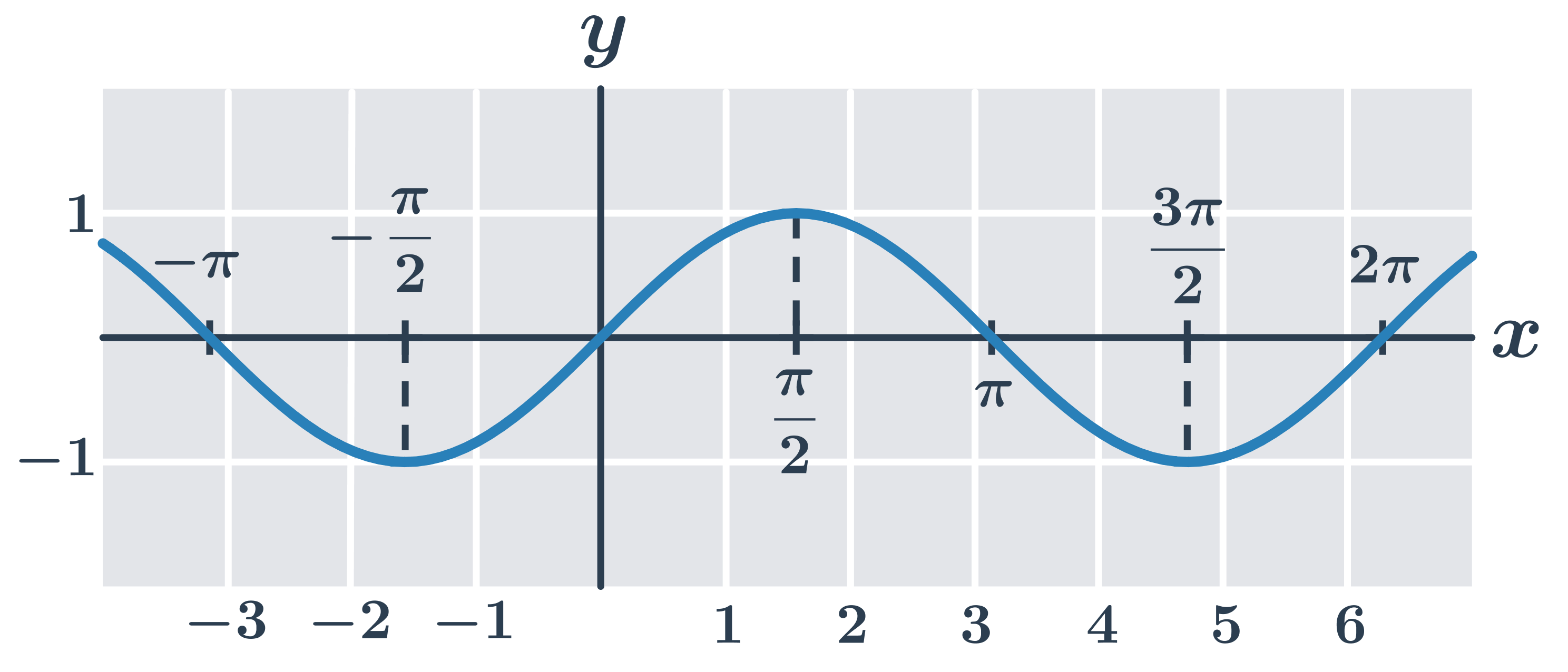
Funkce cosinus y=\cos x:
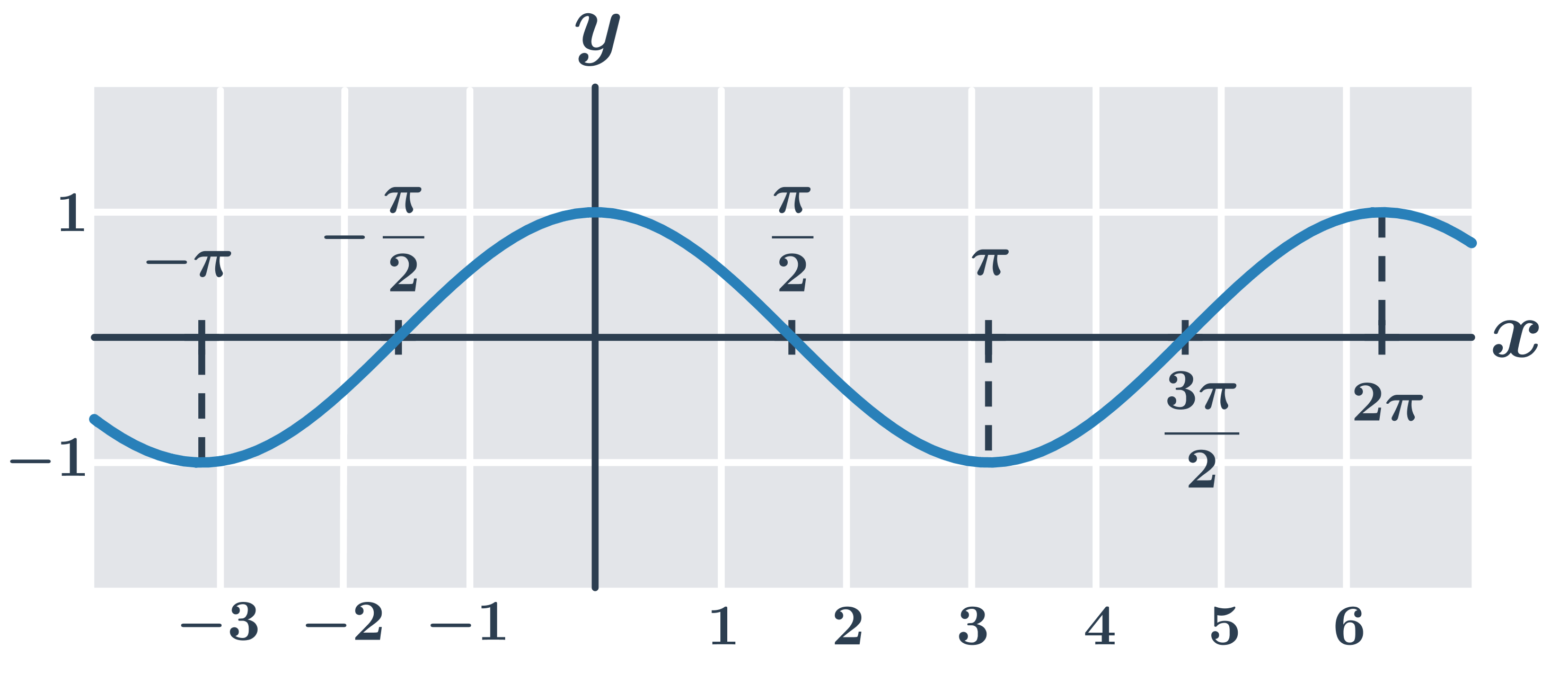
Funkce tangens y=\tan x:
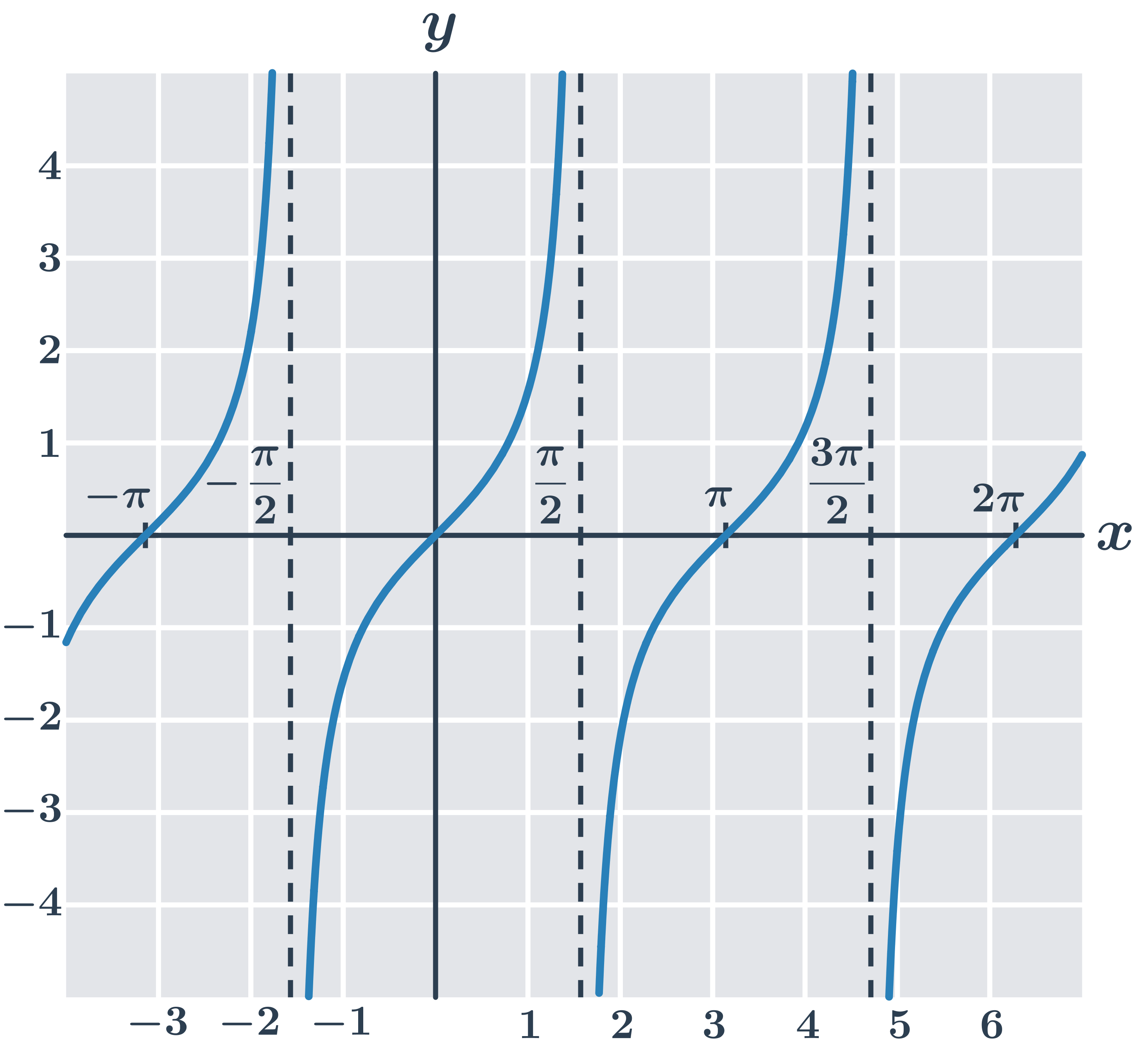
Funkce cotangens y=\cot x:
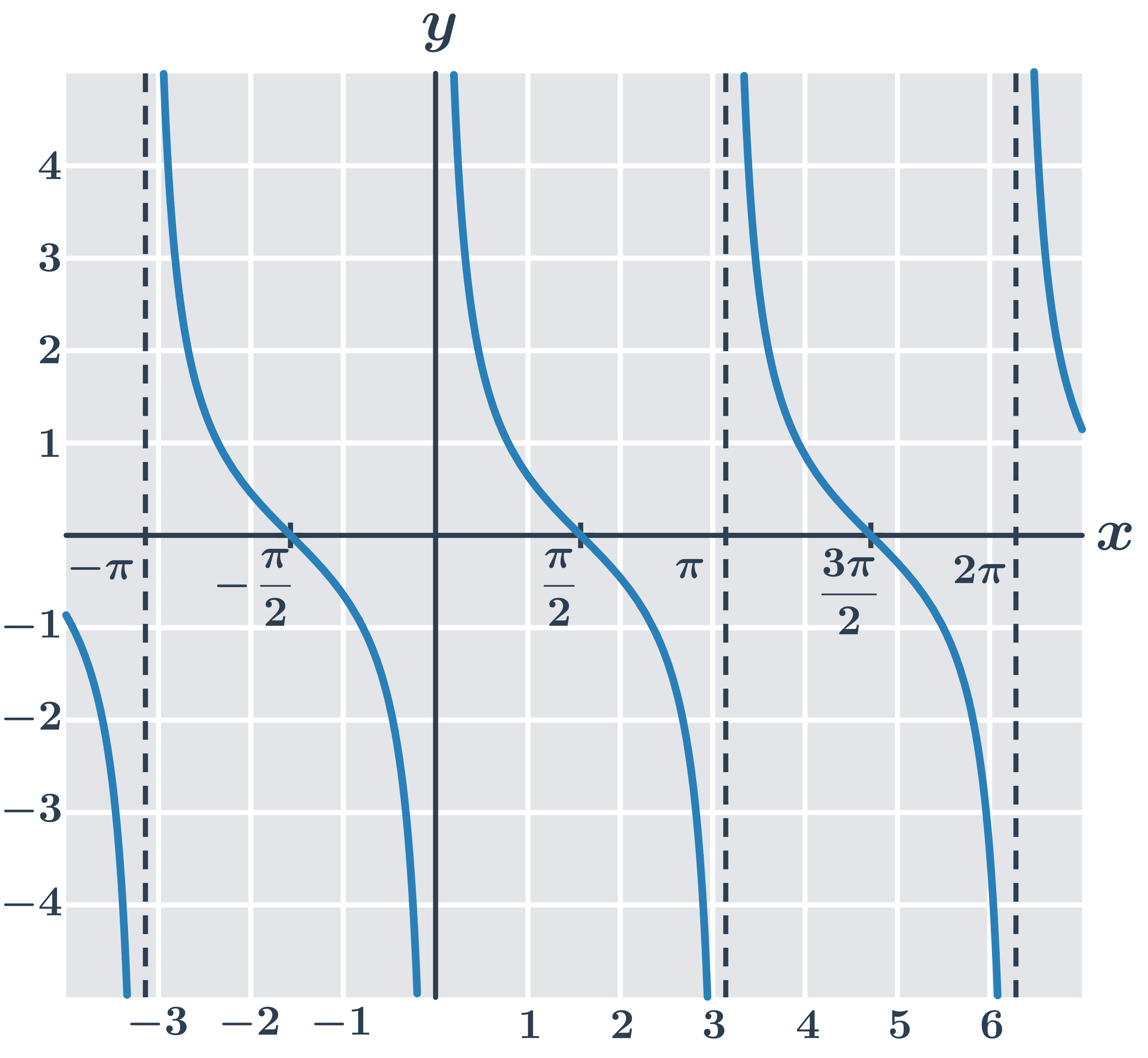
Dopad úprav funkce na graf
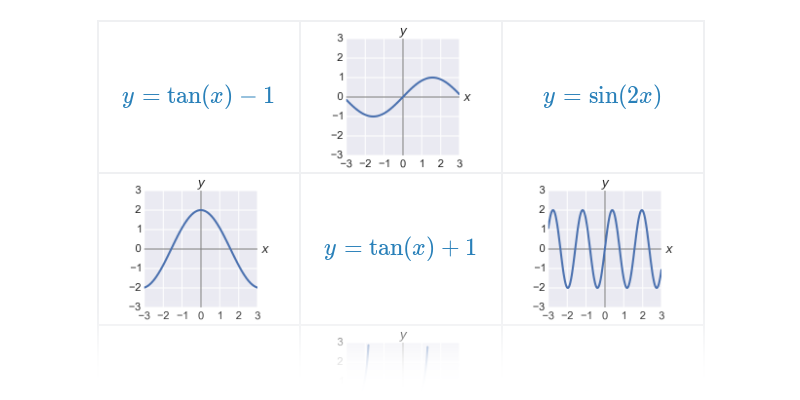
Obrázek ukazuje grafy několika úprav funkce \sin x.
| \sin(x+1) | posun grafu ve směru osy x |
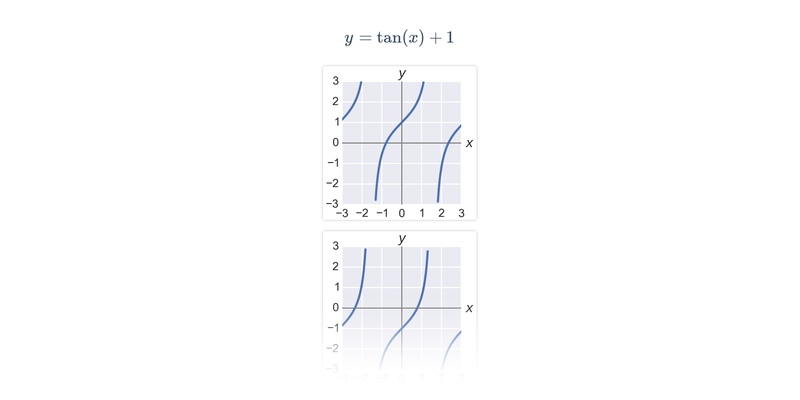
| \sin(x)+1 | graf je posunutý ve směru osy y |
| \sin 2x | funkce má změněnou délku periody (v uvedeném příkladu je graf „zmáčknutý“ ve směru osy x, funkce má poloviční délku periody oproti \sin x) |
| 2\sin x | změní se maximální a minimální funkční hodnota (v uvedeném příkladu je graf „roztažený“ ve směru osy y na dvojnásobnou výšku) |
Zajímavost: fyzikální popis některých úprav
| \sin(x+1) | graf má posunutou fázi |
| 2\sin x | změnila se velikost amplitudy |
Souhrn mi pomohl
Souhrn mi nepomohl
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Grafy goniometrických funkcí 
Zobrazit souhrn tématu
těžké
Grafy goniometrických funkcí (těžké)
zadání: 44
Typicky zabere: 5 min
Pexeso
Hledání dvojic, které k sobě patří.
Grafy goniometrických funkcí
Zobrazit souhrn tématu
těžké
Grafy goniometrických funkcí (těžké)
zadání: 9
Typicky zabere: 5 min
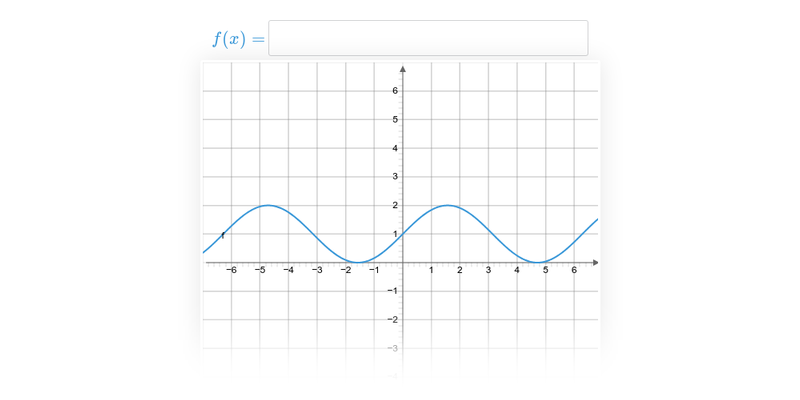
Grafař
Specializované cvičení na práci s grafem a funkcemi.
Grafy goniometrických funkcí
Zobrazit souhrn tématu
těžké
Grafy goniometrických funkcí (těžké)
zadání: 38
Typicky zabere: 11 min
