Grafy lineárních lomených funkcí

G4H

umime.to/G4H

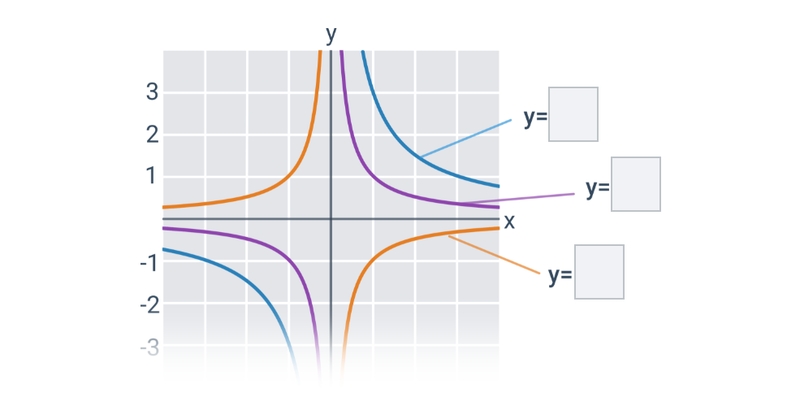
Grafem lineární lomené funkce je hyperbola, která má asymptoty rovnoběžné se souřadnými osami x a y.

Asymptota rovnoběžná s osou y prochází bodem, který nepatří do definičního oboru a má tedy rovnici: x =-\frac{d}{c}.

Pro nalezení rovnice asymptoty rovnoběžné s osou x vydělíme čitatele a jmenovatele a funkční předpis y =\frac{ax+b}{cx+d} upravíme na tvar y =\frac{a}{c}+\frac{n}{ax+b}. Asymptota rovnoběžná s osou x má rovnici: y =\frac{a}{c}.

Průsečík grafu s osou x je bod, pro který ax+b=0. V tomto bodě je hodnota funkce nulová, tedy čitatel zlomku \frac{ax+b}{cx+d} je nulový.

Průsečík grafu s osou y je bod, který dostaneme dosazením hodnoty x=0 do funkčního předpisu.

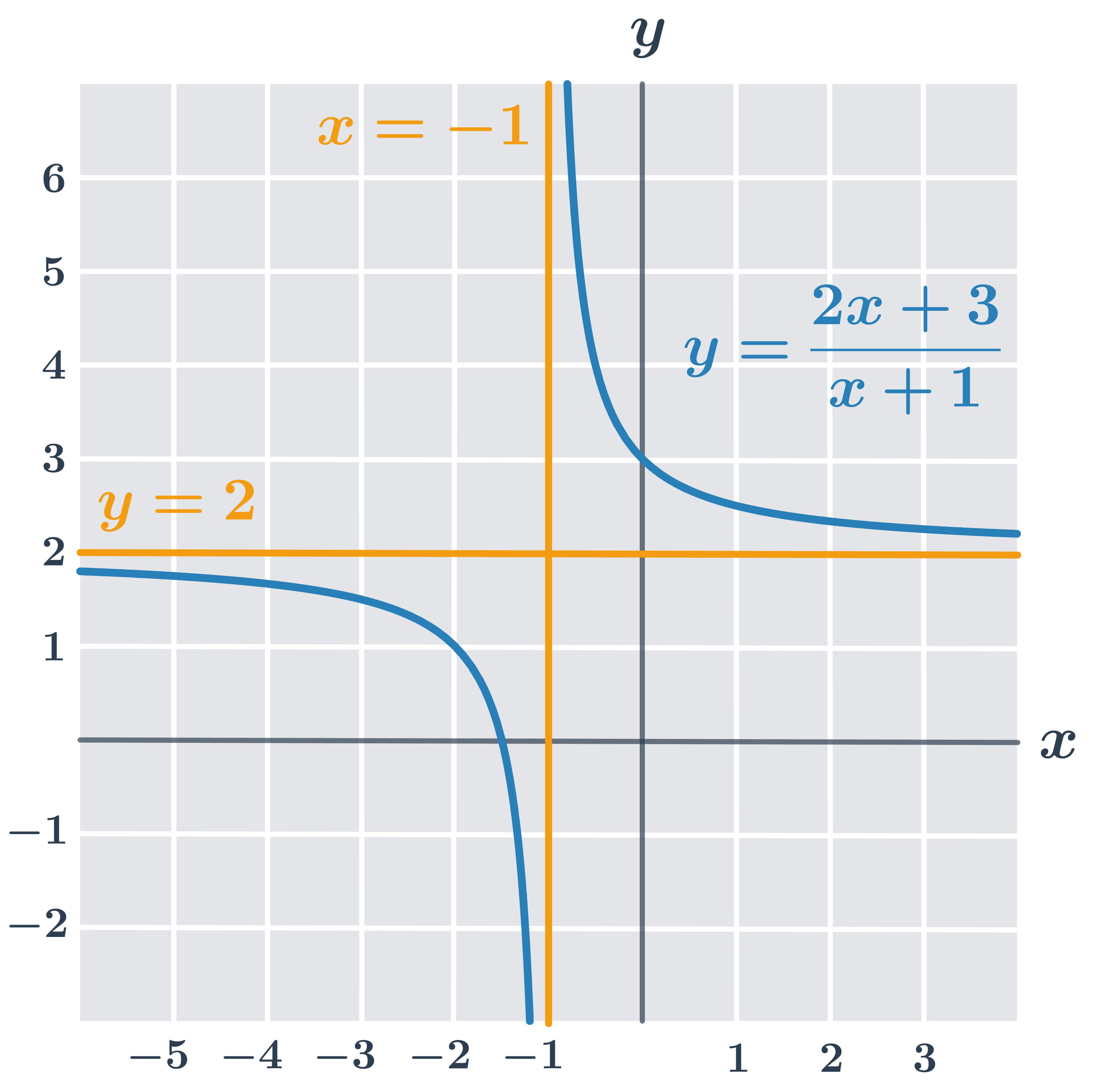
Příklad – funkce y =\frac{2x+3}{x+1}

Rozeberme si graf funkce z obrázku výše:

definiční obor D(f)=\R - \{-1\}, protože x+1\neq0
asymptota rovnoběžná s osou y má rovnici x =-1 (pro x=-1 není funkce definovaná, toto číslo neleží v jejím definičním oboru)
asymptota rovnoběžná s osou x má rovnici y =2, což zjistíme úpravou funkčního předpisu: y =\frac{2x+3}{x+1}=2+\frac{1}{x+1}
průsečík grafu s osou x je bod [0;-\frac{3}{2}] (řešení rovnice: 2x+3=0)
průsečík grafu s osou y je bod [3;0], dosazením hodnoty x=0 do y =\frac{2x+3}{x+1}