Lomené výrazy: úpravy a výpočty

GXJ

umime.to/GXJ

Stáhnout QR kód

S lomenými výrazy počítáme podobně jako se zlomky, pouze musíme úpravy provádět s mnohočleny.

Příklad: úprava výrazu \frac{3}{4x} + \frac{2}{3x}

Převedeme oba výrazy na společný jmenovatel: \frac{9}{12x} + \frac{8}{12x}.
Sečteme: \frac{9+8}{12x} = \frac{17}{12x}.

Příklad: úprava výrazu \frac{x+y}{x^2-y^2}

Jmenovatel rozepíšeme pomocí vzorce x^2-y^2=(x+y)(x-y).
Dostáváme \frac{x+y}{(x+y)(x-y)}.
Pokrátíme na \frac{1}{x-y}.

Souhrn je skryt.

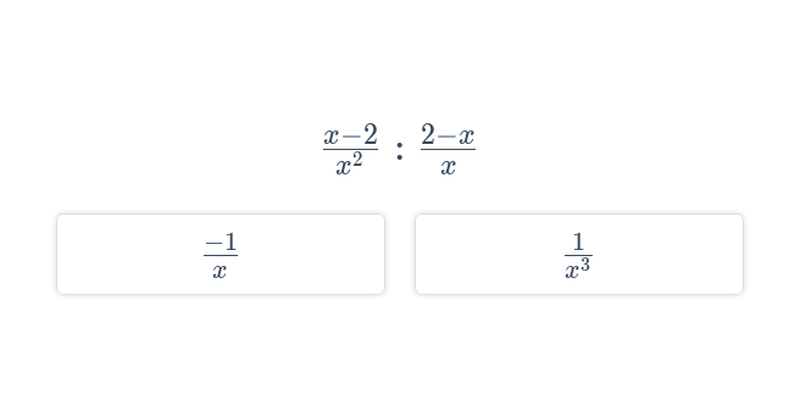
Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Lomené výrazy: úpravy a výpočty

Úpravy lomených výrazů

Rozhodovačka • střední

Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Lomené výrazy: úpravy a výpočty

Početní operace s lomenými výrazy

Krok po kroku • střední

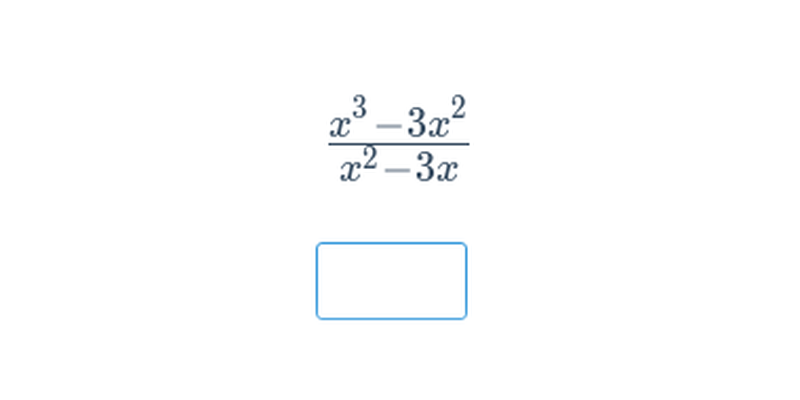
Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Lomené výrazy: úpravy a výpočty

Psaná odpověď • střední

Předcházející

Navazující

Cvičení

Lomené výrazy: úpravy a výpočty

umime.to/GXJ

Rozhodovačka

Úpravy lomených výrazů

Krok po kroku

Početní operace s lomenými výrazy

Psaná odpověď