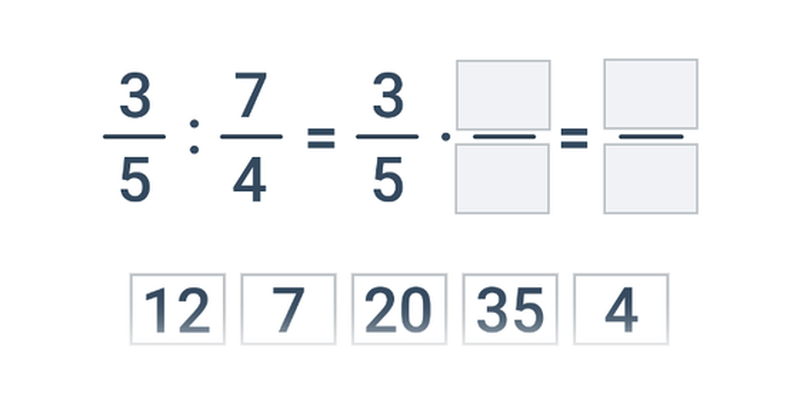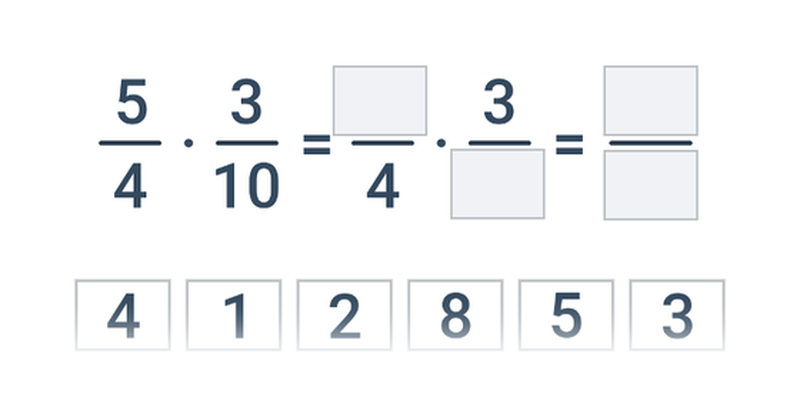Násobení a dělení zlomků

FVO

umime.to/FVO

Násobení zlomků si můžeme představit skrze čokoládu. Pokud násobíme \frac45\cdot \frac23 je to jako bychom brali čtyři z pěti sloupečků a dva ze tří řádků. Kolik čtverečků čokolády takto vezmeme? Osm z patnácti, tedy \frac{8}{15}.

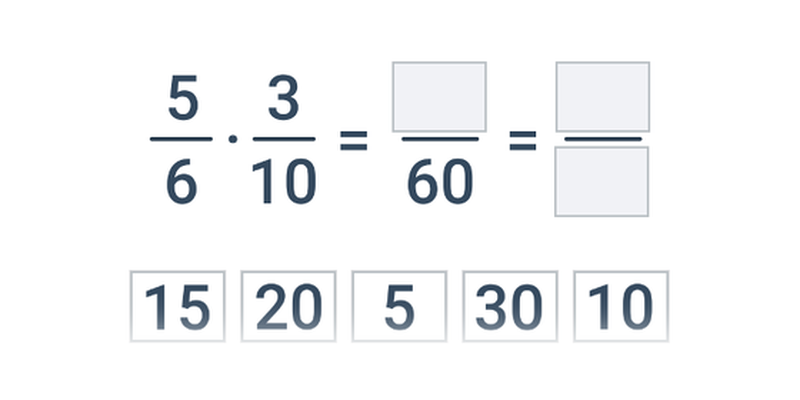
Při násobení zlomků tedy prostě vynásobíme čitatele prvního zlomku a čitatele druhého zlomku a dostaneme výsledný čitatel, podobně pro jmenovatele: \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d}. Pokud si chceme ušetřit násobení velkých čísel, můžeme zlomky krátit, a to i „do kříže“.

Příklady násobení zlomků

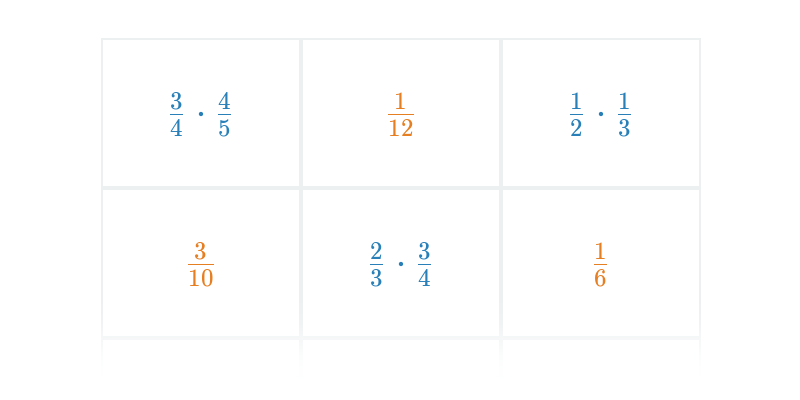
\frac{2}{3}\cdot\frac{1}{5} = \frac{2\cdot 1}{3\cdot 5}=\frac{2}{15}
\frac{2}{3}\cdot\frac{3}{4} = \frac{2\cdot 3}{3\cdot 4}=\frac{2}{4}=\frac{1}{2} (všimněte si, že neroznásobujeme, ale hned krátíme)

Dělení zlomků je to stejné jako násobení převráceným zlomkem: \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}.

Příklady dělení zlomků

\frac13:\frac12 =\frac13\cdot \frac21 = \frac23
\frac{2}{5}:\frac{3}{4}=\frac{2}{5}\cdot \frac{4}{3} = \frac{2\cdot 4}{5\cdot 3} = \frac{8}{15}

Souhrn je skryt.

Přesouvání

Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.

Násobení a dělení zlomků

Přesouvání • lehké

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Násobení a dělení zlomků

Rozhodovačka • střední

Pexeso

Hledání dvojic, které k sobě patří.

Násobení a dělení zlomků

Pexeso • střední

Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Násobení a dělení zlomků

Krok po kroku • střední

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Násobení a dělení zlomků

Psaná odpověď • střední

Předcházející

Navazující

Cvičení

Násobení a dělení zlomků

umime.to/FVO

Přesouvání