Výpočty se zlomky

Základní výpočty se zlomky jsou následující:

Krácení zlomků

• Zlomky se krátí tak, že čitatel i jmenovatel vydělíme jejich společným dělitelem.
• Zlomek \frac{9}{12} můžeme zkrátit na \frac{3}{4}, protože čitatel i jmenovatel mají společný dělitel 3.

Sčítání a odčítání zlomků

• Pro sčítání a odčítání zlomků je nutné převést zlomky na společný jmenovatel.
• \frac{1}{4} + \frac{1}{6} převedeme na společný jmenovatel 12 a dostaneme \frac{3}{12} + \frac{2}{12} = \frac{5}{12}.

Násobení a dělení zlomků

• Násobení se provádí tak, že vynásobíme čitatele i jmenovatele mezi sebou.
• \frac{2}{3} \cdot \frac{3}{4} = \frac{6}{12} = \frac{1}{2}
• Dělení se provádí násobením převráceného zlomku.
• \frac{2}{3} : \frac{3}{4} = \frac{2}{3} \cdot \frac{4}{3} = \frac{8}{9}

Zlomky a procenta

• Převod zlomku na procenta se provádí pomocí násobení 100.
• \frac{3}{4} = 0{,}75 = 75 \%

Zlomky a desetinná čísla

• Zlomky převedeme na desetinná čísla tak, že čitatele vydělíme jmenovatelem. Naopak desetinné číslo lze převést na zlomek pomocí roznásobení mocninami desítky.
• \frac{2}{5} = 2 : 5 = 0{,}4
• 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100}, což po zkrácení dává \frac{1}{4}

Kombinace operací se zlomky

• Zadání kombinující různé aritmetické operace se zlomky.

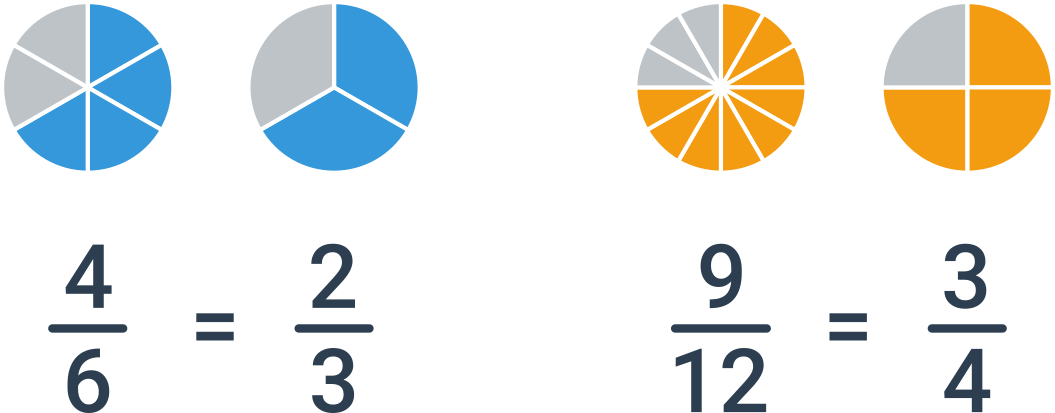
Stejnou hodnotu můžeme vyjádřit mnoha zlomky, například \frac23 = \frac46 = \frac{10}{15} = \frac{200}{300}. Jen jedno možné vyjádření ovšem považujeme za základní tvar. Zlomek je v základním tvaru, pokud jsou čitatel a jmenovatel nesoudělní, tj. nemají žádného společného dělitele kromě jedničky. V uvedeném příkladě je v základním tvaru zlomek \frac23.

Jako krácení zlomku se označuje operace, kdy čitatele i jmenovatele vydělíme stejným, nenulovým číslem. Krácení zachovává hodnotu zlomku. Pokud chceme zlomek převést do základního tvaru, krátíme největším společným dělitelem čitatele a jmenovatele.

Opačnou operací je rozšíření zlomku, kdy čitatele i jmenovatele vynásobíme stejným nenulovým číslem. Rozšíření zlomku se používá při sčítání a odčítání zlomků.

Než se pustíme do sčítání zlomků, je dobré mít jasno v tom, co je čitatel („to nahoře“) a jmenovatel („to dole“). Ve zlomku \frac{3}{7} je 3 čitatel, 7 jmenovatel.

Sčítání zlomků se stejným jmenovatelem

Pokud mají sčítané zlomky stejného jmenovatele, stačí prostě sečíst čitatele. Jmenovatele necháme stejného, tedy \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.

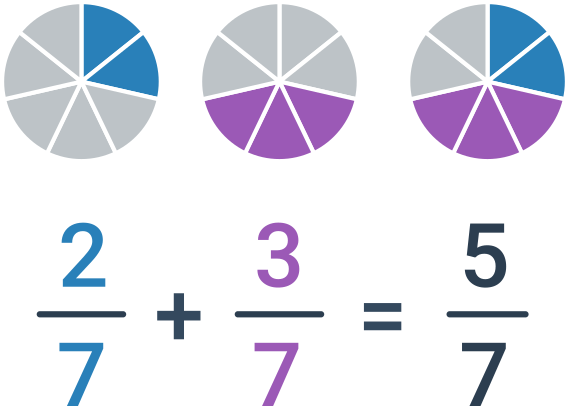
Sčítání zlomků s různými jmenovateli

Pokud mají sčítané zlomky různého jmenovatele, musíme je nejprve rozšířit tak, aby měly stejného jmenovatele. Nejvýhodnější je rozšířit zlomky na nejmenší společný násobek původních jmenovatelů. Jakmile mají zlomky stejného jmenovatele, sečteme je výše uvedeným postupem.

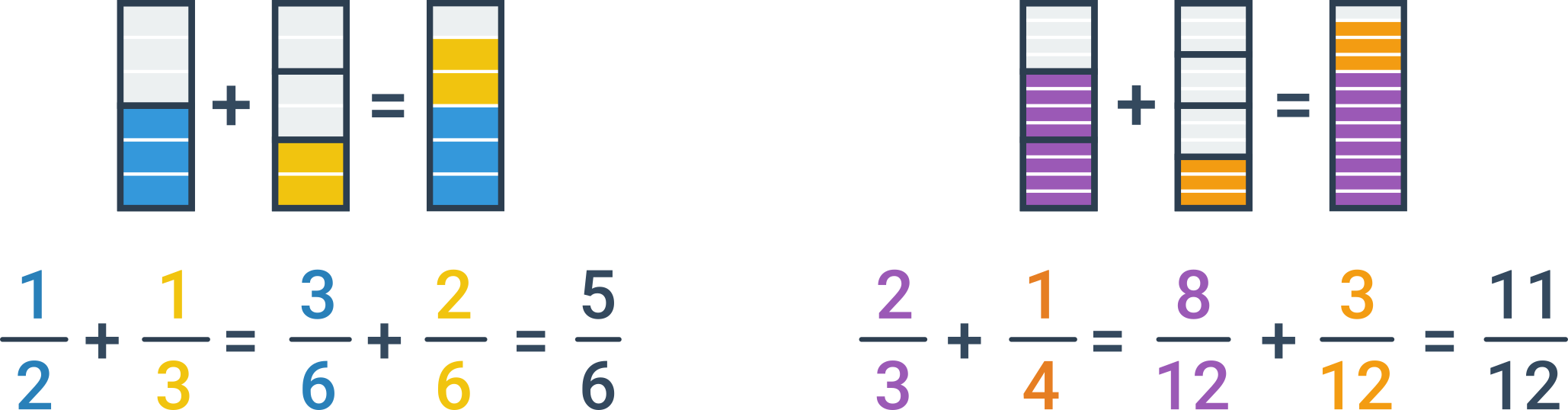
Úpravy a odčítání

Výsledný zlomek většinou ještě krátíme, abychom dostali výsledek v základním tvaru. Odčítání zlomků funguje stejným způsobem.

Příklady

Pracovní list

Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:

• Sčítání a odčítání zlomků: zadání
• Sčítání a odčítání zlomků: řešení

Násobení zlomků si můžeme představit skrze čokoládu. Pokud násobíme \frac45\cdot \frac23 je to jako bychom brali čtyři z pěti sloupečků a dva ze tří řádků. Kolik čtverečků čokolády takto vezmeme? Osm z patnácti, tedy \frac{8}{15}.

Při násobení zlomků tedy prostě vynásobíme čitatele prvního zlomku a čitatele druhého zlomku a dostaneme výsledný čitatel, podobně pro jmenovatele: \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d}. Pokud si chceme ušetřit násobení velkých čísel, můžeme zlomky krátit, a to i „do kříže“.

Dělení zlomků je to stejné jako násobení převráceným zlomkem: \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}.

Převod procent na zlomek v základním tvaru

Jedno procento je to stejné jako jedna setina, tj. \frac{1}{100}. Vynásobíme tedy číslo (udávající procenta) zlomkem \frac{1}{100} a následně zlomek vykrátíme (pomocí dělení největším společným dělitelem) na základní tvar. Příklady:

• 45\ \% = 45 \cdot \frac{1}{100} = \frac{45}{100} = \frac{5\cdot 9}{5\cdot 20}= \frac{9}{20}
• 12\ \% = 12 \cdot \frac{1}{100} = \frac{12}{100} = \frac{4\cdot 3}{4\cdot 25}= \frac{3}{25}

Převod zlomku na procenta

Chceme zlomek \frac{a}{b} vyjádřit jako p\ \%. Protože jedno procento je jedna setina, musí tedy platit \frac{a}{b} = \frac{p}{100}. Takže p = \frac{a}{b}\cdot 100. Stačí tedy zlomek vynásobit číslem 100. Příklady:

• \frac{2}{5} = \frac{2}{5} \cdot 100\ \% = \frac{200}{5}\ \% = 40\ \%
• \frac{3}{20} = \frac{3}{20} \cdot 100\ \% = \frac{300}{20}\ \% = 15\ \%

Převod desetinného čísla na zlomek

Desetinné číslo roznásobíme pomocí mocniny desítky tak, abychom se „zbavili“ desetinné čárky. Následně zlomek vykrátíme (největším společným dělitelem), abychom dostali zlomek v základním tvaru. Příklady:

• 1{,}5 = 1{,}5\cdot \frac{10}{10} = \frac{1{,}5\cdot 10}{10} = \frac{15}{10} = \frac{3}{2}

• 1{,}25 = 1{,}25 \cdot \frac{100}{100} = \frac{1{,}25\cdot 100}{100} = \frac{125}{100} = \frac{5}{4}

Počítání nám může usnadnit, když si zapamatujeme některé užitečné převody, s jejichž pomocí vhodné úvahy vyřešit i další příklady:

• 0{,}01 = \frac{1}{100}

• 0{,}1 = \frac{1}{10}

• 0{,}2 = \frac{1}{5}

• 0{,}25 = \frac{1}{4}

• 0{,}333\ldots = \frac{1}{3}

• 0{,}5 = \frac{1}{2}

Převod zlomku na desetinné číslo

Význam zlomku je prostě podíl čitatele a jmenovatele. Zlomek tedy vyjádříme jako desetinné číslo prostě tak, že podělíme čitatele jmenovatelem (může se hodit postup pro „dělení pod sebou“). Příklady:

• \frac{3}{4} = 3:4 = 0{,}75

• \frac{6}{5} = 6:5 = 1{,}2

• \frac{3}{20} = 3:20 = 0{,}15