Záporné mocniny

FZ9

umime.to/FZ9

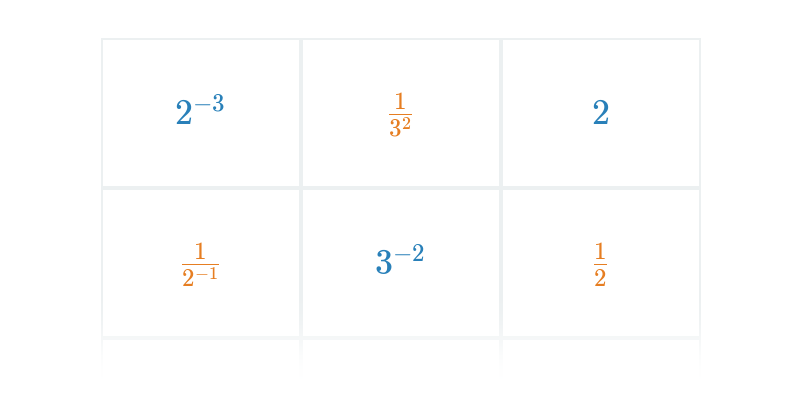
Mocnina se záporným exponentem odpovídá převrácené hodnotě příslušné mocniny s kladným exponentem. Tedy x^{-n} = \frac{1}{x^n}. Toto pravidlo je důsledkem vlastnosti násobení x^n\cdot x^m = x^{n+m}. Musí tedy platit x^{-n} \cdot x^n = x^{-n+n} = x^0 = 1.

Příklady:

2^{-1} = \frac{1}{2} = 0,5
2^{-2} = \frac{1}{2^2} = \frac{1}{4} = 0,25
10^{-2} = \frac{1}{10^2} = 0,01
0,5^{-1} = 2^1 = 2

Souhrn je skryt.

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Záporné mocniny

Rozhodovačka • těžké

Pexeso

Hledání dvojic, které k sobě patří.

Záporné mocniny

Pexeso • těžké

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Záporné mocniny

Psaná odpověď • těžké

Předcházející

Navazující

Cvičení

Záporné mocniny

umime.to/FZ9

Rozhodovačka