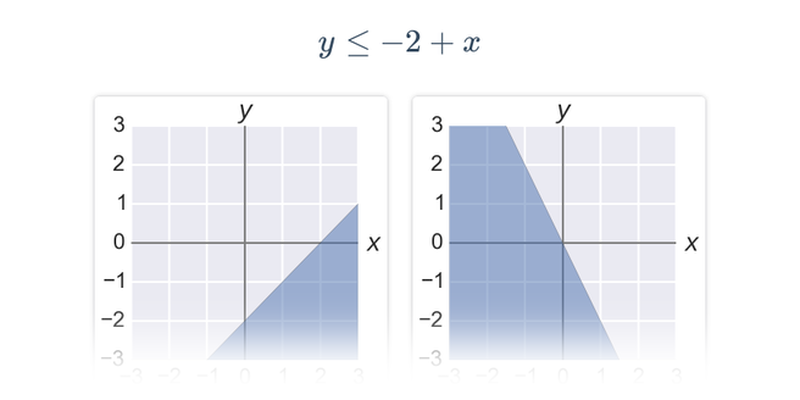
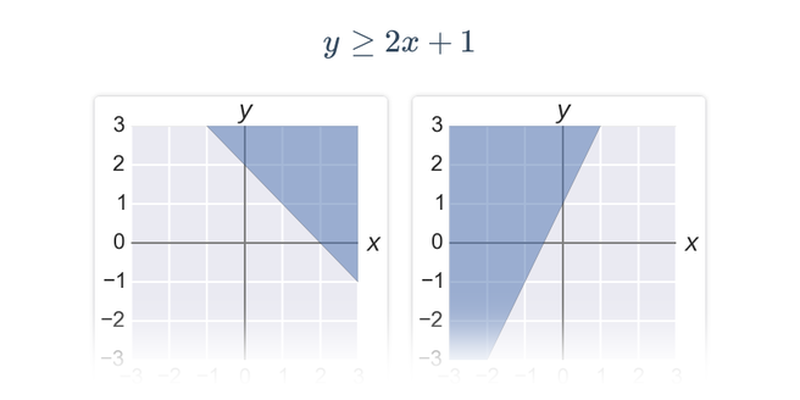
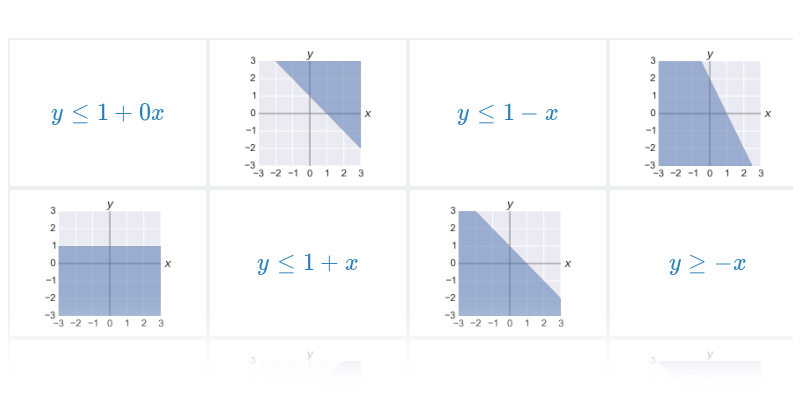
Grafem funkce dané předpisem y= ax+b je přímka. Množinou řešení lineární nerovnice budou všechny body [x,y] ležící v polorovině s hraniční přímkou y= ax+b. Může nastat jedna ze čtyř možností:
| y\geq ax+b | Nerovnost splňují všechny body v rovině, které leží přímo na přímce dané rovnicí y=ax+b nebo “nad” touto přímkou (se souřadnicí y větší než ax+b). |
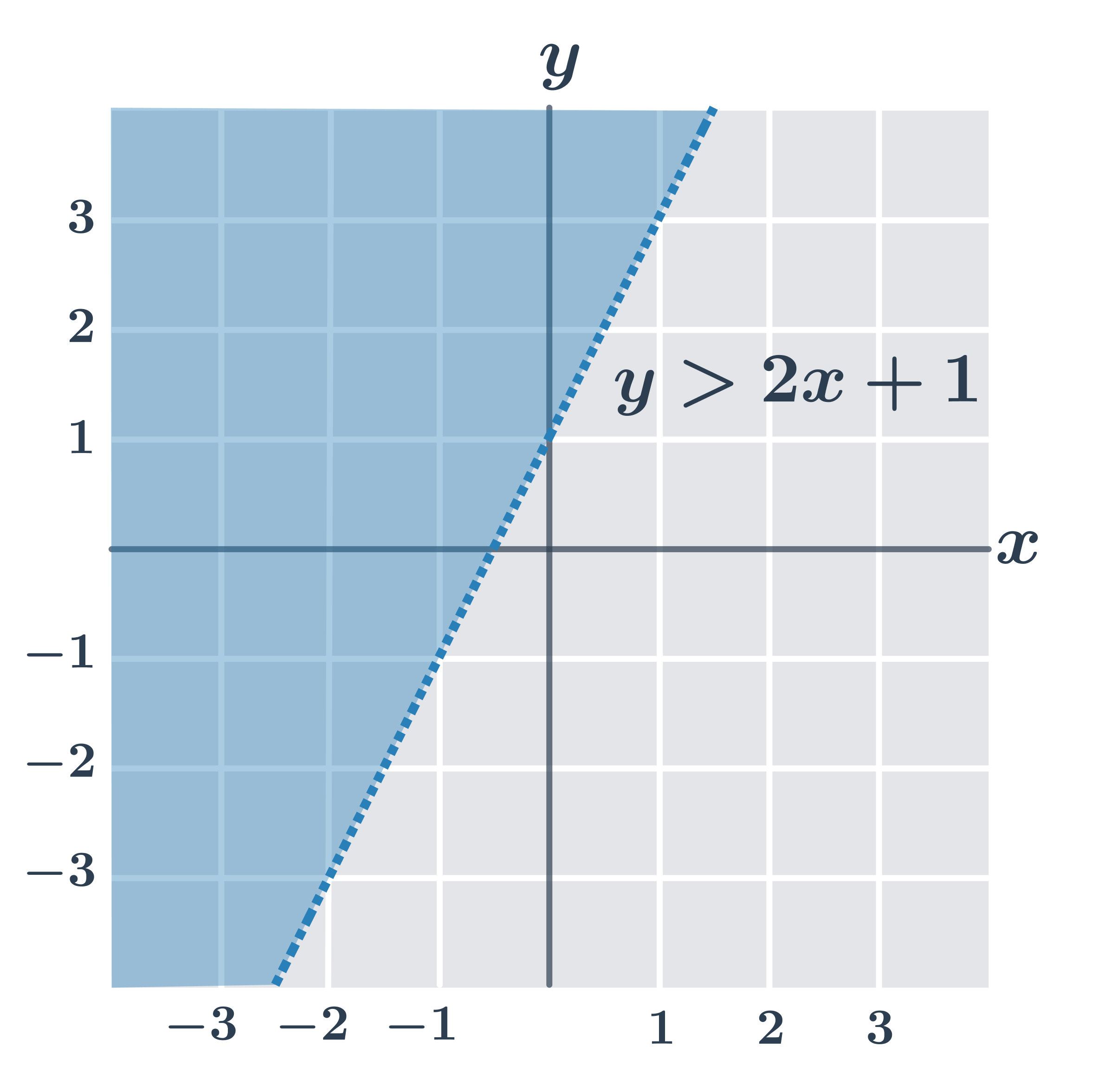
| y \gt ax+b | Nerovnost splňují všechny body v rovině, které leží “nad” přímkou o rovnici y=ax+b. |
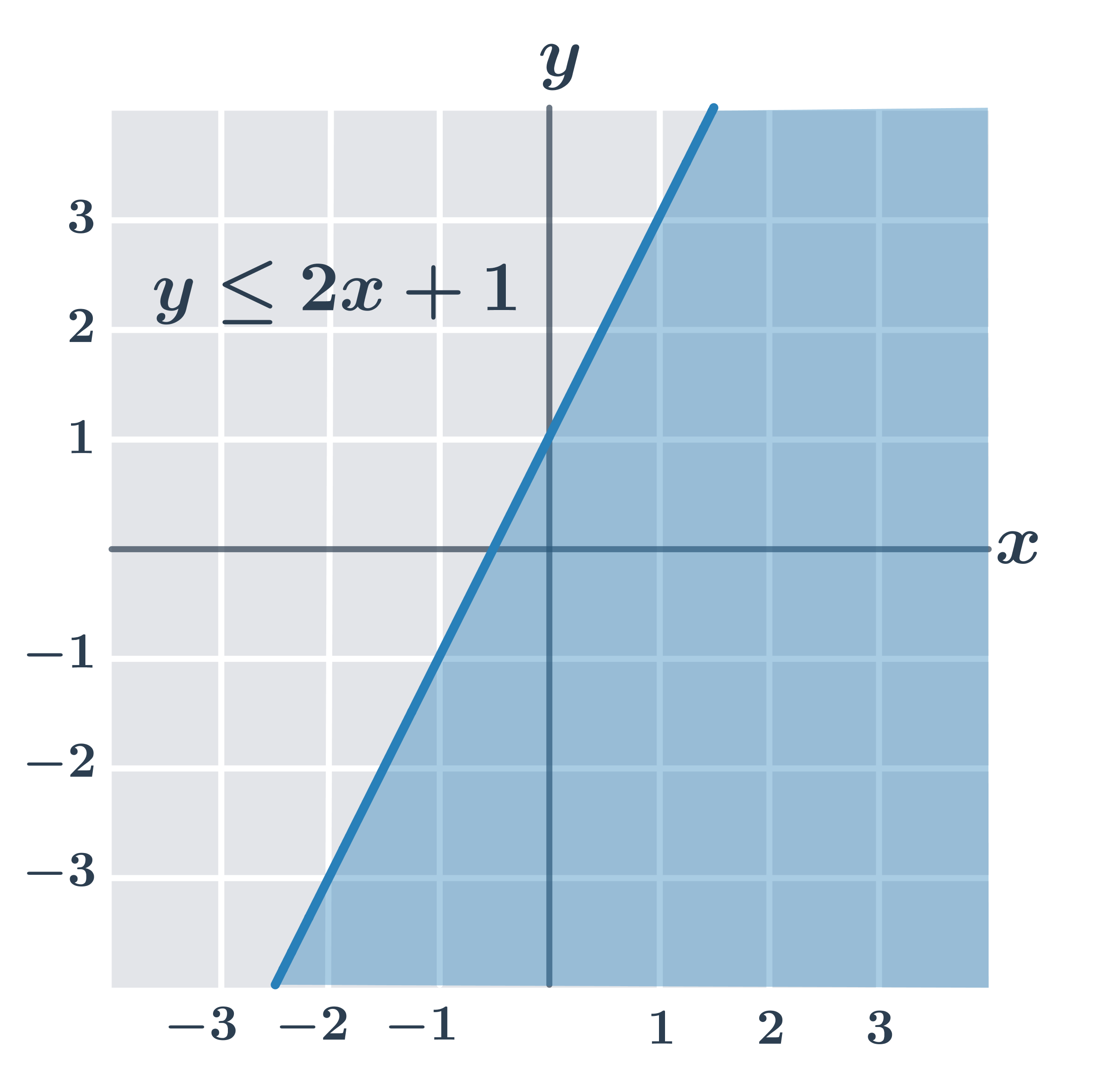
| y\leq ax+b | Nerovnost splňují všechny body v rovině, které leží na přímce o rovnici y=ax+b nebo “pod” touto přímkou (se souřadnicí y menší než ax+b). |
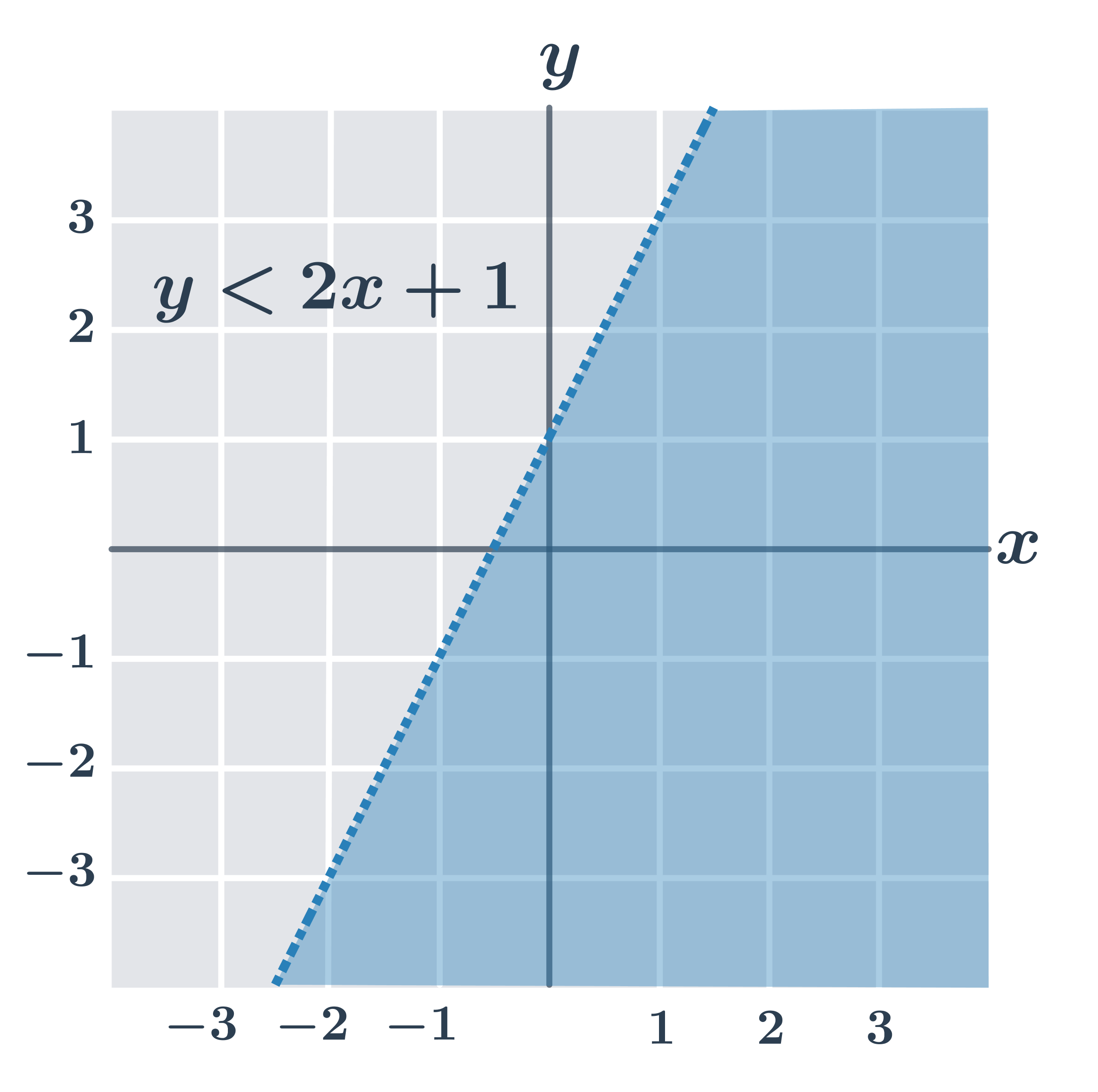
| y \lt ax+b | Nerovnost splňují všechny body v rovině, které leží “pod” přímkou o rovnici y=ax+b. |
Na obrázcích jsou řešení všech typů lineárních nerovnic (všimněte si, že pokud je v nerovnici jen znaménko \gt nebo \lt, body přímo na hraniční přímce lineární nerovnici nesplňují).
- y\geq 2x+1
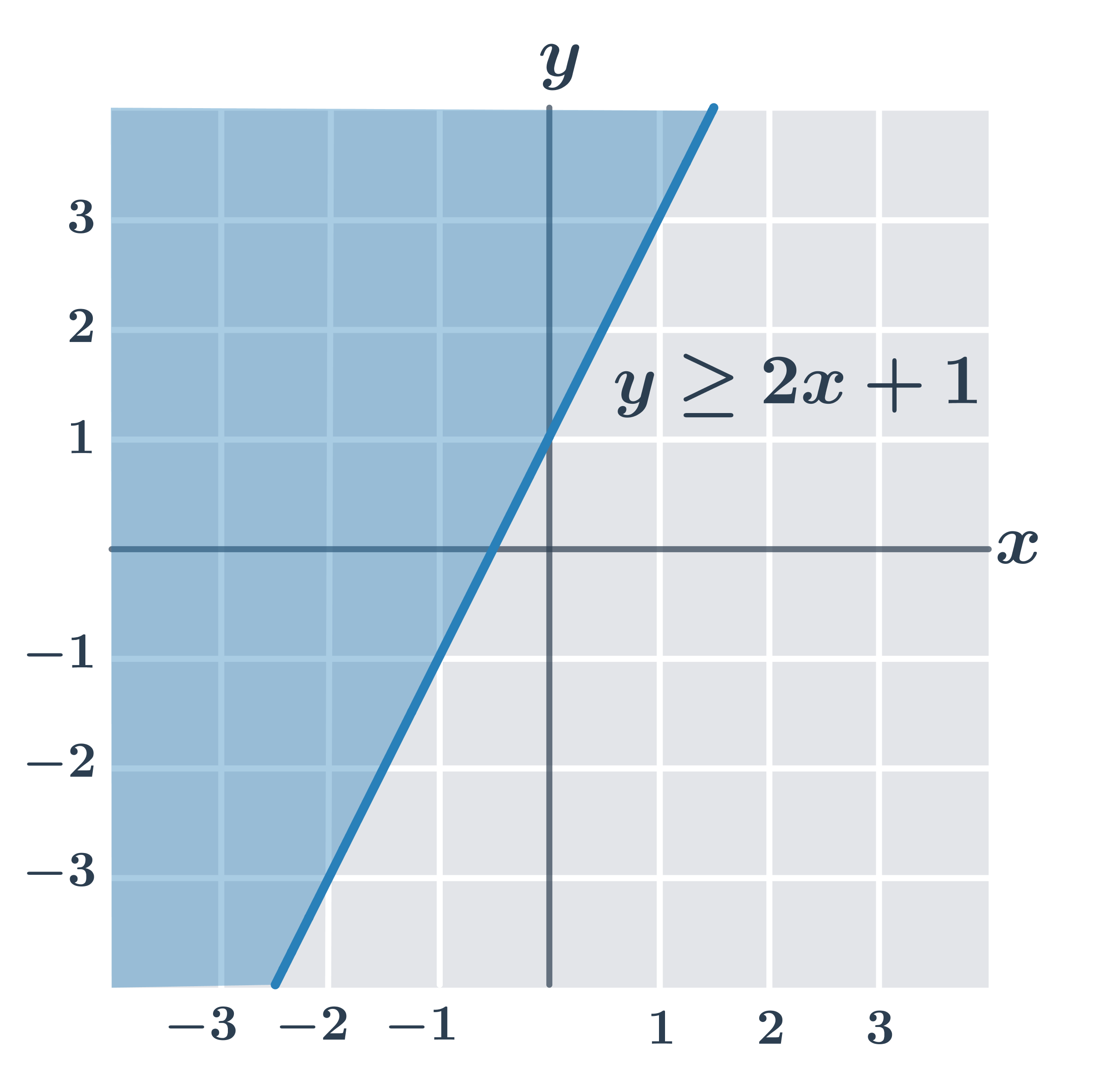
- y \gt 2x+1
- y\leq 2x+1
- y \lt 2x+1
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.