Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Výpis souhrnů
Objem
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Objem krychle a kvádru
Objem kvádru s délkami hran a,b,c je: V=a\cdot b\cdot c
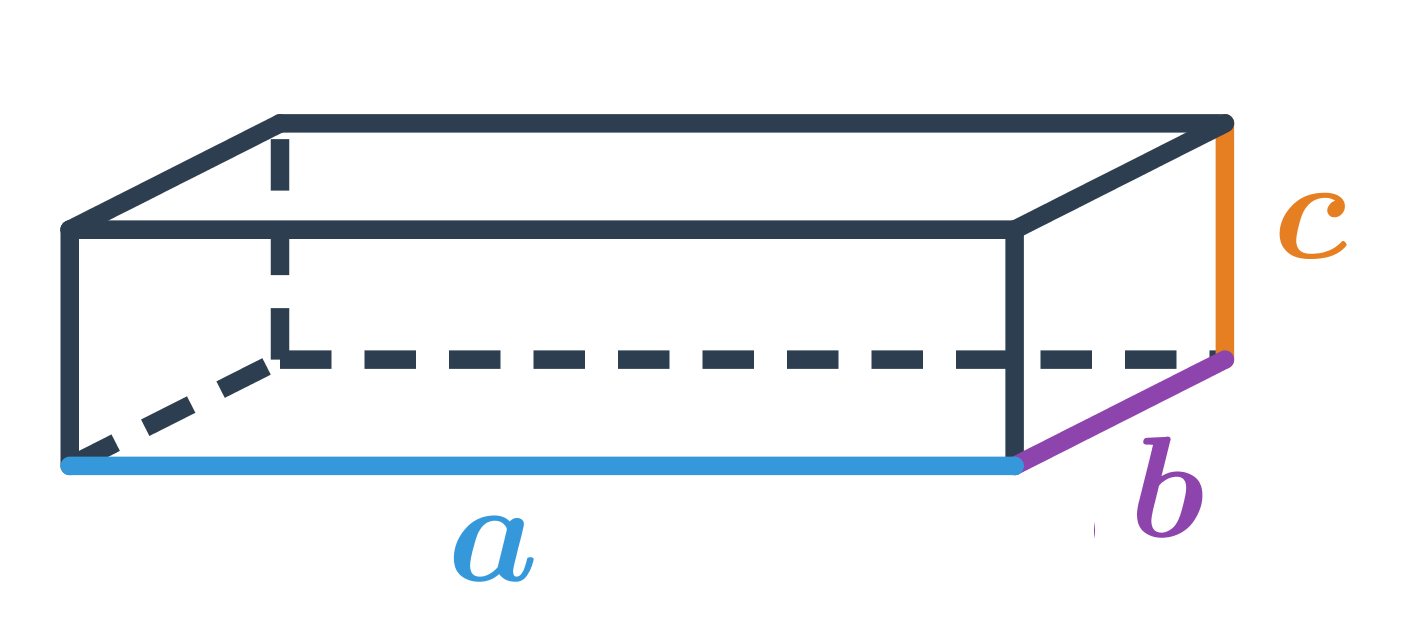
Objem krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako objem kvádru s a=b=c, tedy: V=a\cdot a\cdot a=a^3
NahoruObjem hranolu
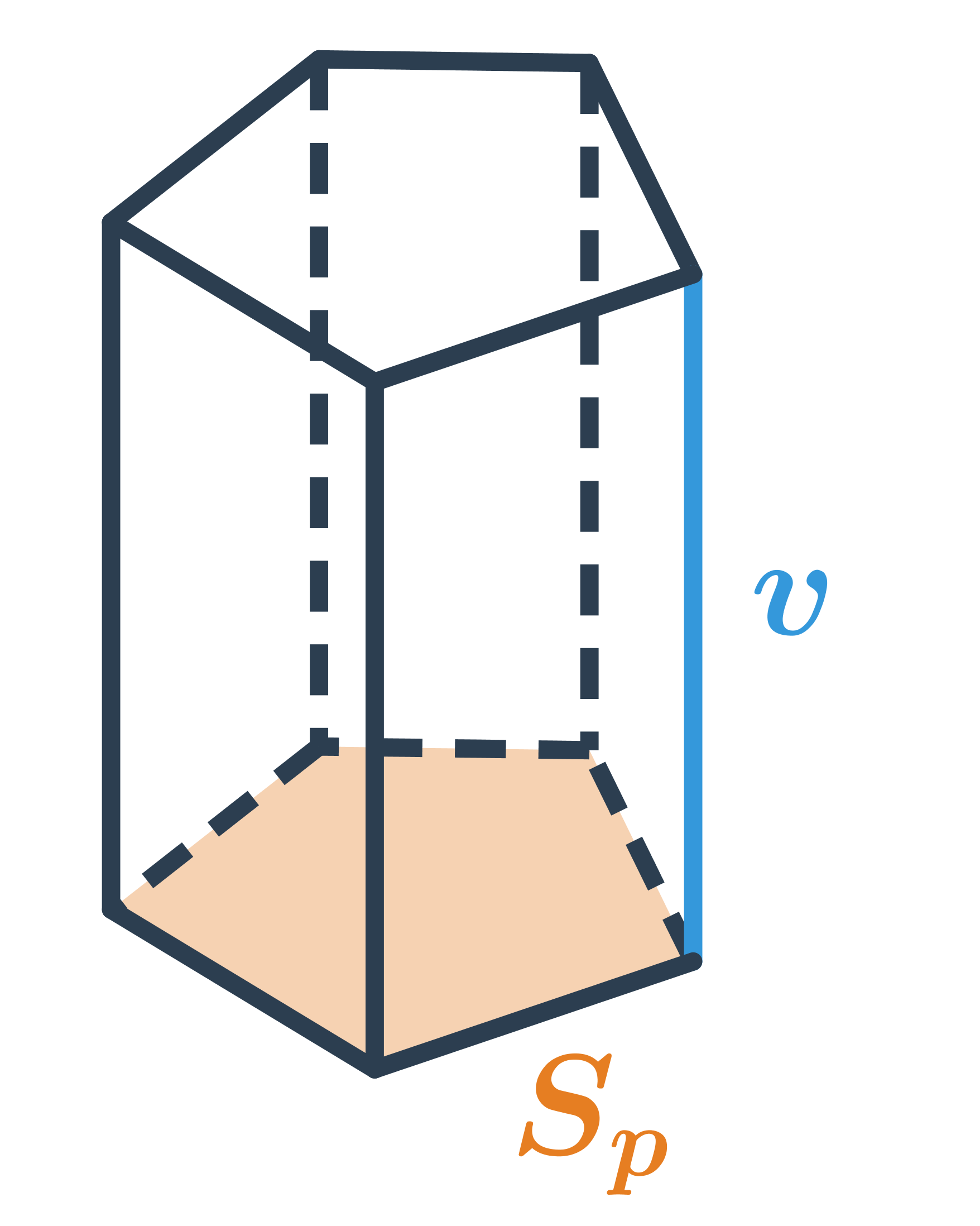
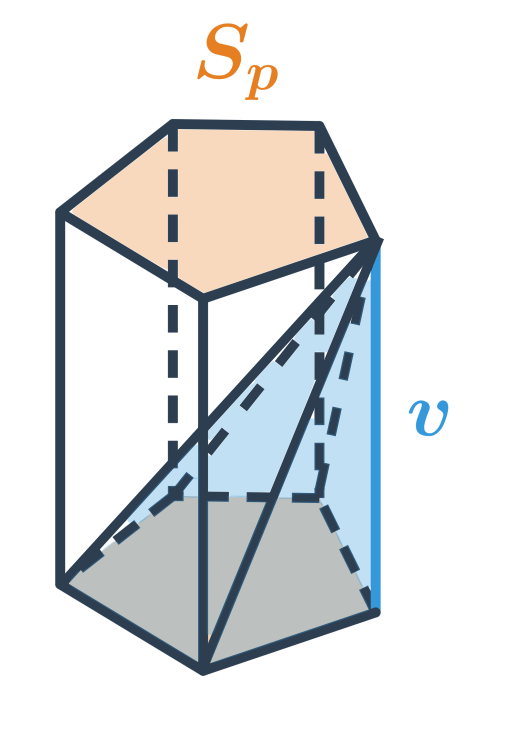
Objem hranolu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=S_p \cdot v.
Objem jehlanu
Objem jehlanu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=\frac{1}{3} S_p \cdot v.
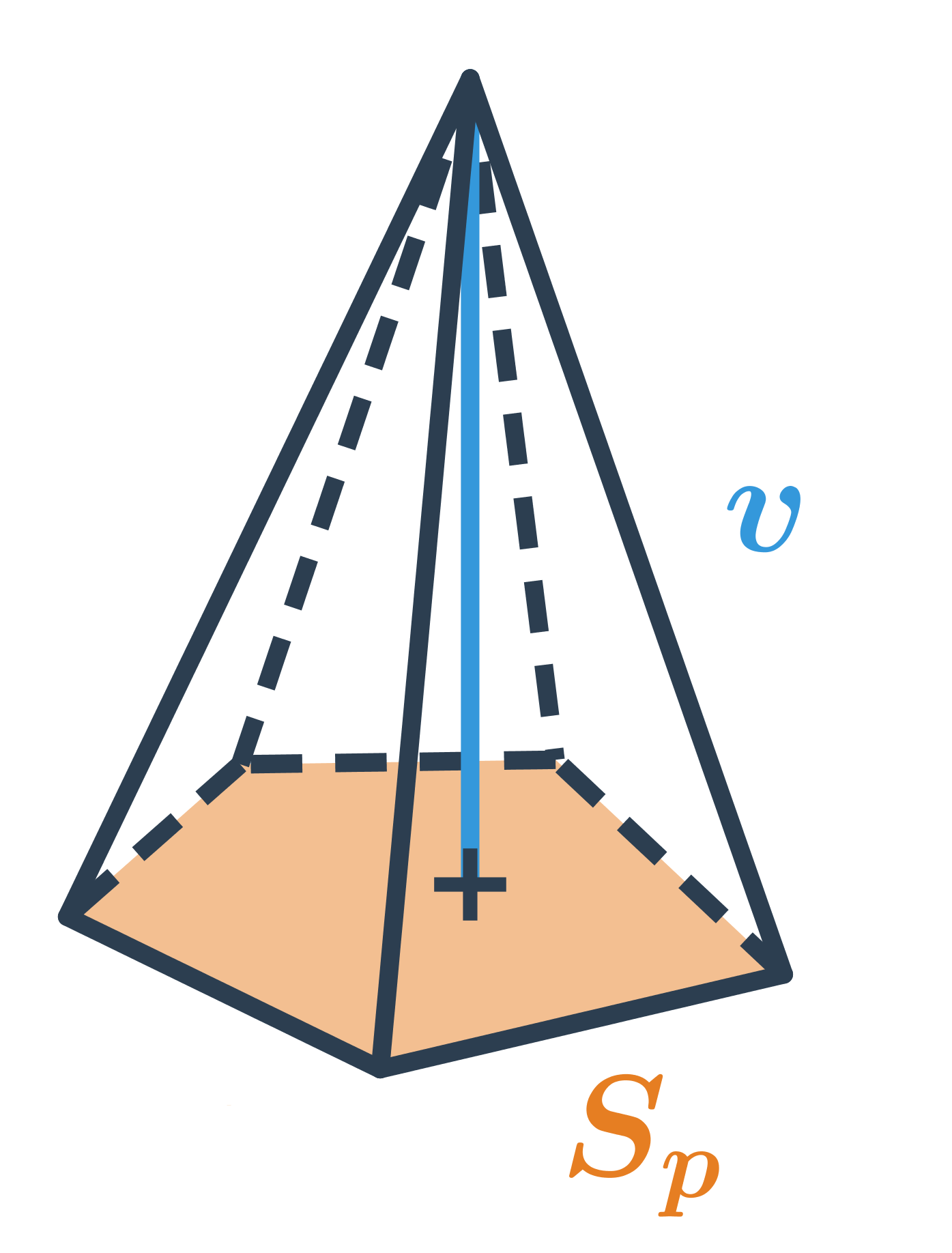
Oproti hranolu se stejnou výškou a tvarem podstavy má jehlan třikrát menší objem.
Objem hranatých těles
Vzorce pro objem „hranatých“ těles vychází z obsahu podstavy a výšky tělesa.
Objem libovolného hranolu je součin obsahu podstavy a výšky: V=S_p\cdot v.
Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = abc. Objem krychle vypočítáme stejným způsobem. Protože v krychli jsou všechny hrany stejně dlouhé, výraz se zjednoduší na V = a^3.
Příklad: objem krychle
Určete objem krychle o hraně délky 4 m.
- Objem krychle o hraně délky a spočítáme jako V=a^3.
- Dosadíme za a známou délku hrany.
- Takže daná krychle má objem V = 4^3 = 64 m³.
Délka hrany je zadaná v metrech, proto je výsledný objem krychle v metrech krychlových.
Příklad: objem kvádru
Určete objem kvádru s hranami 3, 6 a 10 cm.
- Objem kvádru s hranami a,b,c spočítáme jako V=a\cdot b\cdot c.
- Dosadíme za a,b,c známé délky hran.
- Takže daný kvádr má objem V = 3\cdot 6 \cdot 10 = 180 cm³.
Délky hran jsou zadány v centimetrech, proto je výsledný objem kvádru v centimetrech krychlových.
Objem jehlanu je jedna třetina součinu obsahu podstavy a výšky, tj. V=\frac{1}{3}S_p\cdot v. Pro pravidelný čtyřboký jehlan pak tedy V=\frac{1}{3} a^2v.
Příklad: objem pravidelného čtyřbokého jehlanu
Určete objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany 6 cm a výškou 4 cm.
- Objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany a a výškou v spočítáme jako V=\frac{1}{3} \cdot a^2 \cdot v.
- Dosadíme za a a v známé hodnoty.
- Takže daný jehlan má objem V=\frac{1}{3} 6^2 \cdot 4 = 48 cm³.
Délka hran podstavy a velikost výšky jsou zadány v centimetrech, proto je výsledný objem jehlanu v centimetrech krychlových.
Objem válce
Objem válce s poloměrem podstavy r a výškou v spočítáme jako: V=\pi \cdot r^2 \cdot v
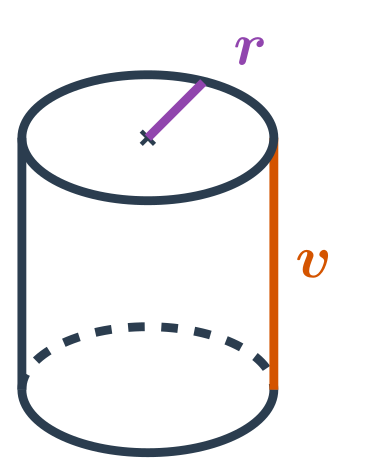
Platí V=S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
NahoruObjem kužele
Objem kužele s poloměrem podstavy r a výškou v spočítáme jako: V=\frac{1}{3} \pi \cdot r^2 \cdot v
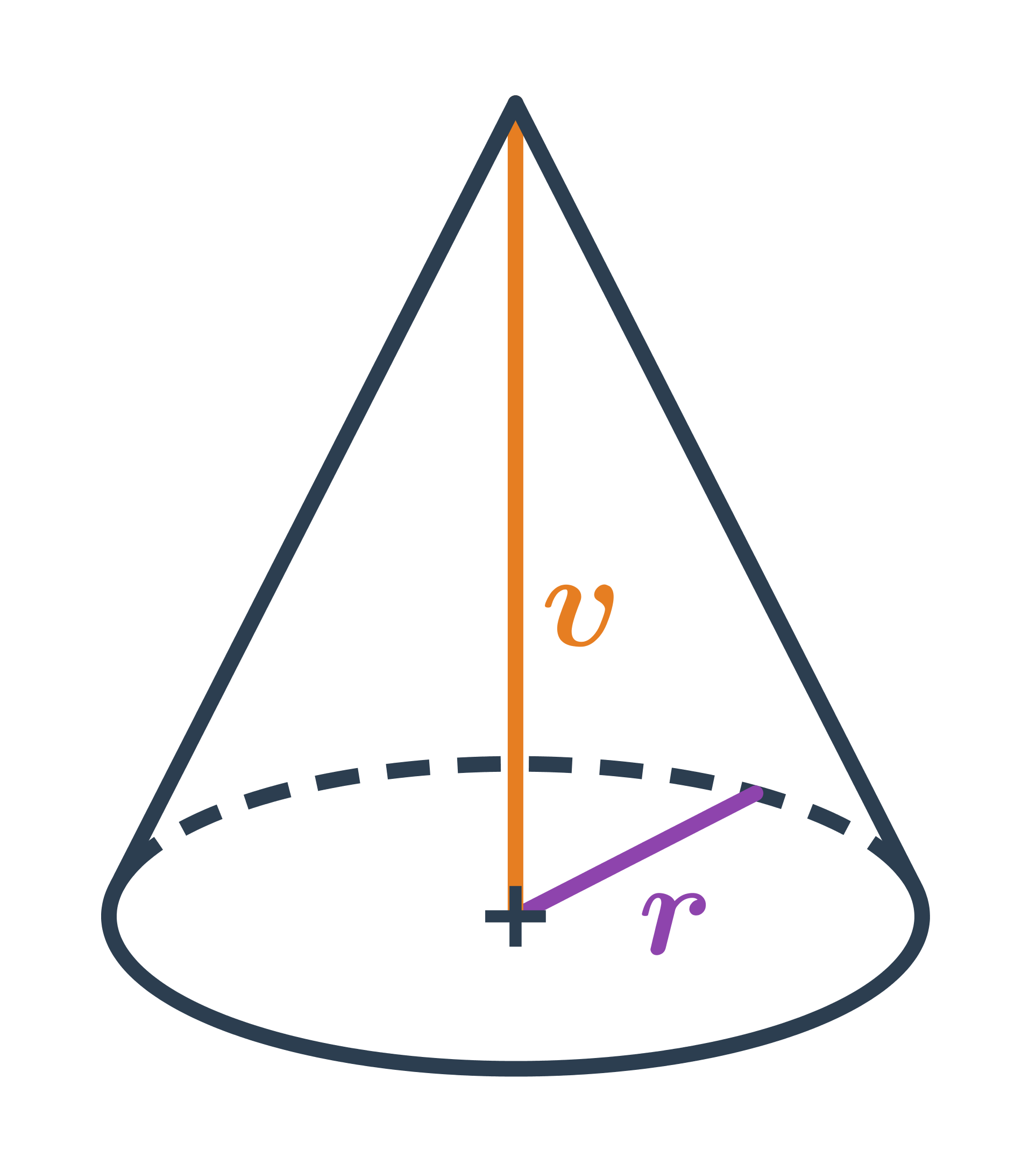
Pro kužel platí V=\frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
Oproti válci se stejnou výškou a poloměrem podstavy má kužel třikrát menší objem.
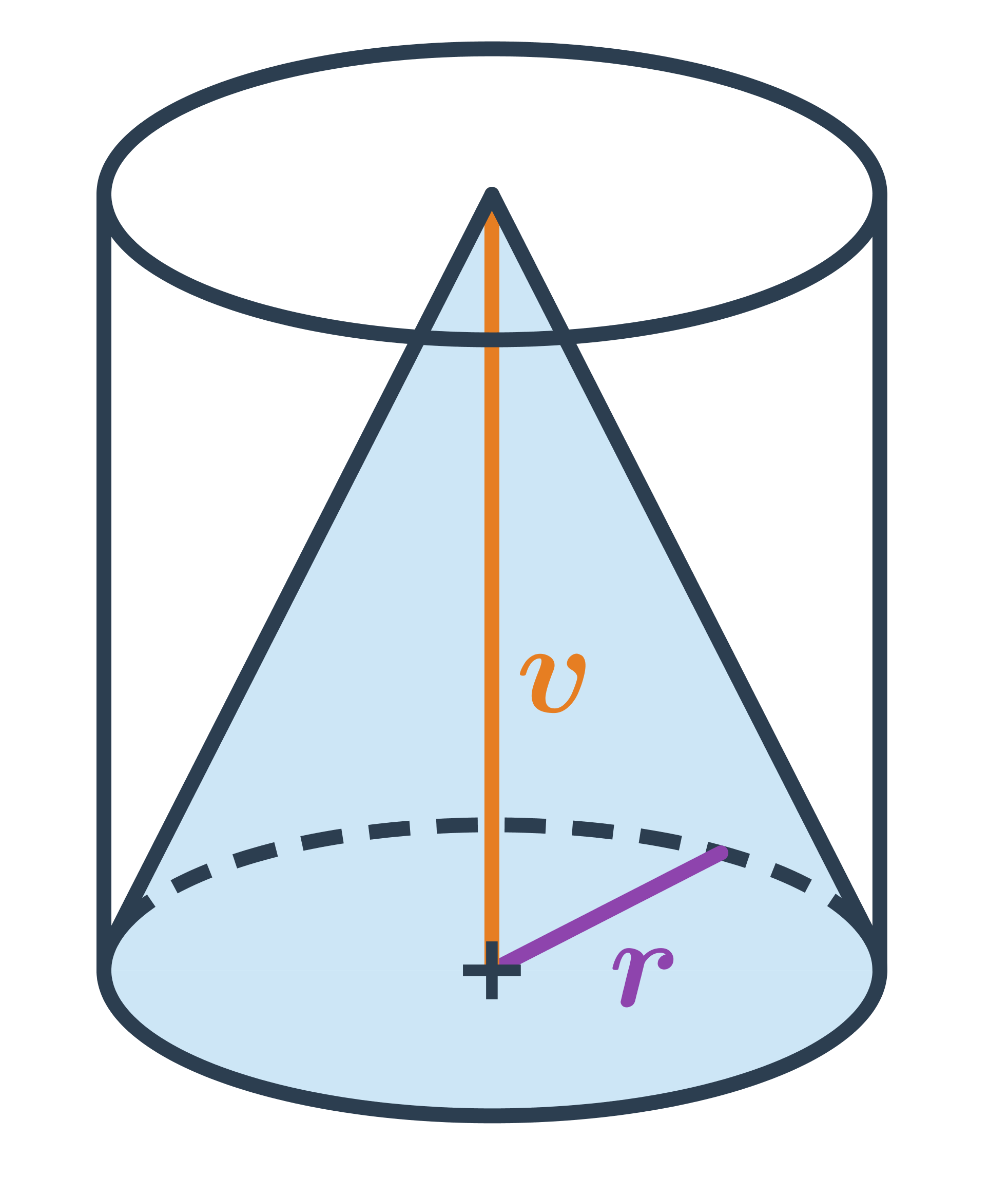
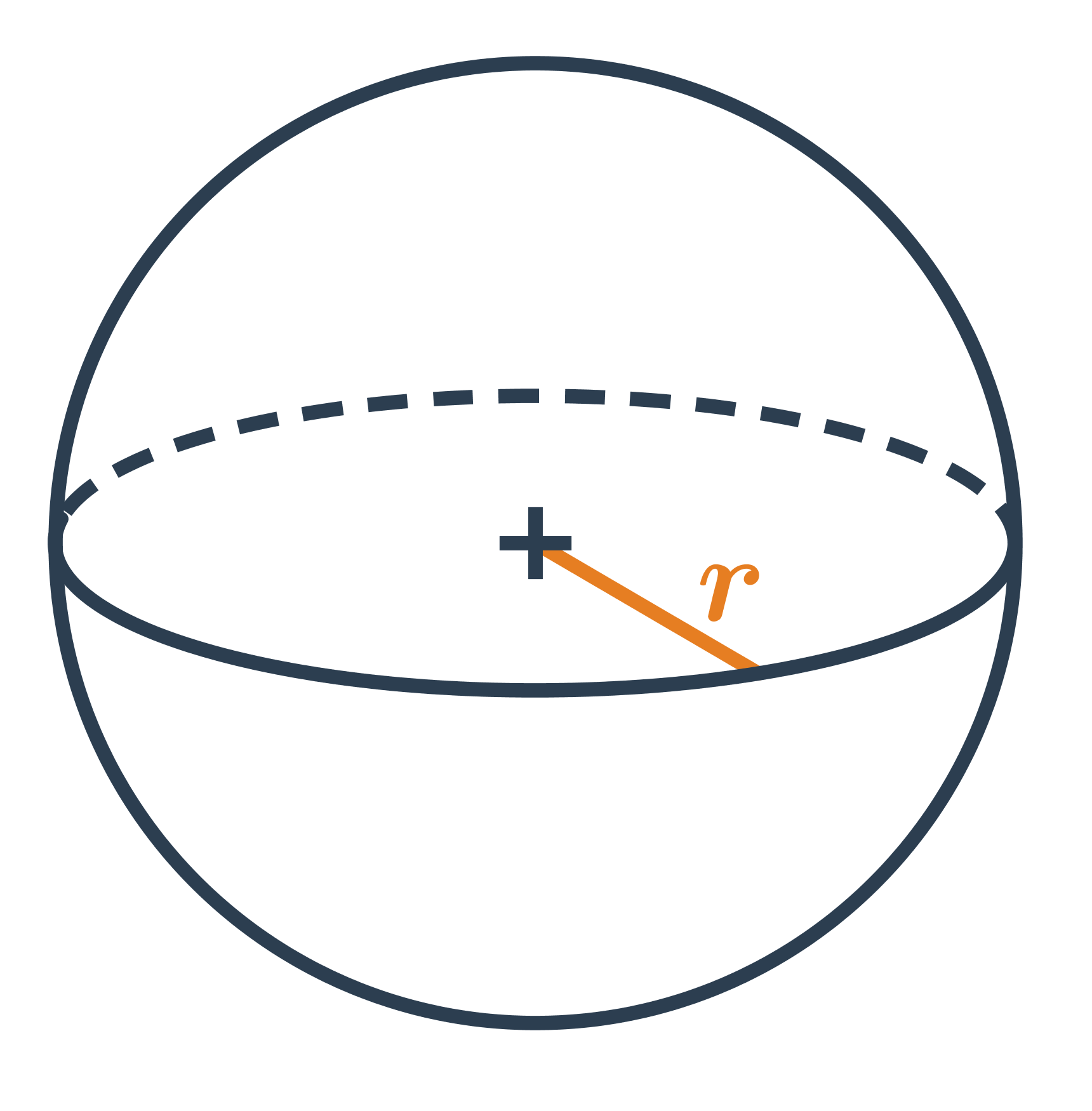
Objem kulatých těles
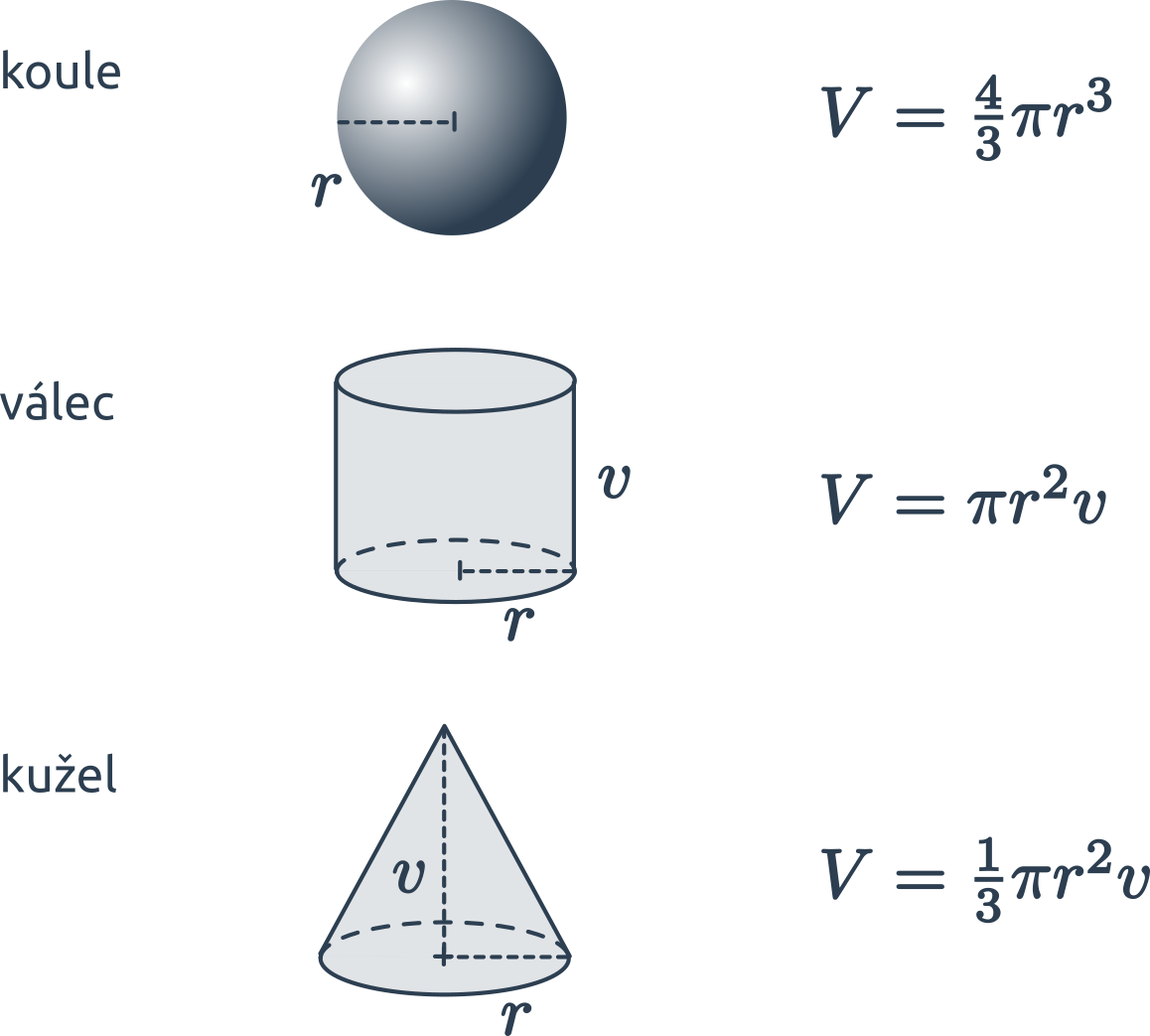
Objem „kulatých“ těles vypočítáme za využití konstanty \pi \approx 3{,}14 159 265. Ve vzorcích označuje r poloměr (koule či podstavy) a v výšku válce.
- Objem koule je V = \frac43 \pi r^3.
- Objem válce je obsah (kruhové) podstavy vynásobený výškou, tedy V = S_p \cdot v = \pi r^2 v.
- Objem kužele je jedna třetina obsahu podstavy vynásobeného výškou, tedy V = \frac13 S_p \cdot v = \frac13 \pi r^2 v.
Příklad: objem koule s daným poloměrem
Určete objem koule o poloměru 3 m.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Dosadíme za r známou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 3^3 m³ = 36 \pi m³ \doteq 113 m³
Velikost poloměru je zadaná v metrech, proto je výsledný objem koule v metrech krychlových.
Příklad: objem koule s daným průměrem
Určete objem koule o průměru 4 dm.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Známe průměr, proto umíme určit poloměr koule jako polovinu průměru r=\frac42=2 dm
- Dosadíme za r spočítanou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 2^3 dm³ = \frac{32}{3} \pi dm³ \doteq 33{,}5 dm³
Velikost průměru je zadaná v decimetrech, proto je výsledný objem koule v decimetrech krychlových.
Příklad: objem válce
Určete objem válce o poloměru podstavy 5 mm a výšce 0{,}1 cm.
- Poloměr podstavy a výšku máme v různých jednotkách. Převedeme velikost výšky na milimetry, abychom měli všechny údaje v mm.
- r=5 mm, v=0{,}1 cm = 1 mm
- Objem válce se známým poloměrem podstavy r a výškou v spočítáme jako: V = \pi r^2 v
- Dosadíme za r a v známé hodnoty v mm.
- Daný válec má objem: V = \pi \cdot 5^2 \cdot 1 mm³ = 25 \pi mm³ \doteq 78{,}5 mm³
Výpočty provádíme s velikostí poloměru i výšky v milimetrech, proto je výsledný objem válce v milimetrech krychlových.
