Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Výpis souhrnů
Vektory
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Vektor je množina všech shodně orientovaných úseček, které mají stejnou délku. Každou z těchto úseček nazýváme umístěním vektoru.
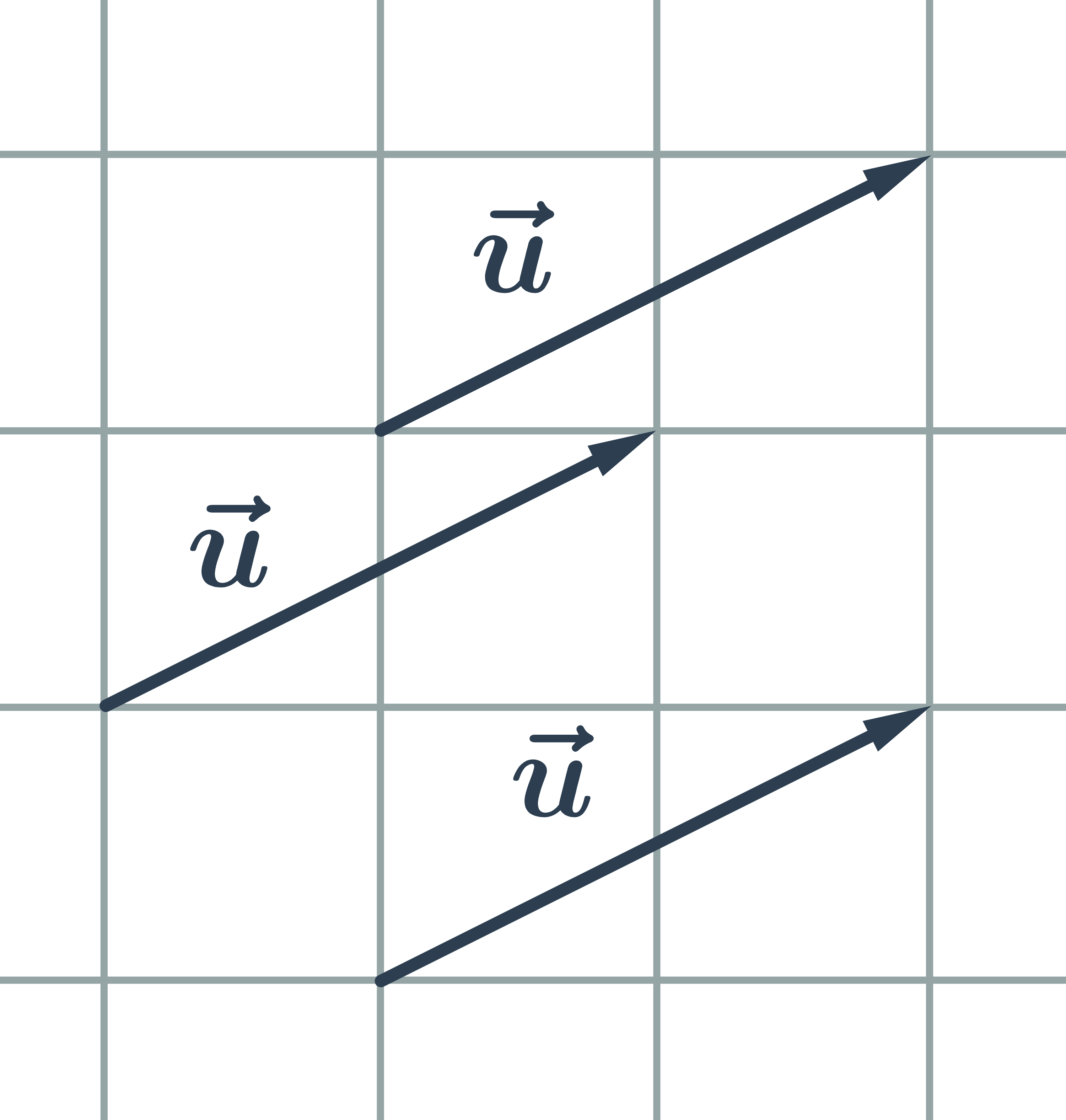
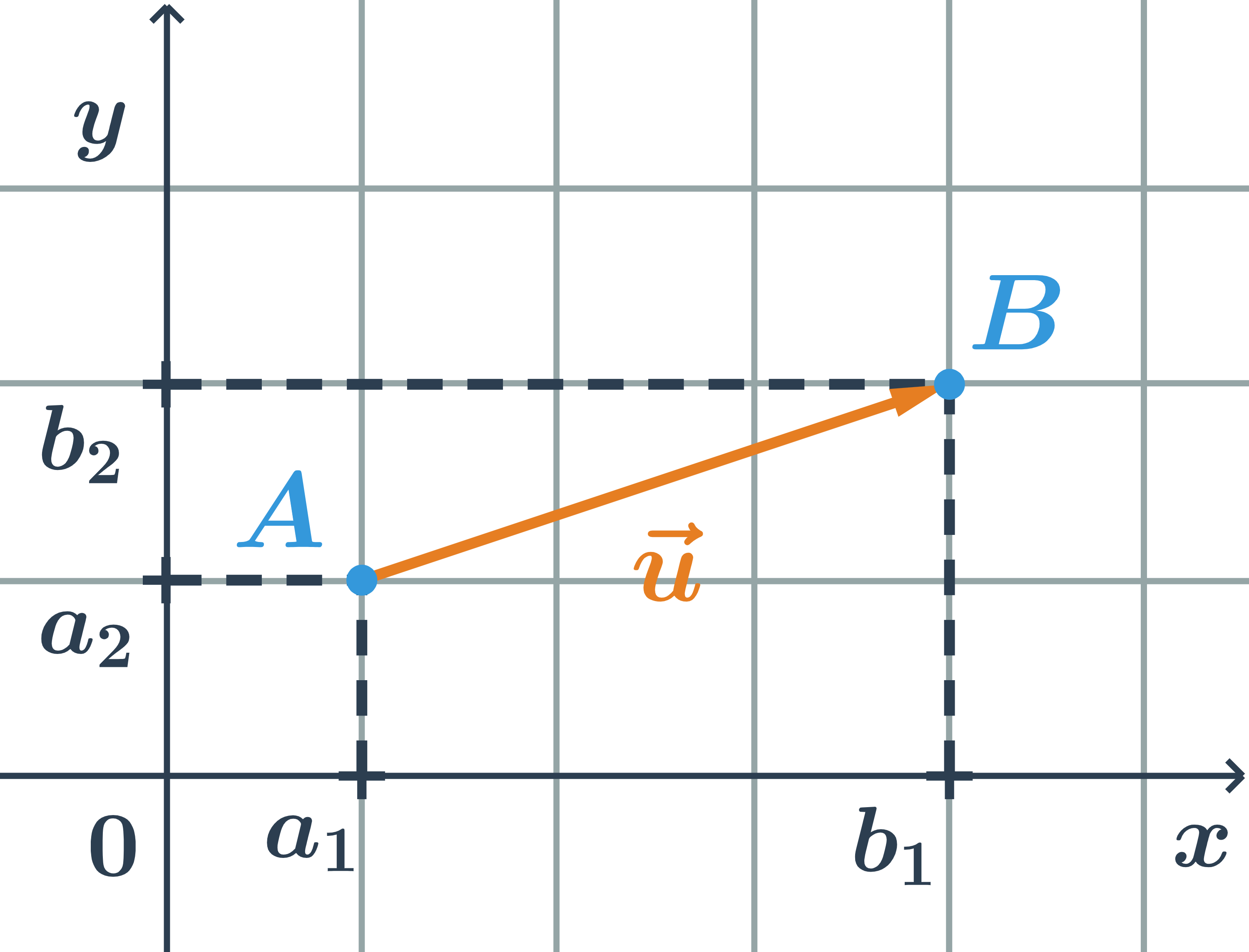
Vektor je určený počátečním a koncovým bodem, graficky znázorňujeme se šipkou u koncového bodu, zapisujeme: \vec{u}=\overrightarrow{AB}
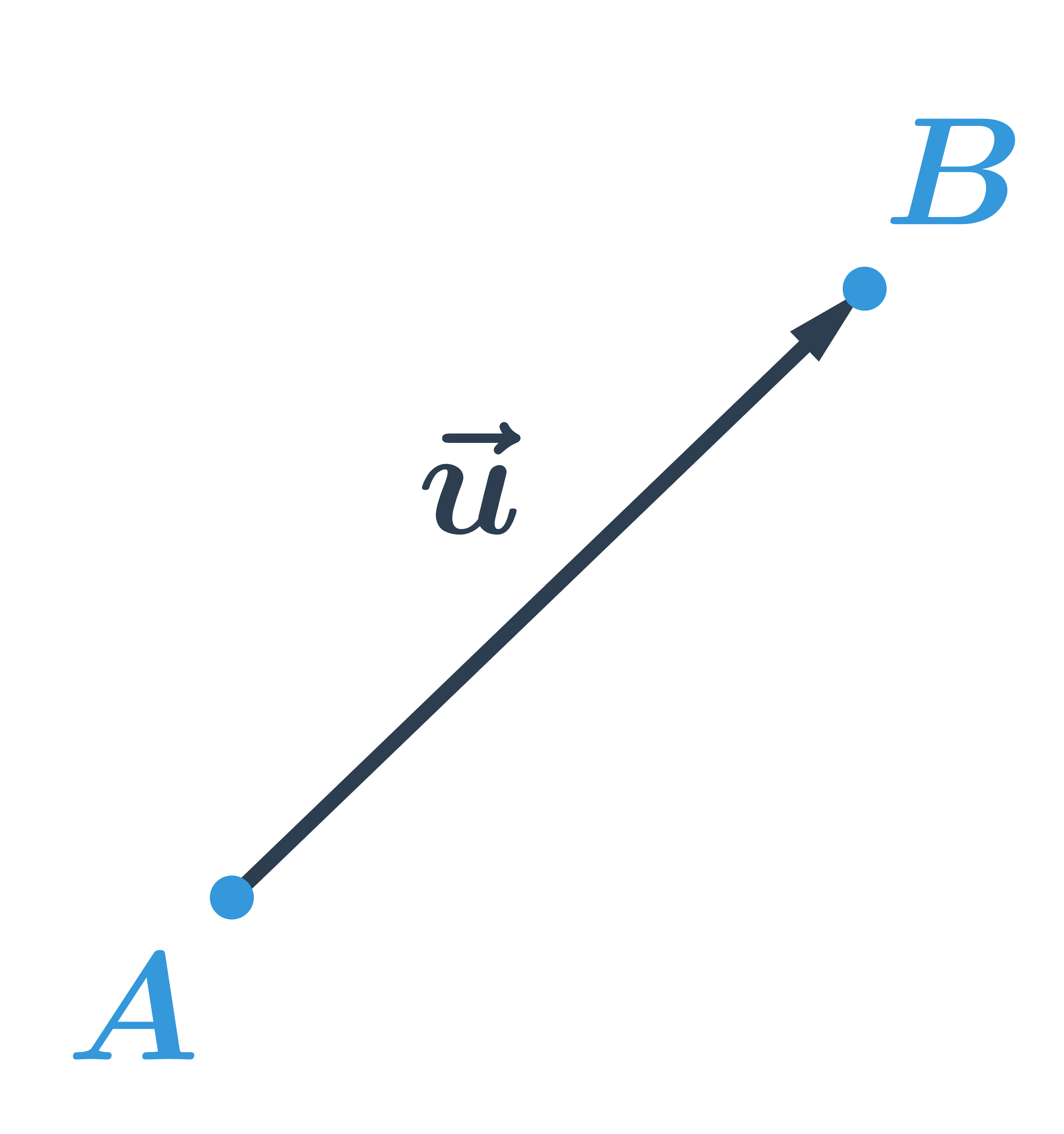
Na obrázku je A počáteční bod vektoru \vec{u}, B je koncový bod vektoru \vec{u}.
NahoruVektory: pojmy
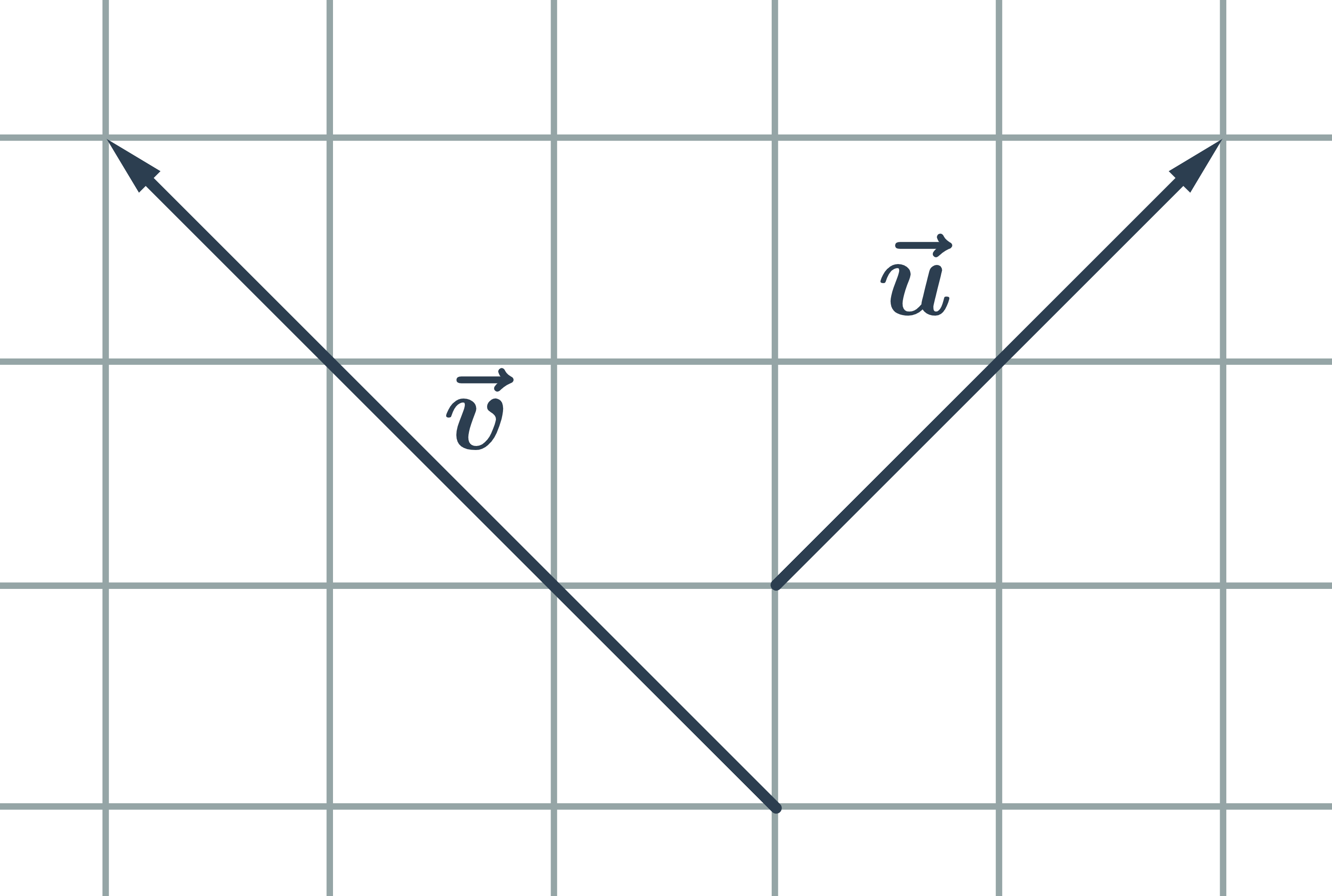
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci:
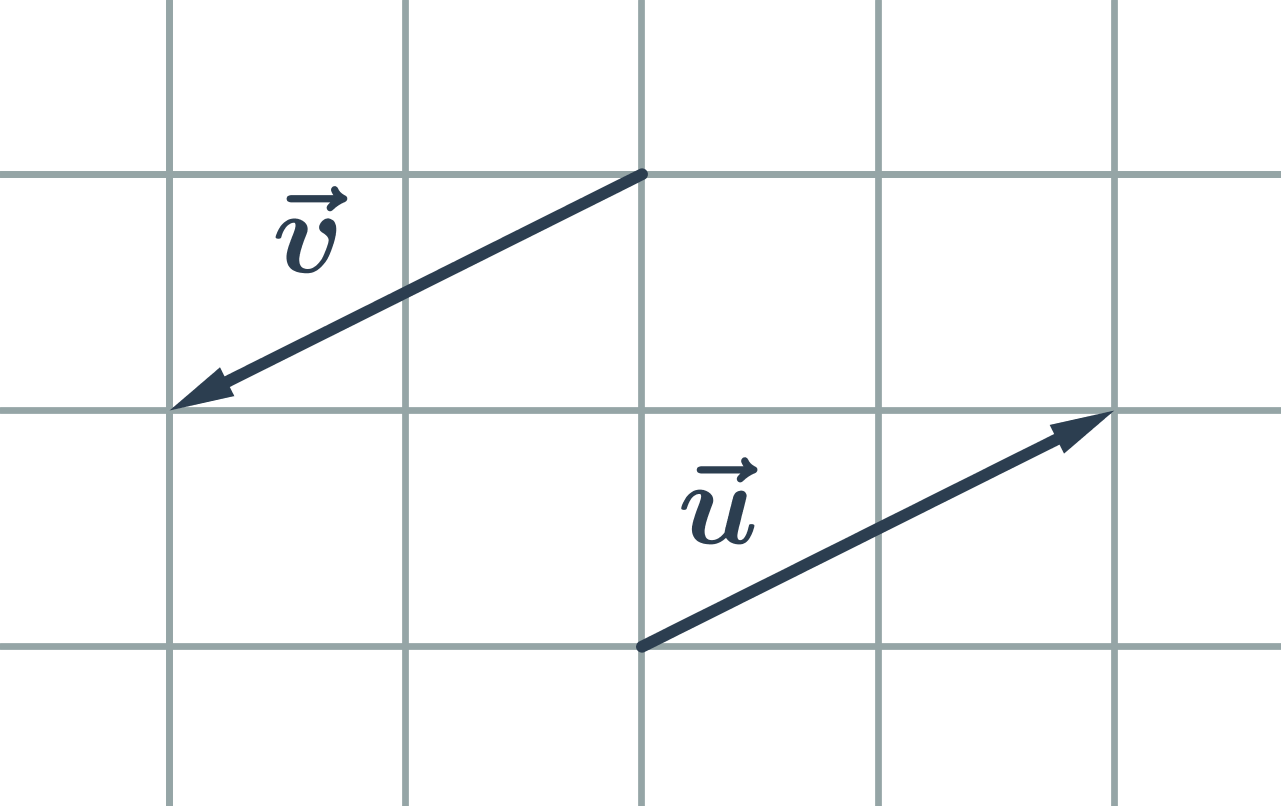
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. Tedy nemusí mít stejnou délku, mohou mít stejnou nebo opačnou orientaci:
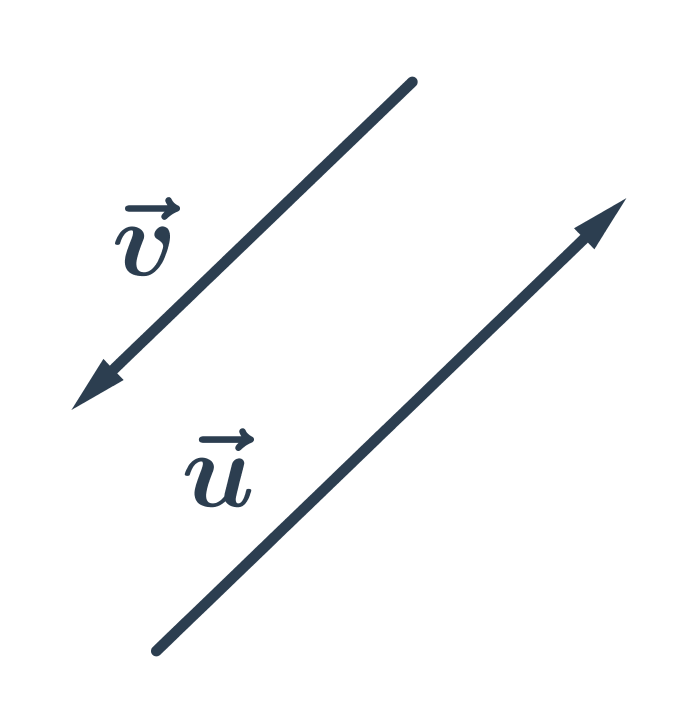
Kolmé vektory jsou vektory, které svírají pravý úhel:
Souřadnice vektoru jsou pravoúhlé průměty vektoru do souřadných os, tedy vektor \vec{u}=\overrightarrow{AB} má souřadnice: \vec{u}=(u_1;u_2)=(b_1-a_1;b_2-a_2)
Velikost vektoru \vec {u}=\overrightarrow{AB} je délka úsečky AB, značíme \left| \vec{u} \right| a platí: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
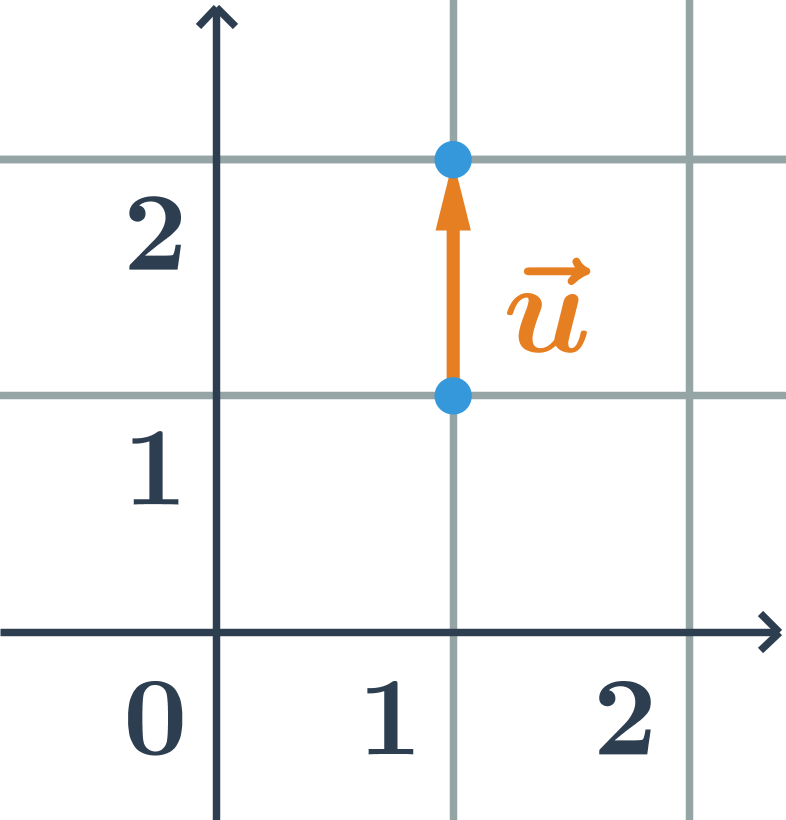
Jednotkový vektor má délku 1.
Nulový vektor má nulovou délku, tedy splývá jeho počáteční a koncový bod.
NahoruSouřadnice vektoru
Již víme, že vektor je množina nekonečně mnoha orientovaných úseček, jedna z nich má počátek v počátku souřadného systému, v bodě O=[0;0]. Souřadnice koncového bodu jsou souřadnice daného vektoru.
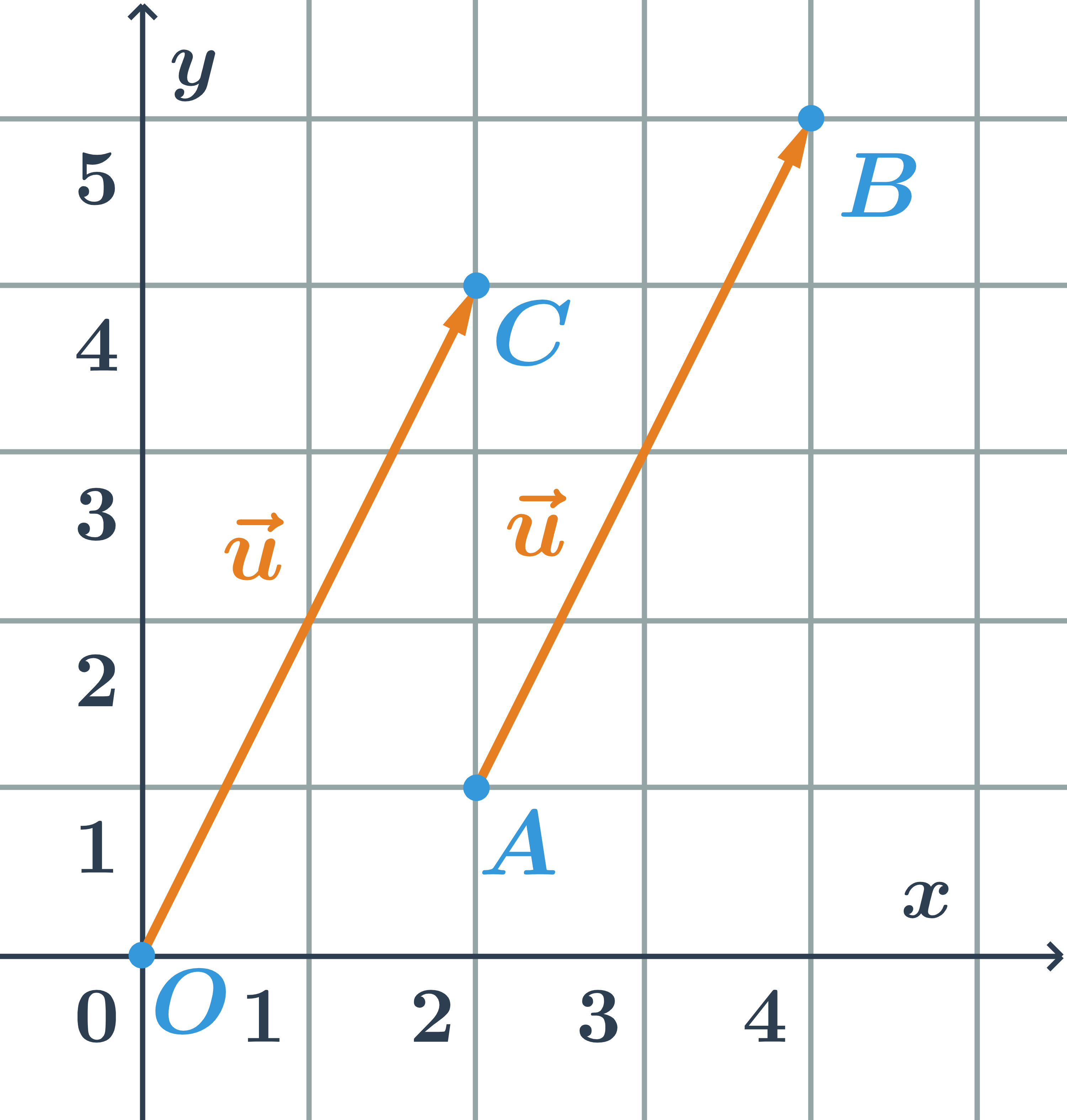
Souřadnice vektoru \overrightarrow{AB}
- Chceme-li vektor \overrightarrow{AB} posunout do počátku souřadného systému, posuneme ho o dva čtverečky vlevo a o jeden čtvereček dolů.
- Bod A se posune do bodu O, bod B se posune do bodu C. Tento posun můžeme vyjádřit takto:
- A se posune na [2-2;1-1]=[0;0]
- B se posune na [4-2;5-1]=[2;4]
- Souřadnice vektor na obrázku jsou: \vec{u}=\overrightarrow{AB}=\overrightarrow{OC}=(2;4)
Všimněte si, že souřadnice vektoru \overrightarrow{AB} jsme získali odečtením souřadnic bodu A od souřadnic bodu B
Pro souřadnice vektoru \overrightarrow{AB} určeného body A=[a_1;a_2], B=[b_1;b_2] platí: \overrightarrow{AB}=B-A=(b_1-a_1;b_2-a_2)
NahoruVelikost vektoru
Velikost vektoru \overrightarrow{AB} je délka úsečky AB. Vektor, který má délku 1, se nazývá jednotkový vektor:
Vektor, který má nulovou délku (počáteční a koncový bod vektoru splývá) se nazývá nulový vektor:
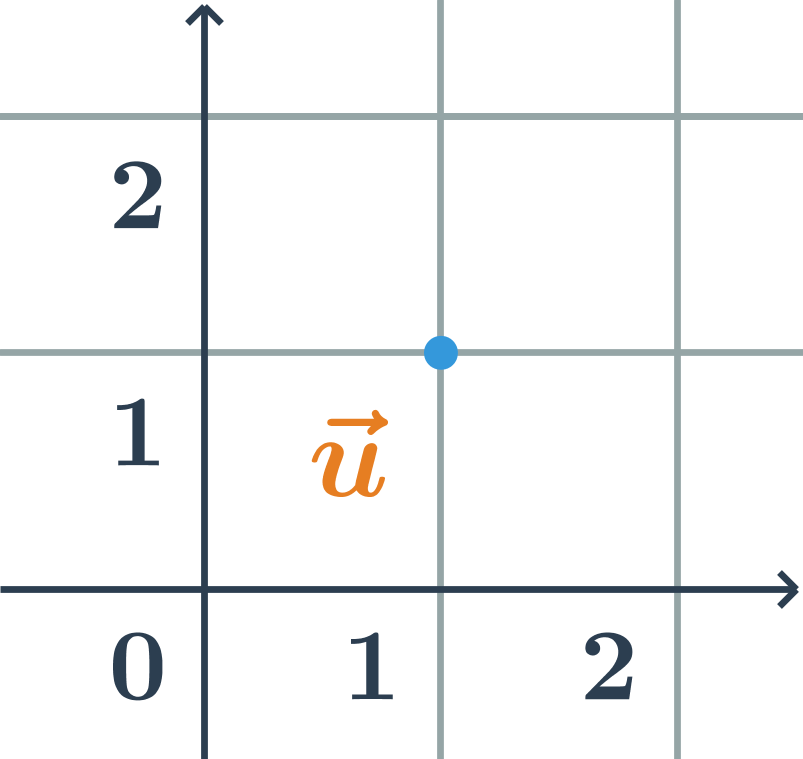
Velikost vektoru \vec{u}=(u_1;u_2) určíme s využitím Pythagorovy věty: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
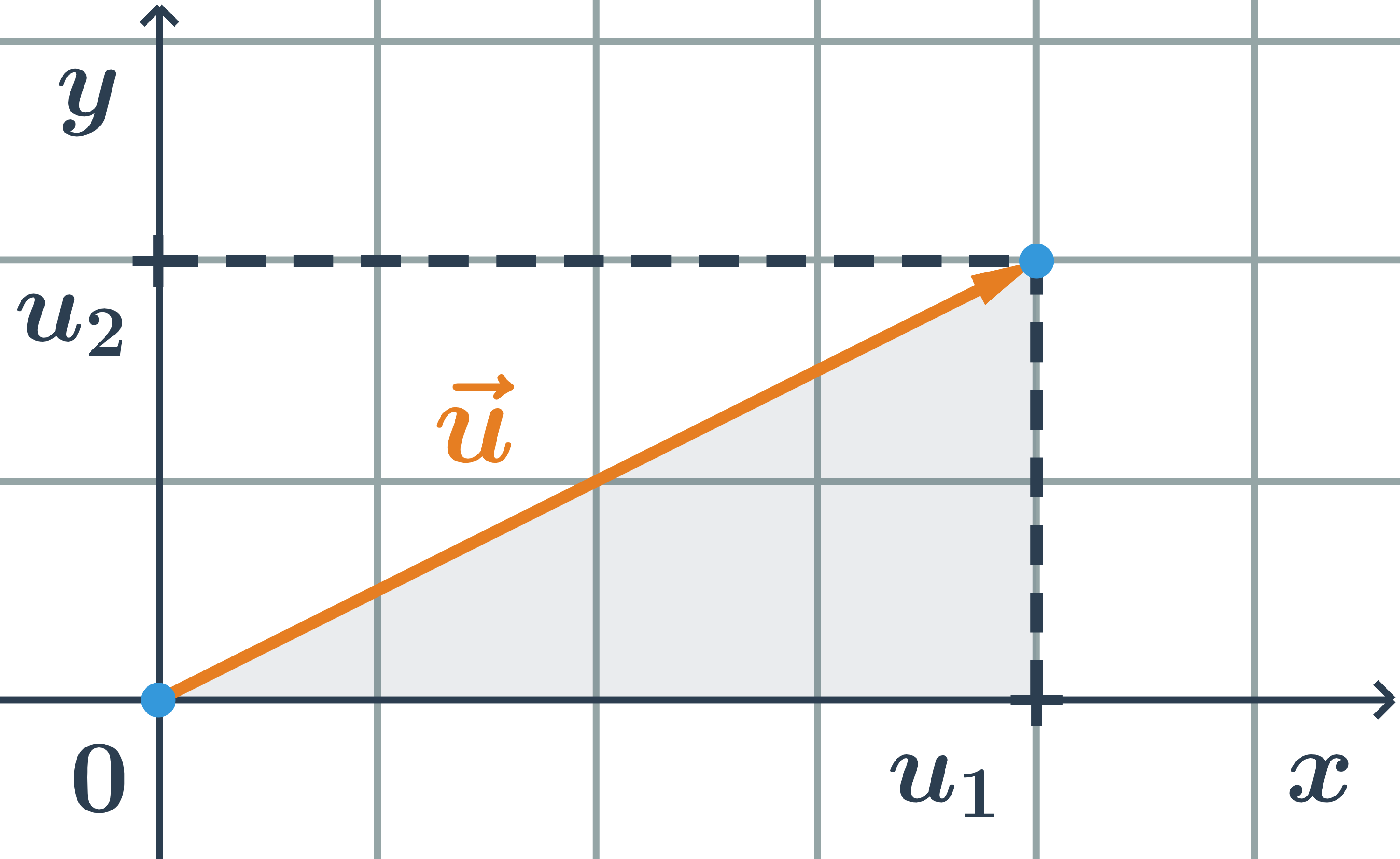
Ve vybarveném trojúhelníku je délka vektoru přepona, odvěsny mají délky u_1 a u_2.
Příklad: velikost vektoru
Určete velikost vektoru na obrázku:
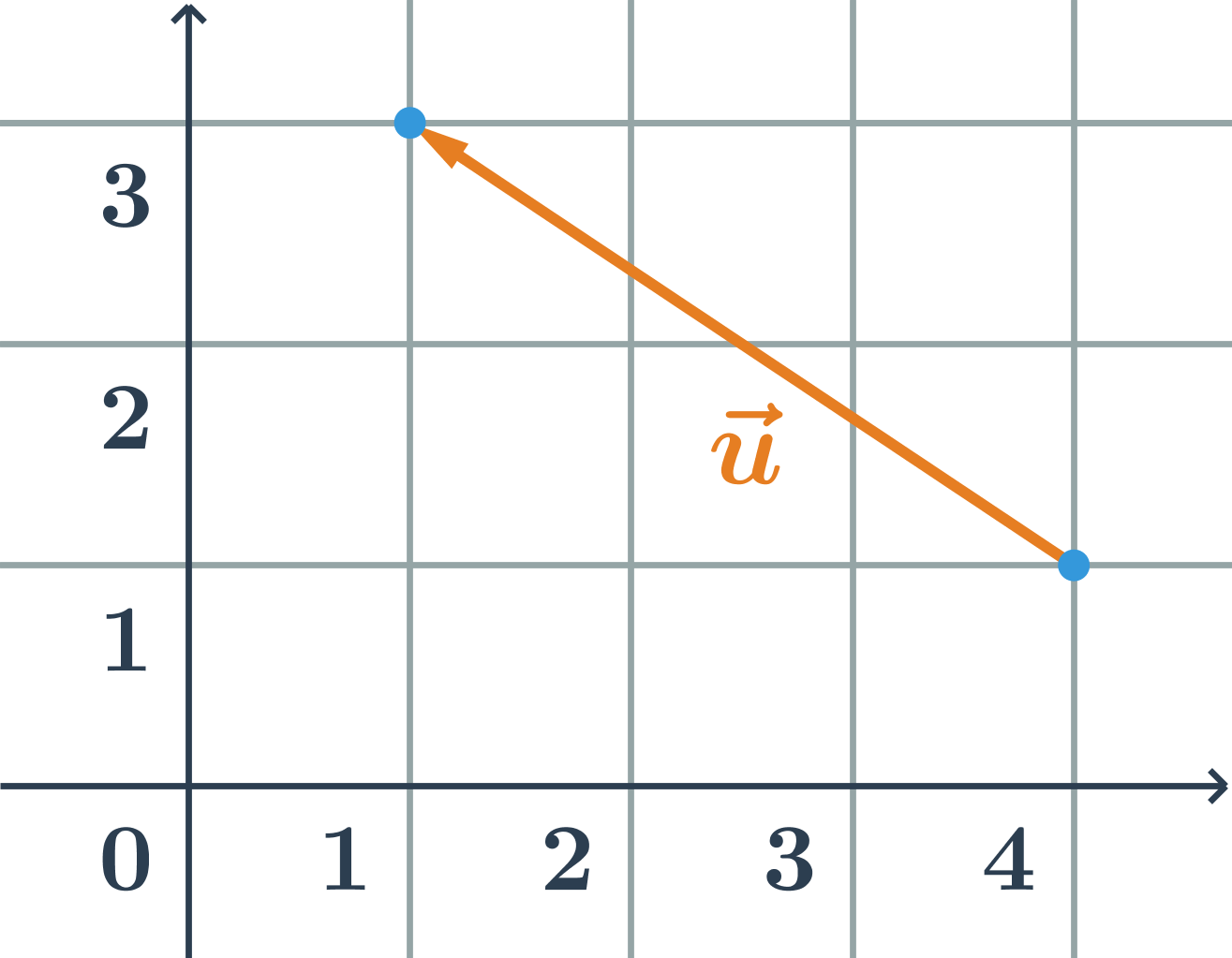
Vektor na obrázku má souřadnice \vec{u}=(-3;2), jeho velikost je \left| \vec{u} \right|=\sqrt{(-3)^2+2^2}=\sqrt{(-3)^2+2^2}=\sqrt{13}
Vzájemná poloha vektorů
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci. K vektoru \vec{u}=(u_1;u_2) je opačný vektor \vec{v}=(-u_1;-u_2)
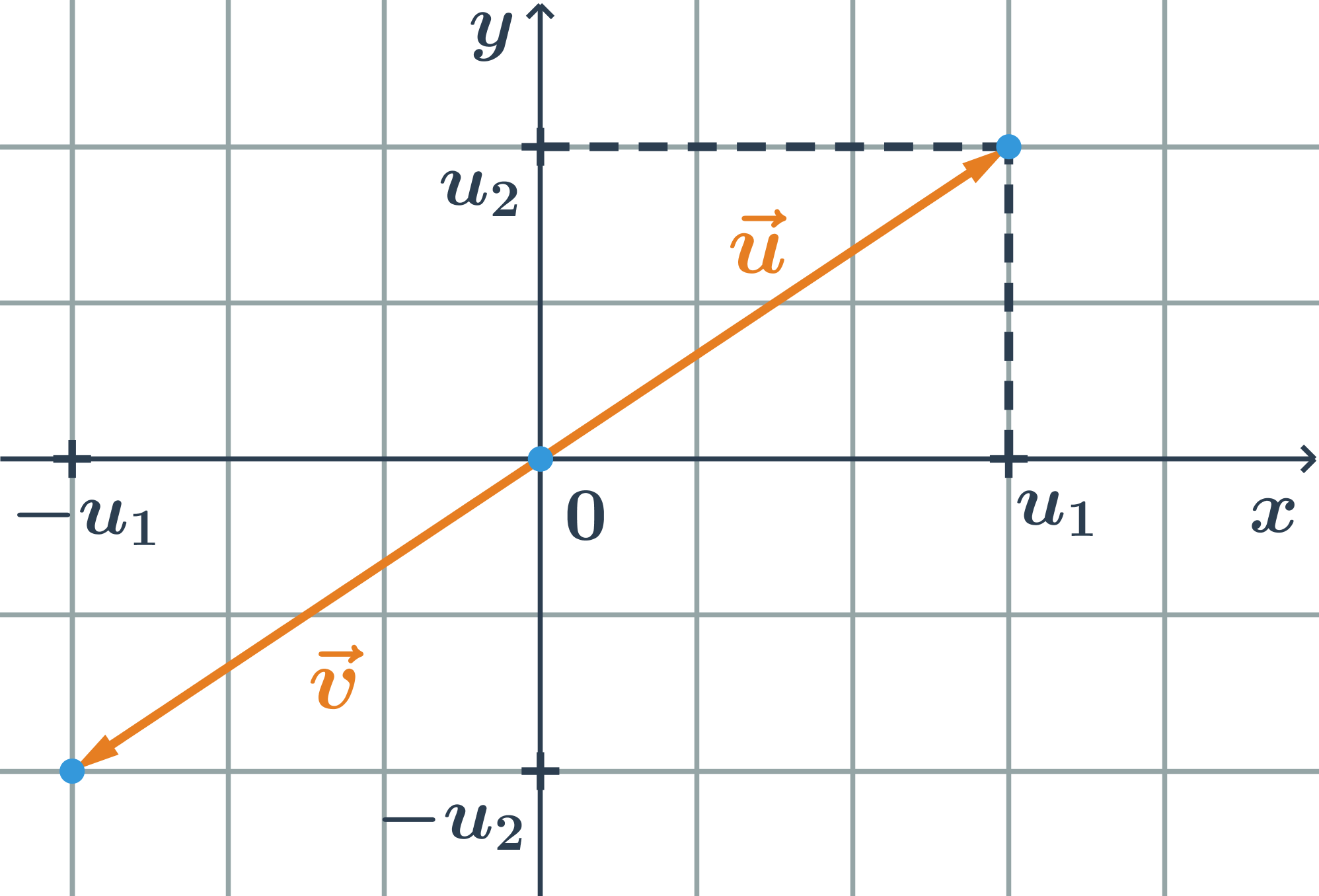
Příklad opačný vektor
- Určete opačný vektor k vektoru \vec{u}=(3;-1).
- Opačný vektor \vec{v} k vektoru \vec{u} má souřadnice: (-u_1;-u_2)=(-3;1)
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. S vektorem \vec{u}=(u_1;u_2) je kolineární každý vektor \vec{v}=(k\cdot u_1;k \cdot u_2), kde k je reálné nenulové číslo. Pro k>0 vektory mají stejný směr, pro k<0 mají vektory opačný směr.
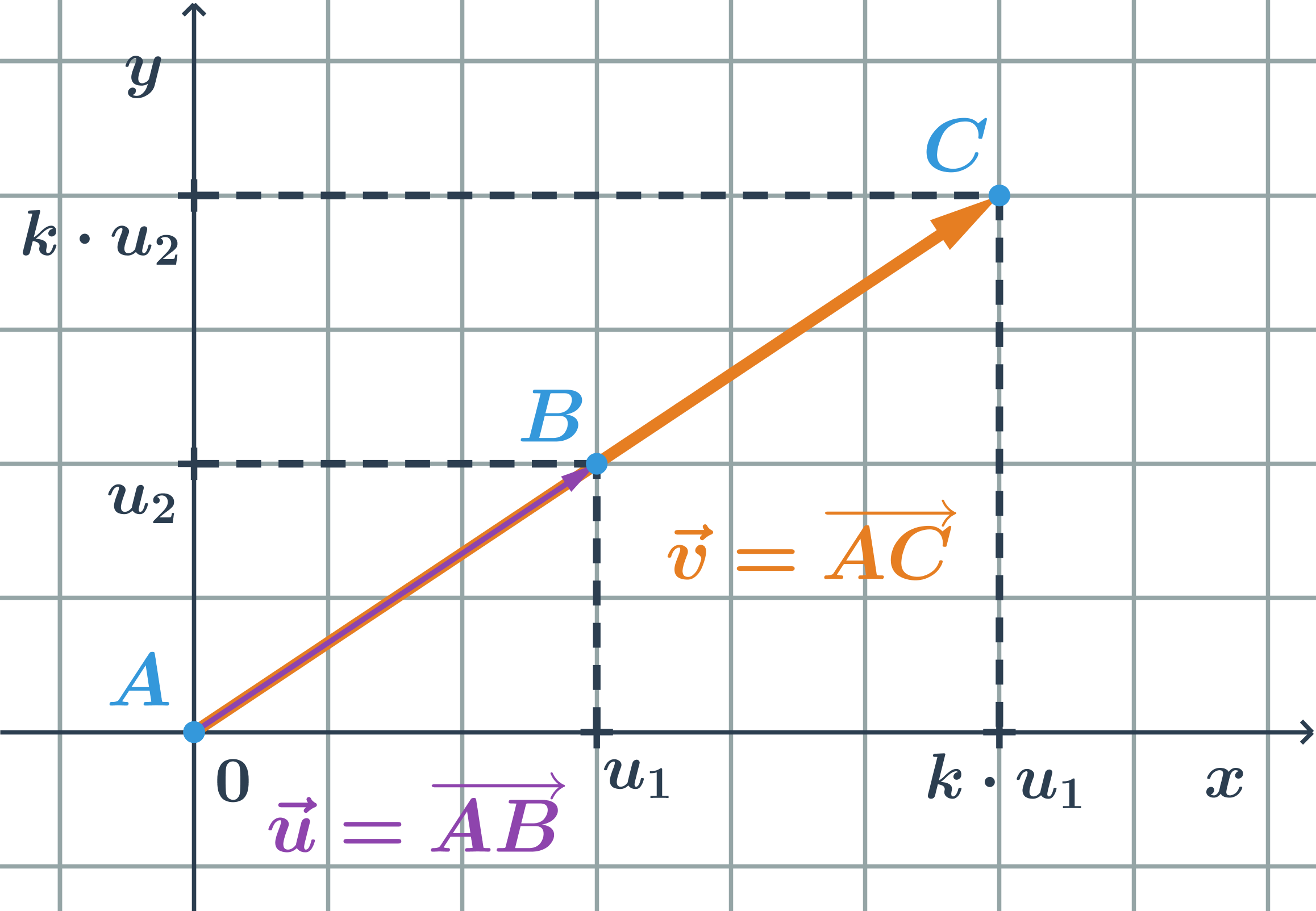
Příklad kolineární vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;3) tak, aby byl kolineární s vektorem \vec{u}=(2;-1).
- Pro druhou souřadnici platí: v_2=3, u_2=-1, tedy v_2= (-3) \cdot u_2
- Vidíme, že k=-3 je záporné, tj. \vec{u} a \vec{v} mají opačnou orientaci
- Pro první souřadnici musí platit: v_1= (-3) \cdot u_1= (-3)\cdot2=-6.
Kolmé vektory jsou vektory, které svírají pravý úhel K vektoru \vec{u}=(u_1;u_2) je kolmý každý vektor \vec{v}=(-k\cdot u_2;k \cdot u_1), kde k je reálné nenulové číslo.
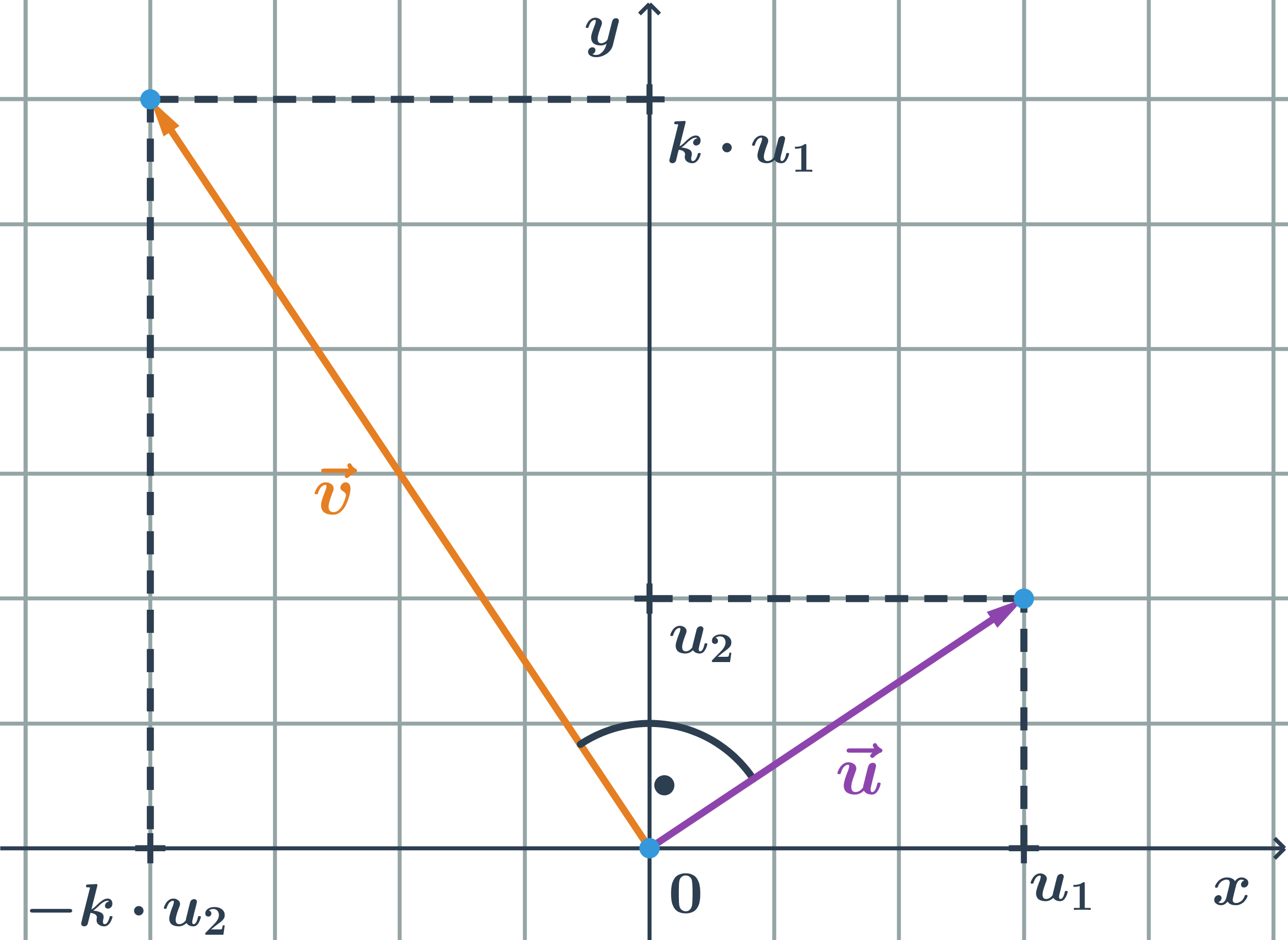
Příklad kolmý vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;4) tak, aby byl kolmý k vektoru \vec{u}=(2;-1).
- Platí: v_2=2 \cdot u_1, tedy musí platit: v_1 = - 2 \cdot u_2.
- Máme tedy v_1 = - 2 \cdot u_2 = -2 \cdot (-1) = 2.
