Výpis souhrnů
Operace a vlastnosti v rovině
Podtémata
Operace a vlastnosti v rovině
Základní intuitivní představa pro jednotlivé operace a vlastnosti:
- Osová souměrnost – děláme „zrcadlový“ obraz útvaru podle přímky
- Středová souměrnost – překlápíme útvar podle bodu
- Shodnost – dva útvary jsou shodné, pokud „mají stejný tvar a velikost“ (mohou se lišit natočením a umístěním)
- Otočení – otočíme útvar okolo určitého bodu o nějaký úhel po směru nebo proti směru hodinových ručiček
- Posunutí – posuneme útvar o určitou vzdálenost daným směrem
- Podobnost – dva útvary jsou podobné, pokud „mají stejný tvar“ (mohou se lišit velikostí, natočením a umístěním)
- Stejnolehlost – vzdálenost bodů útvaru vzhledem k danému bodu se mění v daném poměru
Podtéma určení zobrazení v rovině se pak zabývá rozlišováním mezi jednotlivými zobrazeními.
Podle velikosti a umístění útvarů v rovině lze rozhodnout, jestli je jeden útvar obrazem druhého v nějakém geometrickém zobrazení.
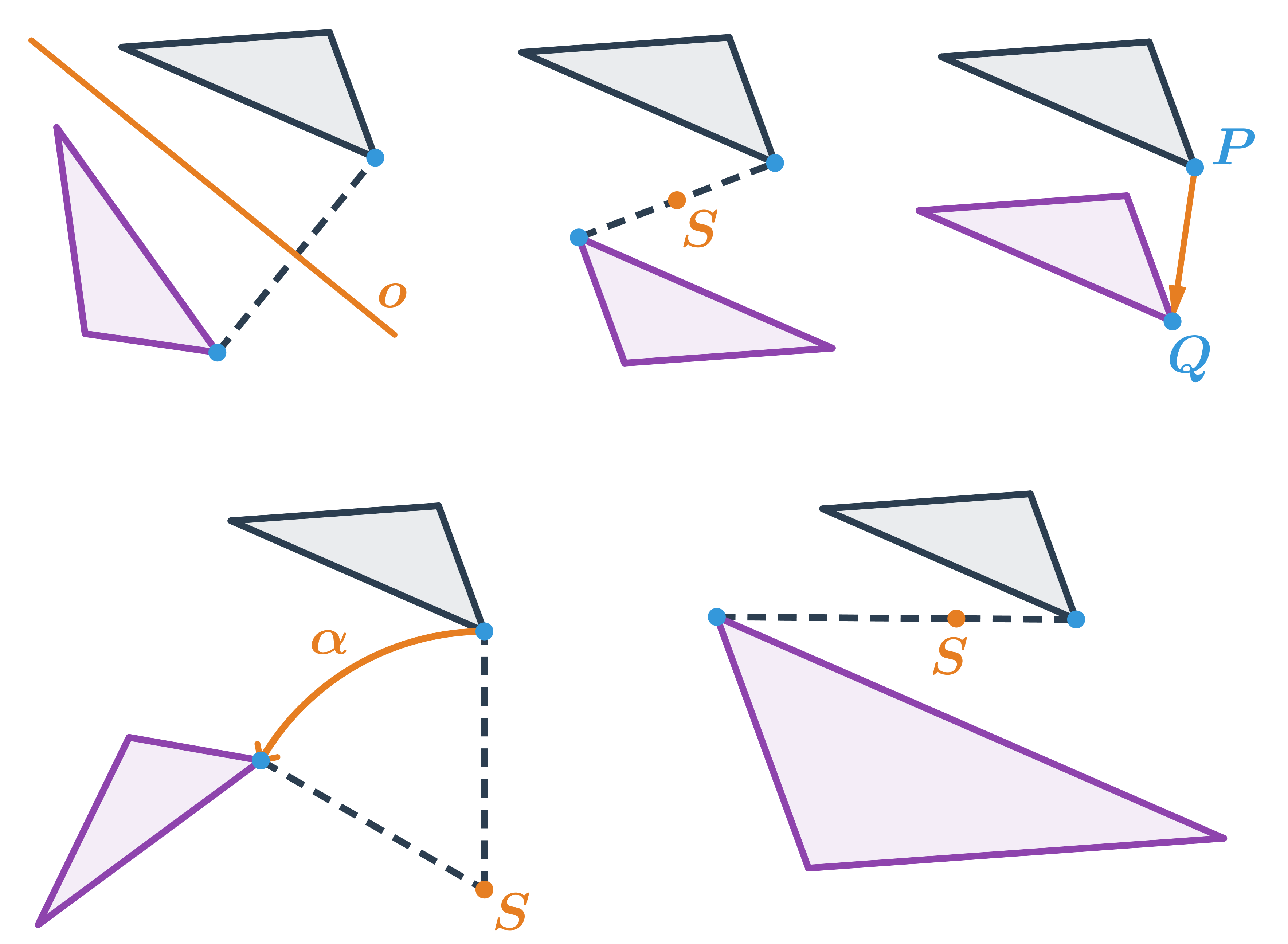
Na obrázku je obraz trojúhelníku v těchto zobrazeních:
- osová souměrnost s osou o
- středová souměrnost se středem S
- posunutí dané orientovanou úsečkou \overrightarrow{PQ}
- otočení dané středem S a orientovaným úhlem \alpha
- stejnolehlost daná středem S a koeficientem -2
Osová souměrnost
Osová souměrnost je dána přímkou o a přiřazuje každému bodu X mimo osu takový bod X', že přímka o je osou úsečky XX'. Jinými slovy: obraz má od osy stejnou vzdálenost jako původní bod a spojnice bodů je kolmá na osu. Osová souměrnost zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
Příklady
Modré a oranžové útvary jsou vzájemně osově souměrné podle osy o:
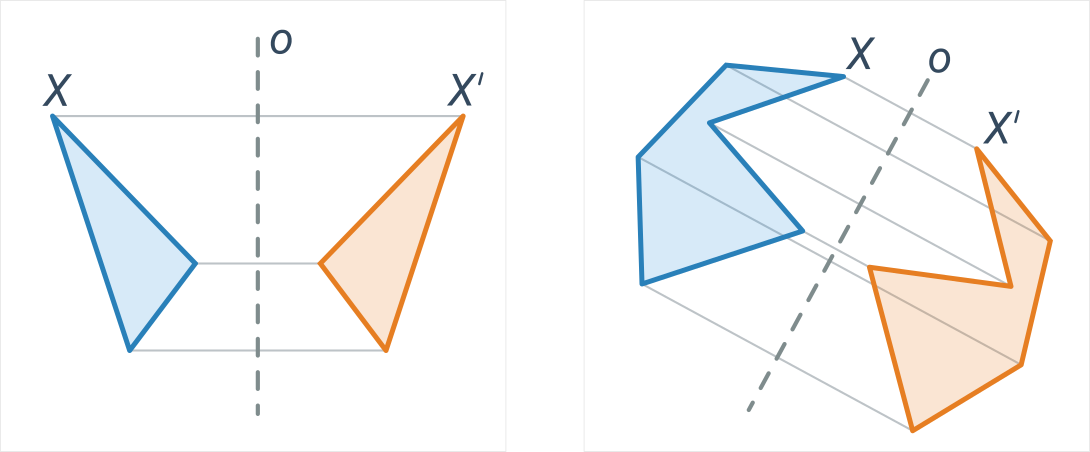
Pro lepší pochopení může být užitečné porovnat osovou a středovou souměrnost.
Osově souměrný útvar
Útvar označujeme za osově souměrný, pokud je v nějaké osové souměrnosti obrazem sebe sama. Osu této souměrnosti pak nazýváme osou útvaru. Obrázek uvádí příklady útvarů osově souměrných (zelené, s vyznačenými osami souměrnosti) i těch nesouměrných (červené):
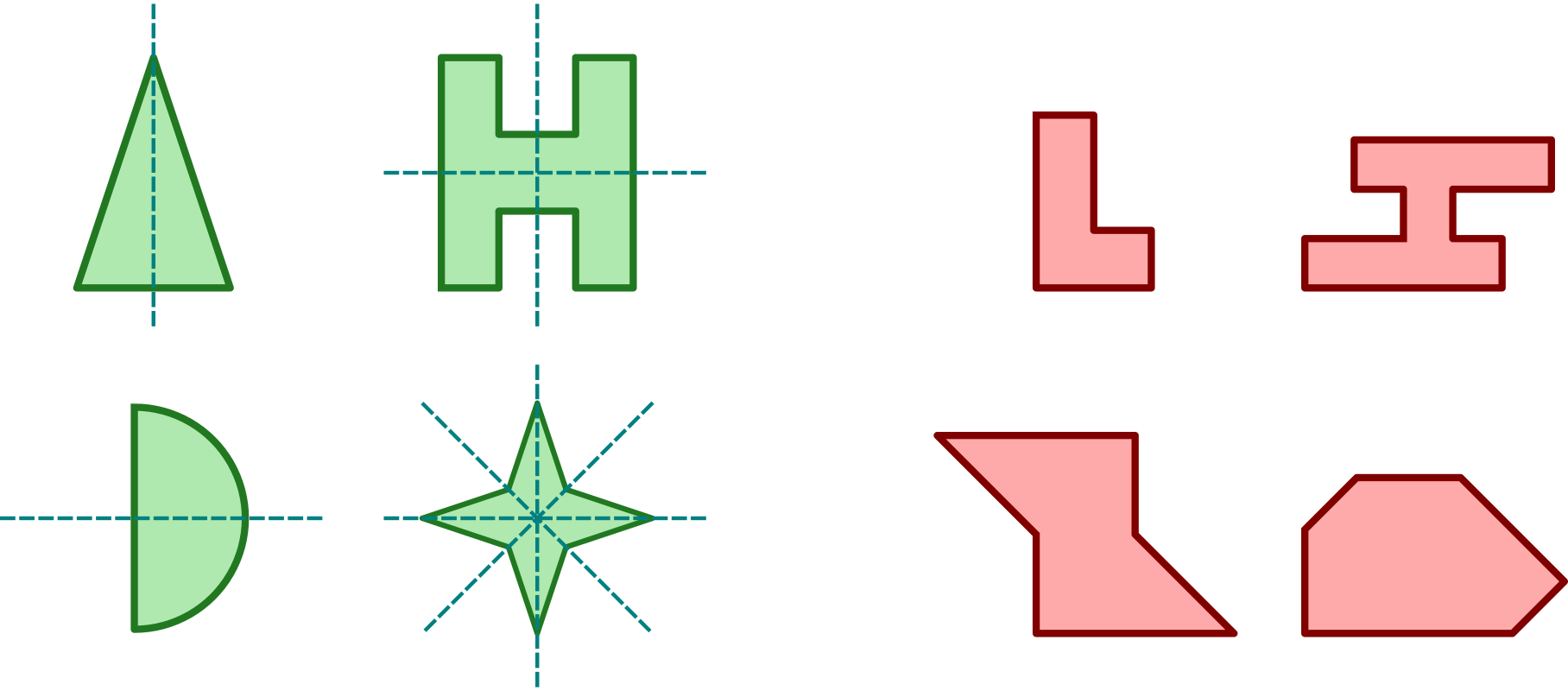
Další příklady:
- Úsečka je osově souměrná a má v rovině jedinou osu souměrnosti (kolmici v jejím středu).
- Rovnoramenný trojúhelník je osově souměrný.
- Trojúhelník, který není rovnoramenný, není osově souměrný.
- Všechny pravidelné mnohoúhelníky jsou osově souměrné. Počet os souměrnosti je roven počtu vrcholů mnohoúhelníku.
- Kruh je osově souměrný a má nekonečně mnoho os souměrnosti.
Komiks pro zpestření
Středová souměrnost
Středová souměrnost je dána bodem S a přiřazuje každému bodu X takový bod X', že bod S je středem úsečky XX'. Jinými slovy: obraz má od středu stejnou vzdálenost jako původní bod a leží na polopřímce opačné k SX.
Středová souměrnost zachovává vzdálenosti i úhly, jde tedy o druh shodnosti. Středová souměrnost se středem v bodě S je shodná s otočením o 180 stupňů podle středu S.
Příklady
Modré a oranžové útvary jsou vzájemně středově souměrné podle středu S:
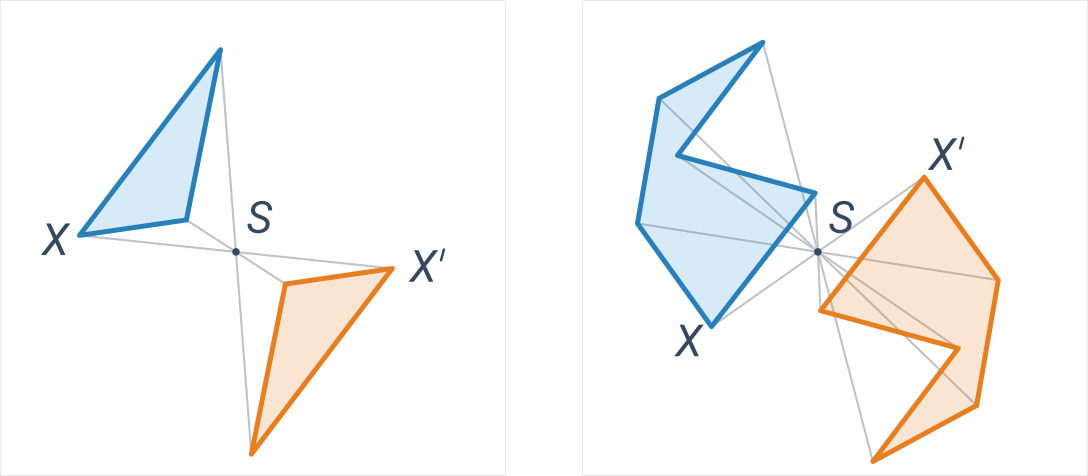
Pro lepší pochopení může být užitečné porovnat středovou a osovou souměrnost.
Středově souměrný útvar
Útvar označujeme za středově souměrný, pokud je v nějaké středové souměrnosti obrazem sebe sama. Střed této středové souměrnosti pak nazýváme středem souměrnosti objektu. Obrázek uvádí příklady útvarů středově souměrných (zelené, s vyznačeným středem souměrnosti) i těch nesouměrných (červené):
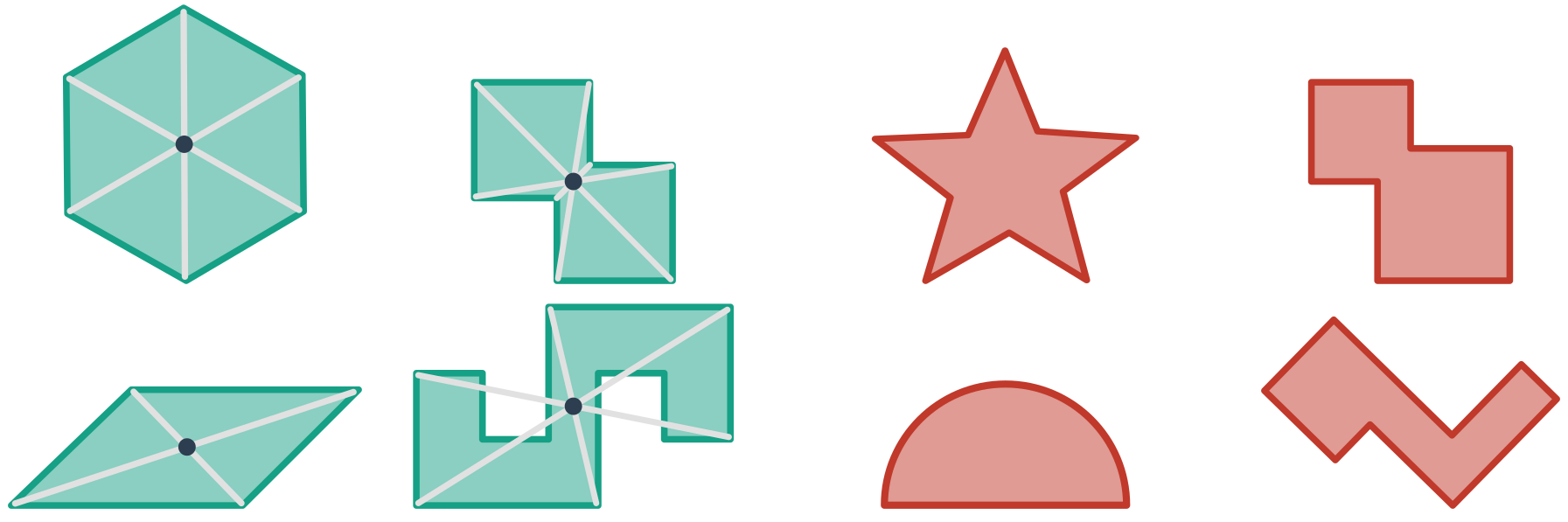
Další příklady:
Úsečka, obdélník, čtverec, kosočtverec, pravidelný šestiúhelník a kruh jsou středově souměrné.
Žádný trojúhelník není středově souměrný.
Dva geometrické útvary jsou shodné, pokud mají stejný tvar a velikost. Na následujícím obrázku mají shodné útvary stejnou barvu.

Značení
Mějme dva pojmenované útvary, např. dva trojúhelníky ABC a GEF.
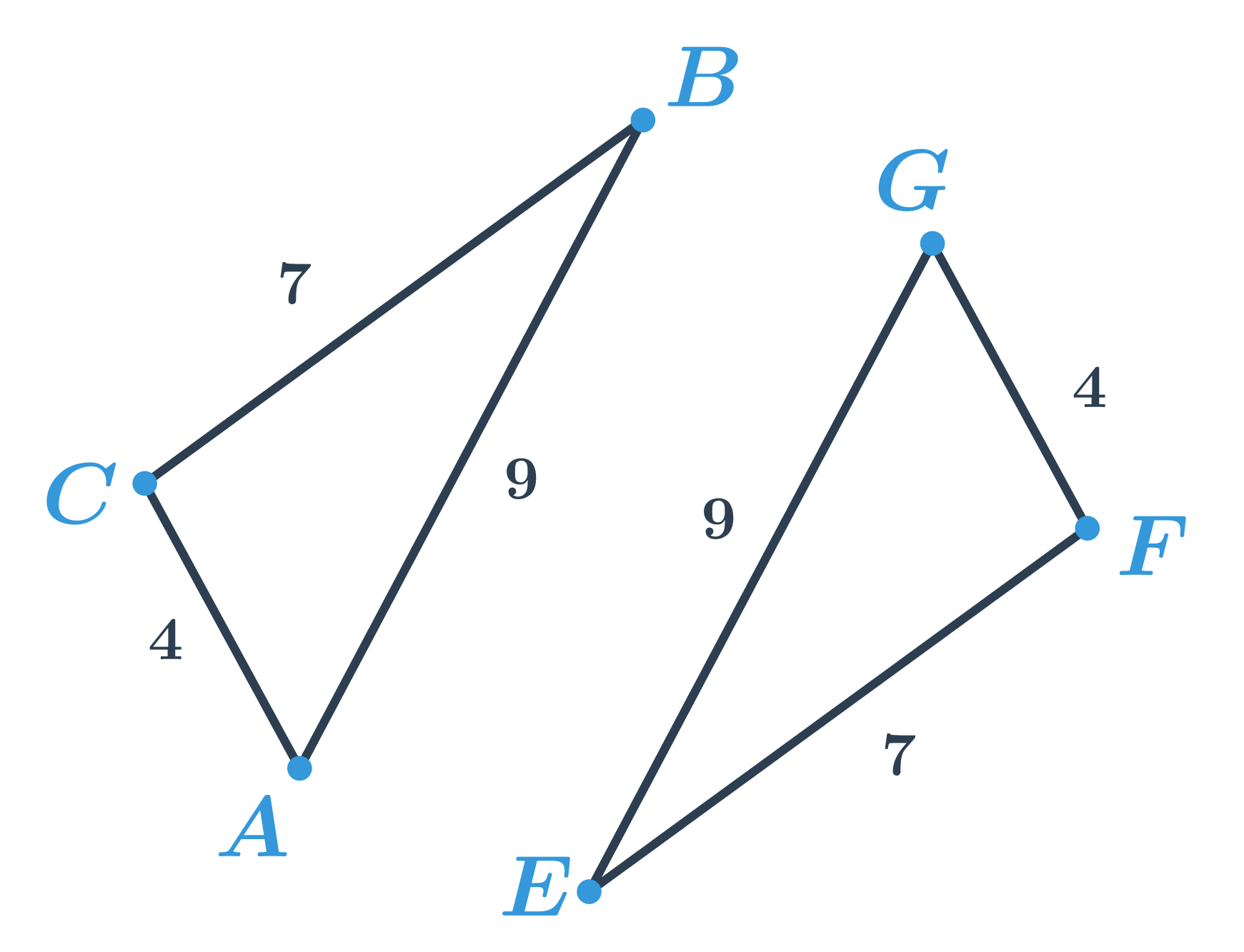
- \left|AB\right|=\left|GE\right|
- \left|BC\right|=\left|EF\right|
- \left|AC\right|=\left|GF\right|
Tyto dva trojúhelníky mají stejné délky stran, jsou tedy shodné. Zapíšeme jako ABC \cong GEF – pozor, na pořadí písmen záleží. Pořadí písmen v názvu trojúhelníku určuje, který vrchol ABC odpovídá kterému vrcholu trojúhelníku GEF. Máme \left|AB\right|=\left|GE\right|, ale \left|AB\right|\neq \left|EF\right|, takže ABC \ncong EFG.
NahoruPodobnost
Dva geometrické útvary jsou si podobné, pokud oba mají stejný tvar (bez ohledu na velikost). Na následujícím obrázku mají podobné útvary stejnou barvu:

Přesněji řečeno, útvary jsou podobné, pokud jeden můžeme získat z druhého kombinací rovnoměrného zmenšení či zvětšení a následným posunutím, otočením nebo překlopením.
Podobnost zachovává velikost úhlů a poměr délek.
Poměr délek odpovídajících úseček v obou útvarech se nazývá koeficient podobnosti.
Příklad 1
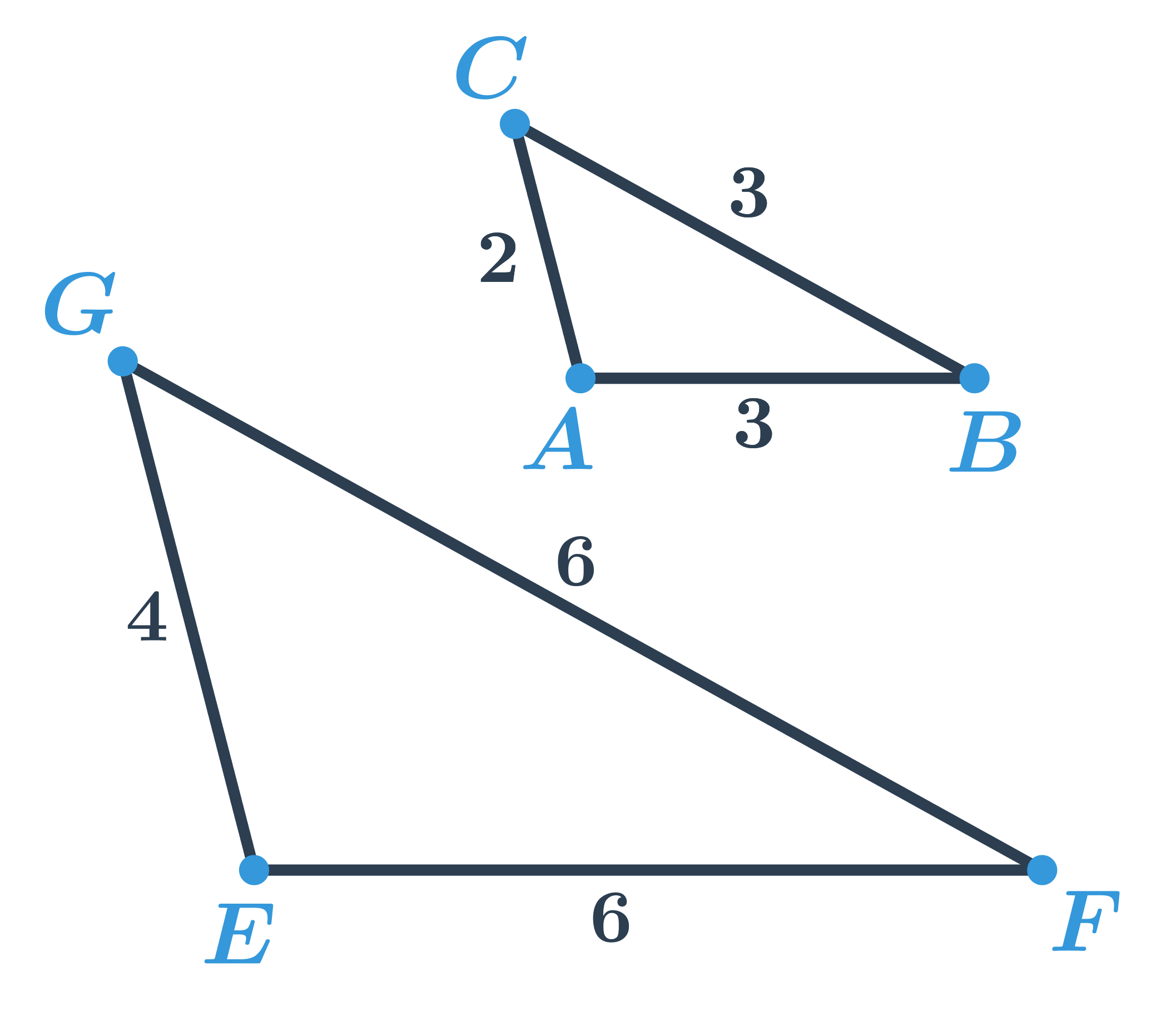
Trojúhelníky ABC a EFG jsou si podobné, protože poměr délek odpovídajících stran je stejný:
- \frac{EF}{AB}=\frac{6}{3}=2
- \frac{FG}{BC}=\frac{6}{3}=2
- \frac{GE}{CA}=\frac{4}{2}=2
Zapisujeme \bigtriangleup EFG\sim \bigtriangleup ABC, koeficient podobnosti je 2.
Příklad 2
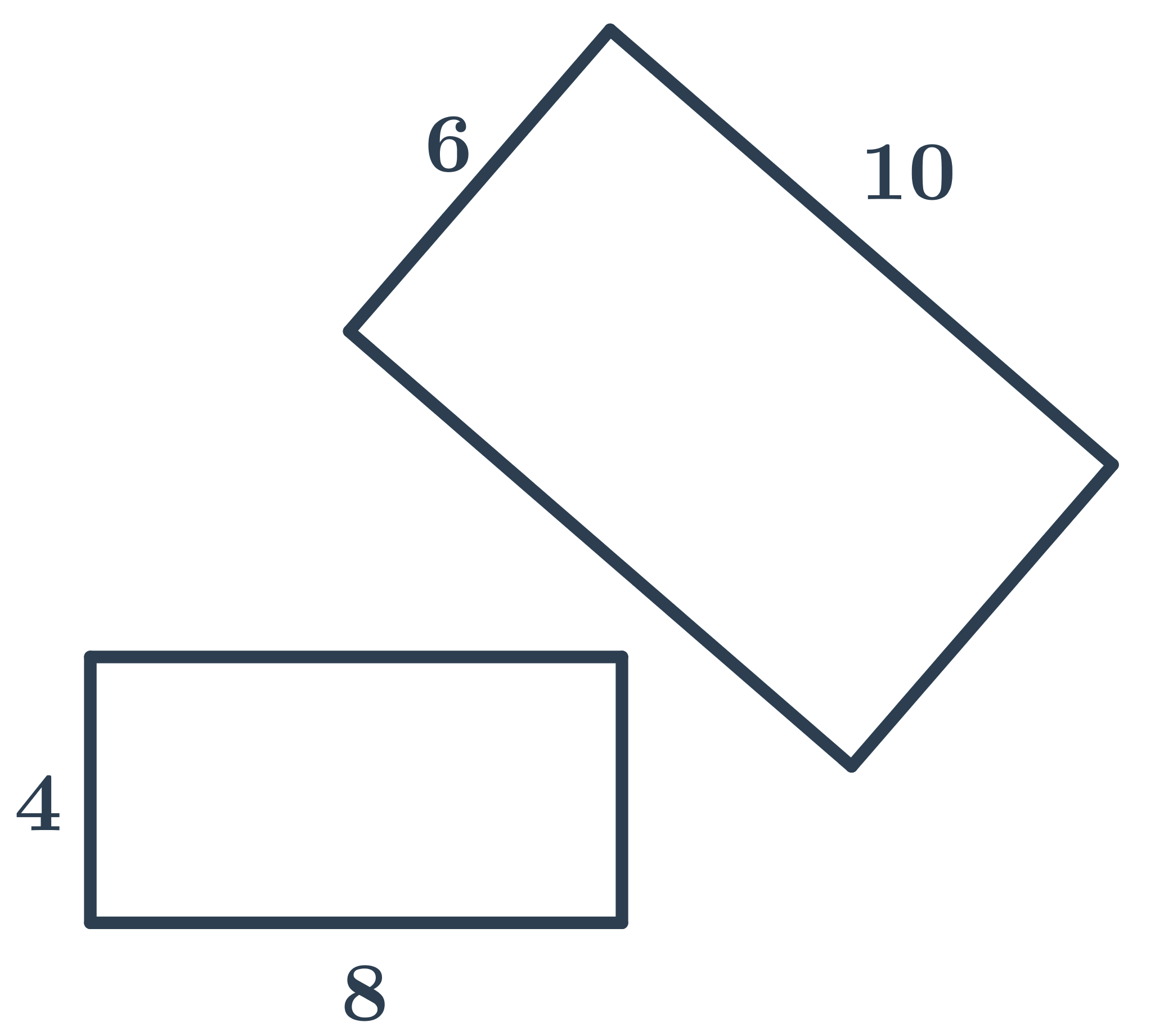
Obdélníky na obrázku nejsou podobné, protože poměr délek odpovídajících stran není stejný:
- poměr delších stran je \frac{10}{8}=\frac{5}{4}
- poměr kratších stran je \frac{6}{4}=\frac{3}{2}
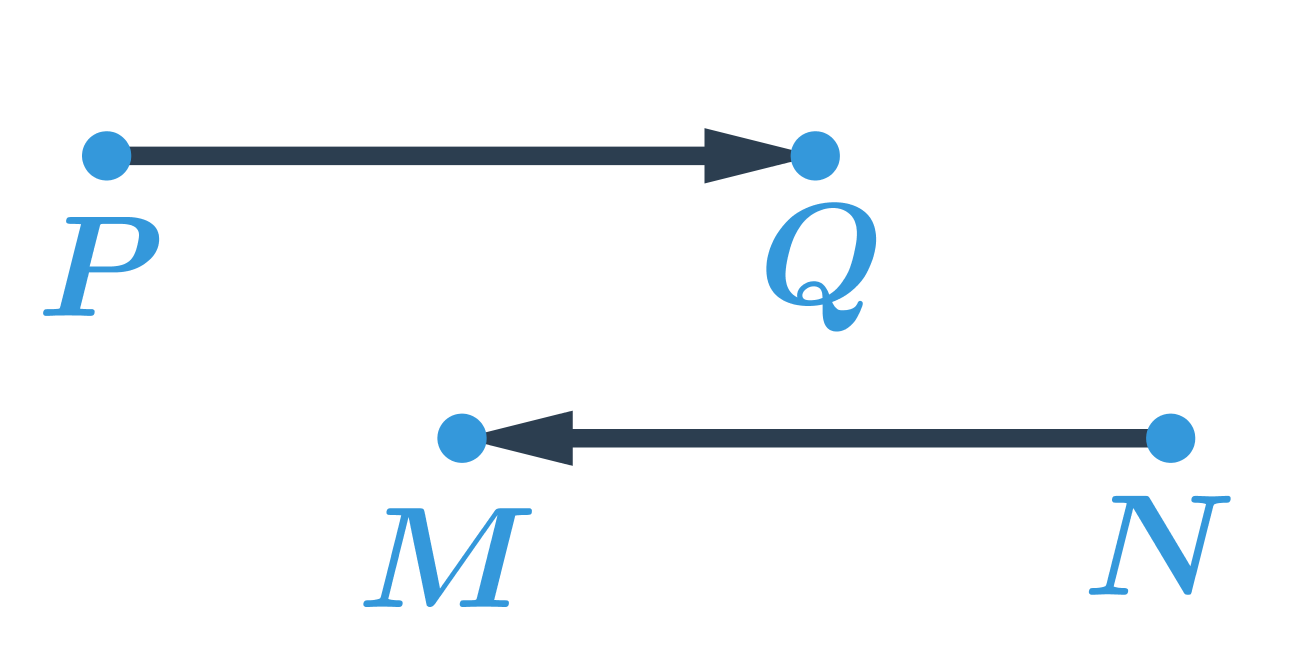
Posunutí je dané orientovanou úsečkou. Tato úsečka určuje směr a délku posunutí. Orientovaná úsečka je úsečka, u které rozlišujeme, který bod je počáteční a který koncový. Orientovanou úsečku označíme šipkou, která určí její směr. Zápis \overrightarrow{PQ} znamená, že počátečním bodem orientované úsečky je bod P a koncovým bodem bod Q. Na obrázku jsou orientované úsečky \overrightarrow{PQ} a \overrightarrow{NM}. Tyto úsečky mají stejnou délku, ale opačný směr.
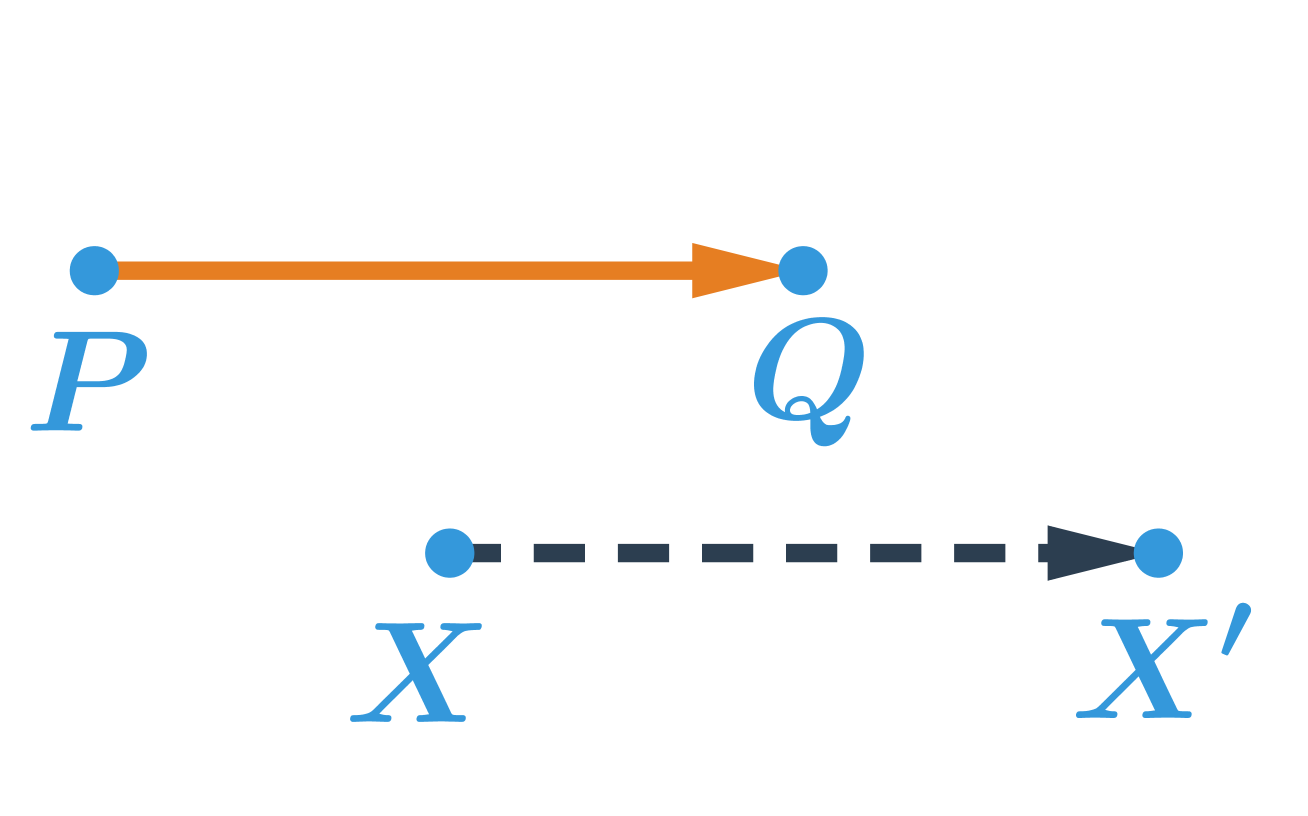
Obrazem bodu X v posunutí, které je určené orientovanou úsečkou \overrightarrow{PQ} je bod X', pro který platí, že orientovaná úsečka \overrightarrow{XX'} má stejnou velikost a stejný směr jako orientovaná úsečka \overrightarrow{PQ}.
Příklad: posunutí bodu
Obrazem bodu X v posunutí, které je určené orientovanou úsečkou \overrightarrow{PQ} je bod X':
Příklad: posunutí trojúhelníku
Obrazem trojúhelníku ABC v posunutí, které je určené orientovanou úsečkou \overrightarrow{PQ} je trojúhelník A'B'C': 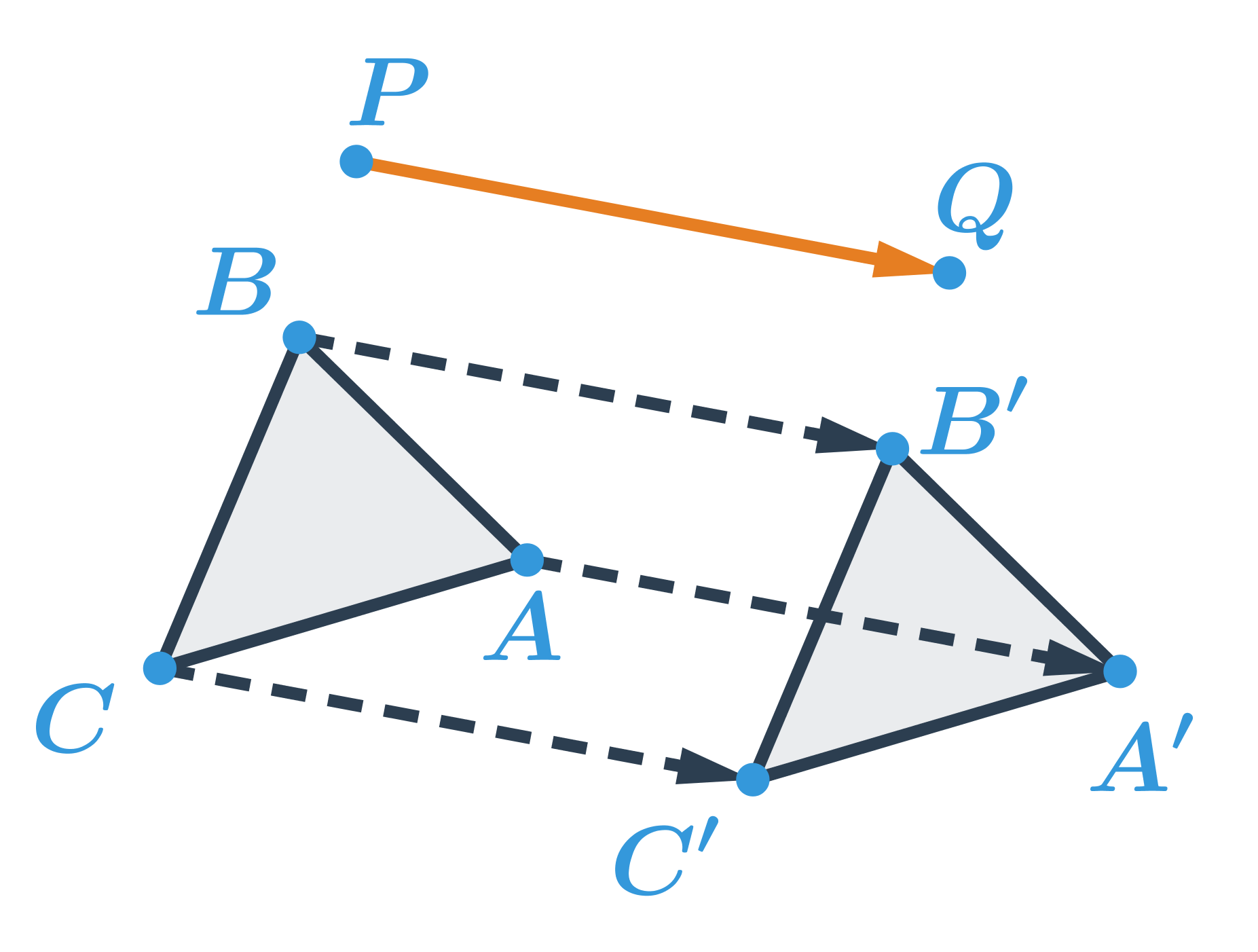
Posunutí zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
Posunutí s použitím vektorů
Posunutí můžeme definovat ještě druhým způsobem, známe‑li vektory. Posunutí je pak dané vektorem posunutí \vec{u}. Obrazem bodu X je bod X', pro který platí, že vektor \overrightarrow{XX'} má stejnou velikost a stejný směr jako vektor \vec{u}.
Příklad: posunutí bodu dané vektorem
Obrazem bodu X v posunutí, které je určené vektorem \vec{u} je bod X'
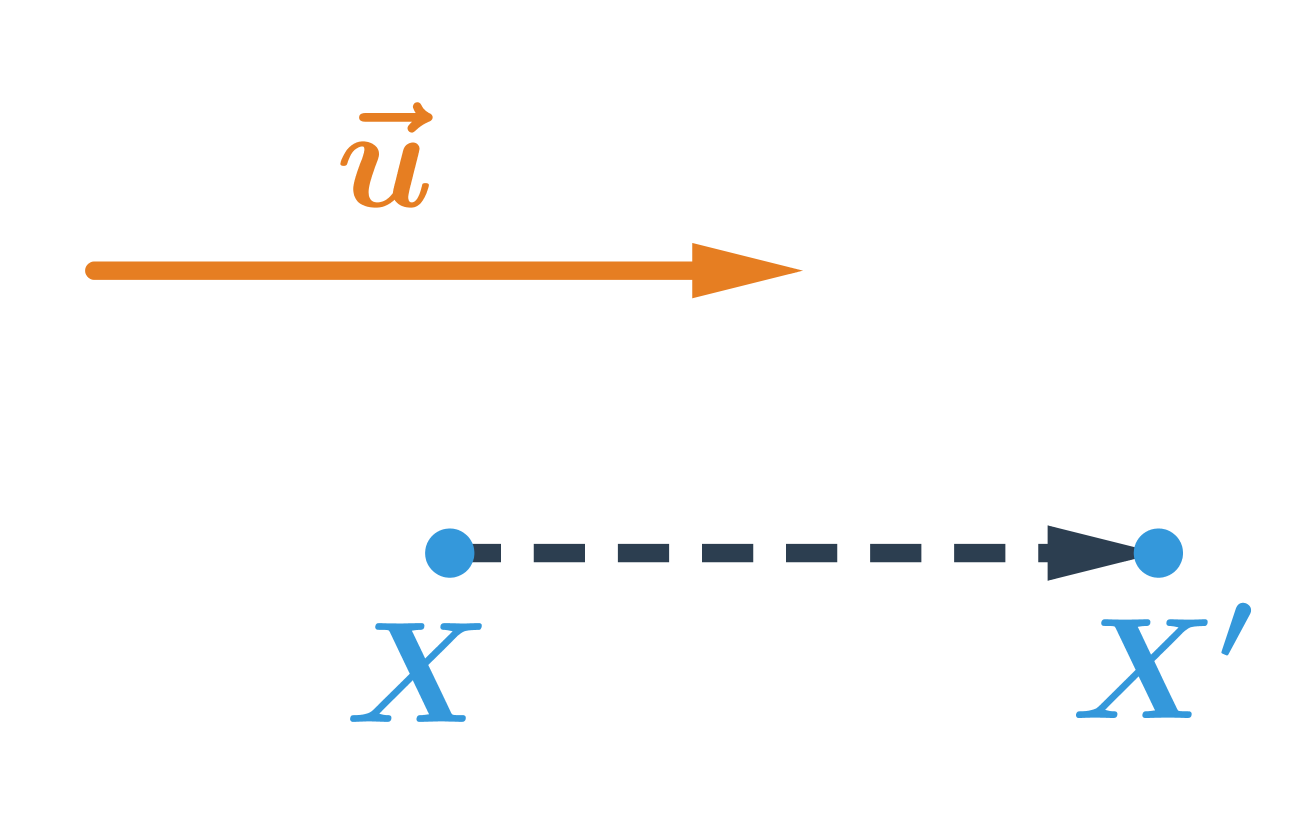
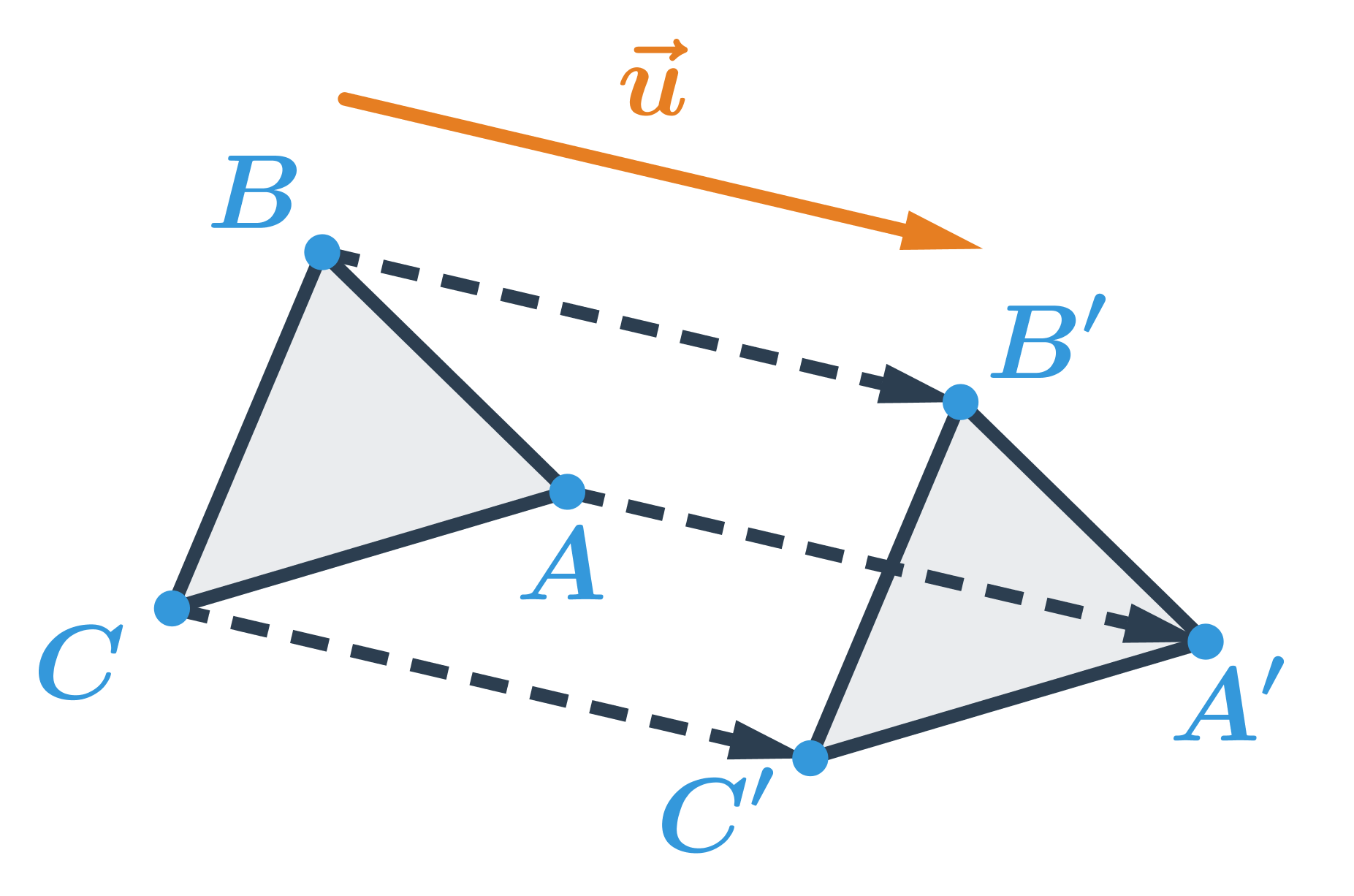
Příklad: posunutí trojúhelníku dané vektorem
Obrazem trojúhelníku ABC v posunutí, které je určené vektorem \vec{u} je trojúhelník A'B'C'
Otočení (rotace) je dané bodem S a orientovaným úhlem \alpha. Bod S se nazývá střed otočení. Pojem orientovaný úhel znamená, že rozlišujeme, zda otáčíme proti směru hodinových ručiček (kladný směr) nebo po směru hodinových ručiček (záporný směr). Obrazem bodu X je bod X', který má stejnou vzdálenost od středu S jako bod X a úhel XSX' má velikost \alpha.
Příklady
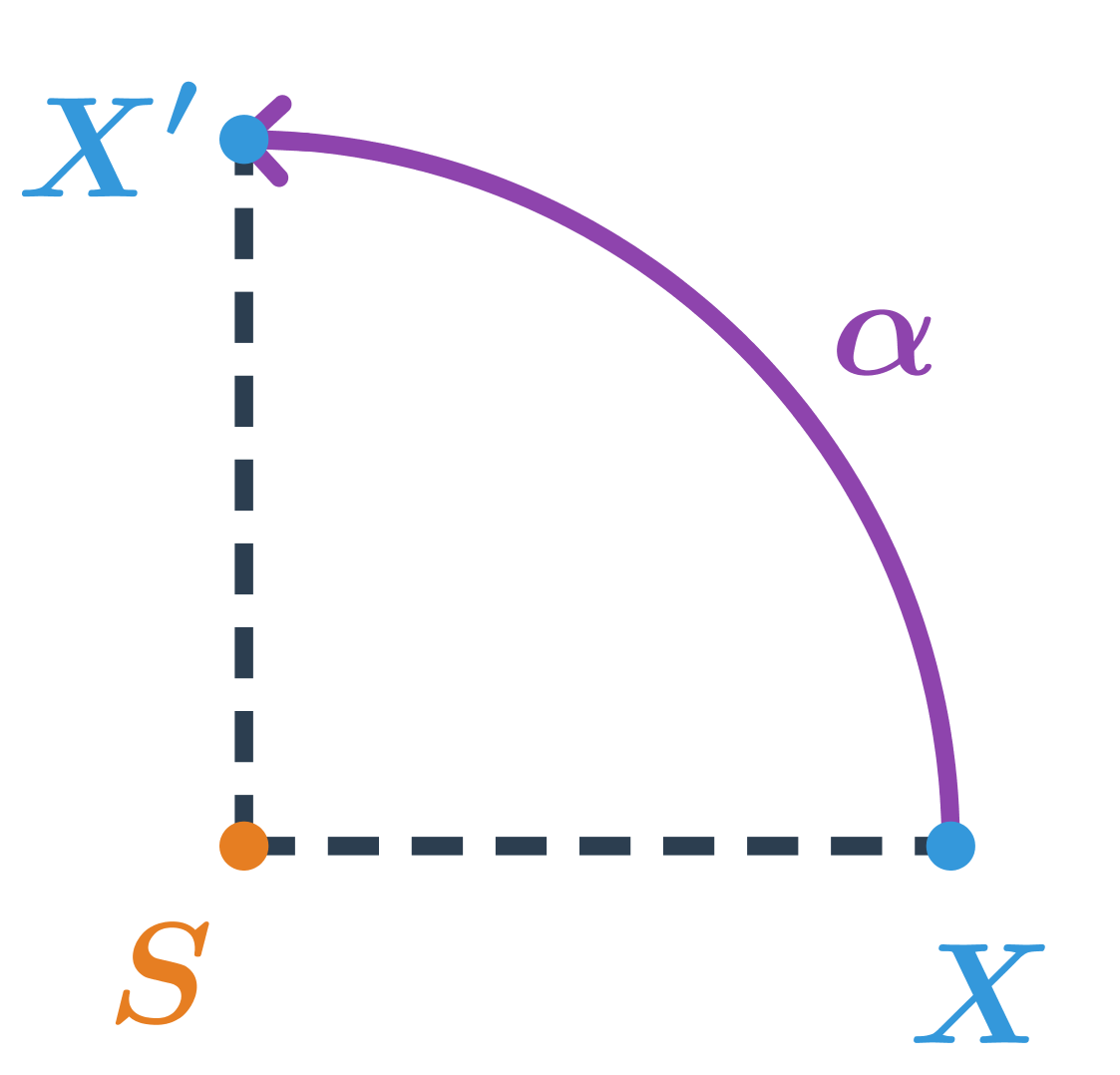
Bod X je otočený kolem středu S o 90^\circ proti směru hodinových ručiček.
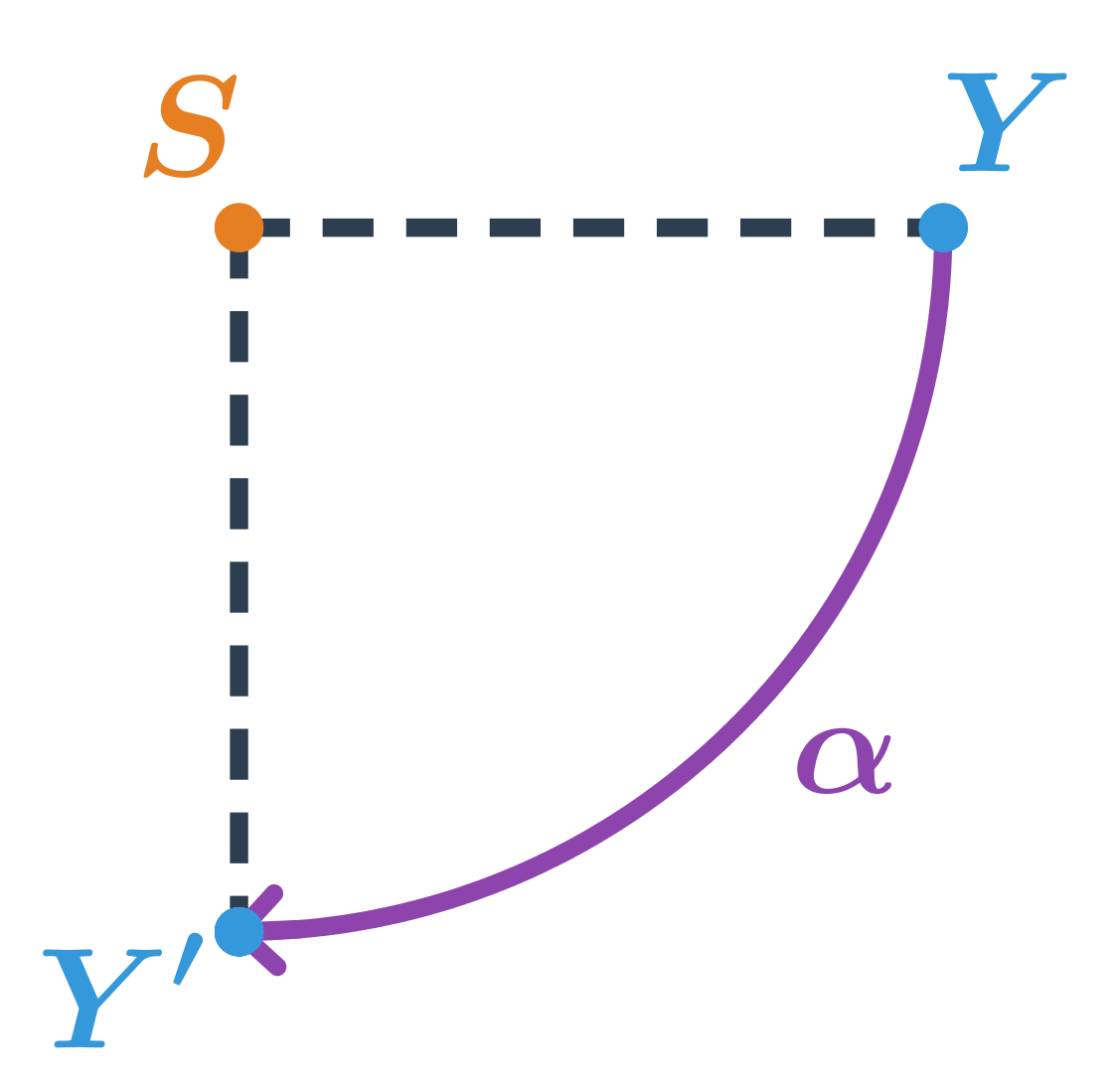
Bod Y je otočený kolem středu S o 90^\circ ve směru hodinových ručiček, tedy o úhel \alpha=-90^\circ.
Trojúhelník ABC je otočený kolem středu S o 60^\circ ve směru hodinových ručiček, tedy o úhel \alpha=-60^\circ.
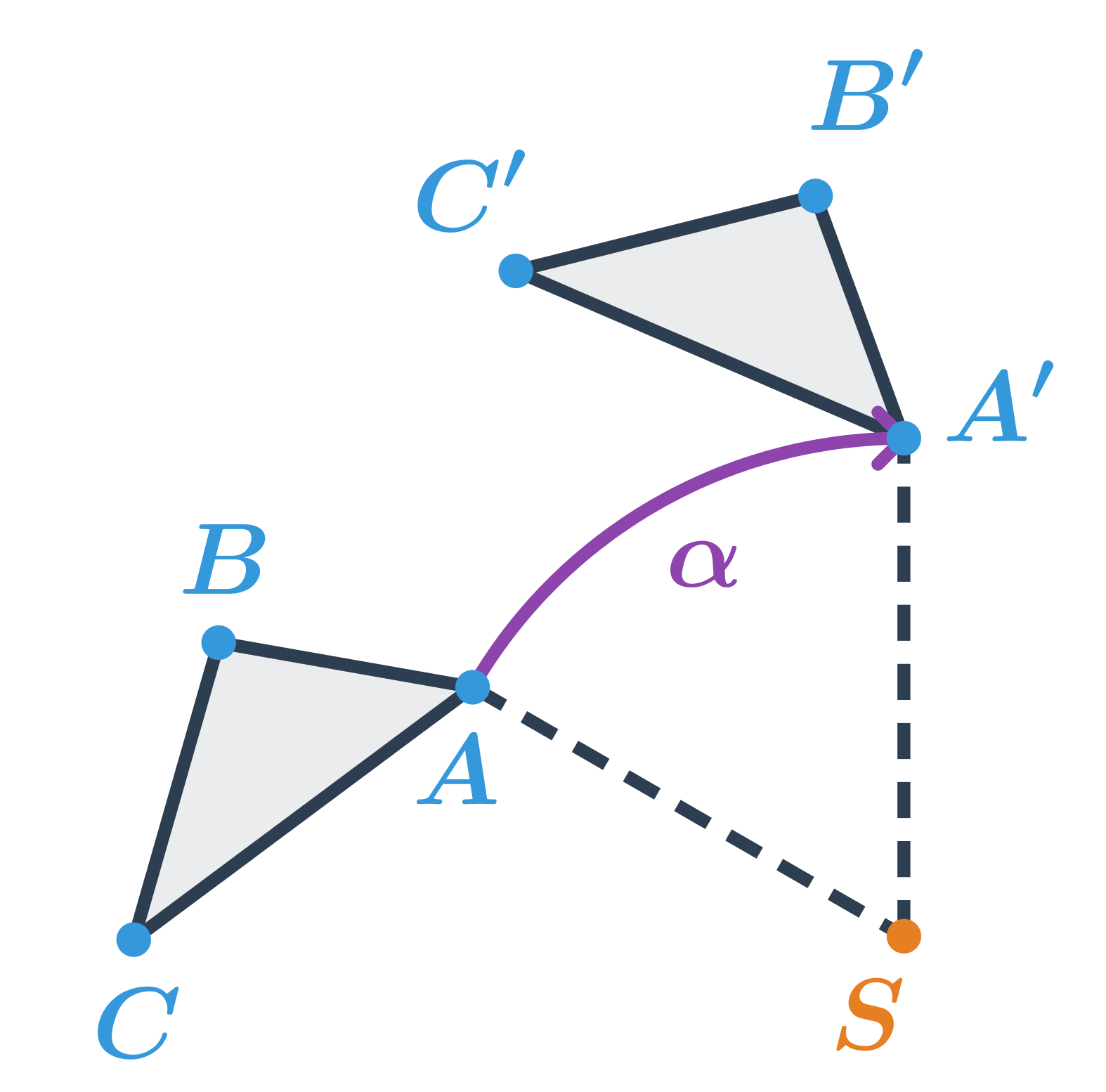
Otočení zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
NahoruStejnolehlost
Stejnolehlost je dána bodem S a nenulovým číslem \lambda. Bod S se nazývá střed stejnolehlosti, číslo \lambda je koeficient stejnolehlosti.
Obrazem bodu X je bod X', pro který platí:
- |SX'|=|\lambda| \cdot |SX|
- pro \lambda \gt 0 leží X, X' na stejné polopřímce s počátkem S
- pro \lambda \lt 0 leží X, X' na opačných polopřímkách s počátkem S
Na obrázku je vidět, kde leží obraz X' bodu X v závislosti na hodnotě koeficientu \lambda:
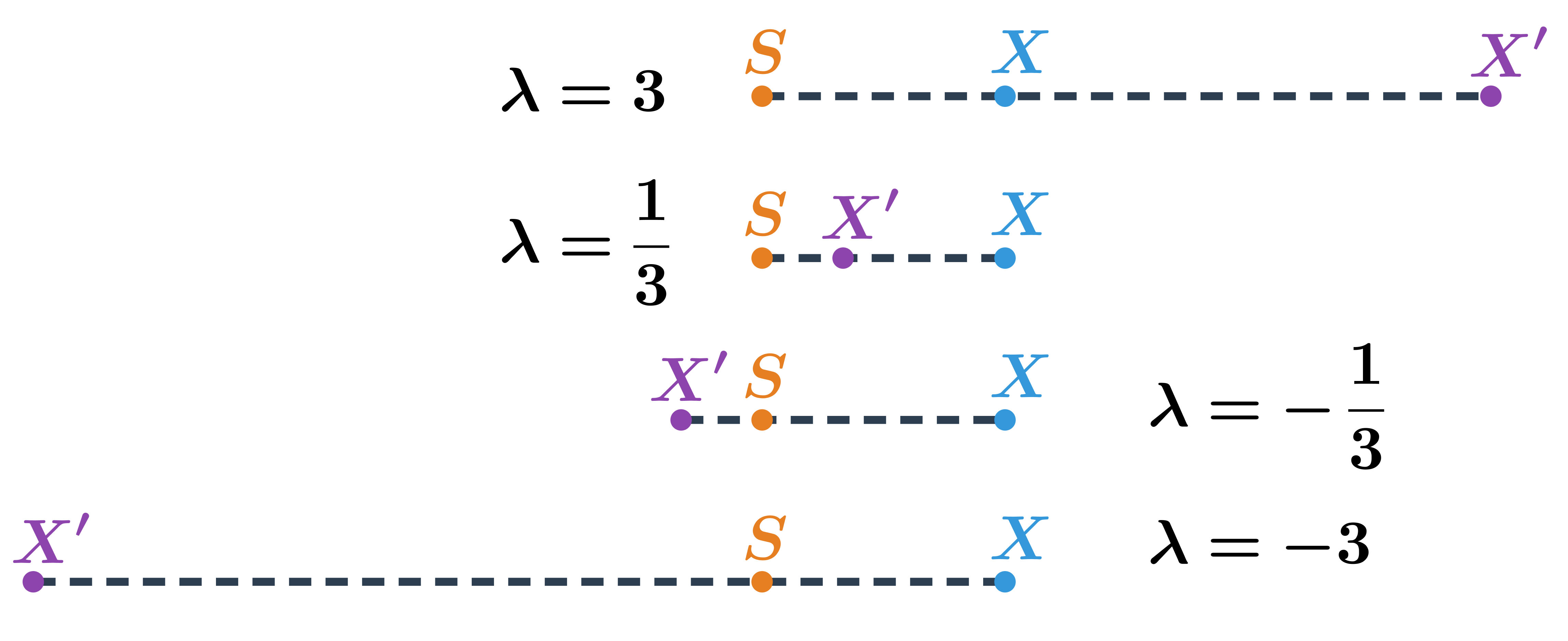
Přehled vlastností obrazu X' bodu X ve stejnolehlosti se středem S pro různé hodnoty koeficientu \lambda:
| \lambda \gt 0 | bod X' leží na polopřímce SX |
| \lambda \lt 0 | bod X' leží na polopřímce opačné k SX |
| |\lambda| \gt 1 | bod X' má od středu S větší vzdálenost než bod X |
| |\lambda| \lt 1 | bod X' má od středu S menší vzdálenost než bod X |
Příklad 1: obraz trojúhelníku ve stejnolehlosti
Obraz trojúhelníku ABC ve stejnolehlosti se středem S a koeficientem \lambda =\frac{1}{2}
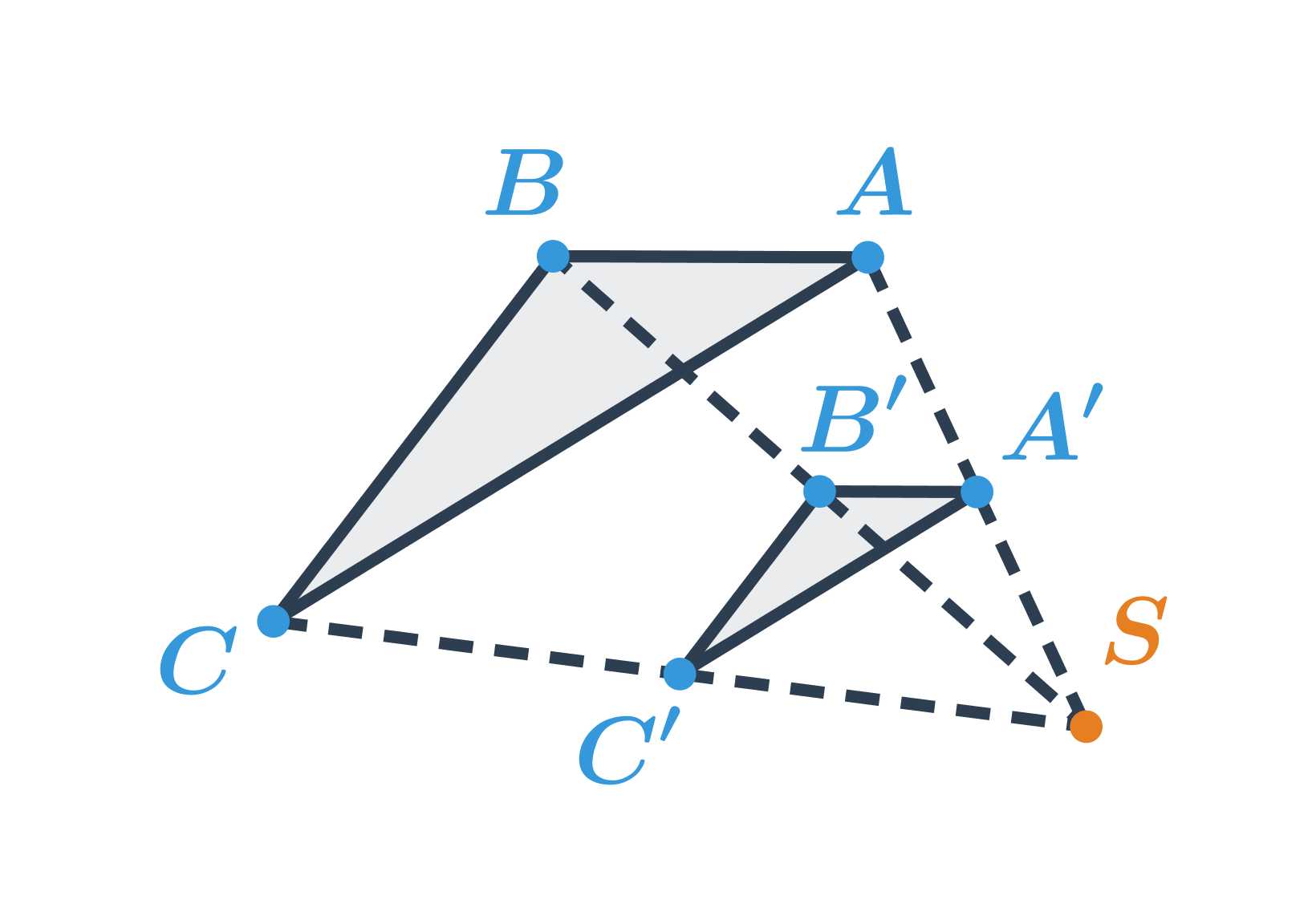
Pro délky odpovídajících si úseček platí: \frac{|SA'|} {|SA|}=\frac{|SB'|} {|SB|}=\frac{|SC'|} {|SC|}=\frac{1}{2}
Příklad 2: obraz kružnice ve stejnolehlosti
Obraz kružnice k ve stejnolehlosti se středem S a koeficientem \lambda =-3.
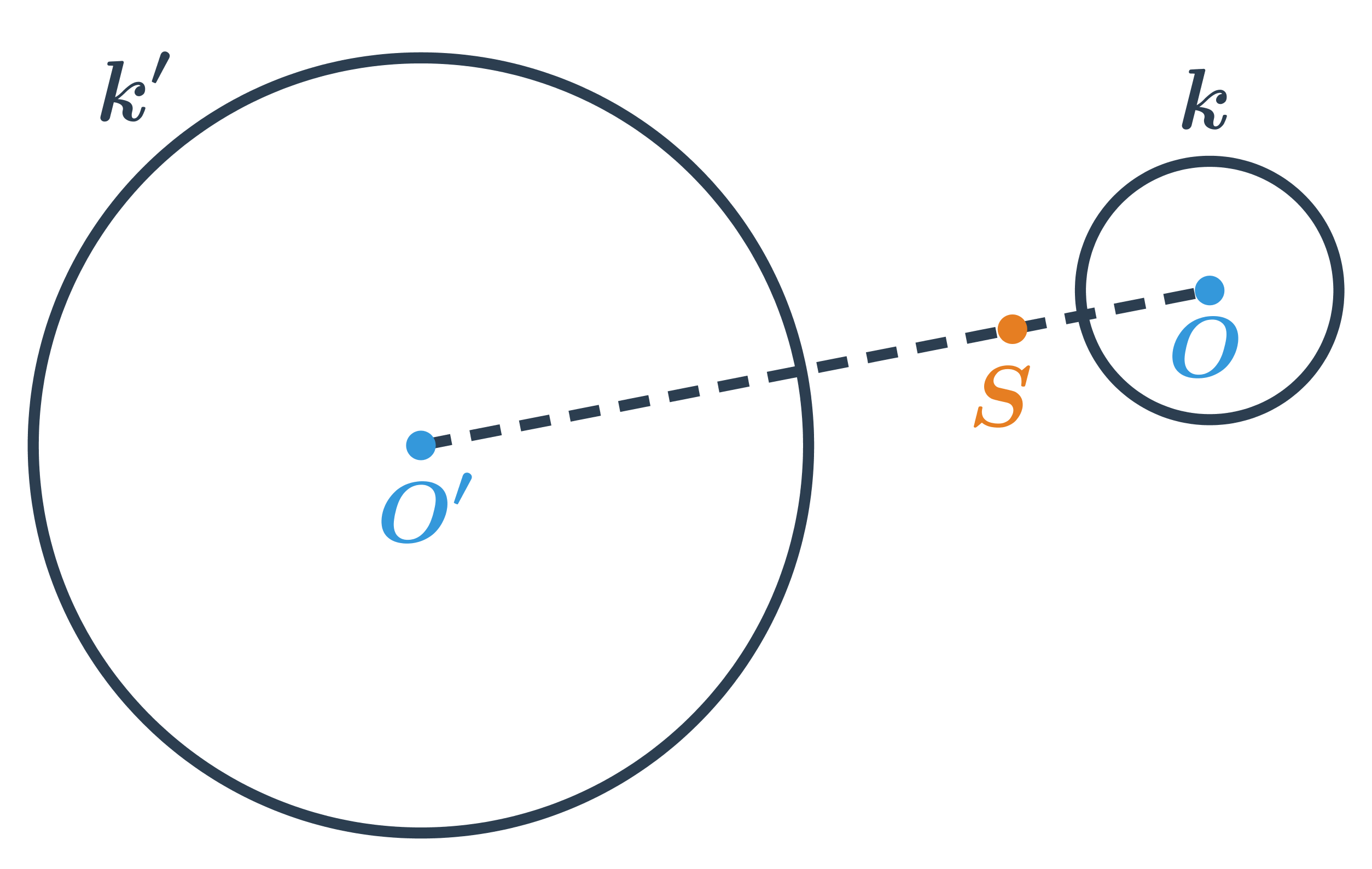
Stejnolehlost zachovává úhly a poměr délek, jde tedy o druh podobnosti.
Nahoru
