Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Výpis souhrnů
Délka a obvod
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Obvod trojúhelníku
Obvod trojúhelníku spočítáme jako součet délek jeho stran: o=a+b+c
Příklad: obvod trojúhelníku
Trojúhelník na obrázku má délky stran a=10, b=8, c=14, takže jeho obvod je o=a+b+c=10+8+14=32.
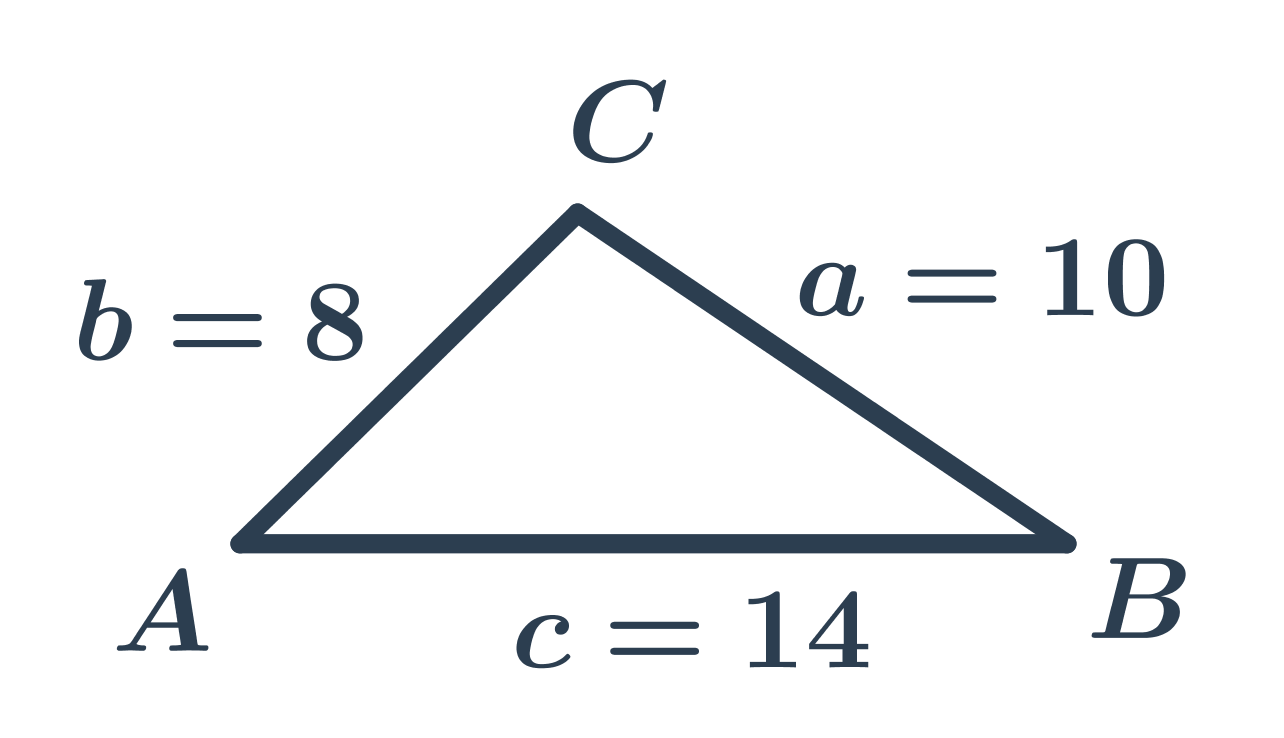
Obvod čtverce a obdélníku
Obvod čtverce o straně délky a je o=a+ a+a+a= 4a.
Obvod obdélníku se stranami o délkách a,b je roven o=a + b + a + b = 2\cdot (a+b).
NahoruObvod rovnoběžníku
Obvod rovnoběžníku se stranami o délkách a,b je roven S=a + b + a + b = 2\cdot (a+b).
NahoruObvod lichoběžníku
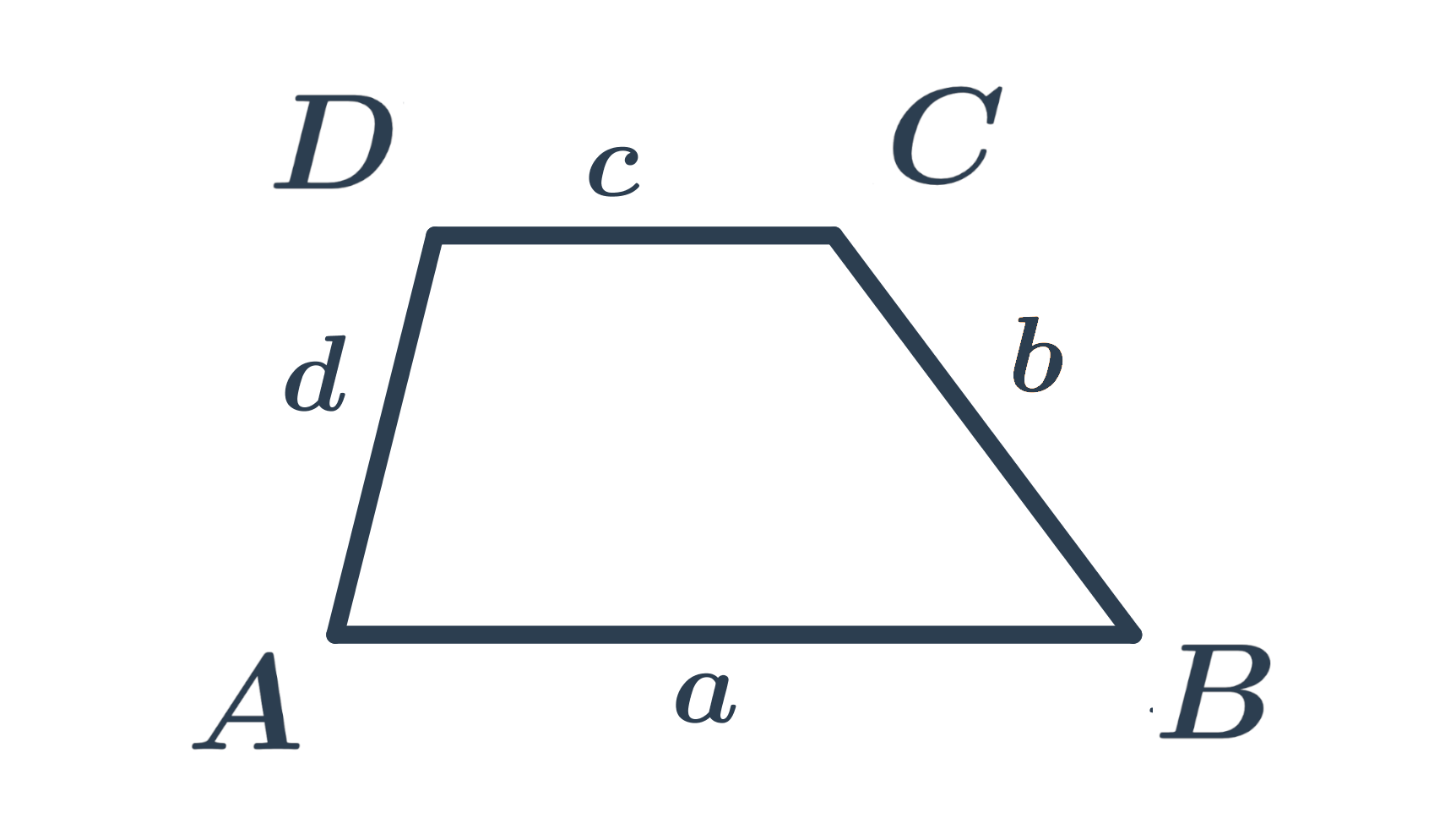
Obvod lichoběžníku je součet délek jeho stran. Tedy obvod lichoběžníku ABCD se stranami o délkách a,b,c,d vypočítáme podle vzorečku o=a+b+c+d.
Obvod kruhu, délka kružnice
Vzorec pro obvod kruhu
Obvod kruhu (i kružnice) o poloměru r je o=2\pi r. Pro průměr d platí o = \pi d.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obvodu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru r nebo průměru d = 2r. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obvodu kruhu přibližuje níže uvedený obrázek. Obvod oranžového čtverce je 8\cdot r. Obvod kruhu je „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.
Příklady: obvod kruhu
- Mějme kruh o poloměru 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Kružnice o průměru 2 cm má délku \pi \cdot 2 \approx 6,3 cm.
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud jej chceme obejít po jeho okrajové čáře, ujdeme 2 \pi \cdot 9{,}1 \approx 57 metrů.
Délka oblouku
Délku oblouku, který na kružnici o poloměru r odpovídá středovému úhlu \alpha spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Příklad – délka oblouku odpovídajícího 90^{\circ}
Délka oblouku na obrázku je:
\frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
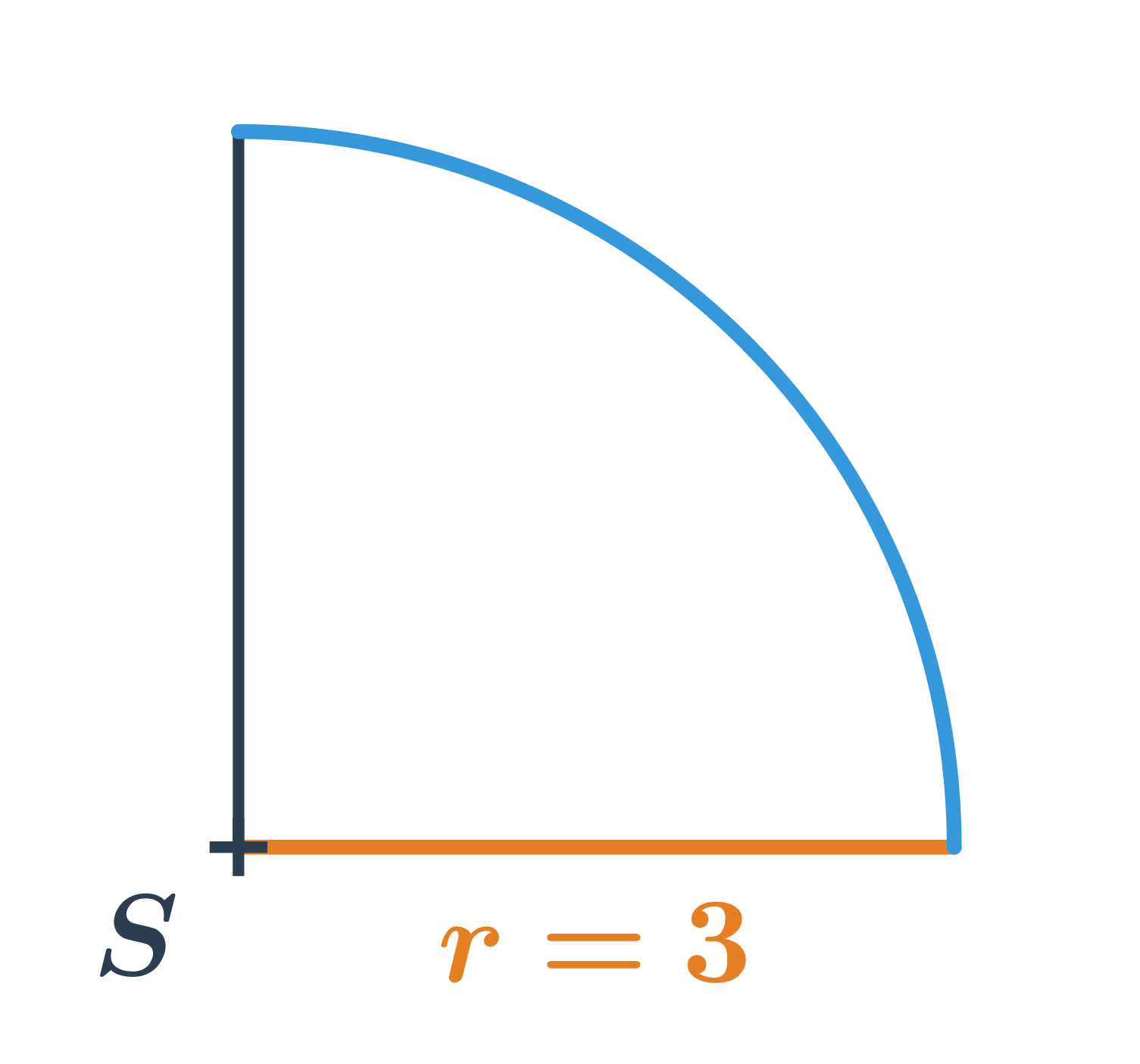Jedná se o čtvrtinu délky kružnice.
Příklad – délka oblouku odpovídajícího 360^{\circ}
Délka celé kružnice (tedy pro celých 360^{\circ}) je:
\frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obvod: mix
Obvod u trojúhelníků a čtyřúhelníků je prostě součet délek jejich stran.
| Útvar | Vlastnosti | Obvod |
|---|---|---|
| trojúhelník | strany a, b, c | o = a + b + c |
| čtverec | strana a | o = 4a |
| obdélník | strany a, b | o = 2(a+b) |
| rovnoběžník | strany a, b | o = 2(a+b) |
| obecný čtyřúhelník | strany a, b, c, d | o = a+b+c+d |
