Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Výpis souhrnů
Goniometrické funkce
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Goniometrické funkce
Goniometrické funkce (nebo též trigonometrické funkce) jsou skupinou funkcí, které dávají do vztahu úhel v pravoúhlém trojúhelníku a poměr dvou jeho stran. Mají široké využití v geometrii a mnoho praktických aplikací – například v navigaci, nebeské mechanice nebo geodézii. Tyto funkce se vyskytují i v dalších oblastech matematiky, jako jsou komplexní čísla nebo nekonečné řady.
Základními goniometrickými funkcemi jsou sinus, kosinus a tangens. Méně často pak můžeme narazit také na sekans, kosekans a kotangens. Inverzní funkce ke goniometrickým funkcím se nazývají cyklometrické (například arkus sinus a arkus tangens).
Podrobněji se goniometrickými funkcemi zabývají tato podtémata:
- Goniometrické funkce a pravoúhlý trojúhelník – základní vztah mezi úhlem a poměrem stran v pravoúhlém trojúhelníku
- Hodnoty goniometrických funkcí – často používané hodnoty základních goniometrických funkcí pro základní úhly (např. 0°, 30°, 45°, 60°, 90°)
- Goniometrické funkce: vztahy a vzorce – klíčové vztahy mezi jednotlivými goniometrickými funkcemi a využití těchto vztahů
- Vlastnosti goniometrických funkcí – vlastnosti goniometrických funkcí, jako jsou periodičnost, symetrie
- Grafy goniometrických funkcí – grafické znázornění goniometrických funkcí
K dispozici je také pomůcka k vytištění Goniometrické funkce: přehled.
NahoruGoniometrické funkce a pravoúhlý trojúhelník
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
- Sinus (\sin) úhlu \alpha je poměr délky odvěsny protilehlé úhlu \alpha a délky přepony.
- Kosinus (\cos) úhlu \alpha je poměr délky odvěsny přilehlé úhlu \alpha a délky přepony.
- Tangens (\tan) úhlu \alpha je poměr délky odvěsny protilehlé úhlu \alpha a délky odvěsny přilehlé úhlu \alpha.
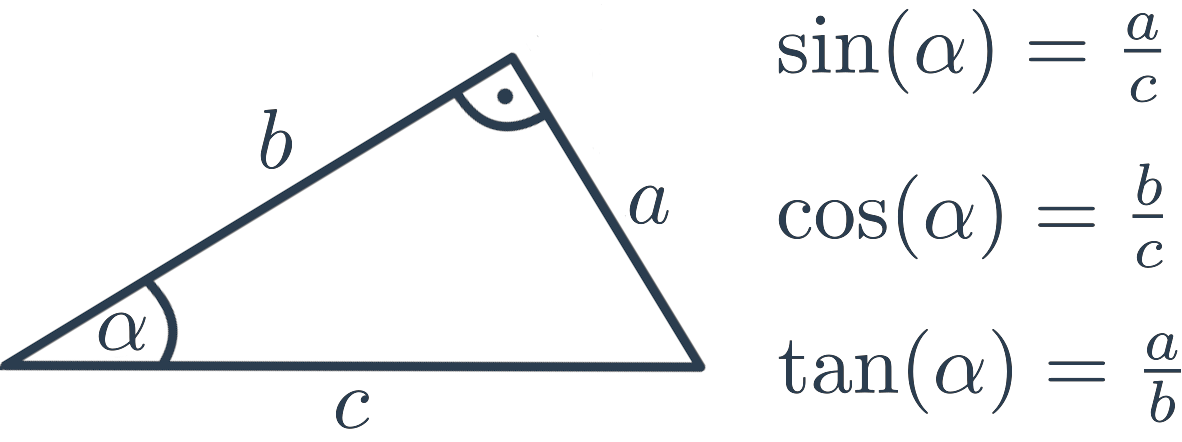
Pokud si pamatujeme význačné hodnoty goniometrických funkcí (jako např. \sin 30^{\circ}=\frac{1}{2}), nebo aspoň máme k dispozici kalkulačku nebo matematické tabulky, znamená pro nás znát hodnotu \sin, \cos nebo \tan některého úhlu v pravoúhlém trojúhelníku totéž jako znát velikost samotného úhlu.
Příklad: známe strany pravoúhlého trojúhelníku, dopočítáme úhly
Pravoúhlý trojúhelník ABC má délky stran a=24, b=10, c=26. Jaké jsou velikosti jeho vnitřních úhlů?
- Pokud je trojúhelník pravoúhlý, je velikost úhlu \gamma naproti nejdelší straně c rovna 90^{\circ}.
- Víme, že \sin \alpha je podíl protilehlé strany a přepony, tedy \sin \alpha=\frac{a}{c}.
- Dosadíme známé velikosti stran: \sin \alpha = \frac{24}{26}\doteq 0{,}923
- Příslušná velikost úhlu je: \alpha \doteq 67^{\circ}
- Z \alpha+\beta+\gamma=180^{\circ} dopočítáme, že \beta je zhruba 23^{\circ}.
Kontrola:
- Víme, že \cos \beta je podíl strany přilehlé k úhlu \beta a přepony, tedy \cos \beta = \frac{a}{c}.
- Dosadíme známé velikosti stran: \cos \beta = \frac{24}{26}\doteq 0{,}923
- Příslušná velikost úhlu je: \beta \doteq 23^{\circ}
Příklad: známe úhel, dopočítáme délku strany pomocí \sin
Mějme pravoúhlý trojúhelník ABC s pravým úhlem u vrcholu C, ve kterém platí \sin \alpha = \frac{1}{2} a délka přepony je c=10. Jaká je délka strany a?
- Víme, že hodnotu \sin \alpha spočítáme jako podíl délky strany protilehlé k úhlu \alpha a délky přepony, tedy \sin \alpha = \frac{a}{c}.
- Dosadíme do této rovnosti za \sin \alpha a za c.
- \frac{1}{2} = \frac{a}{10} \Rightarrow a=5
- Délka strany a je 5.
Příklad: známe úhel, dopočítáme délku strany pomocí \cos
Mějme pravoúhlý trojúhelník ABC s pravým úhlem u vrcholu C, ve kterém platí \cos \alpha = \frac{3}{5} a délka přepony je c=15. Jaká je délka strany a?
- Víme, že hodnotu \cos \alpha spočítáme jako podíl délky strany přilehlé k úhlu \alpha a délky přepony, tedy \cos \alpha = \frac{b}{c}.
- Dosadíme do této rovnosti za \cos \alpha a za c.
- \frac{3}{5} = \frac{b}{15} \Rightarrow b=9
- Délka strany b je 9. Chtěli jsme spočítat délku strany a, což zvládneme ze známých hodnot b,c jednoduše pomocí Pythagorovy věty.
- a^2 = c^2-b^2=255-81=144 \Rightarrow a=12
- Délka strany a je 12.
Příklad: známe úhel, dopočítáme délku strany pomocí \tan
Mějme pravoúhlý trojúhelník ABC s úhlem \alpha = 60^{\circ} a s délkou delší odvěsny 6. Jaká je délka druhé odvěsny?
- Víme, že v pravoúhlém trojúhelníku ABC jsou vnitřní úhly 60^{\circ}, 90^{\circ}, dopočítáme zbývající úhel.
- \beta=180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}
- Vidíme, že \beta < \alpha.
- Delší odvěsna bude v trojúhelníku proti většímu úhlu, takže máme a=6.
- \tan \alpha je podíl odvěsny protilehlé úhlu \alpha a odvěsny přilehlé, tedy \tan \alpha = \frac{a}{b}.
- Dosadíme za \tan \alpha hodnotu \tan 60^{\circ} = \sqrt{3} (zjistíme z tabulek nebo z kalkulačky), dosadíme také b=6.
- \sqrt{3} = \frac{6}{b} \Rightarrow b= \frac{6}{\sqrt{3}} = 2\sqrt{3}
- Délka kratší odvěsny je b=2\sqrt{3}.
Hodnoty goniometrických funkcí
Často používané hodnoty goniometrických funkcí ilustruje tento obrázek jednotkové kružnice:
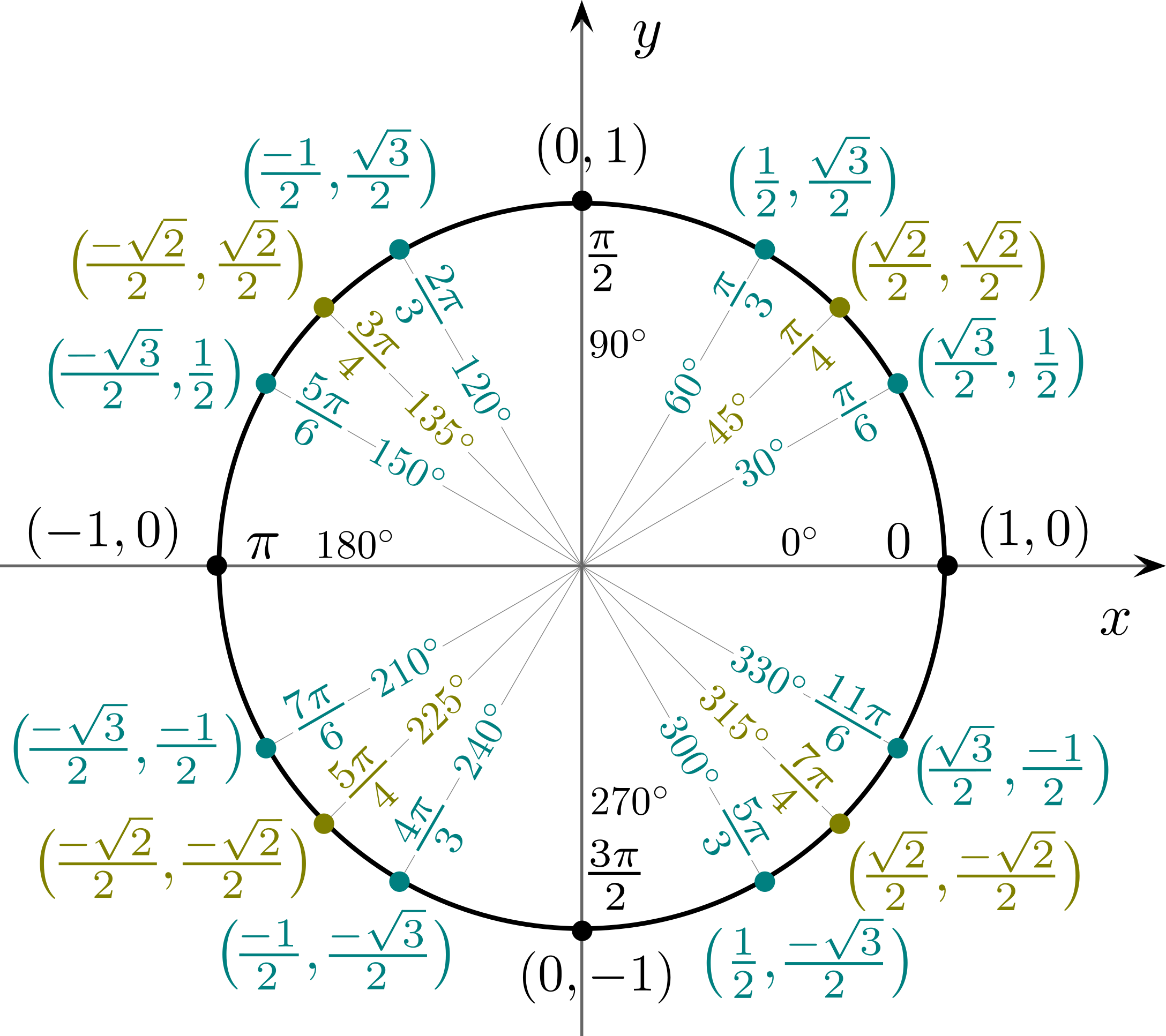
Polopřímka, která svírá úhel \alpha s kladnou částí osy x a začíná v počátku souřadnic, protíná jednotkovou kružnici v bodě se souřadnicemi [\cos \alpha; \sin \alpha], neboli:
- x-ová souřadnice bodu odpovídá hodnotě \cos daného úhlu,
- y-ová souřadnice bodu odpovídá hodnotě \sin daného úhlu.
Příklad: sinus a kosinus úhlu 30°
Polopřímka, která svírá s kladnou částí osy x úhel 30° (to je \frac{\pi}{6} radiánů), protíná jednotkovou kružnici v bodě [\frac{\sqrt{3}}{2}; \frac12]. Takže máme:
- \cos 30^{\circ} = \frac{\sqrt{3}}{2}
- \sin 30^{\circ} = \frac12
Goniometrické funkce: vztahy a vzorce
Pro goniometrické funkce platí celá řada vztahů a vzorců. Výběr těch základních:
Pro záporné hodnoty úhlů
| \sin(-x) = -\sin x (lichá funkce) |
| \cos(-x) = \cos x (sudá funkce) |
| \tan(-x) = -\tan x (lichá funkce) |
Vztahy mezi funkcemi a posuny
| \sin^2 x + \cos^2 x = 1 |
| \tan x = \frac{\sin x}{\cos x} |
| \sin(x+\frac{\pi}{2}) = \cos x |
| \sin(x+2\pi) = \sin x (perioda 2\pi) |
| \sin(x+\pi) = -\sin x |
Vzorce pro goniometrické funkce součtu argumentů
| \sin(x+y) = \sin x \cos y+\cos x \sin y |
| \sin(x-y) = \sin x \cos y - \cos x \sin y |
| \cos(x+y) = \cos x \cos y - \sin x \sin y |
| \cos(x-y) = \cos x \cos y + \sin x \sin y |
Vzorce pro součet hodnot goniometrických funkcí
| \sin x + \sin y = 2 \sin(\frac{x+y}{2})\cos(\frac{x-y}{2}) |
| \sin x - \sin y = 2\cos(\frac{x+y}{2})\sin(\frac{x-y}{2}) |
| \cos x + \cos y = 2\cos(\frac{x+y}{2})\cos(\frac{x-y}{2}) |
| \cos x - \cos y = -2 \sin(\frac{x+y}{2})\sin(\frac{x-y}{2}) |
Dvojnásobný argument
| \sin 2x = 2\sin x \cos x |
| \cos 2x = \cos^2 x - \sin^2 x |
| \tan 2x = \frac{2\tan x}{1-\tan^2 x} |
Vlastnosti goniometrických funkcí
Pro obě funkce \sin x a \cos x platí:
- definiční obor je množina reálných čísel,
- obor hodnot je interval \langle -1, 1 \rangle,
- funkce je omezená,
- funkce je periodická s periodou 2\pi,
- funkce není prostá.
Pro funkci \sin x platí:
- je lichá,
- nulové hodnoty nabývá v bodech x=k\pi.
Pro funkci \cos x platí:
- je sudá,
- nulové hodnoty nabývá v bodech x=(2k+1)\frac{\pi}{2}.
Pro funkci \tan x platí:
- definiční obor je \{x \in \mathbb{R}: x \neq (2k+1)\frac{\pi}{2} \},
- obor hodnot je množina reálných čísel,
- funkce je lichá,
- funkce je periodická s periodou \pi,
- funkce je neomezená,
- nulové hodnoty nabývá v bodech x=k\pi.
Grafy goniometrických funkcí
Grafy základních goniometrických funkcí intuitivně
Všimněte si
- graf které funkce protíná osu y v bodě x=0, y=0? (\sin, \tan)
- graf které funkce protíná osu y v bodě x=0, y=1? (\cos)
- která funkce je definovaná pro všechna x \in \mathbb{R}? (\sin, \cos)
Grafy goniometrických funkcí s popsanými osami
Funkce sinus y=\sin x:
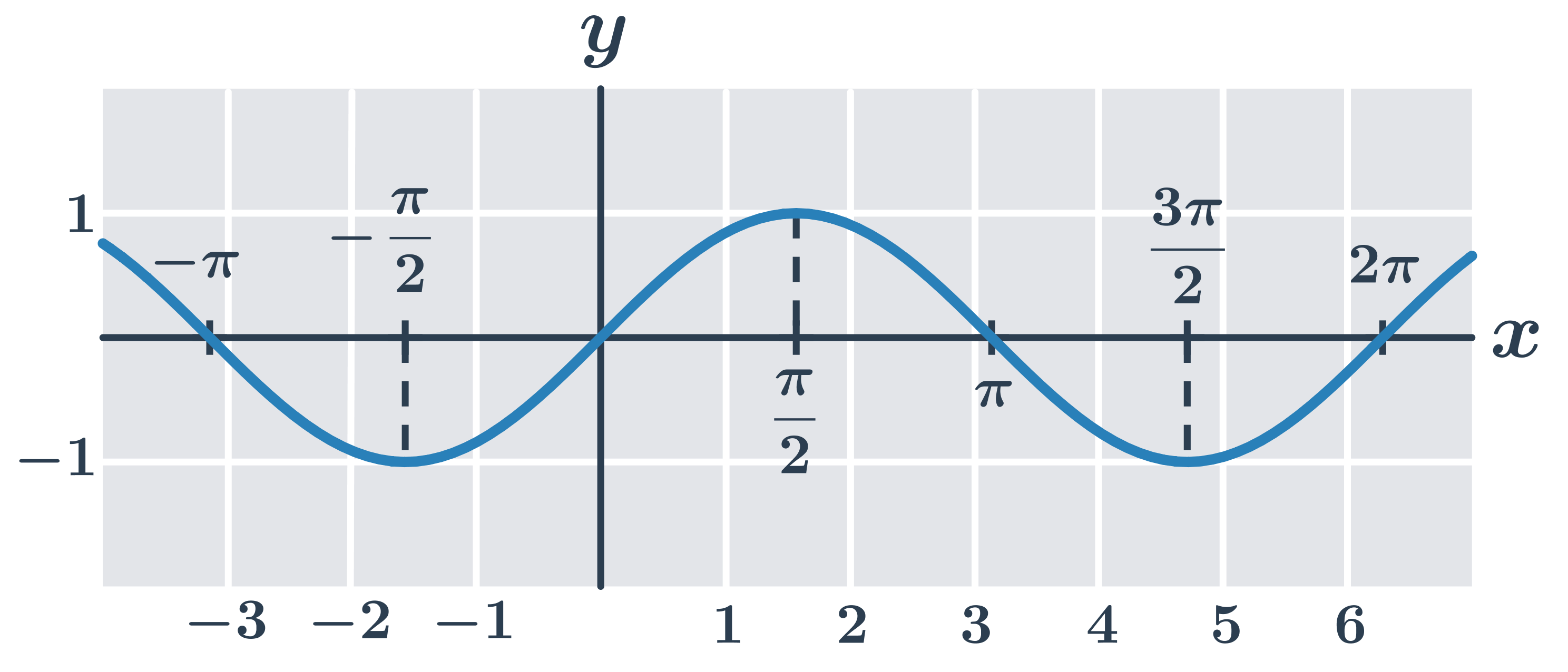
Funkce cosinus y=\cos x:
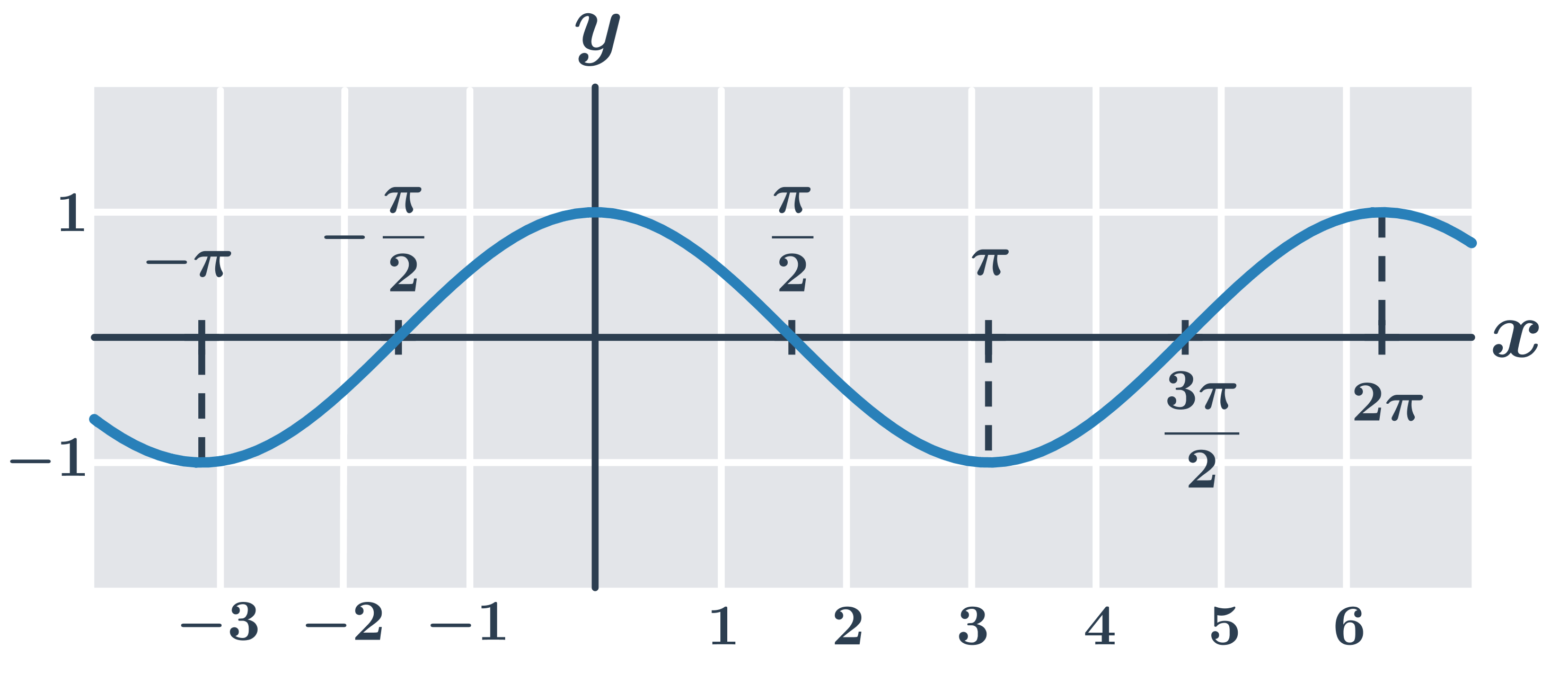
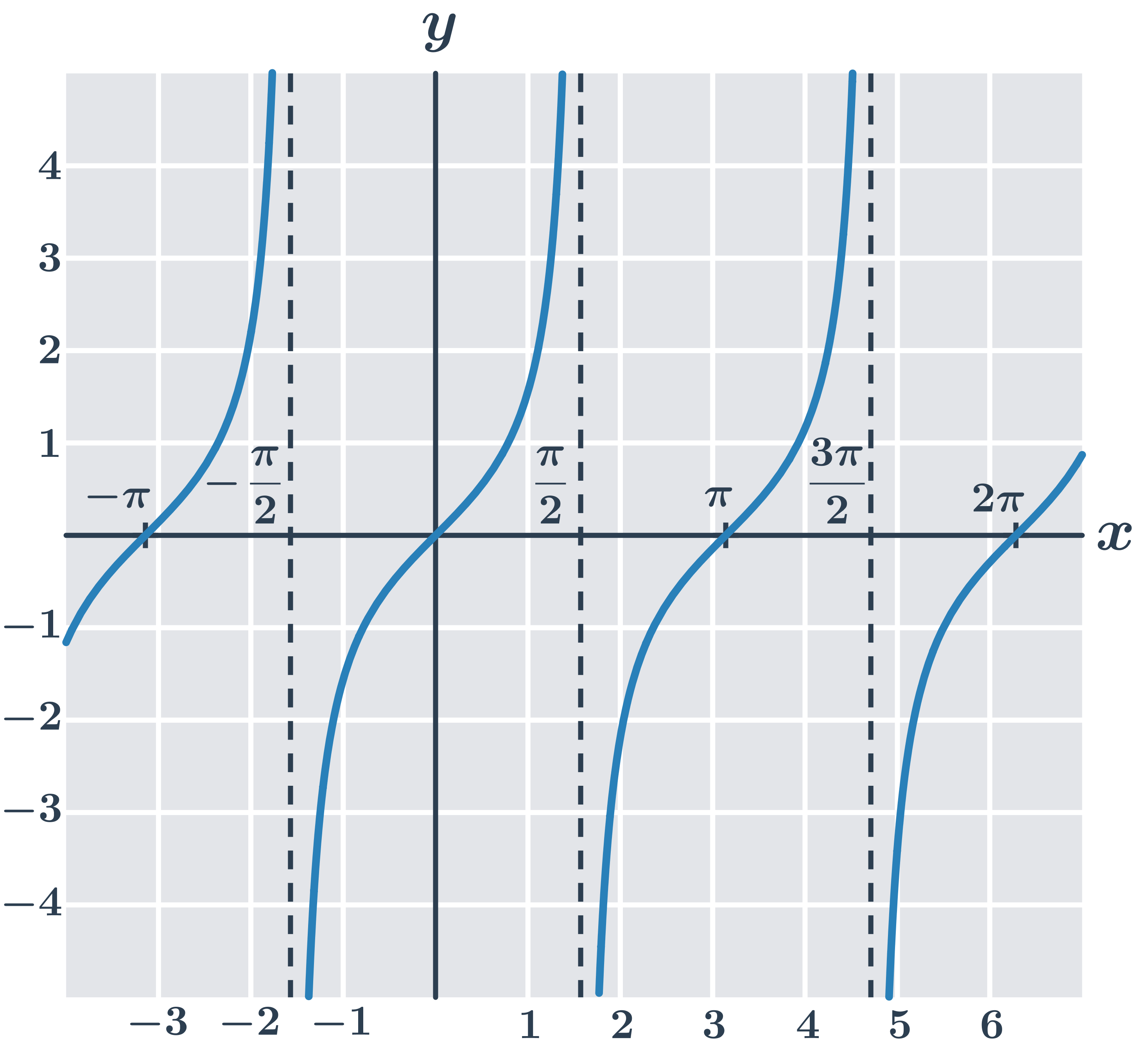
Funkce tangens y=\tan x:
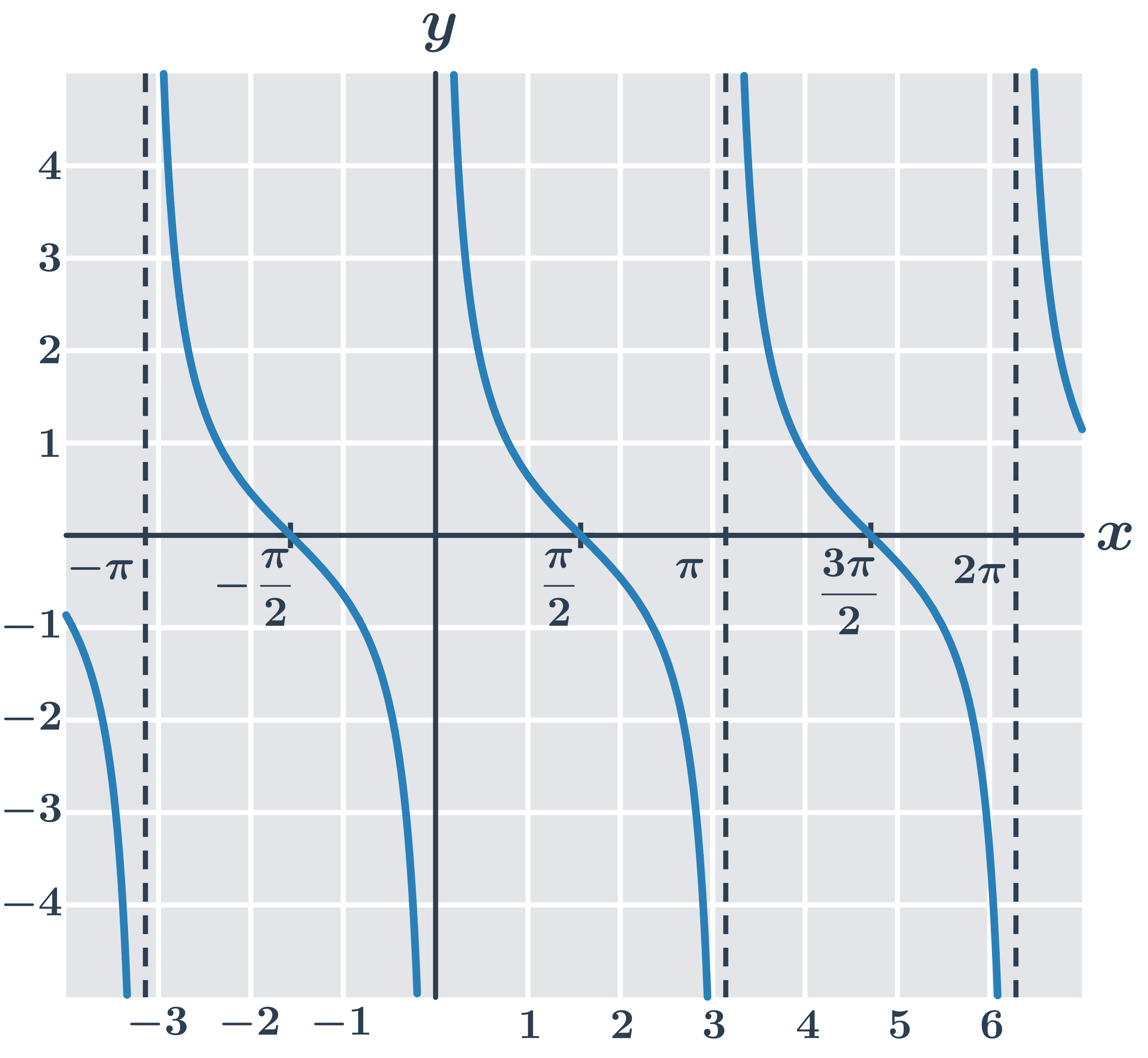
Funkce cotangens y=\cot x:
Dopad úprav funkce na graf
Obrázek ukazuje grafy několika úprav funkce \sin x.
| \sin(x+1) | posun grafu ve směru osy x |
| \sin(x)+1 | graf je posunutý ve směru osy y |
| \sin 2x | funkce má změněnou délku periody (v uvedeném příkladu je graf „zmáčknutý“ ve směru osy x, funkce má poloviční délku periody oproti \sin x) |
| 2\sin x | změní se maximální a minimální funkční hodnota (v uvedeném příkladu je graf „roztažený“ ve směru osy y na dvojnásobnou výšku) |
Zajímavost: fyzikální popis některých úprav
| \sin(x+1) | graf má posunutou fázi |
| 2\sin x | změnila se velikost amplitudy |
