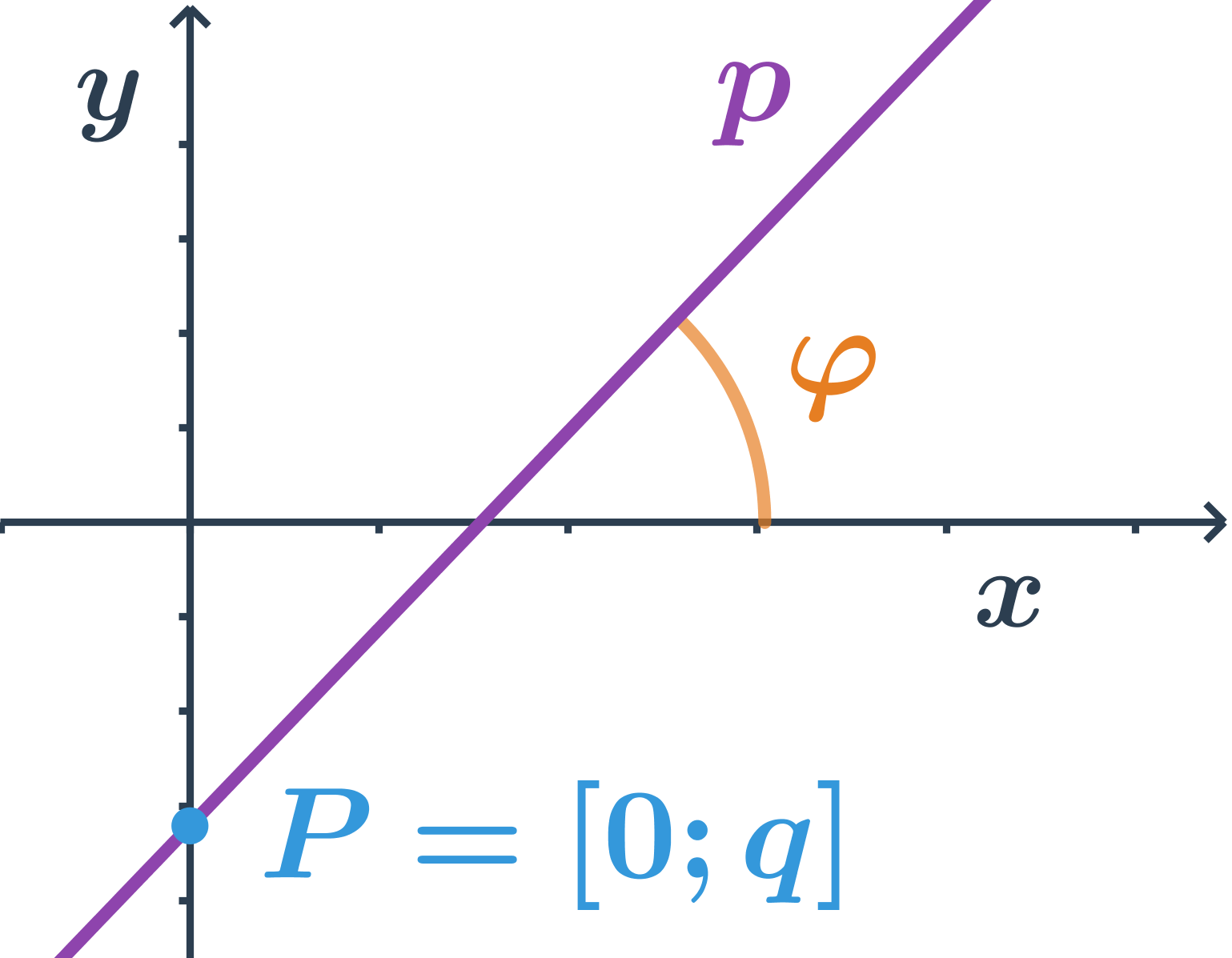Čeština
Angličtina
Informatika
Biologie
Umíme to
Němčina
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Týmovka
Rozhodovačka
Směrnicový tvar rovnice přímky
Procvičujte neomezeněVáš denní počet odpovědí je omezen. Pro navýšení limitu či přístup do svého účtu s licencí se přihlaste.
Přihlásit se
GUD
QR kód
Kód / krátká adresa
Zkopírujte kliknutím.
Nastavení cvičení
Pozor, nastavení je platné pouze pro toto cvičení a předmět.
Směrnicový tvar rovnice přímky
Každou přímku p, která není rovnoběžná s osou y můžeme vyjádřit ve tvaru: y=kx+q, kde k,q\in\mathbb{R}.
Tento tvar se nazývá směrnicový tvar rovnice přímky.
Konstanta k se nazývá směrnice a její hodnota je tangens úhlu, který svírá přímka p s kladnou částí osy x, tedy: k=\tan \varphi.
Konstanta q určuje průsečík přímky p s osou y, souřadnice průsečíku jsou: P=[0;q]. Pro přímku, která prochází počátkem je q=0, tedy směrnicový tvar její rovnice je: y=kx.
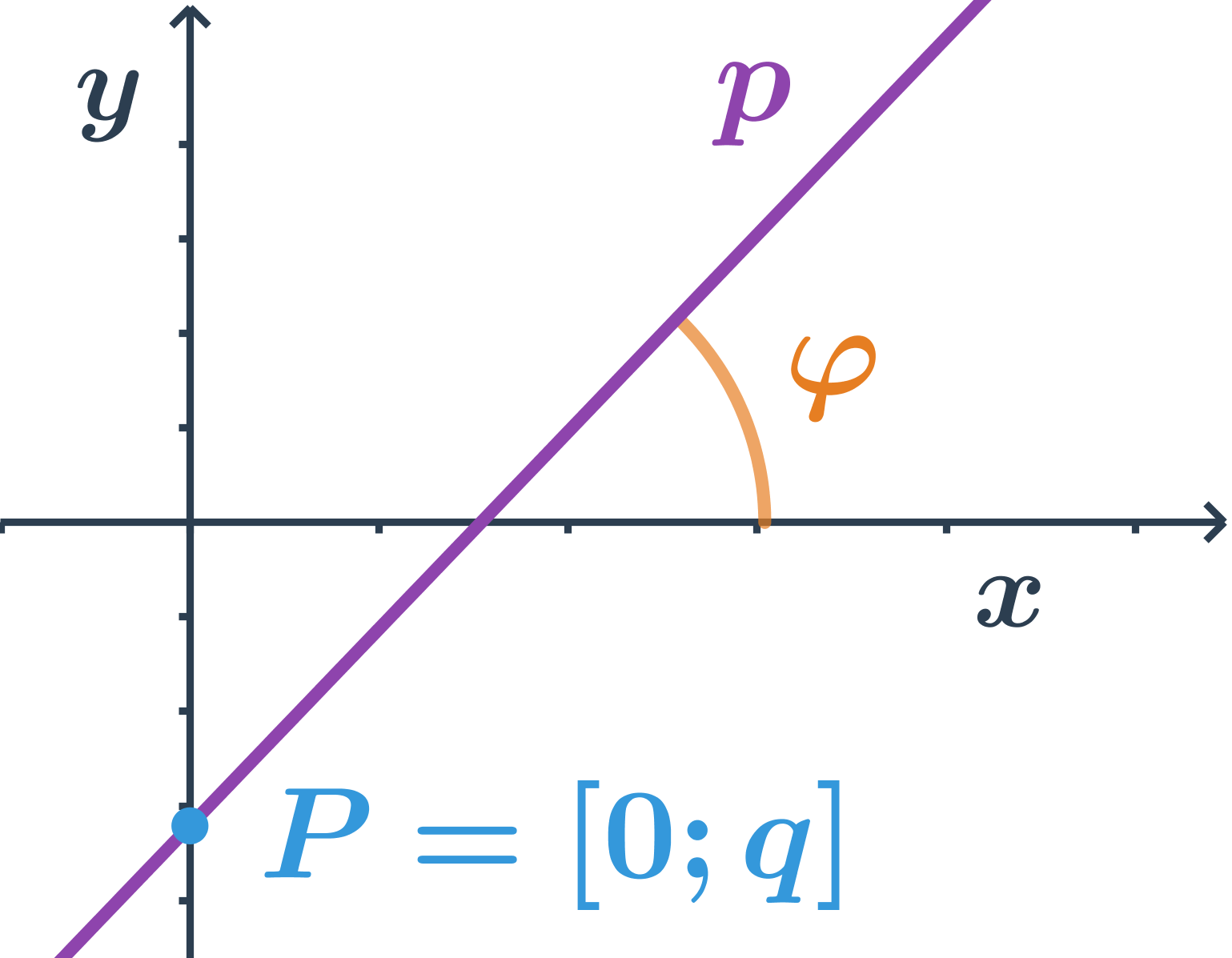
Směrnice přímky, která má směrový vektor \vec{u}=(u_1;u_2) je podíl souřadnic směrového vektoru:
k=\tan \varphi=\frac{u_2}{u_1}
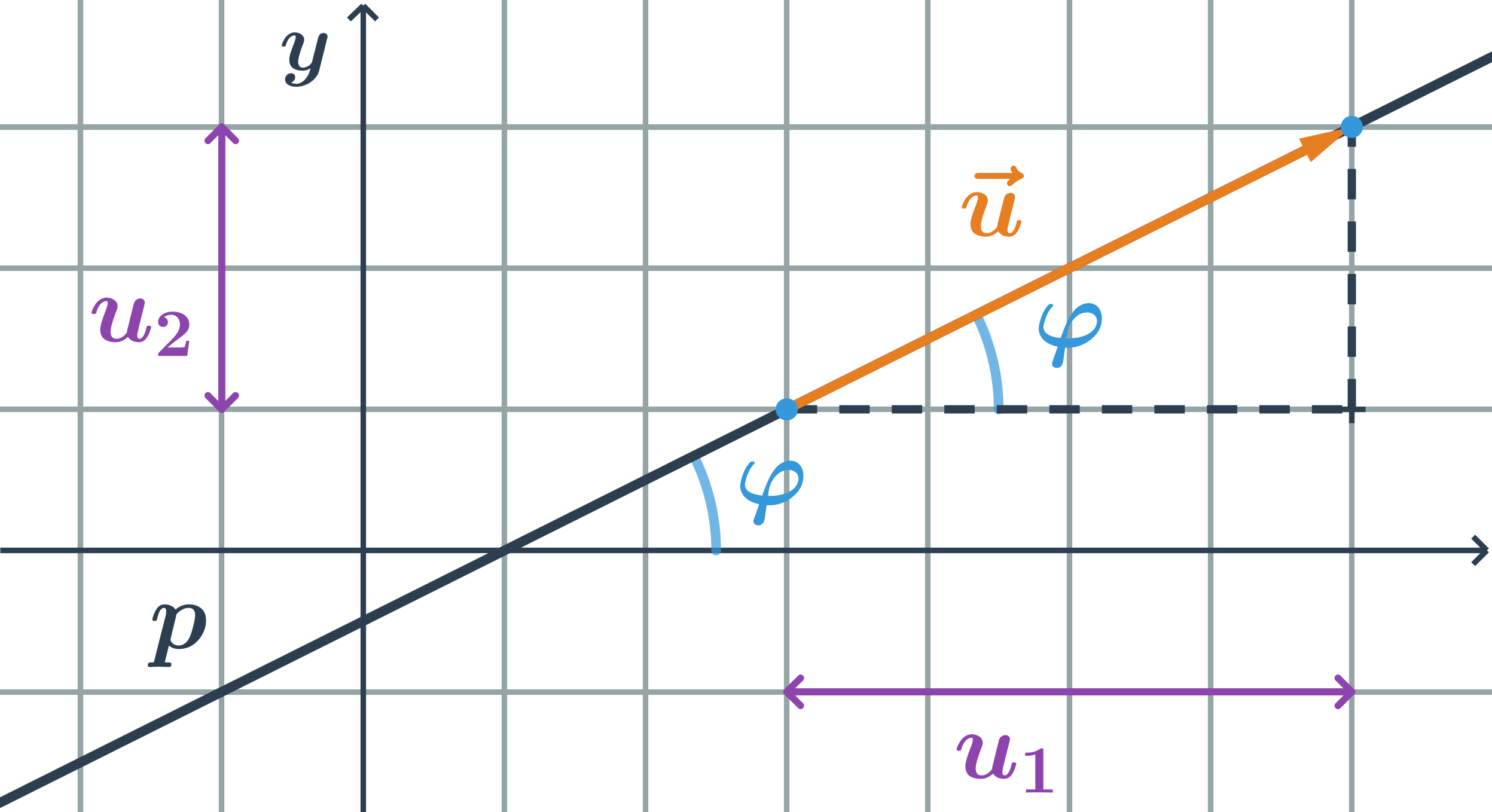
Různé hodnoty směrnice
- Směrnice přímky p: k_1=\tan \varphi_1=\frac{1}{2}
- Směrnice přímky q: k_2=\tan \varphi_2=\frac{1}{1}=1
- Směrnice přímky r: k_3=\tan \varphi_3=\frac{2}{1}=2
- Čím větší odchylka od kladné části osy x, tím větší hodnota směrnice k.
- Přímka rovnoběžná s osou x svírá s kladnou částí osy x úhel 0^\circ a tedy její směrnice je \tan 0^\circ=0.
- Přímka rovnoběžná s osou y svírá s kladnou částí osy x úhel 90^\circ a pro tuto hodnotu funkce tangens není definována, proto nemůžeme určit směrnici.
Směrnicový tvar přímky z obrázku
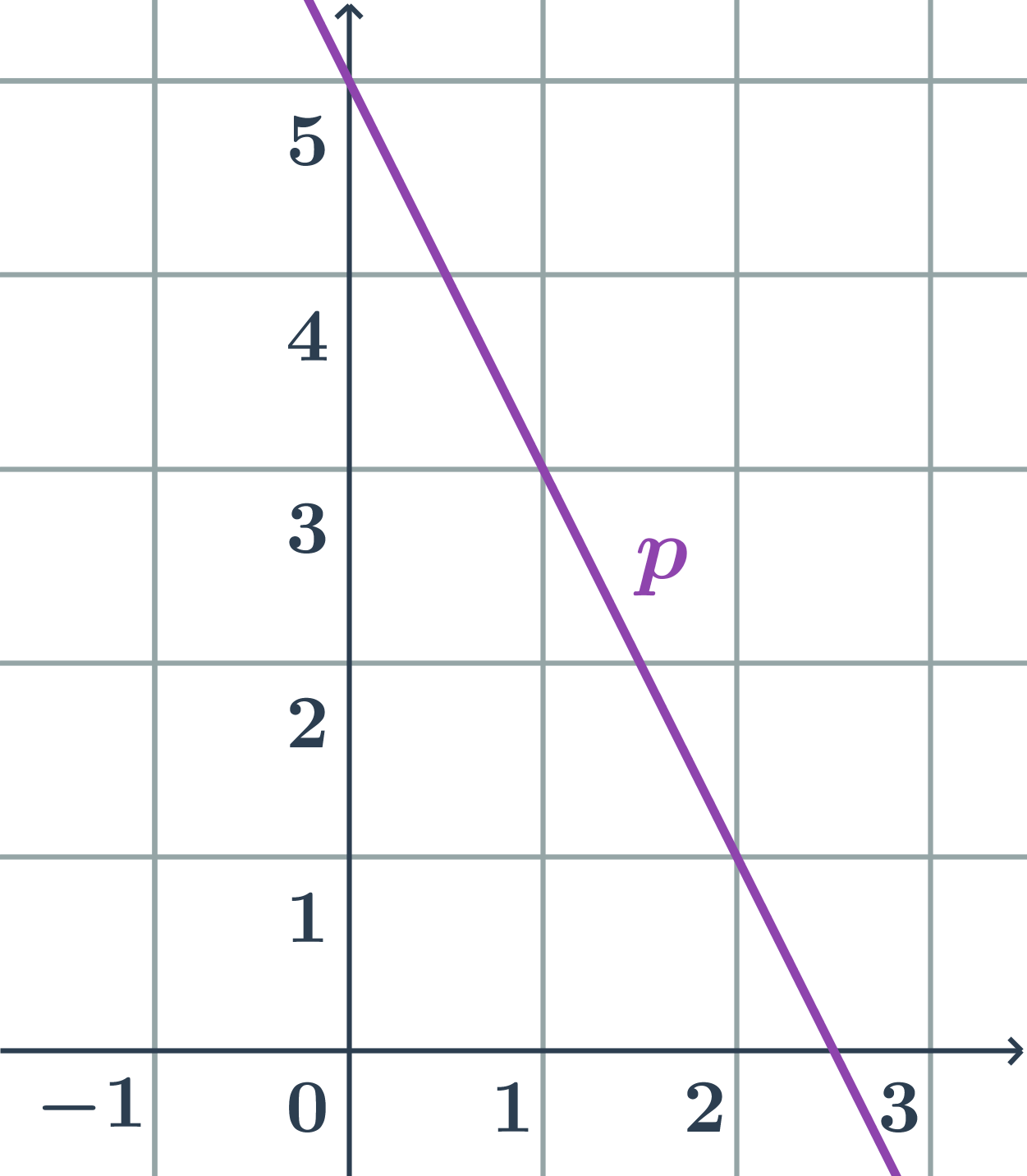
Hledáme směrnicový tvar rovnice přímky: y=kx+q.
- Pro nalezení konstant k a q určíme směrový vektor přímky p a průsečík s osou y.
- směrový vektor přímky: \vec{u}=(1;-2)
- směrnice: k=\tan \varphi=\frac{u_2}{u_1}=\frac{-2}{1}=-2
- průsečík přímky s osou y: P=[0;5]
- konstanta q=y_P=5
- přímka na obrázku má směrnicový tvar y=-2x+5
Dvě přímky
Dvě rovnoběžné přímky svírají s kladnou částí osy x stejný úhel, mají tedy stejnou směrnici.
Pro dvě k sobě kolmé přímky platí:
- přímka p má směrový vektor \vec{u}=(u_1;u_2) a tedy směrnicí: k=\frac{u_2}{u_1}
- každá přímka k ní kolmá má směrový vektor (-u_2;u_1) a tedy směrnici: \frac{-u_2}{u_1}=-\frac{1}{k}
Směrnicový tvar rovnice přímky (střední)
Vyřešeno:
