Výpis souhrnů
Operace s vektory
Podtémata
Operace s vektory
Vektory v rovině mohou být zapsané jako dvojice čísel – souřadnic v rovině, podobně trojrozměrné vektory lze zapsat jako trojice čísel – souřadnic v prostoru.
Operace jako součet, rozdíl a vynásobení reálným číslem, které umíme jednoduše provádět s čísly, lze s vektory provádět po jednotlivých souřadnicích. Tím se zabývá kapitolka Vektory: násobení konstantou, součet, rozdíl. Příklady praktického použití těchto operací s vektory:
- vrabec letí stejným směrem jako moucha a dvakrát rychleji než moucha – vektor rychlosti vrabce získáme, když vektor rychlosti mouchy vynásobíme konstantou 2,
- satelitní snímky ukazují, že ráno ještě vozítko Marka Watneyho stálo na marsovské základně, za dnešek ujel 50 km na východ – jeho novou polohu získáme, když k souřadnicím základny přičteme vektor (50;0),
- šnek přelezl rovně po monitoru z levého horního rohu (souřadnice v pixelech [0;0]) do bodu [1007;555] – vektor, jehož souřadnice jsou počty pixelů, co šnek ulezl v horizontálním a vertikálním směru získáme jako rozdíl jeho umístění na konci pohybu a jeho umístění na začátku pohybu.
Speciální operace, kterou lze provést se dvěma vektory stejné dimenze (mají stejný počet souřadnic), je skalární součin. Vstup této operace jsou dva vektory, výstup je reálné číslo.
Díky skalárnímu součinu můžeme vypočítat kupříkladu jaký úhel vektory svírají, speciálně jestli jsou na sebe kolmé (v takovém případě jejich skalární součin vyjde nulový).
NahoruVektory: násobení konstantou, součet, rozdíl
Součet vektorů
Vektory \vec{u} a \vec{v} sečteme takto: počáteční bod vektoru \vec{v} posuneme do koncového bodu vektoru \vec{u}. Součet vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má počáteční bod stejný jako vektor \vec{u} a koncový bod stejný jako vektor \vec{v}. Píšeme: \vec{u}+\vec{v}=\vec{w}
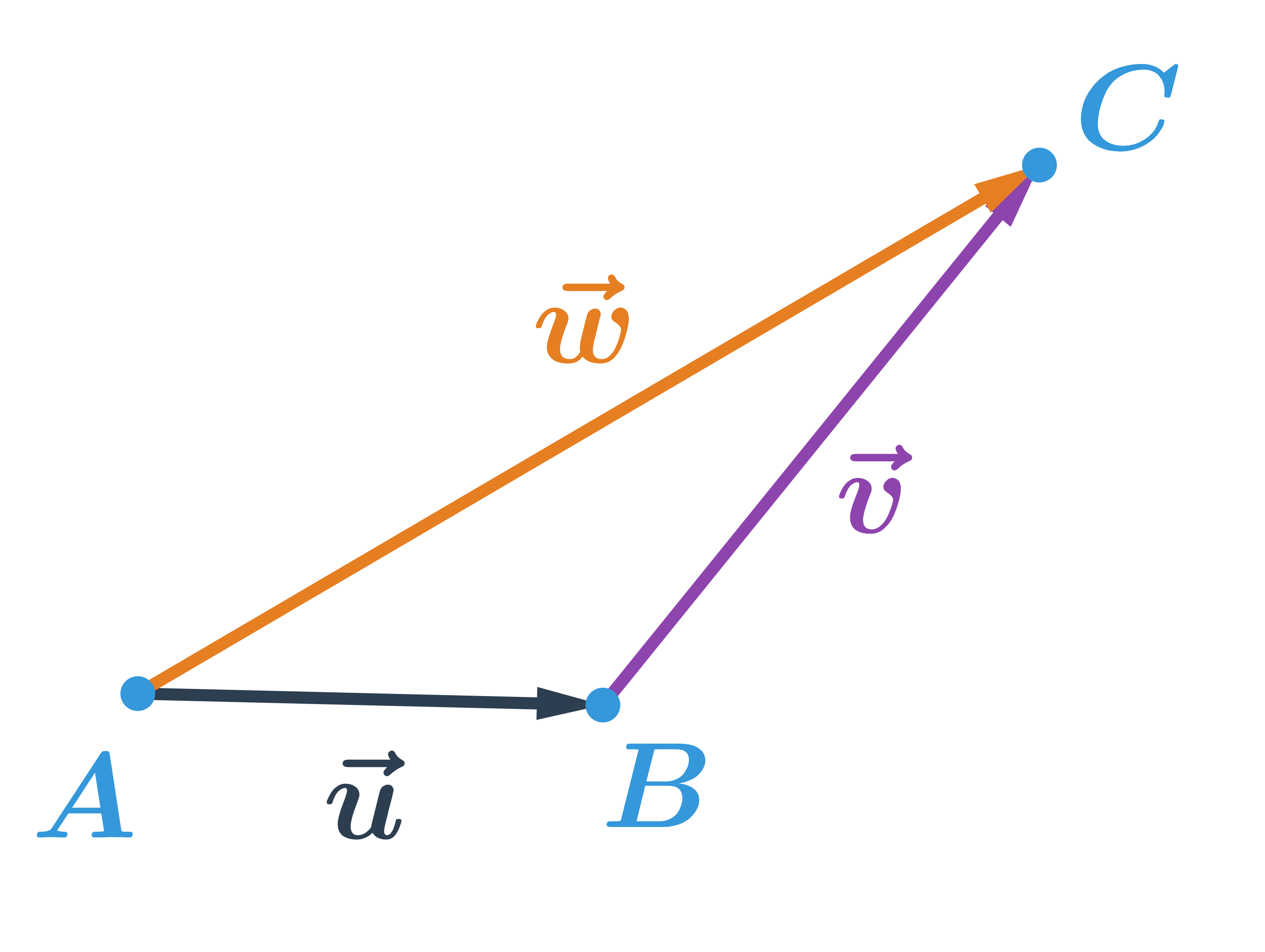
Vektory na obrázku jsou označené \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{BC}. Součet těchto vektorů: \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}
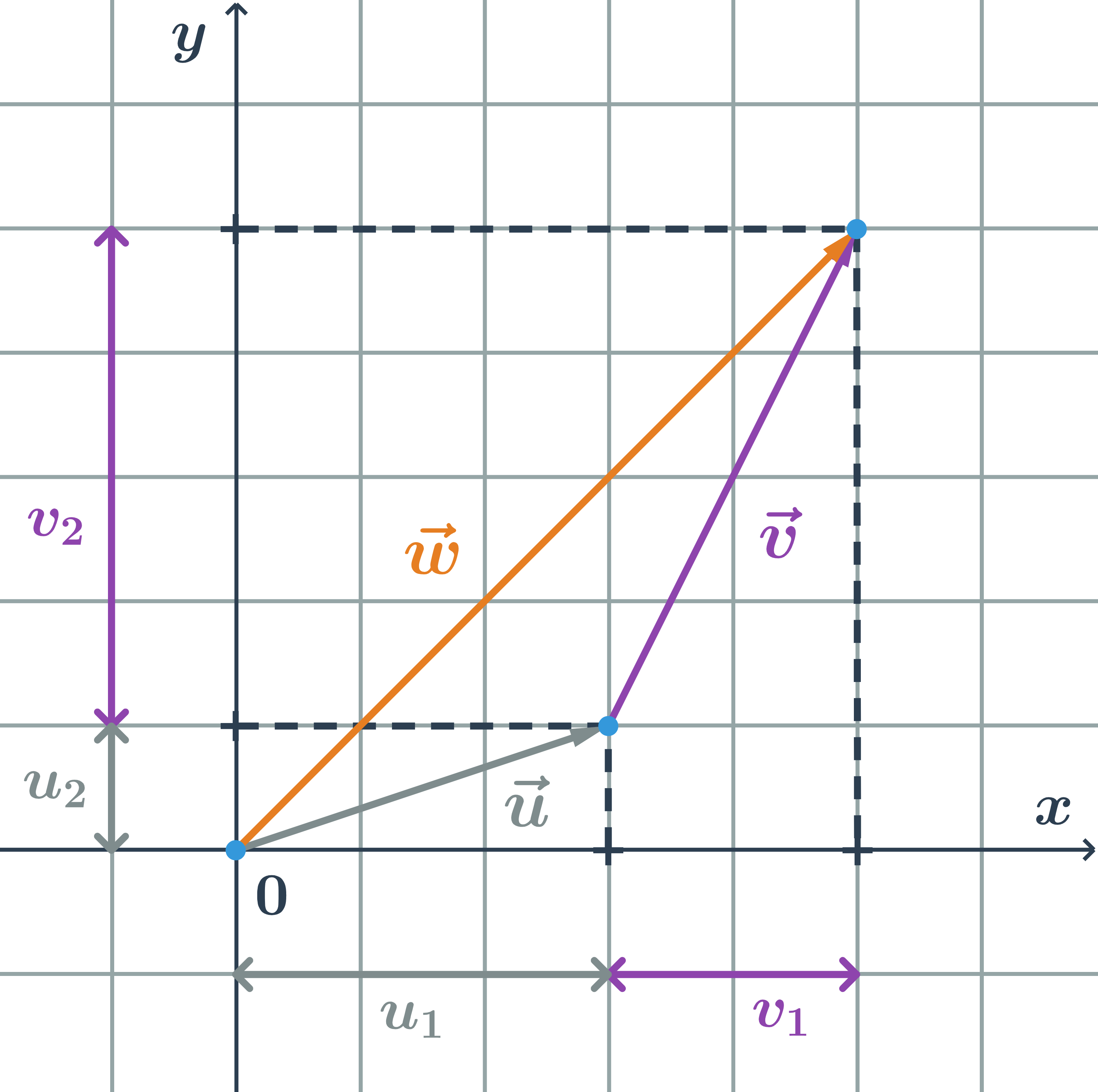
Mějme vektory se souřadnicemi \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2). Pak součet vektorů \vec{u} a \vec{v} je vektor \vec{w} se souřadnicemi \vec{w}=(u_1+v_1; u_2+v_2).
Rozdíl vektorů
Rozdíl vektorů \vec{u} a \vec{v} je součet vektoru \vec{u} s vektorem opačným k \vec{v}. Tedy:
\vec{u}-\vec{v}=\vec{u}+(-\vec{v})
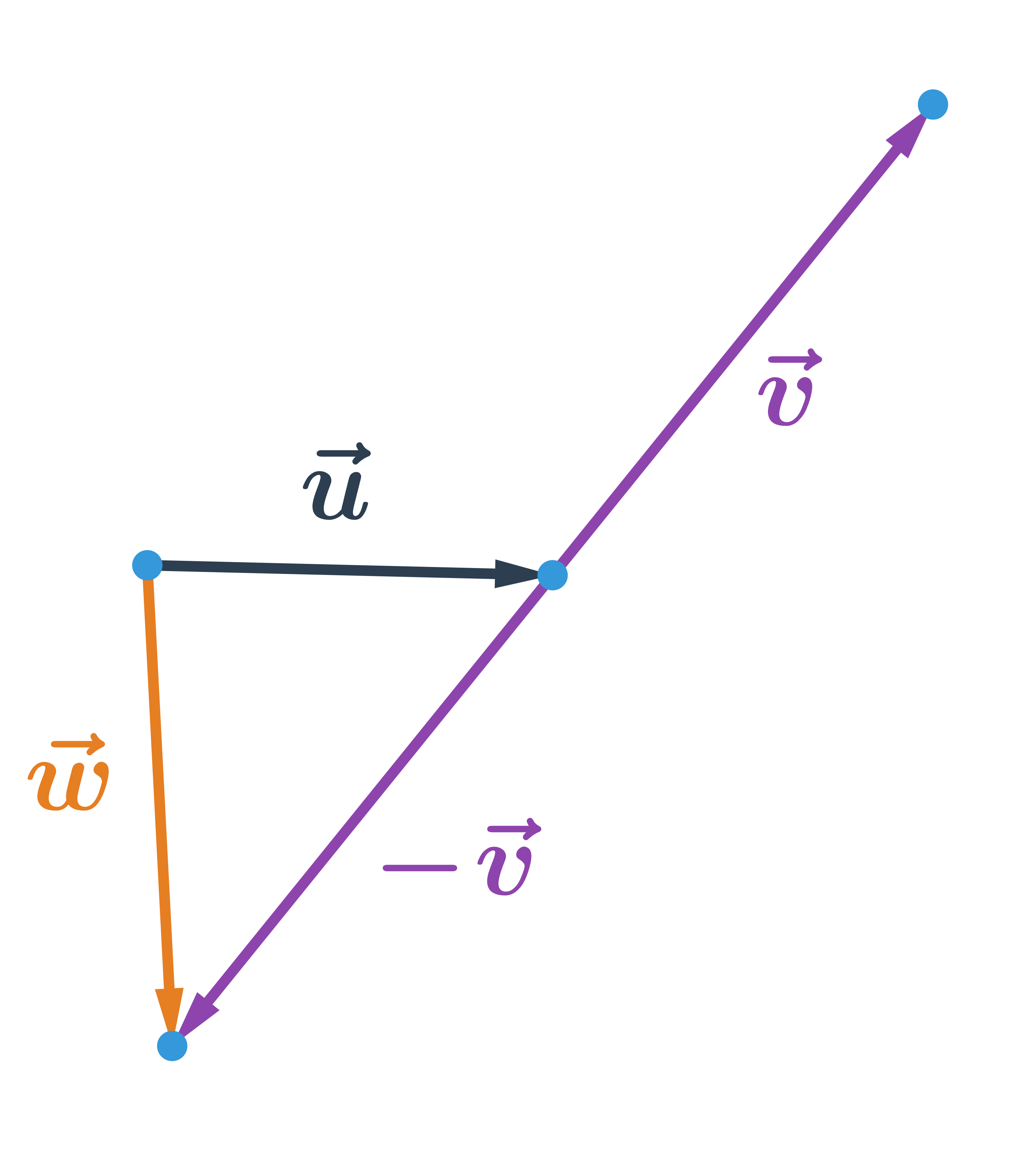
Máme-li souřadnice vektorů: \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), pak rozdíl vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má souřadnice: \vec{w}=(u_1-v_1; u_2-v_2).
Násobek vektoru
Vektor \vec{u} můžeme vynásobit libovolným reálným číslem k. Dostaneme vektor \vec{v}, kterému říkáme násobek vektoru. Píšeme \vec{v}=k \cdot \vec{u}
- Pokud k \gt 0, vektory \vec{u} a k \cdot \vec{u} mají stejný směr
- Pokud k \lt 0, vektory \vec{u} a k \cdot \vec{u} mají opačný směr
- Pokud k=0, vektor k \cdot \vec{u} je nulový vektor
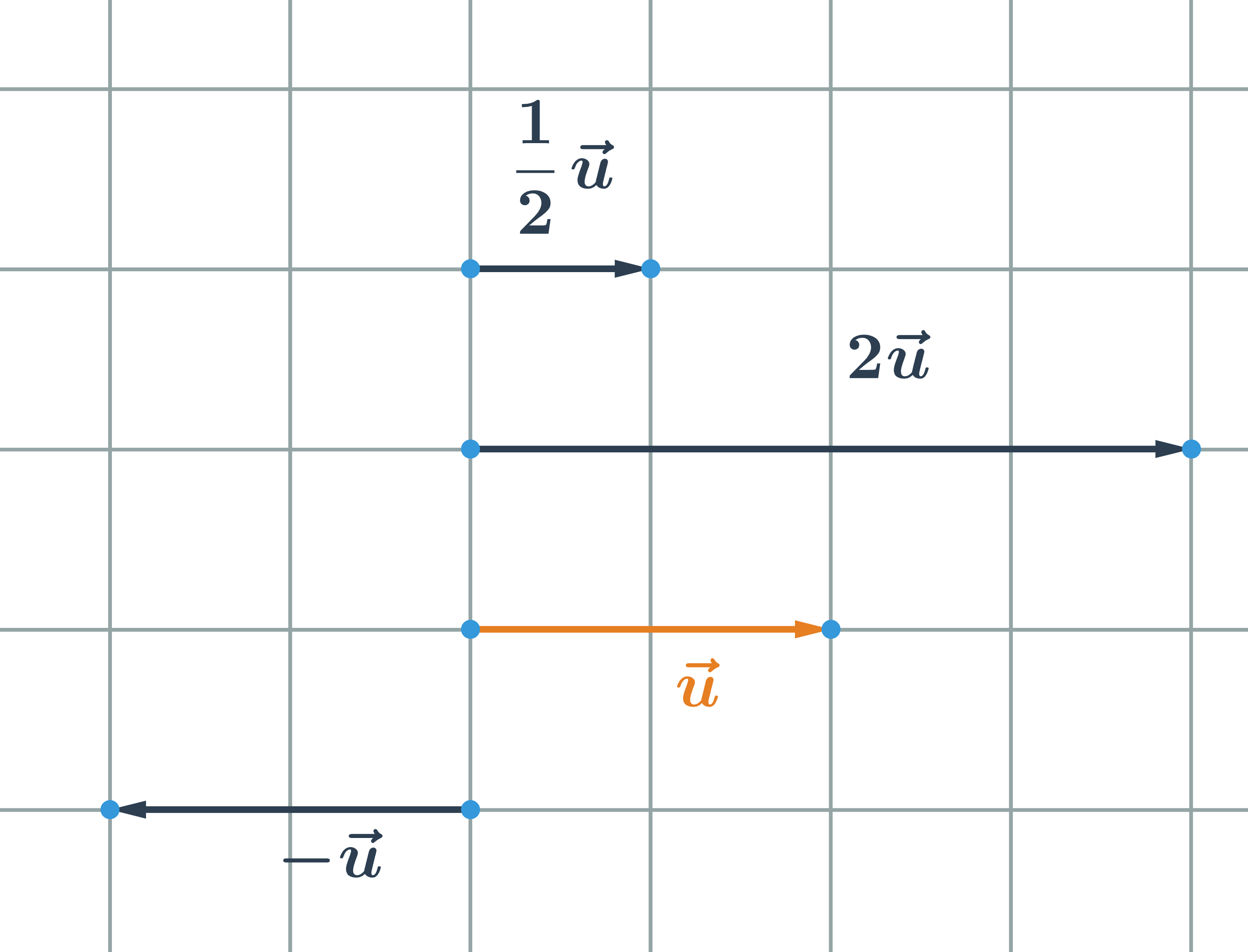
Máme-li souřadnice vektoru \vec{u}=(u_1;u_2), pak jeho násobek \vec{v}=k \cdot \vec{u} má souřadnice \vec{v}=(k \cdot u_1; k\cdot u_2).
Příklad součet a násobek vektoru graficky
Načrtněte vektor \vec{w}=2\vec{a}-\vec{b}+\vec{c}.
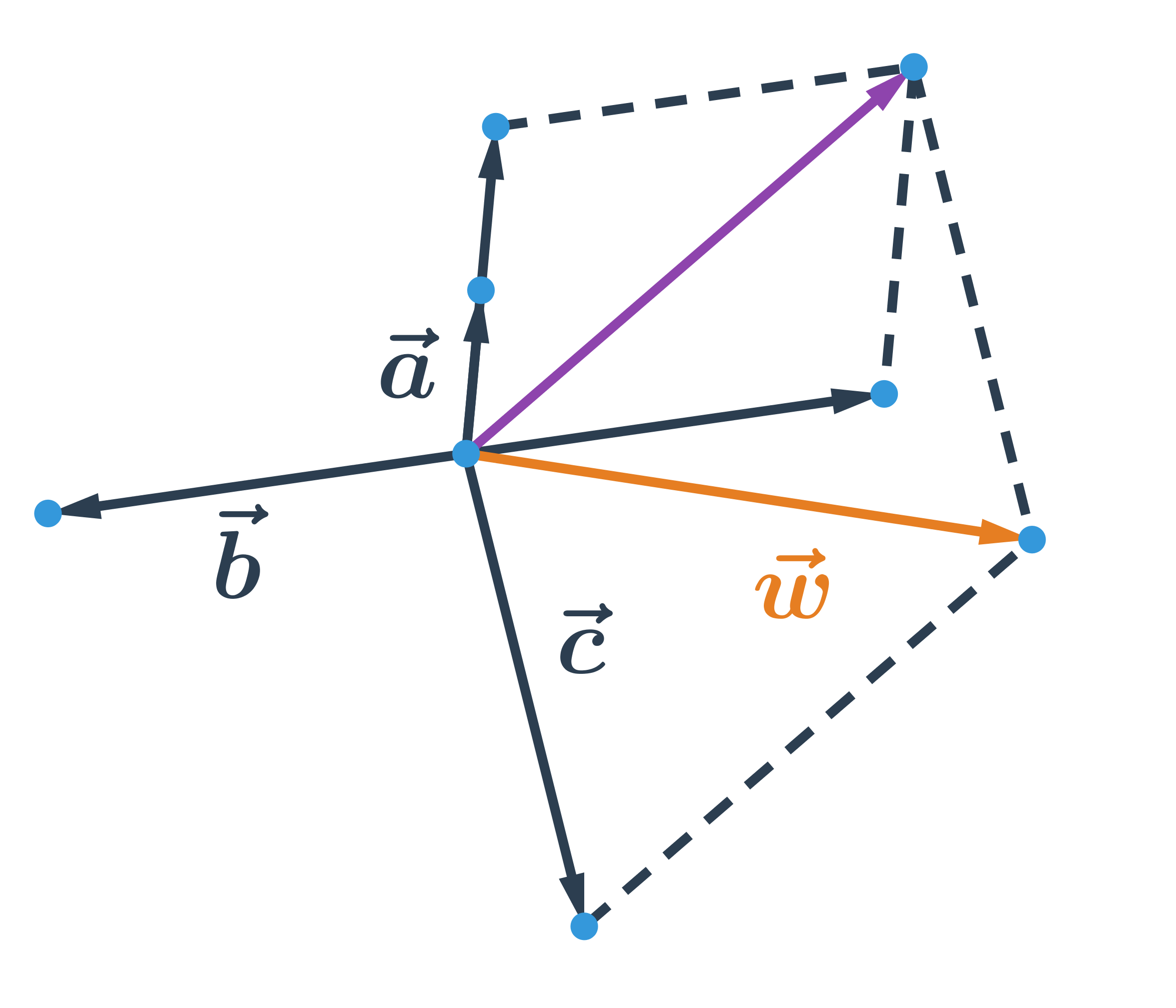
Příklad součet a násobek vektoru v souřadnicích
Jsou dány vektory \vec{u}=(2;-3), \vec{v}=(4;1). Určete souřadnice vektoru \vec{w}=\vec{u}-4\cdot \vec{v}.
- w_1=u_1-4\cdot v_1=2-4\cdot 4=-14
- w_2=u_2-4\cdot v_2=-3-4\cdot 1=-7
Vektory: skalární součin
Skalární součin vektorů \vec{u} a \vec{v} označujeme \vec{u}\cdot \vec{v}. Pro vektory \vec{u}, \vec{v} o velikostech \left| \vec{u} \right| a \left| \vec{v} \right|, které spolu svírají úhel \alpha, je skalární součin definován následovně:
\vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
Vlastnosti skalárního součinu
- Výsledkem skalárního součinu dvou vektorů je číslo (neboli skalár).
- Skalární součin nulového vektoru s libovolným jiným vektorem je vždy roven 0.
- Skalární součin vektorů, které jsou na sebe kolmé, je také roven nule.
Výpočet pomocí souřadnic
Máme-li souřadnice vektorů \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), pak hodnota jejich skalárního součinu je:
u_1\cdot v_1+u_2 \cdot v_2
Poznámka: další typy součinu vektorů
Kromě skalárního součinu existují i jiné typy součinu vektorů (vektorový, smíšený), proto je důležité psát o jaký součin se jedná.Příklad: skalární součin vektorů
Určete skalární součin vektorů, jestliže platí: \left| \vec{u} \right|=4, \left| \vec{v} \right|=3 a vektory svírají úhel 60°.
- Vzoreček: \vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
- Dosadíme známé hodnoty: \vec{u}\cdot \vec{v}=4\cdot3\cdot \cos 60°=4\cdot3\cdot\frac{1}{2}=6
Určení úhlu svíraného dvěma vektory
S využitím vztahu pro skalární součin můžeme určit úhel vektorů: \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}
Příklad: úhel svíraný vektory
Určete úhel vektorů \vec{u}=(3;3) a \vec{v}=(2;0).
- Platí \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}.
- Pomocí známých souřadnic vektorů umíme spočítat skalární součin \vec{u}\cdot\vec{v} a velikosti vektorů \left| \vec{u} \right|, \left| \vec{v} \right|:
- \vec{u}\cdot \vec{v}=u_1\cdot v_1+u_2 \cdot v_2=3\cdot2+3\cdot0=6
- \left| \vec{u} \right|=\sqrt{u_1^2 + u_2^2}=\sqrt{3^2+3^2}=\sqrt{18}
- \left| \vec{v} \right|=\sqrt{v_1^2 + v_2^2}=\sqrt{2^2+0^2}=\sqrt{4}
- Dosadíme tyto hodnoty do vztahu pro výpočet \cos \alpha:
- \cos \alpha =\frac {6}{\sqrt{18}\cdot\sqrt{4}}=\frac{6}{3\sqrt{2}\cdot2}=\frac{1}{\sqrt{2}}
- Úhel vektorů je 45°.

