Výpis souhrnů
Prostorová představivost
Podtémata
Prostorová představivost
Prostorová představivost nám pomáhá vnímat a rozumět tvarům kolem nás, ať už na papíře nebo ve skutečném světě. Procvičování je děleno do více podtémat rozličné obtížnosti:
- Prostorová představivost v rovině – práce s tvary na ploché rovině
- Prostorová představivost: 3D objekty – schopnost představit si, jak vypadá trojrozměrné těleso z jiného úhlu pohledu
- Nárys, půdorys, bokorys – různé způsoby zobrazení objektů
- Počty vrcholů, stěn, hran – počítání základních prvků prostorových těles
- Síť krychle – skládání krychle z plochých částí
- Sítě těles – navazuje na předchozí téma a zabývá se i složitějšími 3D tělesy
- Řezy krychle – řezání krychle rovinou
- Řezy těles – řezání dalších prostorových těles
Prostorová představivost v rovině
Představivost v rovině využíváme, aniž bychom si to uvědomili, v každodenním životě - při orientaci ve městě, v přírodě, při práci s mapu i při pohledu do zrcadla. Měli bychom být schopni rozeznat vzájemnou polohu dvou objektů, určit jejich sjednocení, průnik nebo změnu polohy.
Doplňování v rovině
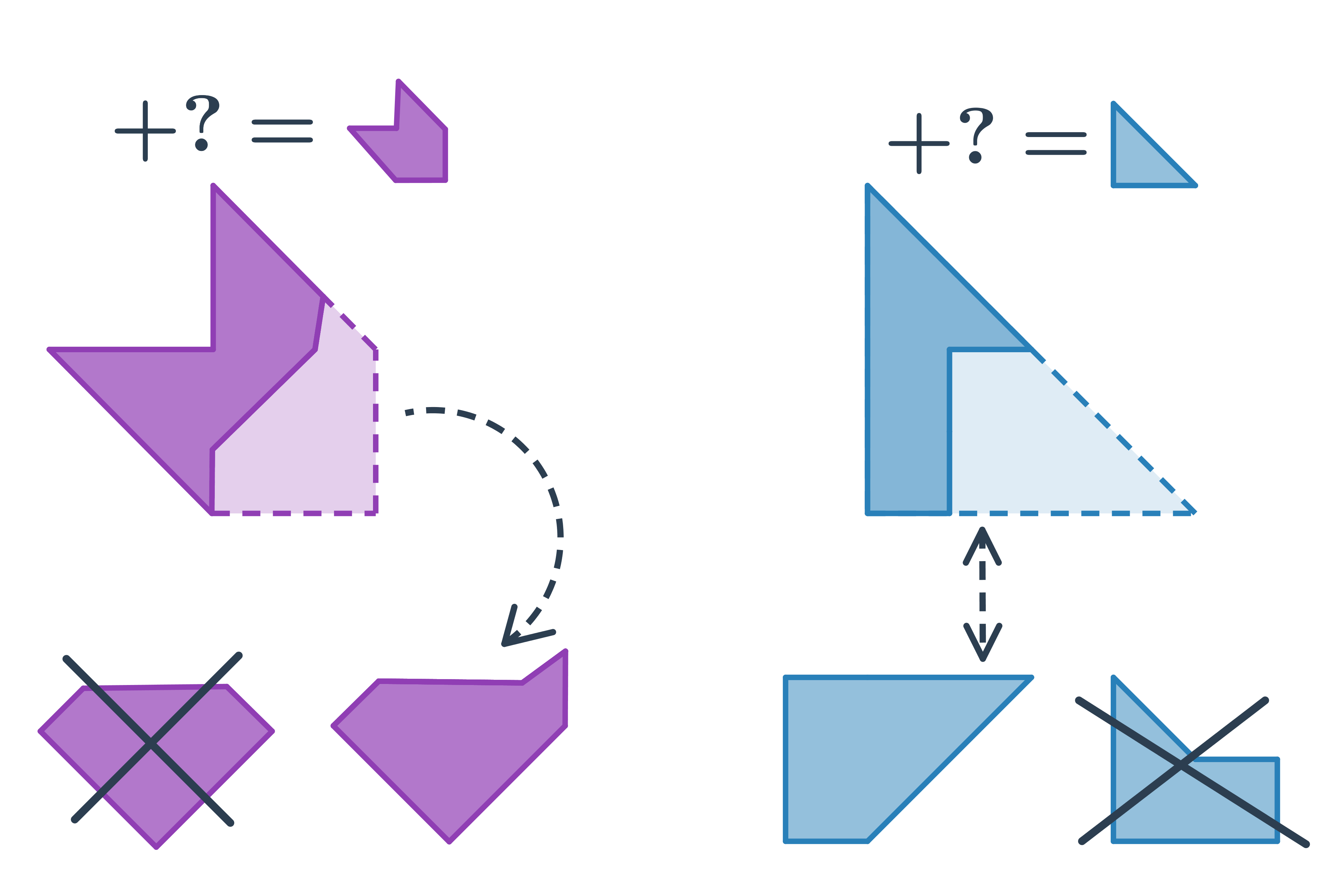
Při doplňování v rovině budeme pracovat nejen se základními rovinnými útvary, ale i s jejich kombinacemi - hvězdy, domečky, sítě. Při řešení úloh je vhodné si, v duchu či na papíře, představit, jak má výsledný tvar vypadat. Pozor, chybějící dílek může být otočený či překlopený.
Otočení a překlopení v rovině
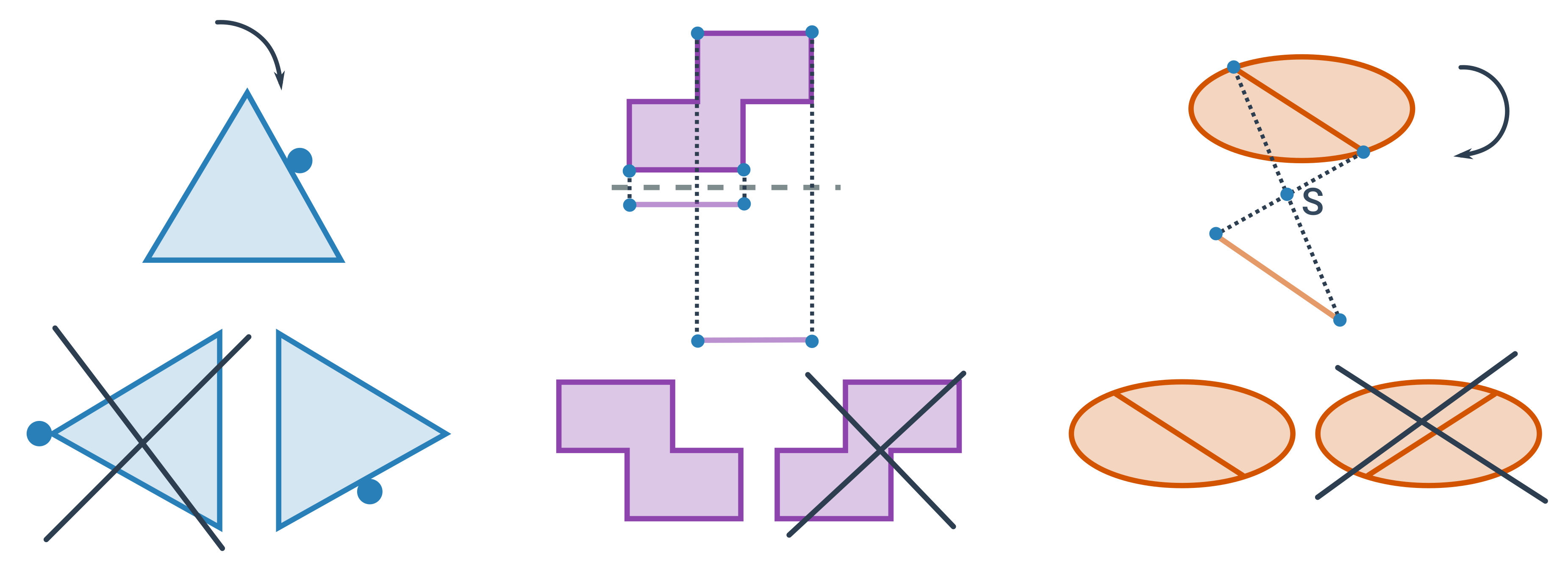
Při hledání správného dílku, který vznikne otočením nebo překlopením daného útvaru využíváme základních vlastností otáčení, osové a středové souměrnosti.
Stačí si pamatovat pár jednoduchých pravidel:
- Při otočení ani překlopení nemění jednotlivé části objektů své vzájemné polohy. Například, pokud je kruh na straně trojúhelníku, nemůže se „přestěhovat“ na vrchol.
- Překlopení je osová souměrnost. To mimo jiné znamená, že bod, který je nejdál od osy překlopení, bude i v překlopení nejdál od osy.
- Otočení o 180° je středová souměrnost.
Prostorová představivost: 3D objekty
Při zobrazení prostorových objektů (těles, staveb z kostek a jiných) narážíme na základní problém: papír či obrazovka má pouze dva rozměry a neumíme tedy reálně modelovat prostorové situace.
Při zobrazení 3D objektů často využíváme pravoúhlého promítání z přední, boční a horní strany, tzv. nárys, bokorys a půdorys.
Při řešení úloh s prostorovou tematikou můžeme například postupovat takto:
- Začneme u jednodušších pohledů.
- Zaměříme se na odlišnosti, tedy zkusíme najít, v čem se dané útvary liší.
Příklad: Výběr správného pohledu na těleso

- Úkol: Vyberte, který ze tří dolních obrázků je jiným pohledem na těleso nad nimi.
- Pozorování: Těleso se skládá ze dvou delších ramen a jednoho kratšího ramene.
- Můžeme tedy škrtnout první obrázek. Na něm má těleso jedno dlouhé a dvě kratší ramena.
- Stejně tak můžeme škrtnout i třetí obrázek, na kterém má těleso tři stejně dlouhá ramena.
- Řešením je prostřední obrázek.
Nárys, půdorys, bokorys
Nárys, bokorys a půdorys slouží k dvojrozměrnému zakreslení trojrozměrného objektu pomocí pravoúhlého promítání. Každý z nich zachycuje pohled na objekt z jiného směru.
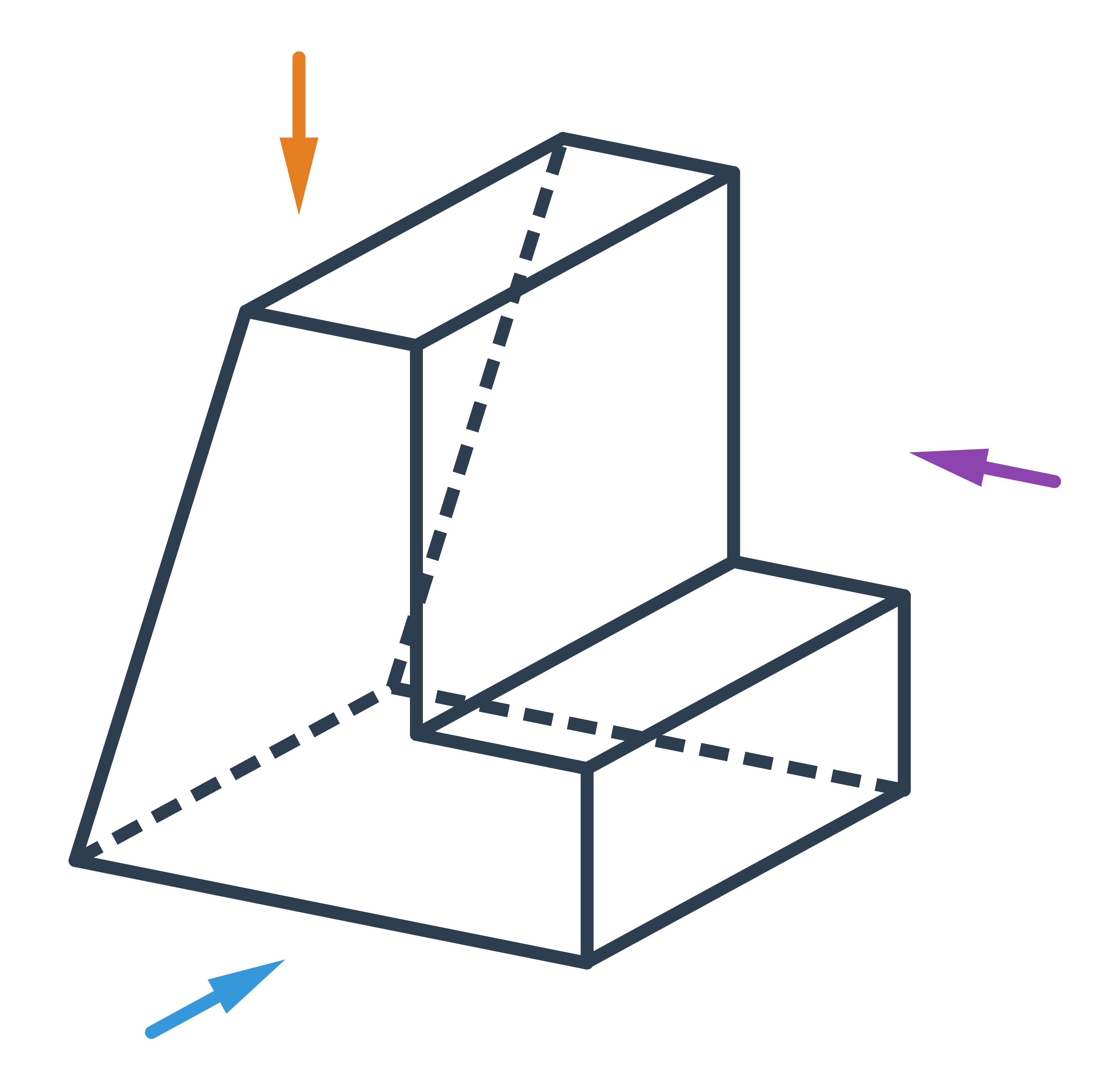
Nárys je pohled na těleso zepředu: 
Bokorys je pohled z boční strany: 
Půdorys je pohled shora: 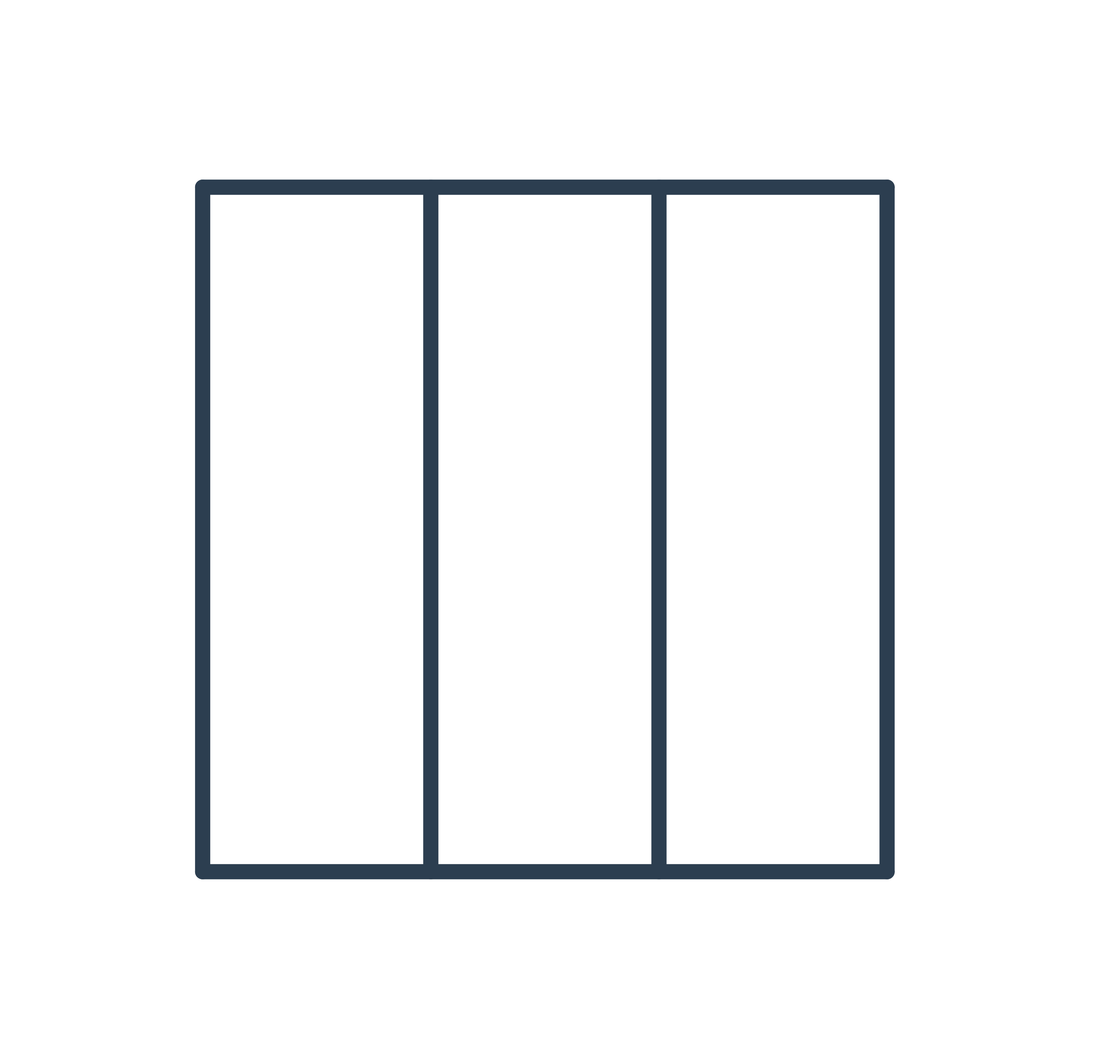
Příklad: 3 pohledy na těleso
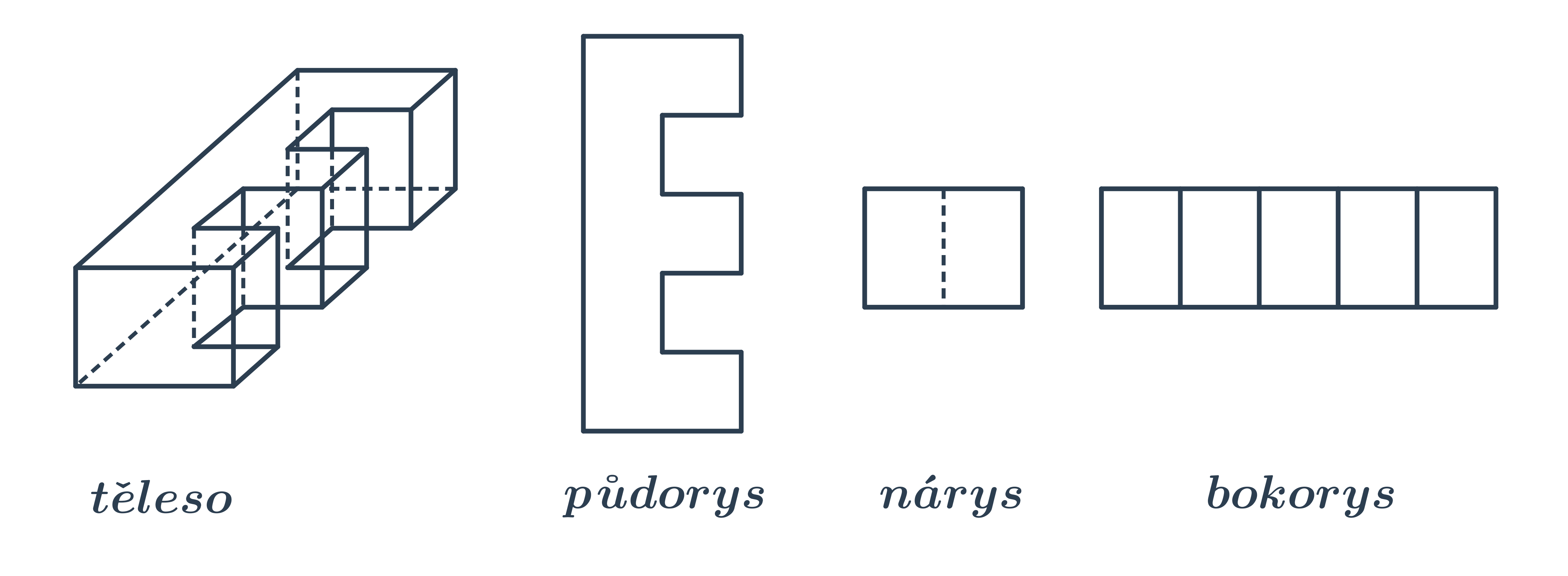
Nejčastěji se v technických aplikacích používá jen půdorys a nárys. Někdy však tyto dva pohledy nestačí.
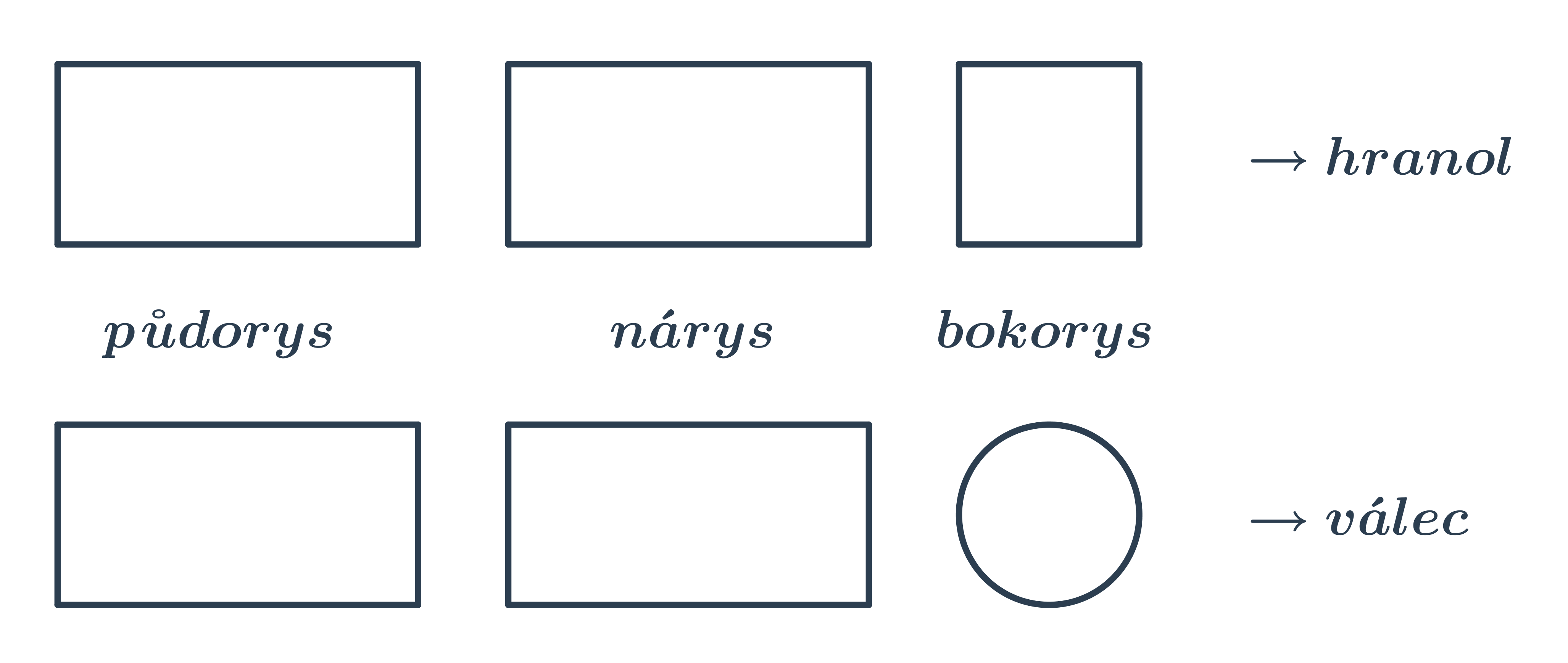
Příklad: Je to hranol nebo není?
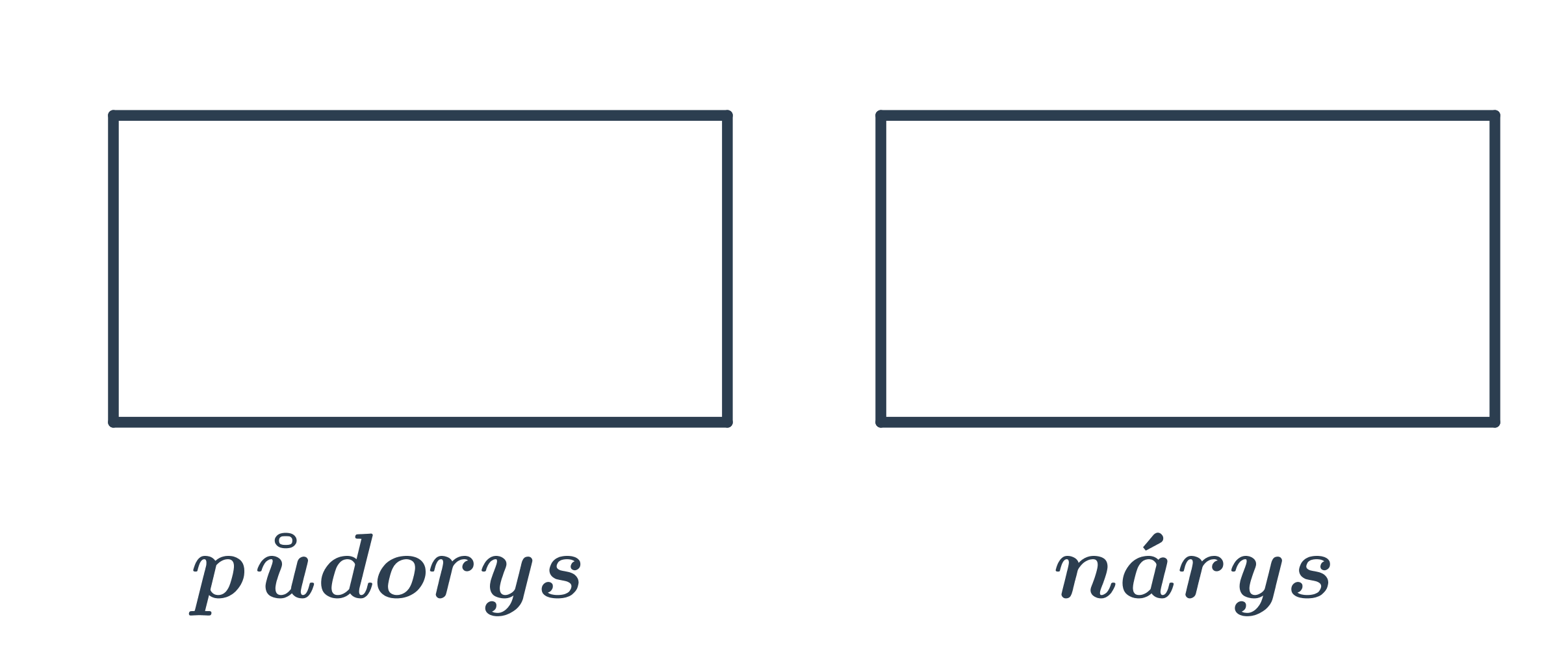
Jaké těleso vidíme na obrázku?
V tuto chvíli řešení není zcela jednoznačné. Těleso může být hranol (což nás asi napadne nejdřív), ale i válec. Aby bylo řešení jednoznačné, museli bychom přidat i bokorys.
Počty vrcholů, stěn, hran
Pro počet vrcholů v, hran h a stěn s konvexního mnohostěnu platí Eulerova věta: v - h + s = 2.
Počty vrcholů, stěn a hran pro pravidelné mnohostěny:
| mnohostěn | počet stěn | počet vrcholů | počet hran |
|---|---|---|---|
| čtyřstěn | 4 | 4 | 6 |
| krychle | 6 | 8 | 12 |
| osmistěn | 8 | 6 | 12 |
| dvanáctistěn | 12 | 20 | 30 |
| dvacetistěn | 20 | 12 | 30 |
Sítě těles
Síť tělesa je rovinné zakreslení, ze kterého jde poskládat plášť tělesa. Příklady sítí:
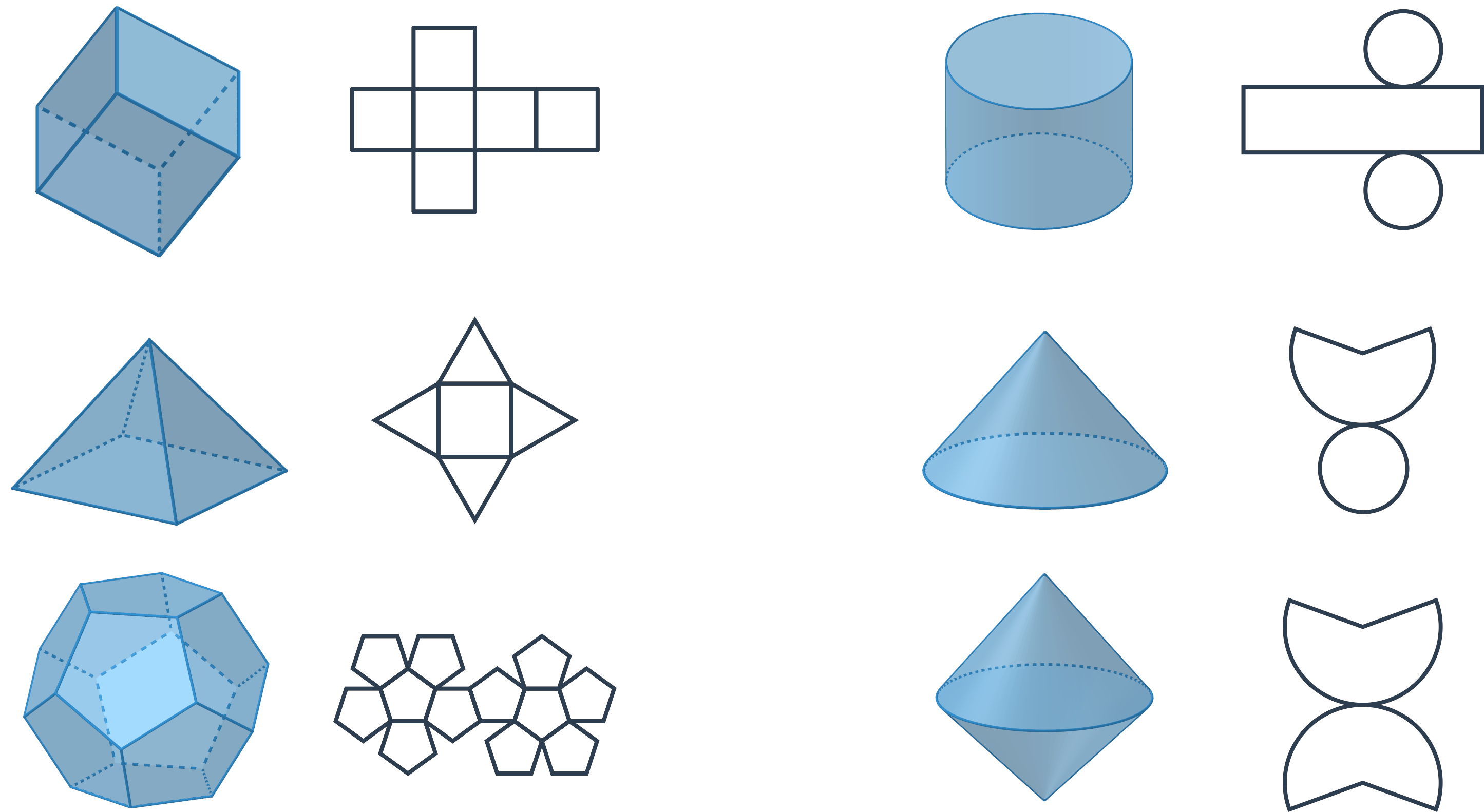
Síť tělesa jde většinou zakreslit mnoha různými způsoby. Síť krychle můžeme zakreslit takto:
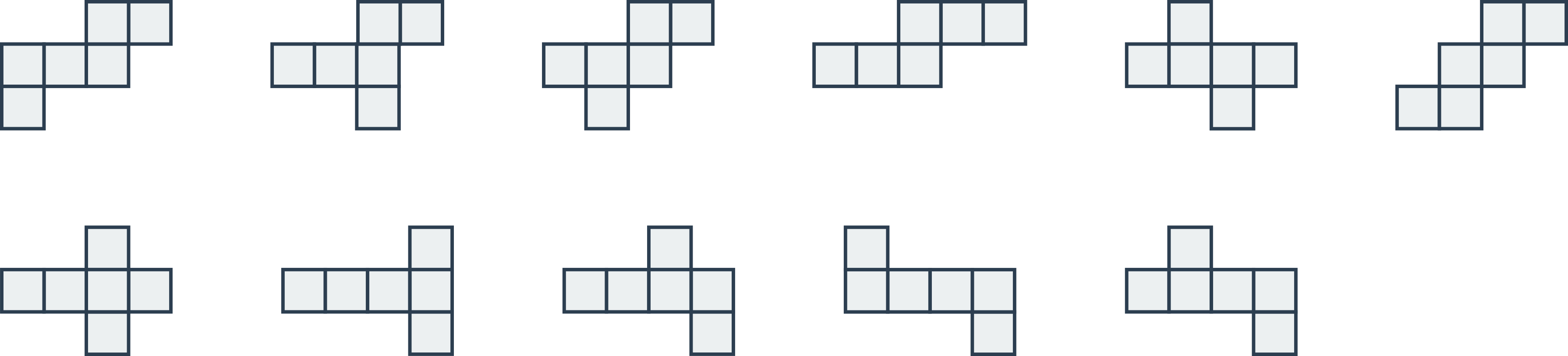
Řezy krychle
Sestrojit řez krychle znamená sestrojit průnik roviny a krychle. Půjde o mnohoúhelník, který leží v rovině řezu a jeho strany jsou okraje řezu, tedy čáry, kudy rovina řízne stěny krychle. Tyto průsečnice řezné roviny se stěnami tělesa chceme sestrojit. Při konstrukci řezů (nejen krychle) můžeme použít tři základní pravidla:
- Pokud leží dva různé body v rovině, pak přímka, která jimi prochází, leží také v této rovině. Když známe ve stěně tělesa dva různé body, které oba leží v rovině řezu, nakreslíme jejich spojnici. Průnik stěny a této spojnice je jednou stranou řezu.
- Dvě rovnoběžné roviny protíná každá další k nim různoběžná rovina ve dvou rovnoběžných přímkách. To znamená, že strany řezu v rovnoběžných stěnách jsou navzájem rovnoběžné.
- Tři navzájem různoběžné roviny se vždy protínají v jednom bodě. Tímto bodem prochází všechny tři průsečnice jednotlivých dvojic rovin. Tedy dvě průsečnice rovin dvou sousedních stěn s rovinou řezu a přímka, na které leží společná hrana stěn, se protínají v jednom bodě.
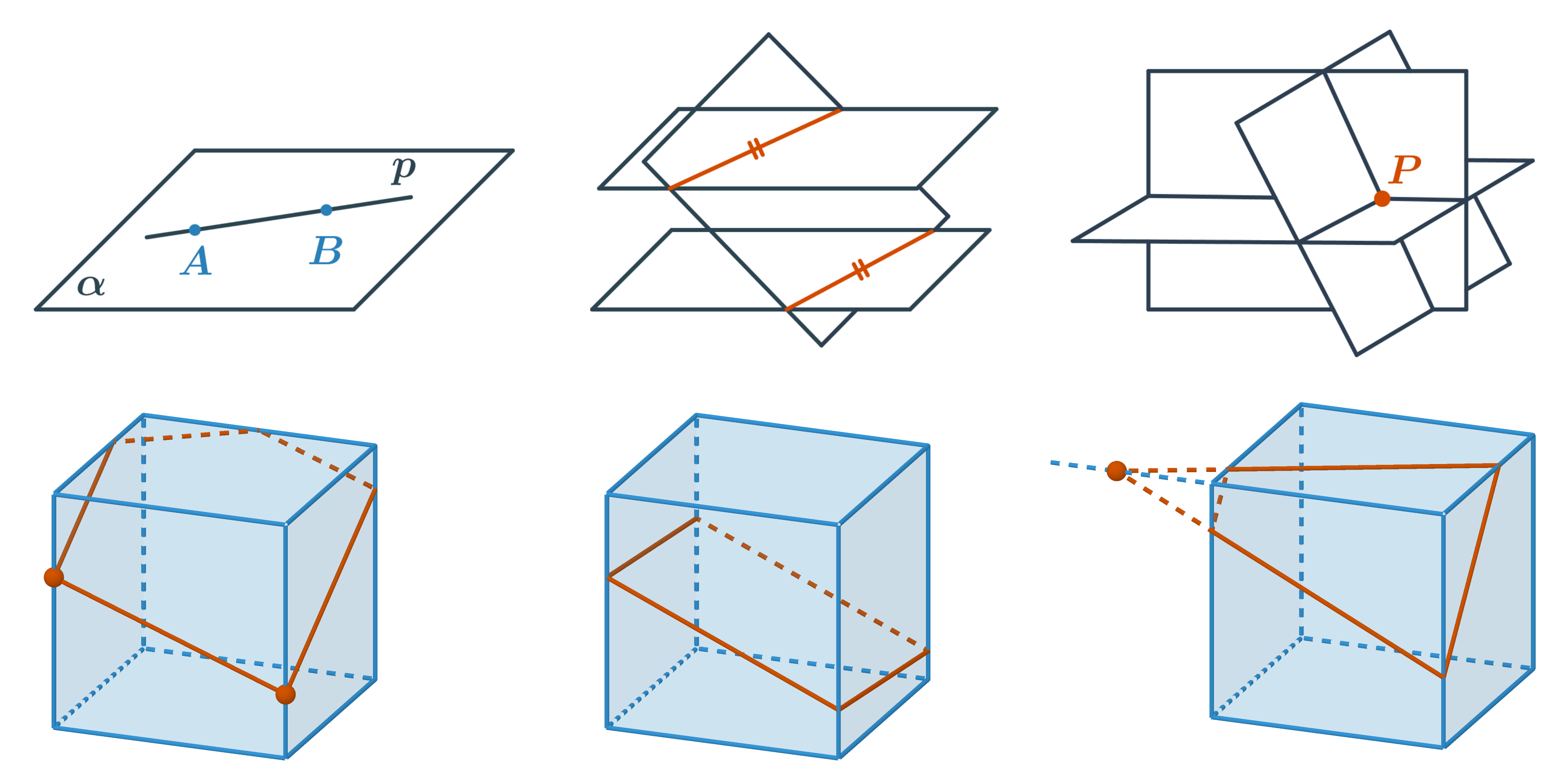
Pozor si dáváme na nejčastější chyby:
- zalomení řezu v jedné stěně (část řezu v jedné stěně musí vždy tvořit jedna úsečka)
- čára řezu jde vnitřkem nebo vnějškem tělesa (okraj řezu musí být celý ve stěnách tělesa)
- čára řezu nekončí na hraně (těleso na hraně končí, řez tělesa také)
Řez krychle rovinou procházející body K, L, M.
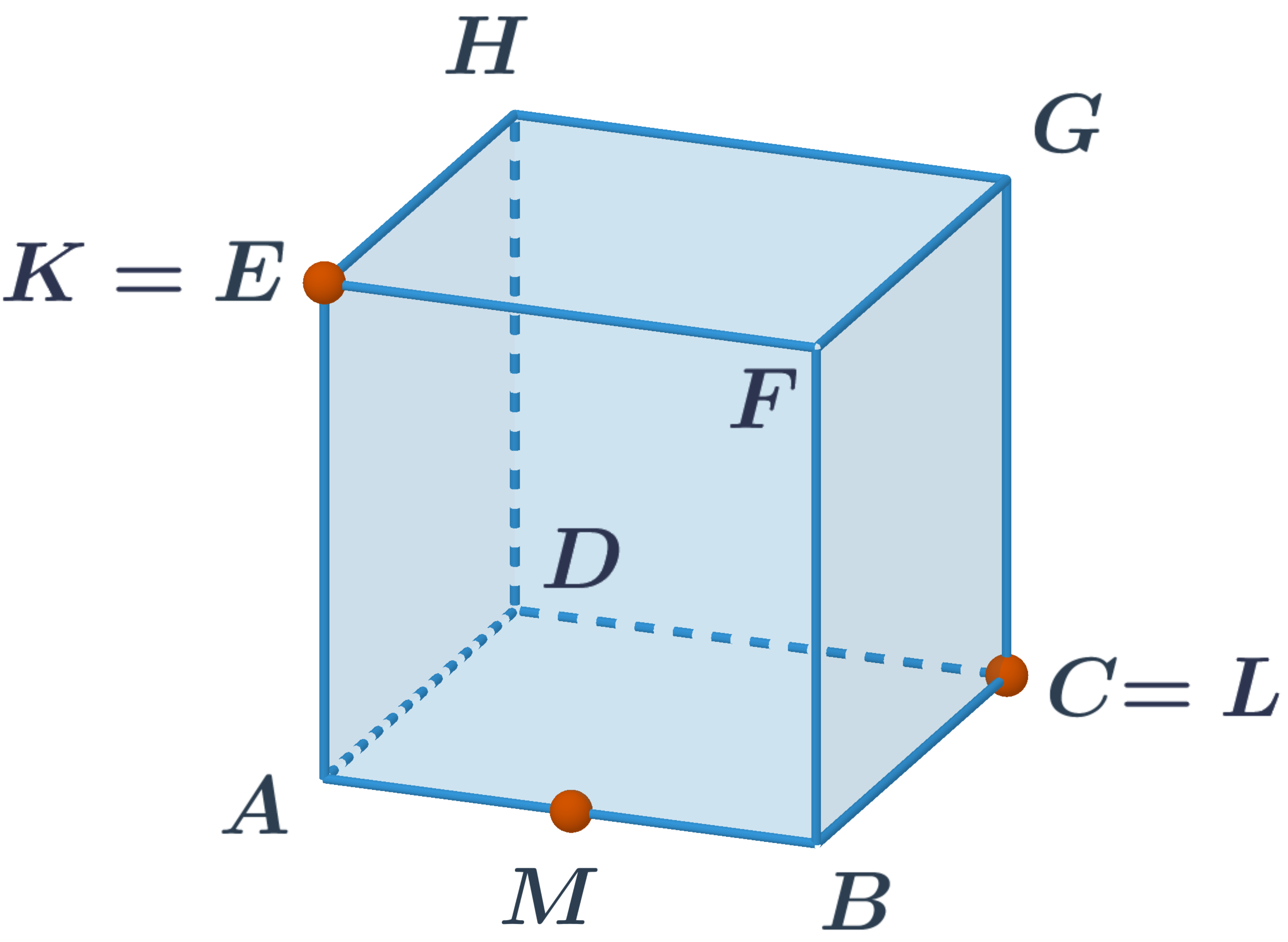
- Body K, M leží v jedné rovině – v přední stěně ABFE. Úsečka KM je tedy první část řezu.
- Stejně tak body L, M leží v jedné rovině – v dolní stěně ABCD. Úsečka LM je tedy druhá část řezu.
- Bod K leží v horní stěně EFGH. Ta je rovnoběžná se stěnou ABCD. Další část řezu KN je tedy rovnoběžná s úsečkou LM.
- Podobně je i poslední část řezu NL v zadní stěně CDHG rovnoběžná s úsečkou KM ve stěně ABFE.
- Řezem je v tomto případě rovnoběžník.
Řezy těles
Sestrojit řez tělesa znamená sestrojit průnik roviny a tělesa. K základní principům konstrukce řezů, které známe z řezů krychle si u složitějších případů přidáme ještě jedno pravidlo:
- Když známe jednu stranu řezu, můžeme ji protáhnout do ostatních stěn. Průsečíky s ostatními stěnami určíme tak, že protáhneme společnou hranu hranu stěny, kde leží známá úsečka řezu a stěny, ve které chceme řez najít. Výhodné je najít průsečnici roviny podstavy a roviny řezu.
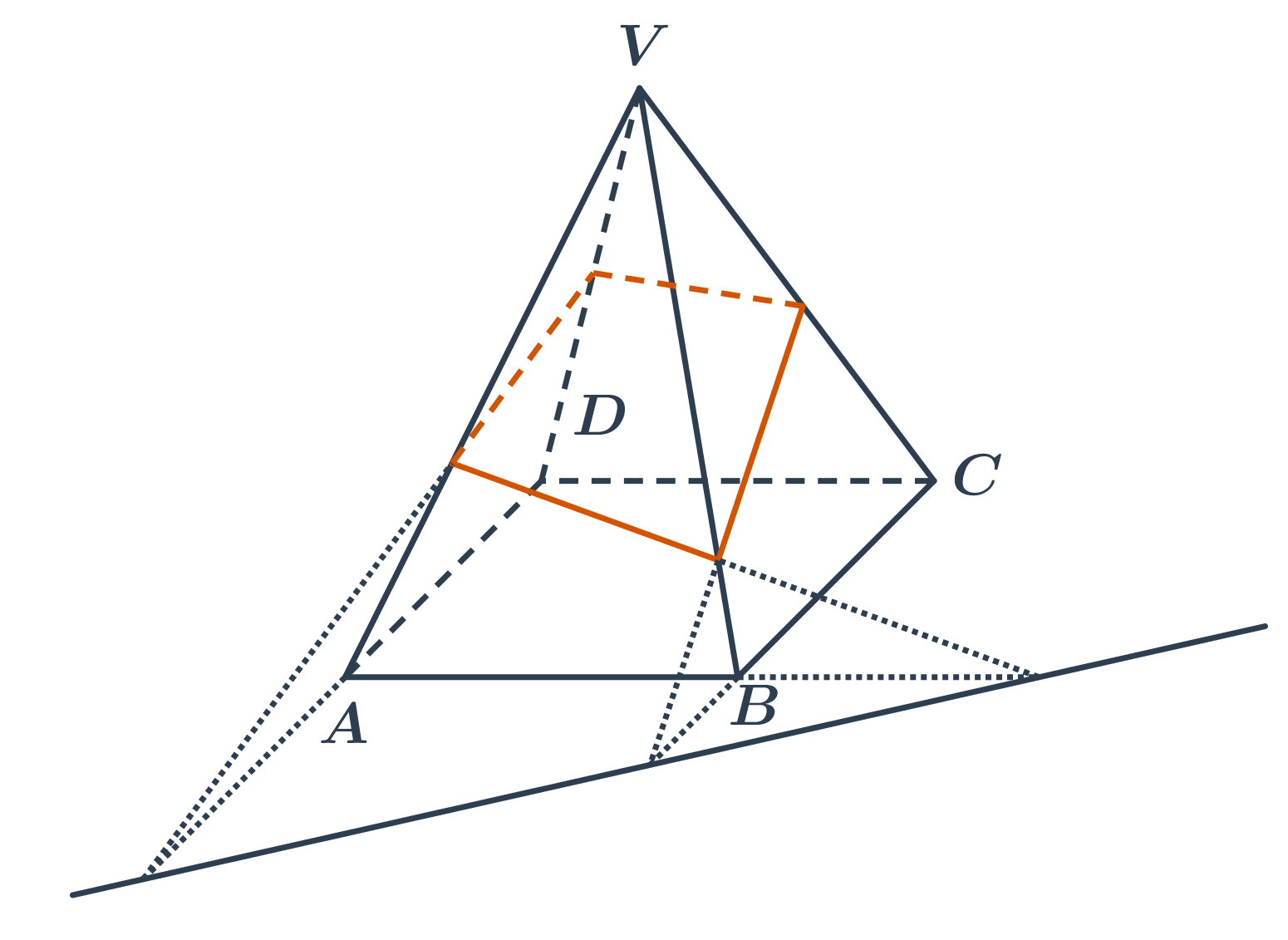
Zobecněním tohoto principu je tzv. středová kolineace, která se využívá pro přesné sestrojení řezu jehlanu a kužele.
Řez jehlanu rovinou procházející body K, L, M.
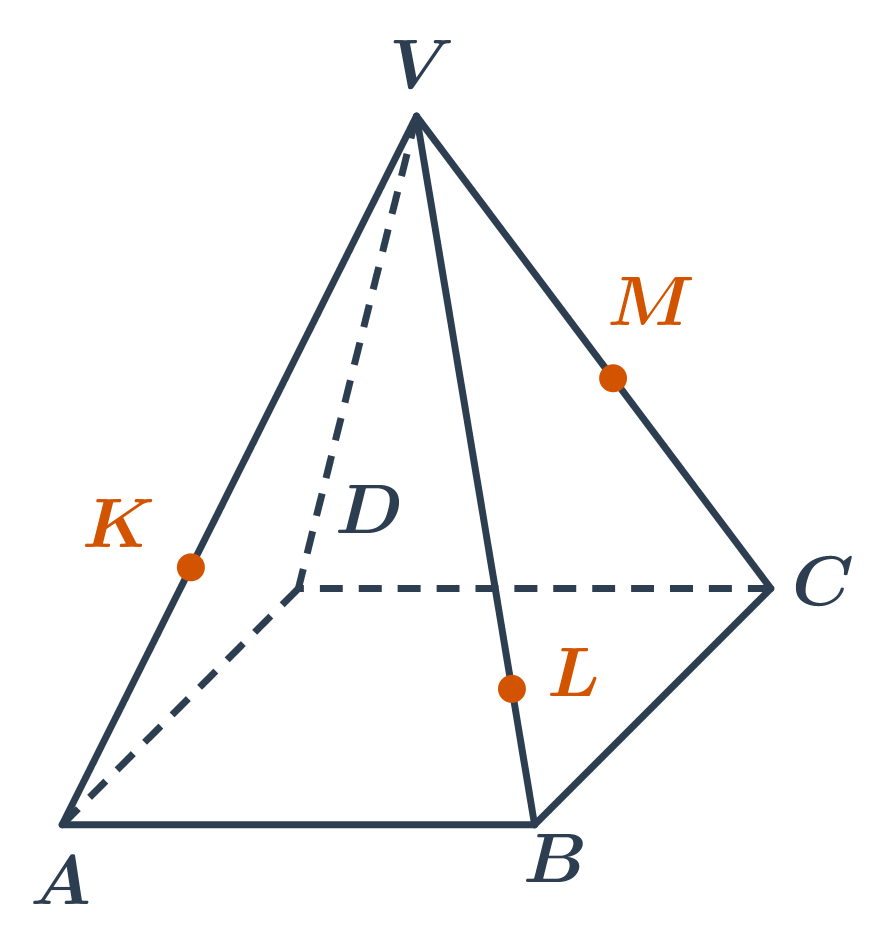
- Známe body na hranách, můžeme rovnou sestrojit dvě části řezu - úsečky KL a LM.
- Najdeme průsečnici roviny podstavy a roviny řezu. Ve stěne BCV leží hrana podstavy BC a úsečka LM. Jejich protažením získáme společný bod P tří rovin: roviny stěny BCV, roviny podstavy a roviny řezu.
- Stejným způsobem získáme společný bod Q tří rovin: roviny stěny ABV, roviny podstavy a roviny řezu. Přímka PQ je pak průsečnice roviny podstavy a roviny řezu.
- Protažením hrany AD získáme na průsečnici bod R. Na přímce RK pak leží další část řezu ve stěně ADV.
- V zadní stěne CDV nyní máne na hranách dva body řezu a můžeme doplnit poslední stranu řezného čtyřúhelníku.
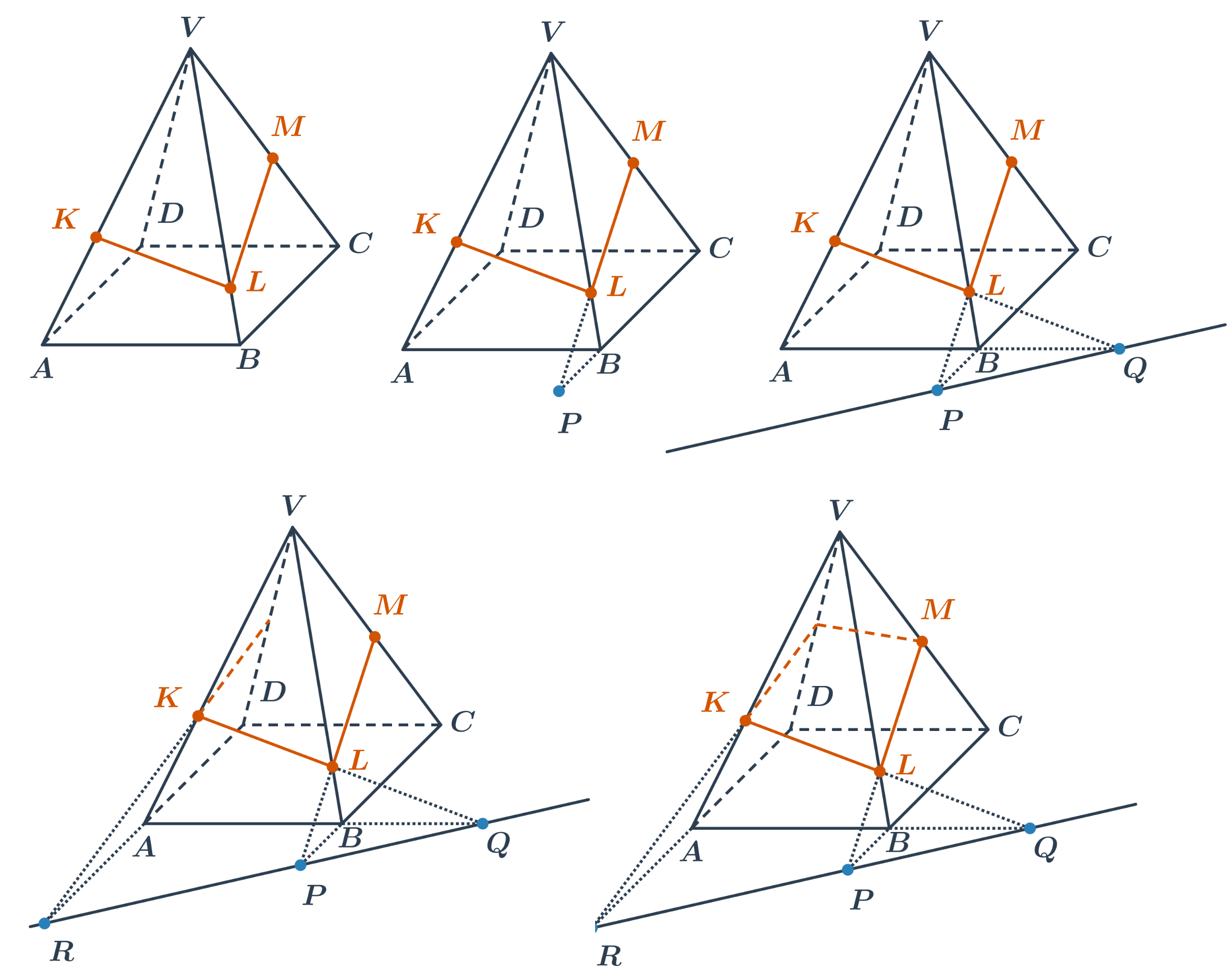
Stejně jako u řezu krychle záleží na poloze roviny a tělesa:
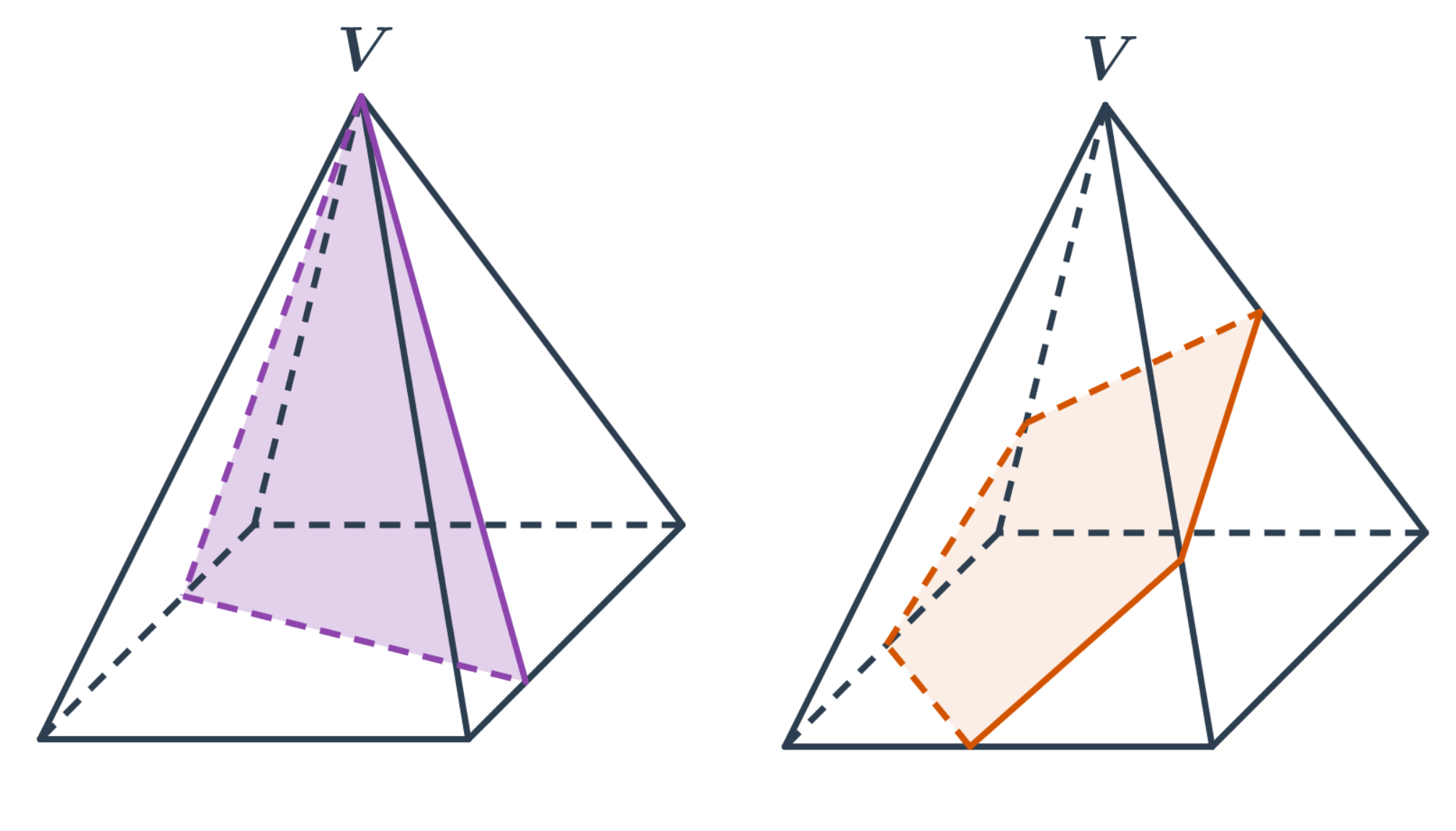
Jehlan
- Rovina prochází vrcholem jehlanu - řezem je trojúhelník.
- Rovina neprochází vrcholem - řezem je obecný n-úhelník.
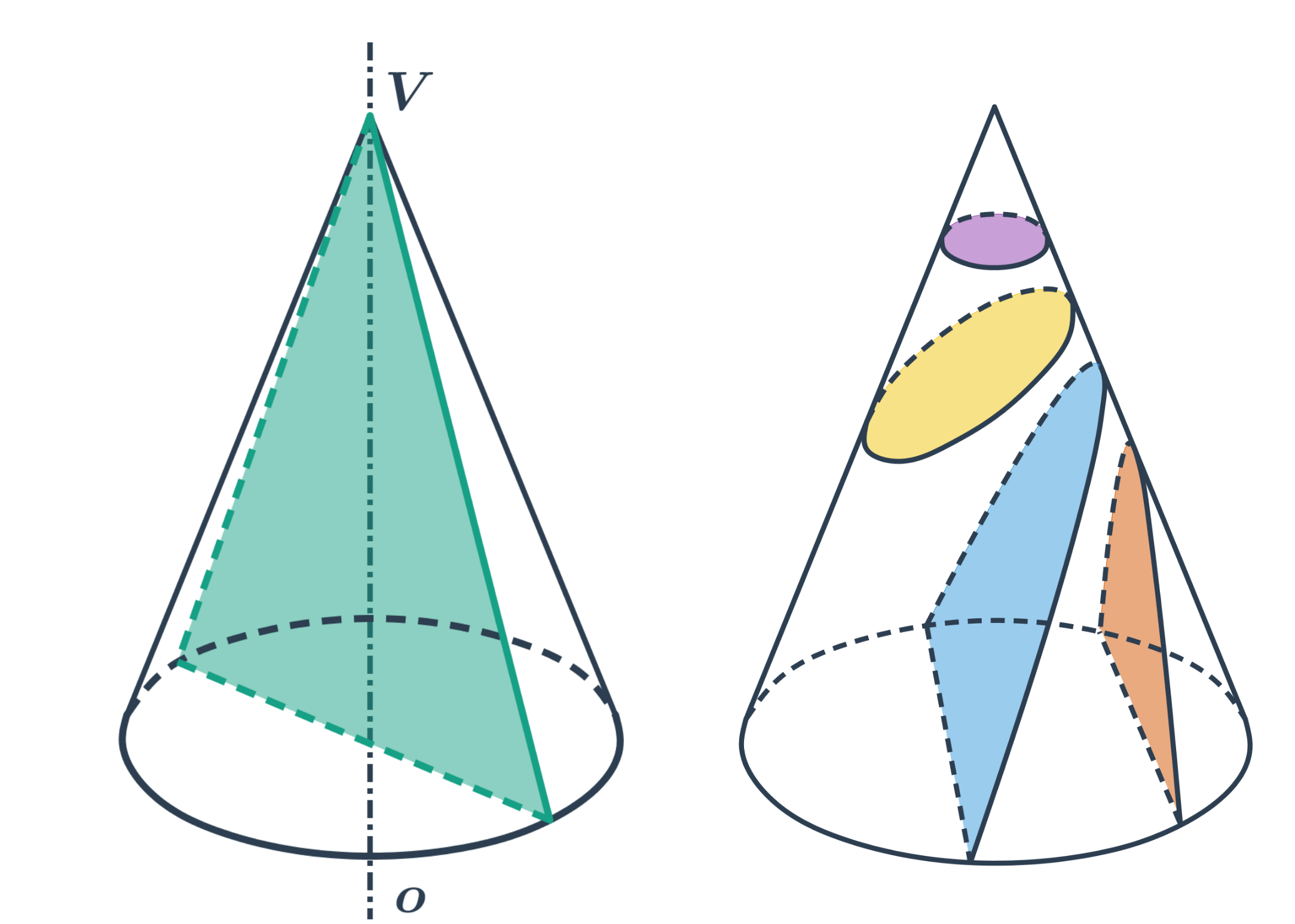
Kužel
- Rovina prochází vrcholem kužele - řezem je trojúhelník.
- Rovina neprochází vrcholem - řezem je kuželosečka.
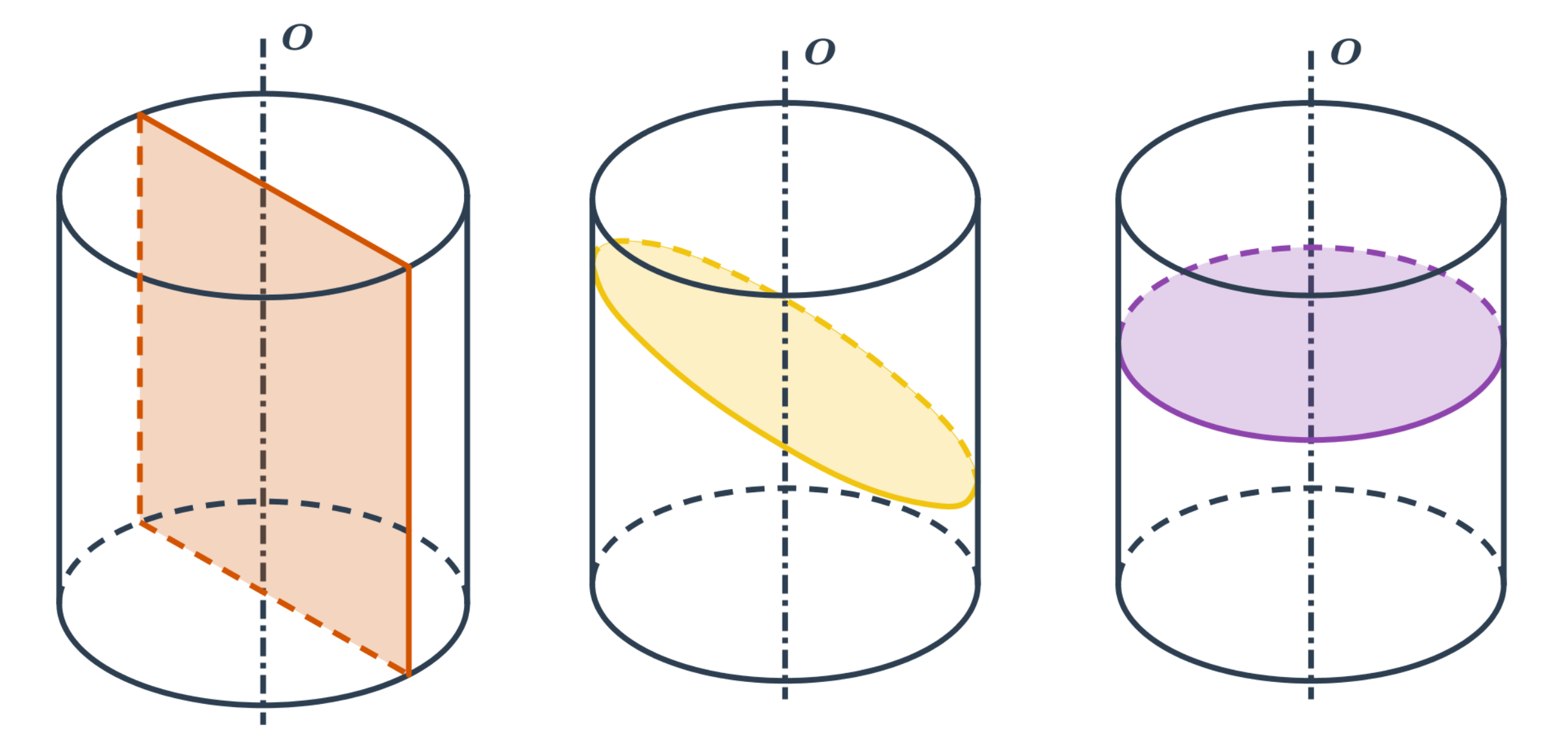
Válec
- Rovina je rovnoběžná s osou válce - řezem je obdélník.
- Rovina není rovnoběžná s osou válce - řezem je kružnice nebo elipsa.
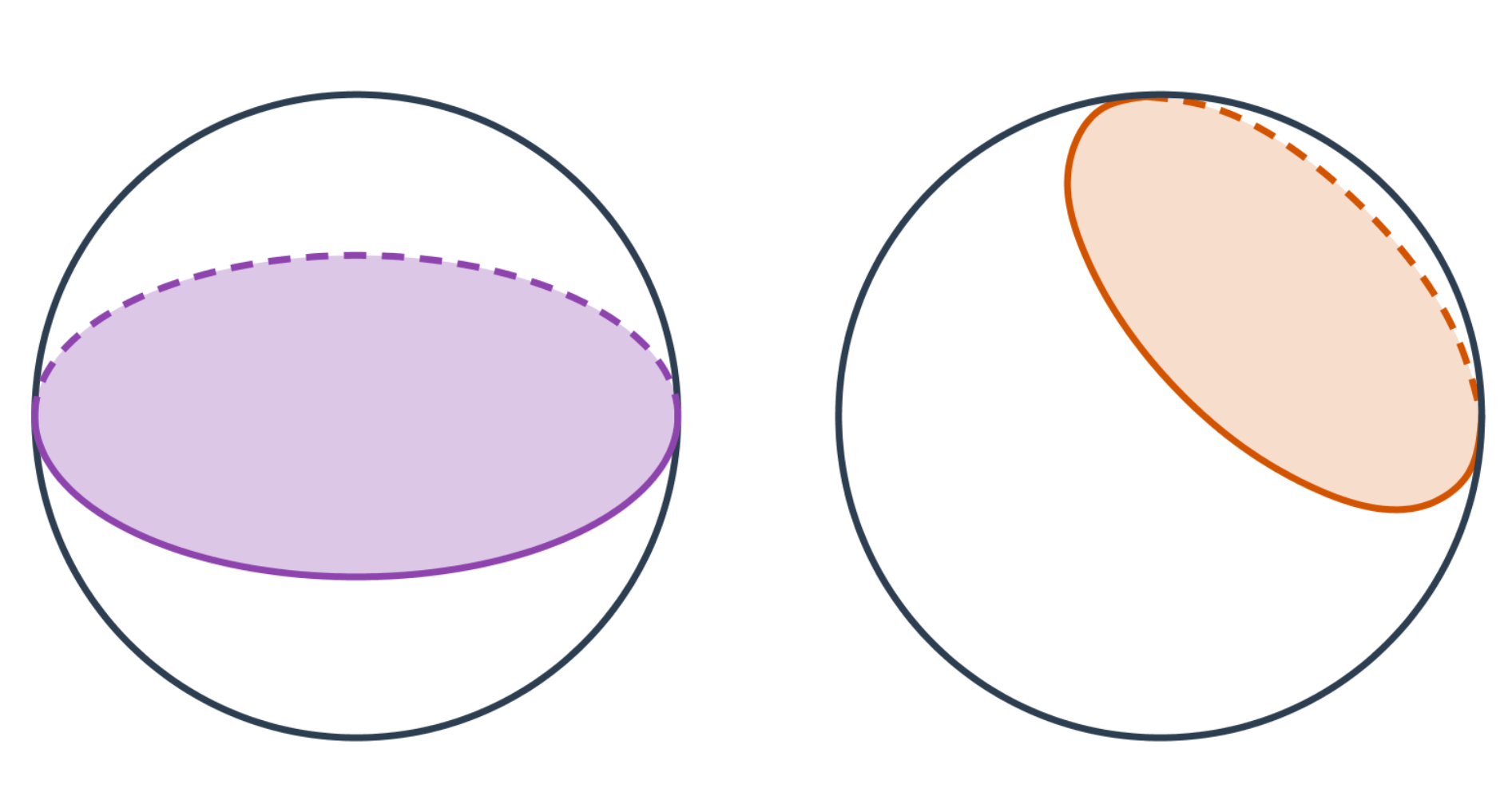
Koule
Řezem koule je vždy kružnice. Na papíře či obrazovce ji ale můžeme vidět i jako elipsu.