Výpis souhrnů
Lineární lomené funkce
Podtémata
Lineární lomené funkce
Lineární lomenou funkci můžeme vyjádřit jako podíl dvou lineárních funkcí, tedy ve tvaru
f:y =\frac{ax+b}{cx+d},
kde a,b,c,d jsou konstanty.
Definičním oborem lineární lomené funkce je množina všech reálných čísel kromě hodnoty, ve které by jmenovatel zlomku \frac{ax+b}{cx+d} byl nulový:
D(f)=\mathbb{R} - \{-\frac{d}{c}\}
Úpravou podmínky pro nenulovost jmenovatele zlomku dostaneme vyjádření definičního oboru pomocí nerovnice: cx+d\neq0\Rightarrow x\neq -\frac{d}{c}
Kdy je funkce nelineární a nekonstantní (a graf je hyperbola, nikoliv přímka)
K tomu, aby f:y=\frac{ax+b}{cx+d} nebyla lineární ani konstantní funkce, musí být splněno několik podmínek. Pro konstanty a,b,c,d musí platit: c\neq0 a bc-ad\neq0.
- pro c=0 bychom měli lineární funkci danou rovnicí y =\frac{a}{d}\cdot x+\frac{b}{d}
- pro bc-ad=0 bychom měli konstantní funkci y =\frac{a}{c}
Vysvětlení podmínky bc-ad\neq0
| Pro lineární lomenou funkci danou předpisem \frac{ax+b}{cx+d} provedeme dělení čitatele zlomku \frac{ax+b}{cx+d} jeho jmenovatelem: |
| \begin{array}{lrrrr} \hspace{0.3cm}(\hspace{0.4cm}ax+\hspace{0.47cm}b)&:&(cx+d)&=&\frac{a}{c}\\\underline{-( \frac{a}{c}\cdot cx+\frac{a}{c}\cdot d)\hspace{0.5cm}}& \\ \hspace{1.05cm}0+b-\frac{a}{c}\cdot d\\ \end{array} |
| Vyšel nám tedy podíl \frac{a}{c} a zbytek b-\frac{a}{c}\cdot d. |
| Pokud by platilo b-\frac{a}{c}\cdot d=0, mohli bychom funkci y =\frac{ax+b}{cx+d} zapsat zjednodušeně ve tvaru y =\frac{a}{c} a to není lineární lomená funkce, ale funkce konstantní. |
| Abychom měli lineární lomenou funkci, musí tedy platit b-\frac{a}{c}\cdot d\neq0. Tuto podmínku můžeme vynásobením obou stran hodnotou c upravit na tvar: bc-ad\neq0 |
Speciálním případem lineární lomené funkce je nepřímá úměrnost vyjádřená ve tvaru y =\frac{k}{x}.
NahoruVlastnosti lineární lomené funkce
Lineární lomená funkce f:y =\frac{ax+b}{cx+d} má definiční obor D(f)=\R - \{-\frac{d}{c}\}, což můžeme také zapsat jako sjednocení dvou intervalů: D(f)=(-\infty, -\frac{d}{c}) \cup (-\frac{d}{c}, \infty)
Pokud c\neq0 a bc-ad\neq0, pak pro lineární lomenou funkci platí:
- je prostá
- není periodická
- nemá maximum ani minimum
- není shora ani zdola omezená
Další vlastnosti závisí na hodnotách koeficientů a, b, c, d:
- pro bc-ad \gt 0 je lineární lomená funkce klesající na intervalu (-\infty, -\frac{d}{c}) a také klesající na intervalu (-\frac{d}{c}, \infty)
- pro bc-ad \lt 0 je lineární lomená funkce rostoucí na intervalu (-\infty, -\frac{d}{c}) a také je rostoucí na intervalu (-\frac{d}{c}, \infty)
- pro a=0 a d=0 má lineární lomená funkce tvar: f:y =\frac{b}{cx} a je to lichá funkce (f(x) = - f(-x))
Příklad: vlastnosti funkce f:y =\frac{3x+1}{4x+2}
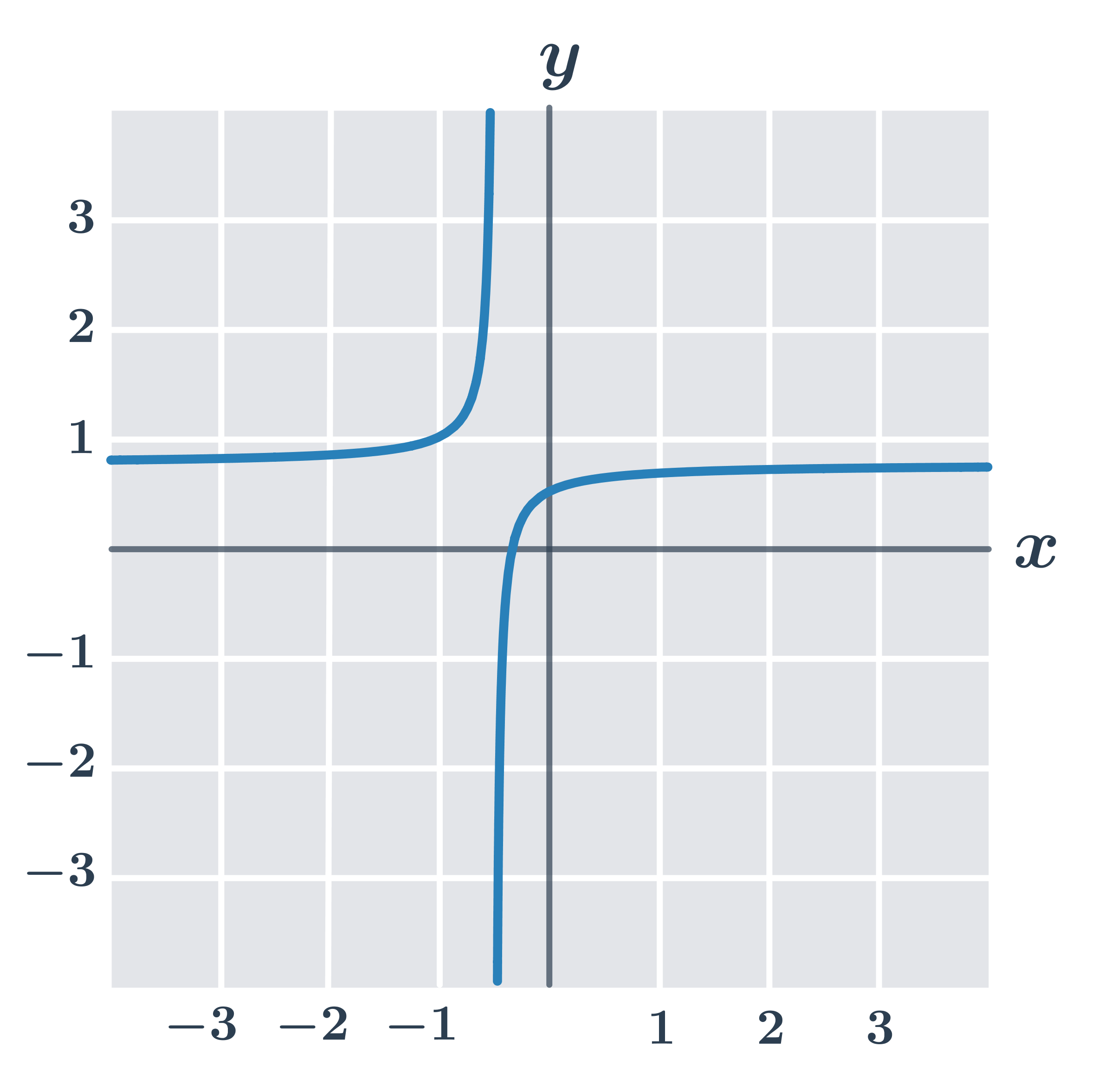
- Definiční obor D(f)=\R - \{-\frac{1}{2}\}.
- Funkce je prostá.
- Funkce je rostoucí na intervalu (-\infty,-\frac{1}{2}) a také je rostoucí na intervalu (-\frac{1}{2},\infty) – snadno poznáme z grafu, ale zároveň můžeme ověřit splnění podmínky bc-ad \lt 0: pro danou funkci bc-ad=1\cdot4-3\cdot2=-2.
Příklad: vlastnosti funkce f:y =\frac{3}{2x}
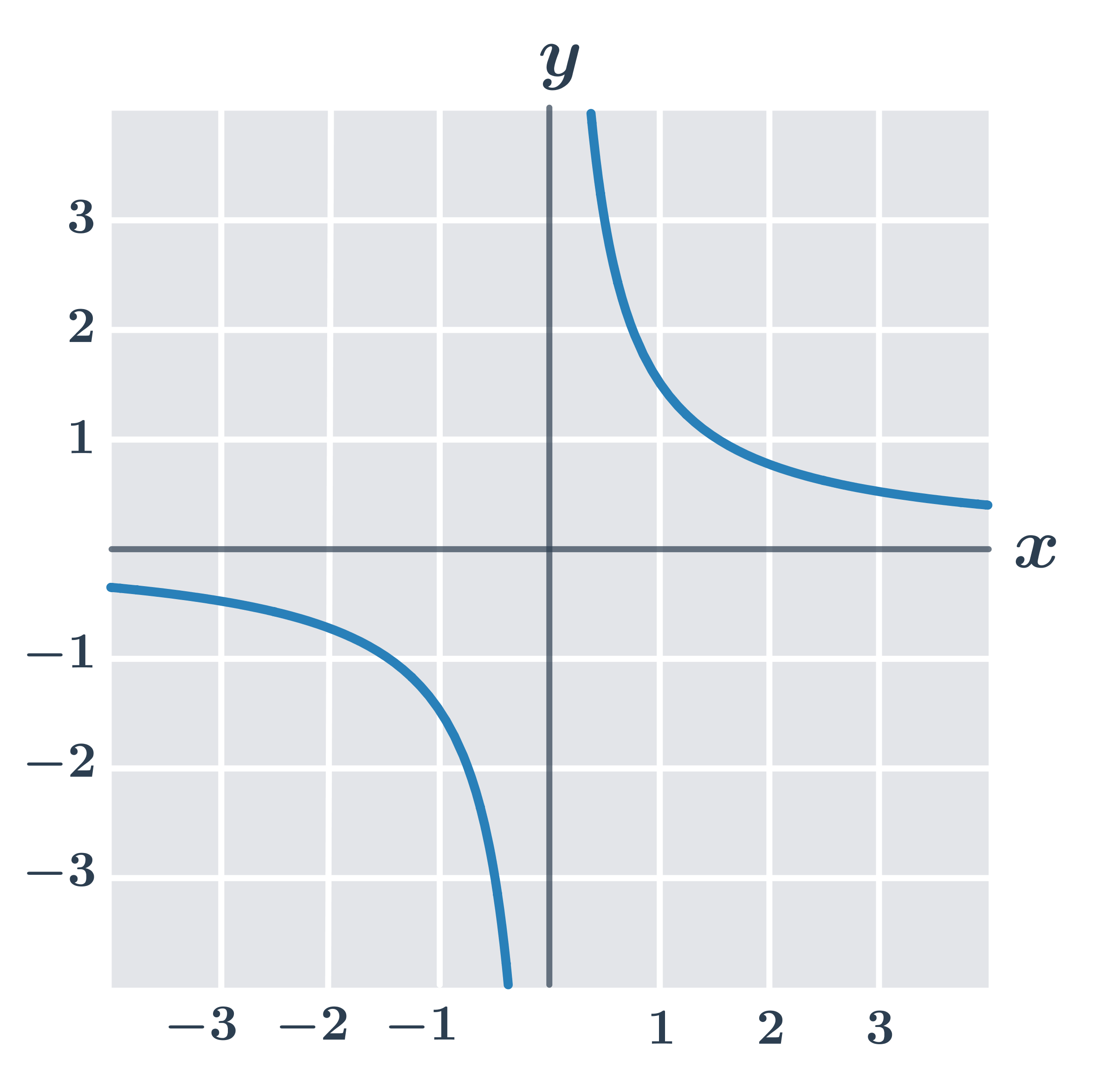
- Definiční obor D(f)=\R - \{0\}.
- Funkce je prostá.
- Funkce je klesající na intervalu (-\infty,0) a také je klesající na intervalu (0,\infty).
- Funkce je lichá – graf je souměrný podle počátku (pro lineární lomené funkce, kde a=0 a d=0).
Poznámka: omezenost lineární lomené funkce
- Definiční obor lineární lomené funkce tvoří vždy dva intervaly.
- Pokud si budeme všímat vlastností funkce jen na jednom z těchto intervalů, jedná se o funkci omezenou zdola nebo shora. Například funkce na obrázku f:y =\frac{2x+3}{x+1}:
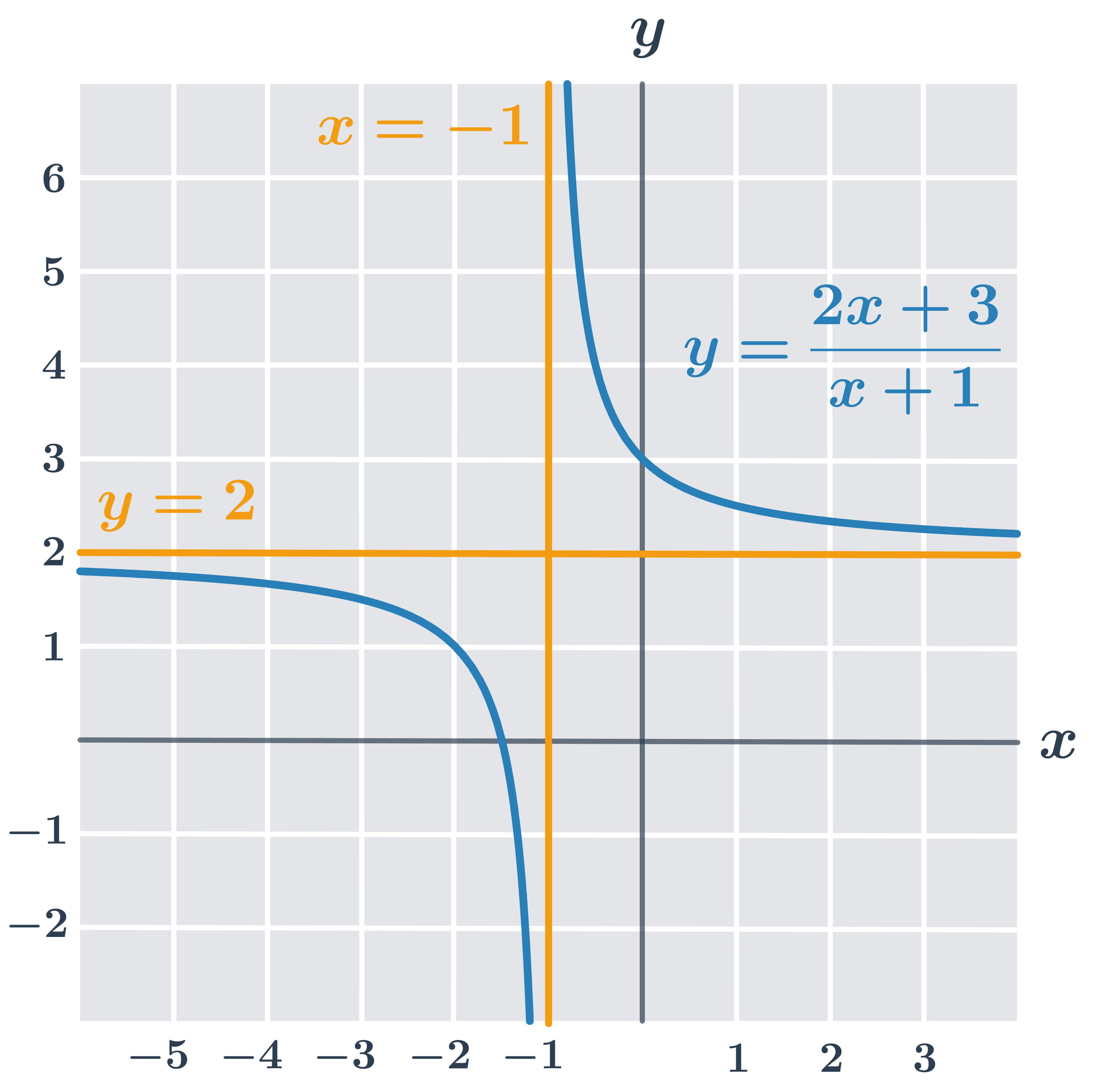
- Definiční obor D(f)=\R - \{-1\}, tedy intervaly (-\infty;-1) a (-1;\infty).
- Na intervalu (-\infty;-1) je funkce shora omezená a na intervalu (-1;\infty) zdola omezená.
Grafy lineárních lomených funkcí
Grafem lineární lomené funkce je hyperbola, která má asymptoty rovnoběžné se souřadnými osami x a y.
Asymptota rovnoběžná s osou y prochází bodem, který nepatří do definičního oboru a má tedy rovnici: x =-\frac{d}{c}.
Pro nalezení rovnice asymptoty rovnoběžné s osou x vydělíme čitatele a jmenovatele a funkční předpis y =\frac{ax+b}{cx+d} upravíme na tvar y =\frac{a}{c}+\frac{n}{ax+b}. Asymptota rovnoběžná s osou x má rovnici: y =\frac{a}{c}.
Průsečík grafu s osou x je bod, pro který ax+b=0. V tomto bodě je hodnota funkce nulová, tedy čitatel zlomku \frac{ax+b}{cx+d} je nulový.
Průsečík grafu s osou y je bod, který dostaneme dosazením hodnoty x=0 do funkčního předpisu.

Příklad – funkce y =\frac{2x+3}{x+1}
Rozeberme si graf funkce z obrázku výše:
- definiční obor D(f)=\R - \{-1\}, protože x+1\neq0
- asymptota rovnoběžná s osou y má rovnici x =-1 (pro x=-1 není funkce definovaná, toto číslo neleží v jejím definičním oboru)
- asymptota rovnoběžná s osou x má rovnici y =2, což zjistíme úpravou funkčního předpisu: y =\frac{2x+3}{x+1}=2+\frac{1}{x+1}
- průsečík grafu s osou x je bod [0;-\frac{3}{2}] (řešení rovnice: 2x+3=0)
- průsečík grafu s osou y je bod [3;0], dosazením hodnoty x=0 do y =\frac{2x+3}{x+1}

