Krychle a kvádr

Krychle a kvádr jsou oba prostorové geometrické útvary, které patří mezi mnohostěny, speciálněji jde o zvláštní případy hranolů.

Krychle je prostorový útvar, který má šest stěn, tvar každé stěny je čtverec. Všechny hrany krychle mají stejnou délku a všechny vnitřní úhly jsou pravé, tedy jejich velikost je 90°. Příklady krychle v běžném životě zahrnují kostky cukru nebo Rubikovu kostku.

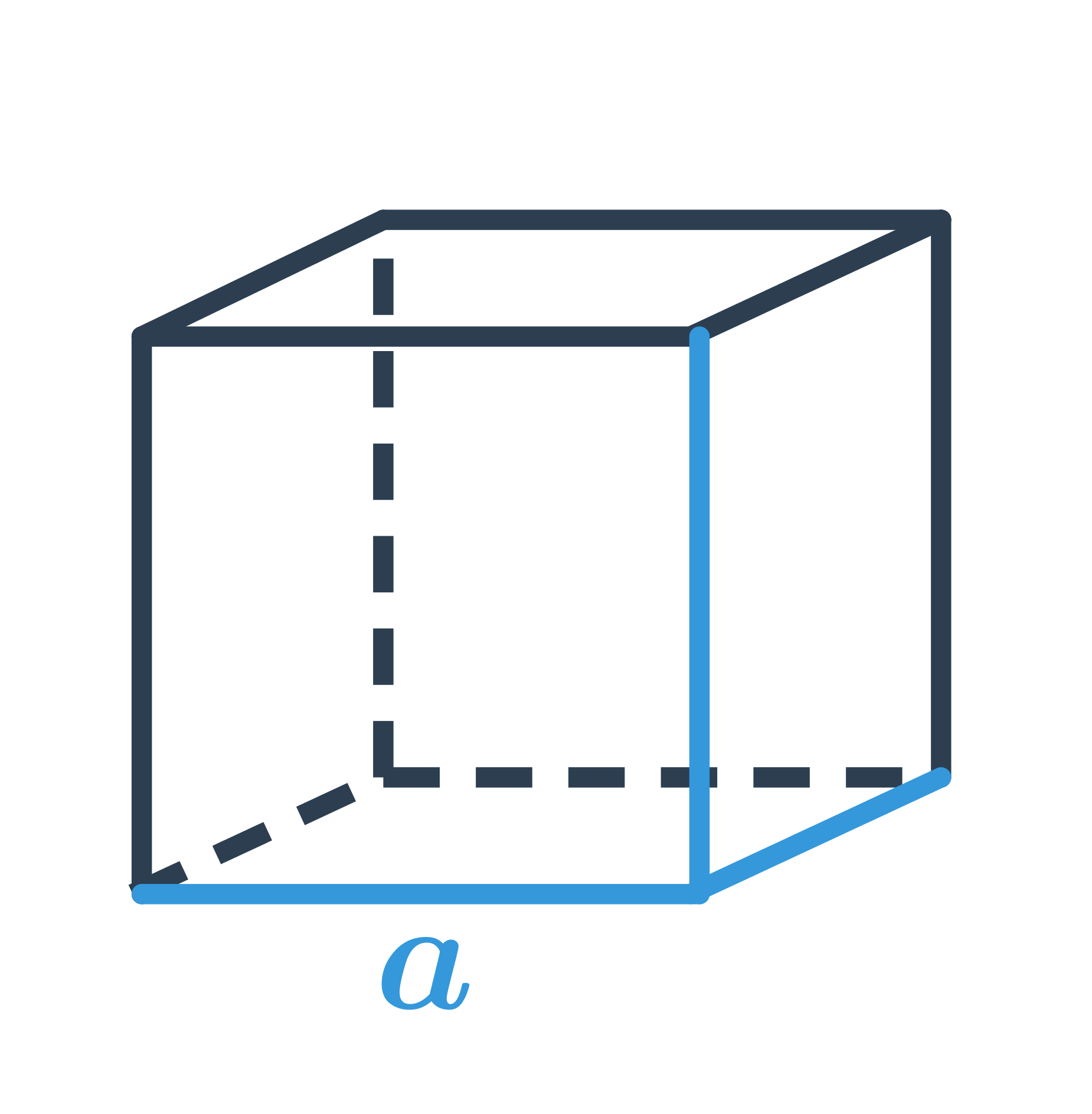
Pro výpočet objemu krychle použijeme vzorec V = a^3, kde a je délka hrany krychle.

Povrch krychle s délkou hrany a se vypočítá pomocí vzorce S = 6a^2.

Kvádr je také hranol, ale na rozdíl od krychle mají jeho stěny tvar obdélníků. Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle. Kvádr má šest stěn, tvar každé stěny je obdélník nebo čtverec, pokud jsou všechny stěny tvaru čtverce, jde o krychli.

Příklady kvádrů v běžném životě zahrnují krabice, knihy nebo cihly.

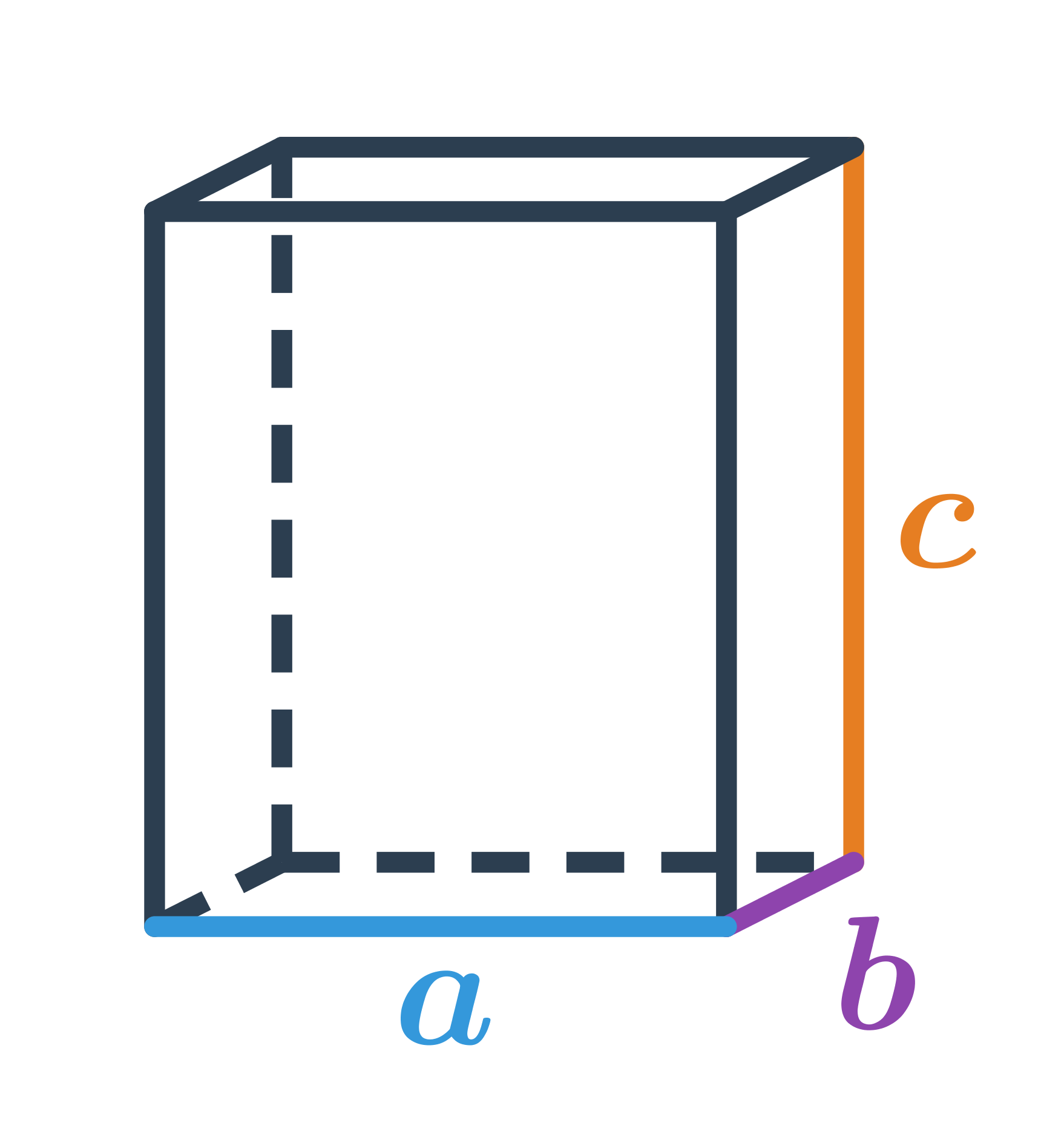
Objem kvádru získáme vzorcem V = a \cdot b \cdot c, kde a,b,c jsou rozměry kvádru.

Povrch kvádru vypočítáme jako součet obsahů všech jeho šesti obdélníkových stěn S = 2(ab + bc + ac). Dvojice protějších stěn jsou shodné obdélníky, proto mají stejné obsahy.

Objem kvádru s délkami hran a,b,c je: V=a\cdot b\cdot c

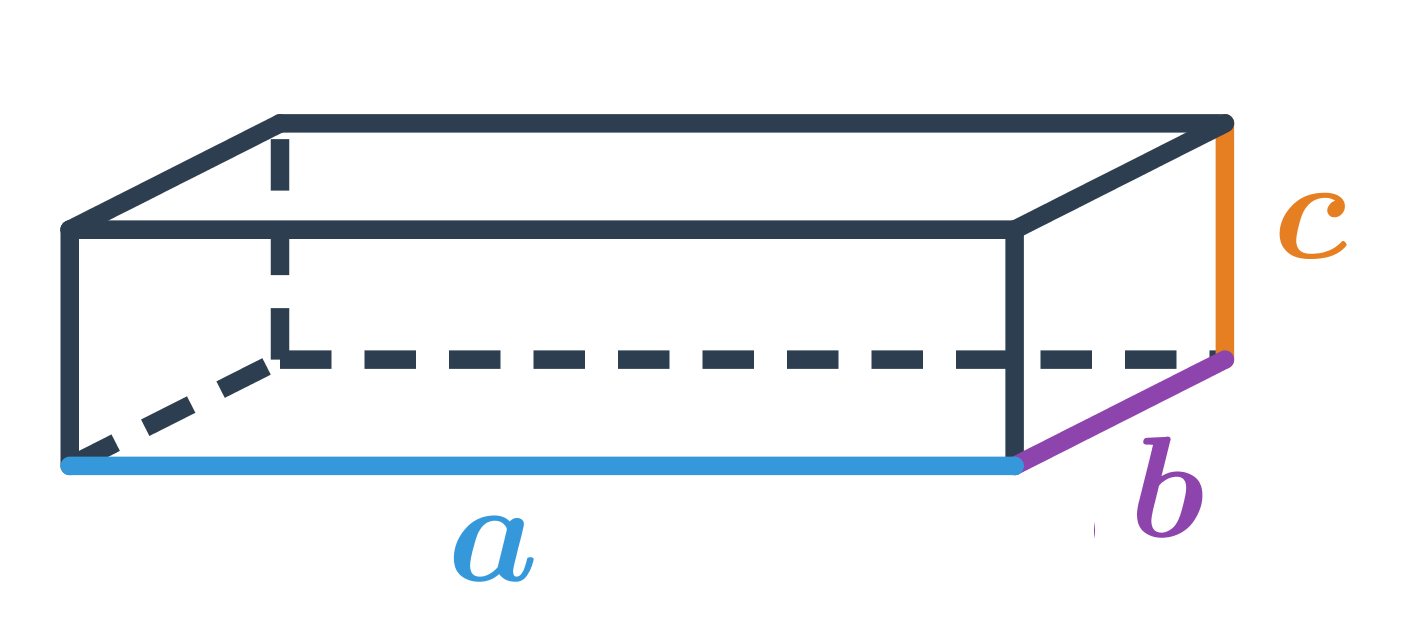
Objem krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako objem kvádru s a=b=c, tedy: V=a\cdot a\cdot a=a^3

Povrch kvádru s délkami hran a,b,c spočítáme jako součet obsahů všech jeho stěn. Tedy: S=2 (a\cdot b + a\cdot c + b \cdot c)

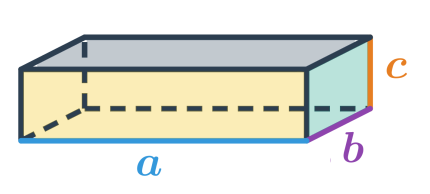
Povrch krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako objem kvádru s a=b=c, tedy šestkrát obsah jedné čtvercové stěny krychle: S = 6\cdot a\cdot a = 6a^2

Síť krychle můžeme zakreslit 11 různými způsoby:

Sestrojit řez krychle znamená sestrojit průnik roviny a krychle. Půjde o mnohoúhelník, který leží v rovině řezu a jeho strany jsou okraje řezu, tedy čáry, kudy rovina řízne stěny krychle. Tyto průsečnice řezné roviny se stěnami tělesa chceme sestrojit. Při konstrukci řezů (nejen krychle) můžeme použít tři základní pravidla:

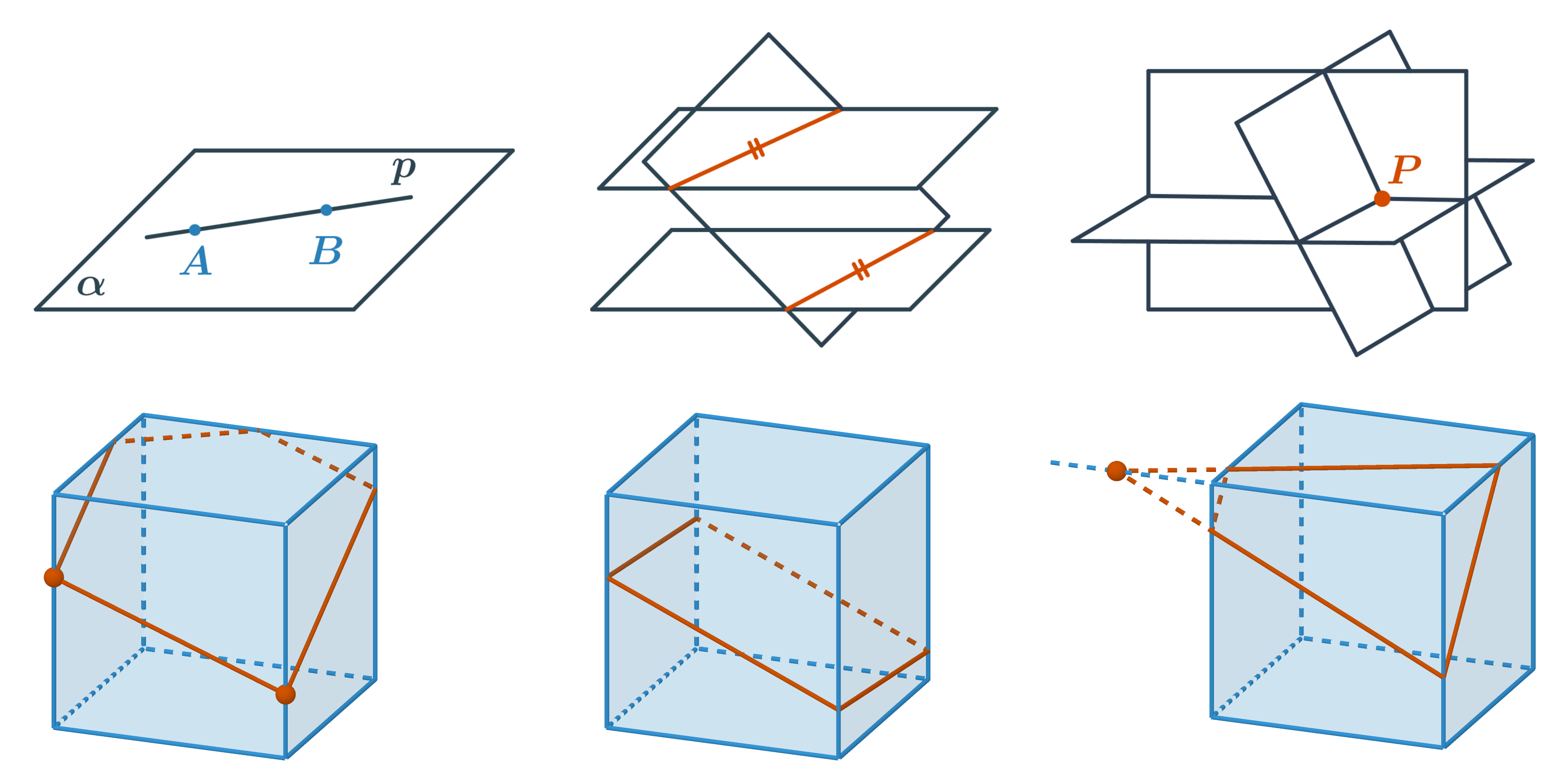
• Pokud leží dva různé body v rovině, pak přímka, která jimi prochází, leží také v této rovině. Když známe ve stěně tělesa dva různé body, které oba leží v rovině řezu, nakreslíme jejich spojnici. Průnik stěny a této spojnice je jednou stranou řezu.
• Dvě rovnoběžné roviny protíná každá další k nim různoběžná rovina ve dvou rovnoběžných přímkách. To znamená, že strany řezu v rovnoběžných stěnách jsou navzájem rovnoběžné.
• Tři navzájem různoběžné roviny se vždy protínají v jednom bodě. Tímto bodem prochází všechny tři průsečnice jednotlivých dvojic rovin. Tedy dvě průsečnice rovin dvou sousedních stěn s rovinou řezu a přímka, na které leží společná hrana stěn, se protínají v jednom bodě.

Pozor si dáváme na nejčastějsí chyby:

• zalomení řezu v jedné stěně (část řezu v jedné stěně musí vždy tvořit jedna úsečka)
• čára řezu jde vnitřkem nebo vnějškem tělesa (okraj řezu musí být celý ve stěnách tělesa)
• čára řezu nekončí na hraně (těleso na hraně končí, řez tělesa také)

Řez krychle rovinou procházející body K, L, M.

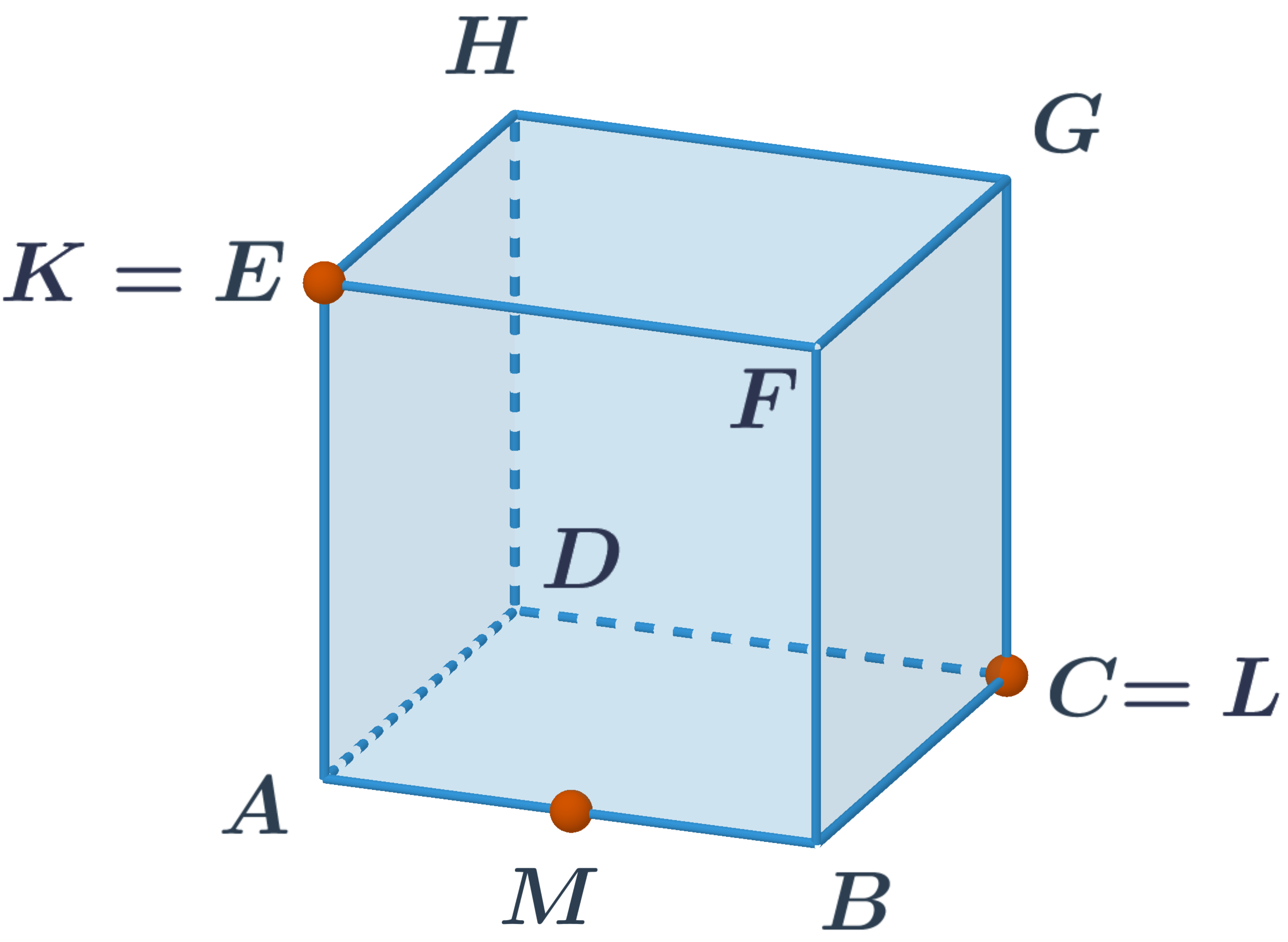
• Body K, M leží v jedné rovině – v přední stěně ABFE. Úsečka KM je tedy první část řezu.
• Stejně tak body L, M leží v jedné rovině – v dolní stěně ABCD. Úsečka LM je tedy druhá část řezu.
• Bod K leží v horní stěně EFGH. Ta je rovnoběžná se stěnou ABCD. Další část řezu KN je tedy rovnoběžná s úsečkou LM.
• Podobně je i poslední část řezu NL v zadní stěně CDHG rovnoběžná s úsečkou KM ve stěně ABFE.
• Řezem je v tomto případě rovnoběžník.