Body

Uvažujeme‑li body v rovině nebo v prostoru, kde máme zavedenou kartézskou soustavu souřadnic (v rovině se dvěma osami x,y nebo v prostoru se třemi osami x,y,z), můžeme body popsat číselně souřadnicemi v rovině, případně souřadnicemi v prostoru.

Pomocí souřadnic pak umíme spočítat vzdálenost dvou bodů „vzdušnou čarou“ – délku úsečky v rovině, případně v prostoru.

Souřadnice bodů většinou zapisujeme pomocí kartézské soustavy souřadnic v rovině, která má jako osy dvě kolmé přímky. Vodorovná přímka se tradičně označuje x a souřadnice podél této osy se zapisuje první. Svislá přímka se tradičně označuje y a souřadnice podle této osy se zapisuje druhá. Přímky x, y se protínají v bodě [0;0].

Přímky x a y jsou souřadné osy, bod [0;0] je počátek soustavy souřadnic.

Příklad: Souřadnice bodu A

Bod A na obrázku je v dané soustavě souřadnic určen jako x=1, y=2, což můžeme zapsat jako A[1;2].

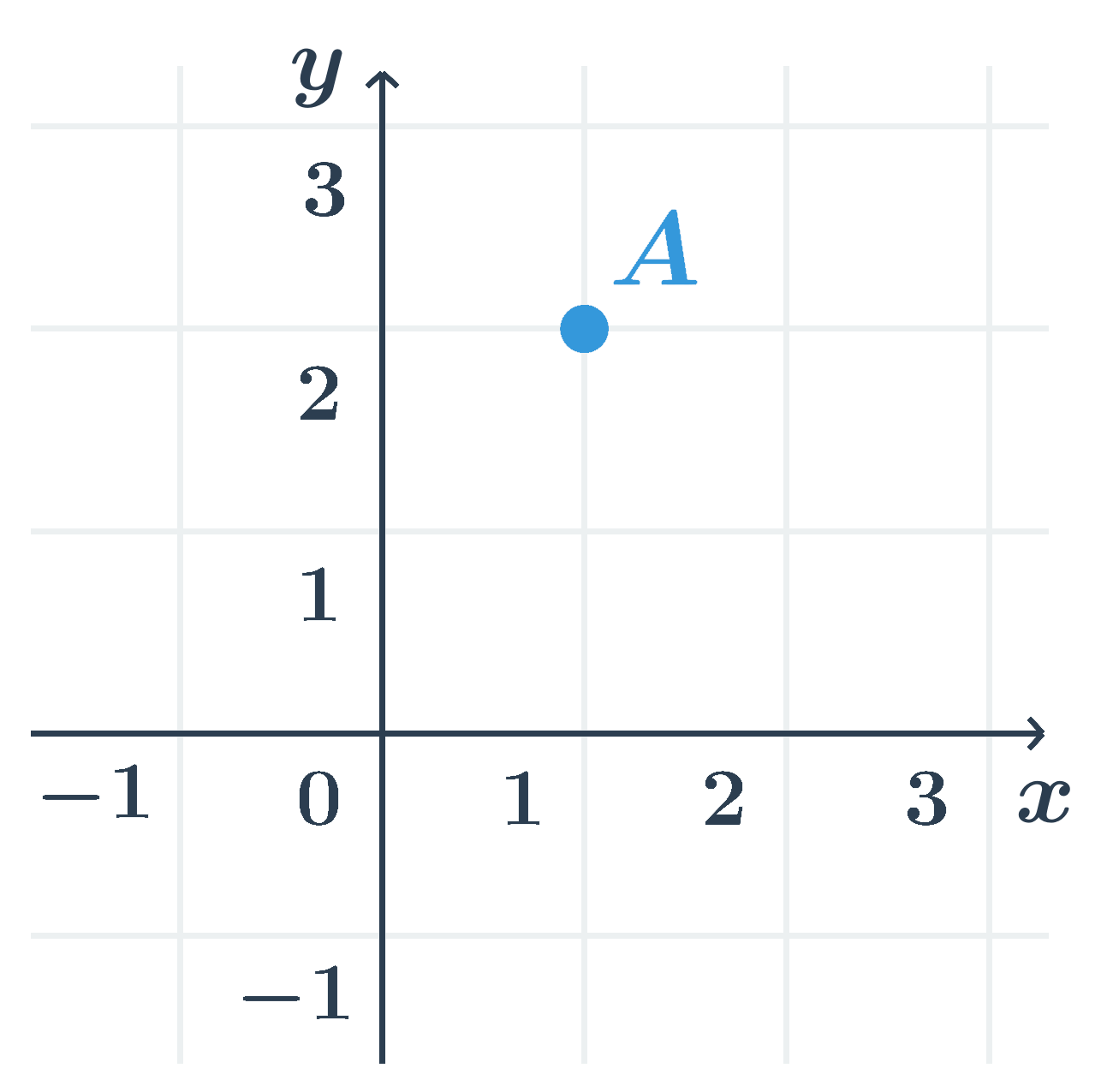
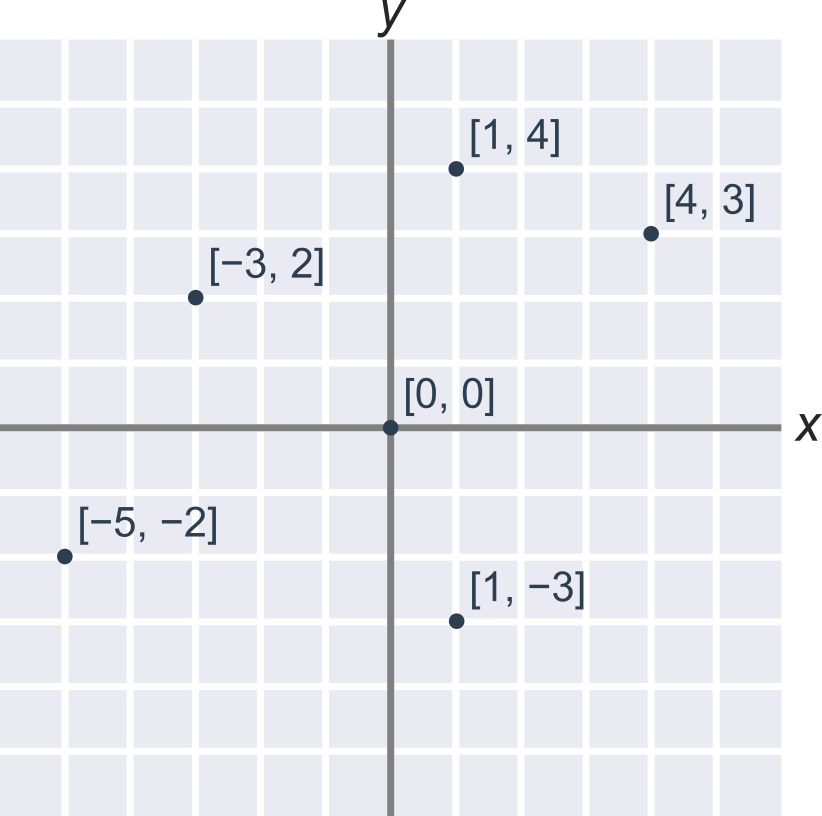
Další příklady souřadnic bodů

Kartézská soustava souřadnic v rovině je daná trojicí navzájem kolmých číselných os x,y,z, které se protínají v bodě [0;0;0].

Přímky x,y,z jsou souřadné osy v prostoru, bod [0;0;0] je počátek soustavy souřadnic.

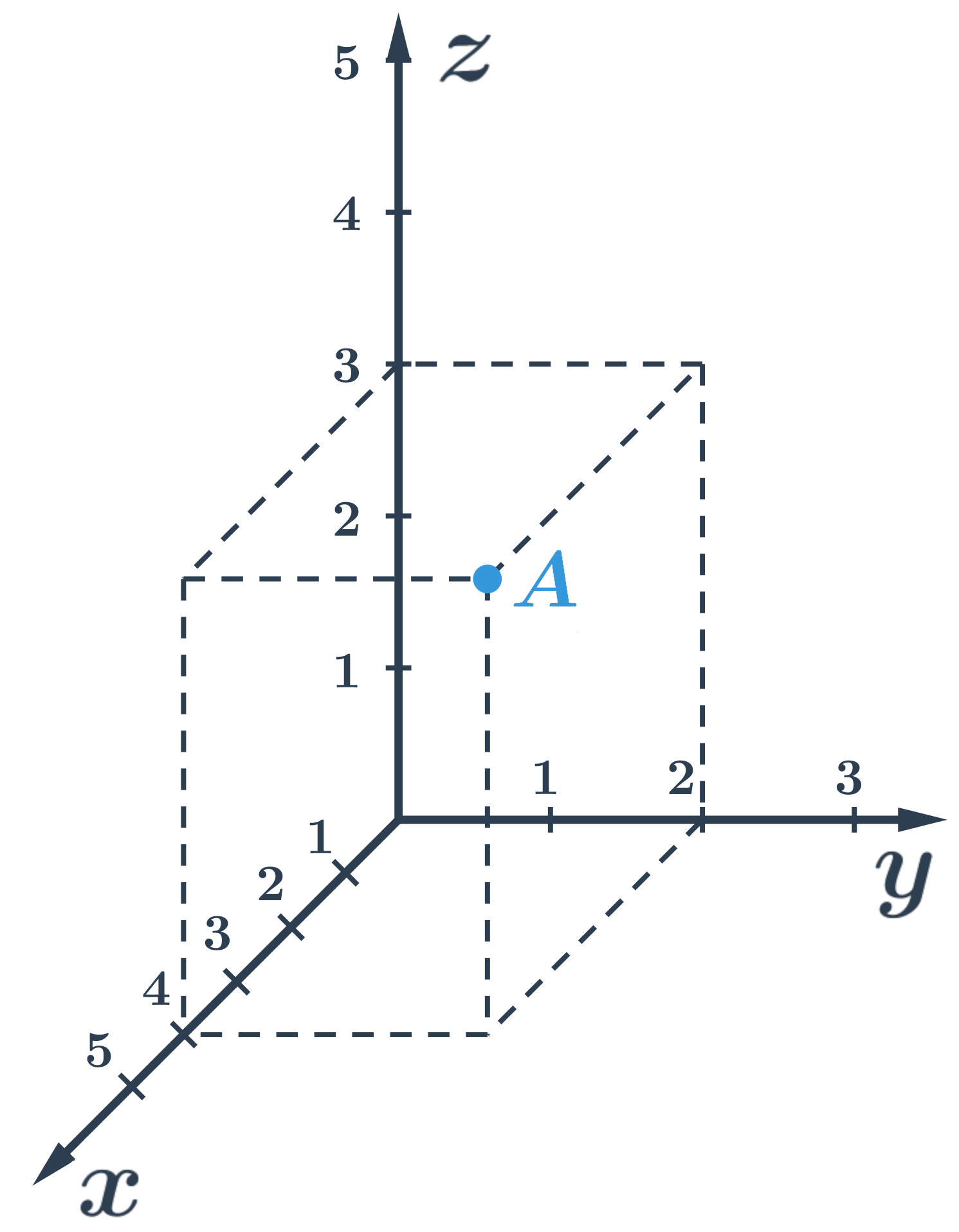
Příklad: Souřadnice bodu A

Bod A na obrázku je v dané soustavě souřadnic určen jako x=4, y=2, z=3, což můžeme zapsat jako A[4;2;3].

Vzdálenost dvou bodů v rovině můžeme spočítat, když známe jejich souřadnice.

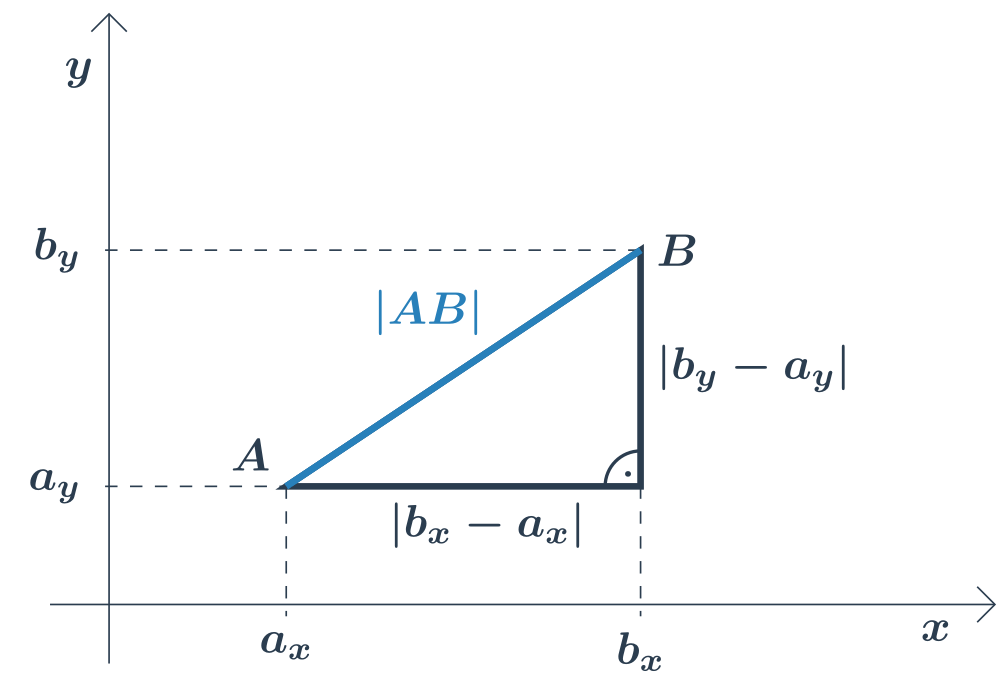
Jsou‑li dány souřadnice A=[a_x,a_y], B=[b_x,b_y], je vzdálenost bodu A od bodu B:

|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2}

Vzoreček vychází z Pythagorovy věty. Všimněme si pravoúhlého trojúhelníku s délkami odvěsen (b_x-a_x) a (b_y-a_y), jehož přepona má délku |AB|.

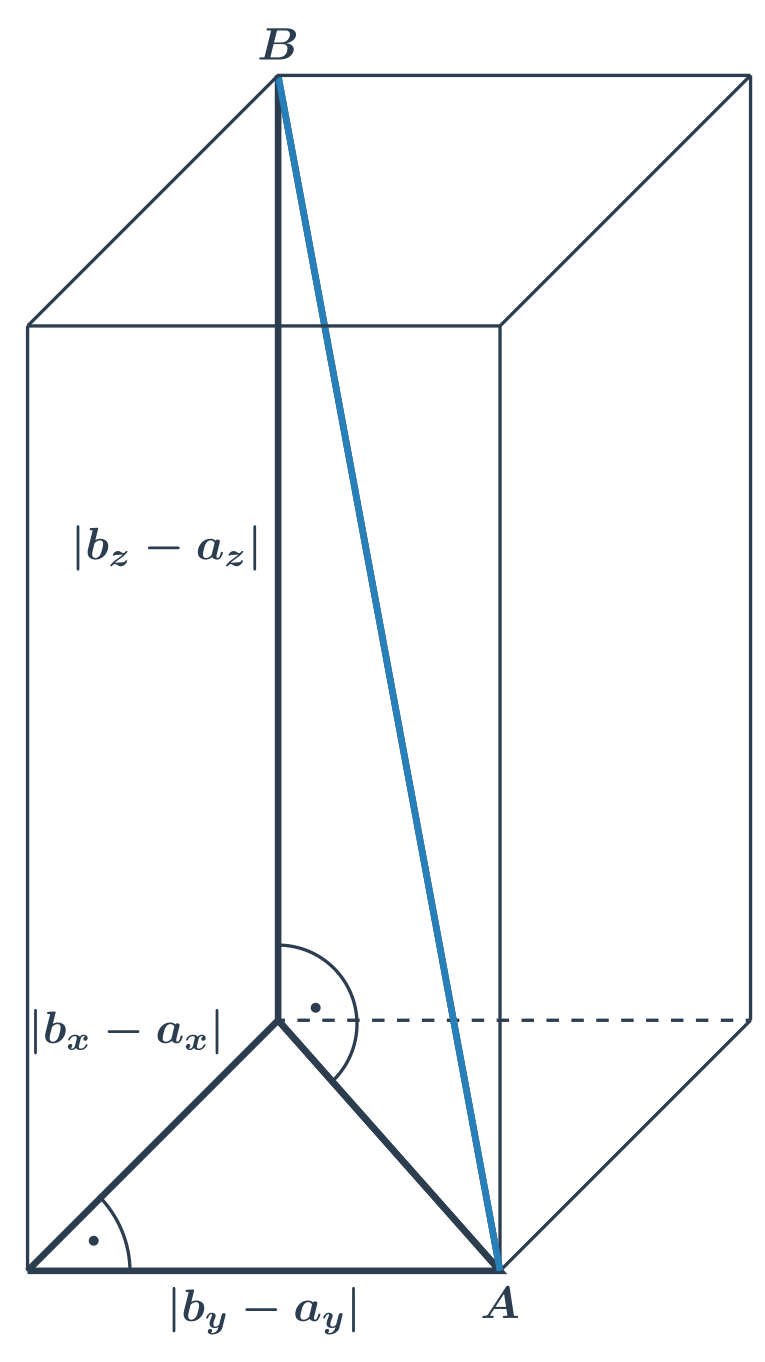
Vzdálenost dvou bodů v prostoru spočítáme podobně jako v rovině pomocí jejich souřadnic. Máme‑li souřadnice bodů A=[a_x,a_y,a_z], B=[b_x,b_y,b_z], můžeme jejich vzdálenost určit takto:

|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2 + (b_z-a_z)^2}

Podobným způsobem (dvakrát po sobě použijeme Pythagorovu větu) počítáme délku tělesové úhlopříčky kvádru.