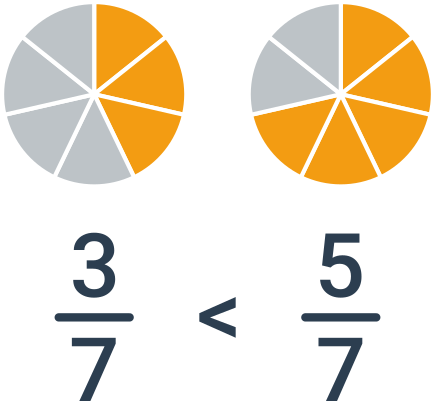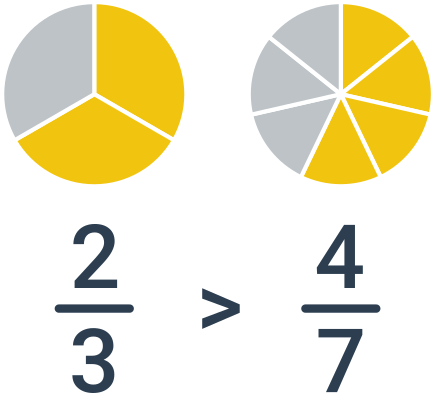Než se pustíme do porovnávání zlomků, je dobré mít jasno v tom, co je čitatel („to nahoře“) a jmenovatel („to dole“). Ve zlomku \frac{3}{7} je 3 čitatel, 7 jmenovatel.

Porovnávání zlomků se stejným jmenovatelem

Porovnávání zlomků se stejným jmenovatelem je jednoduché: stačí prostě porovnat čitatele. Pokud například porovnáváme zlomky \frac{3}{7} a \frac{5}{7}, je větší druhý zlomek. Oba zlomky vyjadřují sedminy z celku a je prostě víc, když máme sedmin pět.

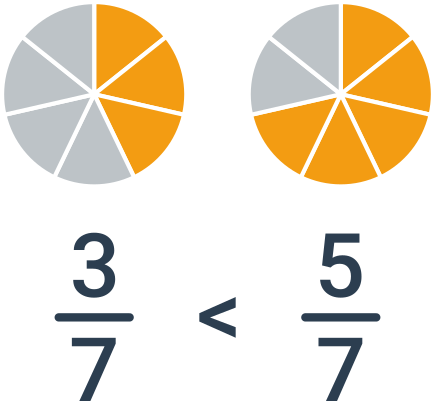
Porovnávání zlomků se stejným čitatelem

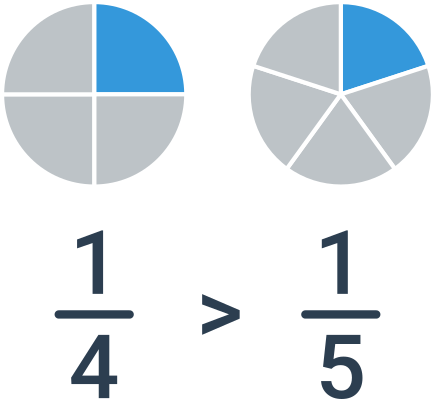
Pokud mají zlomky stejného čitatele, pak stačí porovnat jmenovatele. V tomto případě je však pořadí zlomků opačné než pořadí jmenovatelů. Pokud porovnáváme třeba zlomky \frac{1}{4} a \frac{1}{5}, je větší jedna čtvrtina: dostanu větší kousek pizzy, pokud se bude dělit mezi 4 lidi, než když se bude dělit mezi 5 lidí.

Odlišný jmenovatel i čitatel

V tomto případě potřebujeme zlomky nejprve převést na společného jmenovatele a teprve následně provést porovnání podle čitatelů. Příklad: porovnání zlomků \frac{2}{3} a \frac{4}{7}. Nejmenší společný jmenovatel je 21, po rozšíření dostáváme dvojici zlomků \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} a \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Protože 14 > 12, je větší první zlomek, tj. \frac{2}{3}.

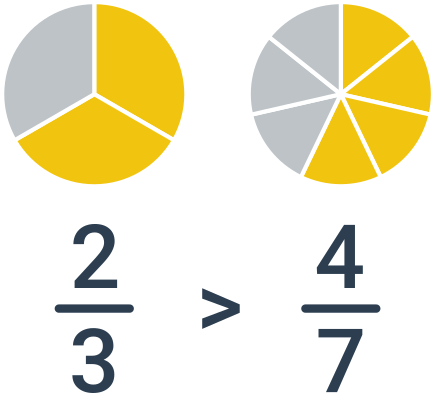
Porovnání bez výpočtu

Často můžeme provést porovnání i bez detailního výpočtu, pokud si zlomky správně představíme nebo porovnáme s vhodnou hodnotou „mezi“:

• Zlomky \frac{2}{3} a \frac{7}{6}. První z nich je menší než 1, druhý je větší než 1. Platí tedy \frac{2}{3} < \frac{7}{6}.

• Zlomky \frac{1}{3} a \frac{4}{5}. První z nich je určitě menší než polovina, druhý je výrazně větší než polovina. Platí tedy \frac{1}{3} < \frac{4}{5}.