
Vektory: násobení konstantou, součet, rozdíl

Součet vektorů
Vektory \vec{u} a \vec{v} sečteme takto: počáteční bod vektoru \vec{v} posuneme do koncového bodu vektoru \vec{u}. Součet vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má počáteční bod stejný jako vektor \vec{u} a koncový bod stejný jako vektor \vec{v}. Píšeme: \vec{u}+\vec{v}=\vec{w}
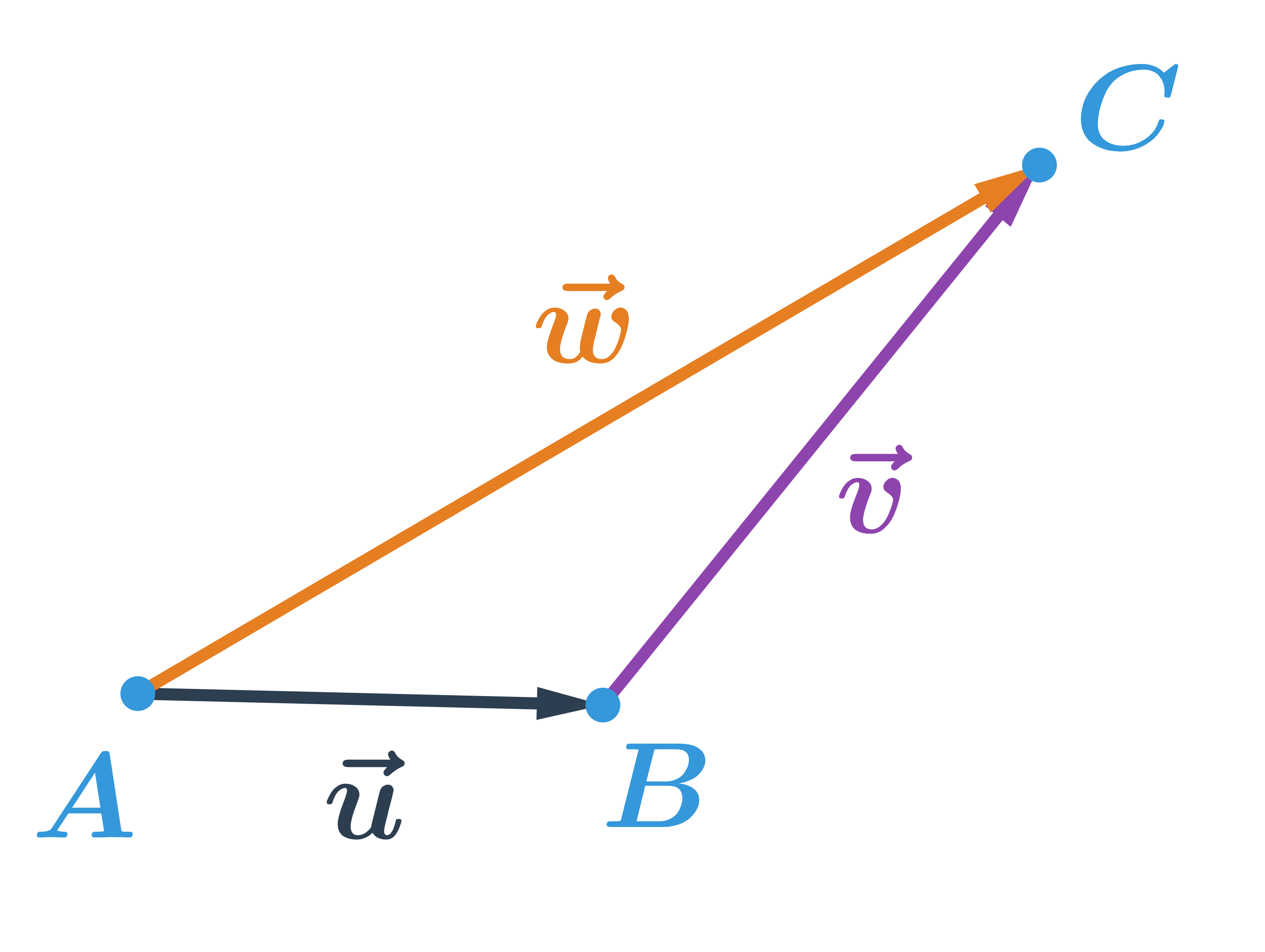
Vektory na obrázku jsou označené \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{BC}. Součet těchto vektorů: \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}
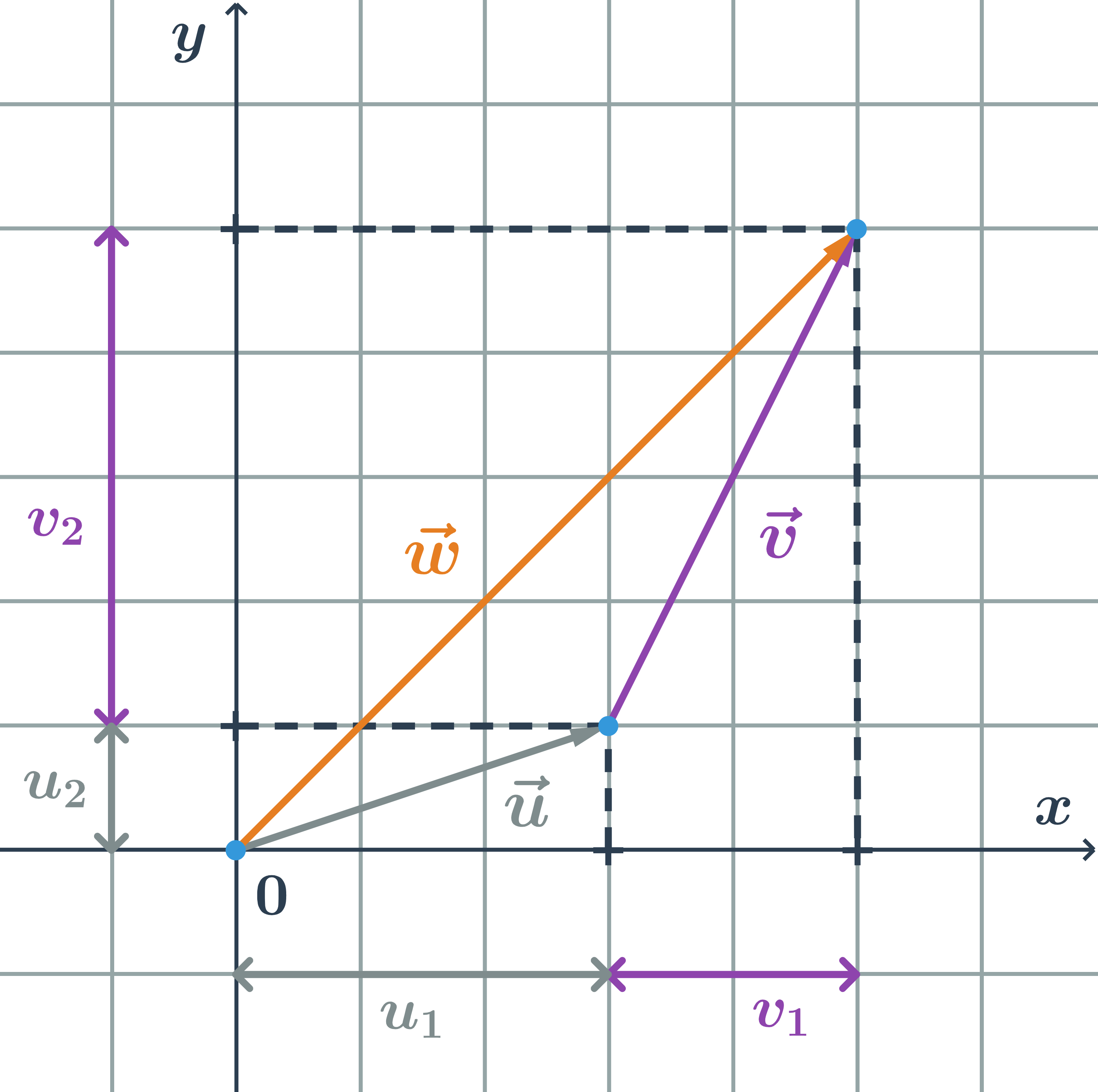
Mějme vektory se souřadnicemi \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2). Pak součet vektorů \vec{u} a \vec{v} je vektor \vec{w} se souřadnicemi \vec{w}=(u_1+v_1; u_2+v_2).
Rozdíl vektorů
Rozdíl vektorů \vec{u} a \vec{v} je součet vektoru \vec{u} s vektorem opačným k \vec{v}. Tedy:
\vec{u}-\vec{v}=\vec{u}+(-\vec{v})
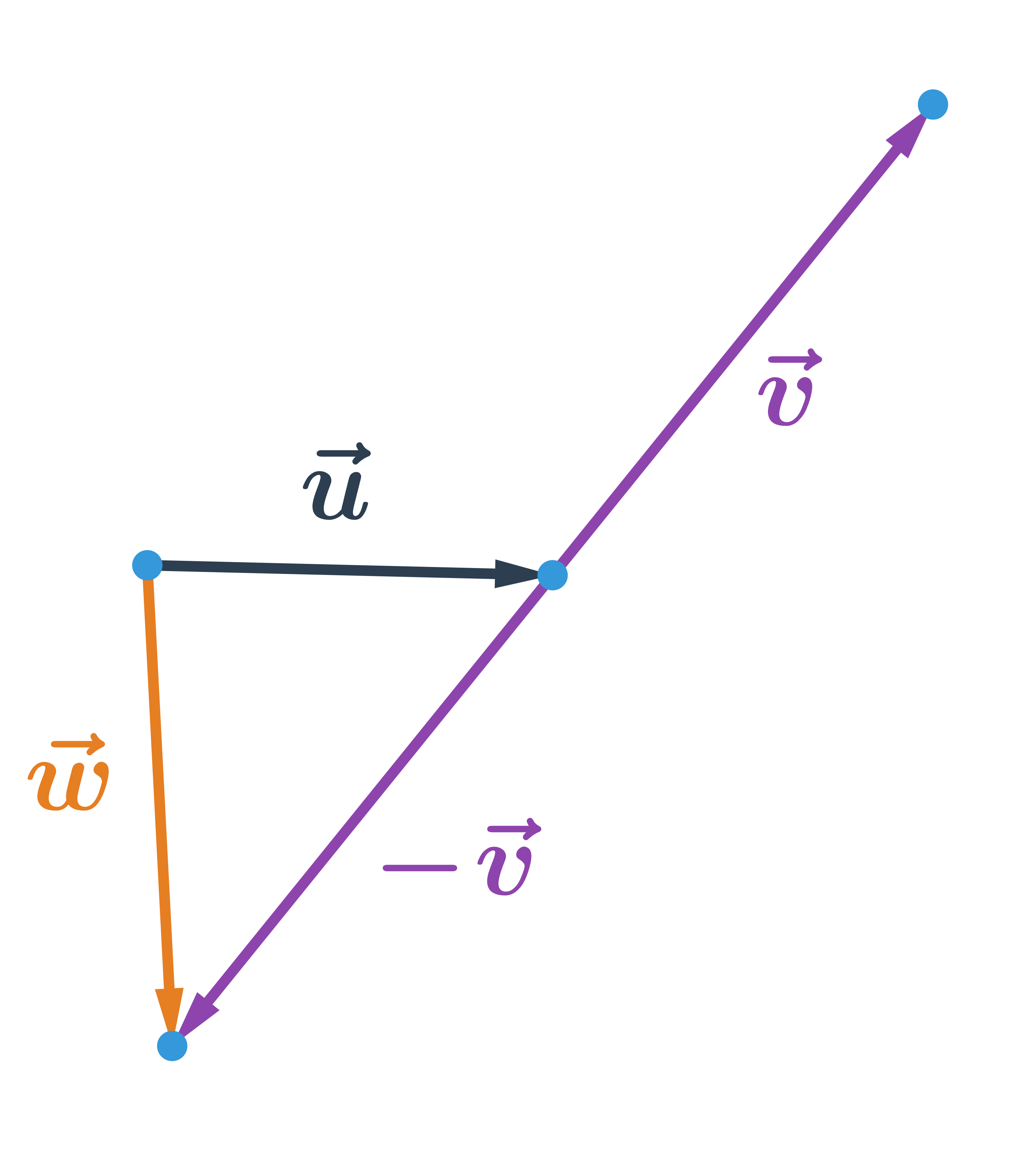
Máme-li souřadnice vektorů: \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), pak rozdíl vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má souřadnice: \vec{w}=(u_1-v_1; u_2-v_2).
Násobek vektoru
Vektor \vec{u} můžeme vynásobit libovolným reálným číslem k. Dostaneme vektor \vec{v}, kterému říkáme násobek vektoru. Píšeme \vec{v}=k \cdot \vec{u}
- Pokud k \gt 0, vektory \vec{u} a k \cdot \vec{u} mají stejný směr
- Pokud k \lt 0, vektory \vec{u} a k \cdot \vec{u} mají opačný směr
- Pokud k=0, vektor k \cdot \vec{u} je nulový vektor
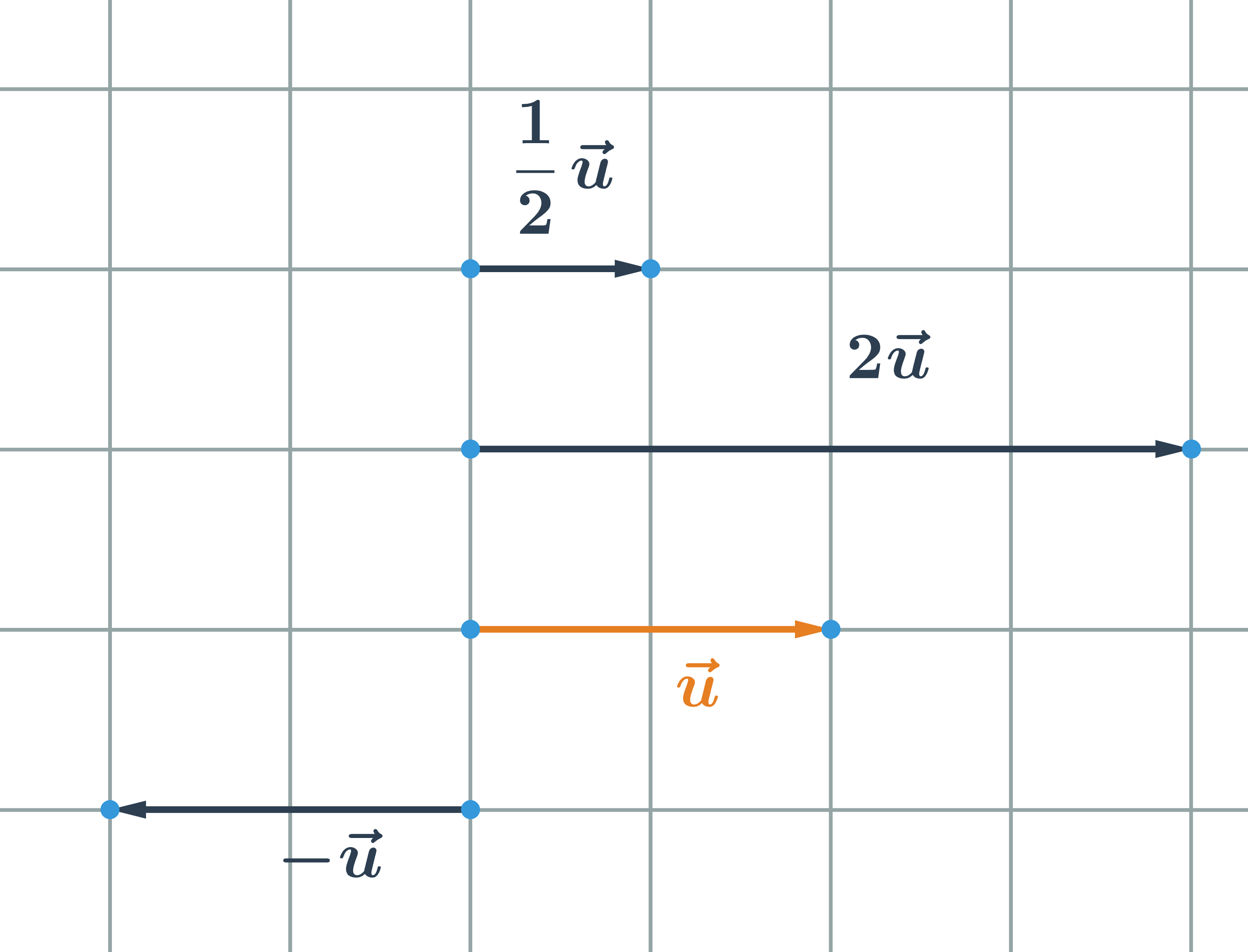
Máme-li souřadnice vektoru \vec{u}=(u_1;u_2), pak jeho násobek \vec{v}=k \cdot \vec{u} má souřadnice \vec{v}=(k \cdot u_1; k\cdot u_2).
Příklad součet a násobek vektoru graficky
Načrtněte vektor \vec{w}=2\vec{a}-\vec{b}+\vec{c}.
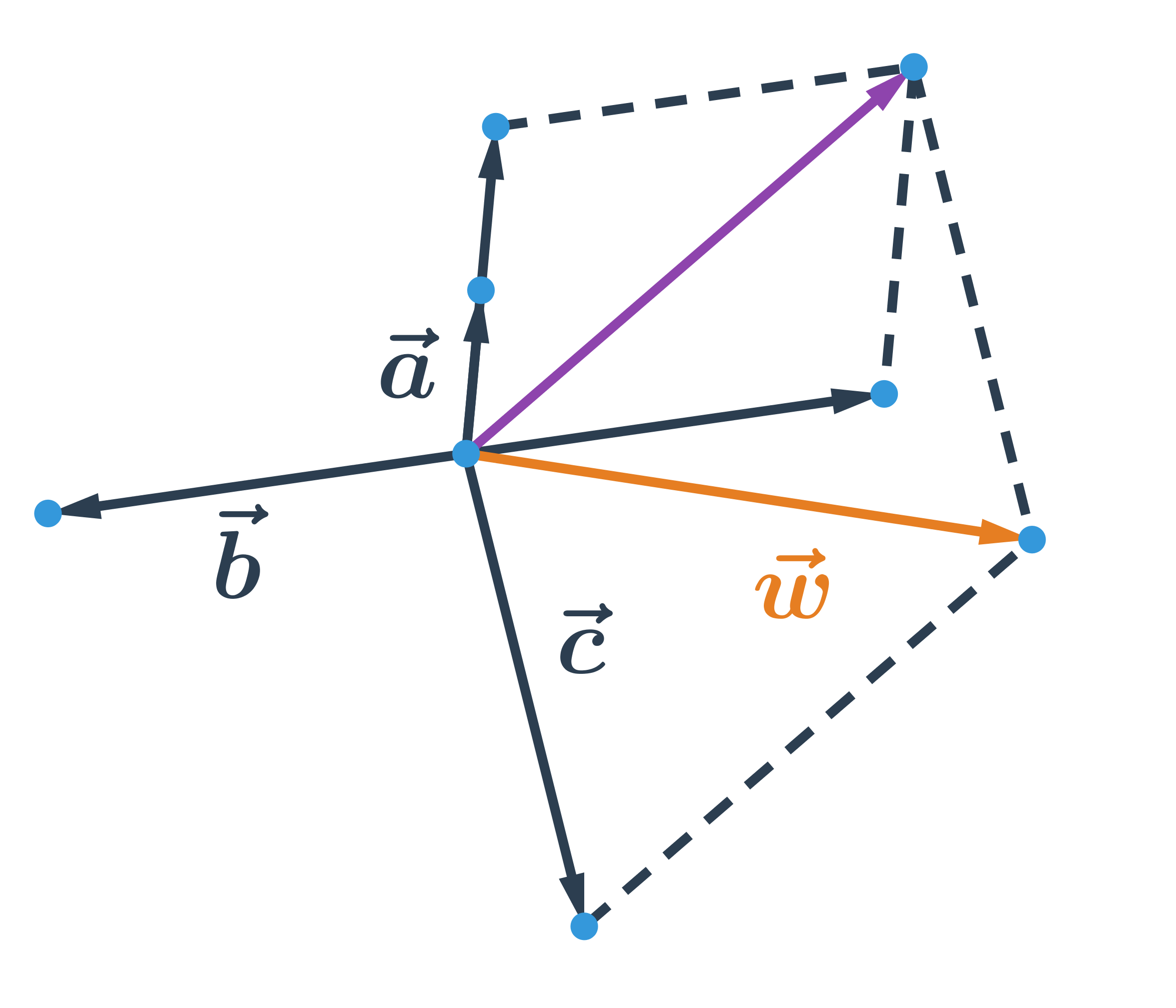
Příklad součet a násobek vektoru v souřadnicích
Jsou dány vektory \vec{u}=(2;-3), \vec{v}=(4;1). Určete souřadnice vektoru \vec{w}=\vec{u}-4\cdot \vec{v}.
- w_1=u_1-4\cdot v_1=2-4\cdot 4=-14
- w_2=u_2-4\cdot v_2=-3-4\cdot 1=-7
Zavřít














