Skvěle, štít %% dosažen
Úsečky » Rozhodovačka »
Úsečky
Rozhodovačka
Procvičujte neomezeněVáš denní počet odpovědí je omezen. Pro navýšení limitu či přístup do svého účtu s licencí se přihlaste.
Přihlásit se
GM4
QR kód
Kód / krátká adresa
Zkopírujte kliknutím.
Nastavení cvičení
Pozor, nastavení je platné pouze pro toto cvičení a předmět.
Střed úsečky v rovině
Střed úsečky dělí úsečku na dvě stejné části. Pokud leží krajní body úsečky AB na číselné ose a jejich polohám odpovídají hodnoty a a b, potom jejímu středu S odpovídá číslo s=\frac{a+b}{2}. Střed úsečky je „průměrem“ jejích krajních bodů.
Pro úsečku v rovině bude situace následující.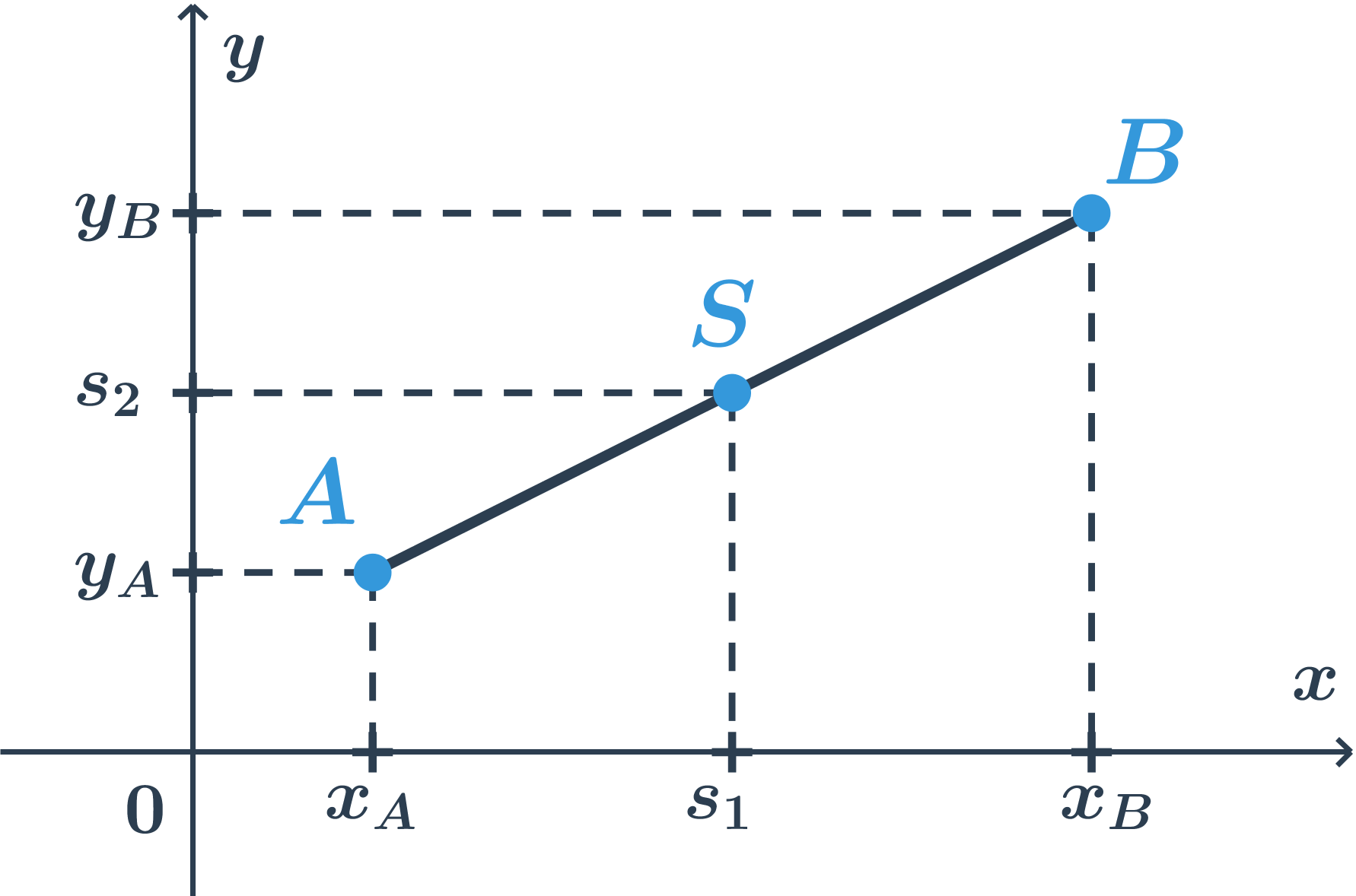 
Situace na obou souřadných osách je stejná jako předtím. Spočítáme obě souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Pro střed S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Příklad: určení středu úsečky
Najděte střed úsečky AB: A[6;-1], B[2;3]
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Střed úsečky AB je bod S[4;1]
Příklad: určení druhého krajního bodu úsečky
Určete souřadnice druhého krajního bodu úsečky AB, je‑li dán bod A[-3;0] a její střed S[1;3].
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Dopočítáme neznámé x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Bod B má souřadnice [5;6].
Střed úsečky v rovině (střední)
Nyní se mohou opakovat už vyřešená zadání.