Odmocňování v matematice je částečně inverzní (opačnou) operací k umocňování. Druhá odmocnina z čísla x je takové nezáporné číslo a, pro které platí a^2 = x. Druhou odmocninu značíme \sqrt{x}.

Obecně pak n-tá odmocnina z x je takové číslo a, pro které platí a^n = x, n-tou odmocninu značíme \sqrt[n]{x}.

Odmocňování má i geometrický význam. Pokud máme čtverec o obsahu S, pak tento čtverec má délku strany rovnou druhé odmocnině \sqrt{S}. Pokud máme krychli o objemu V, pak tato krychle má délku hranu rovnou třetí odmocnině \sqrt[3]{V}. Odmocniny hojně využijeme například při aplikaci Pythagorovy věty.

Graf funkce odmocnina

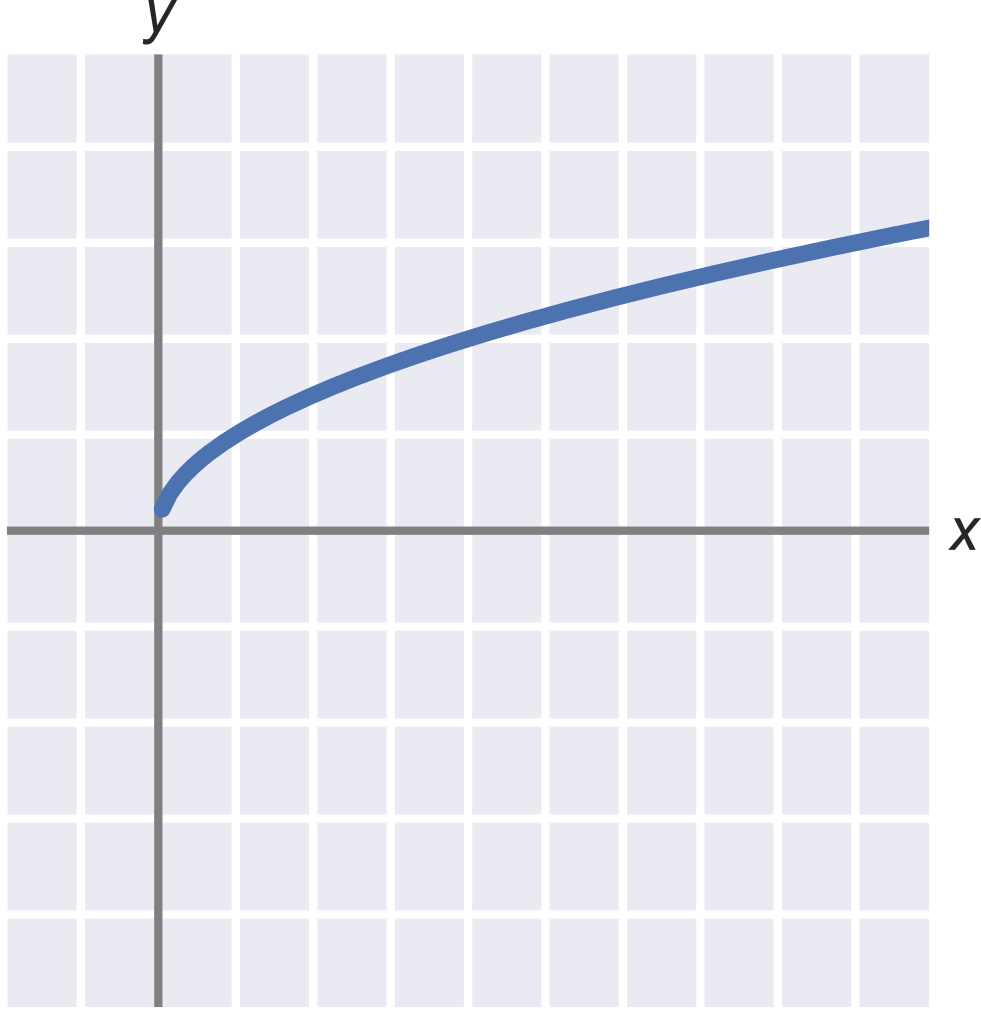
Odmocnina a záporná čísla

Když hledáme odmocninu třeba z 25, tak hledáme číslo, které po umocnění dá 25. To splňuje 5\cdot 5, ale také (-5)\cdot (-5). Odmocnina je však definována jako nezáporné číslo, takže \sqrt{25} = 5.

Druhou odmocninu můžeme počítat pouze z kladných čísel, protože jakékoliv číslo umocněné na druhou je kladné. Odmocnina ze záporných čísel není definována. Nebo vlastně je, ale to musíme zavést komplexní čísla (což je velice zajímavý a užitečný nástroj, ale trochu pokročilý a ten tu nebudeme rozebírat).

Pro běžná reálná čísla můžeme počítat odmocniny ze záporných čísel pro liché stupně n.