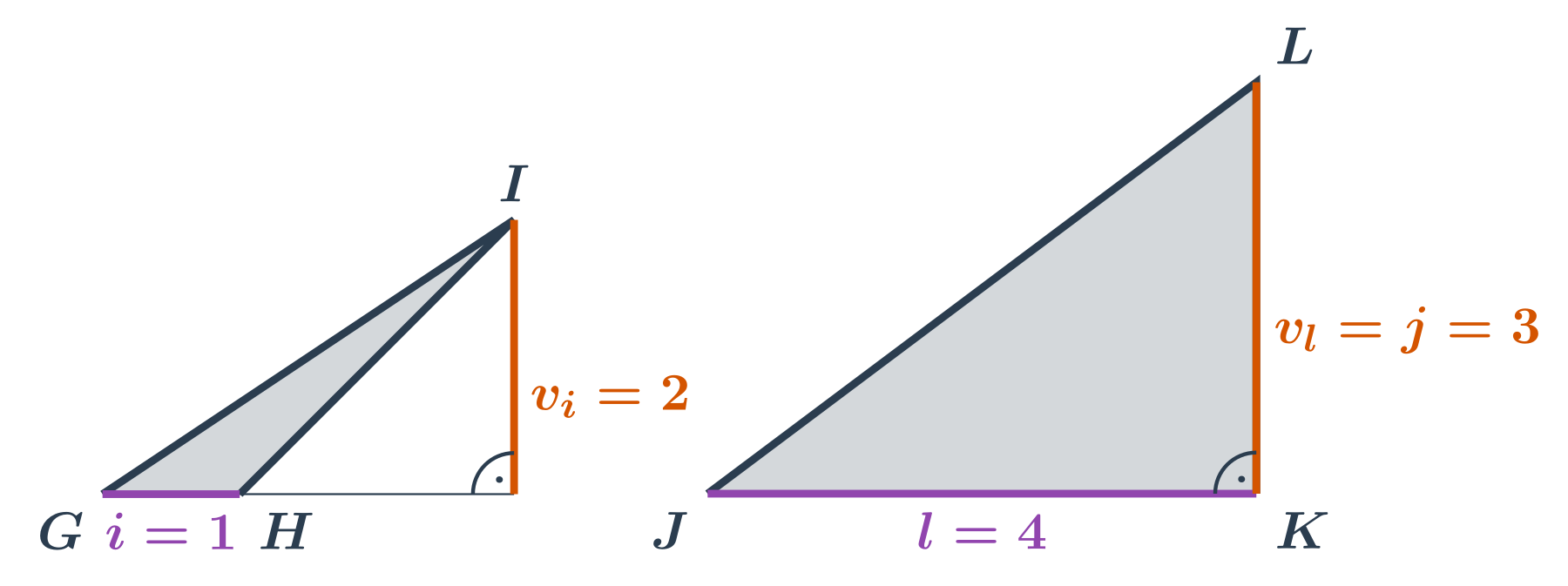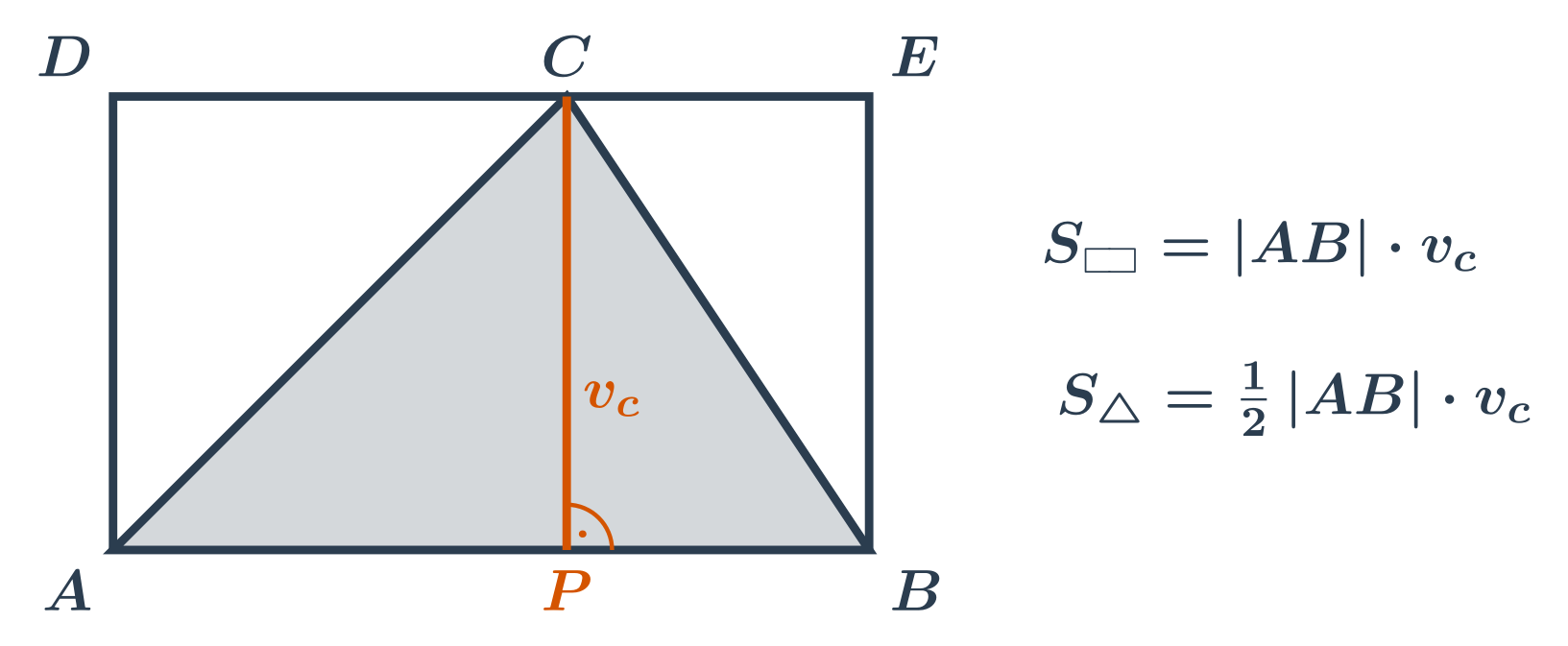
Obsah trojúhelníku spočítáme jako součin délky libovolné strany trojúhelníka a výšky příslušné k této straně, takže: S_{\triangle} = \frac12 \cdot a \cdot v_a = \frac12 \cdot b \cdot v_b = \frac12 \cdot c \cdot v_c

Což si můžeme představit jako polovinu obsahu obdélníku, ve kterém je náš trojúhelník takto vepsán:

Příklady k obsahu:

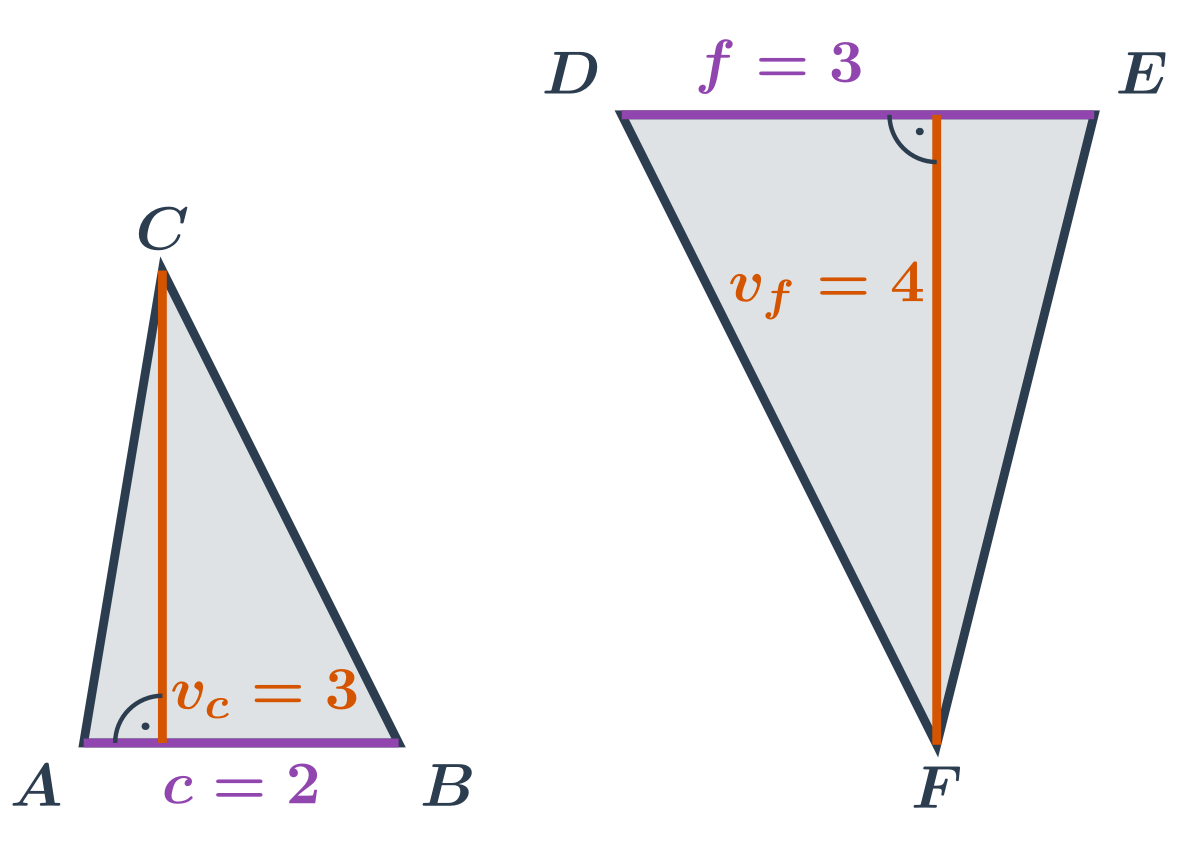
• Trojúhelník ABC: Délka strany \left| AB \right| je 2. Velikost k ní příslušné výšky v_c je 3. Obsah trojúhelníku ABC je roven \frac12 \cdot 2 \cdot 3 = 3.
• Trojúhelník DEF: Nevadí nám, že trojúhelník na náčrtku vypadá zvláštně natočený. Známe délku strany \left| DE \right|, což je 3. Velikost k ní příslušné výšky v_f je 4. Obsah trojúhelníku DEF je roven \frac12 \cdot 3 \cdot 4 = 6.

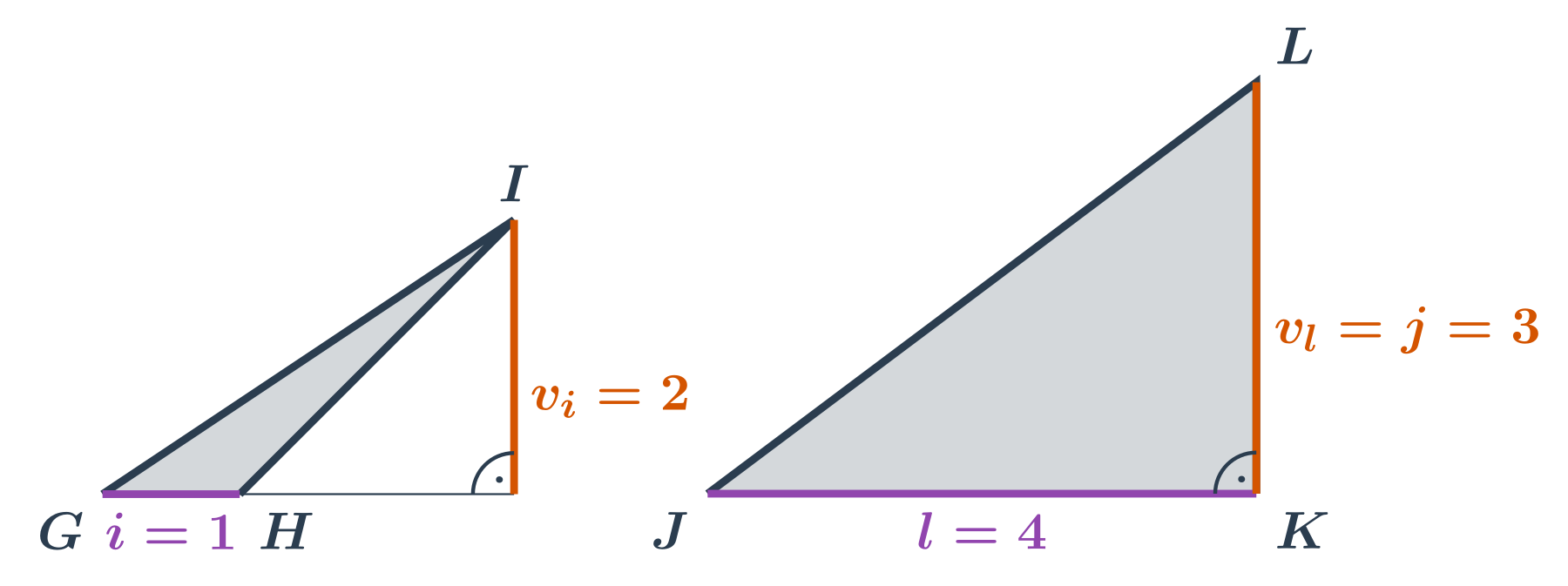
• Trojúhelník GHI: Nevadí nám ani když je pata kolmice, na které leží výška, mimo stranu trojúhelníka. Délka strany \left| GH \right| je 1. Velikost k ní příslušné výšky v_i je 2. Obsah trojúhelníku GHI je \frac12 \cdot 2 \cdot 1 = 1.
• Trojúhelník JKL: S pravoúhlým trojúhelníkem si také poradíme. Délka strany \left| JK \right| je 4. Velikost k ní příslušné výšky v_l je 3 (a je to zároveň i délka strany KL našeho trojúhelníku). Obsah trojúhelníku JKL je \frac12 \cdot 4 \cdot 3 = 6.