
Elipsa

Elipsa je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý součet vzdáleností 2a, který je větší než vzdálenost ohnisek. 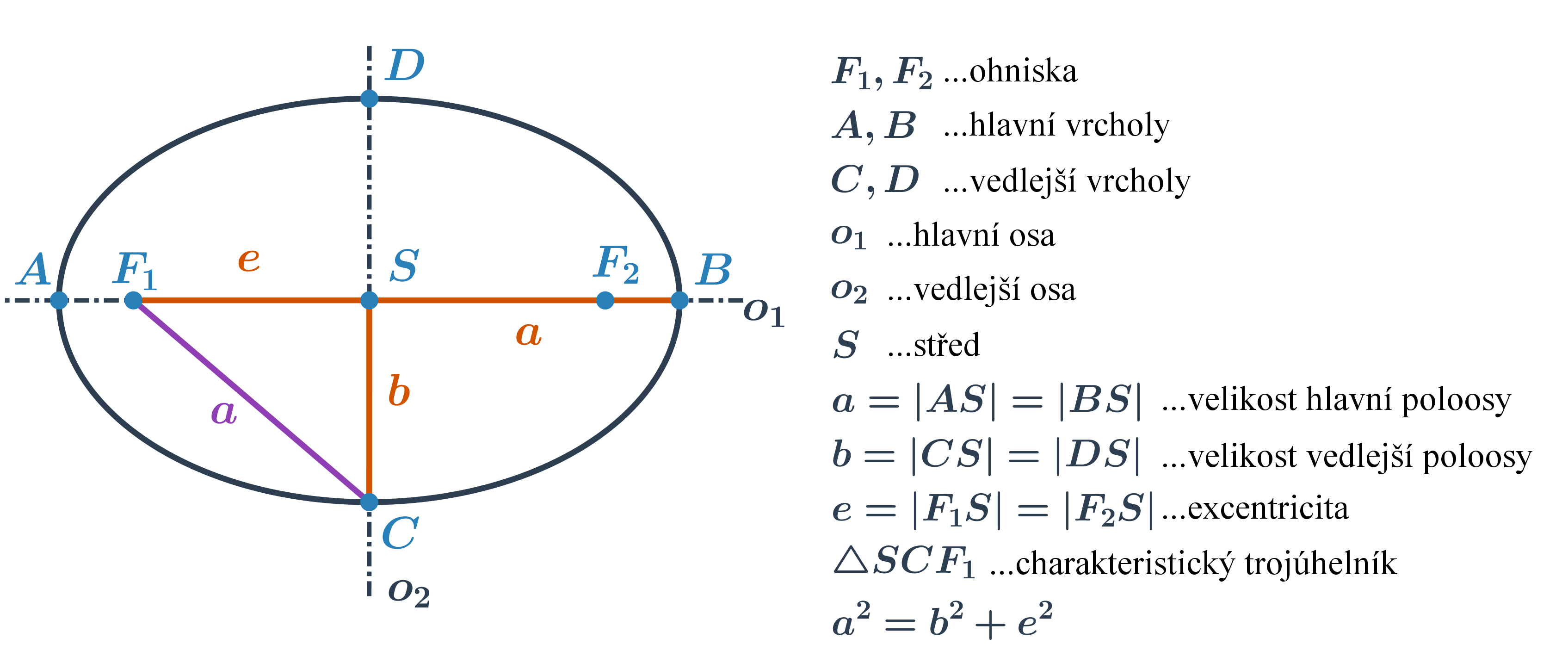
Středová rovnice elipsy
Tvar středové rovnice elipsy o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a a b závisí na poloze hlavní osy:
hlavní osa je rovnoběžná s osou x, rovnice je ve tvaru: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 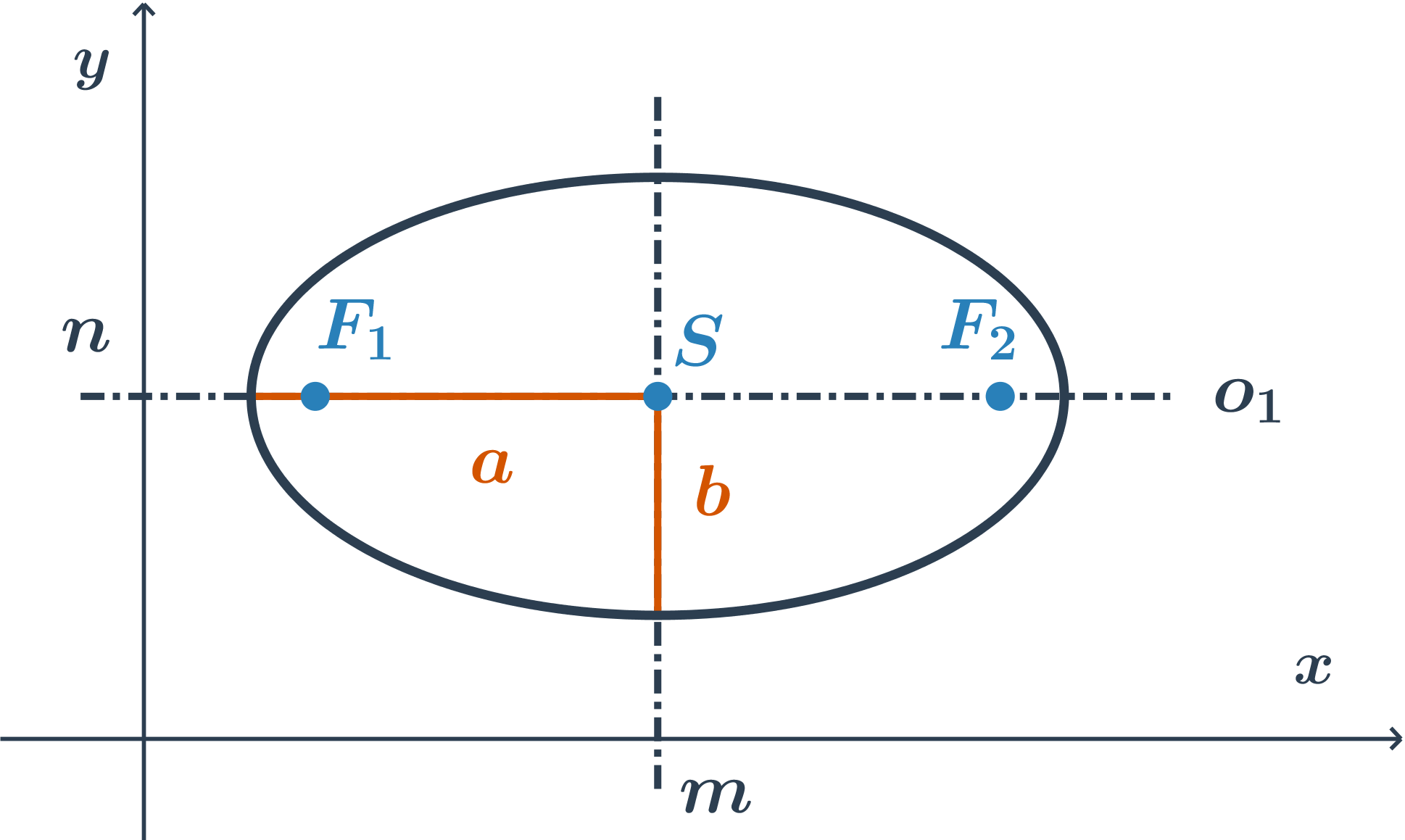
hlavní osa je rovnoběžná s osou y, rovnice je ve tvaru: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 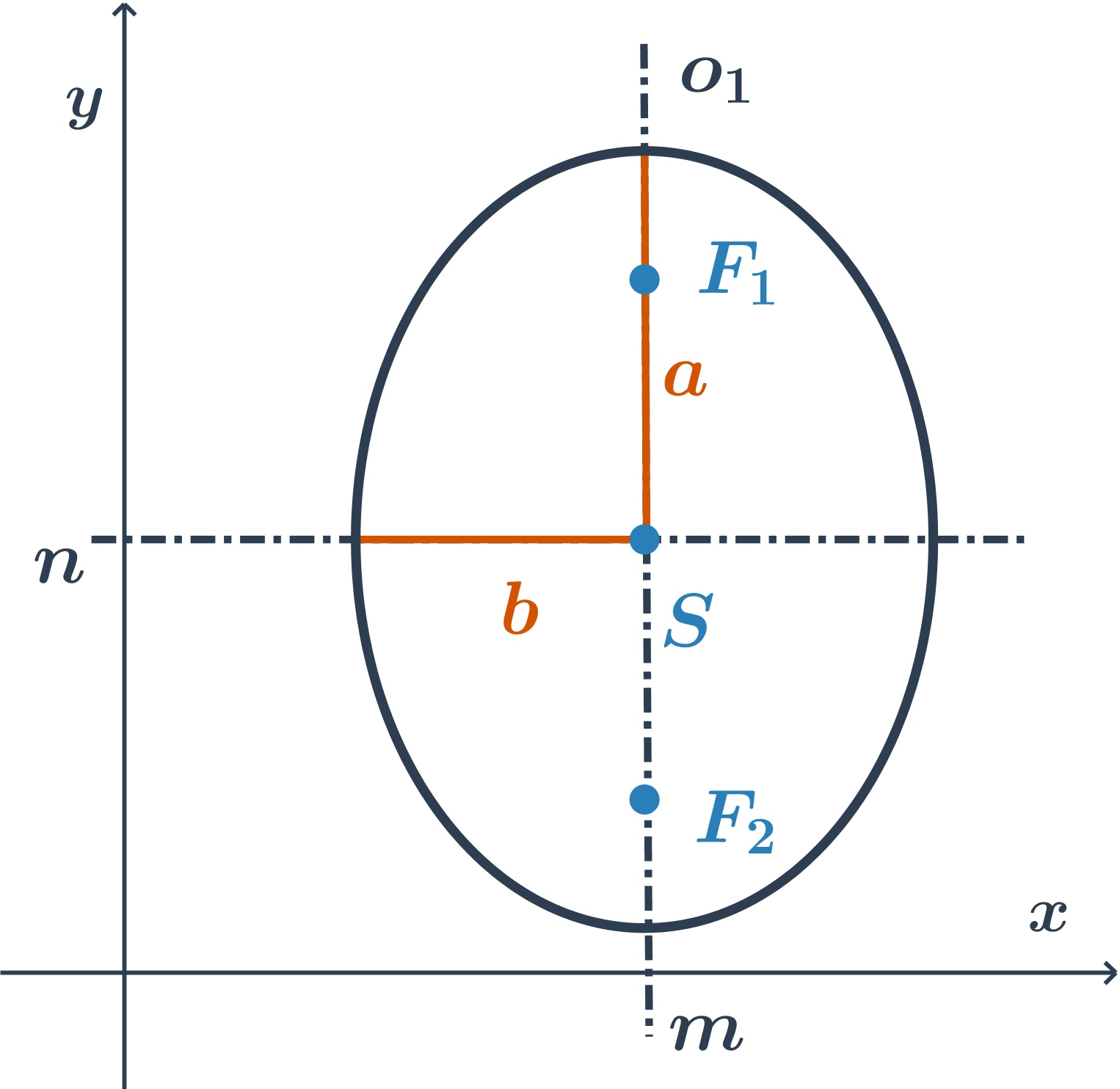
Návod: jak z rovnice poznat, se kterou souřadnou osou je rovnoběžná hlavní osa elipsy
- Podíváme se do jmenovatelů.
- Větší jmenovatel je druhá mocnina velikosti hlavní poloosy (a menší jmenovatel je druhá mocnina velikosti vedlejší poloosy).
- Proměnná v daném čitateli (zlomku s větším jmenovatelem) pak určuje, se kterou osou je hlavní osa elipsy rovnoběžná.
- Stručně řečeno: je‑li větší číslo například ve jmenovateli s proměnnou x, je hlavní osa rovnoběžná s osou x
Příklad: určení středové rovnice elipsy s daným středem, velikostmi poloos a směrem hlavní osy
Určete středovou rovnici elipsy se středem v bodě S[-2;3], je‑li a=3, b=2 a hlavní osa je rovnoběžná s osou y.
- Středová rovnice je ve tvaru \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
- Dosadíme souřadnice středu a velikosti hlavní a vedlejší poloosy. Při dosazení si dáme pozor na to, že souřadnice středu odčítáme: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
- Po úpravě: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1
Obecná rovnice elipsy
Podobně jako existuje několik rovnic přímky, můžeme i rovnici elipsy zapsat jiným způsobem. Obecná rovnice elipsy je ve tvaru:
Ax^2 +By^2+Cx+Dy+E=0, A\ne B, A\cdot B>0.
Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí elipsy. Praktické ověření, zda se jedná o elipsu provádíme převedením na středovou rovnici.
Příklad: určuje daná rovnice elipsu?
Rozhodněte, zda rovnice x^2+3y^2+8x-18y+31=0 určuje elipsu.
- Nejprve si uspořádáme členy: x^2+8x+3y^2-18y+31=0.
- Ze členů s proměnnou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
- K oběma stranám rovnice přičteme konstanty 16 a 27, abychom členy s proměnnými x a y mohli upravit podle vztahu (a\pm b)^2=a^2 \pm 2ab +b^2.
- Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
- A upravíme: (x+4)^2 +3(y-3)^2+31=43
- Převedeme konstantu 31 na druhou stranu rovnice: (x+4)^2 +3(y-3)^2=12
- Na závěr rovnici vydělíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
- Jedná se tedy o elipsu.
Elipsa a přímka
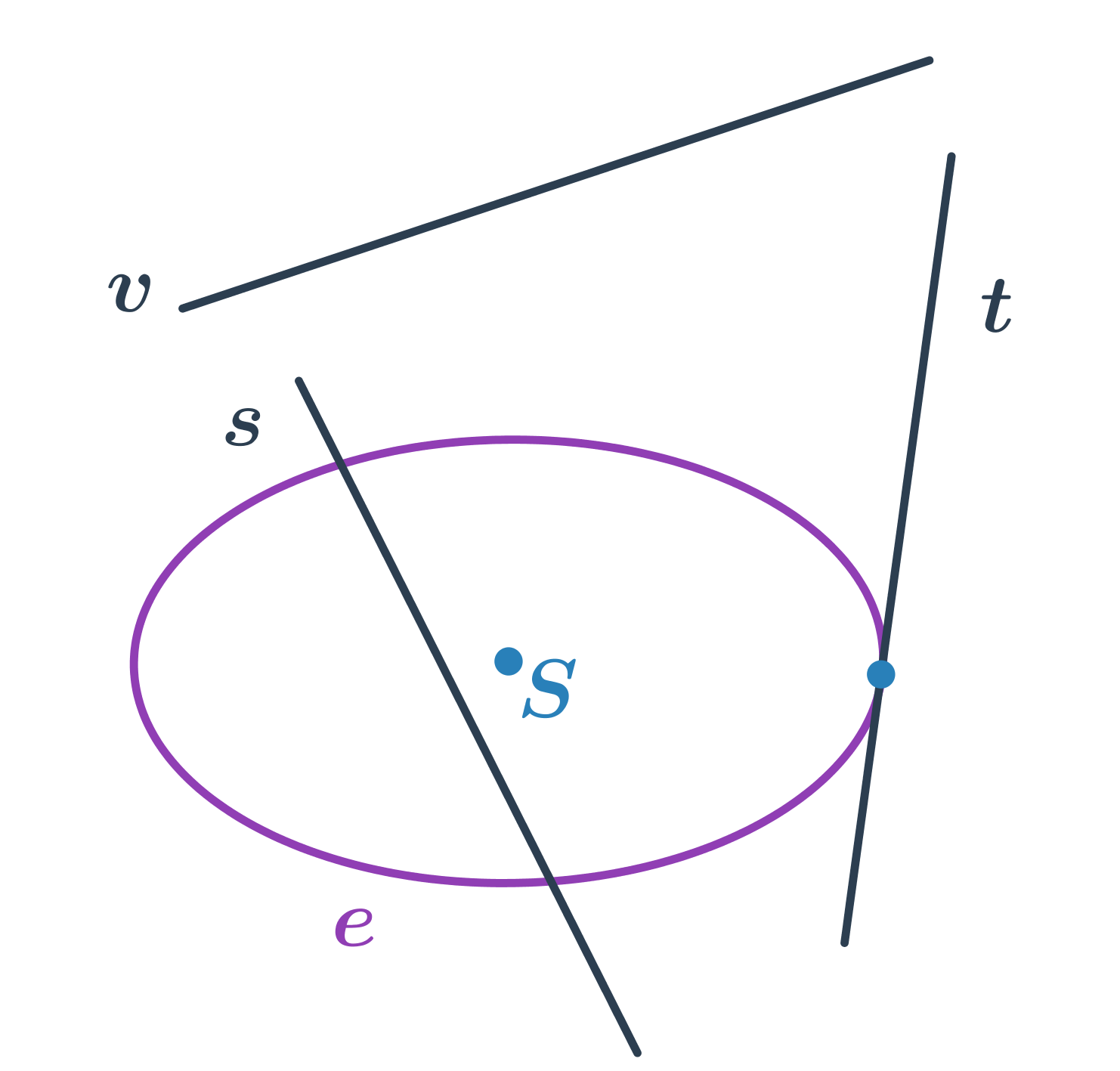
- přímka s protíná elipsu ve dvou bodech – sečna elipsy
- přímka t protíná elipsu v jednom bodě – tečna elipsy
- přímka v elipsu neprotíná – vnější přímka elipsy
Rovnice tečny elipsy v bodě, který leží na elipse
Elipsa daná rovnicí \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bodě T[x_0;y_0] tečnu určenou rovnicí:
\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1
Podobně můžeme zapsat i rovnici tečny elipsy, která má hlavní osu rovnoběžnou s osou y.
Příklad: určení rovnice tečny elipsy v jejím daném bodě
Určete rovnici tečny elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jejím bodě T[1;-2].
- Ověříme, zda bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
- Tečna má rovnici \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
- Dosadíme souřadnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
- Zbavíme se zlomků: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
- Roznásobíme závorky: -2x+4 -4y+8=18
- A dostaneme obecnou rovnici tečny: x+2y+3=0
Zavřít













