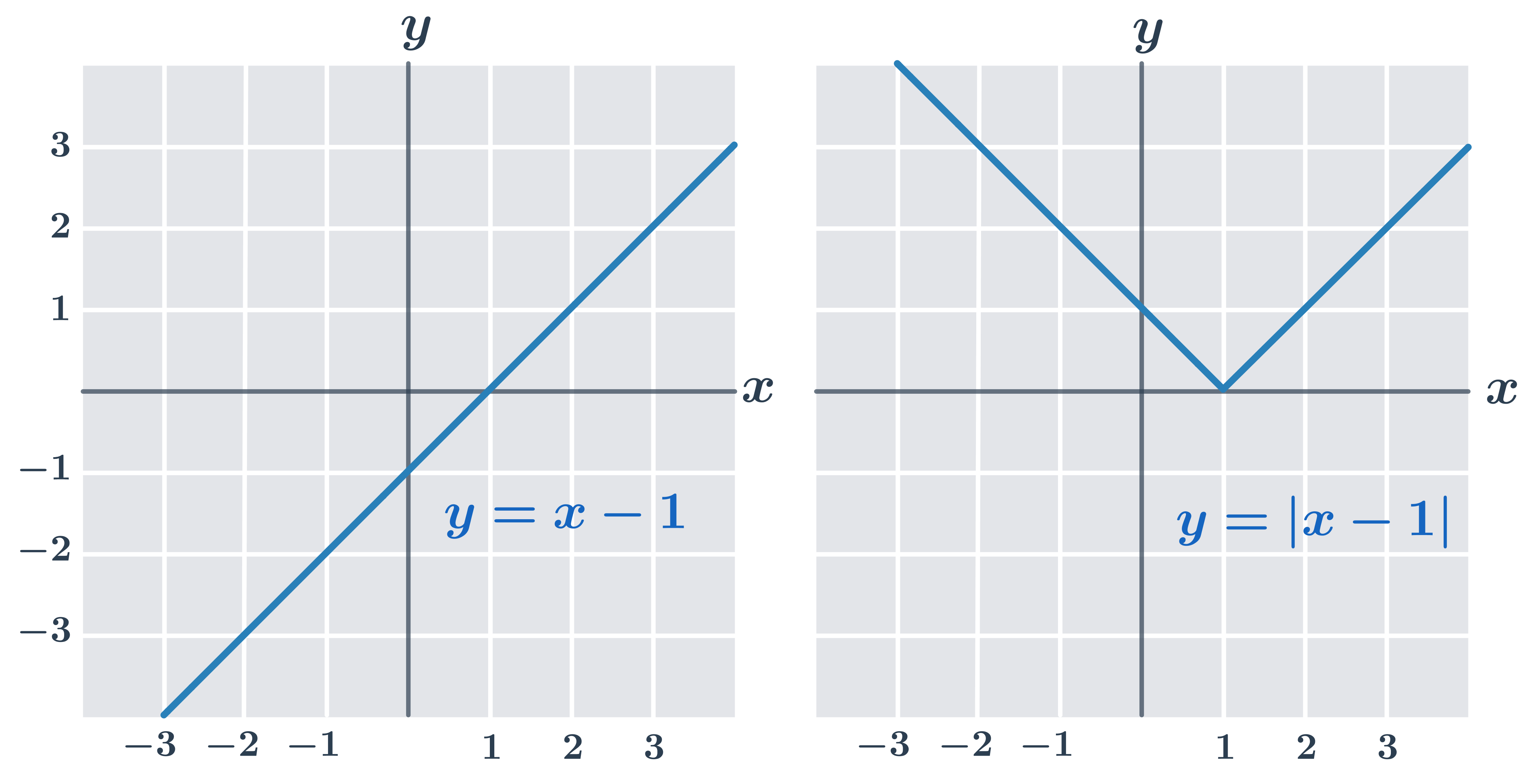Grafy funkcí s absolutní hodnotou (těžké)

QR kód

Stáhnout Na celou obrazovku

Kód / krátká adresa

Zkopírujte kliknutím. Zkopírováno!

E6E

umime.to/E6E

Grafy funkcí s absolutní hodnotou

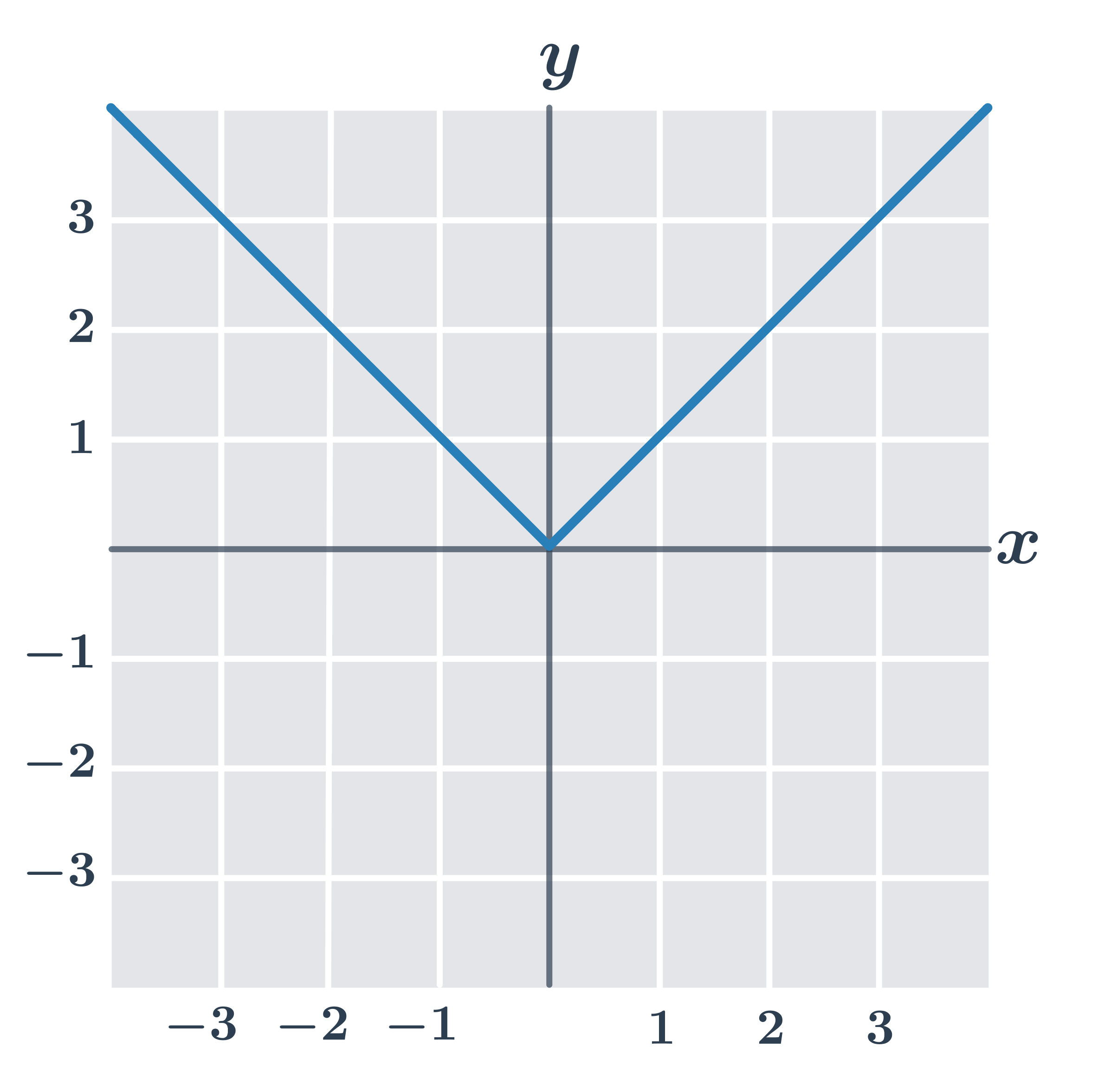
Na obrázku je graf funkce y=|x|. Tento graf tvoří dvě polopřímky s počátkem v bodě [0;0], protože pro absolutní hodnotu platí:

absolutní hodnota kladného čísla je rovna tomuto číslu: |x|=x
absolutní hodnota záporného čísla je rovna opačnému číslu: |x|=-x
absolutní hodnota čísla nula je rovna nule: |0|=0

x > 0	Grafem funkce y=\|x\| je polopřímka s počátkem v bodě [0;0] daná rovnicí y=x.
x < 0	Grafem funkce y=\|x\| je polopřímka s počátkem v bodě [0;0] s rovnicí y=-x.
x = 0	Bod [0;0] je počátek polopřímek, které vytvoří graf funkce y=\|x\|.

Pokud chceme nakreslit graf funkce y=|f(x)| postupujeme tak, že nakreslíme graf y=f(x) a potom záporné funkční hodnoty nahradíme opačnými. V oblasti, kde jsou funkční hodnoty záporné, se tedy graf překlopí kolem osy x.

Příklad 1: graf funkce y=|x-1|

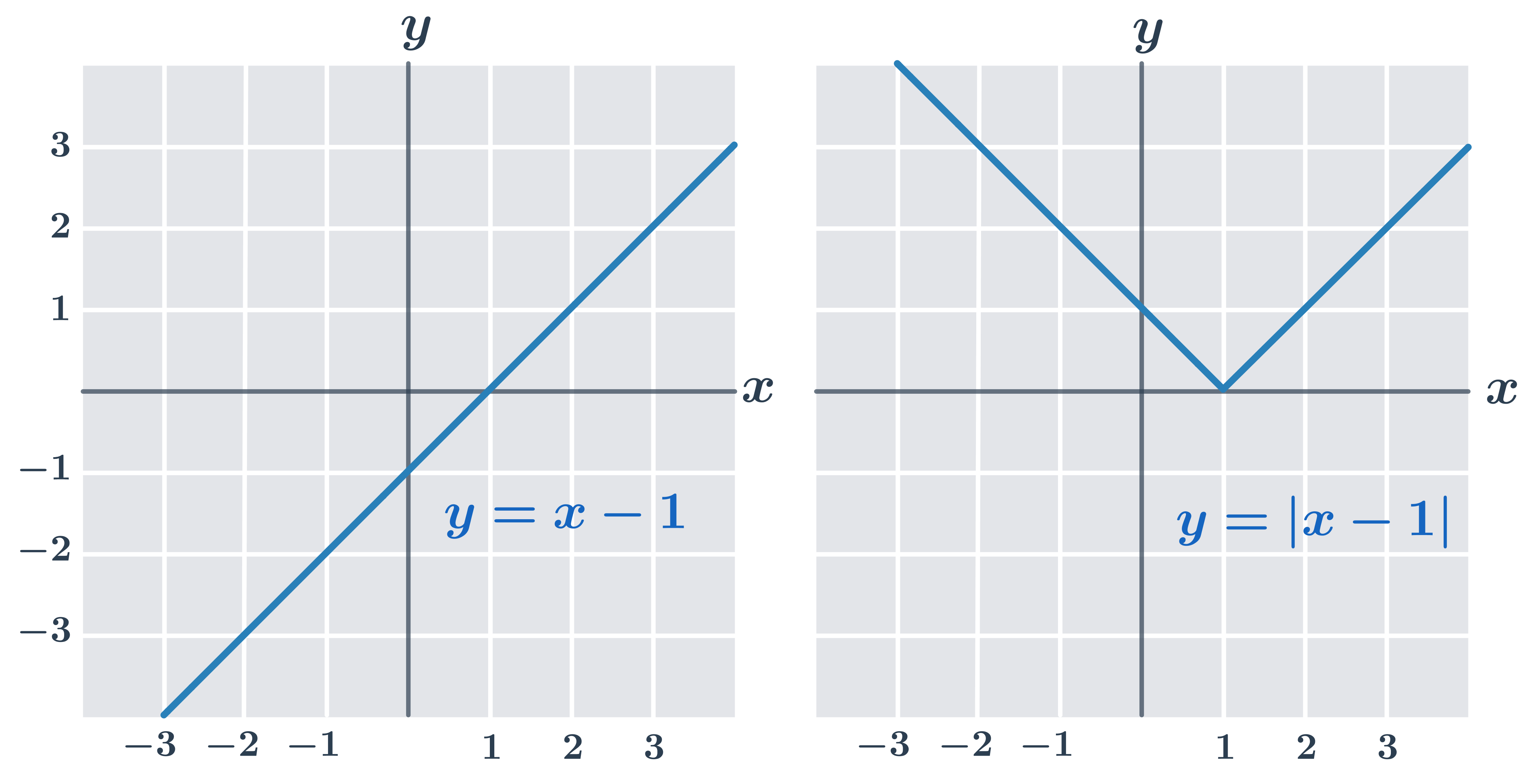
Pro čísla x < 1 má funkce y=x-1 záporné funkční hodnoty.

Funkce y=|x-1| má v intervalu (-\infty;1) opačné hodnoty než funkce y=x-1 (graf y=|x-1| je vůči grafu y=x-1 v tomto intervalu překlopený podle osy x).

V intervalu (1;\infty) jsou grafy funkcí y=x-1 a y=|x-1| stejné.

Příklad 2: graf funkce y=|x^2-4|

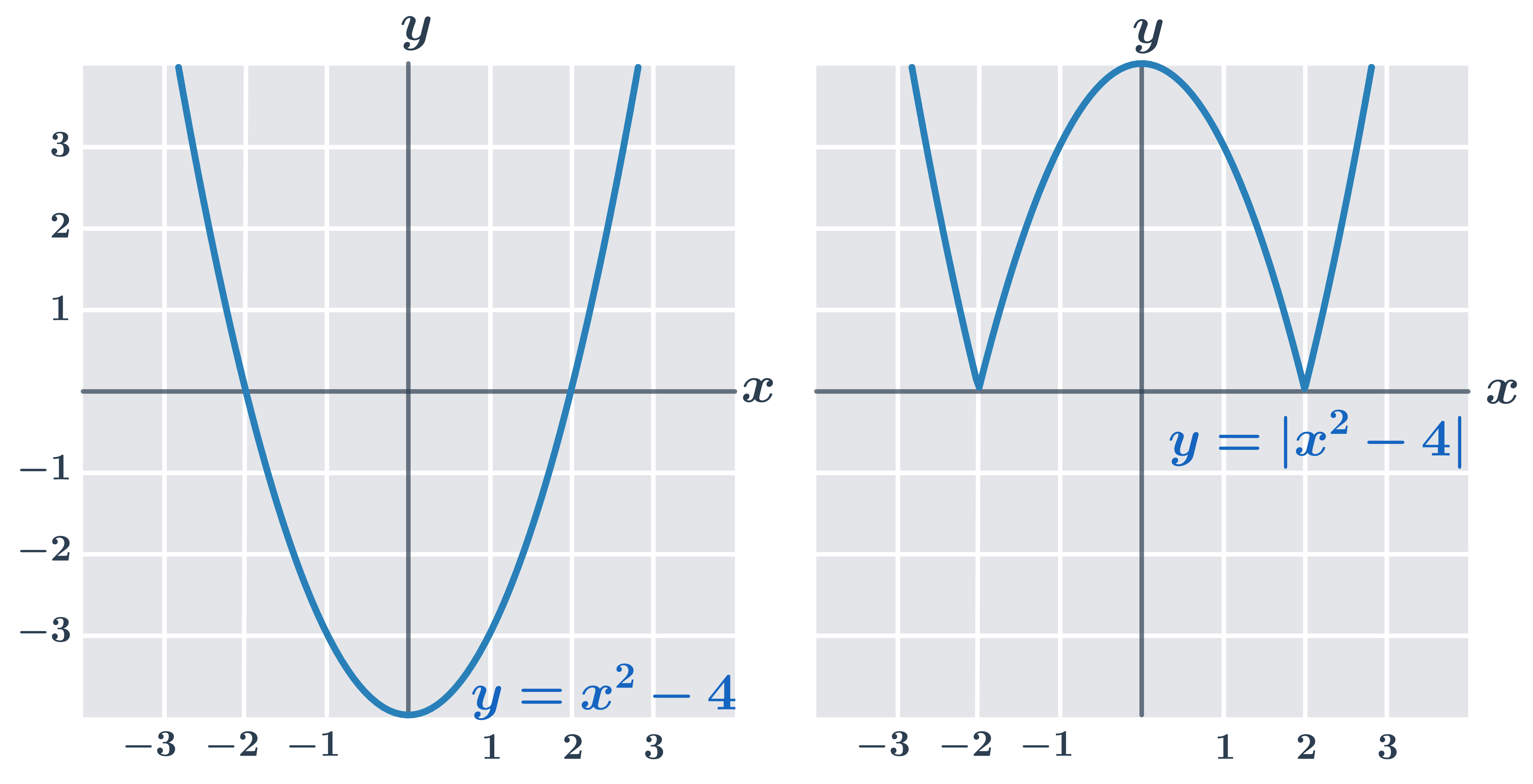
V intervalu (-2;2) má funkce y=x^2-4 záporné funkční hodnoty.

Funkce y=|x^2-4| má v intervalu (-2;2) opačné hodnoty než funkce y=x^2-4 (graf je překlopený podle osy x).

V intervalech (-\infty;-2) a (2;\infty) jsou grafy funkcí y=x^2-4 a y=|x^2-4| stejné.

Zavřít

Grafy funkcí s absolutní hodnotou (těžké)

Vyřešeno:

QR kód

Kód / krátká adresa

umime.to/E6E

Grafy funkcí s absolutní hodnotou

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?