Kužel

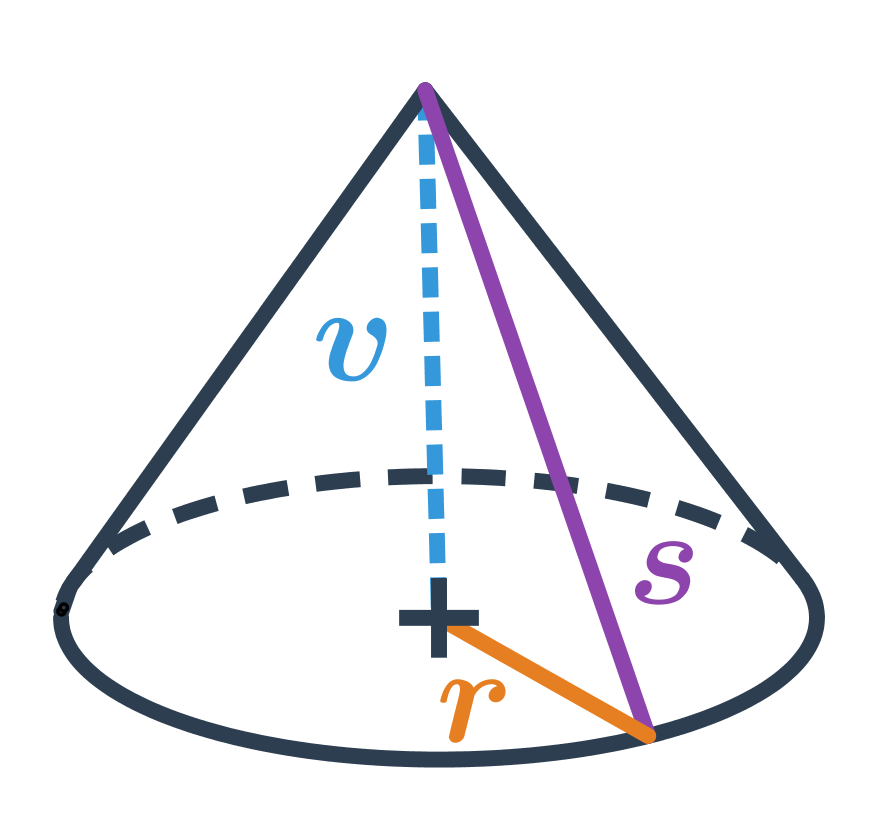
Kužel je prostorový geometrický útvar s kruhovou podstavou. Zužuje se směrem k jednomu bodu zvanému vrchol. Jde o útvar, který vznikne, když se kolem své osy otáčí rovnoramenný trojúhelník. Příkladem kuželu v běžném životě je kornout zmrzliny nebo dopravní kužel. 

Vzorce pro objem a povrch

Objem kuželu lze vypočítat pomocí vzorce: V = \frac{1}{3} \pi \cdot r^2 \cdot v, kde r je poloměr podstavy a v je výška kuželu, což je vzdálenost vrcholu od roviny, ve které leží podstava kuželu.

Povrch kuželu získáme sečtením obsahu základny a obsahu pláště S = \pi \cdot r^2 + \pi \cdot r s, kde s je tzv. strana kuželu, což je délka úsečky spojující vrchol kuželu s okrajem jeho základny.

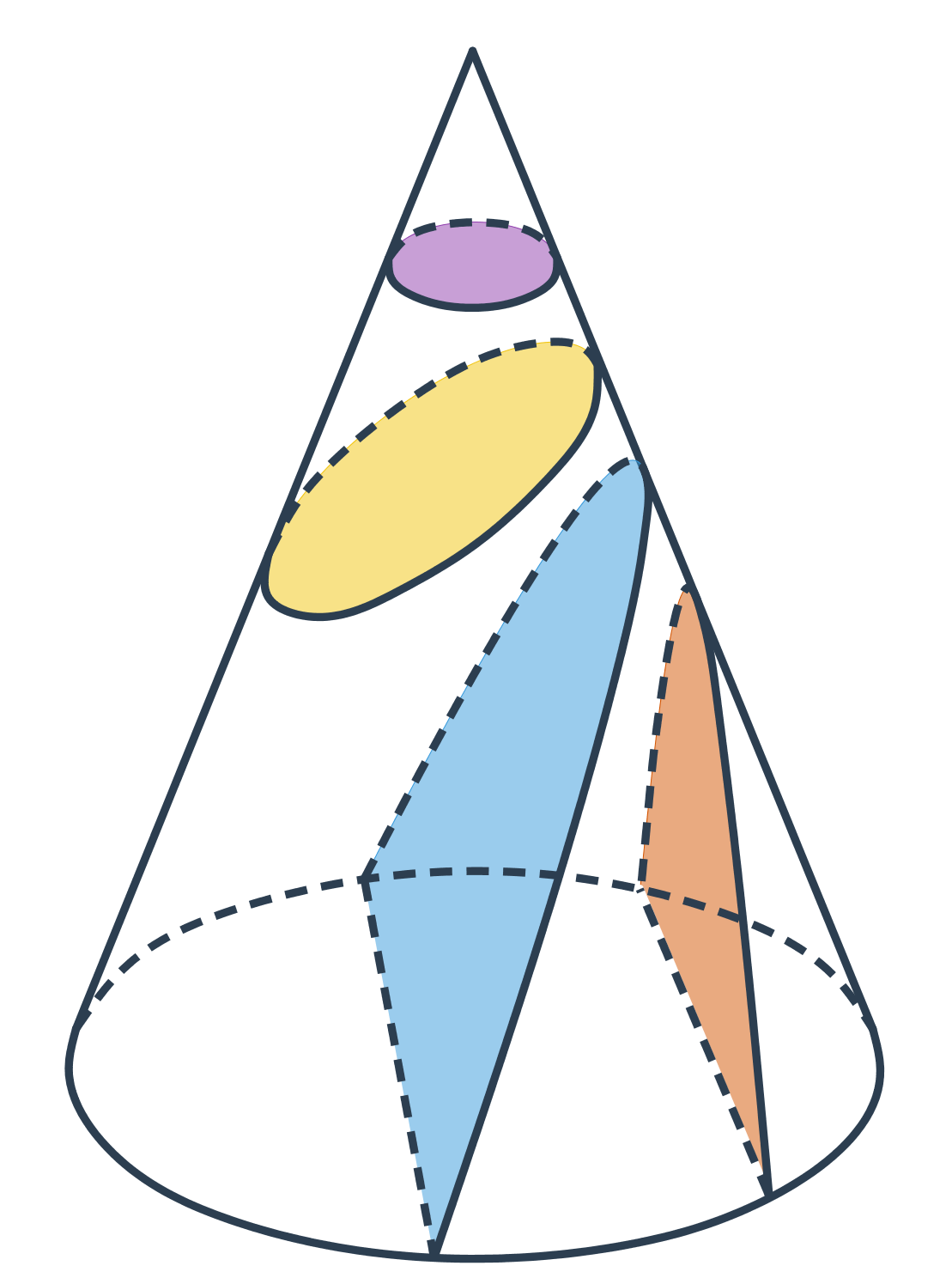
Kuželosečky

Křivky, které vznikají průnikem kuželového povrchu s rovinou se nazývají kuželosečky. Patří mezi ně například kružnice, elipsa, parabola a hyperbola.

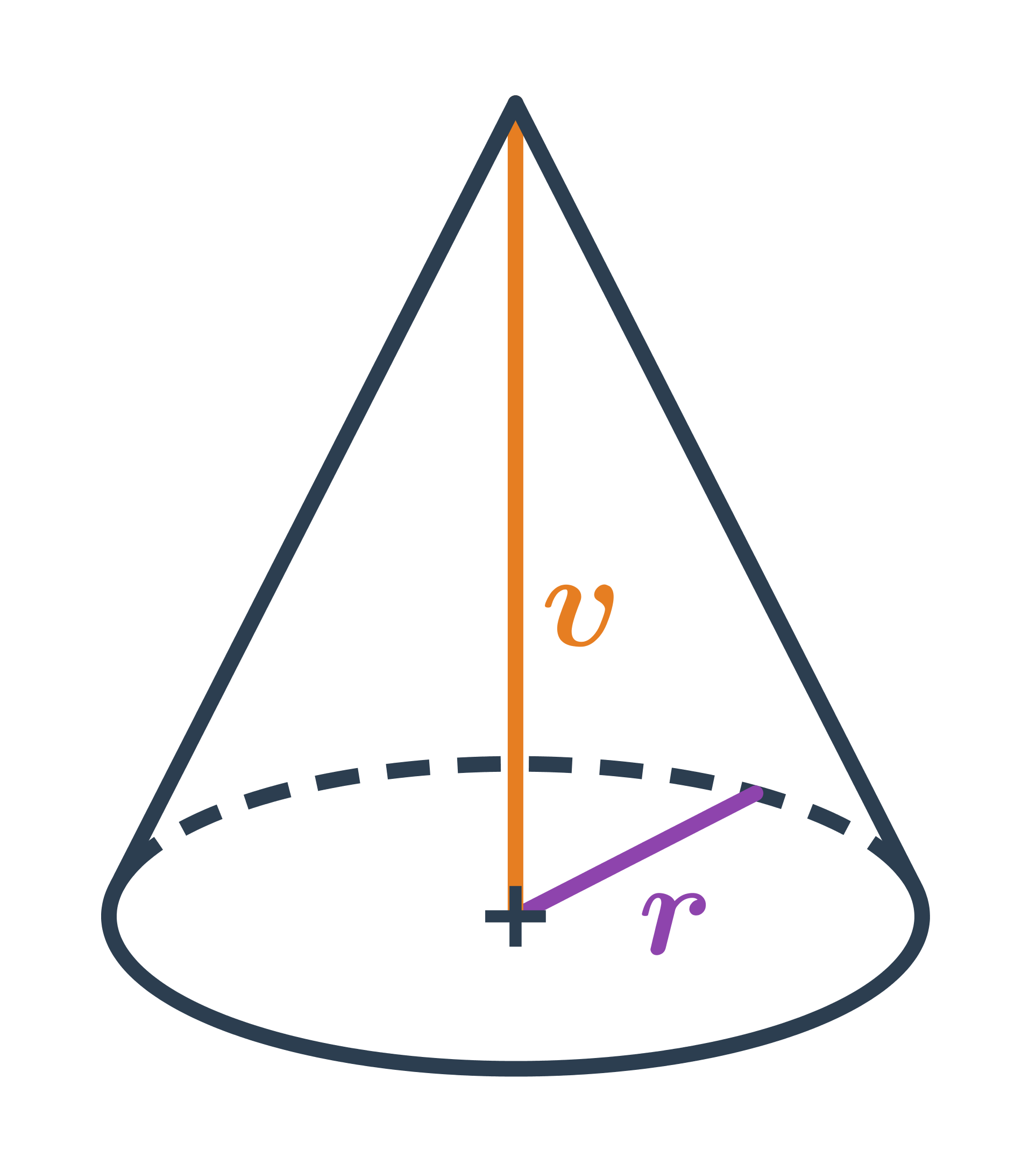
Objem kužele s poloměrem podstavy r a výškou v spočítáme jako: V=\frac{1}{3} \pi \cdot r^2 \cdot v

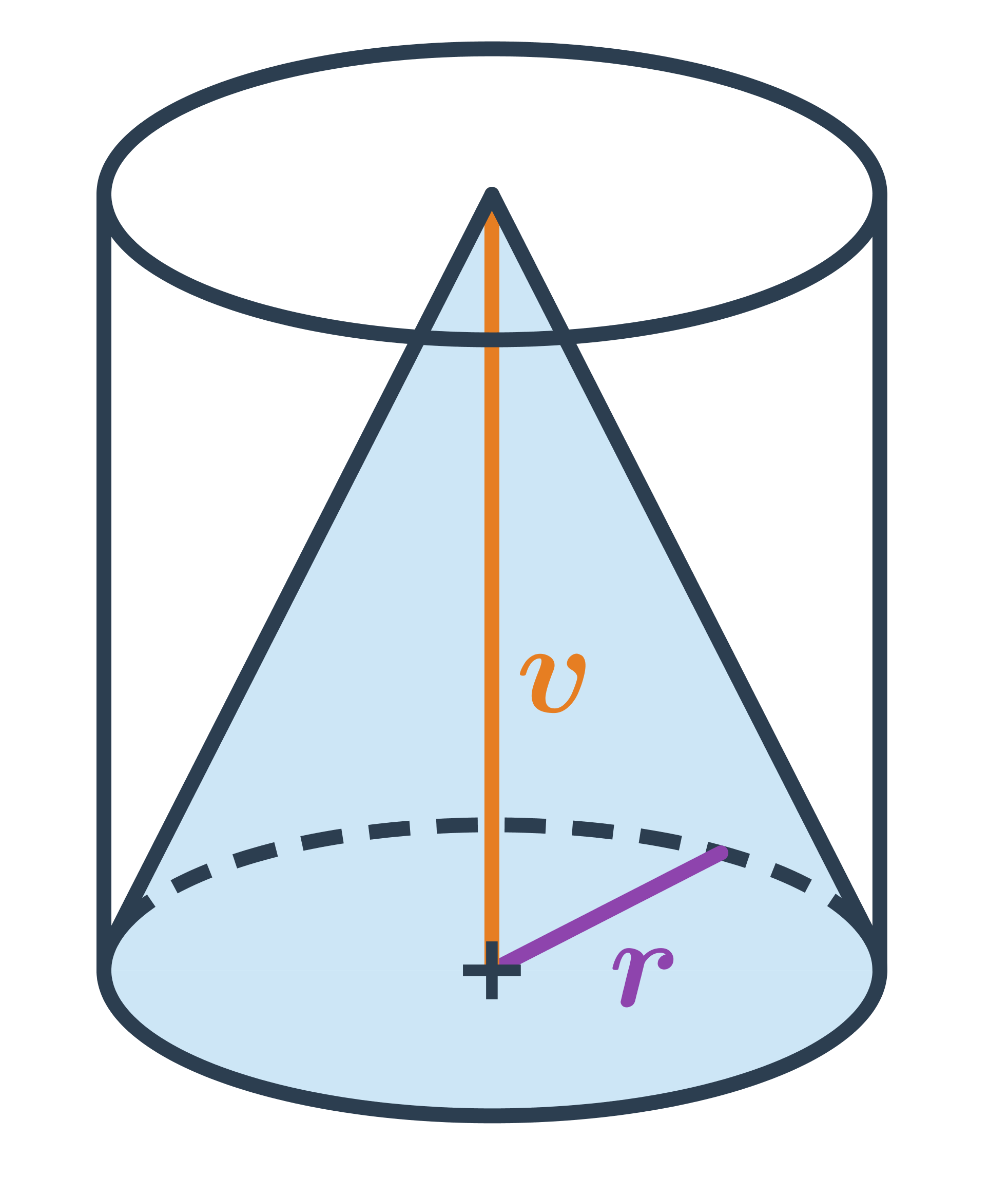
Pro kužel platí V=\frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2

Oproti válci se stejnou výškou a poloměrem podstavy má kužel třikrát menší objem.

Povrch kužele s poloměrem podstavy r a délkou strany s spočítáme takto: V=\pi r^2 + \pi r s = \pi r \cdot (r+s)

Může se stát, že známe poloměr r podstavy kužele a jeho výšku v, ale nemáme zadanou jeho stranu s. Potom si stranu můžeme dopočítat jako přeponu pravoúhlého trojúhelníka s odvěsnami o délkách v a r. Platí: s=\sqrt{v^2+r^2}

• Obsah podstavy kužele: \pi r^2
• Obsah pláště kužele: \frac{1}{2} \cdot 2 \pi r \cdot s = \pi r s